A comparison of risk prediction methods using repeated observations: An application to Electronic Health Records for Hemodialysis

Abstract

An increasingly important data source for the development of clinical risk prediction models are Electronic health records (EHRs). One of their key advantages is that they contain data on many individuals collected over time. This allows one to incorporate more clinical information into a risk model. However, traditional methods for developing risk models are not well suited to these irregularly collected clinical covariates. In this paper, we compare a range of approaches for using longitudinal predictors in a clinical risk model. Using data from an EHR for patients undergoing hemodialysis, we incorporate five different clinical predictors to a risk model for patient mortality. We consider different approaches for treating the repeated measurements including use of summary statistics, machine learning methods, functional data analysis and joint models. We follow-up our empirical findings with a simulation study. Overall, our results suggest that simple approaches perform just as well, if not better, than more complex analytic approaches. These results have important implication for development of risk prediction models with EHRs.

1. Introduction

Electronic health records (EHRs) data constitute a new and exciting resource for clinical research. They present the opportunity to observe dense and diverse information on many patients. However, because EHR data are not collected for research purposes, there are also many challenges in their analysis. One of the key opportunities as well as challenges with EHR data is the longitudinal nature of the data. Unlike well designed clinical studies, the longitudinal data in EHRs are collected irregularly. Some measurements may be very dense over time (e.g. blood pressure measurements from the intensive care unit) while others may be more sparsely collected (e.g. glucose measurements for diabetic patients).

One of the key ways that EHRs have been used is for the development of risk prediction models. Using EHRs to develop risk models are appealing for a multitude of reasons: large sample sizes allow one to model rarer events; many predictors are available; and the risk score is directly applicable to the clinical population used to derive the model. However, a key analytic question is how best to handle repeated predictor measurements.

A recent review of EHR based prediction studies by our group found that out of 107 studies only 36 (33%) used longitudinal predictors [1]. Among these studies, most aggregated the repeated measures into summary statistics such as mean/median or extreme values and only 9 (25%) incorporated disaggregated time varying data. It is possible that such summarization is a missed analytic opportunity. However, there has been some recent work that has suggested that simpler summarization based approaches are just as effective as more sophisticated techniques [2].

The purpose of this paper is to describe and assess the performance for different methods for using repeated measures in a risk model. Since we do not believe that any approach is universally “best”, our goal is to present a resource for other investigators to refer to in their own work and to understand some of the conditions under which different approaches work better. We ground our work in the analysis of EHRs and use five different predictor variables from the same data set to illustrate some differences. We describe the data in Section 2. In Section 3 we present the different analytic approaches. In Section 4 we evaluate the different methods. To provide additional insights we present results from a simulation analysis in Section 5. We finish with some concluding thoughts.

2. Motivating Data

We focus our work on the analysis of EHR data. Some motivating situations we have encountered in our collaborative work include the use of glucose measurements for diabetic patients collected sporadically over the previous year to assess risk of cardiovascular events, vital signs collected densely over a hospital stay to assess risk of decompensation and patterns of service utilization to assess risk of hospital readmission. In all of these scenarios a series of measurements are observable over time where both the value and temporality are potentially useful for developing a risk model.

In the present study, we consider EHR data from dialysis clinics where some clinical measurements are collected densely over time (e.g. blood pressure) and others are collected more sporadically (e.g. lab values), with the goal of predicting near-term mortality. Our data are derived from the EHR of a national chain of hemodialysis clinics. Patients with end stage renal disease (ESRD) require hemodialysis until they receive a kidney transplant or die. They have high morbidity and mortality with a median survival of approximately 5 years, with 20% dying within the first year of diagnosis [3]. Owing to this high mortality rate, there is great interest in developing risk models for patient mortality.

In the US, patients typically receive hemodialysis three times a week. At each treatment session, different clinical measurements are collected. In this analysis we consider three clinical factors collected at the beginning of every session: systolic blood pressure, diastolic blood pressure and weight. In addition to these densely collected factors we consider two laboratory tests collected more sporadically: serum albumin (which is collected monthly) and serum hemoglobin concentration (which is collected bi-weekly). In addition to the above mentioned clinical factors, we abstracted information on patient age, sex and race and used these as baseline predictors. All covariates were available for all patients. We acknowledge that additional information on comorbidities, service utilization, medications and demographics also could have been extracted and incorporated into the risk model.

Our study sample consists of newly incident patients at the dialysis facilities in 2010. Patients had to initiate dialysis at the facility within 30 days of diagnosis of ESRD. We followed patients until their 90th day after diagnosis, which we will refer to as the “landmark day.” In analyses of ESRD patients it is typical to assess patients after Day 90 because this is when patients are eligible for Medicare coverage and therefore linkable with administrative data. We linked patients with United States Renal Dialysis System (USRDS), an administrative database, to determine dates of ESRD diagnosis and mortality. Our database had follow-up through 2011, providing a minimum of one-year of potential follow-up for all patients.

There were 18,846 patients available for analysis. Within the sample 2,655 (14%) died within one year of incidence (Figure 1). We note that nobody dies during the first 90 of ESRD, prior to the landmark time. Table 1 shows descriptive data on the considered longitudinal predictors. Over the 60-day period, patients had on average 24 vitals measurements which are collected at every session. They had fewer laboratory measurements. Figure 2 shows individual measurements for 5 random people over time. One thing we note is the relative diversity in the patterns over time. The blood pressure measurements are quite variable while the weight measurements are much more stable. We note that weight is prone to greater variability in this population than the general population.

Figure 1.

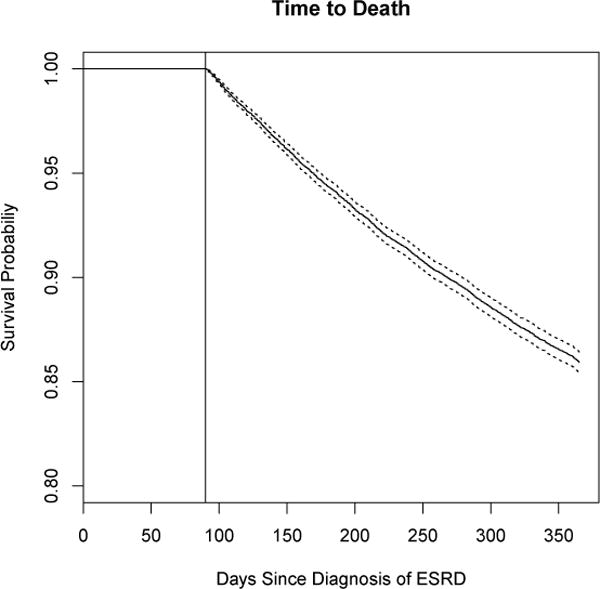
Time to death for the full sample. The vertical line indicates the landmark time (Day 90) from which predictions will be made.

Table 1.

Descriptives of clinical predictors. Data cover the 60 day period prior to the landmark time of Day 90 (i.e. days 30 – 90). Measures are averaged per-person over this period.

	Mean Value	Mean Std Deviation	Mean Number of Measurements
Systolic BP	147.74	17.94	23.80
Diastolic BP	77.41	10.57	23.80
Weight	83.47	1.91	23.89
Hemoglobin	11.45	0.84	5.78
Albumin	3.61	0.16	2.27

Figure 2.

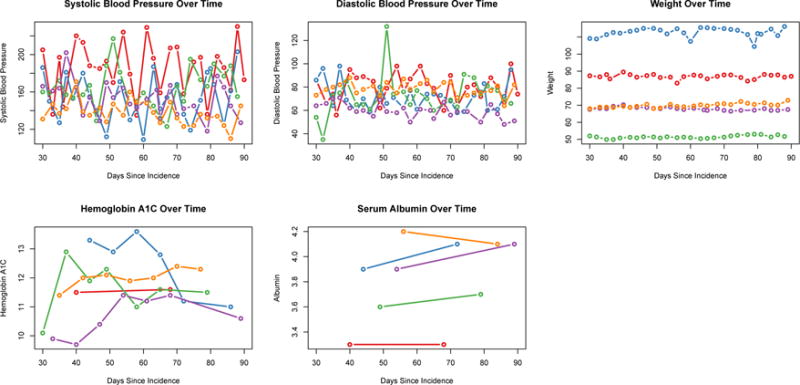
Clinical Measurements for 5 people over time.

3. Methodology

Our analytic task is to derive a prediction model for a time to event outcome that best takes advantage of repeated measurements. While there are many methods for developing risk models, few are well adapted to exploit the dependency within the repeated measurements in some of the predictors. In our present case, the predictor variables consist of two distinct sets of covariates: baseline or time invariant covariates, and longitudinal covariates. For each patient i, we observe the set of time invariant covariates: [W_ik: i ∈ 1, …, n and k ∈ 1, …, K], where n is the number of patients and K is the number of time invariant covariates, as well as the set of longitudinal covariates as [X_ilj, s_ilj: i ∈ 1, …, n and l ∈ 1, …, L and j ∈ 1, …, m_il], where L is the number of longitudinal covariates and m_il is the number of longitudinal observations measured on covariate l for patient i and $s_{\mathit{ilj}}\in \mathcal{S}$, a bounded, closed interval. Here, m_il is the number of times the covariate is observed and s_ilj are the time points at which the covariate is observed. This allows each of the l longitudinal covariate to be observed at different time points for each person. We refer to the collection of observed covariates for each patient as Z_i = {W_ik, X_ilj}. For simplicity we drop the subscripts, k and l moving forward.

In our data, this time domain is measured in days, but this can represent any domain relevant to the way the data are collected. While the length of $\mathcal{S}$ is potentially large, each individual’s set of observed values may be sparse or dense relative to $\mathcal{S}$. Finally, the time period $\mathcal{S}$ is prior to the landmark time, i.e. all measurements are observed before one begins risk assessment. This use of historical information differs from a dynamic risk model where one wants to update risk assessment based on newly observed data. While we do not specifically consider dynamic models, all of the discussed approaches can be adopted within a dynamic context.

To analyze the data, we consider variations of the Cox proportional hazards model. Using the typical Cox model framework [4], we define T_i as the survival time for person i, and C_i the corresponding censoring time. We observe Y_i = min(T_i, C_i) and let δ_i = I(T_i ≤ C_i). The Cox proportional hazards model is given as

$$h_i(t;\gamma )=h_0(t)\mathit{exp}(Z_i\gamma )$$ (1)

where h_i(t; γ) is the hazard at t time given a set of covariates Z_i with parameter vector γ and baseline hazard h₀(t).

To do risk prediction with this model we predict the probability of being alive at any given time t. This predicted probability is generated based on the baseline hazard and the individual’s observed covariates and compared against whether the person is actually alive at the given time point. Different methods for evaluating risk predictions in the presence of censoring have been studied elsewhere (see for example [5]).

The analytic challenge is how to analyze the observed X_ij. While we make no over-arching assumptions regarding the distribution or pattern of the X_ij each analytic approach will treat them differently, with their own embedded assumptions. The following subsections present the different methodologies we consider for analyzing repeated measures data.

3.1. Most Recent Observation

The simplest approach is to use the last observed clinical value as a single predictor in a Cox model. This basic approach can be thought of as a single landmark analysis, using day 90, s_i,90, or the closest observed date, as the landmark point [6]. Such an analysis makes the (reasonable) assumption that the most predictive clinical value is the one recorded at time s_i,90. This approach has been used successfully with EHR data by others [7].

3.2. Aggregated Data

Instead of using only the most recent value as a predictor we could instead aggregate the time varying data into different summary statistics. In our review of risk models [1], 25% of studies used summary statistics to model time varying predictors. The most common statistic used was the extreme value of the time period (max/min; 13% of studies). Other metrics included the number of measurements (10%), mean/median values (7%), trend/slope (3%) and variability (2%).

We comment briefly on the number of times a measurement is taken since this is particularly unique to EHR data. Since patients do not interact with an EHR system randomly the number of measurements may indicate the overall health of the patient, regardless of the actual value. In previous work, we have referred to this as ‘informed presence’ [8]. In our case, since the data are derived from outpatient clinics and visits should be regular, fewer measurements may indicate a sicker individual, suggesting s/he has been hospitalized during the 60 day period.

The choice of best summary statistic will depend on how variation in the X_ij relate to the hazard of death. In our analysis we calculated the mean, min, max, standard deviation and count of each of the clinical measurements and incorporate them into a Cox model.

3.3. Ignoring Temporal Dependence: Machine Learning Methods

Another analytic option is to ignore the temporal dependency of the X_ij and treat each observed data point independently. If each individual had data observed at each time point, i.e. blood pressure was measured every day, we would have a well aligned dataset and could employ any traditional analytic approach for developing risk models. Since all variables are not observed at all time points in $\mathcal{S}$, but instead sporadically observed, we need to impute, or fill-in, data into those unmeasured time points. Given the longitudinal nature of the data, the simplest form of imputation is last-observation-carried-forward, however we also consider another more complex approach involving smoothing across the longitudinal trajectory.

Since the time domain, $\mathcal{S}$, is large and multiple predictors can be used, the dimension of the data grows very quickly. In such cases machine learning approaches are useful. In our analysis we considered two popular, but different machine learning methods that have been adapted for time to event outcomes: LASSO [9] and Random Forests [10].

The LASSO implementation for survival models is a direct extension of the Cox model above, where the parameter vector γ is penalized on the $ℒ1$ norm to increase model stability. Random Forests is a very different analytic approach that uses a collection of classification and regression trees to form a non-parametric estimate of survival. We note that other machine learning methods could also have been considered.

3.4. Modeling the Repeated Measures

The next two approaches take into account the temporal dependence inherent in this type of data: functional data analysis (FDA) and joint models (JM). Both approaches have seen extensive development in recent years. While they each approach the underlying longitudinal process of the X_ij differently, the FDA and JM methodologies employed in this paper are able to handle data observed both densely or sparsely over the time domain.

3.4.1. Functional Data Analysis

Functional data models have been well developed over the past 15 years (see [11] for review). While the general functional regression model is not specific to repeated measures data, it is well adapted to it. Specifically, the model assumes that the longitudinal predictor X_ij = X_i(s_ij) and we assume that each X_i(·) is a square-integrable random smooth functions over $\mathcal{S}$. Without loss of generality, we can assume E[X_i(s)] = 0 and $\mathcal{S}=[0,1]$.

These predictor functions can be measured with or without error and can be observed densely or sparsely. To account for both sparsity and noise in the observed data, it is common to first smooth the X_i using functional principal components [12].

In the case when the predictor functions are observed on a dense grid of points and without noise the scalar-on-function regression model [13] allows one to regress a scalar outcome onto a functional process(es) and other scalar covariates. This has been extended for time to event outcomes [14] as:

$$h_i[t;\omega ,\beta (\cdot )]=h_0(t)\mathit{exp}(W_i\omega +{\displaystyle {\int }_0^1{X}_i(s)\beta (s)ds})$$ (2)

where W_i are scalar covariates with corresponding parameter vector ω and X_i(s) is the functional process with smooth parameter vector β(s). As described by [14], β(s) serves as a weight function for X_i(s) in order to obtain the overall contribution towards one’s hazard. Since the integral in equation (2) represents an infinite dimensional process, X_i(s) is typically approximated using regression splines.

While early work for the functional regression model focused on inference for β(s), recent work has centered on techniques for flexibly modeling the covariate process to aid in prediction. This has included work in variable selection [15], interactions [16], and non-linear effects [17]. The functional model can also be adapted for dynamic risk assessment using an historical functional linear model [18]. Empirical work has shown that different formulations of the functional model perform better in different settings [19]. For simplicity, in our present analysis, we focus on the basic functional regression model formulated by [13], adapted by [14] for survival data and using functional principal components to pre-smooth the data.

3.4.2. Joint Models

Like FDA, JMs have been well studied over the past 15 years and described elsewhere (see for example [20] and [21]). Where functional data methods treat the longitudinal trajectory as a fixed, smooth process, potentially measured with error, JMs take a different approach. They consider the longitudinal process as a random process to be modeled and then incorporated into a survival model. As such the JM, as the name implies, is a combination of two models: a survival model and longitudinal sub-model. While all parameters are typically estimated together, they can conceptually be thought of as two separate models. First one uses a mixed model to estimate the longitudinal covariate process, X_ij:

$$X_{ij}=m_{ij}+{\epsilon }_{ij}=D_{ij}\omega +G_i{b}_i+{\epsilon }_{ij}$$ (3)

where D_ij are a set of covariates — that include both time, $\mathcal{S}$, and baseline factors W_i — and G_i are the set of random effects. The longitudinal process over $\mathcal{S}$ is modeled flexibly, typically via cubic splines. Allowing m_ij to represent the longitudinal history estimated above, we next incorporate this into a survival model as:

$$h_i(t|M_i(t),W_i^{\ast })=h_0(t)\text{exp}(W_i^{\ast }{\omega }^{\ast }+\alpha m_{ij})$$ (4)

where $W_i^{\ast }$ may represent the same or different baseline covariates as above. In the estimation process, all of the parameters in equations (3) and (4) are estimated simultaneously either via an EM-algorithm or an MCMC approach within a Bayesian formulation. One deviation from the typical JM formulation and our formulation is that the event time period, T, and the covariate time period, S, overlap, i.e. data are observed while people can fail. This aspect makes JMs well suited for dynamic prediction [22].

Just as in the functional model, the JM has a high degree of flexibility in its specification: one has a choice as to how to model the longitudinal process, the survival process and then how to bring these processes together. One interesting aspect of the JM is that one can allow either the observed values or the rate of change (i.e. derivative) of the longitudinal process to impact the survival outcome. One challenge of the JM, is that compared to the other techniques they are quite computational. This is particularly the case when one has multiple longitudinal processes. Therefore, while proposals have been made for incorporating multiple longitudinal covariates [23], these methods have not yet been incorporated into available software. Therefore we only test the JM in the scenario where one has a single longitudinal covariate.

3.5. Combination Approaches

While the above methods have been presented as distinct approaches, it is also possible to combine many of these as well. For example, we considered using the summary metrics as a covariate in the functional and JMs. Additionally, we assessed using FDA to perform the imputation for the machine learning methods. Instead of doing one observation carried forward, this estimates each persons curve over $\mathcal{S}$ and imputes in. Finally, while not considered here, one can take a stacking approach and fit all the methods separately and and combine them together [24].

4. Empirical Evaluation

We first consider how the different analytic approaches perform on our dataset. We were interested in two primary questions: prediction performance and prediction stability. Moreover, we were interested in how these metrics varied based on the size of the training data.

4.1. Methods

4.1.1. Training, Validation & Testing Data

Since some of the methods required a fair amount of tuning, we divided the data into training, validation and testing sets. Our overall sample consisted of 18,846 individuals. We created validation and testing sets of 5,000 individuals each, leaving 8,846 individuals for training. We used the training data to build the initial models, evaluating tuning parameters and settings on the validation data. All final results are reported on the test data.

One of our interests was the impact of training set size. To test this, we randomly subsampled the training data into training sets of size n = 250, 500, 1000, & 5000 people, fitting the training data with each method and testing on the validation data. Once optimal parameter settings were established we repeated the sampling process and tested on the testing data. In order to test the stability of the predictions, we repeated this sampling and testing on the test data 10 times.

4.1.2. Analytic Techniques

All analyses were performed in R version 3.3. We tested out each of the above mentioned analytic techniques on each of the five clinical predictors (Table 2).

Table 2.

Analyses Performed

Approach	Abbreviation	R Function
Baseline Covariates	Base	coxph
Last Observation	Last	coxph
Summary Statistics
Mean Value	Mean	coxph
Maximum Value	Max	coxph
Minimum Value	Min	coxph
Standard Deviation	SD	coxph
Number of Measurements	Count	coxph
All Summary Statistics	Summary	coxph
Machine Learning
Random Forests	RF	rfsrc
Cox-LASSO	LASSO	glmnet
Random Forests w/FDA imputation	RF.FDA	rfsrc
LASSO w/FDA Imputation	LASSO.FDA	glmnet
Model Based Approach
Joint Model	JM	jointModel
FDA	FDA	pcox
Joint Model with Summary	JM.Summary	jointModel
FDA With Summary	FDA.Summary	pcox

We first fit a baseline Cox model using only patient age, sex and race. These covariates were included in each subsequent model. The first model consisted of the last observed clinical value closest to Day 90. To assess summary statistics, we fit separate models for each of the five summary metrics as well as a sixth overall model. To fit the regularized Cox model we used the glmnet package. The optimal lambda was chosen via 10-fold cross-validation. To fit Random Forests we used the randomForestSRC package using 2,000 trees. We performed functional principal components with the refund package and fit the functional Cox model using the pcox package available on github through the package’s author. Finally we used the JM package to fit the JM. The longitudinal process was estimated via a cubic spline and a random intercept.

We considered a number of combination approaches. We incorporated the mean covariate value into both functional and JMs. We also used the fits from the functional principal components to impute for LASSO and Random Forests. Finally, we applied each of the analytic approaches, using all five of the longitudinal covariates at the same time. Since there is no publicly available software for the JM with multiple predictors this was not explored.

4.1.3. Evaluation

To assess model performance, we calculated the c-statistic, a metric of the ability of a model to discriminate between events and non-events, with 1.0 indicating perfect separation and 0.5 indicating no-separation. A moderately strong c-statistic for a clinical model is at least 0.70. There are multiple ways to compute the c-statistic for time-to-event models [5], with most requiring the specification of a point of time at which to evaluate. We used the cumulative incidence procedure by [25], which counts all events up though the specified time point. Using the validation data we tested different time horizons ranging from 30 days to 1 year. Sixty-days after the landmark time of 90 days proved to be the optimal prediction period (i.e. day 150 after ESRD). However, inference from the results did not differ across different evaluation points. Since each person had a minimum of one-year of follow-up there was no censoring. We present box-plots of the c-statistics across the 10 runs to observe both the average and variability of the performance.

4.2. Empirical Results

Figure 3 shows boxplots across the 10 runs for the performance for the different models using systolic blood pressure as a predictor. The additional clinical predictors are shown in the appendix. Figure 4 shows all variables combined. Using just age, gender and race a modestly strong and stable predictor with a median c-statistic ranging from 0.68 (IQR: 0.67,0.70) to 0.70 (0.70,0.70) depending on training sample size. Among the clinical variables, the strongest individual predictor was serum albumin. It is worth noting that serum albumin is the most sparsely observed predictor, with each person have a median of two observations. Using the last observed value and a training sample size of 5,000, the c-statistic was 0.81 (0.80,0.81). Not surprisingly using all clinical predictors had the best performance 0.84 (0.83, 0.84).

Figure 3.

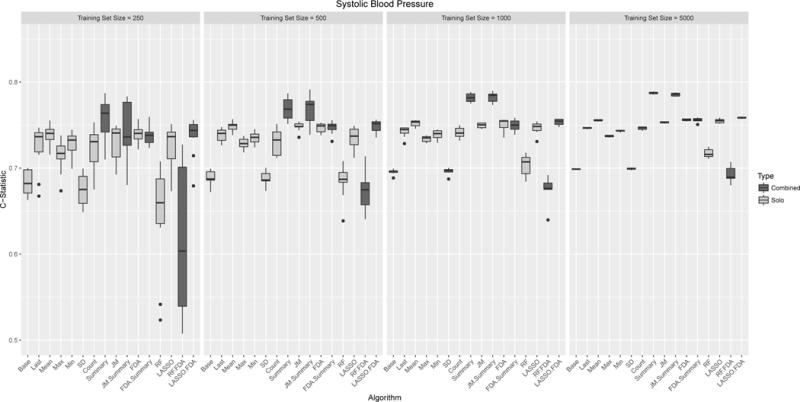
Box plots of model performance (C-statistics) for multiple measurements of Systolic Blood Pressure. Each panel refers to different training set sizes ranging from 250 – 5,000 people, with each analysis run 10 times. Each model was evaluated was evaluated on the same test set of 5,000 people. Models are grouped based on whether multiple methods were grouped together (red/blue).

Figure 4.

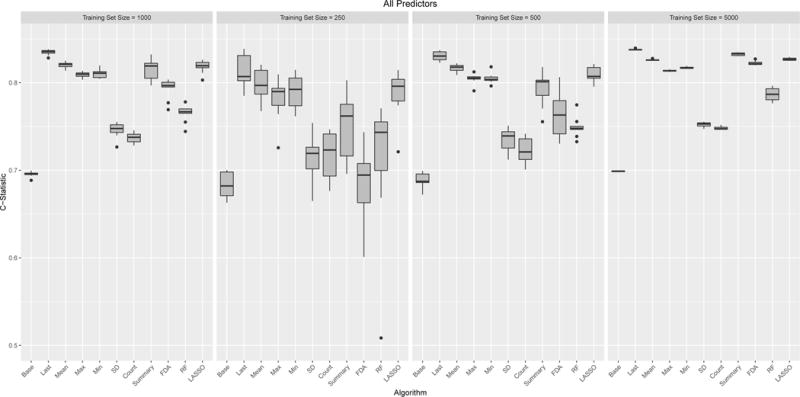
Box plots of model performance (C-statistics) when combining all five clinical predictors into a single model. Each panel refers to different training set sizes ranging from 250 – 5,000 people, with each analysis run 10 times. Each model was evaluated was evaluated on the same test set of 5,000 people. Since the standard implementation of Joint Models does not handle multiple predictors they are not included.

The training sample size was an important aspect in algorithm stability. Table 3 shows the standard deviation of each algorithm’s c-statistic averaged over the five clinical predictors. Most algorithms became relatively stable at a training sample size of 1,000 with very high stability at 5,000. Random Forests was the one exception, still exhibiting a degree of variability even at higher training sizes. Another aspect of stability is convergence of the algorithm. We had some convergence problems with JMs. Overall, the model failed to converge 21% of the time. Lack of convergence was associated with training sample size —30% vs 14% for training sets of size 250 and 5000 respectively —as well as clinical predictor —40% for weight versus 7.5% for Hemoglobin.

Table 3.

Average standard deviation of the c-statistics

	250	500	1000	5000
Base	0.014	0.009	0.003	0.001
Last	0.023	0.010	0.004	0.001
Mean	0.017	0.008	0.004	0.001
Max	0.021	0.007	0.004	0.001
Min	0.017	0.009	0.005	0.001
SD	0.018	0.011	0.006	0.001
Count	0.021	0.013	0.006	0.002
All Summary	0.028	0.014	0.007	0.002
JM	0.032	0.028	0.009	0.002
FDA	0.019	0.012	0.006	0.002
RF	0.048	0.026	0.013	0.008
LASSO	0.042	0.022	0.007	0.002

The best algorithm ultimately depended on the specific clinical predictor (Table 4). The simplest approach, using the last observation, often performed quite well. The use of all summary statistics was often among the best performing algorithms, however, the best individual summary statistics depended on the specific predictor. One noteworthy observation, was the relative performance of the number of times a clinical predictor was measured. The number of times measured was not predictive for the labs but was for the vital measurements. This is likely due to the fact that labs are taken on a scheduled basis, while the number of vitals signs (e.g. blood pressure) is an indication of how many treatment sessions a patient attended. The use of JMs and FDA, which attempt to model the longitudinal trajectory were never the best performing approach, though did show comparable performance for albumin and hemoglobin. The two machine learning based approaches showed different performance with LASSO performing better than Random Forests.

Table 4.

C-statistics at a training sample size of 5,000

	ALB	HEMO	SBP	DBP	WT	ALL
Base	0.70	0.70	0.70	0.70	0.70	0.70
Last	0.81	0.76	0.75	0.71	0.69	0.84
Mean	0.80	0.75	0.76	0.72	0.69	0.83
Max	0.78	0.75	0.74	0.70	0.70	0.81
Min	0.81	0.73	0.74	0.72	0.70	0.82
SD	0.72	0.70	0.70	0.70	0.73	0.75
Count	0.70	0.71	0.75	0.75	0.75	0.75
All Summary	0.80	0.75	0.79	0.77	0.76	0.83
JM	0.79	0.74	0.75	0.72	0.69	—
FDA	0.80	0.74	0.76	0.72	0.70	0.82
RF	0.75	0.69	0.72	0.69	0.73	0.79
LASSO	0.81	0.76	0.76	0.72	0.71	0.83

Finally, we explored combining some of the analytic approaches. Adding in summary metrics to JMs and FDA led to poorer (i.e. more variable) performance with smaller training sizes but better performance with larger training sizes. This lack of stability is likely due to over-fitting and less in the smaller training sets. Using FDA to impute in data for LASSO and Random Forests, also led to slightly better performance.

5. Simulation

The empirical results suggest that summary metrics perform just as well, if not better, than than model based approaches. However, these results may be due to a lack of regularity in the underlying longitudinal process. To test this hypothesis we performed a simulation where the longitudinal covariate process was regular and should be well handled by either FDA or JM methods.

5.1. Simulation Methods

We followed the simulation strategy performed in [14] and adapted from [13]. Specifically we considered the model where the data generating distribution contains one longitudinal predictor, X_i(s), observed over a grid of length S = 60. For each subject i ∈ 1, …, N, we generate survival times T_i using the model h_i = h₀(t) exp(η_i), where h_i(t) is the hazard of T for subject i and h₀(t) is the baseline hazard. As in [14], ${\eta }_i=\frac{1}{J}{\displaystyle {\sum }_{j=1}^J{X}_i(s_j)\beta (s_j)}$, $X_i(s_j)={\mu }_{i1}+{\mu }_{i2}{s}_j+{\displaystyle {\sum }_{k=1}^{10}\{v_{ik1}\text{sin}(2\pi k{s}_j)+v_{ik2}\text{cos}(2\pi k10s_j)\}}$, μ_i1 ∼ N(0, 25), μ_i2 ∼ N(0, 4), and v_ik1, v_ik2 ∼ N(0, 1/k²). We generated survival times under a Weibull distribution with shape parameter 1.25 following the method of [26]. To mimic our data, we set the median survival at 5 years and censored observations after 1 year.

We considered two data generating coefficients for β(s): β₁(s) = 2(s/10)² and ${\beta }_2(s)=2\text{sin}\left(\frac{\pi s}{5}\right)$. As shown in figure 5, β₁ places successively more weight on observations further along in time, where β₂ varies weight across the time domain. While we would be inclined to believe that β₁ more likely represents the true underlying effect, we wanted to consider a more complex function like β₂ that would not overly benefit some of the simpler analytic approaches.

Figure 5.

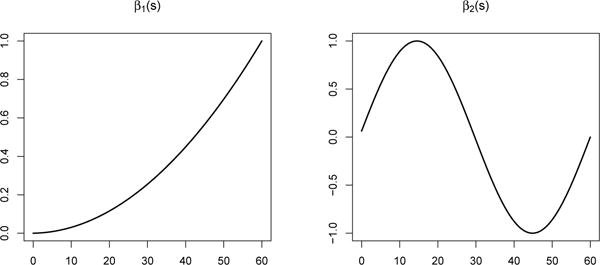
Simulated β coefficient vectors

As in our data application, we were interested in the impact of sparsity of the observed data. We considered two degrees of sparsity: where 50% of the data points were observed and where 10% of the data points were observed. Finally, for each of the two data generating distributions we considered two different training set sample sizes: 500 and 1,000. As in the data example, we fixed the test set size at 5,000. This gave us a total of 8 different simulation designs: 2 βs, 2 sparsities, 2 sample sizes. We performed each simulation 100 times and calculated the c-statistic for the overall model fit [27].

5.2. Simulation Results

Figures 6 – 7 show the results for the two considered β functions. Overall the results are very similar showing strong performance for all prediction methods. The one exception is the standard deviation which, not surprisingly shows no predictability. The primary difference between the two simulations is that the use of the last observed value performs slightly better compared to the other methods under β function 1 compared to β function 2. This is not surprising given the nature of the underlying function. Finally, it is interesting to note, that the degree of sparsity in the observed data had virtually no impact on predictive performance. This is not very dissimilar from the empirical results, which had the most sparsely observed covariate, albumin, being the most predictive.

Figure 6.

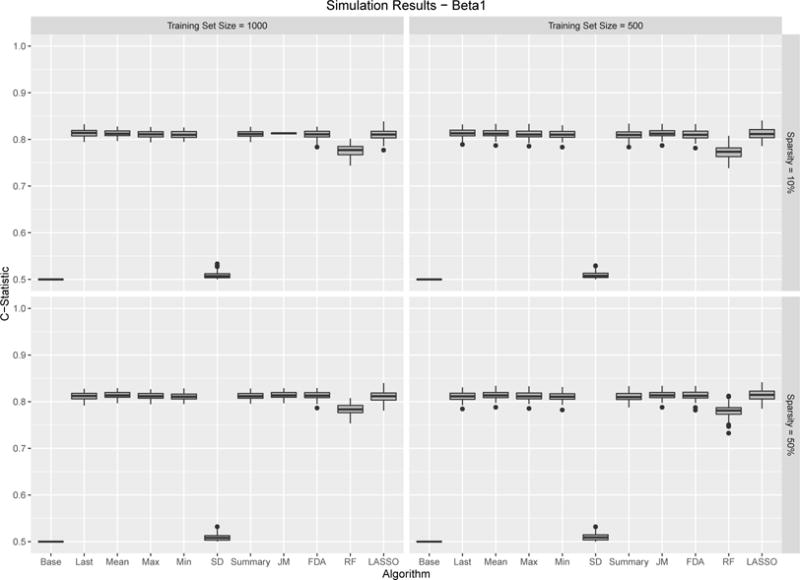
β₁ Results. Boxplots for C-Statistics for 100 simulations across different sample algorithms, training sample set sample size and sparsity. Results are relatively consistent with most algorithms performing well.

Figure 7.

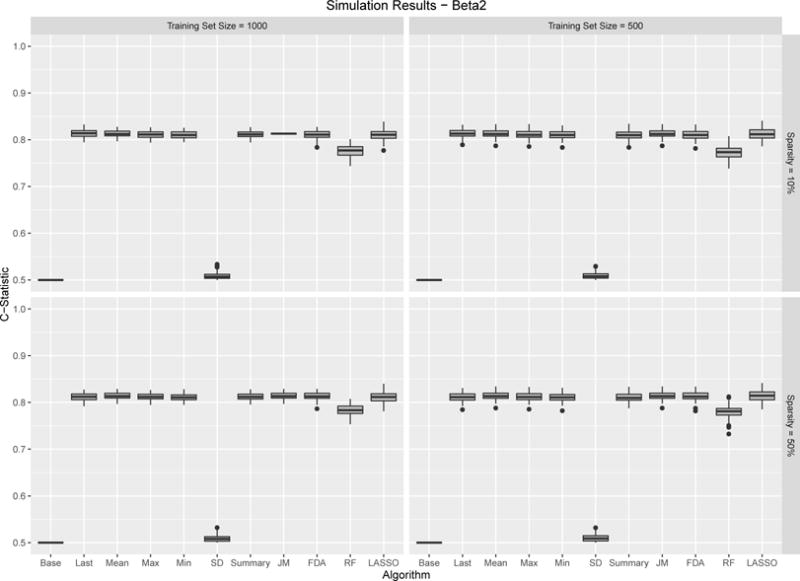
β₂ Results. Boxplots for C-Statistics for 100 simulations across different sample algorithms, training sample set sample size and sparsity. Results are relatively consistent with most algorithms performing well.

6. Discussion

Both our empirical and simulation results suggest that the use of simple analytic techniques are sufficient for robust risk prediction. In real data settings, simpler approaches such as the use of the last observed value or simple summary statistics may be preferable as they are less sensitive to noisy data. Moreover, when the underlying process is smooth and regular, simpler methods still do just as well as more complex approaches. These results have important implications for the development of risk prediction models with EHR data. EHR data are characterized by having many irregularly measured longitudinal predictors. Most recent efforts have used simple approaches to incorporate these predictors [1]. These results support the validity of these approaches.

While many complex analytic strategies exist to derive risk models, other authors have similarly noted that simpler approaches often work well. In a similar analysis, [2] examined modeling a single longitudinal predictor (blood pressure) from a large epidemiological cohort. The authors found that simpler methods for incorporating longitudinal data performed just as well as more complex methods such as JMs. In another context, [28] examined different Bayesian methods for analyzing fMRI data and found that simple regularization performed best. Finally, [29] compared different machine learning methods for predicted clinical outcomes and noted that logistic regression performed better. Our analysis extends these findings to the context of EHR data, which contain diverse sets of longitudinal predictors, where it is not always apparent how best to incorporate these variables into a risk model.

In developing EHR based prediction models, simpler analytic approaches have appeal for a number of reasons. Firstly, due to the irregularly observed data, placing all observations on the same time scale can be challenging, requiring either binning or imputation. Moreover, depending on the time scale, the dimension of the problem can grow rapidly, making summary statistics more parsimonious. Another challenge are the number of potential risk predictors. In our data example we only considered five clinical variables but easily could have incorporated dozens of labs and other vitals. Finally, while not discussed, simpler models make implementation easier. The goal of many EHR based risk models is to incorporate them into clinical decision support tools. If the clinical covariates can be represented simply, this becomes easier. This is especially the case with JMs which can be quite computational for generating new predictions.

One of the interesting findings was that different summary statistics performed better for different clinical predictors. For example, the minimum serum albumin concentration was the best summary metric while the standard deviation was the best for weight. Clinically these findings make sense but highlight that attention needs to be paid even when using summary statistics. We also note the predictability of the raw number of clinical measurements - regardless of the actual value. It was interesting to observe that the count was useful only for the vital signs. Such ‘informative presence’ is a hallmark of EHRs and can be exploited for risk prediction purposes. These results highlight the importance of still being mindful regarding which summary metrics are used.

One possible explanation for why the simpler analytic approaches work better is that clinical data in general, and EHR data particularly, can be quite noisy. It is noted that the standard deviation of the longitudinal measurements was often a strong predictor. Therefore analytic approaches that require a degree of regularity or smoothness may be ill suited. However, even in our simulation, where regularity was imposed, we did not find that more complex methods performed better. Instead, all methods performed equally well. The lack of variability in prediction performance, compared with the empirical data, highlights that under regular conditions all of these methods obtain the same targets. Therefore it is in noisy, real data settings, that the added value of simplicity is realized.

These results do not indicate that more complex approaches such as JMs and FDA are not worthwhile. While not explored here, these approaches can be extremely useful for understanding the nature of the relationship between the predictor and the outcome; both approaches allow one to associate the longitudinal process with an outcome. This can be useful both from an inferential perspective as well as helping to refine a risk model. For example, estimation and visualization of the parameter vector β(s), can inform which summary statistics are likely to be most predictive.

In an effort to focus on the role of the longitudinal predictors, there are some components to model building that we have not fully considered. Firstly, EHR data are characterized by their diversity of clinical predictors, each with different utility in risk prediction [30]. Incorporating data such as comorbidities, service utilization history and additional demographics, would raise the dimension of the problem likely making simpler methods even more appealing. Another aspect we do not fully explore is the role of imputation. Using the machine learning methods require one to align the data and impute unobserved values. We considered two imputation methods that exploit the temporality of the data, but more complex approaches could have been considered [31]. Thirdly, it is possible that a binary modeled focused on 60-day mortality would have performed better. While not discussed fully here, all of these methods could be adopted for a binary outcome. In our testing, the inference was similar with simpler approaches performing better. Finally, many of the modeled effects may have non-linear relationships with the outcomes. For example, both high and low blood pressure are risk factors for mortality among those with ESRD. Each of these methods could be adopted to incorporate these non-linearities. While machine learning methods like random forests naturally handle such non-linearities, splines or quadratic terms could be added to the prediction model.

There are still important questions future work should consider. While our data were relatively dense (an average of 24 blood pressure measurements per-person) it is possible to extract even denser data. For example, real time blood pressure measurements derived from an intensive care unit may be sampled on the order of minutes providing hundreds of observations per-person. Similarly, personal tracking and monitor data will be very dense, perhaps providing opportunities for FDA or other analytic approaches to shine. Additionally, our analysis ignores the question of developing dynamic risk predictions. While our results suggest that one can ignore the temporality of the historical data, this does not suggest that one should not develop risk models that update over time. Future work should compare different approaches for developing such dynamic models.

In summary, these results suggest that while consideration needs to be taken for the best risk model, there is confidence that simpler approaches may be sufficient.