Moving slowly is hard for humans: limitations of dynamic primitives

Complementing a large body of prior work showing advantages of composing primitives to manage the complexity of motor control, this paper uncovers a limitation due to composition of behavior from dynamic primitives: while slower execution frequently makes a task easier, there is a limit and it is hard for humans to move very slowly. We suggest that this remarkable limitation is not due to inadequacies of muscle, nor to slow neural communication, but is a consequence of how the control of movement is organized.

Abstract

Mounting evidence suggests that human motor control uses dynamic primitives, attractors of dynamic neuromechanical systems that require minimal central supervision. However, advantages for control may be offset by compromised versatility. Extending recent results showing that humans could not sustain discrete movements as duration decreased, this study tested whether smoothly rhythmic movements could be maintained as duration increased. Participants performed horizontal movements between two targets, paced by sounds with intervals that increased from 1 to 6 s by 200 ms per cycle and then decreased again. The instruction emphasized smooth rhythmic movements without interspersed dwell times. We hypothesized that 1) when oscillatory motions slow down, smoothness decreases; 2) slower oscillatory motions are executed as submovements or even discrete movements; and 3) the transition between smooth oscillations and submovements shows hysteresis. An alternative hypothesis was that 4) removing visual feedback restores smoothness, indicative of visually evoked corrections causing the irregularity. Results showed that humans could not perform slow and smooth oscillatory movements. Harmonicity decreased with longer intervals, and dwell times between cycles appeared and became prominent at slower speeds. Velocity profiles showed an increase with cycle duration of the number of overlapping submovements. There was weak evidence of hysteresis in the transition between these two types of movement. Eliminating vision had no effect, suggesting that intermittent visually evoked corrections did not underlie this phenomenon. These results show that it is hard for humans to execute smooth rhythmic motions very slowly. Instead, they “default” to another dynamic primitive and compose motion as a sequence of overlapping submovements.

NEW & NOTEWORTHY Complementing a large body of prior work showing advantages of composing primitives to manage the complexity of motor control, this paper uncovers a limitation due to composition of behavior from dynamic primitives: while slower execution frequently makes a task easier, there is a limit and it is hard for humans to move very slowly. We suggest that this remarkable limitation is not due to inadequacies of muscle, nor to slow neural communication, but is a consequence of how the control of movement is organized.

one of the delightful paradoxes of motor neuroscience is that human agility and dexterity vastly exceed modern robots—despite much slower actuation, information transmission, and computation. One possible resolution of this paradox is the hypothesis that human actions are composed of “dynamic primitives”: dynamic primitives may be implemented without continuous intervention from higher levels of the central nervous system, yet each generates highly dynamic behavior (Hogan 2017; Hogan and Sternad 2012, 2013; Sternad 2008; Sternad et al. 2000). The proposed dynamic primitives are members of at least three distinct classes of “dynamic attractors” that may arise from the interaction of neural networks: submovements, oscillations, and mechanical impedances, the latter to account for physical interaction with external objects. Submovements and oscillations in particular are conceived as arising from dynamic attractors that generate observable discrete and rhythmic movements, respectively. An operational definition of submovements is provided in the appendix. Definitions of discrete and rhythmic movements are provided in Hogan and Sternad (2007).

While this strategy, combining complex actions from limited classes of dynamic primitives, may “work around” the sluggish response of biological “hardware” and “wetware” by reducing the need for continuous central intervention, it may also have disadvantages. In particular, we hypothesize that it may impose limitations on motor behavior. The experimental study presented here probed simple arm movements to test whether they exhibited limitations that arose from being composed of dynamic primitives (submovements and oscillations).

Support for motor primitives underlying motor actions is evident in several different lines of prior work (Bizzi et al. 2008; Flash and Hochner 2005; Giese et al. 2009; Giszter 2015). Several studies have provided evidence that discrete and rhythmic movements are mediated by different neural circuits. For example, Hira et al. (2015) showed that distinct regions in the motor cortex of rodents are associated with rhythmic and discrete movements. A human neuroimaging study revealed significantly different cerebral activation for the two types of movements (Schaal et al. 2004): in continuous rhythmic wrist movements, cerebral activation was largely confined to unilateral primary motor areas, whereas discrete movements elicited strong additional activity in the bilateral parietal cortex and cerebellum. Transcranial magnetic stimulation-induced activation of the tibialis anterior has revealed different responses during rhythmic and discrete movements (Goto et al. 2014). Concomitant behavioral results reinforced these differences. For example, Ikegami et al. (2010) showed that adaptation to altered visuomotor conditions was almost fully transferred from discrete to rhythmic performance, while there was minimal transfer in the reverse direction. Howard et al. (2011) reported that, during learning of reaching movements in two force fields with different directions, interference was reduced when movements in different fields were performed in a different manner, rhythmic or discrete. Furthermore, neurological evidence supporting dynamic primitives underlying motor behavior is found in persons recovering after cerebral vascular accident (stroke). Their earliest recovering movements are distinctly “quantized,” exhibiting fluctuations with highly stereotyped velocity profiles (Krebs et al. 1999). Remarkably, as recovery proceeds, these submovements overlap and blend to approximate more closely the smoothness of unimpaired movements (Rohrer et al. 2002, 2004). A more recent study of stroke survivors showed that rhythmic movements were better preserved than discrete movements (Leconte et al. 2016).

Evidence of limitations arising from the composition of motor actions from dynamic primitives was demonstrated in a recent study (Sternad et al. 2013). The discreteness of a sequence of movements could not be sustained as their pace increased. Subjects switched to rhythmic performance of oscillatory movements; dwell times disappeared and the movements merged to smooth rhythmic performance. [A quantitative distinction between rhythmic and discrete movements was proposed in Hogan and Sternad (2007)]. This transition from discrete to rhythmic performance could not be dismissed as a shortcoming of peripheral biomechanics, because an auditory cue changed the pace at which the transition occurred.

That study of accelerating discrete movements showed that the parameters of these dynamic primitives are limited; in particular, a periodic sequence of discrete movements could not be sustained as its pace increased. The present study complements and extends that prior work by examining decelerating oscillatory movements made by moving the hand between two targets in a plane while paced by a metronome. It was designed to test our hypothesis that oscillatory primitives are characterized by a limited range of parameters. In particular, we predict that sufficiently slow oscillatory movements cannot be executed smoothly by oscillatory primitives. Hypothesis 1: Oscillatory motion smoothness decreases as period increases. We quantify smoothness by harmonicity, i.e., deviation from harmonic motion.

Instead, we propose that when rhythmic movements are executed sufficiently slowly, they “fall apart” into discrete movements. Discrete movements are separated by dwell times, a nonzero interval where both velocity and acceleration are zero (Hogan and Sternad 2007). In addition, even without decomposition into discrete movements, we propose that slowing down oscillatory movements engenders an unavoidable increase of irregularity. To corroborate this change in kinematics, we conducted a finer-grained analysis to identify submovements: Assuming a lognormal shape as a basis function, we performed an optimization procedure that fit submovements to each velocity profile. Importantly, the underlying submovements differ from discrete movements in that they may overlap in time. Hypothesis 2: Slower oscillatory motions are executed as a sequence of discrete movements, separated by dwell times; furthermore, individual movements show an increasing number of submovements. We tested this hypothesis in two ways: first, we measured dwell time, i.e., the time spent at rest at the end of each movement, a distinctive signature of discrete movements; second, we measured the number of submovements underlying each movement. We predict that both measures increase as period increases.

In nonlinear systems that have multiple stable states, transitions between different states typically depend on the history of states such that transitions in opposite directions may exhibit an asymmetry termed “hysteresis.” This is particularly the case in systems that have a lag between input and output, as in numerous physical systems, and clearly also in biological systems, and in particular motor systems. For example in human locomotion the transition from walking to running typically happens at a speed higher than the transition from running to walking, although the reverse has also been reported (Diedrich and Warren 1995; Getchell and Whitall 2004; Hreljac 1995; Li 2000; Thorstensson and Roberthson 1987). Hence we expect that any transition from one class of primitives (e.g., oscillations of the kind that might be generated as limit-cycle behavior) to another class (e.g., submovements of the kind that might be generated as point-attractor behavior) exhibit a behavioral asymmetry or hysteresis. Hypothesis 3: The transition between oscillatory and submovement primitives when periods increase differs from when they decrease. Specifically, we predict that if oscillatory movements slow down, a transition to a sequence of submovements will occur at longer periods than the reverse transition (submovements to smooth oscillations) when movements speed up, because the system tends to persist in its current state.

An alternative theory is that submovements emerge from an intermittent feedback control process as visually evoked corrections to an ongoing movement (Craik 1947; Meyer et al. 1988, 1990). If that is the case, removing visual feedback should eliminate the irregularity due to intermittent control, or at least substantially reduce it. Hypothesis 4: Removing visual feedback substantially restores smoothness to slow oscillatory motions. Specifically, we compare movements with and without visual feedback.

Observations consistent with hypotheses 1 and 2 would represent motor limitations exclusively due to wetware—the neural organization of motor control—rather than the more obvious shortcomings of neuromechanical hardware. Confirmation of hypothesis 3 would inform details of how the wetware may be implemented, i.e., as interacting nonlinear dynamic systems. Confirmation of hypothesis 4 would support an alternative control mechanism that might generate irregularity in slow oscillatory motions, due to visual corrections of deviations from a desired trajectory.

To test these hypotheses, we conducted experiments in which unimpaired subjects were instructed to perform smooth, rhythmic arm movements (i.e., with no dwell time at zero speed) between two targets, both with and without visual feedback, in synchrony with a metronome that dictated progressively longer periods. We found that humans could not perform slow, smooth, oscillatory movements. Harmonicity decreased with cycle period, consistent with composition as a sequence of submovements. Despite instructions, we observed dwell times at movement extremes which became increasingly prominent at the slower speeds. We found only weak evidence of asymmetry (hysteresis) in the transition between these two classes of movement. We also found that eliminating vision had no effect, suggesting that intermittent visual feedback did not underlie this phenomenon.

METHODS

Ten volunteers with no (self-reported) neurological or biomechanical abnormalities participated in this experiment (19–43 yr old, 6 male and 4 female). Nine subjects were right-handed according to the Edinburgh handedness test; one subject was left-handed (Oldfield 1971). One of the 10 subjects did not comply with task instruction and performed with periods that significantly and unsystematically deviated from the metronome. Those data were eliminated from further analysis. Prior to data collection, participants were informed about the experimental procedure and signed an informed consent form; the study protocol was approved by MIT’s Institutional Review Board.

Experimental Apparatus and Data Collection

Participants were seated in front of a table, with the sternum close to the table edge (Fig. 1). To fixate shoulder position, two belts tied the upper body to the back of the chair. For reference to place subjects in comparable positions, a location was marked on the table. This reference mark was in the subject’s midsagittal plane, 23 cm away from the edge of the table (in the anterior-posterior direction) and ~26 cm distant from the subject’s sternum. The height of the chair was adjusted to position the subject’s upper arm to be ~45° from horizontal; the forearm rested lightly on the table. From this neutral position, the subject could perform a reaching movement forward and backward in the sagittal direction, involving both shoulder and elbow joints without reaching the limits of their workspace. The forearm was mounted on a low-friction skid that reduced surface static and kinetic friction. A brace stabilized the wrist to discourage wrist rotation.

Fig. 1.

Experimental setup. Subjects held a handle with a magnetic sensor attached that measured hand position and displayed it on a monitor. Subjects were instructed to perform continuous smoothly rhythmic movements forward (away from the body) and backward (toward the body) in the parasagittal plane, sliding on the horizontal table surface. Movement amplitude was indicated by 2 large circles on the monitor.

Two circular targets were shown on a vertical screen to instruct movement amplitude (Fig. 1). Targets were at a distance of ±14 cm from the neutral position corresponding to the reference mark on the table, specifying a movement distance of 28 cm. The targets had a diameter of 10 cm, which was intentionally large so that accuracy requirements were minimal. The screen was placed at a distance of ~65 cm from the eyes and the display gain was 0.5, showing targets and movements at half their real size. Subjects were asked to move the hand back and forth from target to target on the table in a parasagittal plane. A computer-generated audio signal prescribed movement timing.

Subjects grasped a handle onto which a magnetic Flock of Birds sensor was attached (Ascension Technologies, Burlington, VT). Its static accuracy and resolution were 0.25 cm and 0.08 cm, respectively. The combined weight of the sensor and handle was ~70 g, which is ~1/8 of the weight of the hand. The sampling frequency was 100 Hz. This frequency was sufficient as the frequency content of the motion was significantly below 50 Hz and antialiasing was not required. Position was zeroed with the handle in the neutral position shown by the reference mark on the tabletop. Position in the plane of the table was displayed in real time by a cursor on the screen. Care was taken to ensure that all participants were similarly able to reach both targets. To reach the distant target, subjects had to extend their arms, although not completely; reaching to the target nearest the subject was not difficult. Data collection for off-line analysis was controlled by a custom-made software routine written in C and Tcl/Tk on a computer running the Linux operating system.

Experimental Conditions and Procedure

At the beginning of each trial participants placed their hand at the reference position. All participants used their dominant hand. They were then instructed to perform smooth forward-and-backward cyclic movements between targets in synchrony with the metronome sounds (one sound per back-and-forth cycle) but without stopping at the ends, i.e., with no dwell time. All metronome sounds had a duration of 50 ms. The metronome sequence took the following form for all trials: The trial began with 10 sounds separated by an interval of 1 s, presenting a constant periodic signal for 10 s. Subsequently, 25 sounds were produced where each interval increased by 200 ms, ending at an interval of 6 s. This long interval was sustained for 5 sounds, equivalent to a duration of 30 s. After this constant periodic interval, another 25 sounds with a decreasing interval of 200 ms followed. The trial ended with 10 sounds of 1-s cycle interval. The total trial duration was 225 s for a sequence of 75 cycles. Figure 2 shows the sequence of cycle intervals as a function of time and also as a function of cycle number. The figure also includes the change of intersound interval as a percentage of the previous intersound interval to highlight that the changes were initially large at 20% but then decreased to a minimum of 4%.

Fig. 2.

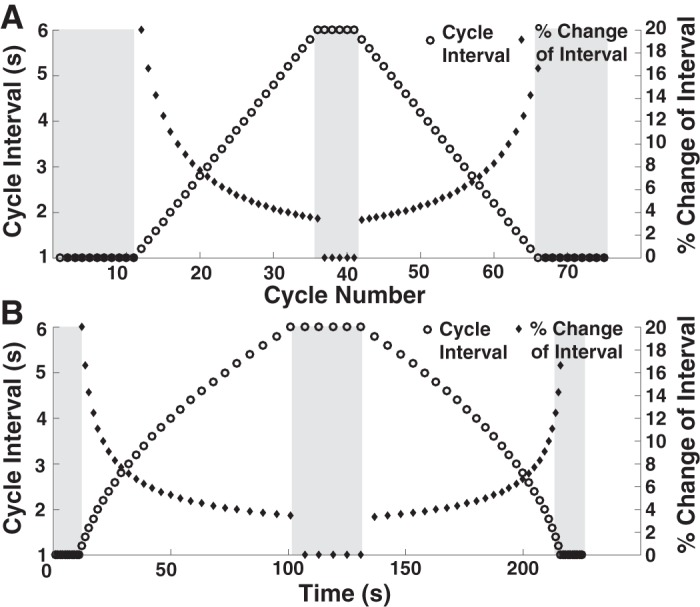
The sequence of metronome intervals and their corresponding percentage change as a function of cycle number (A) and time (B). The shaded areas mark the segments with constant periods.

This same timing sequence was presented in two different perceptual conditions. In the “vision” condition, subjects had their eyes open and executed their movements to the targets displayed on the monitor. In the “no-vision” condition, subjects were asked to make the same amplitude movements with their eyes closed, which removed explicit visual feedback. These two conditions were repeated twice, both times starting with the vision condition, followed by the no-vision condition. The total duration of these four experimental trials was ~20 min, with short breaks inserted between trials. Prior to data collection, each participant performed several movements with the metronome to familiarize him/herself with the task.

Data Reduction and Analysis

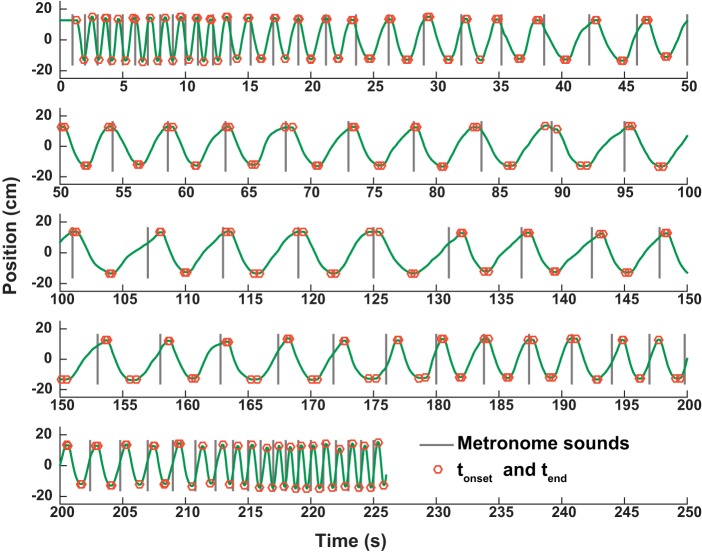
Of the 3D signals from the Flock-of-Birds sensor only horizontal displacements in the parasagittal direction were processed. Figure 3 shows a complete time series of one trial, divided into five segments for display. The time series reveals the change in kinematic shape from the initial faster movements to the slower paced sections of the trial. The vertical lines denote the onset of the metronome sound; the red dots mark the onset and offset of each movement (defined below).

Fig. 3.

A complete time history of 1 trial. Gray vertical lines indicate the onset of the metronome sounds. Red dots mark the onset and offset of each movement (see methods).

Before extracting quantitative markers, the position data were smoothed using a five-sample moving average filter with centered filtering, using the “smooth” function in MATLAB to avoid phase lag. Velocity was obtained numerically from the two-sample difference of the position signal, and was smoothed again with the same five-sample moving average filter. This differentiation introduced a delay of approximately half a sample (5 ms), which was considered negligible.

Parsing into Single Movements

For all analyses, the continuous kinematic data were parsed into single movements, delimited by t_onset and t_end. Both onset and offset of one movement were defined by the time when velocity crossed a threshold, defined as 3% of the peak velocity of the same movement. Given that subsequent measures depended on this temporal demarcation, alternative thresholds of 1 and 5% were compared for their influence on subsequent analyses. No significant differences were identified and we opted to use 3% throughout. To minimize the possibility of false detection of dwell time between movements (e.g., due to noise in the data), linear regressions of velocity onto time were applied to the velocity samples between t_end of one movement and t_onset of the next. The number of samples for this regression varied between 3 for fast movements up to 100 for slow movements. If the linear fit was sufficiently good (defined by R²>0.70) and the regression slope, or acceleration, was greater than 0.25 cm/s², the segment was considered part of a continuous trajectory. In this case, t_onset and t_end (shown respectively by the forward-facing and backward-facing triangles in Fig. 4) were merged into one time point, defined by the sample with the lowest speed in this segment. This point then defined the common time that separated adjacent movements. If the regression slope was less than 0.25 cm/s², t_onset and t_end were regarded as distinct and were retained, i.e., there was a dwell time DT between movements. If the linear fit was poor (defined by R²<0.70) the demarcation points t_onset and t_end were retained and the dwell time between them was calculated. The threshold value of R² prevented intervals with very noisy samples from being misidentified as a continuous trajectory with nonzero slope. Multiple prior tests of R² values between 0.5 and 0.9 showed that the threshold was sufficiently conservative in classifying dwell times. The results reported here were not sensitive to the specific value of R².

Fig. 4.

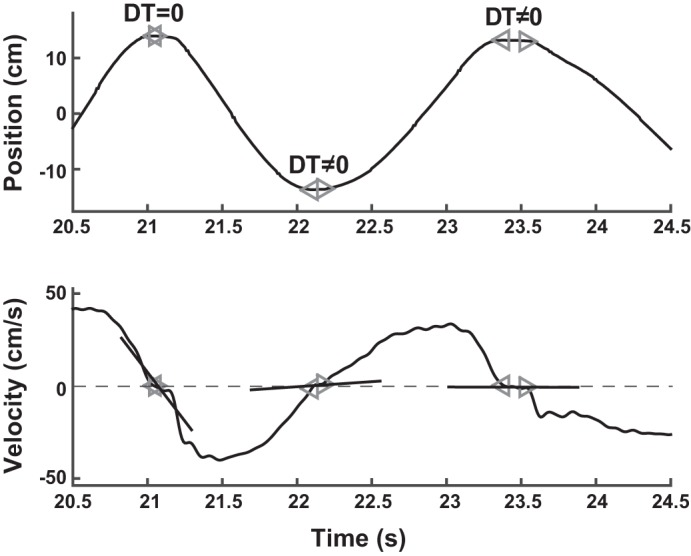
Estimation of dwell time based on position and velocity of a short trial segment. For each movement, its onset t_onset (forward-facing triangle) and end t_end (backward-facing triangle) was first assigned to the time when velocity rose above and (respectively) fell below 5% of the peak velocity of the intervening movement. A linear regression of velocity onto time was then applied to the samples between t_end of one movement and t_onset of the next. If the regression slope reliably exceeded 0.25 cm/s² (i.e., with R² > 0.70) the adjacent t_end and t_onset were merged into a single time point. This occurred at t ≅ 21 s in the data above. If the regression slope was less than 0.25 cm/s² or was unreliable (R² < 0.70), the distinct values of t_end and t_onset were retained and dwell time was nonzero. This occurred at t ≅ 22 s and t ≅ 23.5 s in the data shown.

Cycle Time, Movement Time, and Dwell Time

Cycle time CT_i was defined as the interval between two adjacent forward-movement onsets

$$C{T}_i=t_{onset,i+1}-t_{onset,i}\hspace{0.17em}$$

Movement time of one move MT_j was defined as

$$M{T}_j=t_{end,j}-t_{onset,j}\hspace{0.17em}$$

where j denotes the movement number.

Hogan and Sternad defined discrete movements as characterized by a nonzero dwell time between adjacent movements (Hogan and Sternad 2007). If distinct values of t_onset and t_end were retained following the regression slope test described above, the time between two adjacent movements defined the dwell time DT_j

$$D{T}_j=t_{onset,j+1}-t_{end,j}$$

where j and j+1 denote adjacent movement numbers. Conversely, if t_onset and t_end were merged into one time point, DT was zero.

Analysis of Rhythmicity

A common measure of rhythmicity is harmonicity, or closeness to a sinusoidal trajectory. Several quantifiers have been suggested in previous studies (Guiard 1993; Hogan and Sternad 2007). For each of the trajectories the velocity profile between t_onset and t_end was fit with a half sinusoid using least-square regression

$$\widehat{v}(t;A)=A\sin \left(\pi \frac{t-t_{onset}}{t_{end}-t_{onset}}\right),\hspace{0.17em}\hspace{0.17em}t\in (t_{onset},t_{end})$$

As the movement time was determined by t_end−t_onset, only the amplitude had to be fit. The Goodness of Fit (GoF) was defined for each movement as

$$GoF=100\left(1-\frac{{\displaystyle \int \Vert v(t)-\widehat{v}(t)\Vert dt}}{{\displaystyle \int \Vert v(t)\Vert dt}}\right),\hspace{0.17em}\hspace{0.17em}GoF\le 100\%$$

Note that the above computations of onset, offset, movement time, cycle time, dwell time, and harmonicity were independent of the subsequent analysis of submovements.

Submovement Extraction

The velocity profile of each single movement (between t_onset and t_end) was parsed into a sum of submovements using the globally optimal algorithm described in Rohrer and Hogan (2003, 2006). Each submovement had a lognormal velocity profile with bounded support. This versatile shape can be lepto- or platykurtic with positive or negative skewness and has been shown to provide the best fit to upper extremity movements of 19 alternative candidates (Plamondon et al. 1993; Vaisman et al. 2013). The speed profile was described by

$$\Lambda (t;t_0,T,\mu ,\sigma ,A)=\frac{A{T}^2}{4\sigma (t_0+T-t)(t-t_0)}\cdot \exp \left\{-{\left[\ln \left(\frac{t-t_0}{t_0+T-t}\right)-\mu \right]}^2\cdot \frac{1}{2{\sigma }^2}\right\},\hspace{0.17em}\hspace{0.17em}t\in (t_0,t_0+T)$$

where t₀ is the onset time, T is a duration parameter, A is a scale factor of the profile, μ represents the skewness of the profile, and σ is similar to a standard deviation (larger values yield wider profiles). The algorithm maximized GoF for a fixed number of submovements k, starting with k = 1 in the first iteration; this number was increased by one in each subsequent iteration. GoF of the reconstruction of each single movement was defined as

$$GoF\text{=100}\left(1-\frac{{\displaystyle \int \Vert v(t)-\tilde{v}(t)\Vert dt}}{{\displaystyle \int \Vert v(t)\Vert dt}}\right),\hspace{0.17em}\hspace{0.17em}GoF\le \text{100\%}$$

where ṽ is the reconstruction of each single movement, i.e., the sum of k submovements.

The algorithm stopped when the improvement of the GoF measure due to adding one more submovement was less than 1%. For an alternative algorithm for submovement analysis see Gowda et al. (2015).

Parameter Bounds

The number of submovements per movement was limited to 10, although this limit was never reached with the chosen GoF threshold. T and t₀ were limited so that all submovements started between t_onset and t_end and lasted no longer than t_end − t_onset. The other bounds were set to A∈[0.1,1]×max v(t); μ∈[−1,1]; σ∈[0.3,0.8]. At shorter periods this procedure typically yielded two submovements per half-cycle; at longer periods, five. As discussed below, these parameter bounds did not limit the fitting results.

Submovement Latency, Skewness, and Duration

Latency L_k between adjacent submovements was defined as

$$L_k=t_{0,k+1}-t_{0,k}$$

where t_0,k and t_0,k+1 denote the onset times of adjacent submovements with index k and k+1. Note that submovements could overlap; the separation of submovements is conceptually quite different from dwell time determined based on the measured velocity profile.

Skewness was quantified by μ_k/σ_k. The submovement profile could be strongly skewed (up to μ_k/σ_k = ±3.33) with a long “tail” at its beginning or end. As a result, the parameter T_k overrepresented the duration of the kth submovement. To mitigate distortion due to skewness, submovement duration was quantified by the time interval between ascending and descending crossings of half of the peak submovement velocity.

Statistical Analyses

Comparison of the different measures in the two conditions was performed using two-way repeated-measures analysis of variance (ANOVA). A first analysis of variance compared the three steady-state segments of each trial, cycle 1–10, 36–40, and 66–75, using a 3 (segment) × 4 (trial) repeated-measures ANOVA. A second analysis of variance examined the accelerating and decelerating portions using a two-way 2 (segment) × 4 (trial) ANOVA. Multiple pairwise comparisons (paired-sample t-tests) with Bonferroni corrections were run to perform post hoc analyses. Degrees of freedom were adjusted based on the Greenhouse-Geisser correction when sphericity was violated. Prior to analysis, values that exceeded 3 standard deviations from the mean were excluded from data analysis. A significance level of P = 0.05 was used for all analyses.

RESULTS

Cycle Times

Our first concern was whether subjects competently performed the task. Figure 5, A and B respectively plot cycle time against the corresponding cycle number for all trials of one subject and means of all subjects and standard deviation. In general, subjects followed the metronome, although variability increased as the instructed interval increased. A first analysis focused on cycle times in the three steady-state segments. A 3 (segment) × 4 (trial) ANOVA identified a significant main effect for segment, F_1.1,8.8 = 2,995.50, P < 0.001, but not for trial, F_1.4,11.3 = 0.83, P = 0.423, nor for their interaction, F_1.5,12.3 = 0.74, P = 0.463. As expected, post hoc analysis confirmed that the cycle time in the middle segment was significantly longer (P < 0.001), while no significant difference was detected between the first and last segments (P = 1). The mean cycle times and their standard error in the three segments were 0.97 ± 0.03, 5.76 ± 0.23, and 0.97 ± 0.07 s, which were close to the metronome intervals of 1.0 s and 6.0 s as instructed.

Fig. 5.

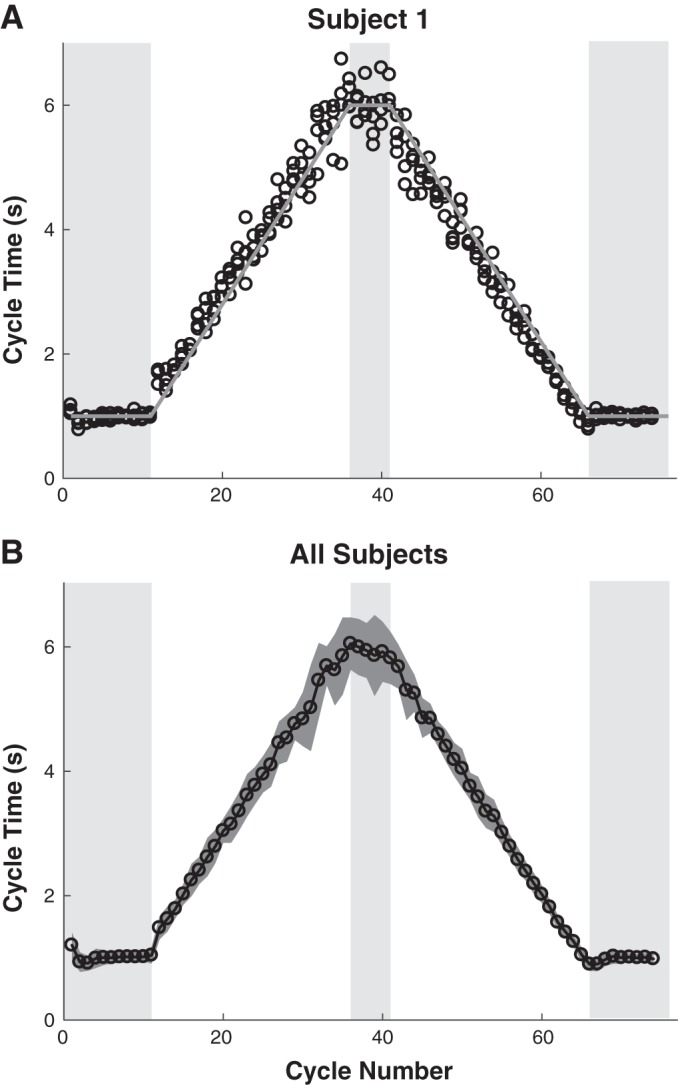
Cycle time as a function of cycle number. A: data for all 4 trials of 1 exemplary subject. Gray line indicates period prescribed by the metronome. The shaded areas mark the segments with constant periods. B: mean values of all subjects and trials. Means are calculated across 9 subjects and 4 trials and for both movements within a cycle. The gray shading depicts the standard deviation.

To examine performance in the two transient segments, two separate linear regressions of cycle time onto cycle number were performed for the accelerating and decelerating segments within each trial. The R²-value was submitted to a 2 (segment) × 4 (trial) ANOVA. The segment effect was significant, F_1,8 = 9.29, P = 0.016, but neither the trial effect, F_3,24 = 0.71, P = 0.557, nor the interaction were significant, F_2.0,16.2 = 0.81, P = 0.465. These results indicated that the cycle times in the increasing segment deviated more from the metronome (R² =0.90 ± 0.07) than in the decreasing segment (R² = 0.95 ± 0.05). This might signal that it is more difficult to synchronize with lengthening intervals than with shortening intervals. Despite these subtle differences, we concluded that subjects followed instructions adequately.

The absence of a trial effect indicated that there was no evidence of learning, nor any evidence that vision or its absence affected performance.

Harmonicity

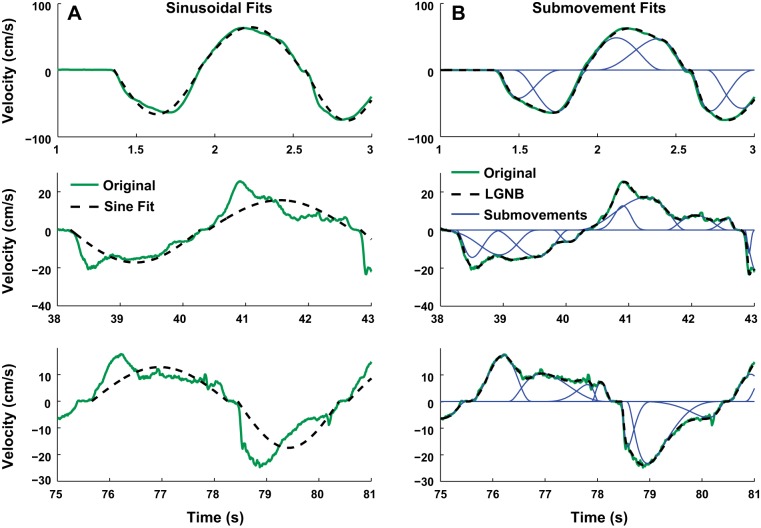
Hypothesis 1 predicts that humans cannot perform slow, smooth oscillatory motions. The most evident feature of performance, common to all subjects, was that the shape of the speed profile changed with duration, becoming visibly more irregular as movements slowed. To quantify this effect, each half-cycle (forth or back) was fit with a half-sinusoid as described above. Figure 6A shows exemplary measured speed profiles with the best-fit half-sinusoid superimposed for 1) movements in the initial segment with an instructed cycle time of 1 s (top row); 2) movements in the transient segment where instructed cycle time changed continuously (middle row), and 3) movements in the segment with an instructed cycle time of 6 s (bottom row). In all cases, the speed profiles were not strictly sinusoidal and at best only approximately periodic (Hogan and Sternad 2007). However, the slower speed profiles deviated significantly more from sinusoidal. Harmonicity was quantified by the GoF between the measured speed profile and the “best-fit” sinusoid and is plotted against the cycle number for one subject across the four trials in Fig. 7A; the average and standard error of the mean over all subjects are presented in Fig. 7B.

Fig. 6.

Exemplary fits of half-sinewaves (A) and submovements (B) to measured velocity profiles in 3 different segments of a trial (top row: fast; middle row: transient; bottom row: slow). The dashed lines show the fit to the measured velocity, shown as continuous green lines. The continuous blue lines show the submovements used to fit the measured velocity.

Fig. 7.

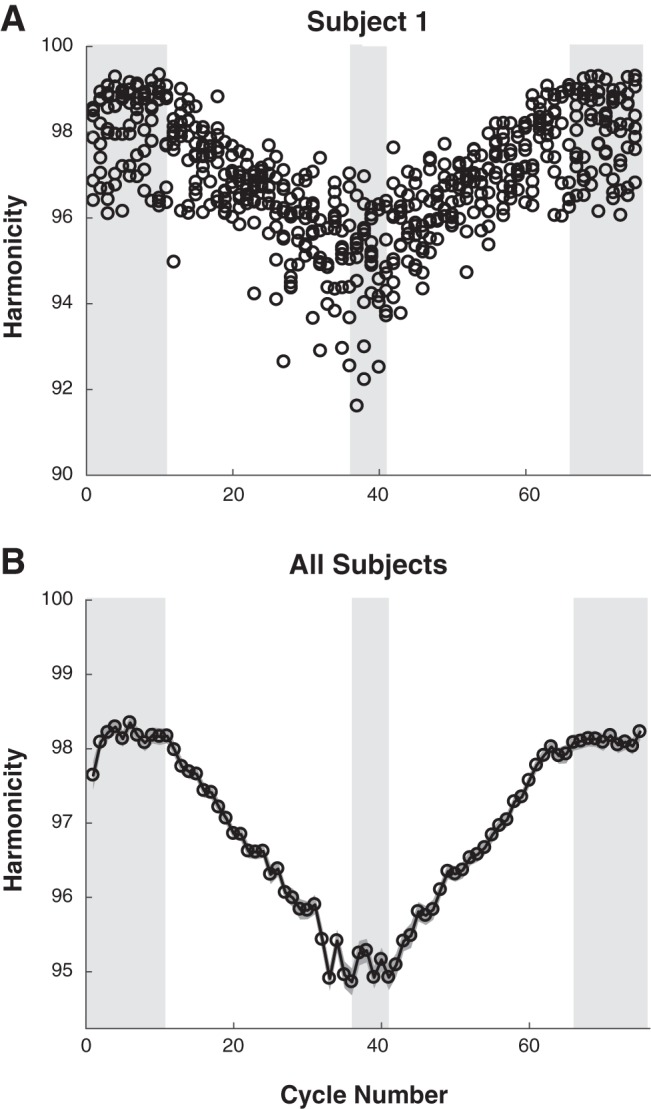
Harmonicity as a function of cycle number. A: data for all 4 trials of 1 exemplary subject. The shaded areas mark the segments with constant periods. B: mean values of all subjects and trials. Means are calculated across 9 subjects and 4 trials and for both movements within a cycle. The gray shading depicts the standard error of the mean.

The same ANOVA compared harmonicity in the three steady-state segments and across the four trials. We found a significant effect for segment, F_2,16 = 213.56, P < 0.001, but again no trial effect, F_3,24 = 0.94, P = 0.439, nor an interaction, F_3.2,25.3 = 0.65, P = 0.688. The significant segment effect was due to the longer middle segment (P = 0.021); there was no significant difference between the first and last segments, F_1,8 = 2.95, P = 0.372. The harmonicity measures in the three segments were 88 ± 2.7, 69 ± 4.2, and 90 ± 1.8. The significant difference between steady-state segments strongly supports hypothesis 1.

The same ANOVA compared harmonicity in the two transient segments but found no significant effects: segment: F_1,8 = 0.23, P = 0.883; trial: F_3,24 = 1.03, P = 0.397; interaction: F_3,24 = 0.77, P = 0.521. The absence of any significant difference between transient segments contradicts hypothesis 3. The absence of any trial effect indicated that there was no evidence of learning. Neither was there any evidence that vision or its absence affected performance, contradicting hypothesis 4.

Dwell Time

Hypothesis 2 predicts that slower oscillatory movements are executed as a sequence of discrete movements, separated by increasing dwell times between t_onset and t_end—the distinctive signature of discrete movements. Figure 8A shows dwell times of a single subject in a single trial. Figure 8B shows the mean of dwell time for all subjects combined. Note that in the single subject’s data there is a gap between the zero dwell times and those of nonzero duration. This minimum nonzero duration was not due to sampling nor an artifact of the dwell time calculations. The minimum dwell time for all subjects was 30 ms (3 samples). Dwell times were visibly longer in slower movements, while for many cycles in the initial and final segment, dwell time was zero. To test this observation statistically, the dwell times of all subjects were submitted to two ANOVAs. The first compared the steady-state segments and identified a significant difference, F_1.0,8.1 = 37.38, P < 0.001; again, neither the trial effect, F_1.5,11.9 = 1.24, P = 0.310, nor the interaction were significant, F_1.5,11.8 = 1.29, P = 0.299. The mean dwell times in the first, middle, and last steady-state segments were: 9 ± 6, 167 ± 81, and 5 ± 3 ms, respectively (Fig. 8B). Post hoc tests revealed that the segment effect was due to long dwell times in the middle segment (P < 0.001); the values in the first and last segments were not significantly different from each other (P = 0.594). The significant increase in dwell time at the longer periods strongly supports hypothesis 2. The absence of any trial effect indicated no evidence of learning and no evidence that vision or its absence affected performance, contradicting hypothesis 4.

Fig. 8.

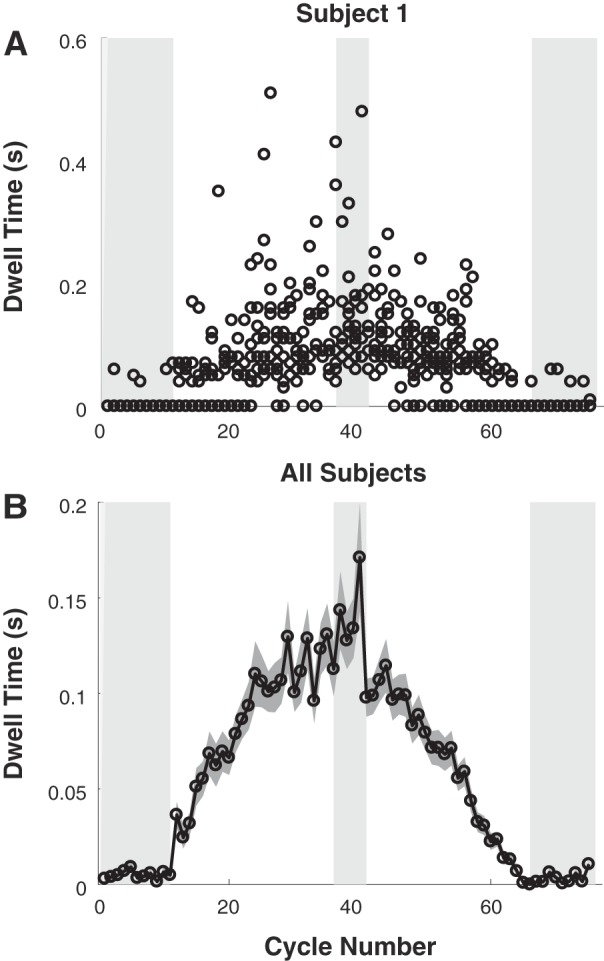
Dwell time as a function of cycle number. A: data for all 4 trials of 1 exemplary subject. The shaded areas mark the segments with constant cycle intervals. B: mean values of all subjects and trials. Means are calculated across 9 subjects and 4 trials and for both movements within a cycle. The gray shading depicts the standard error of the mean.

The second analysis examined the transient segments. The 2 × 4 ANOVA detected a significant segment difference between the ascending and descending segment, F_1,8 = 16.22, P = 0.004, and a trial main effect, F_3,24 = 5.08, P = 0.007, but no interaction, F_3,24 = 2.63, P = 0.073. The segment effect indicated that dwell times in the segment where period increased (movements slowed) were significantly longer than in the segment where period decreased: increasing, 99 ± 45 ms; decreasing, 71 ± 36 ms (Fig. 8B). This difference may be indicative of the higher demands to synchronize with lengthening compared with shortening periods, as already seen in the periods above, indicating potential hysteresis. Post hoc analyses of the trial main effect revealed that dwell time in trial 1 was significantly longer than in trial 4 (P = 0.048). The significant trial effect indicated that some familiarization with the task may have occurred. However, the trial effect could not be attributed to the presence or absence of vision. Dwell times in trials 1 to 4 were 101 ± 48, 90 ± 45, 85 ± 48, and 63 ± 30 ms, respectively. Dwell time tended to decrease between trials 1 and 2 as vision was removed (not significant, P = 0.32, uncorrected), but dwell time also tended to decrease further between trials 2 and 3 as vision was restored (not significant, P = 0.64, uncorrected). The absence of a significant effect of vision is strong evidence against hypothesis 4.

Submovements

The unambiguous evidence of increasing dwell time as movements slowed motivated the finer-grained decomposition of the speed profiles into submovements. Using the method described above, each half-cycle (forth or back) was fit to a set of submovements that could temporally overlap. Compared with the half-sinusoid fit used to assess harmonicity, submovements yielded a better fit to the measured speed profiles for movements of all durations as they could overlap in time (Fig. 6B).

Number of submovements.

As mentioned in the introduction, we hypothesized that oscillatory primitives are only available with a limited range of periods and that sufficiently slow rhythmic movements become replaced by submovements. A corollary of hypothesis 2 is that the number of submovements should increase systematically with movement duration. Figure 9 shows the distribution of the number of submovements per movement (half cycle) plotted against cycle number. To construct the histogram, data were parsed into bins of five nonoverlapping cycles and the numbers of submovements pooled across trials and subjects. The number of submovements per movement was lowest in the first 10 and last 10 cycles, showing typically two submovements. As the cycle time increased, the number gradually increased, typically reaching five at the longest cycle interval. This pattern was reversed as the cycle time decreased.

Fig. 9.

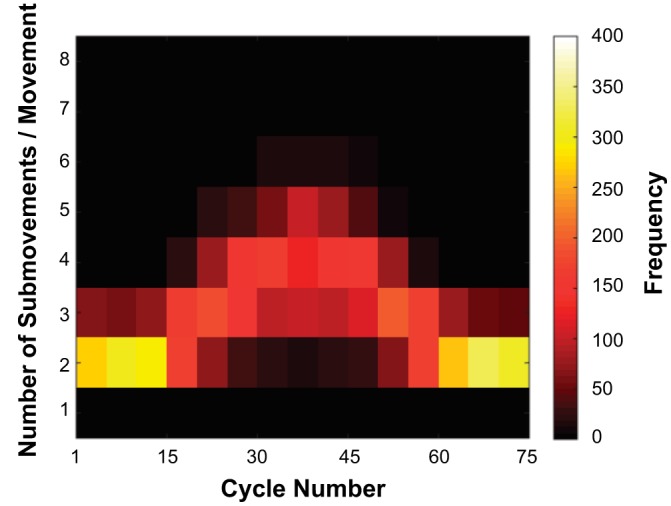
Distribution of the number of submovements per movement as a function of cycle number for all subjects and all trials. Cycles were parsed into bins of 5. Colors denote the frequency of the number of submovements per movement in each bin (legend on the right margin).

Hypothesis 3 predicts that the accelerating and decelerating segments would differ in the transition between execution as a primitive oscillation and as a sequence of submovements. To examine whether the number of submovements per movement changed asymmetrically in the decelerating and accelerating segments, the slope and GoF of a linear regression of submovements per movement onto cycle number was compared between the two transient sections. The 2 (segment) × 4 (trial) ANOVA failed to show any significant effects for GoF: trial: F_3,24 = 1.15, P = 0.351; segment: F_1,8 = 0.53, P = 0.486; interaction: F_3,24 = 0.09, P = 0.963. Similarly, there were no differences for slope: segment: F_1,8 = 0.81, P = 0.394; trial: F_3,24 = 0.90, P = 0.458; interaction: F_3,24 = 0.14, P = 0.935. These data do not support hypothesis 3. The absence of any trial effect indicated no evidence of learning and no evidence that vision or its absence affected performance, contradicting hypothesis 4.

The remaining analyses aimed to test the reliability of our submovement extraction algorithm. Reliably extracting overlapping submovements from a continuous kinematic record is a notoriously hard problem. For example, the common practice of examining zero-crossings of progressively higher derivatives is fundamentally misleading. Even aside from the practical difficulty of obtaining reliable higher-order derivatives from kinematic data, a composition of two single-peaked speed profiles may yield a composite speed profile with one, two, or three speed peaks, hence one to five zero-crossings in the acceleration profile (Rohrer and Hogan 2003). The algorithm we used was designed to avoid these problems and was shown to identify submovements reliably, even in the presence of substantial noise (Rohrer and Hogan 2003). The analysis described next attempted to test whether the submovement sequences we derived might be an artifact of the extraction algorithm or, instead, reflected the structure underlying motor behavior.

Submovement duration.

For practical reasons, the submovement extraction algorithm assumed that the submovement parameters duration, latency, and skewness lay within a limited range of values (see methods). Mathematically, any smooth data history may be fit with arbitrary precision by a sum of basis functions, provided those functions have finite support (they are zero except for a finite range of their argument). As a result, a sufficiently large number of sufficiently short submovements could have fit our observed data with any specified degree of precision. In that case, we might expect the number of extracted submovements to cluster at the upper end of the allowable range and their durations to cluster at the shorter end of their allowable range.

In fact, they did not. Pooling data for all subjects and trials, the number of extracted submovements per movement was much less than 10, the maximum allowable (Fig. 9). Figure 10A shows histograms of submovement durations plotted against cycle number. Each histogram was computed for a group of five nonoverlapping cycles. In all cases, submovement durations were clustered away from the bounding values permitted by the submovement extraction algorithm. Moreover, this pattern became more pronounced for slower movements.

Fig. 10.

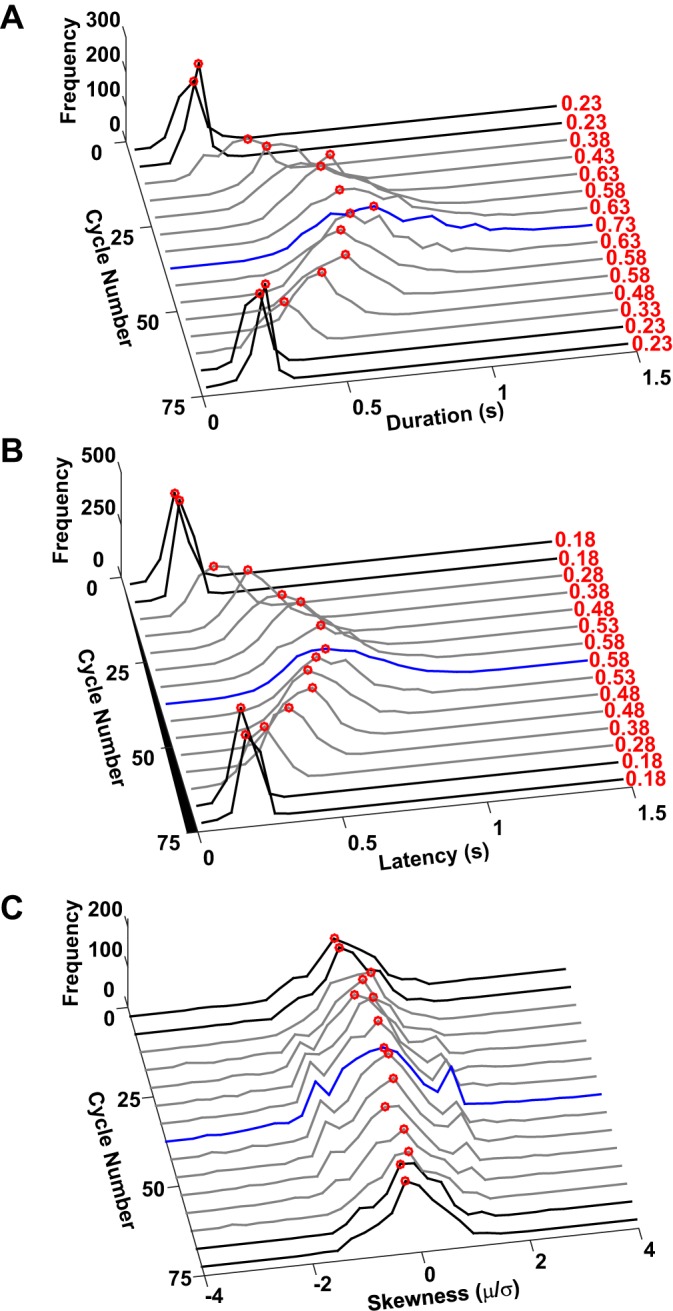
Histograms of submovement parameters duration, latency, and skewness as a function of cycle number for all subjects and all trials. Cycles were parsed into bins of 5. Black lines denote the faster initial and final steady-state segments; blue line denotes the slow steady-state segment in the middle of each trial; gray lines denote transient segments. A: histogram of duration against cycle number. Red numbers denote the most frequent duration for each histogram. Note that all histograms are clustered away from their short-duration limits and that this pattern is more pronounced as movements slow. B: histogram of latency against cycle number. Red numbers denote the most frequent latency for each histogram. Note that all histograms are clustered away from their short-latency limits and that this pattern is more pronounced as movements slow. C: histogram of skewness against cycle number. Unlike duration and latency, skewness is insensitive to cycle number.

Latency.

Pooling data for all subjects and trials, Fig. 10B shows histograms of submovement latencies plotted against cycle number. As above, each histogram was computed for a bin of five cycles. In all cases, submovement latencies were clustered away from zero, consistent with a minimum “refractory period” between submovements. Again, this pattern became more pronounced for slower movements. Note that latency is also nonzero for continuous oscillatory movements in the initial and final segments, highlighting that latency is defined at the submovement level and is independent of and distinct from dwell time.

Skewness.

Pooling data for all subjects and trials, Fig. 10C shows histograms of submovement skewness plotted against cycle number. As above, each histogram was computed for a group of five nonoverlapping cycles. In all cases, submovement skewness was clustered around zero, far from the bounding values permitted by the submovement extraction algorithm. We conclude that our submovement extraction algorithm performed acceptably. Especially for the slower movements with lower harmonicity, it did not generate submovement sequences that were not present in the structure of the experimental data. This is confirmed by the excellent fit evident in Fig. 6B.

DISCUSSION

This study set out to explore possible limitations due to motor control based on dynamic primitives. A previous study showed that human subjects were unable to sustain a periodic sequence of discrete movements (i.e., separated by dwell times) as their pace increased; instead, they switched to oscillatory movements (Sternad et al. 2013). Importantly, the pace at which the transition occurred varied with sensory information conditions. This meant that the transition could not be dismissed as a shortcoming of peripheral biomechanics but reflected a limitation consistent with composing motor behavior from dynamic primitives—i.e., a consequence of the “software” architecture underlying motor control.

The study presented here complemented that previous work by exploring movements that gradually decreased in speed. While the previous study exposed limitations of discrete movements, the present study “stressed” continuous rhythmic movements to expose the limits of oscillatory primitives. We asked human subjects to maintain a smoothly rhythmic movement with long periods (up to 6 s). Results showed that, despite the auditory display of period, and with or without vision of the cursor movement, hand speed profiles became significantly and substantially more irregular as movements slowed (Figs. 6 and 7). In addition, despite explicit instructions to the contrary, epochs in which the hand dwelt at zero velocity were observed. In the first and last steady-state segments, dwell times were within the temporal resolution of our measurements, but they became significantly and substantially more prominent as movements slowed (Fig. 8). Together, these observations support hypothesis 1, that smoothness decreases as period increases. Instead, as predicted by hypothesis 2, as movements slowed they started to exhibit dwell times, a definitive delimiter of discrete movements.

It is important to note that the above conclusions are based on standard analyses of movement kinematics and are completely independent of our method of identifying submovements. Our finer-grained submovement analysis provided further strong support for hypothesis 2, showing that the number of submovements increased systematically with longer cycle times. However, we found only weak evidence of an asymmetry in the decelerating and accelerating transitions between execution by oscillations and by sequences of submovements, as hypothesis 3 predicted. The only support for hypothesis 3 was found in the pattern of dwell times: the ascending segment showed a faster increase and longer dwell times than the descending segment, irrespective of practice. The presence or absence of vision had no effect on any of our observations; hypothesis 4 was not supported.

The observed inability to produce slow, smooth oscillatory movements exposes a limitation due to the composition of motor behavior from dynamic primitives—i.e., a consequence of the software architecture underlying motor control. Smooth rhythmic movements are replaced by a sequence of submovements, when moving sufficiently slowly. Before interpreting the data furthermore, we first discuss and rule out possible artifacts that might provide alternative explanations.

Possible Artifacts

Measurement noise.

Could the observed kinematic irregularity be an artifact of our experimental measurement procedures? Kinematic data were obtained as a sequence of positions sampled at 100 Hz. Velocity was computed based on zero-lag smoothing of the position, numerical differentiation with a half-sample delay, and further zero-lag smoothing. Although this reduced measurement artifact, due to the finite resolution of the position measurement and the finite sampling interval, velocity measurements at slow speeds necessarily had relatively higher variability than at high speeds—i.e., the signal-to-noise ratio was poorer. Nevertheless, this cannot account for our observations.

An upper bound on the magnitude of measurement noise was obtained from our submovement extraction procedure. That analysis fit progressively more submovements to the velocity profiles until adding more submovements did not improve the fit; that is, the algorithm stopped when the GoF improvement achieved by adding another submovement fell below 1% (see methods). However, the root-mean-square deviation between the resulting submovement sequence and the experimental velocity profile could exceed 1% of the experimental data’s RMS variation. In fact, it was found to range between ~1 and 2%, the latter at longer periods, consistent with the expected poorer signal-to-noise ratio. As measurement noise was the same for all subjects, this indicated the worst-case noise magnitude. Measurement noise of this strength—1–2% of signal magnitude—cannot account for the kinematic irregularity we observed (see Fig. 6).

Friction.

Subjects lightly rested their forearm on the table while making movements. Although we provided a low-friction skid (made of Teflon) to minimize static and dynamic friction, we did not completely eliminate friction. Dry friction is commonly characterized by static friction (when velocity is zero) that is larger than kinetic (sliding) friction, a phenomenon colloquially known as “stiction.” This might conceivably have induced dwell periods at the extremes of movement (due to “sticking” when velocity declined to zero). Moreover, this might have become more prominent during slower movements, when the forces required to overcome inertia and generate movement would have been smaller, hence more time may have been required to exceed the threshold of static friction.

Two observations argue against this account. The foremost is that the kinematic irregularities we observed occurred throughout the movements (see Fig. 6). Kinematic irregularities due to stiction would have been confined to the regions where velocity was zero—i.e., clustered at the movement extremes. In fact, the deviations from smooth rhythmicity occurred throughout. They were well approximated as a sequence of submovements with onset times distributed throughout the movement duration, not clustered at the ends.

In addition, to assess the role of friction empirically, we performed an ad hoc experiment in which subjects were asked to perform similar oscillatory arm movements at a constant period between two visually presented targets under two contrasting conditions: 1) with the hand sliding over a horizontal surface similar to this experiment; or 2) with the hand and forearm unsupported, i.e., moving “in air.” Arm positions in 3D were measured at 200-Hz sampling rate and differentiated as described above to compute velocity. There was no measureable difference between the two conditions. We conclude that friction cannot account for our observations.

Motor noise.

Could the observed kinematic irregularity be an artifact of force production in the peripheral neuromuscular system? All torques required to accelerate and decelerate limb inertia (including Coriolis and centrifugal accelerations) are proportional to the inverse square of movement time. As times increased from 1 to 6 s, the required inertial forces decreased by a factor of 36 while the irregularity increased. Therefore, the complex interaction torques required to produce the approximately straight hand paths we observed cannot account for speed fluctuations that increased as movements slowed.

Because muscles may need to overcome the apparent viscosity due to muscle force-velocity characteristics (or other phenomena), muscle force may not decline as rapidly as the forces required to overcome inertia. Nevertheless, mechanical physics dictates that slower motions require lower muscle forces. Could the fluctuations we observed be due to “signal-dependent noise,” which has been proposed to account for several aspects of motor behavior (Harris and Wolpert 1998; Jones et al. 2002)? Signal-dependent noise is usually assumed to be proportional (or at least monotonically related) to the magnitude of the underlying signal. If so, motor noise in force production should decline as force declines. This is opposed to our observation that kinematic irregularity increased as movements slowed and mechanically required forces decreased. Further evidence is provided by a recent simulation that showed that signal-dependent noise is far too small to cause the large kinematic irregularities observed in upper limb movements (Salmond et al. 2016). As demonstrated in other work, signal-dependent noise may not be as prominent as is often assumed (Sternad et al. 2011).

But might sufficiently low muscle forces exhibit fluctuations that reflect the action of individual motor units? In contrast to the pattern usually assumed for signal-dependent noise, force fluctuations due to the actions of individual motor units would yield “noise” magnitudes that increased as the underlying (mean) force declined. However, Slifkin and Newell (1999) showed that, though the noise-to-signal ratio of force production actually increased for sufficiently small forces, the magnitude of the “noise” in force decreased monotonically with mean force (see Fig. 3 in Slifkin and Newell (1999). Therefore, noise in muscle force cannot account for our observation that kinematic fluctuations increased as movements slowed.

Finally, compelling evidence against attributing the observed behavior to motor noise came from the observed dwell times, which increased with movement duration and became most pronounced in the slowest movements. This effect is consistent with previous results (Adam and Paas 1996; van der Wel et al. 2010). The probability that noise of magnitude sufficient to account for the observed speed fluctuations (Fig. 6) could also yield epochs with speed below 3% of peak for significant durations (Fig. 8) is essentially zero. These dwell times are an unambiguous signature of discrete movements.

Relation to Prior Work

As our observations cannot be dismissed by these possible artifacts, they support our hypothesis that sufficiently slow motions cannot be executed by oscillatory primitives—i.e., the parameters of an oscillatory dynamic primitive are limited. Our data suggest that these slower movements are executed using a sequence of submovements that we propose are the dynamic primitives underlying discrete movements. These findings extend several other studies that showed that repetitive movements, if performed sufficiently slowly, transition to a sequence of discrete movements or movements composed of overlapping submovements (Adam and Paas 1996; Doeringer and Hogan 1998a, 1998b; Hogan et al. 1999; van der Wel et al. 2010). Previous reports of submovements in slow discrete movements are found in studies of persons recovering after cerebral vascular accident (stroke) (Dipietro et al. 2012; Krebs et al. 1999; Rohrer et al. 2002, 2004). However, in those studies, it is unclear whether the presence of submovements in slow discrete movements is a consequence of neural injury or a fundamental feature of motor control.

Intermittent feedback control.

It has been proposed that submovements arise from an intermittent feedback control process. The notion of submovements due to intermittent feedback control has a long history. As early as 1899, Woodworth investigated line-drawing tasks and reported irregularities just before acquiring a target. He interpreted this as the signature of a corrective, or “current control” phase that reduced errors in a series of discrete steps, distinct from an “initial transport” or ballistic phase (Woodworth 1899). For discrete aiming movements to small targets, irregularities have been reported in the velocity trace, in contrast to the smooth bell-shaped velocity profile shown for simple reaching movements (compare Meyer et al. 1988, 1990 with Atkeson and Hollerbach 1985; Flash and Hogan 1985). Movements to smaller targets that required higher precision evoked greater irregularity, consistent with a greater number of corrective submovements (Milner 1992; Milner and Ijaz 1990).

Craik (1947) observed that when participants tracked a pseudo-randomly moving target, their response included directional changes at frequencies other than the target frequency. These were termed “intermittency” (Vince 1948). Intermittency has been demonstrated in many visuomotor tracking tasks, testing completely predictable to pseudo-random targets with various display properties (Miall et al. 1993; Poulton 1974; Vince 1948; Weir et al. 1989; Wickens 1984). A number of possible explanations for intermittency were proposed, including an internal clock controlling the timing of the actor's corrective responses (Bekey 1962), a physiological refractory period delaying the production of the next response (Smith 1967; Vince 1948) and an error dead zone around the target within which no adjustments are detected or deemed necessary (Wolpert et al. 1992). Central to all these interpretations is the view that humans are intermittent feedback controllers (Craik 1947; Miall et al. 1993; Neilson et al. 1988a, 1988b; O’Dwyer and Neilson 1998; Poulton 1974; Weir et al. 1989).

The present study showed that these explanations, however appealing, are not sufficient to account for our results. Hypothesis 4 was not supported: the increase of kinematic fluctuations (decrease of harmonicity) as movements slowed was neither eliminated nor even significantly reduced by removing visual feedback. To some extent this is not surprising: our experimental protocol was deliberately designed without continuous tracking and with minimal accuracy requirements, thereby reducing the need for visually evoked correction. Previous results also support our observations: though Miall et al. (1993) reported that removal of visual feedback reduced intermittency, removing visual feedback had no effect on an oscillatory phase-space drawing task (Doeringer and Hogan 1998a, 1998b). Of course, alternative sources of feedback (e.g., proprioceptive) were still available, but the performance of an intermittent feedback controller should improve for slower movements (with more time to acquire, process, and respond to sensory information). We observed the opposite: harmonicity declined and dwell periods increased in slower movements.

Relation between kinematic variables and submovement parameters.

It is important to stress that our extraction of submovements was completely independent of our quantification of kinematic variables dwell time, harmonicity, and cycle period. Nevertheless, comparison of the pattern of the kinematic variables (cycle time, dwell time, and harmonicity) with those of the submovement parameters (number, duration, and latency) revealed very similar changes with cycle number (compare Figs. 5, 7, and 8 with Figs. 9 and 10). Some more specific correlations suggest interesting speculations about the underlying processes.

In principle, a movement could exhibit nonzero dwell time with no submovements; conversely, a movement could be composed of submovements, yet exhibit no dwell time. In fact, both measures clearly increased with movement duration (Figs. 8 and 9), but the correlation between dwell times and number of submovements was modest, ranging between R = 0.10 and R = 0.55 over nine subjects. To gain further insight, we tested how strongly the two measures were correlated with movement time by calculating Spearman’s rank correlation within single participants. While both were significantly correlated with movement time (P < 0.0005), dwell time was significantly (P = 0.02) less correlated than the number of submovements (mean of individual correlation coefficients 0.58 vs. 0.75). This was most likely due to the highly skewed distribution of dwell times toward lower values, including zero dwell times even within the slowest movements. The covariation of two independent measures (dwell time and submovements) indicates that both were consequences of a common underlying neural process.

In effect, submovement extraction provides a finer-grained analysis of that underlying process; the number of submovements may increase before dwell time deviates from zero. Closer examination of submovement parameters is informative: One remarkable observation was that, while movement time and submovement durations were strongly correlated (R = 0.93), submovement duration did not increase beyond ~1 s. Whereas our finding speaks to a limitation of oscillatory primitives—they cannot support arbitrarily slow periodic behavior—this suggests a similar limitation on “discrete” primitives: they, too, cannot be arbitrarily slow. As movement time increased, submovement duration increased, but only up to a point; thereafter, additional submovements were recruited, consistent with our observation that submovement number increased with movement duration.

Dynamic primitives and nonlinear dynamics.

Oscillations due to nonlinear dynamics with stable limit-cycle behavior were discussed in much previous work on rhythmic manual coordination (Kay et al. 1987; Schöner and Kelso 1988). Specifically, Russell and Sternad (2001) studied a task in which subjects tracked a periodic visual signal with effectors prepared to have different natural frequencies. The observed phase leads and lags varied with the mismatch between target period and the effector’s natural frequency, consistent with phase and frequency locking of coupled oscillators. Unlike in Russell and Sternad (2001), the metronome period in the present study changed continuously and therefore required adjustments at every cycle. If phase locking underlay the behavior, it would require corrections when mismatch with the metronome was observed. That would be most likely at the ends of movements, which is not consistent with our findings of “irregularities” throughout. Hence, phase locking with adjustments is a less likely candidate for our observations.

An alternative is that primitive oscillations and submovements emerge from the nonlinear dynamics of neural networks; this is one reason we refer to them as dynamic primitives. Nonlinear dynamic systems exhibit distinctive interactions. If control were based on feedback and/or feedforward control (e.g., based on an internal model of the neuromuscular periphery), it should be possible to superimpose or merge discrete and rhythmic movements in any task-specified way, subject only to the shortcomings of the biomechanical system. Sternad and colleagues examined movements that combined oscillations and submovements in unimanual and bimanual, single-joint and multijoint tasks. Experimentally probing superposition of oscillations and submovements at random phasing revealed that transient displacements preferentially occurred in limited phase windows of ongoing rhythmic movements (Sternad et al. 2000, 2002; Sternad and Dean 2003; Wei et al. 2003). Without nonlinear dynamics, discrete and rhythmic movements could be superimposed arbitrarily. The fact that they could not strongly supports a nonlinear dynamic origin of these primitive actions.

These interactions between discrete and rhythmic movements are reminiscent of interactions identified in rhythm generation of mammalian limbs. Going beyond pure rhythm generation, discrete perturbations such as sensory stimulation have induced phase resetting. To account for this observation, Rybak and colleagues proposed a two-layered central pattern generator structure consisting of a pattern-formation unit and a rhythm-generating unit (Rybak et al. 2006). Connected via interneurons, the two-layered model could simulate a more varied pattern of observations, such as phase-resetting and nonresetting perturbations.

Several alternative neural architectures underlying motor primitives are considered in Giszter 2015, e.g., Fig. 3 of that paper). While the rhythm generator of Rybak et al. (2006) is clearly associated with a rhythmic dynamic primitive, it is less clear how a submovement primitive might emerge from this architecture. The “burst generators” proposed by Hägglund et al. (2013) may be the origin of submovements such as we report here. An alternative to the dynamic submovements that we define is the notion of time-varying synergies introduced by d'Avella et al. (2003). Time-varying synergies combine temporal structure with the pattern of muscle recruitment. However, a study in frogs showed that time-varying synergies could not account for limb trajectories, whereas premotor drive pulses could (Kargo and Giszter 2008). The latter are consistent with our view of submovements as dynamic primitives. However, whether the evolution of the human nervous system has preserved these structures found in mouse and frog remains for future study.

Another distinctive feature of nonlinear interactions is an asymmetry usually termed hysteresis. In the context of the experiments reported here, hysteresis would manifest as a different transition between oscillatory motion and a sequence of submovements when periods increased and decreased. Our companion study on accelerating discrete movements showed at most weak evidence of hysteresis (Sternad et al. 2013). The present study showed some evidence of hysteresis, although only in one variable, dwell time. Although there was no evidence of an abrupt switch (typical of hysteretic phenomena in dynamical systems), dwell time increased significantly faster than it decreased in the two transition segments. However, the submovement composition of the discrete movements did not reflect a similar asymmetry. Another possible explanation for the asymmetry in the dwell times is that for lengthening intervals the current performance does not receive an error signal until after the movement is finished. In contrast, for shortening intervals the metronome sound or error signal arrives before the end of the movement, allowing adjustment in the immediate next cycle. Given these considerations, we refrain from placing much emphasis on the hysteresis result.

These observations (limited evidence of hysteresis, nor an abrupt switch) may have been due to the fact that this task—synchronizing with a slowly decelerating transiently periodic auditory signal—appears to have been quite difficult. Even though the biomechanical demands of this task were trivial (move slowly between two large targets a short distance apart), there was no evidence that harmonicity increased with practice. However, we did find evidence that the dwell times in the transient segments on the fourth trial were significantly shorter than in the first trial. This suggests that the demands of the task (synchronize with a slowly decelerating or accelerating auditory signal) may have been challenging. The concomitant variability (see Figs. 5, 7, and 8) may have masked more visible evidence of hysteresis. Further work is required to resolve this question.

Implications and Conclusions

The importance of limitations.

Limitations such as we report here strongly support the biological plausibility of our core hypothesis that motor control is based on dynamic primitives. Without limitations, this idea might be dismissed as experimentally indistinguishable from mathematical “curve fitting.” In the context of the experiments reported here, any (almost-) periodic behavior such as we observed during the steady-state segments could in principle be reconstructed with arbitrary precision as a sum of components with (almost-) periodic behaviors; this is the essence of Fourier analysis. However, such curve-fitting reconstruction would be equally competent for all periods. Our observation that it was not (see Figs. 6 and 7) shows that our data exhibits structure that cannot be dismissed as simple curve fitting. Moreover, the appearance of submovement sequences in slow movements is fully consistent with our proposal that motor control is based on dynamic primitives (Hogan and Sternad 2012).

Our observations strongly support hypothesis 1, that slow rhythmic movements cannot be executed by oscillatory dynamic primitives. A crude estimate of the longest period of an oscillatory motor primitive may be obtained by examining the variation of the number of fitted submovements with metronome interval. Referring to Fig. 9, the number of submovements begins to increase at a period of ~3 s. This is similar to the reported limit on the time-horizon estimated in time perception and human behavior, which is also close to 3 s (Fraisse 1984; Schleidt et al. 1987). This raises the intriguing possibility that the dynamic primitives underlying action may also play a role in perception. For example, the increasing dwell times could be the result of an inaccurate estimation of the requested cycle time. Further work is required to assess this speculation.

Our observations are also consistent with the proposal that there may be a refractory period between adjacent submovements. Although our algorithm to identify submovements permitted two or more of them to start simultaneously, in fact they did not; the distribution of latencies was clustered well away from zero (Fig. 10B). However, it is unclear whether any refractory period is a “hard-wired” limitation or a feature of the software responsible for initiating submovements. Our data appear to suggest the latter, but further work is required.

Why dynamic primitives?

The main finding of this study and the companion study (Sternad et al. 2013) is that upper extremity motor control exhibits limitations due to its software, the organization of motor behavior as a composition of dynamic primitives. In particular, slow motions are difficult. This appears to be a drawback of control via dynamic primitives; is it offset by some advantage? The most obvious benefit is simplification. Specifying an action as a sequence of submovements, limited in duration, rather than as a continuous and extended time course of neural activity, dramatically reduces the dimensions of the control problem and places fewer demands on a limited capacity for neural information processing and transmission. This is the main reason why we believe that control based on dynamic primitives may resolve the “paradox of human dexterity”; it suggests how humans perform so much better than robots despite vastly inferior hardware and wetware.

GRANTS

D. Sternad was supported by the National Institutes of Health R01-HD045639, R01-HD087089, and the National Science Foundation DMS-0928587 and NSF-EAGER-1548514. S. Charles was supported by a Whitaker Graduate Fellowship. N. Hogan was supported by NIH R01-HD087089, NSF-EAGER-1548514 and by the Eric P. and Evelyn E. Newman fund and the Gloria Blake fund.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.K.C. performed experiments; S.-W.P., H.M., and D.S. analyzed data; S.-W.P., D.S., and N.H. interpreted results of experiments; S.-W.P. prepared figures; S.-W.P. and N.H. drafted manuscript; S.-W.P., S.K.C., and D.S. edited and revised manuscript; S.-W.P., H.M., S.K.C., D.S., and N.H. approved final version of manuscript.

APPENDIX

We define a submovement as an attractor that describes a smooth sigmoidal transition of a variable from one value to another with a stereotyped time profile. For limb position, the variable is a vector in some coordinate frame, e.g., hand position in visually relevant coordinates, x = [x₁,x₂,…x_n]^t. Each coordinate’s speed profile has the same shape which is nonzero for a finite duration d = e − b, where b is the time when the submovement begins and e is the time it ends, i.e., it has finite support:

$${\dot{x}}_j(t)={\widehat{v}}_j\sigma (t),j=\mathrm{1...}n$$

where v̂_j is the peak speed of element j; σ(t) > 0 iff b < t < e and σ(t) = 0 if t ≤ b or e ≤ t. The speed profile has only one peak: there is only one point t_p∈(b,e) at which σ̇(t_p) = 0, and at that point, σ(t_p) = 1.