Disharmony in neural oscillations

Abstract

Cross-frequency phase coupling (PPC) may play an important role in neural processing and cognition. However, a new study unveils a statistical bias in how PPC is detected in neural recordings, questions prior evidence for PPC in hippocampus, and shows PPC tests are dramatically flawed by their confounds with oscillation harmonics.

neural oscillations are taking a greater prominence in our study of the neural bases of cognition. Their capacity to orchestrate the activity of large populations of neurons is arguably instrumental in many cognitive operations. More and more theoreticians and experimentalists are now wondering whether the coupling of these oscillations across distinct frequencies provides refined temporal organization of neural activity involved in sophisticated cognitive processes. While cross-frequency coupling (CFC) comes in different flavors (Jensen and Colgin 2007), phase-phase coupling (PPC, or n:m coupling) has been thoroughly studied by theoreticians (Canavier 2015) and is unique for its capacity to control precisely the timing of neural spiking at distinct time scales. In particular, Belluscio and colleagues’ findings that the phase of theta and gamma rhythms are coupled in rodent hippocampus (Belluscio et al. 2012) strongly support CFC-mediated schemes for the representation of sequences in this region (Lisman and Jensen 2013). A growing number of studies have reported PPC and other signatures of CFC across many areas and putatively linked it to specific cognitive operations (see Hyafil et al. 2015 for review).

A new study by Scheffer-Teixeira and Tort (Scheffer-Teixeira and Tort 2016) adds a disharmonic voice to the choir, by questioning the existence and relevance of PPC in the brain. The implications of the study are threefold: methodological, experimental, and conceptual. First, the authors show how current methods for detecting PPC create many false positives (even to the point that significant PPC is detected in pure white noise). Such bias emerges as the filtering procedure, applied before measuring coupling levels, creates short-lived artifactual linear relationships between the extracted phase of the two filtered signals. In turn, these temporary links yield straight lines in phase-phase plots (plots showing how phases of the two filtered signals coevolve) that can be confounded with genuine PPC, unless appropriate surrogates are used, as nicely demonstrated by the authors.

Second, on the experimental side, in contrast to Belluscio and colleagues, Scheffer-Teixeira and Tort hardly found any trace of PPC in hippocampal traces when using appropriate surrogates, despite having tested a large variety of data sets and analysis techniques. In at least one data set weak yet significant coupling between theta and gamma phases was encountered, but the authors suggested that the modulation was too weak to play any role in cognition. The authors conclude that participation of theta-gamma coupling to neural coding is restricted. However it should be noted that the experimental measure probably underestimates the actual coupling strength, because of measurement noise, and since LFP is a very indirect measure of population activity. Theta-gamma coupling may be important only at some specific times, and the long recording epoch could have washed out this coupling by averaging with periods of lower coupling. Moreover, there is to my knowledge no computational study that shows the level of phase coupling required to achieve a significant role in brain function. Besides, the very low P values (as low as 10⁻¹²) as found in the phase-phase plots of the original hippocampal data by Belluscio and colleagues would likely survive the correction for multiple comparison proposed by Scheffer-Teixeira and Tort. Thus theta-gamma phase coupling appears as a robust (yet possibly weak) property of hippocampus. Whether it is strong enough to significantly influence neural coding remains under discussion. This debate calls for a step forward in the convergence of modeling and experimental approaches in neurophysiology, where models of neural phase coupling should be evaluated not only on their qualitative but also on their quantitative similarity with empirical data (in this case level of CFC coupling).

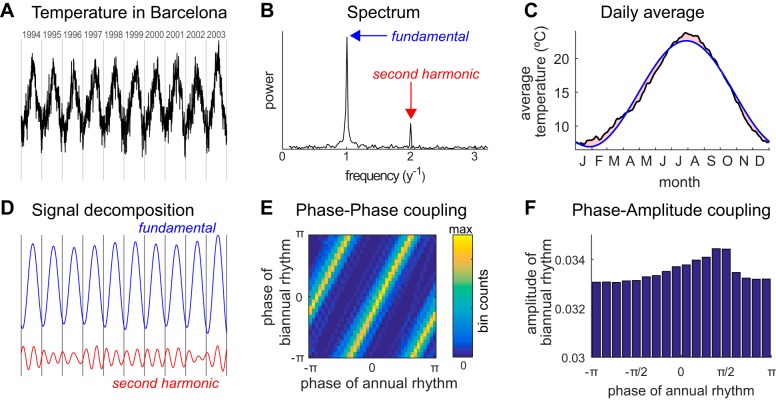
Third, and fundamentally, the authors stress a severe conceptual flaw in the way that PPC is evaluated empirically. Current measures, even when appropriate surrogates are applied, will test positive for PPC whenever the slow oscillation is nonsinusoidal (and even in the absence of high oscillations). The point is illustrated on the daily temperature time series from the city of Barcelona (Fig. 1A). Temperatures are subject to yearly fluctuations due to Earth revolution, visible in the time series spectrum (the strong peak at 1 yr⁻¹) and daily average over years (Fig. 1, B and C). This oscillation is not purely sinusoidal, as evidenced by a secondary peak in the spectrum at 2 yr⁻¹; this second harmonics is visible in the difference between the daily averages and a pure sinusoidal fit (red area in Fig. 1C). This secondary peak should of course not be interpreted as an independent 6-mo oscillation in surface temperature of the Earth. Yet if the signal is decomposed into a yearly and a biyearly rhythm (Fig. 1D), as would be done using standard CFC techniques, we notice a consistent phase relationship between the two rhythms, which is exactly what the PPC measure tests for. Indeed, Fourier analysis specifies that any periodic variable can be decomposed into harmonics which hold a constant phase relationship. Building phase-phase plane between the two decomposed rhythms (Fig. 1D) misleads us into concluding that there is very strong 2:1 phase coupling between an annual and a biannual rhythm in Earth temperatures. A similar analysis shows phase-amplitude coupling is also present between the two same rhythms (Fig. 1). In other words, PPC in this case measures coupling between the harmonics of a unique (nonsinusoidal) signal, not between distinct oscillatory processes. This is very problematic since prominent neural oscillations including hippocampal theta (Buzsaki et al. 1985; Belluscio et al. 2012) and visual alpha (Mazaheri and Jensen 2008) are nonsinusoidal. Indeed, in nonlinear systems such as the brain is, nonsinusoidality is the rule rather than the exception. So, in presence of positive PPC measures, nonsinusoidality of the slower oscillation provides a more parsimonious account than genuine CFC.

Fig. 1.

Cross-frequency coupling in daily Barcelona temperature time series. A: daily temperature in Barcelona Fabra Observatory (Spain) in period 1994–2003. Vertical lines mark change of year. B: spectrum on entire time series (1913–2014) shows large peak at 1 yr⁻¹ (i.e., one cycle per year) corresponding to fundamental frequency of annual temperature fluctuations, and a weaker peak at 2 yr⁻¹ (two cycles per year), corresponding to the second harmonic of the annual rhythm. C: average temperature per day of the year (black line) is compared with sinusoidal fit (blue line). The difference (light red) marks the nonsinusoidality of the signal, dominated by the second harmonic. D: corresponding annual (blue line) and biannual (red line) rhythms obtained by filtering of original times series (Kaiser filter applied on 0.8–1.2 yr⁻¹ and 1.6–2.4 yr⁻¹, respectively), as would be performed on neural recordings. E: phase-phase plot showing the very strong coupling between phase of the filtered annual and biannual rhythms (check the consistent phase of the filtered biannual rhythm at each change of year in D). Color denotes the number of days in time series falling in the phase-phase 2D bin. F: phase-amplitude coupling between filtered annual and biannual rhythms. The phase of annual rhythm modulates the amplitude of biannual rhythm weakly but reliably (P = 10⁻³, modulation index computed according to Tort et al. 2010).

The same caveat also holds for phase-amplitude coupling, as was recognized as early as 2008 (Kramer et al. 2008). However, this and further warnings (Aru et al. 2015; Hyafil 2015; Lozano-Soldevilla et al. 2016) have been widely ignored by many experimentalists, with whom CFC tests have become recently very popular. As illustrated above, the issue lies in that current methods decompose neural signal into separate frequency bands before testing for a link between these bands, regardless of whether the distinct bands actually depend on separate generative mechanisms (as would be the case for genuine CFC). The corollary problem of identifying how the different rhythms are generated is a tough one. Ideally, it would be resolved by going down at the circuits level and identifying subcircuits responsible for each of the oscillations. In the case of hippocampal theta and gamma, in vitro recordings have nicely shown that theta predominate in longitudinal slices while gamma predominate in transverse slices (Gloveli et al. 2005). This demonstrates that hippocampal gamma is not (at least not always) reducible due to theta harmonics. When this approach is not affordable and one only has access to large-scale signals such as EEG or LFP, one could seek evidence that the two bands do not always coexist in time. For example, the presence of the higher band at times when the lower band is absent would be a strong indication for separable sources, and thus, possibly, for genuine CFC. Note that detecting PPC between distant signals in the brain does not ensure that the two bands are independent, even when conduction effects are accounted for. An alternative explanation would be phase coupling between two oscillations of the same frequency in the two signals, one of them being nonsinusoidal; this would transitively induce cross-frequency phase coupling between the fundamental frequency in one signal and the harmonics of the other signal.

A more systematic and grounded approach could use comparison between (stochastic) generative models of time series. One class of model would include a single nonlinear oscillatory generation process (for example nonlinear autoregressive model) that generates nonsinusoidal periodic signal, while the other would include separate coupled generative dynamics. Bayesian techniques could in principle distinguish these different accounts of CFC (independent coupled signals vs. nonsinusoidal signal) based on likelihood scores. Moreover, such a modeling approach allows to represent neural signals in terms of minimal dynamical systems that can later be compared with physiological models: this approach would provide a leap forward in the convergence of microscopic and macroscopic neurophysiology.

Coincidentally, a new method for detecting CFC in multivariate data, published a couple of weeks following the paper by Scheffer-Teixeira and Tort, again in eLife, provides a first important step in this direction. The technique, termed generalized eigendecomposition cross-frequency coupling (gedCFC), precisely uses a modeling approach by dimensionality reduction (Cohen 2017). The method gains traction by looking at spatial and spectral decompositions of the signal that maximize CFC between decomposed signals. It is not clear, however, how the nonsinusoidality caveat should be avoided since it does not account for nonlinear oscillatory generation. A future extension of the method that also detect cross-frequency phase coupling would constitute a very valuable asset for the experimentalist.

In summary, the new and compelling cry by Scheffer-Teixeira and Tort should call experimentalists to adopt a more cautious stance toward evidence for CFC and invite theoreticians to devise better-grounded methods to separate the CFC wheat from the nonsinusoidal chaff. Testing the hypotheses regarding how brain oscillations shape neural coding will inevitably require convergence of the quantitative descriptive models from single neuron physiology to macroscopic neural signals.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.H. analyzed data; interpreted results of experiments; prepared figures; drafted manuscript; edited and revised manuscript; approved final version of manuscript.