Afferent motor feedback determines the perceived location of tactile stimuli in the external space presented to the moving arm

We show that proprioceptive feedback of arm motion rather than efferent motor signals contributes to tactile localization during an arm movement. Data further show that localization errors depend on arm velocity, not displacement per se, suggesting that instantaneous velocity feedback plays a role in the underlying computations. Model simulation using Bayesian inference suggests that these errors depend not only on spatial but also on temporal uncertainties of sensory and motor signals.

Abstract

People make systematic errors when localizing a brief tactile stimulus in the external space presented on the index finger while moving the arm. Although these errors likely arise in the spatiotemporal integration of the tactile input and information about arm position, the underlying arm position information used in this process is not known. In this study, we tested the contributions of afferent proprioceptive feedback and predictive arm position signals by comparing localization errors during passive vs. active arm movements. In the active trials, participants were instructed to localize a tactile stimulus in the external space that was presented to the index finger near the time of a self-generated arm movement. In the passive trials, each of the active trials was passively replayed in randomized order, using a robotic device. Our results provide evidence that the localization error patterns of the passive trials are similar to the active trials and, moreover, did not lag but rather led the active trials, which suggests that proprioceptive feedback makes an important contribution to tactile localization. To further test which kinematic property of this afferent feedback signal drives the underlying computations, we examined the localization errors with movements that had differently skewed velocity profiles but overall the same displacement. This revealed a difference in the localization patterns, which we explain by a probabilistic model in which temporal uncertainty about the stimulus is converted into a spatial likelihood, depending on the actual velocity of the arm rather than involving an efferent, preprogrammed movement.

NEW & NOTEWORTHY We show that proprioceptive feedback of arm motion rather than efferent motor signals contributes to tactile localization during an arm movement. Data further show that localization errors depend on arm velocity, not displacement per se, suggesting that instantaneous velocity feedback plays a role in the underlying computations. Model simulation using Bayesian inference suggests that these errors depend not only on spatial but also on temporal uncertainties of sensory and motor signals.

action influences perception. For example, a brief stimulus presented near the time of an eye or arm movement is systematically mislocalized in space, such as a visual flash near the time of a saccade (Richard et al. 2009; Ross et al. 1997; Schlag and Schlag-Rey 2002) or a haptic stimulus near the time of an arm movement (Dassonville 1995; Maij et al. 2013; Watanabe et al. 2009). The localization error depends systematically on when the stimulus is presented during the movement; the errors are in the direction of the movement at the beginning of the movement and in the opposite direction at the end of the movement (e.g., Dassonville 1995; O’Regan 1984; Watanabe et al. 2009).

Computationally, to determine the location of a stimulus requires that its location on the sensory surface is combined with position of the sensory surface at the time of the stimulus (Pola 2007; Ross et al. 2001; Schlag and Schlag-Rey 2002). Errors could simply arise because this integration process operates with delayed and time-varying signals due to the movement (Dassonville 1995; Maij et al. 2011; Pola 2007; Ross et al. 2001; Schlag and Schlag-Rey 2002; Teichert et al. 2010).

Maij and colleagues (Maij et al. 2011, 2013) recently modeled this interaction between perception and action using Bayesian inference. In their model, the temporal uncertainty in the processing of the stimulus is converted into a spatial likelihood of where this stimulus was given during the movement, a conversion that involves a Jacobian transformation that depends on the kinematics of the movement. The model (Maij et al. 2011), derived to explain perisaccadic mislocalization, could also account for tactile mislocalization during arm movements, including the different error patterns between slow and fast arm movements (Maij et al. 2013).

Although the model includes movement kinematics in its computations (e.g., movement amplitude and duration), it is unclear whether this signal is based on an efferent motor command or derived from afferent feedback. By design the model rules out the use of an impending displacement signal (Sommer and Wurtz 2004a, 2004b, 2006) because it can make different predictions for the same displacement, depending on the velocity. This leaves open the possibility of using a corollary discharge signal that encodes the instantaneous position (Guthrie et al. 1983) vs. using a dynamic sensory feedback signal about the position (Vliegen et al. 2005).

The first objective of this study was to distinguish the contributions of efferent motor signals and afferent proprioceptive feedback by comparing tactile localization errors during self-generated, active movements vs. robot-imposed, passive arm movements. Because of sensory processing times, afferent proprioceptive feedback is inherently delayed (by ~50–100 ms; see Bourguignon et al. 2015) compared with internally generated feedback based on instantaneous efferent motor signals. These efferent motor signals are present only during self-generated movements. Therefore, if efferent motor commands are involved in tactile localization, the mislocalization pattern during passive movements could be expected to lag in time compared with active movements. If localization patterns of active and passive movements overlap, it could be inferred that afferent signals primarily shape the localization error patterns.

The results reported below support the hypothesis that afferent feedback signals determine the localization errors. Because the arm movements and hence, the afferent feedback signals can be precisely controlled using passive movements, a further question is, which of the arm movement’s characteristics are central to the localization errors? The temporal uncertainty model of (Maij et al. 2013) operates with feedback about instantaneous velocity, but whether the brain has direct access to this signal or only to a filtered, approximated form is not known. Recently, we reported localization differences between slow and fast movements, but these results cannot answer whether differences in the instantaneous or mean velocity caused the effects. Therefore, the second objective of this study was to examine the localization errors during passive movements with the same overall displacement and the same mean velocity but with differently skewed velocity profiles and thus different instantaneous velocity kinematics.

METHODS

Six participants gave informed, written consent to take part in the experiment. All participants (2 women, 4 men, 24–32 yr old, all right-handed) had normal or corrected-to-normal vision and were free of any sensory, perceptual, or motor disorders. The study was part of a research protocol that was approved by the ethics committee of the Social Sciences Faculty of the Radboud University Nijmegen.

Setup.

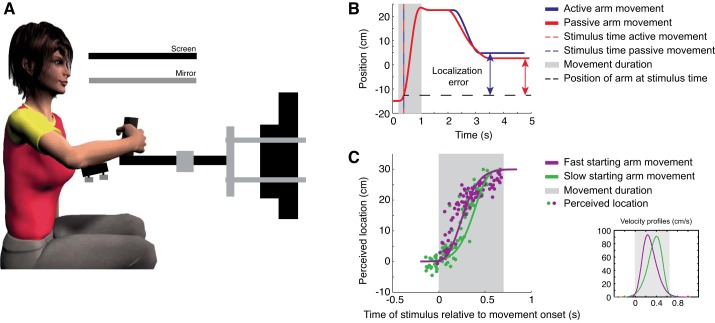
Participants were instructed to hold the handle of a planar robotic manipulandum (Howard et al. 2009) with their right hand in a power grip (thumb up and palm of the hand around the handle) throughout the whole experiment (sampling frequency of 1,000 Hz; see Fig. 1A). The forearm was supported in the horizontal plane by an air sled (custom built, based on the air sled designed in Howard et al. 2009). An electrode connected to an electrical stimulus device (DS7A; Digitimer) was attached to the participant’s right index finger, which produced a tactile stimulus with a duration of 500 µs (square wave) that was just above threshold but well perceived by the participant (4.5–7.3 mA). Participants were tested in two experiments, which were performed in random order, counterbalanced across participants. Prior to each experiment, participants were familiarized with the task by practicing several trials.

Fig. 1.

A: schematic overview of the setup. Participants performed active and passive arm movements. A custom-built air sled supported the forearm to reduce muscle activity to hold the handle of the robot arm. B: single trial representation in the active (blue) and passive (red) condition. Dashed red and blue line indicates the time of the stimulus and the black dashed line the location of the hand at the time of the stimulus. Double arrows indicate the localization error. Movement duration is shown in gray. C: perceived locations (dots) along the trajectory of a single participant in the 2nd experiment. Solid lines represent the trajectories over time. Movement duration is shown in gray. The different velocity profiles are shown at bottom right corner.

Experiment 1: active vs. passive movements (procedure).

Prior to each trial, the participant was instructed to close his or her eyes. An active trial began with the robot moving the right arm to its start position (15 cm to the left of the participant’s midline, ~30 cm from the body). After 500 ms at the start position, a beep instructed the participant to actively generate a fast arm movement of ~30 cm displacement in a left to right direction (so-called movement phase). The movement trajectory was confined to a simulated mechanical channel with a spring constant of 3 kN/m, allowing the hand to move freely in the left to right direction.

Before, during or after the arm movement, a tactile stimulus was presented to the index finger of the participant (randomly drawn from a uniform distribution defined over 1.2 s). After the movement, i.e., 1.5 s after the first beep, another auditory cue instructed the participant to move their right arm within 3 s to the position along the movement path where he or she perceived the tactile stimulus. In a small number of cases when the participant failed to perceive the stimulus, the participant was instructed to move the handle to the right of the end position of the hand to a location where the hand never was during the trial (see data analyses for the percentage of discarded trials). Then, the next trial started.

After the participant had performed a block of 50 active trials, a block of 50 passive trials started. Passive trials were identical to active trials (same trajectory and time of the stimulus for each passive trial), except that the robot displaced the arm during the movement phase, whereas the participant kept the arm relaxed. The movement was confined to a simulated point attractor moving along the trajectory of one of the randomly drawn previous active trials with a spring constant of 3 kN/m. Each of the 50 active trials in the preceding block was passively replayed in randomized order. This procedure was repeated three times, such that participants performed 150 active and 150 passive trials in total. Figure 1B demonstrates a single trial of both trial types.

Experiment 2: passive movements with skewed velocity profiles.

Participants performed passive trials as in experiment 1, the only difference being that one of two differently skewed velocity profiles was imposed (see Fig. 1C). Velocity profiles were based on a Weibull function, whose skewness can be modulated by changing two parameters (its shape and scale parameter). Movement duration was set to 0.65 s, with a velocity that peaked either at 0.39 s (slow-starting trials) or at 0.26 s (fast-starting trials) from movement onset (see Fig. 1C). The time at which the tactile stimuli was presented was drawn from a uniform distribution of 0.9 s. Each velocity profile was tested 100 times.

Data analyses.

Data were analyzed with MATLAB software. The localization error was defined as the recorded position of the fingertip at the perceived stimulus location relative to the actual location of the fingertip when the stimulus was presented. Positive values indicate a localization bias in the direction of the arm movement. Localization errors are shown as a function of time of the stimulus relative to the onset of the movement. Start and end of the movement were determined using a velocity threshold of 5 cm/s. We constructed a localization curve through the data points using a moving Gaussian average with a width of 100 ms.

We discarded trials in which the participant did not perceive the stimulus (8.6 ± 6.2% of the trials in experiment 1 and 5.8 ± 5.4% of the trials in experiment 2; means ± SD) or when the absolute localization error was >20 cm (1.8 ± 1.4% of the trials in experiment 1 and 0.8 ± 0.3% of the trials in experiment 2; means ± SD). In total we analyzed 88.4 ± 8.2% of the active trials and 88.7 ± 4.7% of the passive trials in experiment 1 and 95.9 ± 2.5% of the slow-starting trials and 94.1 ± 5.0% of the fast-starting trials in experiment 2.

We determined the temporal shift between the passive and active localization curve as follows. To do so, we shifted the passive localization curve in time (−150 to 150 ms in steps of 1 ms) and calculated the squared localization error differences with an overall constructed localization curve (using the same moving Gaussian average; calculated from all data points of both conditions) for each time shift. We defined the temporal shift between the two conditions for each participant by minimizing the summed squared error differences with this overall constructed curve (Maij et al. 2009).

Model predictions.

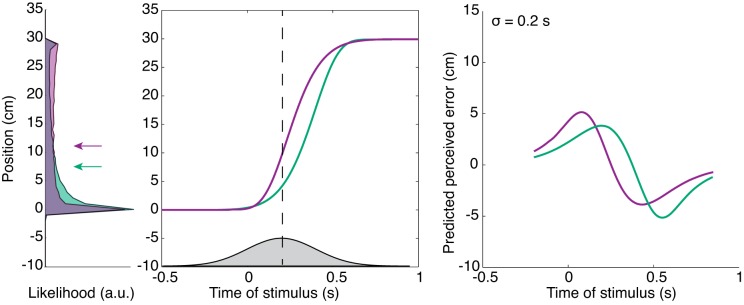
We use a probabilistic approach to explain the results for the skewed velocity profile experiment by means of the temporal uncertainty model for tactile stimuli during arm movements (Maij et al. 2013). In short, in this model we assume that participants are uncertain about the time of the stimulus with respect to the arm movement. This temporal uncertainty is represented by a Gaussian distribution described by sigma (σ) and a delay parameter (d; a mismatch in the perceived time of the stimulus with respect to the time of the arm movement). A positive value for d indicates that the participant’s internal estimate of arm position is d ms ahead of its actual position at the time of the stimulus; a negative value for d indicates that the participant’s internal representation of arm position lags its actual position at the time of the stimulus. By combining a Gaussian distribution (gray Gaussian at t = 0.2 s with σ = 200 ms and d = 0 ms) at the time of the stimulus with the actual arm movement (Fig. 2, purple or green line), we obtain a likelihood of where the stimulus was in space (see distributions in Fig. 2, left). As a result, changing the velocity of the arm during the movement affects the predicted perceived location. Note that this likelihood is not distributed normally, because the arm movement profile is not a normal distribution. We consider the mean of the likelihood to represent the predicted perceived location of the stimulus (see, for example, the green arrow in Fig. 2, left, which represents the mean of the green area denoting likelihood distribution). Note the differences between the arrows for the two different movement profiles for the same time of the stimulus and time relative to movement onset. With this model, we can simulate a localization curve from the predicted perceived locations at all stimulus times relative to the arm movement (see Fig. 2, right).

Fig. 2.

Model predictions of the localization errors for 2 different velocity profiles. Left: gray distribution represents temporal uncertainty (σ = 200 ms) about the tactile stimulus presented at 0.2 s (vertical dashed line) relative to movement onset; note that here we use a delay parameter of 0 ms. Combining this distribution with 2 different arm movement profiles (purple and green lines) results in 2 different likelihoods. The mean of the likelihood (indicated by both the purple and green arrows) represents the predicted perceived error for that time sample. Each time sample provides different likelihoods with corresponding means and results in a predicted localization error pattern for both conditions (as shown at right). Right: 2 predicted localization curves for the fast- and slow-starting movements, using the same parameters as those at left. Note the differences between the 2 localization curves.

As shown, for the condition in which the arm movement velocity is high in the beginning of the movement, the peak of the estimated localization curve is closer to movement onset compared with the estimated localization curve for the condition with a high velocity at the end of the movement. We used a fitting procedure to minimize the squared error between the measured and predicted localization error for all data points.

RESULTS

Experiment 1: active vs. passive arm movements.

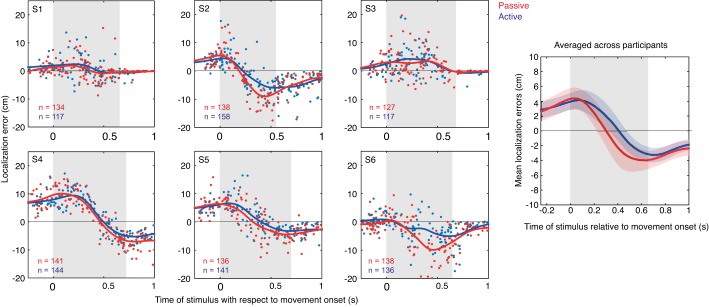
The localization errors for the active and passive trials are shown separately for each participant in Fig. 3. Although the localization curves vary substantially across participants, within participants the localization curves for the passive and active trials are very similar (Fig. 3). For example, compare S2 and S4. S4 shows a clear rise of the errors in the direction of the arm movement and then a clear decrease into the opposite direction of the arm movement, whereas S2 demonstrates not much of an increase at movement onset and then a large decrease in the opposite direction near the end of the movement. Both participants, however, show a close overlap of the localization curves for passive and active trials.

Fig. 3.

Left: localization errors in the passive (red dots) and active (blue dots) trials for each participant. Gray shaded area represents the arm movement duration. Solid line represents a moving Gaussian window (σ = 100 ms). Right: mean localization curves across all participants for both passive and active trials.

We hypothesized that if an efference copy signal were involved in the processing of the perceived localization, we would find a negative temporal shift (active precedes passive location errors). We calculated the temporal shift between the two localization curves for each participant (see methods for more details), and instead of a negative shift we found that the shift was on average +47 ± 15 ms (means ± SD; see Table 1). Statistically, this value corresponds to a significantly positive difference from 0 (t-test, P < 0.05). This clearly shows that we did not find a lag of the passive localization errors but rather a lead, which suggests that the efference copy alone is not causing the localization errors.

Table 1.

Temporal shift between the passive and active localization errors and the difference in peak-to-peak amplitudes of the localization curves

	S1	S2	S3	S4	S5	S6
Temporal shift, ms	66	58	−13	47	81	53
ΔPeak to peak, cm	−0.31	4.06	−1.07	2.43	1.05	4.47

To further investigate this, we also tested whether there are differences between the passive and active trials for the variability and the amplitude of the localization errors. The averaged variability of the localization errors relative to the mean localization curves for the passive vs. the active condition is not significantly higher for all participants (P = 0.30). This shows that errors in the passive trials are not more variable than those of the active trials. Moreover, we tested the difference between the peak-to-peak amplitude between the curves for the two conditions, which was small on average 1.8 ± 0.9 cm (means ± SD; Table 1) and not significantly different from zero (t-test, P = 0.11). The absence of these significant differences is a further argument against the importance of an efference copy signal in deriving the location of tactile stimulus presented to a moving arm.

Experiment 2: passive movements with skewed velocity profiles.

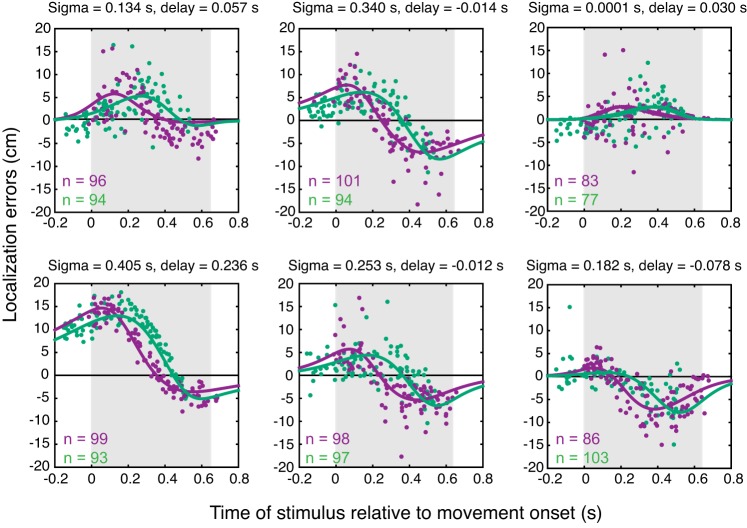
If the central nervous system (CNS) estimates the perceived location based on the instantaneous velocity signal, then two skewed velocity profiles should yield different localization patterns. In a second experiment, we investigated the localization errors for passively performed arm movements using two different skewed velocity profiles. Figure 4 depicts the results of each individual participant, showing clear differences in the localization errors between the fast- and slow-starting trials. We fit our model (see methods) to the data by minimizing the squared difference using only two free parameters for each participant (sigma and delay) independent of velocity condition. The model explains the distinction between the slow- and fast-starting trials quite well (see lines in Fig. 4). Despite the clear idiosyncratic differences in the localization patterns, the fits (shown in Fig. 4) provide a good match to the localization errors for each participant (r² values for the 6 participants: 0.42, 0.73, 0.15, 0.92, 0.52, 0.53). These differences between fast- and slow-starting trials suggest that an instantaneous velocity signal is used in the spatial computations and not a filtered version of such a signal.

Fig. 4.

Localization errors in the 2 skewed velocity conditions plotted separately for each participant. Purple dots, fast-starting trials; green dots, slow-starting trials. Solid lines represent the model fits, with the values of the 2 fitted parameters (sigma and delay) presented above each graph.

DISCUSSION

We report two major findings regarding haptic mislocalization during passively induced and actively generated arm movements. First, the error pattern, specified as a localization curve, did not show a time lag but rather a time lead for the passive compared with the active arm movements. Errors did also not differ in amplitude and variability between passive and active movements. The absence of a time lag suggests that proprioceptive feedback, and not the efferent motor command, dominates in the computations of tactile localization. Second, the localization errors were found to depend critically on the instantaneous arm velocity, which suggests that instantaneous proprioceptive feedback, rather than some averaged, filtered form of this signal is used in tactile localization. This confirmed the predictions of our temporal uncertainty model, operating with instantaneous velocity signals, which nicely resembled the observed localization curves (see Fig. 4). In the following, we will discuss these two findings in more detail.

We expected the passive localization curves to be lagging the active localization curves, given that sensory feedback is delayed compared with internal feedback based on the motor outflow during active conditions. But in fact, contrary to this expectation, we found the opposite, that localization curves of active trials lag the passive trials. Barnett-Cowan and Harris (2011) found similar positive time differences in the perceived onset of active vs. passive head movements. More specifically, they asked whether the presence of efference copy sped up the detection of an active head movement compared with a passive head movement or whether the efference copy caused a suppression of vestibular signals, thereby slowing down the perceived timing. They found evidence for the latter, with the active head movement detected ~35 ms later compared with a corresponding passive movement. In a similar way, Williams et al. (1998) reported sensory suppression of cutaneous stimuli presented to a moving finger or arm, detecting it several tens of milliseconds later compared with a stimulus detected on a stationary body part. Vitello et al. (2006) also found tactile suppression during active compared with passive arm movements. Based on these observations, if the onset of an active arm movement is perceived later than the onset of a passive arm movement due to suppression of the sensory feedback, then the perceived time of the tactile stimulus relative to the perceived movement may also be shifted in time. This could explain why localization curves of the active movement lag the passive curve. One could argue that if sensory suppression explains the lag of the active compared with the passive trials, there should relatively be more active trials in which the stimulus is not perceived than passive trials. However, this was not the case (active trials: 5.7 ± 2.2% vs. passive trials: 4.1 ± 0.8%, means ± SD, P = 0.35), suggesting that stimuli mostly did exceed perceptual threshold but that the perceived time of the tactile stimulus relative to the perceived movement differed between active and passive.

The observation of a positive temporal shift suggests that afferent signals about arm position are primarily causing the localization errors. Muscle spindles (type Ia and II afferents) are generally seen as the major contributors to proprioception (Goodwin et al. 1972). They will play a role in both passive and active arm movements. Golgi tendon organs (type Ib afferents) are sensitive to muscle tension, typically responding when muscles actively contract (for review, see Moore 1984). They are thus relatively insensitive to passive contraction. If localization errors relate to limb estimation (in terms of uncertainty), then we would have expected lower variability in the active condition, when muscle spindles, golgi tendon organs, and efference copy could all provide limb position information. Some studies have indeed reported that efferent signals allow for better limb position estimates (Fuentes and Bastian 2010; Monaco et al. 2010), but others have argued that active proprioception (such as in the active trials) and passive proprioception (such as in the passive trials) provide similar estimates of limb position (Capaday et al. 2013). In the present study, the variability of the localization errors is not different between the active and passive condition, which suggests that afferent signals, likely from muscle spindles, dominate in the localization mechanism. In this respect, our results are consistent with the notion that active and passive proprioception provide similar limb position estimates.

Whereas the results of the first experiment showed the involvement of the afferent signals, the findings of the second experiment revealed which of its characteristics are central to the localization errors. We found a clear difference between the localization patterns observed during the two different velocity profiles, suggesting that the CNS uses the instantaneous velocity signal to judge the location of a stimulus relative to movement onset. This conclusion is in line with the finding of Vliegen et al. (2005), who studied double-step saccades during eye-head gaze control. They propose, based on the findings of Jay and Sparks (1984) (eye position, and not eye displacement, is used for auditory localization during saccades), that the updating of visual target locations across eye and head motion relies on instantaneous kinematic signals rather than on relative displacements. Here, we show that this also holds for localization of tactile targets while making arm movements. For completeness, note that this reliance on instantaneous velocity signals appears in the model as an inversed relation of the signal (see methods and Maij et al. 2013).

Finally, it should be noted that the systematic mislocalization errors that we describe here are different from the systematic errors that participants make when reaching to remembered visual targets presented to relatively stationary eyes (Baud-Bovy and Viviani 1998; Beurze et al. 2006; Soechting and Flanders 1989). Here, the errors arise because the receptor surface is in motion, or close to be moved, and depend strongly on when the stimulus is presented with respect to the motion dynamics.

Our results contribute to a body of work showing that stimuli, whether visual, tactile, or auditory, are erroneously localized in space when presented during an eye or arm movement (Dassonville 1995; Klingenhoefer and Bremmer, 2009; Krügeret al. 2016; Lappe et al. 2000; e.g., Maij et al. 2009, 2011; Mateeff 1978; Matin and Pearce 1965; Rosset al. 1997; Watanabe et al. 2009). This may be taken to suggest that there is some general principle by which the brain combines sensory and motor information in such conditions. Our model proposes a description of this unified principle at the computational level, in which not only spatial but also temporal uncertainties of sensory and motor signals affect the outcome of an optimal integration process.

GRANTS

This research was supported by the Netherlands Organization for Scientific Research (NWO, Rubicon Grant 446-10-015 and Veni Grant 451-12-009 to F. Maij), the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2012)/ERC Grant agreement no. 283567), the Netherlands Organization for Scientific Research (NWO, VICI Grant 400-07-003 to W. P. Medendorp), and the Engineering and Physical Sciences Research Council UK (EP/I031030/1 to A. M. Wing).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

F.M. performed experiments; F.M. analyzed data; F.M., A.M.W., and W.P.M. interpreted results of experiments; F.M. prepared figures; F.M. drafted manuscript; F.M., A.M.W., and W.P.M. edited and revised manuscript; F.M., A.M.W., and W.P.M. approved final version of manuscript.