Abstract
An increasing number of studies have documented phenotypic selection on life-history traits in human populations, but less is known of the heritability and genetic constraints that mediate the response to selection on life-history traits in humans. We collected pedigree data for four generations of preindustrial (1745–1900) Finns who lived in premodern fertility and mortality conditions, and by using a restricted maximum-likelihood animal-model framework, we estimated the heritability of and genetic correlations between a suite of life-history traits and two alternative measures of fitness. First, we demonstrate high heritability of key life-history traits (fecundity, interbirth interval, age at last reproduction, and adult longevity) and measures of fitness (individual λ and lifetime reproductive success) for females but not for males. This sex difference may have arisen because most of the measured traits are under physiological control of the female, such that a male's fitness in monogamous societies may depend mainly on the reproductive quality of his spouse. We found strong positive genetic correlations between female age at first reproduction and longevity, and between interbirth intervals and longevity, suggesting reduced life spans in females who either started to breed relatively early or who then bred frequently. Our results suggest that key female life-history traits in this premodern human population had high heritability and may have responded to natural selection. However genetic constraints between longevity and reproductive life-history traits may have constrained the evolution of life history and facilitated the maintenance of additive genetic variance in key life-history traits.
Keywords: genetic correlation, Homo sapiens, animal model, natural selection, tradeoff
The cultural and biological factors that determine human life-history evolution are of interest to scientists from several different fields of science. Evolutionary biologists and anthropologists are interested in revealing the importance of different life-history traits in affecting fitness and longevity and whether these traits are under natural selection. Many studies have reported phenotypic correlations between different life-history traits, longevity, and measures of fitness in humans, but the nature of such associations is often contradictory. For example, although some studies have shown negative effects of high total reproductive effort on postreproductive longevity (1–3), most studies have found no association, or even positive correlations, between total reproductive effort and longevity (4–10). Likewise, some studies have shown a negative relationship between age at first reproduction (AFR) and postreproductive mortality (1, 11), whereas others found no evidence for such an association (6, 12, 13). In a historical northern Finnish population, the most important component of female fitness (i.e., the phenotypic trait with the highest selection differential) was the number of delivered offspring, but women also gained higher fitness (larger total number of offspring raised to adulthood over lifetime) if they began reproducing earlier, had shorter interbirth intervals, and continued reproducing later (10). Phenotypic covariation between female life-history traits indicated that interbirth intervals were independent both of ages at first and last reproduction, whereas women who started to reproduce early also ceased reproduction young (10). Last, Strassmann and Gillespie (14) showed evidence for a nonlinear relationship between female fecundity and reproductive success in Dogon farmers of Mali because child mortality, rather than fecundity, was the primary determinant of female fitness in this population.
From an evolutionary point of view, these correlations are particularly interesting if they have a genetic basis, because natural selection can lead to an evolutionary response only when it acts on a heritable character. However, estimating the heritability of human life-history traits is problematic, because the effects of common environments shared by close relatives and cultural transmission can inflate estimates of heritability. Twin studies, in which identical twins are raised in different environments, are ideal for investigating such issues, but these kinds of data for humans are scarce. Consequently, little is known about whether the documented phenotypic selection on human life-history traits could lead to changes over time because of the lack of information on the heritability and genetic constraints of reproductive traits in natural-state human populations (15).
An alternative approach to twin studies, which we adopt here, is to use a methodology that controls for common environment effects as much as possible and considers the similarity between pairs of individuals of various degrees of relatedness, for which shared environment may not be such a problem (16). In this study, we applied restricted maximum-likelihood (REML) estimation and an “animal model” to estimate heritabilities and genetic correlations between female and male life-history traits. The advantage of this technique compared with more traditionally used parent–offspring and sibling regression analyses is that it simultaneously incorporates information from a variety of relationships of different degrees, such as offspring, parents, grandparents, full-siblings, and half-siblings, which makes it a more powerful method than the traditional approaches (17, 18). REML analyses also have less strict assumptions about selection patterns or inbreeding and do not require balanced data sets, which makes them considerably more amenable to data from natural populations (17, 18).
In this article, our aims were to (i) estimate the heritability of human life-history traits, (ii) examine genetic correlations between the life-history traits and different fitness measures, and (iii) compare the estimates obtained for male and female traits. We used pedigree data collected from genealogical records from preindustrial Finland. These records cover a historical era before the availability of advanced medical care or modern birth-control methods. We found that the key female life-history traits were highly heritable, allowing rapid evolutionary response to selection, but we also found considerable genetic constraints between reproductive traits and longevity.
Methods
Population Sample. We collected pedigrees of life-history data following four generations of preindustrial Finns by using a large genealogical database (Genealogia Sursilliana CD-2000 database, I. B. Voipio, personal communication) (19). Our data set includes 194 base individuals from the following four different parishes: Oulu, Kokkola, and Kaarlela in western Finland, and Kuusamo in eastern Finland. Base individuals (for whom parents were not known) were born in 1745–1765, and the data set includes all of their descendants to the great-grandchildren level as well as spouses of all married individuals, giving a total of 5,018 individuals with latest birth date of 1903. Complete individual life histories (birth, death, and all reproductive events) were recorded for three generations (a total of 1,894 individuals, of which 904 are female). Of the 904 females with complete life histories, 353 survived to adulthood and reproduction, and these females were included in the analyses. Of the 985 men, 361 survived to reproduction and, thus, were included in the analyses. Because the fate of some children was not known, sample size for lifetime reproductive success (measured as the number of children raised to adulthood, i.e., 15 years of age) is smaller than the sample size for fecundity. For the fourth generation, only lifespan (but not reproductive history) was recorded.
The data set includes known paternities for all individuals, based on the assumption that the male in a household was the genetic father of his wife's children. We expect incidences of extra-pair paternities to be relatively low in the study population, but even if extra-pair paternities had been common, this error should be conservative because, in that case, heritabilities would be underestimated. In the study period from 1745 to the late 19th century, industrialization had not yet begun in Finland, and fertility and mortality rates were high before the introduction of effective contraception or modern medical care (20). The genealogical database that was used to acquire these data includes a relatively high proportion of individuals from wealthier social classes (19). Even though wealthier people suffered from the same causes of child mortality as others and the differences between social classes in general were small in Finland compared with many other countries, child mortality in the wealthier social classes was slightly lower (21). Unfortunately, we have no knowledge of wealth or social class of each of the study families; this would have helped to explain further environmentally caused variation between the families. Because practically all Finns of that time practiced the Lutheran religion, differences caused by religion were absent (22).
Life-History Traits. For all of the studied life-history traits, except for adult lifespan, only individuals who reproduced at all (i.e., gave birth to at least one child) were included in the analyses. Historical data always includes incomplete records, which may introduce censoring bias. For example, records for women with many children are more likely to include a missing record for one child by chance and, thus, may be omitted from the analysis for reproductive success and fitness; in other words, the larger the family, the higher the likelihood that complete follow-up of the whole family will fail. Therefore, we calculated estimates of trait values both by using the highest possible number of individuals (pairwise omission of cases with missing values) and the minimum number of individuals (listwise omission of cases with missing values). We report both estimates in cases in which these estimates differ by >5%, and we use the highest possible number of individuals in all other analyses.
The studied measures of fitness and life-history traits were defined as follows.
Lifetime reproductive success (LRS). LRS was measured as the total number of children produced in a lifetime that survived to adolescence (here, to 15 years of age).
Individual λ (calculated according to the method of McGraw and Caswell, ref. 23). This measure considers at the same time both the timing of reproduction and the number of children raised to adulthood (15 years of age). LRS and λ may rank individuals differently according to their fitness, because children produced at early ages contribute more to the fitness than children produced at later ages. Rate-sensitive λ allows for more accurate estimation of individual fitness in humans, even though overall reproductive success explains >90% of the variation in λ (24). The value of λ was calculated with matlab software (Mathworks, Natick, MA) by using a program written by J.J. (available by request).
Fecundity. This trait was calculated as the number of children produced in a lifetime.
AFR. This trait was calculated as the age in years when a woman gave birth to her first child or a man fathered his first child.
Mean interbirth interval (MIBI). This trait was calculated as the average time in months between successive births. This trait was calculated only for women.
Offspring survival. Survival of children to adulthood was calculated as LRS/fecundity.
Age at last reproduction (ALR). This trait was defined as the age in years when a woman gave birth to her last child. Only individuals who survived at least to 45 years of age and were not widowed before then were included into the analyses to consider only women who were potentially reproducing. ALR was calculated only for females, because the ALR of men depends heavily on the age of the wife (25).
Adult longevity. Age in years at death of individuals that survived past 15 years of age (including nonreproducing individuals) was included in the analyses. Longevity was known for the fourth generation and for most of the spouses of individuals in the data set, so we were able to use a more extensive pedigree and have a larger sample size for analysis of the heritability of longevity than for the other life-history traits.
Table 1 gives a summary of the sample sizes and mean values for the studied life-history traits and measures of fitness (described above) in our study population.
Table 1. Data for all considered traits.
| Trait | Mean | SD | N | VA | VM | VR | h2 + SE | m + SE | CVA | CVM | CVR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Females | |||||||||||
| λ | 0.88 | 0.42 | 136 | 0.15 | 0.00 | 0.05 | 0.761 ± 0.246** | 0.000 ± 0.000 | 44.011 | 0.000 | 24.106 |
| Fecundity, all individuals | 5.76 | 3.56 | 353 | 3.82 | 0.89 | 7.79 | 0.306 ± 0.097** | 0.071 ± 0.059 | 33.932 | 16.378 | 48.456 |
| Fecundity, censored | 5.20 | 3.68 | 136 | 8.07 | 2.71 | 3.55 | 0.563 ± 0.206** | 0.189 ± 0.112 | 11.224 | 6.504 | 7.444 |
| LRS | 3.47 | 2.75 | 138 | 3.62 | 0.00 | 4.14 | 0.466 ± 0.198* | 0.000 ± 0.000 | 54.831 | 0.000 | 58.637 |
| AFR | 25.31 | 4.82 | 353 | 1.27 | 10.28 | 12.93 | 0.052 ± 0.102 | 0.420 ± 0.066*** | 4.453 | 12.668 | 14.207 |
| MIBI, all individuals | 34.09 | 25.65 | 292 | 176.41 | 0.00 | 468.67 | 0.287 ± 0.093** | 0.000 ± 0.000 | 38.961 | 0.000 | 63.505 |
| MIBI, censored | 30.20 | 19.68 | 96 | 84.354 | 0.000 | 318.176 | 0.210 ± 0.197 | 0.000 ± 0.000 | 36.288 | 0.000 | 70.476 |
| ALR | 40.02 | 5.93 | 179 | 14.36 | 0.00 | 19.55 | 0.424 ± 0.162** | 0.000 ± 0.000 | 9.470 | 0.000 | 11.049 |
| Adult lifespan | 61.31 | 20.10 | 1226 | 70.60 | 9.10 | 324.11 | 0.175 ± 0.054** | 0.023 ± 0.035 | 13.705 | 4.920 | 29.364 |
| Offspring survival | 0.69 | 0.31 | 138 | 0.00 | 0.00 | 0.09 | 0.000 ± 0.006 | 0.000 ± 0.000 | 0.000 | 0.000 | 43.959 |
| Males | |||||||||||
| λ | 0.90 | 0.35 | 125 | 0 | 0.062 | 0.069 | 0.000 ± 0.000 | 0.474 ± 0.125*** | 0.000 | 27.653 | 29.172 |
| Fecundity, all individuals | 5.68 | 3.30 | 361 | 0.247 | 1.037 | 9.544 | 0.023 ± 0.043 | 0.096 ± 0.062 | 8.743 | 17.915 | 54.349 |
| Fecundity, censored | 4.94 | 3.28 | 125 | 0.000 | 3.018 | 7.958 | 0.000 ± 0.000 | 0.275 ± 0.100** | 0.000 | 6.864 | 11.146 |
| LRS | 3.39 | 2.45 | 125 | 0.000 | 0.873 | 5.207 | 0.000 ± 0.000 | 0.144 ± 0.108 | 0.000 | 27.546 | 67.273 |
| AFR | 29.60 | 6.21 | 361 | 5.083 | 1.475 | 30.767 | 0.136 ± 0.102 | 0.144 ± 0.081 | 7.618 | 4.104 | 18.742 |
| Adult lifespan, all individuals | 56.80 | 18.86 | 1388 | 58.361 | 26.981 | 263.346 | 0.167 ± 0.047** | 0.077 ± 0.032* | 13.449 | 9.144 | 28.568 |
| Adult lifespan, censored | 55.52 | 19.78 | 125 | 0.000 | 234.866 | 200.918 | 0.000 ± 0.000 | 0.539 ± 0.114*** | 0.000 | 60.551 | 56.004 |
| Offspring survival | 0.72 | 0.3 | 125 | 0.000 | 0.000 | 0.088 | 0.000 ± 0.008 | 0.000 ± 0.000 | 0.000 | 0.000 | 41.168 |
Sample sizes are trait-specific because not all individuals in the data set have complete records. To assess the magnitude of censoring bias, we calculated two estimates for each trait. We primarily report estimates calculated by using all available individuals (pairwise omission of missing values). We also calculated censored estimates based on those individuals for which we had complete records for calculation of λ (listwise omission of missing values). We report the censored estimates if the difference in trait means was >5%. We also report censored estimates of heritability if they are not within the confidence intervals of estimate based on all available individuals. N, sample size; VA, additive genetic variance); VM, maternal-effect variance; VR, residual variance; h2, heritabilities; m, maternal effects; CVA, coefficient of additive genetic variances; CVM, coefficient of maternal effects; CVR, coefficient of residual variance. *, P < 0.05; **, P < 0.01.
Heritabilities and Coefficients of Variation. Variance components and heritability values were estimated by using a multivariate restricted maximum-likelihood mixed-model procedure (vce; ref. 26). The form of mixed model that we used here is known as an animal model in which a phenotype of each individual animal (here, a person) was broken down into its components of additive genetic value and other random and fixed effects as follows:
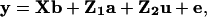 |
[1] |
where y is a vector of phenotypic values; b is a vector of fixed effects; a is a vector of random effects of the additive genetic merit (or breeding value) of each individual; u is a vector containing other random effects to be included in the model (discussed below); e is a vector of residual values; and X, Z1, and Z2 are design matrices relating a given phenotypic observation to its corresponding fixed or random effects (17). Design (or incidence) matrices are simply matrices of 0s and 1s that are constructed to link each phenotypic observation on an individual with the necessary fixed and random effects in the model. Their use is standard in linear models of many forms, for example, in mixed models such as the animal model used here (see ref. 17, p. 746). The variance–covariance structure for the additive genetic effects a is determined by the pedigree of the population, and the residual terms e are assumed to be normally distributed. Therefore, the model exploits the covariance between pairs of relatives of all types of relatedness, making optimal use of the data available in complex, multigenerational pedigrees (17). The software package vce (26) then estimates variance components for the random effects by using a restricted maximum-likelihood procedure. Although the traits used in this analysis showed some departure from a normal distribution, the restricted maximum-likelihood estimation procedure that is used is fairly robust to departures from normality; deviations may affect optimality properties, but estimates remain unbiased (17, 27).
One advantage of this technique is the possibility to fit fixed and random effects to explain environmental variation. For example, by including mother's identity as a random factor in our analyses, it is possible for us to model maternal effects in the form of covariance between offspring of the same mother, in addition to that due to genetic effects (refs. 17, pp. 767–774, and 18). Hence, for all traits maternal identity was fitted as a random effect, to prevent shared maternal environment being mistaken for shared genetic effects. Paternal identity was also fitted as a random effect, but because it did not explain a significance proportion of variation when maternal identity had been included in the model, and because in most of the cases siblings were full siblings sharing the same mother and father, we present here only estimates from models with maternal identity as a random effect. Birth parish of a base individual was fitted as a fixed effect for all of the traits to take into account differences in lifestyle and life history between parishes. Birth cohorts of 20 years were also fitted as a multilevel fixed effect for all traits to incorporate temporal variation across the study period. Birth order of individuals was also considered, but because it did not significantly explain any variation in any of the traits, it was left out from the final models. All analyses were performed separately for males and females.
Therefore, by using the animal model, we can partition the total phenotypic variance (VP) into the following three components:
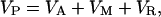 |
[2] |
where VA is the additive genetic variance, VM is the maternal effect variance, and VR is residual variance, which will include environmental effects not incorporated in the maternal effects, nonadditive genetic effects (dominance and epistatic), and error variance (16). The narrow-sense heritability (16) is defined as follows by the ratio of additive genetic variance to the total phenotypic variance: h2 = VA/VP. Maternal effects were quantified in a similar manner as follows: m = VM/VP. Significance of heritabilities and maternal effects were determined by t tests.
It is argued sometimes that heritabilities may not provide a good means of comparing genetic variation between traits or populations (17, 28), especially where levels of environmental variation differ between traits (29). Therefore, we also estimated the coefficient of additive genetic variance CVA, for which the variance component was scaled by the trait mean (X) rather than total variance: CVA = 100 × √VA/X. Coefficients of residual variance and maternal effects were calculated similarly.
Genetic Correlations Between Traits. Genetic correlations were estimated by specifying a multivariate version of the animal model (outlined explicitly in ref. 17, p. 775). For two traits, the genetic covariance between them is estimated from the comparison of phenotypic covariance in the traits expressed in relatives of differing degrees (i.e., Y in mother and X in daughter; and Y in father and X in brother, etc.), in exactly the same way as the genetic variance is estimated from the covariance between relatives in the same trait. Restricted maximum-likelihood analyses are not affected by unbalanced data sets (which is one of the reasons why they are so widely used), so the different sample sizes for different traits does not affect the analysis; the model simply uses information from all available relationships. The additive genetic correlations between traits were estimated with the same analysis package as described above.
Life-history traits are often correlated; for example, LRS and λ are composite measures, and AFR and longevity are their components. We calculated additive genetic correlations between traits that we considered to be biologically meaningful (i.e., excluding correlations between composite measures and their components: AFR–longevity, ALR–longevity, AFR–ALR, MIBI–longevity, AFR–MIBI, and ALR–MIBI).
Results
Heritabilities and Coefficients of Variance. Female traits. The heritability estimates (h2) for all of the measured traits of females were significantly different from zero, with the exception of AFR and child survival, indicating the existence of additive genetic variation in these traits (Table 1). The significant heritability estimates for the different life-history traits ranged from 0.18 for adult longevity to 0.42 for ALR. We also detected significant heritability for our estimates of lifetime fitness; LRS had a heritability of 0.47 and λ of 0.76. AFR was the only trait that had a significant maternal effect (m) of 0.46, indicating that although additive genetic variation in this trait was too small to be statistically significant, the maternal environment affected AFR. Values of coefficients of additive, maternal, and residual variances ranged from 4.45 for AFR to 54.83 for lifetime-reproductive success (Table 1). In general, coefficients of additive genetic variances corresponded with the heritabilities; traits having relatively large estimates of heritability showed also the largest estimates of CVA values. However, ALR had a high heritability (0.42) but a relatively low CVA value.
Comparison of the censored sample, including only individuals for whom it was possible to estimate fitness, to that of all individuals, suggests that fitness was underestimated because of censoring bias (Table 1). Individuals in the censored sample had lower average fecundity and shorter birth interval than individuals in the larger sample (Table 1). The heritability estimate for fecundity was higher for the censored sample, suggesting that estimates of heritability may be biased upwards in the censored data set. An estimate for ALR using the censored sample could not be calculated, because of problems in model convergence. However, the heritability estimates for fitness and lifetime reproductive success still remain high even if they include some censoring bias.
Male traits. In contrast to females, adult longevity was the only life-history trait of males that had significant heritable variation (Table 1). Male longevity had a small, but significant, estimate of maternal effect of 0.08, and λ had a significant estimate of maternal effect of 0.47. There was no detectable significant additive genetic variation in any of the other life-history traits and measures of fitness in males, and CVA values corresponded to the heritability values (Table 1).
Correlations Between Traits. We calculated additive genetic correlations only for female traits, because male traits (except for adult lifespan) did not have additive genetic variance, and thus, genetic correlations would not be meaningful. There was a significant positive genetic correlation between female AFR and longevity (Table 2). This correlation suggests a genetic tradeoff between reproducing at young age and longevity, indicating that senescence rate may be higher when starting reproduction early. The genetic correlation between mean-birth interval and longevity was significantly positive. Therefore, shorter interbirth intervals would also be associated with shorter lifespan, suggesting another genetic tradeoff. ALR was nearly significantly negatively correlated with mean birth intervals, possibly suggesting that long interbirth intervals are also associated with earlier age of finishing reproduction. These genetic correlations remained qualitatively similar when the analysis was restricted to censored sample (data not shown). Other additive genetic correlations between traits were insignificant (Table 2).
Table 2. Additive genetic correlations between life-history traits of women.
| Traits | Additive genetic correlation | SE | P |
|---|---|---|---|
| AFR-longevity | 0.997 | 0.199 | <0.001 |
| ALR-longevity | -0.301 | 0.301 | 0.32 |
| MIBI-longevity | 0.595 | 0.294 | 0.04 |
| AFR-ALR | -0.194 | 0.733 | 0.79 |
| AFR-MIBI | 0.537 | 0.741 | 0.47 |
| ALR-MIBI | -0.693 | 0.367 | 0.06 |
Bold values indicate significant genetic correlations between traits (P < 0.05).
Discussion
We found significant heritability of female life-history traits in a human population living under premodern conditions. The evolution of human life-history traits by natural selection has been a controversial topic because of the substantial cultural components in human life-history trait expression. Earlier studies have revealed phenotypic selection on key life-history traits (1–14), but studies rarely have been able to comment on the genetic basis of those traits (for exceptions, see refs. 15 and 30). Our results suggest that important human life-history traits contained significant additive genetic variation and, therefore, would have been able to evolve by natural selection. However, some of the key traits were also involved in genetic tradeoffs in the form of antagonistic genetic correlations. Such tradeoffs may have constrained any responses to selection and can also play a fundamental role in the maintenance of additive genetic variation in traits under selection (31, 32).
Studies of wild animal populations have also reported significant heritabilities of life-history traits (29, 33, 34), but our estimates are relatively high compared with those from animal populations in natural environments. There are several possible explanations for this difference. First, estimates of heritability may be confounded by the magnitude of residual variance (17, 28), with the high heritability estimated here for a rural preindustrial human population being due to relatively low environmental and residual variation compared with wild animal populations. Indeed, low heritabilities of fitness-related traits are often explained by high environmental variation that would obscure underlying additive genetic variation (28, 35). However, coefficients of additive genetic variance (which are not affected by levels of residual variance) of the measured traits were also high, with good correspondence between values of CVA and heritabilities: traits with the highest values of h2 generally also had the highest values of CVA. Second, in human studies, the inflation or confounding of heritability estimates due to cultural transmission within families must also be considered. In this study, we hoped to overcome this problem at least partly by taking into account effects of the common environment (by fitting mother's identity in the model to estimate variance between mothers) and by using all possible relationships available in the pedigree, across multiple generations in the animal-model framework analyses. We cannot rule out the possibility that our estimates of heritability may also be affected by some cultural effects within families that we were not able to separate from additive genetic variation. Nevertheless, this study is, to our knowledge, the first attempt to use an animal model (rather than less efficient analyses such as parent–offspring regressions) to estimate quantitative genetics parameters of human life-history traits and fitness.
All of our measures of fitness (λ, fecundity, and lifetime-reproductive success) had high heritabilities in females (0.76, 0.31, and 0.47, respectively), which compare well with heritability estimates in humans for fecundity from other studies (e.g., parent–offspring regression estimates ranging from 0 to 0.40; ref. 30). Censoring bias may have affected these estimates differently, but the estimates calculated for the censored sample (Table 1) should be directly comparable (0.76, 0.53, and 0.47, respectively, for fitness, fecundity, and LRS). It has been suggested that higher additive genetic variance of fitness traits compared with other life-history traits could result from fitness being a composite character (35). Additive genetic variance in fitness is likely to be affected by additive genetic variance in components of fitness; morphological, physiological, behavioral, and life-history traits will all contribute to additive genetic variation in fitness. This explanation is appealing, recognizing that λ is composed of more traits (and, hence presumably, loci) than LRS and fecundity.
An additional factor that can maintain additive genetic variance in traits under strong selection is the existence of antagonistic additive genetic correlations, or antagonistic pleiotropy (16, 36). Although these are often expected for fitness components, reviews from animal studies show that empirical evidence for negative genetic correlations is generally rare (18, 36). However, here we found significant genetic tradeoffs between key female life-history traits, specifically longevity and AFR, and longevity and MIBI. Their existence implies that females who start to breed relatively late, or who have longer interbirth intervals, will have relatively longer lifespans, supporting the hypothesis that the rate of reproduction should trade off with longevity (37–39). These tradeoffs may have had important implications for the evolution of human life history, because human females may gain fitness benefits by outliving their own reproductive capacity by improving the reproductive success of their offspring and the survival of their grand offspring (40, 41). Such positive fitness effects of postreproductive survival would intensify the selection for genes increasing longevity, but our results suggest the existence of constraints on any response to such selection imposed by countervailing selection favouring early or frequent breeding. Therefore, antagonistic correlations could serve to maintain the significant additive genetic variance observed for longevity.
Among females, the two exceptions to the general pattern of high heritability were offspring survival and AFR. The mortality of children in our study population was relatively high, with ≈30% of children in this sample dying before the age of 15 years. The most common causes of death among children in Finland at the time were infectious diseases, such as smallpox, measles, typhus, and pulmonary tuberculosis (42). Therefore, because there are several disease-related causes of mortality, we might not necessarily expect a significant additive genetic component in offspring survival. Instead, epistatic genetic interactions are more likely to be involved in resistance to diseases (43), and thus, genes inherited both from mother and father may be important. AFR also did not have a significant amount of additive genetic variance in our study population in contrast to modern Australian women, whose AFR has a significant heritability of 0.21 and also significant shared environmental effects of 0.18 (15). Variation in AFR in females is unlikely to reflect the age at maturation, which usually occurs at ≈12–16 years of age (44), as indicated by the high average AFR in these women (Table 1). Rather, it is likely that in populations living in harsh environmental conditions with limited resources, such as the subjects of our study in preindustrial Finland, AFR was heavily influenced by family effects, such as wealth, which we detected as a significant maternal effect for females. Also, note that, in contrast to AFR, ALR in females had a high heritability of 0.42, which is close to the value of heritability of 0.44 for age at menopause in a contemporary human population, which had small but significant shared environmental effects (15). However, in contrast to some studies reporting positive phenotypic correlations between ALR and longevity in humans (8, 10, 11, 45), we did not find any significant genetic correlation between these two traits.
Last, one of the striking differences between males and females revealed in our study was the high heritability of life-history traits and fitness in female traits compared with male traits. To our knowledge, no other study has attempted to estimate heritabilities for male fitness or life-history traits, such as age at first and last reproduction, in humans. This lack of significant heritability estimates for males is unlikely to be caused by possible misassigned paternity in the pedigrees used in this study, for the estimates of heritabilities of male and female traits were made by using the same pedigrees: i.e., paternity information contributed to the analysis of female traits as much as to males (so that, for example, the analysis could use the covariance between paternal half-sisters, or between a female and her paternal grandmother, and so on). If extra-marital relationships were introducing error into the pedigrees, this would have lowered heritabilities for the female traits as well as for the male traits. Instead, the lack of significant estimates of heritability of fitness and life-history traits in males (with the exception of adult longevity) might be due to the fact that in monogamous societies such as our study population, reproductive traits depend heavily on female quality and are physiologically under female control (men do not give birth or produce milk to feed offspring). Therefore, there may be little phenotypic covariance between male relatives. It is plausible that our data have excluded traits that were important for male fitness, such as the ability to attract a young and fertile partner by ensuring economic resources (25), and other studies have shown that certain male physical attributes, such as body height, which correlate with attractiveness to females and with reproductive success (46, 47), have significant heritabilities in modern human populations (48). However, the results presented here imply that, at least for this population, such effects do not necessarily translate into heritability of reproductive success.
In conclusion, we found relatively high heritabilities of fitness measures and fitness-related life-history traits in this preindustrial human population, even though life-history traits (or any fitness-correlated traits) are generally expected to have low additive genetic variance (16, 30). How this additive variance is maintained in the population is outside of the scope of our study (see refs. 49 and 50 for review), but one reason could be antagonistic pleiotropy arising from negative genetic correlations. The genetic tradeoffs between longevity and mean birth intervals and AFR that we detected provide compelling support for this hypothesis. These correlations are also interesting because they suggest some underlying genetic mechanism affecting age of first reproduction and longevity and another mechanism affecting rate of reproduction and longevity. The relatively large additive genetic variance and genetic constraints between key life-history traits that we found in this human population suggest that human life history has had the potential to evolve by optimizing natural selection, as classical life-history theory predicts. The significance of the maternal effects for female AFR and male fitness further emphasize that social aspects, like wealth of the family, also play an important role in human life-history evolution. Future studies could attempt to show how phenotypic selection on life-history traits translates into genetic response to selection in human populations.
Acknowledgments
We thank I. Voipio for providing data, Mirkka Lahdenperä for collection of the data set used here, and Juha Merilä and J. M. Cano Arias for assistance with the vce program. This work was supported by the European Commission Marie Curie Fellowship Association (J.E.P.), The Academy of Finland (J.E.P., V.L., and J.J.), and The Royal Society of the United Kingdom (L.E.B.K. and V.L.).
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: AFR, age at first reproduction; LRS, lifetime reproductive success; MIBI, mean interbirth interval; ALR, age at last reproduction.
References
- 1.Westerndorp, R. G. J. & Kirkwood, T. B. L. (1998) Nature 396, 743–746. [DOI] [PubMed] [Google Scholar]
- 2.Thomas, F., Teriokhin A. T., Renaud F., De Meeûs, T. & Guégan, J. F. (2000) J. Evol. Biol. 13, 409–414. [Google Scholar]
- 3.Doblhammer, G. & Oeppen, J. (2003) Proc. R. Soc. Lond. B. 270, 1541–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Knodel, J. E. (1998) Demographic Behavior in the Past (Cambridge Univ. Press, New York).
- 5.Voland, E. & Engel, C. (1989) in The Sociobiology of Sexual and Reproductive Strategies, eds. Rasa, A. E., Vogel, C. & Voland, E. (Chapman & Hall, London), pp. 194–205.
- 6.Le Bourg, E., Thon, B., Légaré, J., Desjardinds, B. & Charbonneau, H. (1993) Exp. Gerontol. 28, 217–232. [DOI] [PubMed] [Google Scholar]
- 7.Wrigley, E. A., Davies, R. S., Oeppen, J. E. & Schofield, R. S. (1997) English Population History from Family Reconstitution 1580–1837 (Cambridge Univ. Press, Cambridge).
- 8.Korpelainen, H. (2000) Proc. R. Soc. London Ser. B. 267, 1765–1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Helle, S., Käär, P. & Jokela, J. (2002) J. Evol. Biol. 15, 803–807. [Google Scholar]
- 10.Helle, S., Lummaa, V. & Jokela, L. (2005) Proc. R. Soc. London Ser. B 272, 29–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Doblhammer, G. (2000) Popul. Stud. 54, 169–176. [DOI] [PubMed] [Google Scholar]
- 12.Kumle, M. & Lund, E. (2000) in Sex and Longevity: Sexuality, Gender, Reproduction, Parenthood, eds. Robine, J.-M., Kirkwood, T. B. L. & Allard, M. (Springer, Berlin), pp. 117–128.
- 13.Menken, J., Duffy, L. & Kuhn, R. (2003) Popul. Dev. Rev. 29, 405–426. [Google Scholar]
- 14.Strassmann, B. I. & Gillespie, B. (2002) Proc. R. Soc. London Ser. B 269, 553–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kirk, K. M., Blomberg, S. P., Duffy, D. L., Heath, A. C., Owens, I. P. F. & Martin, N. G. (2001) Evolution (Lawrence, Kans.) 55, 423–435. [DOI] [PubMed] [Google Scholar]
- 16.Falconer, D. S. & Mackay, T. F. C. (1996) Introduction to Quantitative Genetics (Longman, Essex, U.K.).
- 17.Lynch, M. & Walsh, B. (1998) Genetics and Analysis of Quantitative Traits (Sinauer, Sunderland, MA).
- 18.Kruuk, L. E. B. (2004) Philos. Trans. R. Soc. London B 359, 873–890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kojonen, E., ed. (1971) Sursillin Suku. Genealogia Sursilliana (Weiling & Göös, Tapiola, Finland).
- 20.Soininen, A. M. (1974) Old Traditional Agriculture in Finland in The 18th and 19th Centuries (Forssan Kirjapaino Oy, Forssa, Finland).
- 21.Wirilander, K. (1974) Herrasväkeä: Suomen Säätyläistö 1721–1870 (Suomen Historiallinen Seura, Helsinki).
- 22.Morning, B. (1999) Hist. Fam. 4, 159–184. [DOI] [PubMed] [Google Scholar]
- 23.McGraw, J. B. & Caswell, H. (1996) Am. Nat. 147, 47–64. [Google Scholar]
- 24.Käär, P. & Jokela, J. (1998) Proc. R. Soc. London Ser. B 265, 2415–2420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Käär, P., Jokela, J. Helle, T. & Kojola, I. (1996) Proc. R. Soc. London Ser. B 263, 1475–1480. [DOI] [PubMed] [Google Scholar]
- 26.Neumaier A, Groeneveld E. (1998) Genet. Sel. Evol. 30, 3–26. [Google Scholar]
- 27.Shaw, R. G. (1987) Evolution (Lawrence, Kans.) 41, 812–826. [DOI] [PubMed] [Google Scholar]
- 28.Houle, D. (1992) Genetics 130, 195–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kruuk, L. E. B., Clutton-Brock, T. H., Pemberton, J. M., Brotherstone, S. & Guinness, F. E. (2000) Proc. Natl. Acad. Sci. USA 97, 698–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fisher, R. A. (1958) The Genetic Theory of Natural Selection (Dover, New York).
- 31.Reznick, D. (1992) Trends Ecol. Evol. 7, 42–45. [Google Scholar]
- 32.Roff, D. A. (1992) The Evolution of Life Histories: Theory and Analysis (Chapman & Hall, New York).
- 33.Réale, D., Berteaux, D., McAdam, A. G. & Boutin, S. (2003) (Lawrence, Kans.) 57, 2416–2423. [DOI] [PubMed] [Google Scholar]
- 34.Sheldon, B. C., Kruuk, L. E. B. & Merilä J. (2003) (Lawrence, Kans.) 57, 406–420. [DOI] [PubMed] [Google Scholar]
- 35.Price, T. & Schluter, D. (1991) (Lawrence, Kans.) 45, 853–861. [Google Scholar]
- 36.Roff, D. A. (1997) Evolutionary Quantitative Genetics (Chapman & Hall, New York).
- 37.Williams, G. C. (1957) (Lawrence, Kans.) 11, 398–411. [Google Scholar]
- 38.Kirkwood, T. B. L. (1977) Nature 270, 301–302. [DOI] [PubMed] [Google Scholar]
- 39.Kirkwood, T. B. L. & Rose, M. R. (1991) Phil. Trans. R. Soc. London Ser. B 332, 15–24. [DOI] [PubMed] [Google Scholar]
- 40.Hawkes, K., O'Connell, J. F., Jones, N. G., Alvarez, H. & Charnov, E. L. (1998) Proc. Natl. Acad. Sci. USA 95, 1336–1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lahdenperä, M., Lummaa, V., Helle, S., Tremblay, M. & Russell, A. F. (2004) Nature 428, 178–181. [DOI] [PubMed] [Google Scholar]
- 42.Turpeinen, O. (1978) Popul. Stud. 32, 523–533. [DOI] [PubMed] [Google Scholar]
- 43.Moore, J. H. (2003) Hum. Hered. 56, 73–82. [DOI] [PubMed] [Google Scholar]
- 44.Ellison, P. (2001) On Fertile Ground (Harvard Univ. Press, Cambridge, MA).
- 45.Perls, T. T., Alpert, L. & Fretts, R. C. (1997) Nature 339, 133. [DOI] [PubMed] [Google Scholar]
- 46.Pawlowski, B., Dunbar, R. I. M. & Lipowicz, A. (2000) Nature 403, 156. [DOI] [PubMed] [Google Scholar]
- 47.Mueller, U. & Mazur A. (2001) Behav. Ecol. Sociobiol. 50, 302–311. [Google Scholar]
- 48.Silventoinen, K., Kaprio, J. & Lahelma, E. (2000) Behav. Genet. 30, 477–485. [DOI] [PubMed] [Google Scholar]
- 49.Charlesworth, B. in (1987) Sexual Selection: Testing the Alternatives, eds. Bradbury, J. W. & Andersson, M. B. (Wiley, New York), pp. 21–40.
- 50.Merilä, J. & Sheldon, B. C. (1999) Heredity 83, 103–109. [DOI] [PubMed] [Google Scholar]


