Density Functional Calculations for Prediction of ⁵⁷Fe Mössbauer Isomer Shifts and Quadrupole Splittings in β-Diketiminate Complexes

Abstract

The relative ease of Mössbauer spectroscopy and of density functional theory (DFT) calculations encourages the use of Mössbauer parameters as a validation method for calculations, and the use of calculations as a double check on crystallographic structures. A number of studies have proposed correlations between the computationally determined electron density at the iron nucleus and the observed isomer shift, but deviations from these correlations in low-valent iron β-diketiminate complexes encouraged us to determine a new correlation for these compounds. The use of B3LYP/def2-TZVP in the ORCA platform provides an excellent balance of accuracy and speed. We provide here not only this new correlation and a clear guide to its use but also a systematic analysis of the limitations of this approach. We also highlight the impact of crystallographic inaccuracies, DFT model truncation, and spin states, with intent to assist experimentalists to use Mössbauer spectroscopy and calculations together.

Introduction

Since the discovery of recoilless nuclear resonance absorption of γ-rays in 1957 by Rudolf Mössbauer,¹ the spectroscopy bearing his name has become a powerful technique in transition metal and bioinorganic chemistry to obtain information regarding the electronics and magnetic properties of metal centers.² The Mössbauer effect has been observed for more than 80 nuclides, but ⁵⁷Fe Mössbauer spectroscopy is the most common.³⁻⁶ Mössbauer spectroscopy using the ⁵⁷Fe nucleus has become ubiquitous in both bioinorganic and coordination chemistry because of the ability to selectively probe Fe environments in a sample, even in the presence of large protein scaffolds or complex ligands that have numerous other atoms.⁵ Each unique iron environment typically exhibits a doublet in a Mössbauer spectrum when the applied field is small (“zero field”) (Figure 1). Fitting the zero-field doublet yields two parameters, the isomer shift (δ) and the absolute value of the quadrupole splitting (|ΔE_Q|).³

Figure 1.

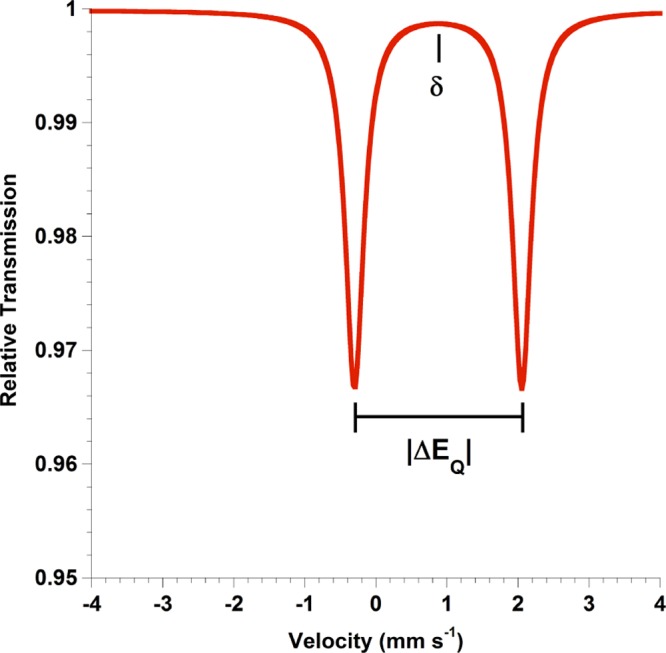
Diagram of a typical zero-field Mössbauer spectrum with isomer shift (δ) and quadrupole splitting parameters (|ΔE_Q|) indicated.

The isomer shift, δ, which lies at the midpoint of the doublet, reflects the electron density at the iron nucleus and is often used to interpret the oxidation state and spin state of the iron center. For example, high oxidation states tend to give lower isomer shifts in high-spin compounds, and for the same oxidation state, low-spin compounds tend to give lower isomer shifts than high-spin compounds.³ However, the ligand field has a substantial influence on the isomer shift, and additional trends are evident based on the ligand identities (more covalency tends to give lower δ) and the geometry at the metal (lower coordination numbers tend to give lower δ). These trends have been usefully summed up by the generalization that shorter bonds give lower δ, a principle that unites the trends with oxidation state, coordination number, and spin state.³ However, due to the number of (often competing) influences, it may be difficult to predict the isomer shift adequately with these qualitative relationships.

The quadrupole splitting, which represents the peak-to-peak separation of the doublet, reflects the asymmetry in electron distribution around the nucleus and therefore can offer insight into the occupancy of the 3d orbitals. For high-symmetry iron centers with octahedral and tetrahedral coordination environments, interpretation of the quadrupole splitting can be straightforward, but in more complex systems with less symmetry and orbital mixing, interpretation is typically more complicated.³

The complexity of interpreting the spectral values for understanding of electronics and bonding has led chemists to use density functional theory (DFT) computations to predict Mössbauer parameters for a given structure.^6,7 The ability to accurately calculate the experimental values has also become a valuable way to validate a computational model.^7,8 Computation of the isomer shift and quadrupole splitting for an iron site requires calculation of the electron density and the electric field gradient (EFG) at the iron nucleus, respectively. Calculating the isomer shift is problematic because of systematic errors of common basis sets in describing the electron density very close to the iron nucleus. As a result, calculation of isomer shift values generally depends on an empirically determined correlation between the calculated electron density and the experimental isomer shift.^6,9 These fits are typically linear, but the fit parameters only apply when using a specific set of computational parameters (functional, basis set, relativistic corrections). The calculated EFG yields a predicted quadrupole splitting through the relationship given in eq 1, where e is the charge of an electron, Q is the quadrupole moment of the ⁵⁷Fe nucleus (0.16(1) barn,³ and V_zz is the major component of the EFG. Comparison of these to experiment is complicated by the fact that the sign of the experimental quadrupole splitting is not determined in a zero-field measurement, and thus most researchers simply use the absolute value of the quadrupole splitting for comparison to experiment.

1

Though the number of DFT studies on Mössbauer parameters is too large to describe them all, a few are particularly worth noting. Oldfield et al. established an early precedent for predicting Mössbauer parameters of paramagnetic complexes in various spin states as well as the use of relativistic corrections for improving isomer shift predictions.^6d Noodleman et al. examined different classes of iron complexes and proteins with particular focus on iron-nitrosyl and iron-sulfur species, and extended their results to prediction of intermediates in metalloproteins, such as ribonucleotide reductase.^{6c,6f,6g,7e,9f} Neese et al. compared pure and hybrid functionals along with various basis sets for the prediction of Mössbauer parameters for simple iron compounds.^6b,6e,9b Filatov et al. reported a new method based on energy derivatives due to the excitation of the ⁵⁷Fe nucleus enabling isomer shift calculations without a correlation with experimental results.¹⁰ Friesner et al. benchmarked many functionals and basis sets on a broad range of iron compounds, established the use of X-ray structures for Mössbauer parameter predictions, and extended their results to assessing the validity of proposed methane monooxygenase intermediates.^9c Pápai et al. published an extensive benchmark study using a wide range of iron compounds, and compared GGA and hybrid functionals, STO and GTO basis sets, and effects of solvation models on Mössbauer parameter predictions.^9d They also discussed potential difficulties with the correlation of computation to experiment, including low-lying excited states, geometrical isomerism, and spin state changes. More recent reports have focused on expansion of these ideas to new ligand systems, inclusion of experimental error in the development of the correlation fits, as well as new methods for structure optimization, including systems requiring periodic boundary conditions.¹¹

We became interested in computing Mössbauer parameters for reduced β-diketiminate supported iron complexes to validate calculations on their electronic structures.⁸ These showed us that the existing correlations have few examples of multimetallic complexes, redox-active ligands, low-valent, and low-coordinate iron complexes. Additionally, the established correlations use continuum solvation models with the polarity of water^9b or methanol,^9d whereas the iron complexes of interest to our group are often studied experimentally in less polar solvents, such as toluene. When using the isomer shift correlation reported by Neese and co-workers, we often calculated isomer shifts that had systematic deviations from experiment (0.1–0.2 mm s⁻¹ lower in the calculations) despite the optimized geometries agreeing quite well with the crystal structure geometries.^8a,8e The need to address these issues and the large number of zero-field Mössbauer spectra that we have now collected on related systems encouraged us to seek a more applicable correlation as well as the most facile method for the calculations. Others have also noted that the isomer shift correlations in the literature often need to be “tuned” to different kinds of environments, for example iron-sulfur clusters.¹²

Herein, we report a revised set of correlation parameters between the calculated electron density and the experimental isomer shift. We use ORCA, a free platform for computations that has implemented a simple readout for Mössbauer parameters,¹³ and utilize the common functional B3LYP, which has been validated in many earlier studies. Importantly, the new correlation comes from a representative subset of β-diketiminate complexes as a training set, and we test the effectiveness of this correlation for prediction of Mössbauer parameters using a test set of different complexes. Furthermore, we test the correlation more generally using other low-valent iron complexes with different ligand types having various donors (carbon donors, phosphines, thiolates, and hydrides). The power of the same computations for prediction of quadrupole splitting values is also evaluated for all complexes. As experimentalists ourselves, we were also motivated to evaluate the tools that are often used to make computations feasible for the nonspecialist. Thus, we describe the effects of ligand truncation in the computations, and the effect of the spin state on predicted isomer shift and quadrupole splitting values in selected examples.

Results

Nine iron β-diketiminate complexes were chosen as a training set to calibrate the relationship between the calculated electron densities and the experimental isomer shifts. The complexes were specifically chosen because they had very high-quality X-ray structures with no disorder and span a variety of oxidation states, spin states, and coordination numbers. We purposely chose a small representative training set because we wanted to be able to test the quality of this correlation with independent compounds and structures that are not part of the training set. A list of the training set complexes along with coordination number, formal oxidation state, spin state, and experimental isomer shifts are given in Table 1, and the labeling scheme is given in Figure 2. The isomer shift is temperature dependent due to the second-order Doppler shift, which is often minimal (<0.02 mm s^–1) at liquid N₂ temperatures and below, however the exact contribution depends on the effective mass of the absorber and bonding environment.^3,14 Due to the lack of a generality of this dependence, we chose to include data irrespective of the temperature of measurement. Only literature spectra referenced to α-Fe at 298–300 K were chosen.

Table 1. Training Set for Establishing a Correlation between Computed Electron Densities (ρ) and Experimental Isomer Shift.

compound	C.N.a	formal ox. stateb	Sc	exp. δ (mm s−1)d	refe
K2[LMeFeNNFeLMe]	3	0	2	0.47	(15)
LMeFeBr(THF)	4	+2	2	0.89	(16)
MeLMe,Me2Fe	4	+2	2	0.84	(22)
MeLMe,MeFeCl2	4	+3	5/2	0.33	(17)
MeLMe,MeFe(Cl)2K(18-crown-6)	4	+2	2	0.88	(17)
MeLMe,MeFe(μ-S)2FeMeLMe,Me	4	+3	0	0.28	(18)
LMeFe(η6-C6H6)	5	+1	1/2	0.70	(16)
MeLMe,MeFe(CNXyl)3f	5	+1	1/2	0.17	(19)
MeLMe,MeFe(CO)3	5	+1	1/2	0.12	(19)

^aCoordination number of iron.

^bFormal oxidation state of the iron center(s) based on charge counting.

^cExperimental spin of the system.

^dExperimental isomer shifts were collected at 80 K with a small applied magnetic field of 0.07 T referenced to α-Fe or iron foil at 298–300 K.

^eReference containing crystal structure and Mössbauer parameters.

^fCNXyl = 2,6-dimethylphenyl isocyanide.

Figure 2.

Structure and labeling scheme of β-diketiminate ligands L^Me, L^tBu, and ^MeL^Me,Me.

We chose to fit the training set results with a single line for each basis set choice (eq 2), a strategy that was employed by Neese and by Pápai to generalize single correlations without need to select fit parameters based on oxidation state of the metal center.^9b,9d Some other studies break down the test sets into smaller groups using parameters such as oxidation state and ligand sphere, and then establish a linear correlation for each subset,^9c but we disfavor this strategy because it cannot be applied to complexes with redox-active ligands or with unusual environments in which there is no independent, unambiguous determination of the oxidation state. Also note that many of the complexes examined in this report contain π-accepting ligands or redox-active ligands that can drastically affect the electron density at the iron center. In these cases, Mössbauer spectroscopy has been useful in assigning the “true” oxidation state of the metal center over the formal oxidation state established by charge counting, which can differ substantially.^9c

2

In eq 2, δ is the isomer shift, ρ(0) is the calculated electron density at Fe, α and β are calibration constants with C as an unrefined constant that is subtracted from ρ(0) to avoid a fit where the β parameter is unreasonably large. Parameters for the fits developed from the training set of compounds, the square of the correlation coefficient (R²), the mean absolute error (MAE), and the maximum deviation from experiment (max. dev.), are given in Table 2 and shown in Figure 3. The fit values of α are within error of the experimental value of 0.31 ± 0.04 a₀³ mm s^–1, which has been estimated from the change in electron capture rate of ⁵²Fe in different iron compounds.²⁰

Table 2. Fit Parameters and Statistics for the Linear Fit of the Training Set Compounds for the Prediction of Isomer Shifts, Using the B3LYP Functional.

basis set	α (a03 mm s–1)a	β (mm s–1)a	C (a0–3)a	(R2)b	MAE (mm s–1)c	max. dev. (mm s–1)d
def2-TZVP	–0.32 ± 0.02	1.18 ± 0.04	13 780	0.985	0.038	0.11
CP(PPP)	–0.30 ± 0.02	1.49 ± 0.06	14 760	0.983	0.040	0.13

^aCalibration coefficients for eq 2 for each choice of basis set on iron.

^bSquare of the correlation coefficient from the linear fits of the training set.

^cMAE between the linear fit and experiment.

^dMaximum deviation between the linear fit and experimental isomer shift for the training set.

Figure 3.

Plots of calculated electron density at Fe against the experimentally observed isomer shifts for the training set compounds for def2-TZVP (top) and CP(PPP) (bottom). Data are shown in red and the linear fits are shown in black with given fit parameters (α and β) as well as the square of the correlation coefficient (R²).

With the correlation established and fits for eq 2 showing excellent agreement with the experimental isomer shifts, we tested the predictive power of the new correlations toward other compounds reported by our group as well as the generality toward other ligand classes, the ability of the correlation to evaluate different spin states, and the efficacy in predicting Mössbauer parameters for spectra collected at temperatures other than 80 K. These “test” compounds and their corresponding experimental isomer shifts are shown in Table 3 along with the isomer shifts calculated using the fit parameters established above for both def2-TZVP and CP(PPP).

Table 3. Identity and Parameters of Test Compounds for Prediction of Isomer Shift Values.

compound	C.N.a	formal ox. state	Sb	exp. δc	calc. δ def2-TZVPd	calc. δ CP(PPP)e	T (K)f	ref
LMeFe(NCtBu)2g	4	+1	3/2	0.72	0.72	0.73	80	(8c)
LMeFe(tBu-Py)2h	4	+1	3/2	0.79	0.82	0.83	80	(8d)
LtBuFeCH3	3	+2	2	0.48	0.47	0.48	4.2	(21)
LtBuFeCl	3	+2	2	0.74	0.76	0.77	4.2	(21)
LtBuFeNHtolyli	3	+2	2	0.71	0.65	0.66	4.2	(21)
LtBuFe(HCCPh)	3	+1	3/2	0.44	0.48	0.49	150	(21)
[LtBuFeH][K(18-crown-6)]	3	+1	3/2	0.47	0.46	0.47	80	(8b)
[LtBuFeH][K(crypt)]j	3	+1	3/2	0.40	0.40	0.41	80	(8b)
MeLMe,MeFe(η6-C6H6)	5	+1	1/2	0.68	0.77	0.77	80	(19)
MeLMe,MeFe(η5-Ind)k	5	+2	1	0.67	0.70	0.71	80	(22)
MeLMe,MeFe(Py)(μ-N2C10H10)(Py)FeLl	4	+2	4	0.76	0.70, 0.71	0.71, 0.72	80	(8e)
MeLMe,MeFe(Py)(μ-Py)FeMeLMe,Mel	4, 4	+2, +2	3	0.67, 0.76	0.71, 0.73	0.71, 0.74	80	(8e)
LMeFe(AdNNNNAd)m	4	+2	3/2	0.69	0.62	0.63	80	(8a)
LS,SFe(THF)2n	4	+2	2	0.89	0.79	0.80	80	(23)
(SiPiPr3)FeCOSi(CH3)3o	5		0	0.061	0.10	0.11	80	(24)
Cr(iPrNPPh2)3Fe-PMe3p	5		3/2	0.25	0.27	0.28	110	(25)
[Cp*Fe(S2Ph)(N2H2)FeCp*]PF6q	6	+2.5	1/2	0.29	0.47	0.47	80	(26)
Cp2Fer	6	+2	0	0.53	0.68	0.69	80	(27)
PNPiPrFeCl2s	5	+2	2	0.86	0.85	0.86	80	(28)
PNPtBuFeCl2t	5	+2	2	0.99	0.89	0.91	80	(28)
[(IMes)2FeCl]u	3	+2	2	0.65	0.52	0.54	80	(29)
[(IMes)(Me2-cAAC)-FeCl]u,v	3	+2	2	0.52	0.45	0.47	80	(29)
[(Me2-cAAC)2FeCl]v	3	+2	2	0.49	0.34	0.35	80	(29)
[(cylDep)2Fe][BArF4]w	2	+1	3/2	0.48	0.52	0.52	80	(30)
[(sIDep)2Fe][BArF4]x	2	+1	3/2	0.55	0.47	0.47	80	(30)

^aC.N. is the coordination number of the Fe center.

^bTotal spin of the system.

^cExperimental isomer shift referenced to α-Fe or iron foil at 298–300 K.

^dIsomer shift calculated using the def2-TZVP linear fit from Table 2.

^eIsomer shift calculated using the def2-TZVP/CP(PPPP) linear fit from Table 2.

^fCollection temperature for experimental parameters.

^gThree unique starting geometries were used and the results averaged. “NC^tBu” is tert-butylnitrile.

^h“^tBu-Py” is 4-tert-butylpyridine.

ⁱ“NHtolyl” is 4-methylanilide.

^j“crypt” is 2.2.2-cryptand.

^k“Ind” is indenyl.

^l“Py” is pyridine. “N₂C₁₀H₁₀” is 4H,4′H-[4,4′-bipyridine]-1,1′-diide.

^m“AdNNNNAd” is N,N‴-bis(adamantyl)tetrazene.

ⁿ“L^S,S” is 4′,6‴-difluoro-2,2′′′′,4,4′′′′,6,6′′′′-hexaisopropyl-[1,1′,3′,1″,3″,1‴,3‴,1′′′′-quinquephenyl]-2,2′-dithiolate.

^o1,1′,1″-Tris(2-(diisopropylphosphino)phenyl)silane.

^pN-Isopropyl-1,1-diphenylphosphanamide.

^qCp* is 1,2,3,4,5-pentamethylcyclopentadienyl anion and S₂Ph is 1,2-benzenedithiolate.

^rCp is the cyclopentadienyl anion.

^sBis(2-(diisopropylphosphaneyl)ethyl)amine.

^tBis(2-(di-tert-butylphosphaneyl)ethyl)amine.

^uIMes is 1,3-bis(2,4,6-trimethylphenyl)imidazole-2-ylidene.

^vMe₂-cAAC is 3,3,5,5-tetramethyl-1-(2′,6′-diisopropylphenyl)pyrrolidine-2-ylidene.

^wcylDep is 1,3-bis-2′6′-diethylphenyl)-4,5-(CH₂)₄-imidazolin-2-ylidene.

^xsIDep is 1,3-bis-(2′,6′-diethylphenyl)-imidazolin-2-ylidene.

Uncertainty statistics for the isomer shift predictions are given in Table 4, which gives both the MAE and the standard deviation. We also give the largest deviation seen in the test set, which gives the “worst-case” scenario. These data show no clear empirical preference for CP(PPP) over def2-TZVP as the errors for both basis sets are comparable for all classes of compounds examined. Neese and Pápai similarly have seen little improvement in statistics when using CP(PPP), but favor the larger basis set because it is specially designed for core properties.^9b,9d Despite the theoretical justification for the CP(PPP) basis set, def2-TZVP performed comparably to CP(PPP) over the set of compounds examined with a 0.001 mm s^–1 difference in MAE, which is well within the accepted experimental error (±0.02 mm s^–1) for Mössbauer spectroscopy. The computations using CP(PPP) as the basis set on iron took on average 1.46 times longer than when def2-TZVP was used on all atoms. Considering the savings of computational resources along with the comparable accuracy of the two basis sets, we find that def2-TZVP is the most efficient choice for computational predictions of the Mössbauer isomer shift.

Table 4. Error Comparison of def2-TZVP versus CP(PPP) for Prediction of ⁵⁷Fe Mössbauer Isomer Shift Parameter.

	Def2-TZVP			CP(PPP)
	MAEa (mm s–1)	std. dev.b (mm s–1)	largest deviationc (mm s–1)	MAEa (mm s–1)	std. dev.b (mm s–1)	largest deviationc (mm s–1)
training set	0.038	0.050	0.11	0.040	0.053	0.13
all β-diketiminated	0.035	0.045	0.11	0.035	0.045	0.13
othere	0.097	0.12	0.18	0.091	0.11	0.18
all compoundsf	0.054	0.075	0.18	0.053	0.073	0.18

^aMAE between predicted and experimental values.

^bStandard deviation (Std. Dev.) of errors between predicted and experimental values.

^cLargest deviation between predicted and experimental values.

^dStatistics for all β-diketiminate supported complexes.

^eStatistics for non-β-diketiminate complexes.

^fStatistics for all compounds.

We were gratified to discover that this new correlation performed much better for compounds that had been problematic when using the correlation from Neese.^9b For example, in a recent study of diketiminate compounds with bridging pyridine ligands,^8e two compounds were addressed computationally. In one, the experimental isomer shift of 0.76 mm s^–1 was far from the previously calculated value of 0.59 mm s^–1, but the method described here predicted a closer value of 0.70 mm s^–1 (Table 3, row 11). In a diiron compound with inequivalent iron centers, the experimental isomer shifts of 0.76 and 0.67 mm s^–1 were predicted to be 0.62 and 0.52 mm s^–1 using the literature correlation, whereas the method described here predicted much closer values of 0.73 and 0.71 mm s^–1 (Table 3, row 12).

Prediction of Quadrupole Splitting

Previous studies observed larger errors in predicted quadrupole splitting values as the magnitude of the quadrupole splitting increases.^9c,9d Our calculations show similar scattering at larger quadrupole splitting values (Table 5), and therefore we have included the percent error statistics with the caveat that this measure downplays large errors in large values in Table 6. Overall, both basis sets performed equally well at predicting the quadrupole splitting for the compounds examined. Given the much greater computational resources needed for CP(PPP) versus def2-TZVP, we again favor def2-TZVP for computational predictions.

Table 5. Experimental and Calculated Quadrupole Splitting Parameters.

compound	exp. |ΔEQ| (mm s–1)a	def2-TZVP |ΔEQ| (mm s–1)b	CP(PPP) |ΔEQ| (mm s–1)c	ref
K2[LMeFeNNFeLMe]	2.48	2.37, 2.33	2.22, 2.18	(15)
LMeFeBr(THF)	2.36	2.19	2.34	(16)
LMeFe(η6-C6H6)	0.74	0.93	1.14	(19)
MeLMe,Me2Fe	1.80	1.48	1.69	(19)
MeLMe,MeFe(Cl)2	1.23	1.00	1.05	(18)
MeLMe,MeFe(Cl)2K(18-crown-6)	2.10	2.07	2.27	(17)
MeLMe,MeFe(μ-S)2FeMeLMe,Me	1.14	1.18, 1.18	1.15, 1.15	(18)
MeLMe,MeFe(CNXyl)3d	0.81	0.76	0.80	(19)
MeLMe,MeFe(CO)3	0.77	0.79	0.89	(19)
LMe Fe(NCtBu)2e	0.72	1.06	1.20	(8c)
LMeFe(tBu-Py)2f	0.59	0.59	0.56	(8b)
LtBuFeCH3	1.74	2.14	2.10	(21)
LtBuFeCl	1.61	2.05	2.05	(21)
LtBuFeNHtolylg	1.42	1.72	1.66	(21)
LtBuFe(HCCPh)	2.05	2.53	2.44	(21)
[LtBuFeH][K(18-crown-6)]	1.84	2.21	2.25	(8b)
[LtBuFeH][K(crypt)]h	1.93	2.25	2.36	(8b)
MeLMe,MeFe(η6-C6H6)	0.69	0.87	1.08	(19)
MeLMe,MeFe(η5-Ind)i	1.07	1.02	0.89	(22)
MeLMe,MeFe(Py)(μ-N2C10H10)(Py)FeMeLMe,Mej	1.38	1.12, 1.10	1.26, 1.26	(8e)
MeLMe,MeFe(Py)(μ-Py)FeMeLMe,Mej	1.29, 1.66	1.14, 1.22	1.04, 1.37	(8e)
LMeFe(AdNNNNAd)k	1.32	1.53	1.77	(8a)
LS,SFe(THF)2l	3.77	3.81	3.99	(23)
(SiPiPr3)FeCOSi(CH3)3m	1.115	1.12	1.41	(24)
Cr(iPrNPPh2)3Fe-PMe3n	0.31	1.07	1.11	(25)
[Cp*Fe(S2Ph)(N2H2)FeCp*]PF6o	0.74	0.80, 0.80	0.82, 0.82	(26)
Cp2Fep	2.41	2.61	2.97	(27)
PNPiPrFeCl2q	2.89	3.25	3.36	(28)
PNPtBuFeCl2r	2.69	3.09	3.22	(28)
[(IMes)2FeCl]s	2.63	2.23	2.30	(29)
[(IMes)(Me2-cAAC)-FeCl]s,t	2.03	2.94	2.99	(29)
[(Me2-cAAC)2-FeCl]t	2.04	1.84	1.69	(29)
[(cylDep)2Fe][BArF4]u	5.75	5.43	5.40	(30)
[(sIDep)2Fe][BArF4]v	6.82	6.00	5.99	(30)

^aExperimentally observed quadrupole splitting.

^bQuadrupole splitting calculated using the def2-TZVP basis set on all atoms.

^cQuadrupole splitting calculated using the CP(PPP) basis set on iron.

^d“CNXyl” is 2,5-dimethylphenylisocyanide.

^e“NC^tBu” is tert-butylnitrile.

^f“^tBu-Py” is 4-tert-butylpyridine.

^g“NHtolyl” is 4-methylanilide.

^h“crypt” is 2.2.2-cryptand.

ⁱ“Ind” is indenyl.

^j“Py” is pyridine. “N₂C₁₀H₁₀” is 4H,4′H-[4,4′-bipyridine]-1,1′-diide.

^k“AdNNNNAd” is N,N‴-bis(adamantly)tetrazene.

^l“L^S,S” is 4′,6‴-difluoro-2,2′′′′,4,4′′′′,6,6′′′′-hexaisopropyl-[1,1′,3′,1″,3″,1‴,3‴,1′′′′-quinquephenyl]-2,2′-dithiolate.

^m1,1′,1″-Tris(2-(diisopropylphosphino)phenyl)silane.

ⁿN-Isopropyl-1,1-diphenylphosphanamide.

^oCp* is 1,2,3,4,5-pentamethylcyclopentadienyl anion. S₂Ph is 1,2-benzenedithiolate.

^pCp is the cyclopentadienyl anion.

^qBis(2-(diisopropylphosphaneyl)ethyl)amine.

^rBis(2-(di-tert-butylphosphaneyl)ethyl)amine.

^sIMes is 1,3-bis(2,4,6-trimethylphenyl)imidazole-2-ylidene.

^tMe₂-cAAC is 3,3,5,5-tetramethyl-1-(2′,6′-diisopropylphenyl)pyrrolidine-2-ylidene.

^ucylDep is 1,3-bis-2′6′-diethylphenyl)-4,5-(CH₂)₄-imidazolin-2-ylidene.

^vsIDep is 1,3-bis-(2′,6′-diethylphenyl)-imidazolin-2-ylidene.

Table 6. Error Comparison of def2-TZVP versus CP(PPP) for Prediction of ⁵⁷Fe Mössbauer |ΔE_Q| Parameters.

	Def2-TZVP				CP(PPP)
	MAEa (mm s–1)	std. dev.b (mm s–1)	largest deviationc (mm s–1)	% errord	MAEa (mm s–1)	std. dev.b (mm s–1)	largest deviationc (mm s–1)	% errord
training set	0.12	0.14	0.32	4.9	0.15	0.20	0.40	5.9
β-diketiminate complexes	0.27	0.36	0.84	11.0	0.28	0.35	0.70	11.1
non-β-diketiminate complexes	0.35	0.47	0.91	14.0	0.45	0.52	0.96	18.1
all compounds	0.30	0.40	0.91	12.0	0.33	0.41	0.96	13.4

^aMAE between predicted and experimental values.

^bStandard deviation of errors between predicted and experimental values.

^cLargest deviation between predicted and experimental values.

^dAverage percent error between predicted and experimental values.

Testing the Use of Crystallographic Geometries versus Optimized Geometries

Previously, Friesner and co-workers examined the calculation of Mössbauer parameters, comparing between using the geometry from X-ray crystallography versus using a DFT optimized structure.^9c They concluded that as long as the X-ray structure and DFT geometry were in good agreement, the predicted Mössbauer parameters derived from each should not be significantly different. On the other hand, Pápái and co-workers state that the error in X-ray structures due to thermal motion can affect the calculation of Mössbauer parameters and support the use of DFT optimized geometries.^9d Nemykin and Noodleman have employed both methods, with emphasis on the need for geometry optimization to closely match the X-ray structures.^{6c,6f,6g,7e,9a,9f} Common issues not addressed in these studies are the impact of crystal packing effects on the molecular geometry at iron and disorder in the X-ray structures. Our experience is that it is fairly common to have two polymorphs of the same complex or two different crystal structures of the same complex with different solvents of crystallization. Additionally, it is frequently observed that there are two crystallographically independent molecules in an X-ray crystal structure, and sometimes the bond distances/angles differ between the inequivalent molecules. Disorder of ligands can also lead to multiple observed molecular configurations for the same compound. Using X-ray coordinates as a report of molecular geometry also introduces another problem because X-ray diffraction measures electron density rather than nuclear positions, and thus there is systematic shortening of all distances to H atoms (by ∼0.1 Å) in the refined structures.³¹ Below, we show that these crystallographic issues can lead to large inaccuracies in computationally predicted parameters if a full geometry optimization is not performed.

To evaluate this issue, we computationally examined L^MeFe(NC^tBu)₂, a compound reported previously by Cowley et al.^8c It is an ideal test case for the influence of crystal packing because the asymmetric unit in the X-ray crystal structure contained three chemically identical but crystallographically independent molecules of L^MeFe(NC^tBu)₂. In addition to performing point calculations on the crystallographic geometries with only the H atom positions optimized, we also performed a full geometry optimization on each independent molecule. For each of the six resulting geometries, the electron density at the nucleus and quadrupole splitting were calculated (Table 7). (It is most appropriate to compare the electron densities rather than converting them to isomer shifts as the correlation fit parameters reported above are from a fully optimized training set. The predicted isomer shifts are also given to demonstrate the variation.)

Table 7. Comparison of Calculated Parameters for Multiple Geometries from a Single Crystal Using Fully Optimized DFT Geometries and H-Atom Only Optimized Geometries.

structure	exp. IS (mm s–1)	calc. ρ(0)-13780 def2-TZVPa	calc. ρ(0)-14760 CP(PPP)a	exp. |ΔEQ| (mm s–1)	calc. |ΔEQ| def2-TZVP	calc. |ΔEQ| CP(PPP)
LMeFe(NCtBu)2 – 1 H-only	0.72	1.054 (0.843)	2.129 (0.851)	1.87	1.09	1.26
LMeFe(NCtBu)2 – 2 H-only		1.225 (0.788)	2.310 (0.797)		0.85	1.04
LMeFe(NCtBu)2 – 3 H-only		1.076 (0.836)	2.153 (0.844)		0.90	1.08
LMeFe(NCtBu)2 – 1		1.438 (0.720)	2.536 (0.729)		1.08	1.22
LMeFe(NCtBu)2 – 2		1.429 (0.723)	2.528 (0.732)		1.06	1.20
LMeFe(NCtBu)2 – 3		1.436 (0.721)	2.533 (0.730)		1.04	1.18

^aThe numbers in parentheses are the calculated isomer shifts according to our computational method.

For the fully optimized structures the calculated ρ(0) using both def2-TZVP and CP(PPP) vary by less than 0.01 a₀⁻³ among the three structures, as would be expected since these structures should optimize to the same energy minimum regardless of the starting geometry. This would lead to a difference of less than 0.003 mm s^–1 in the calculated isomer shift, well within the uncertainty of the correlation (±0.05 mm s⁻¹) as well as the uncertainty of the measured isomer shift (±0.02 mm s⁻¹). For the structures with only H-atoms optimized, on the other hand, there is significant variation in the computed electron densities of nearly 0.2 a₀^–3. This would correspond to changes in the calculated isomer shift of 0.05 mm s^–1 using the correlations reported here, which is on the order of the error in the isomer shift prediction. Thus, optimizing only H atoms can introduce a significant source of error in cases wherein multiple molecules are present in the asymmetric unit or disorder gives multiple conformations.

Similarly, the calculated quadrupole splitting varied less in the fully optimized geometries (0.04 mm s^–1) than in the H-atom only optimized geometries (0.24 mm s^–1). Again, the magnitude of the error in the predicted quadrupole splitting was similar to the uncertainty in our best correlation (0.27 mm s^–1). In both parameters, less variation is observed for fully optimized geometries leading to the conclusion that a full geometry optimization is best, because systematic error is introduced by selection of a random molecule within the asymmetric unit or a particular polymorph.

It is also useful to comment on the accuracy of X-ray crystallographic structures. Despite the ubiquity of X-ray crystallography and the high level of faith that the inorganic chemistry community places in crystallographic results, it is important to remember that crystallographic analysis gives metrical parameters with an accuracy that is poorer than the “estimated standard deviations” that arise from the refinement protocol.³² Even more serious systematic deviations have been noted in some cases.³³ Treating Mössbauer spectroscopy as an independent check of geometries is therefore valuable. In the case discussed above, the Mössbauer spectrum of the crystalline solid shows narrow lines and Lorentzian line shapes that indicate a relatively unvarying geometry in the crystal, though the bond distances around Fe vary by 0.02 Å and orientations of the nitriles vary by 90° in the crystallographic structure. Our computations show that these would lead to a variation in Mössbauer parameters of ∼0.05 mm s^–1, which would have led to a ∼20% increase in the broadness of the right line of the spectra, as indicated by simulations (Figures S-3 and S-4). The fact that this broadening was not observed implies that the deviations between the geometries of independent molecules in the X-ray crystal structure are not real despite the good R value of 5.4% of the crystal structure. These results emphasize the importance of confirming crystallographic conclusions using an independent measure, whether spectroscopic or computational (or both). Of course, using the DFT-optimized structure is not without danger either, as DFT optimization can give inaccurate geometries, particularly in cases of low-lying excited states, ambiguous spin states, and shallow potential energy surfaces.

Ferrocene presents another interesting test case because the Cambridge Structural Database contains 27 different crystal structures of this molecule, including a polymorph with staggered Cp rings (“staggered 1 & 2”) with two refinements of the same data, a second similar polymorph (“staggered 3”), and a separate structure with eclipsed Cp rings (“eclipsed 1”).³⁴ Because we were unsure of the effect of crystal packing, we independently collected both solid and solution Mössbauer spectra on purified ferrocene samples at 80 K (Figures S-1 and S-2), and both spectra were virtually identical with isomer shifts of 0.53 mm s^–1 and quadrupole splittings of 2.41 mm s^–1 (2.40 mm s^–1 for frozen toluene solution). These match well with the solid-state parameters reported by Foyt et al. at 78 K.²⁷ The minimal difference between the solid-state spectrum and frozen solution spectrum suggests that there is little influence of crystal packing effects on the Mössbauer parameters. Despite the similarity of the experimental parameters for solid-state and solution samples, we observed variation in the H-atom only optimized structures on the order of 0.05 mm s^–1 but only 0.001 mm s^–1 variation in the fully optimized DFT structures (Table 8). The quadrupole splitting for the H-atom only optimizations varied by nearly 0.30 mm s^–1, whereas in the fully optimized structures they varied by only 0.01 mm s^–1. Interestingly, calculations on atomic positional parameters from two different reported refinements of the same neutron diffraction data³⁴ (staggered 1 & 2) led to isomer shifts that differed by more than 0.04 mm s^–1 with both basis sets. These results are consistent with those of the nitrile complex described above, and further support the conclusion that use of an unoptimized geometry from an X-ray crystal structure introduces a source of error when predicting Mössbauer parameters.

Table 8. Comparison of Calculated Parameters for Multiple Geometries from a Single Crystal Using Fully Optimized DFT Geometries and H-Atom Only Optimized Geometries.

structure	exp. IS (mm s–1)	calc. ρ(0)-13780 def2-TZVPa	calc. ρ(0)-14760 CP(PPP)a	exp. |ΔEQ| (mm s–1)	calc. |ΔEQ| def2-TZVP	calc. |ΔEQ| CP(PPP)
FeCp2 staggered 1 H-onlyb,c	0.53	1.621 (0.661)	2.740 (0.668)	2.41	2.64	2.98
FeCp2 staggered 2 H-onlyb,c		1.491 (0.703)	2.603 (0.709)		2.86	3.22
FeCp2 staggered 3 H-onlyd		1.477 (0.707)	2.589 (0.713)		2.91	3.27
FeCp2 staggered 1b,c		1.555 (0.682)	2.674 (0.688)		2.60	2.97
FeCp2 staggered 2b,c		1.555 (0.683)	2.671 (0.689)		2.61	2.97
FeCp2 staggered 3d		1.554 (0.683)	2.671 (0.689)		2.61	2.97
FeCp2 eclipsed 1 H-onlye		1.441 (0.719)	2.548 (0.726)		2.71	3.09
FeCp2 eclipsed 1e		1.598 (0.669)	2.713 (0.676)		2.49	2.87

^aValues in parentheses are the predicted isomer shifts based on the parameters for the correlations given above. Three decimals places are given to demonstrate the similarity for the DFT fully optimized structures and are not significant.

^bStructures from ref (34a).

^cStructures are from two refinement methods of neutron diffraction data.

^dStructure from ref (34b).

^eStructure from ref (34c).

We note that for Cp₂Fe, both the optimized and nonoptimized structures gave a substantial difference in the experimental versus computed isomer shifts (0.53 vs 0.68 mm s^–1) (see below). This is not from a problem with the reported experimental Mössbauer parameters because we independently verified the Mössbauer spectrum (see Supporting Information). We also evaluated whether an eclipsed structure of ferrocene could give rise to the difference. Both an H-atom only optimization and a full DFT optimization of an eclipsed D_5h structure led to isomer shift values very similar to those computed for the staggered structure (<0.02 mm s^–1 difference) consistent with the results reported by Nemykin for the two conformers.^9a Therefore, the structure does not account for the 0.15 mm s^–1 difference between theory and experiment. We do not yet have an explanation for this large deviation, as Nemykin was able to reproduce the experimental isomer shift using B3LYP with Wacheter’s full electron basis set.^9a

Overall, despite the low accuracy of the computations for the prediction of the isomer shift for ferrocene and the quadrupole splitting for L^MeFe(NC^tBu)₂, in each case, the variation in predicted Mössbauer parameters observed in H-atom optimized structures had lower precision than the fully optimized structures. These two case studies demonstrate the importance of full optimization prior to prediction of parameters.

Limitations of the Computational Protocol

Cp and associated derivatives are prevalent ligands throughout inorganic and organometallic chemistry. Ferrocene, a classic example of such Cp compounds, has been examined by DFT calculations previously and attempts to predict the isomer shift have led to deviations from experiment for other authors as well.^9a,9d Using the protocols in this report, we examined ferrocene as well as a recent coordination compound [Cp*Fe(S₂Ph)(N₂H₂)FeCp*]⁻ that contains pentamethylcyclopentadienyl (Cp*). In both cases, the fully optimized geometry matched well with the reported crystal structure and no significant deviations in bond distances were observed. Despite geometric agreement between experimental and computed structures, the predicted isomer shifts for these compounds were overestimated by computations by >0.15 mm s^–1, whereas the predicted quadrupole splittings generally compared quite well with experiment (<10% deviation) (Table 9). On the basis of these results, we do not recommend use of these conditions for prediction of Mössbauer parameters for compounds with Cp-based ligands as there is a systematic error in the isomer shift when compared with that of the experiment. Pápai et al. found better agreement for ferrocene with use of Slater-type (STO) TZP all electron basis set regardless of the functional employed.^9d,9h

Table 9. Comparison of Experimental and Predicted Parameters for Cp Iron Complexes.

structure	ferrocene (staggered)	ferrocene (eclipsed)	[Cp*Fe(S2Ph)(N2H2)FeCp*][PF6]
exp. IS (mm s–1)	0.53		0.29
δ def2-TZVP (mm s–1)	0.68	0.67	0.47
δ CP(PPP) (mm s–1)	0.69	0.68	0.47
exp. |ΔEQ| (mm s–1)	2.41		0.74
|ΔEQ| def2-TZVP (mm s–1)	2.61	2.49	0.80
|ΔEQ| CP(PPP) (mm s–1)	2.97	2.87	0.82

We did not observe consistent deviations for other ligand classes, but we note that low-coordinate N-heterocyclic carbene complexes (NHC) and cyclic alkyl amino carbene (cAAC) complexes showed sporadic larger deviations in both isomer shift (>0.1 mm s^–1) and quadrupole splitting (>0.8 mm s^–1). We also looked for systematic deviations associated with the formal oxidation state of iron and the coordination number of the iron (Tables 10 and 11). On the basis of formal oxidation states, the two basis sets examined have comparable accuracies across all oxidation states with predictions for iron(II) compounds having the greatest errors in predicted isomer shifts when using def2-TZVP. Previous studies have noted iron(II) compounds with S = 1 or 2 can have low-lying excited states or electronically degenerate ground states that can affect the calculated parameters,¹⁰ but we made no special efforts to account for these effects in this study. The results based on the coordination number at iron were comparable for both basis sets for all coordination numbers (2–6). Overall, def2-TZVP performed better than CP(PPP) for most coordination numbers for quadrupole splitting predictions, except 4-coordinate where CP(PPP) was slightly (1.6%) better.

Table 10. Error Statistics for Mössbauer Parameter Predictions Based on the Formal Oxidation State of Iron.

	Def2-TZVP			CP(PPP)
formal ox. state	MAE δ (mm s–1)a	MAE |ΔEQ| (mm s–1)b	% error in |ΔEQ|c	MAE δ (mm s–1)a	MAE |ΔEQ| (mm s–1)b	% error in |ΔEQ|c
0 (2)d	0.031	0.088	3.5	0.028	0.284	11.4
1 (11)d	0.032	0.321	13.0	0.036	0.365	14.7
2 (16)d	0.081	0.291	11.7	0.054	0.325	13.1
3 (2)d	0.046	0.102	4.1	0.069	0.070	2.8

^aMAE between predicted and experimental values in isomer shift.

^bMAE between predicted and experimental values in quadrupole splitting.

^cAverage percent error between predicted and experimental values for quadrupole splitting.

^dNumber of compounds examined with the specified formal oxidation state.

Table 11. Error Statistics for Mössbauer Parameter Predictions Based on the Coordination Number at Iron.

	Def2-TZVP			CP(PPP)
C.N. at Fe	MAE δ (mm s–1)a	MAE |ΔEQ| (mm s–1)b	% error in |ΔEQ|c	MAE δ (mm s–1)a	MAE |ΔEQ| (mm s–1)b	% error in |ΔEQ|c
2-coord. (2)d	0.061	0.568	22.9	0.059	0.595	24.0
3-coord. (9)d	0.036	0.371	14.9	0.031	0.406	16.4
4-coord. (11)d	0.039	0.29	11.7	0.040	0.251	10.1
5-coord. (9)d	0.047	0.223	9.0	0.045	0.329	14.3

^aMAE between predicted and experimental values in isomer shift.

^bMAE between predicted and experimental values in quadrupole splitting.

^cAverage percent error between predicted and experimental values for quadrupole splitting.

^dNumber of compounds examined with the specified C.N.

Distinguishing Spin States Using Mössbauer Correlations

The spin state of a metal center affects the electron distribution within the d-orbital manifold, which in turn influences the isomer shift and quadrupole splitting parameters. Therefore, in cases where the magnetization of a sample is not easily measured or the compound of interest is present in a mixture with other paramagnetic compounds, we hypothesized that DFT calculations can be used to compare computed Mössbauer parameters for various spin states with experimental parameters. Pápái has previously examined the accuracy of quadrupole splitting parameter predictions in spin-crossover compounds wherein two spin states have been experimentally observed.^9d Long explored prediction of Mössbauer parameters for known high- and low-spin pyrazolylborate complexes and clustering of computed parameters was observed based on spin state.^9g We examined the sensitivity of the predicted Mössbauer parameters toward changes in spin state for three of the complexes in the test set: one high spin, one intermediate spin, and one low spin. Each structure was optimized in the high spin, intermediate spin (when applicable), and low spin configurations, and then the Mössbauer parameters were computed (Table 12).

Table 12. Comparison of Computed ⁵⁷Fe Mössbauer Parameters for Various Spin States for Three β-Diketiminate Complexes.

compound	Sa	exp. δb	calc. δ def2-TZVP (mm s–1)c	calc. δ CP(PPP)/def2-TZVP (mm s–1)d	exp. |ΔEQ| (mm s–1)e	calc. |ΔEQ| def2-TZVP (mm s–1)f	calc. |ΔEQ| CP(PPP)/def2-TZVP (mm s–1)g	T (K)h	refj
LtBuFeCH3	1/2		0.22	0.24		1.11	1.40	80	(21)
	3/2		0.39	0.40		2.33	2.28
	5/2	0.48	0.47	0.48	1.74	2.14	2.10
MeLMe,MeFe(η5-Ind)k	1/2		0.58	0.58		3.70	3.91	80	(22)
	3/2	0.68	0.70	0.70	1.07	1.02	0.89
	5/2		0.79	0.80		2.15	2.23
MeLMe,MeFe(CO)3	1/2	0.12	0.12	0.13	0.77	0.79	0.89	80	(19)
	3/2		0.49	0.50		1.11	1.09

^aSpin state of the computed geometry.

^bExperimental isomer shift.

^cIsomer shift calculated using the def2-TZVP correlation fit parameters from Table 2.

^dIsomer shift calculated using the def2-TZVP/CP(PPP) correlation fit parameters from Table 2.

^eExperimental quadrupole splitting.

^fCalculated quadrupole splitting using the def2-TZVP basis set.

^gCalculated quadrupole splitting using the def2-TZVP/CP(PPP) basis set combination.

^hCollection temperature for the experimental parameters.

^jReference with the experimental parameters and crystal structure.

^k“Ind” represents indenyl (C₈H₇).

Using our favored protocol with def2-TZVP as the basis set on iron, the isomer shift became more positive as the total spin increased as is expected.³ The average difference between computed isomer shifts between spin states was 0.17 mm s^–1 with a minimum difference of 0.08 mm s^–1, values that are 5 and 2 times the MAE for the correlation with β-diketiminate complexes described above. The average difference in quadrupole splitting was 1.11 mm s^–1 for different spin states with a minimum difference of 0.18 mm s^–1. The average difference is 4 times larger than the MAE for predicted quadrupole splittings in β-diketiminate complexes (0.27 mm s^–1), whereas the minimum difference is about half of this error. In all three cases, comparison of the optimized geometry and computed Mössbauer parameters agree best with experiment for the spin state that has been experimentally determined. This suggests that computations can indeed aid in determining the spin state of a compound, and we encourage the use of this protocol for compounds whose magnetic susceptibility or spin state cannot be determined by more rigorous means.

Truncating Computational Models

Sterically bulky ligands are often used to control the geometry, solubility, or other properties of iron complexes. However, the size of these ligands greatly increases the computational cost. Therefore, it is common to use truncated computational models to increase the speed of calculations; we have pursued this route with many diketiminate complexes.³⁵ As part of our evaluation, we tested whether truncation can harm the validity of the computed Mössbauer parameters. Specifically, we tested the influence of truncation on the accuracy of the predicted spectral parameters for three complexes with different bulky ligands (Figure 4 and Table 13).

Figure 4.

Complexes examined for effects of ligand truncation on Mössbauer parameter prediction. (a) L^tBuFe(HCCPh), (b) (SiP^iPr₃)FeCOSi(CH₃)₃, (c) L^S,SFe(THF)₂.

Table 13. Calculated Mössbauer Parameters for Truncated Models of Select Compounds.

compound	trunca	exp. δb	calc. δ def2-TZVP (mm s–1)c	calc. δ CP(PPP)/def2-TZVP (mm s–1)d	exp. |ΔEQ| (mm s–1)e	calc. |ΔEQ| def2-TZVP (mm s–1)f	calc. |ΔEQ| CP(PPP)/def2-TZVP (mm s–1)g	T (K)h	refj
LtBuFe(HCCPh)	none	0.44	0.47	0.48	2.05	2.53	2.44	4.2	21
	1		0.44	0.45		2.58	2.52
	2		0.44	0.45		2.73	2.59
	3		0.45	0.47		2.81	2.69
(SiPiPr3)FeCOSi(CH3)3	none	0.06	0.08	0.08	1.12	1.12	1.41	80	24
	1		−0.03	−0.03		1.19	1.47
	2		–0.038	–0.033		1.25	1.55
	3		0.01	0.00		1.10	1.44
LS,SFe(THF)2	none	0.89	0.78	0.79	3.77	3.81	3.99	80	21
	1		0.81	0.81		3.94	4.07
	2		0.82	0.82		3.80	3.92

^aTruncation level, which corresponds to the structures shown in Figure 4.

^bExperimental isomer shift.

^cIsomer shift calculated using the def2-TZVP correlation fit parameters from Table 2.

^dIsomer shift calculated using the def2-TZVP/CP(PPP) correlation fit parameters from Table 2.

^eExperimental quadrupole splitting.

^fCalculated quadrupole splitting using the def2-TZVP basis set.

^gCalculated quadrupole splitting using the def2-TZVP/CP(PPP) basis set combination.

^hCollection temperature for the experimental parameters.

^jReference with the experimental parameters and crystal structure.

Comparison between a DFT optimized geometry and the geometry of the solid-state molecular structure is the most commonly used metric for assessing the validity of a truncated DFT model. In these three examples, a variety of degrees of truncation did not lead to significant deviations from the X-ray structure and, with L^S,SFe(THF)₂, even led to metrics more similar to the crystal structure (Table 14). The predicted isomer shifts in two of the three cases exhibited very little change (≤0.04 mm s^–1). The third case, (SiP^iPr₃)FeCOSi(CH₃)₃, exhibited the largest deviations upon truncation (∼0.1 mm s^–1), which is on the order of errors observed for non-β-diketiminate compounds using the correlations established in this work. The predicted quadrupole splittings did not deviate greatly upon increased truncation for the three examples: it is less than the error for the quadrupole splitting predictions observed for the set of compounds. In each case, the computational time was an order of magnitude less for the greatest degree of truncation compared with that of the parent complex. Thus, the cost in accuracy from truncation appears to be limited relative to the great advantage in computational resources, but all truncation should be done with caution because there are sometimes deviations in the calculated parameters that do not appear to correlate with observed geometry deviations.

Table 14. Average First Coordination Sphere Bond and Angle Deviations from X-ray Structures for Truncated Models.

compound	trunc.a	avg. bond dev.b (%)	avg. angle dev.c (%)	max bond dev.d (%)	max angle dev.e (%)
LtBuFe(HCCPh)	none	1.7	2.8	2.5	3.8
	1	2.1	3.1	2.8	4.4
	2	2.3	2.5	2.8	4.7
	3	2.2	2.1	3.5	4.0
(SiPiPr3)FeCOSi (CH3)3	none	0.9	1.4	1.6	4.8
	1	2.3	4.4	4.0	21.2
	2	2.4	3.9	3.9	22.8
	3	2.6	4.0	4.0	24.6
LS,SFe(THF)2	none	2.3	3.7	3.7	12.7
	1	1.9	3.3	3.9	11.9
	2	1.9	2.6	4.3	7.4

^aTruncation level which correspond to the structures shown in Figure 4.

^bAverage percent deviation of bonds in the first coordination sphere about iron from the crystal structure.

^cAverage percent deviation of angles in the first coordination sphere about iron from the crystal structure.

^dMaximum percent deviation of bonds in the first coordination sphere about iron from the crystal structure.

^eMaximum percent deviation of angles in the first coordination sphere about iron from the crystal structure.

Conclusions

DFT calculations on β-diketiminate compounds with various spin states, geometries, and ligand spheres were used to establish correlations for the prediction of Mössbauer isomer shifts using a set of standard optimization conditions. Our results indicate that def2-TZVP and CP(PPP) are similar in their predictive ability, and the former is preferable due to greater computational expediency. Full geometry optimizations are essential. The predictive power of the correlations was tested with a test set of β-diketiminate complexes as well as a variety of other iron complexes using the same procedure. These correlations have a mean average error (MAE) of 0.035 mm s^–1 for β-diketiminate complexes, an improvement from other previously reported conditions and 0.05 mm s^–1 for all compounds tested, which is comparable to other correlations. Quadrupole splitting parameters were also calculated for the compounds tested showing good agreement with experiment with MAE of 0.30 mm s^–1 for all compounds.

We also tested other factors, such as the use of X-ray geometries and truncation of computational models. We found DFT geometry optimization to be extremely important for obtaining reliable values in the cases we tried. However, it should be remembered that the optimized geometry can be predicted poorly by DFT, and so care should be taken. Comparison of experimental Mössbauer parameters with the computed results from different spin states successfully reproduced experiment in three of three test cases; thus, these computations are powerful in their ability to support spin-state assignment. Similarly, we examined the effects of truncation of large ligands, which showed that even major truncation led to <5% change in geometry metrics around the metal center and minimal changes in Mössbauer parameters predicted. Overall, we anticipate that the protocols established here will assist others for using Mössbauer spectroscopy coupled with computations for reliable characterization of new compounds.

Computational Details

DFT calculations were performed with the ORCA program package, version 3.0.3.¹³ Optimized geometries were computed using the BP86 functional.³⁶ Atom-pairwise dispersion correction with the Becke–Johnson damping scheme (D3BJ),³⁷ the scalar relativistic zero-order regular approximation (ZORA),³⁸ and the scalar relativistically recontracted version of the Aldrichs triple-ζ basis set, def2-TZVP,³⁹ were used on all atoms. Mössbauer parameters were calculated using the B3LYP⁴⁰ functional with either all atoms modeled with the def2-TZVP basis set or a combination of the CP(PPP) for the iron atom with all other atoms modeled with def2-TZVP. It was important to test both because CP(PPP)^6b,6e,9b has been reported as best for calculation of the electronic properties in independent benchmark studies by Neese and Pápai, but has significantly higher resource costs.^9b,9d The conductor-like screening model⁴¹ (COSMO) was used to simulate a toluene solution (ε = 2.4). The choice of solvent model was used to best simulate the environment of organometallic complexes and β-diketiminate complexes in the solid state, wherein the aryl groups of the supporting ligands are most generally the closest contacts between molecules. Resolution of identity (RI) was used to approximate two electron integrals, but this was used only for geometry optimizations; the calculations of Mössbauer parameters did not use RI because we have observed substantial variations in calculated Mössbauer parameters when RI is used. Geometry optimization started from the X-ray crystallographic models and was tightly converged (TightOpt). The SCF calculations were tightly converged (TightSCF) with unrestricted spin (UKS). Numerical integrations during all DFT calculations were done on a dense grid (ORCA grid4), and for Mössbauer calculations a very dense grid (ORCA grid 7) was used on the iron atoms. The calculated structures were confirmed to be minima on the potential energy surfaces by the absence of imaginary frequencies after numerical frequency calculations on the optimized structures. Noncoordinating counterions and solvent were not included in the calculations because previous studies have demonstrated that these have a minimal effect on the calculated Mössbauer parameters.^9b,9c,9e,42

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b00595.

• Mössbauer spectra of ferrocene, computational method, optimized structures, and input files (PDF)

This work was supported by the National Institutes of Health (GM065313 to P.L.H.; GM116463 to S.F.M.).

The authors declare no competing financial interest.