Abstract
Changes to cognition, including memory, following radiation exposure are a concern for cosmic ray exposures to astronauts and in Hadron therapy with proton and heavy ion beams. The purpose of the present work is to develop computational methods to evaluate microscopic energy deposition (ED) in volumes representative of neuron cell structures, including segments of dendrites and spines, using a stochastic track structure model. A challenge for biophysical models of neuronal damage is the large sizes (>100 μm) and variability in volumes of possible dendritic segments and pre-synaptic elements (spines and filopodia). We consider cylindrical and spherical microscopic volumes of varying geometric parameters and aspect ratios from 0.5 to 5 irradiated by protons, and 3He and 12C particles at energies corresponding to a distance of 1 cm to the Bragg peak, which represent particles of interest in Hadron therapy as well as space radiation exposure. We investigate the optimal axis length of dendritic segments to evaluate microscopic ED and hit probabilities along the dendritic branches at a given macroscopic dose. Because of large computation times to analyze ED in volumes of varying sizes, we developed an analytical method to find the mean primary dose in spheres that can guide numerical methods to find the primary dose distribution for cylinders. Considering cylindrical segments of varying aspect ratio at constant volume, we assess the chord length distribution, mean number of hits and ED profiles by primary particles and secondary electrons (δ-rays). For biophysical modeling applications, segments on dendritic branches are proposed to have equal diameters and axes lengths along the varying diameter of a dendritic branch.
Keywords: space radiation, hadron therapy, track structure models, heavy ions, galactic cosmic rays, neuronal dendrites and spines, cognitive changes, central nervous system effects
1. Introduction
Radiation induced impairment of cognition, including changes to memory, involves damage to neuronal cells in the hippocampus and pre-frontal cortex (Greene-Schloesser et al 2012, Cacao and Cucinotta 2016a, Cacao and Cucinotta 2016b, Chakraborti et al 2012, Parihar et al 2015a). Cognitive changes after irradiation with protons and heavy ions are of concern in cancer treatment with particle beams and space radiation exposures to astronauts (Cucinotta et al 2014). The dendrite and synaptic elements of neurons are the locations of chemical and electrical processes central to neuronal cell communication and have been reported to be modified by low doses of protons, heavy ions, and X-rays (Shirai et al 2013, Raber et al 2016).
In this paper we discuss methods to predict ED in microscopic volumes of spherical and cylindrical geometries with the goal of developing models of radiation damage to dendrites and spines of neuron cells. At this time very little is known about the mechanisms leading to changes in dendritic morphology or spine density in neuron cells and how radiation quality dependent effects are manifested (Parihar et al 2014, 2015a, 2015b). Possible mechanisms are direct energy deposition, initial and persistent production of reactive oxygen species (ROS), microglial activation and neuro-inflammation. From published experimental studies with X-rays, protons, and heavy ions, there are clear dependences on radiation quality and dose to the changes observed (Parihar and Limoli, 2014, Parihar et al 2015a; 2015b), which suggest track structure plays an important role in changes to dendritic morphology.
An important computational challenge is the large spatial extent of the dendritic arbors of neuronal cells, which are typically 100’s of microns and dependent on neuronal cell type. Furthermore, possible geometric parameters describing dendrites and spines will be of varying diameter and length. The track structure of high energy particles consists of a core of high ED events close to the particle track (<10’s of nm) and a penumbra of secondary electrons denoted as δ-rays produced through ionization that may extend for 1000’s of microns or more from a primary particles path dependent on the particle velocity and kinematic constraints. Therefore computational approaches must ultimately be developed for microscopic volumes of variable sizes with significant heterogeneity in microscopic ED for different radiation types and primary particle fluence or absorbed dose.
In our previous work we considered details of neuron cell geometries, which have tree like cellular architecture (Ascoli 2006, Cucinotta et al 2014, Alp et al 2015) using a stochastic model of radiation track structure (RITRACKS) which has been show have good agreement with experiments for ionization and excitation cross sections for particles and electrons, LET, and nano-dosimetry measurements (Plante and Cucinotta, 2008; 2019; 2010). Dendritic branches of neurons like cylindrical pipes extend from the cell’s soma and branch out with initial diameter at the range of 2 to 3 microns and thin out at distal ends reaching the light resolution limit to approximately 0.4 micron in microscopy studies (Meijering 2010). Geometrical reconstruction of neuron branches can be made using right circular cylindrical segments of varying length and diameter, with a 3D structure constructed by rotation of azimuthal angle of consecutive segments (Ascoli et al 2007, Ascoli 2015). Continuously varying diameters of dendrites segments sets a biological constraint on geometry and axes lengths of cylinders, which are determined by reconstruction processes in experimental studies, including sectioning of samples and image processing (Kubota et al 2009, Peng et al 2011).
An aim of this paper is to investigate optimal axis length of dendritic segments to evaluate microscopic ED and hit probabilities along the dendritic branches at a given macroscopic dose. The diameter of a dendritic section is a structural constraint on a dendritic branch and can vary from >5 μm close to the soma to <0.5 μm at the further tips of dendrite branches. We consider four cylindrical segments with different aspect ratios (ARs) that are chosen to represent dendritic sections close to soma (thicker diameter with different axes lengths), distal end (thinner diameter, long axis length) and very small protrusions on dendrites (both small diameter and axis length). The presentation of dosimetric parameters of the same volume spheres highlights the effects of ARs in cylinders (Kellerer 1981). An analytical method is also developed to find the mean primary particle microscopic dose in spheres for a given macroscopic dose. The fast analytical method can complement lengthy numerical studies of dose distributions for a given volume. Contributions of the primary core region and δ-rays in the penumbra to the ratio of hits and ED to micro-volumes (Vmicro) are investigated by stochastic Monte-Carlo sampling. The probability (or mean number) of hit(s) by primary beam and δ-rays, chord length distribution of primary beam, distance between δ-ray hits to micro-volumes (impact parameter), and the variance of ED for given geometrical structure are described. This information for the same volume structures can be used to interpret the effects of radiation quality or linear energy transfer (LET) for a given absorbed dose or particle fluence (Kellerer and Chmelevsky 1975, El Naqa et al 2012, Palmans et al 2014). The methods developed herein are applicable to a wide variety of particle types. For Hadron therapy applications we focus on the particle beams; proton, 3He and 12C with kinetic energies of 32, 38, and 59 MeV/n, respectively corresponding to 1 cm from the Bragg peak, which are also important components of space radiation exposures.
2. Materials and methods
2.1. Stochastic track structure with RITRACKS Monte-Carlo simulation tool
The ED events from particle tracks are simulated with RITRACKS (Plante and Cucinotta 2008, 2009), a Monte-Carlo based computer model that calculates the positions of ED events due to ionization and excitation as a particle traverses a medium assumed to be water. The stochastic simulation environment for a given charged particle with an initial energy, propagation direction (e.g. along the z-axis) and entrance point, e.g. (0,0,0) creates ED events at varying positions for the initial particle and the created secondary electrons denoted as δ-rays, which are correlated with the particles path. Energy deposition events are lumped within a predetermined voxel size of 20 nm3. The total ED in a voxel and its coordinates are an output value from the simulation. For a predetermined track length, voxel ED values and their coordinates are calculated, which includes contributions from the primary particle track and δ-rays. This stochastic process is repeated a large number of times using Monte-Carlo techniques with the same initial conditions to create a library of histories for a particle’s ED events.
2.2. Target volume and particle beam simulation geometry
Our simulation platform is designed as the cylindrical or spherical target micro-volume, Vmicro is fixed for randomly distributed particle beams. We consider four equivalent micro-volumes represented by right circular cylinders or spheres with of density. The cylinders and spheres that are labeled as Cyli, Sphi, i=1,2,3,4 have the same volume for given indices. The cylinder height (H), diameter (dCyl), the corresponding ARs defined as H/dCyl and the sphere diameter (dSph) are listed in table 1. The circular base of each cylinder in Cartesian coordinates is located on the x-y plane centered at (0,0,0) and the mass center of the cylinder and the same volume sphere are at (0,0,H/2) along the z-axis.
Table 1.
Geometric factors of the micro-volumes.
| Geometric Descriptor | Vmicro,1 | Vmicro,2 | Vmicro,3 | Vmicro,4 |
|---|---|---|---|---|
| Vmicro (μm3) | 0.085 | 1.131 | 2.011 | 5.655 |
| Sphere: dSph (μm) | 0.545 | 1.293 | 1.566 | 2.210 |
| Cylinder: (H, dCyl) μm, H/dCyl | (0.3, 0.6), 0.5 | (1, 1.2), 0.833 | (4, 0.8), 5 | (5, 1.2), 4.167 |
2.3. Particle beam arrangement
Particle beams of length LBeam (0, LBeam) on the z-axis are constructed from randomly selected 20 μm track histories to comprise a longer track length as described previously (Alp et al 2015). An entrance point for a beam on x-y plane with radius RBeam is randomly chosen. First, the beam is translated by (−LBackward+H/2) on z-axis, then randomly rotated with respect to (0,0,H/2) point. The LBeam and RBeam range for (1H, 3He, 12C) are chosen as (120, 160, 200) μm and (40, 60, 70) μm, respectively. The LBackward is taken as 0.23×LBeam upon analyzing figure S.1 given in the Supplementary information file.
2.4. Scoring algorithm
The scoring algorithm for each random particle beam and Vmicro calculates the chord length (LCh) of a beam crossing, total number of voxels, and total ED per beam. We also consider the so-called LET approximation where a stochastic beam (BeamStch) is reduced to a line (BeamLine) and calculate the chord length; the length section bounded by Vmicro, and if there is a line crossing the volume it is recorded as ‘primary beam hit’. The BeamStch that constitutes voxel coordinates and deposited energy of each voxel is run on a coincidence algorithm to find if any voxels are bounded by the Vmicro. The total number of voxels and total voxel energy per beam are recorded as primary beam properties if there is a LCh value otherwise it is categorized as ‘δ-ray hit’. This rule assigns some tangent BeamStch lines to Vmicro as δ-ray hits. If there is a primary beam and multiple δ-ray crossings all voxel number and total energy values are recorded as primary beam properties as the presence of the LCh has higher priority in the algorithm. Likewise, multiple δ-ray crossings are recorded as a single value if there is no LCh. However the low probability of a Vmicro hit per beam reduces the probability of multiple δ-ray crossings. The results of BeamStch and Vmicro coincidences were calculated and stored as a trial in a library during simulations. In addition, any number of random beams determined by the macroscopic dose can be chosen for statistical sampling to find dose to the Vmicro. The mean number of trials per Vmicro, per particle beam is 11.6 million in this study.
2.5. Theoretical formulation
The mean macroscopic (absorbed) dose D0,F (in units of Gy) of NF charged particles with LET (keV/μm) impinging on area AF (in units of μm2) is given with unit conversion factor 0.16 as,
| (1) |
The fluence of a particle, F, defined as one particle per area (in units of μm2), is given by,
| (2) |
The dose to a Vmicro with mean cross-sectional area, Amicro and total surface area Smicro embedded in larger volume of the uniform isotropic irradiation is calculated as described next.
In the LET approximation of the track, the mean number of primary particle hits, PP to Vmicro at a given fluence is a function of D0,F, LET, and geometric properties of Vmicro,
| (3) |
We denote, as the total ED events by a primary particle traversal and as the δ-ray dose for a single δ-ray hit. The mean number of δ-ray hits, Pδ is calculated by extensive numerical simulations, and the total number of hits are classified by RP and Rδ as the ratios of primary beam and δ-ray hits to total number of hits if there is a hit in a trial that satisfy RP+Rδ=1. Therefore, the mean number of hits to Vmicro by δ-rays at given D0,F is
| (4) |
The dose to Vmicro per hit, Dm,1 is the total energy deposited per unit mass for any type of hit to Vmicro and a combination primary, and ‘total δ-ray dose’, components,
| (5) |
where is
| (6) |
Finally, dose to Vmicro at absorbed dose, D0,F is
| (7) |
where and are the mean of the corresponding dose distributions. Monte-Carlo simulations provide distributions of , and values of Rδ to RP for a given spherical and right circular cylinder micro-volumes.
An analytical approach is developed to find the dose, applicable to spheres. We assign a constant value Ctrack that gives the contribution to energy deposition to Vmicro due to the stochastic track structure, which deviates from the LET approximation of a line. Then, is written
| (8) |
where the chord length, LCh,micro is confined by Vmicro. Expressions of mean chord length, mean cross-sectional area, for convex bodies at isotropic fluence, first discovered by Cauchy (Vickers and Brown, 2001) are given by
| (9) |
The estimate of Ctrack at any entry point on a sphere is described in the next section. The number of primary beam hits that Vmicro will receive at given D0,F is a Poisson process and for k hits the probability is given as
| (10) |
The mean primary dose, to Vmicro over all the hits at D0,F are evaluated as
| (11) |
where the is . Ctrack(0) is analytically calculated for a particle beam that passes through the center of a sphere in the next section.
2.6. Dose to sphere by analytical and stochastic approaches
If the radial profile of ED (figure S.1(a) at the Supplementary file) is known the contribution of ED to a given radial cross section on the same plane can be calculated analytically. Normalized radial ED (RNED) profiles of interest (1H, 3He, 12C) at given energies are numerically calculated. The RNED profiles will be taken as kernels for analytical dose calculations. Figure 1(a) and 1(b) have the complementary images of spherical Vmicro located at (0,0,0) point for analytical and stochastic presentations. The critical geometrical parameters are the radius of the sphere, Rmicro and the impact parameter, b, which is the normal distance between the center of the sphere and the particle beam. The beam can make a direct traversal (red solid arrow, figure 1(a)) or if there are contributions by δ-rays as seen in the volume in figure 1(b), black track structure. The blue curve indicates how the dose drops radially from the propagation direction for each beam. For a track segment longer than the ranges of backscattering and forward scattering distances by δ-rays at the point of interest, longitudinal electronic equilibrium is achieved (Alp et al 2015). The radial component, RNED function determines how source points of length Δzi at points Pi along the z-axis of propagating beam contribute to total dose. The radial contributions are confined to distances −Rmicro < Pi < Rmicro in figure 1(a). For a direct particle traversals (red arrow) source points Pi can be inside (P1) or outside (P2) the sphere. An example area surrounded by a black circle of point P3 for the outside-beam (black arrow) is also shown. Energy deposition contribution of source points P1 and P3 are numerically calculated in detail in panels figure 1(c) and 1(d), respectively. For a finite length energy source at P1 (figure 1(c)), RNED1 determines the ratio of ED in the circular area of radius r1 and the beam source to normal sphere distance b1. RNED(rk,θk) needs to be calculated over all equally spaced angles Δθ, (Δθ=2π/m) where m is the number of steps and (θk=kΔθ). RNED1 on panel figure 1(c) is calculated as;
| (12) |
with
| (13) |
Figure 1.
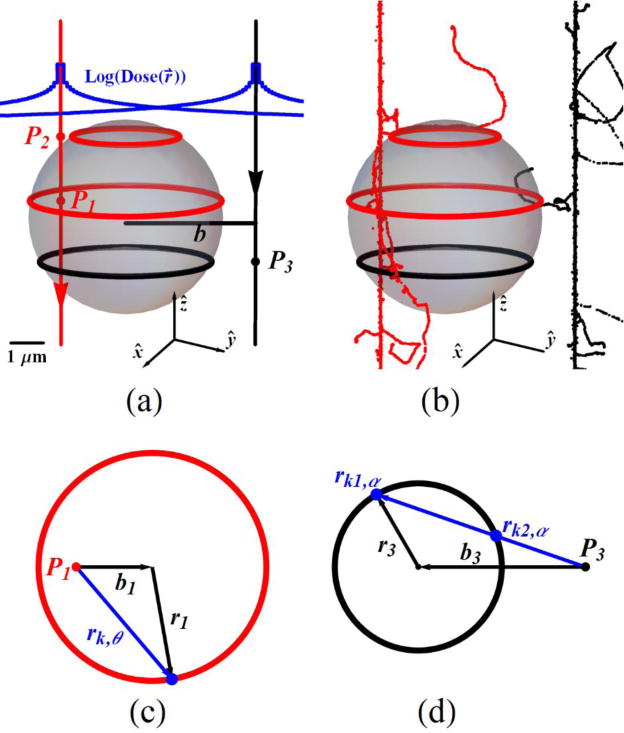
Analytical (a) and (b) stochastic dose calculation in a sphere of particle track beams. The track structure is presented for 12C at 59 MeV/n with a sphere of radius 3 μm (a), (b). The analytical dose calculation described in the text and its derivation from the stochastic simulation, Ctrack is calculated for the cases if track source point is inside (c) and outside (d) the segment of the sphere.
If a point source is outside the cross sectional area of interest, illustrated by the black circle with radius r3 and normal distance between the beam and the center of the circle b3 in figure 1(d), the distances rk1,α and rk2,α are calculated before these distances are substituted to RNED(rk,α). Here the difference RNED(rk2,αk) − RNED(rk,αk) is proportional to final mean value of RNED3. The proportionality constant is αmax = 2ArcSin(r3/b3) and αmax is divided to s pieces (Δα= αmax/s) to sum over αk (= kΔα) with the mean value of RNED3,
| (14) |
Finally, the dose calculated analytically for one particle in the sphere is found as,
| (15) |
where the discrete beam length is Δz = Rmicro/N and N is an integer. Comparing equation (8) with equation (15), shows that the track contribution factor, Ctrack is given by
| (16) |
where the factor of 2 in equation (16) accounts for the Δz stacks from −Rmicro to Rmicro. The Ctrack(0) on equation (11) is calculated at b = 0 to find the and this section covers a generalized traversal track at any point on a sphere.
The stochastic calculations in figure 1(b) are made in a straight forward manner. A long track segment, as discussed above, is constructed randomly out of 20 μm track histories from the RITRACKS code. The total ED to the sphere is calculated by first registering voxels bounded by the spherical volume, then summing all the voxel energies per trial to find the dose to sphere. Many trials (>10,000) are repeated to find mean values to compare with the analytical results.
3. Results
3.1. Chord length analysis of right circular cylinders
The four right circular cylinders (Cyl1 to Cyl4) in table 1 are investigated as sample micro-volumes (VCyl1 to VCyl4) with aspect ratios (=H/dCyl) that span a range of values (0.5 to 5.0). Figure 2(a,b) shows example of stochastic beams (voxels in red) of (1H, 12C) ions and BeamLine as black continuous lines. A primary beam hit by a proton to VCyl1 (figure 2(a)) and a δ-ray from a carbon ion passes through VCyl4 (figure 2(b)). Chord length distribution, f(LCh) for each VCyl in simulations are binned (red dots) to compare with analytical results (black lines) that were numerical evaluated in figure 2(c–f). The maximum chord length, LCh,max is the diagonal length of the cylinder. The f(LCh) is normalized by the LCh,max and named normalized chord length distribution, f(LCh,N) in figure 2. Analytical form of f(LCh) at given AR is independent of specific height or diameter values but depend on their ARs. Analytical expression of f(LCh) is worked out for convex bodies by Kellerer (1971, 1984, 1985) and an integral expression by Langworthy (1988) are used to plot the f(LCh) numerically. The mean value of chord length, for convex bodies is given by equation (9). The standard deviations (SD) of LCh for cylinders are calculated from numerically evaluated f(LCh) and listed in table 2 . The simulation results of for the same VCyl and the particles (1H, 3He, 12C) are presented as deviation from the analytical value in table 2. The two peaks on the f(LCh,N) are located at dCyl/LCh,max, H/LCh,max (LCh,max = (0.671, 1.562, 5.141, 4.079) μm in figure 2(c–f)) and the peak amplitudes are comparable around H/dCyl~1, similar to figure 2(c,d). The peaks unify at H=dCyl (LCh,N=0.7071) and the dCyl/LCh,max peak dominates for H>dCyl in figure 2(e,f). In addition, the coefficient of variation, CV (CV=SD/mean) for a right cylindrical geometry is minimum for aspect ratio of one. Similar visual plots can be found by Mader (1980). The range of CV (0.3536±3×10−6) is nearly equal at the aspect ratios of the cylinders studied.
Figure 2.
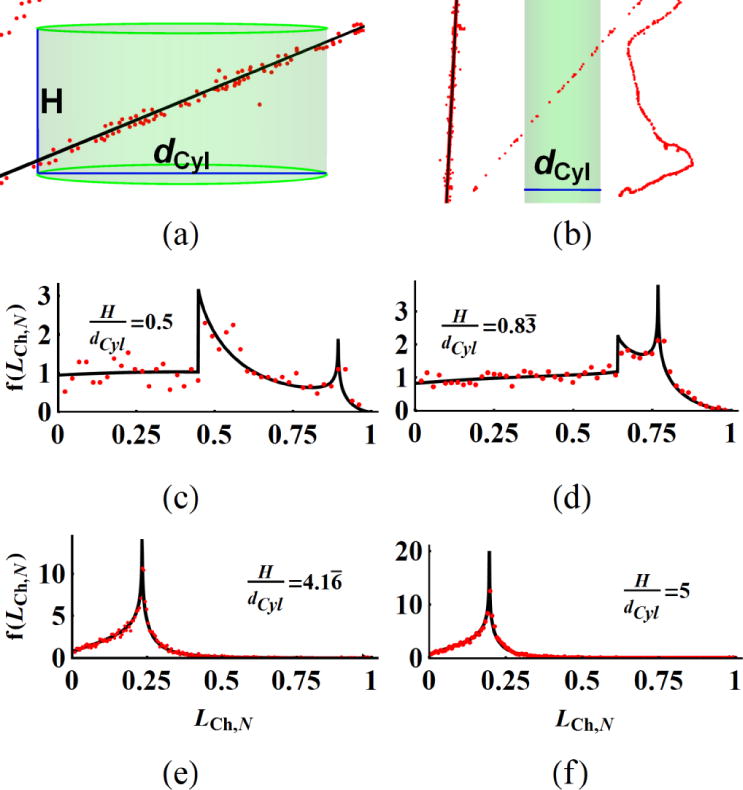
(a) Primary beam and (b) secondary electron tracks pass through the target cylinders and the chord length distribution of primary beam tracks normalized by the maximum length, f(LCh,N) are plotted for cylinders with different ARs (c–f). The red dots on (a,b) represents voxel coordinates and central black line is the line approximation of the same track. Black lines of f(LCh,N) are analytical and red dots are the binned simulation results (c–f) for 1H at 32 MeV.
Table 2.
Analytical and simulation results of mean chord lengths, .
| Geometric Descriptor | Vmicro,1 | Vmicro,2 | Vmicro,3 | Vmicro,4 | |
|---|---|---|---|---|---|
| Sphere: , mean±SD μm | 0.363±0.129 | 0.862±0.305 | 1.044±0.369 | 1.474±0.521 | |
| Cylinder: , mean±SD μm | 0.300±0.163 | 0.750±0.385 | 0.727±0.356 | 1.071±0.552 | |
|
|
1.211 | 1.149 | 1.435 | 1.375 | |
| Sphere: | 0.995±0.003 | 1.003±0.015 | 0.997±0.008 | 1.002±0.023 | |
| Cylinder: | 1.020±0.001 | 1.004±0.028 | 0.993±0.010 | 0.992±0.012 |
; Analytical result
; Simulation result
3.2. Chord length analysis of spheres
Figure 3(a) shows a stochastic primary beam of 3He at 38 MeV/n and BeamLine on VSph1. The chord length distribution f(s) for a sphere of diameter dSph is given by f(s) = 2s/dSph2 where 0<s<dSph. The mean±SD of LCh for a sphere is calculated as and LCh,max is dSph. Table 2 lists the analytical mean chord length and deviation of in simulation results as .
Figure 3.
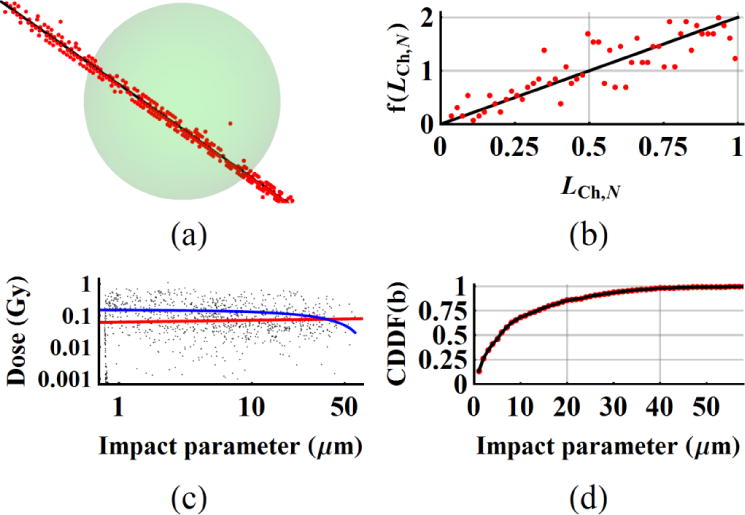
(a) A primary beam track, (b) the chord length distribution of primary tracks normalized by the maximum length, f(LCh,N), (c) as a function of impact parameter, b and (d) CDDF(b) of impact parameter are plotted for spherical target volumes. The results are presented for 3He beam and VSph1 (dSph=0.545 μm) in (a,b) and VSph3 (dSph=2.210 μm) in (c,d). The blue line in figure 4(c) shows the slope on linear scale which fits to a negative slope; 0.1504 – 0.00184×b Gy. Similarly, the slope on log-log scale plotted as a red line in figure 3(c), is positive valued; .
The dose deposition by δ-rays was investigated as a function of impact parameter b, normal distance between BeamLine and center of the sphere (figure 3(c,d)). The points close to RSph3 are generated by secondary electrons along the primary beam line. The δ-rays contribute to for up to about 45 μm for 3He in these simulations. A linear relation as a first approximation is sought between impact parameter and . The mean±SD of is 0.1329±0.1433 Gy. The slope on linear scale fits to a negative slope; 0.1504 – 0.00184×b Gy (blue line in figure 3(c)). Similarly, the slope on log-log scale plotted as a red line in figure 3(c), is positive valued; . Our investigation on all the spheres and particles did not provide conclusive evidence on how the distribution changes with impact parameter.
The energy per voxel increases at the end of a δ-ray track as the electron energy decreases (Cucinotta et al 1998). The mean±SD of voxel numbers of secondary electrons, is 33.14±26.35 and the high number of voxel number per hit may explain the averaging effect over many voxels. As a result, the magnitude of displays a spatial distribution which is independent of impact parameters for given Vmicro ranges. Cumulative dose distribution function (CDDF(b)) as a function of impact parameter in figure 3(d) shows that 50% of events takes place at 4.64 μm from the surface of the sphere with a radius of 0.783 μm.
3.3. Dose deposition profiles in cylindrical and spherical micro-volumes
Tables 3 and 4 include the relevant quantities obtained by simulation results for all the Vmicro. The ratios of hits by primary beam, RP and δ-rays, Rδ for a given particle in Vmicro provide a partition of ED events between primary and δ-ray events. The ratio, Rδ/RP represents the number of hits by δ-rays per primary particle. The mean ratio for (1H, 3He, 12C) particles of all the Vmicro are (0.202±0.031, 0.711±0.063, 5.024±0.313). Division of the mean of these ratios by the LET of the particles results in (0.112, 0.116, 0.125) μm/keV.
Table 3.
Simulation statistics for cylindrical micro-volumes.
| Parameter | Particle | VCyl1 | VCyl2 | VCyl3 | VCyl4 | |
|---|---|---|---|---|---|---|
| RP | 1H | 0.818 | 0.850 | 0.837 | 0.858 | |
| 3He | 0.566 | 0.586 | 0.600 | 0.611 | ||
| 12C | 0.177 | 0.164 | 0.170 | 0.177 | ||
| Rδ | 1H | 0.182 | 0.150 | 0.163 | 0.142 | |
| 3He | 0.434 | 0.414 | 0.400 | 0.389 | ||
| 12C | 0.823 | 0.836 | 0.830 | 0.823 | ||
|
|
1H | 0.8840±0.8916 | 0.1661±0.1466 | 0.0898±0.0852 | 0.0469±0.0400 | |
| 3He | 2.8070±2.1710 | 0.5340±0.3516 | 0.2954±0.1938 | 0.1532±0.0975 | ||
| 12C | 16.9956±10.0948 | 3.6098±1.7878 | 1.8049±0.9395 | 0.9816±0.5352 | ||
|
|
1H | 0.9365±1.5520 | 0.1827±0.2199 | 0.0944±0.1171 | 0.0483±0.0551 | |
| 3He | 0.9827±1.4152 | 0.1745±0.2107 | 0.0952±0.1148 | 0.0476±0.0538 | ||
| 12C | 0.9967±1.5008 | 0.1646±0.2173 | 0.0855±0.1158 | 0.0436±0.0548 | ||
| 1H | 54.22±63.84 | 52.27±30.48 | 51.73±31.24 | 52.00±30.41 | ||
| 3He | 131.90±74.70 | 127.21±70.30 | 129.16±70.30 | 128.82±70.35 | ||
| 12C | 264.22±146.22 | 304.89±148.69 | 282.03±146.20 | 296.15±160.50 | ||
| 1H | 30.08±33.70 | 33.46±31.44 | 31.42±33.47 | 30.73±28.37 | ||
| 3He | 33.40±32.43 | 32.84±28.71 | 32.01±28.14 | 31.04±27.51 | ||
| 12C | 33.74±33.96 | 30.86±29.06 | 29.45±28.71 | 29.41±27.56 | ||
|
|
1H | 31.17 | 31.84 | 32.29 | 31.60 | |
| 3He | 37.60 | 39.56 | 39.51 | 39.24 | ||
| 12C | 112.81 | 111.59 | 110.58 | 109.02 | ||
|
|
1H | 55.01 | 51.45 | 51.91 | 51.85 | |
| 3He | 51.97 | 50.20 | 51.39 | 50.59 | ||
| 12C | 52.42 | 50.26 | 50.14 | 49.07 |
Table 4.
Simulation statistics for spherical micro-volumes.
| Parameter | Particle | VSph1 | VSph2 | VSph3 | VSph4 | |
|---|---|---|---|---|---|---|
| RP | 1H | 0.790 | 0.827 | 0.833 | 0.845 | |
| 3He | 0.555 | 0.563 | 0.593 | 0.607 | ||
| 12C | 0.168 | 0.150 | 0.163 | 0.166 | ||
| Rδ | 1H | 0.210 | 0.173 | 0.167 | 0.155 | |
| 3He | 0.445 | 0.437 | 0.407 | 0.393 | ||
| 12C | 0.832 | 0.850 | 0.837 | 0.834 | ||
|
|
1H | 1.0090±0.8850 | 0.1861±0.1439 | 0.1302±0.1019 | 0.0649±0.0435 | |
| 3He | 3.1468±1.9322 | 0.6208±0.3235 | 0.4319±0.2202 | 0.2125±0.1018 | ||
| 12C | 19.9970±9.1389 | 4.0280±1.5094 | 2.5635±0.9829 | 1.3875±0.4907 | ||
|
|
1H | 0.9303±1.5148 | 0.1826±0.2199 | 0.1238±0.1401 | 0.0600±0.0630 | |
| 3He | 1.0608±1.4632 | 0.1874±0.2147 | 0.1329±0.1433 | 0.0652±0.0559 | ||
| 12C | 1.1226±1.6261 | 0.1807±0.2271 | 0.1170±0.1439 | 0.0562±0.0609 | ||
| 1H | 52.58±24.94 | 51.97±22.99 | 52.24±23.17 | 52.23±21.77 | ||
| 3He | 124.95±49.80 | 128.82±51.49 | 131.19±51.40 | 128.32±49.98 | ||
| 12C | 257.14±107.44 | 295.71±108.98 | 284.33±109.70 | 304.42±108.96 | ||
| 1H | 24.49±27.42 | 28.80±26.75 | 28.72±25.10 | 27.67±23.81 | ||
| 3He | 29.64±26.72 | 33.46±31.43 | 31.41±29.76 | 31.39±25.29 | ||
| 12C | 31.49±29.28 | 29.20±25.64 | 28.00±24.59 | 27.97±22.88 | ||
|
|
1H | 27.96 | 29.38 | 30.01 | 29.81 | |
| 3He | 36.74 | 39.53 | 39.72 | 39.56 | ||
| 12C | 112.06 | 111.73 | 110.77 | 109.32 | ||
|
|
1H | 55.41 | 52.02 | 51.89 | 51.97 | |
| 3He | 52.24 | 49.74 | 50.43 | 50.20 | ||
| 12C | 52.73 | 50.76 | 50.37 | 48.23 |
The frequency mean lineal energy, ; energy per hit over all the hit events normalized by chord lengths of Vmicro are (1537, 5013, 31760) eV/μm for (1H, 3He, 12C) primary beams. Aside from the similarity of mean secondary dose per hit, in tables 3 and 4 and overlap of the cumulative dose distribution of secondary tracks (Supplementary figures S.2 and S.3), we tested the difference of secondary electron tracks for the chord length normalized , the mean number of voxel numbers for δ-ray tracks normalized by the chord length, and the mean voxel energy for δ-ray tracks, by one way ANOVA test for (1H, 3He, 12C) particles over all Vmicro. The chord length normalized for secondary tracks are (1548, 1606, 1513) eV/μm and these values are not different between particles by p<0.26. The value is 30.45 voxel/μm over all particles in tables 3 and 4 and the mean voxel values are not significantly different between (1H, 3He, 12C) particles by p<0.063. Likewise, the is 51.34 eV/voxel over all values in tables 3 and 4 and these results are not different between the particles by p<0.009. Weighting of particle LET values of primary beam hits are reflected by the mean number of voxels normalized by chord length, and the mean voxel energy in table 3 and 4.
3.4. Aspect ratio of cylinders modify the mean chord lengths, cross-sections, and probability of hits
The mean chord length, and cross-section, of a sphere are single valued quantities (4/3RSph, πRSph2). The total surface area, SCyl changes with varying aspect ratio at constant VCyl. The and represent the mean number of any hits by primary (equation (3)) or δ-ray (equation (3)) tracks and depend on the . Figure 4 is based on numerical analysis of equation (9) at given constant Vmicro and compares the changes in cylindrical parameters, , and (black line) for varying aspect ratio with respect to constant spherical values (red line). The closest approach of cylindrical parameters to a sphere occur at the AR=1 with a difference of 14.5%. The products of or by at given AR are equal to the same products for spheres . Our simulation results for different values of RBeam (section 2.2) confirm that the ratio . The analytical values of the mean number of any hits to VCyl,i (i=1,2,3,4) in figure 4(b) are (1.211, 1.149, 1.435, 1.375) for the AR of (0.5, 0.833, 5, 4.167). These values are the same as in table 2. Comparable simulations results at Vmicro averaged over (1H, 3He, 12C) are found as (1.129±0.008, 1.104±0.023, 1.410±0.021, 1.357±0.010).
Figure 4.
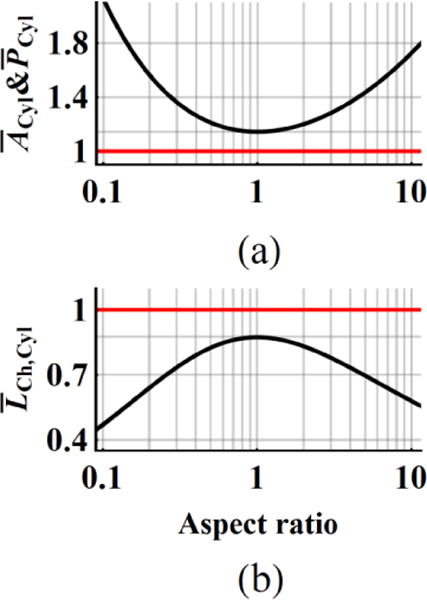
(a) Mean cross-section, , mean number of hits, and (b) mean chord length in cylinders depend on the aspect ratio, AR. The red lines are constant valued quantities for spheres at given Vmicro and black curves for cylinders are plotted by changing the AR and keeping the same Vmicro values.
3.5. Chord length distribution dictates primary beam dose deposition profiles in Vmicro
The normalized chord length distributions f(LCh,N) in figure 2 and figure 3 are frequency plots of random simulations of LCh for uniform isotropic irradiation. The in equation (8) has a linear dependence on LCh, while the profile should follow the product of f(LCh)×LCh. Analysis of figure 5 for VCyl3 and VSph3 for the case of 1H (32 MeV/n) shows that random primary track events peak towards the peaks of f(LCh) that are shown in the insets of figure S.2(a,b). The mean±SD of are (0.08976±0.08519, 0.13024±0.10193) Gy (tables 3 and 4). The red straight lines in figure 5(a) and 5(b) are linear fits to data with slopes of (0.12284, 0.12445) Gy/μm respectively. Nearly equal slopes of the same volume cylinders and spheres for given particle fluence are confirmed in all of the simulations.
Figure 5.
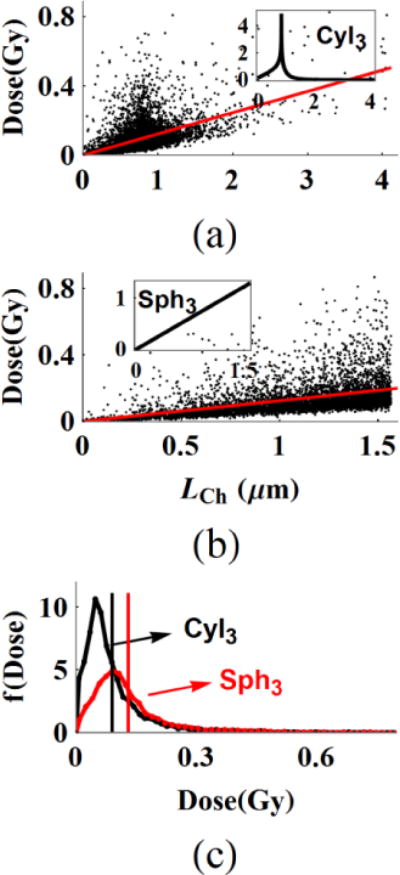
The dose distribution of primary beam hits follow the product of chord length and chord length distribution in cylinders and spheres. The insets in (a, b) are the f(LCh) of the VCyl3 and VSph3. The linear slopes to the data sets, red lines are nearly equal in (a) and (b). The dose-frequency plot in (c) that is normalized by the number of events in the cylinder volume under the same fluence is plotted for the data sets on (a, b). The vertical black and red lines are the mean dose.
Dose frequency histograms f(Dose) of VCyl3 and VSph3 in figure 5(c) give rise to normalized cumulative dose functions of (See figures S.2 and S.3 in the Supplementary file). The mean number of hits, PP under the same fluence is larger for VCyl3 than VSph3 and the ratio of PP,Cyl3/PP,Sph3 is 1.428. This result reflects the ratio of cross-section and the probability of hits between VCyl3 and VSph3 in figure 4. The f(Dose) in figure 5(c) for both VCyl3 and VSph3 are normalized by the number of events in VCyl3. The vertical black and red lines are the above reported mean doses. The ratio of mean is 0.689. Taken together, the product of is expected to give the same D0,F for primary beams and the product of 1.428×0.689=0.984 is close to unity in this example.
3.6. Total voxel number and voxel energy distribution in micro-volumes follow the distributions of ‘core’ and ‘penumbra’ of track histories
To characterize the stochastic nature of the dose deposition of particle tracks in Vmicro, figure 6(a–c) shows the distribution of the primary total voxel numbers, f(T.V.N.) at uniform isotropic field. The mean±SD of the primary voxel numbers, confined by VCyl3 are (37.7±22.7, 93.9±51.1, 206.5±111.2) for the (1H, 3He, 12C). These voxel numbers normalized by and named normalized primary voxel numbers, are listed in table 3. The increase in the primary voxel numbers is correlated with increase in the LET of the particles. The shape of f(T.V.N.) in figure 6(a–c) depends on the distribution of LCh and stochastic nature of ED events along the primary beam in equation (8). The figure 6(d–f) are the voxel energy distribution at the particle libraries of the (1H, 3He, 12C) confined to 100 nm along the particle tracks with mean voxel energies of (28.0, 37.5, 116.4) eV/voxel for the (1H, 3He, 12C) beams, respectively. The confined by the VCyl3 in figure 6(a–c) are (32.3, 39.5, 110.6) eV/voxel for the (1H, 3He, 12C). The voxel energy distributions f(V.E.) in figure 6(d–f) show larger voxel energy tails for increasing LET. Taken together, the voxel energy distribution in VCyl3 can be sampled as the number of voxels per random primary beam hit from column 1 in figure 6 and the energy of each voxel from column 2 to predict dose distribution for a random beam hitting the VCyl3.
Figure 6.
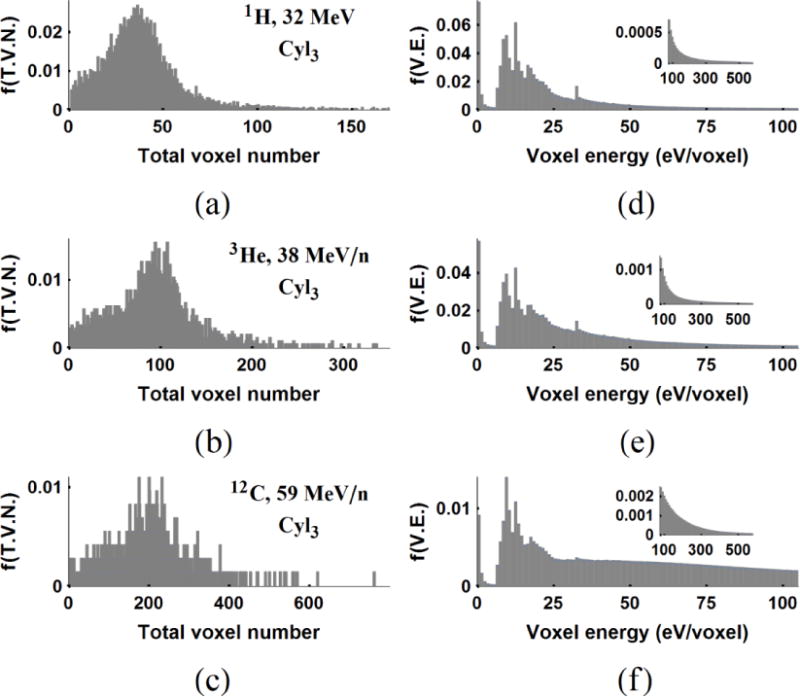
Total voxel number (first column) and voxel energy distribution (second column) of primary beams in VCyl3 (a, b, c) and the core of voxel energy distribution for (1H, 3He, 12C) (d, e, f). The f(T.V.N.) is the distribution of total voxel numbers and the f(V.E.) is the voxel energy distribution of the core region defined as the inner 100 nm radial distance of (1H, 3He, 12C) at (32, 38, 59) MeV/n.
The statistics of normalized by the and the for δ-ray hits are given in section 3.7 for all particles at energies 1 cm from the Bragg peak. The distribution of total number of voxels of δ-ray crossings in VCyl3 are (22.8±21.6, 23.8±20.5, 21.4±20.9) in figure 7(a–c). The f(V.E.) of the penumbra region obtained from the track libraries of the (1H, 3He, 12C) in figure 7(d–f) have the mean voxel energies of (57.9, 56.8, 54.2) eV/voxel, respectively. The confined by the VCyl3 are (51.9, 51.4, 50.1) eV/voxel for (1H, 3He, 12C) in table 4. The mean voxel energies of the described core in figure 6(d–f) and the penumbra regions in figure 7(d–f) are well separated. These results also motivate sampling of ED events in Vmicro by the distributions of voxel numbers and voxel energies of secondary electron tracks. These distributions are quite similar at 1 cm of the BP at given initial maximum electron energies.
Figure 7.
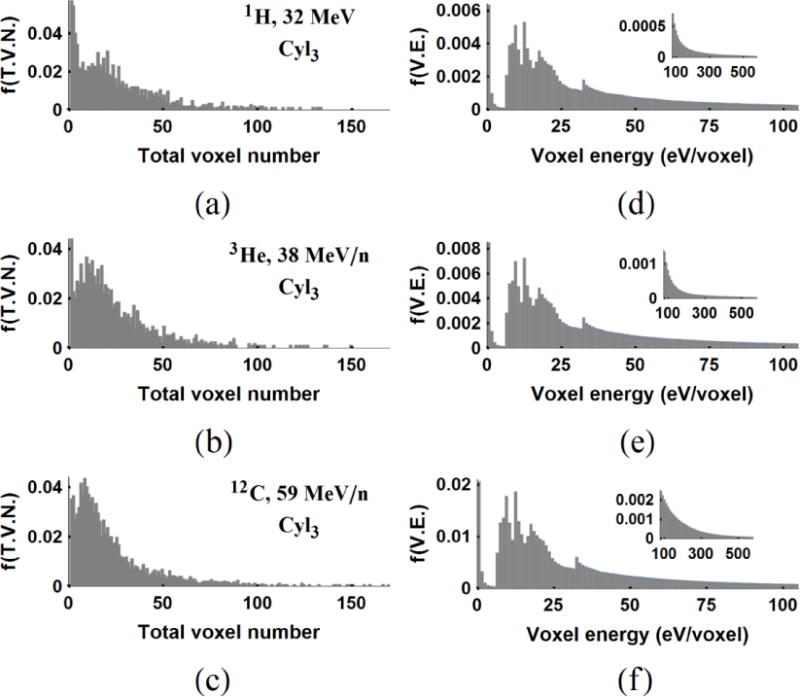
Total voxel number (a, b, c) and voxel energy distribution (d, e, f) of δ-rays confined to VCyl3 for (1H, 3He, 12C). The voxel energy distributions, f(V.E) (d, e, f) are obtained for voxels outside the 100 nm radius of 20 μm tracks generated by the RITRACKS code.
3.7. Dose sampling in micro-volumes at given macroscopic dose, D0,F
A straight forward method to sample D0,F in Vmicro for given particle fluence follows the steps of first finding the number of particles by equation (1) then, randomly picking that number of particles by the Poisson distribution from the simulation library to generate a stochastic dose realization in Vmicro. The same processes are repeated many times to present a dose distribution in Vmicro at D0,F. An alternative method is to use the CDDF of both and in figure S.2 and figure S.3 and the probability of PP and Pδ of hits at given D0,F calculated by RP and Rδ that are listed in tables 3 and 4. Briefly, the mean number of hits by PP and Pδ are sampled by the Poisson distribution and primary and δ-ray dose values are randomly drawn from the appropriate CDDF distributions. The process is repeated many times to obtain a dose distribution in Vmicro at D0,F and the mean dose at Vmicro approaches D0,F. Both methods give nearly identical results for the microscopic dose distribution. The alternative method depends on the accuracy of the CDDF for primary particle and δ-rays.
As an example of a low dose study in micro-volumes in figure 8 we consider normalized dose distributions, f(Dose) at 0.2 Gy which show the extent of the dose deposition in the (VCyl1, VCyl2, VCyl3, VCyl4) that are irradiated by (1H, 3He, 12C) particles. The percentage of no-hit values and the lower threshold for the highest 5% of the dose values obtained in figure 8 listed in table 5. Because the mean dose per hit and the CDDF of the primary and δ-ray doses of protons are very similar, protons have a higher hit probability but the tail of the high dose distribution is narrower compared to other ions. The mean dose of the primary hits of 3He and 12C are well separated from the mean dose of δ-ray hits (tables 3 and 4). This is reflected distinctly in the dose distribution for carbon ions as the higher dose peaks are from the primary track hits and δ-ray, which are distinct. Although the highest LET particle (12C) has the highest dose distribution values, 3He can lead to higher dose than protons and with a higher percentage of dose deposition events than 12C at the Bragg peak of 1 cm. A similar result (not shown) is obtained for spheres.
Figure 8.
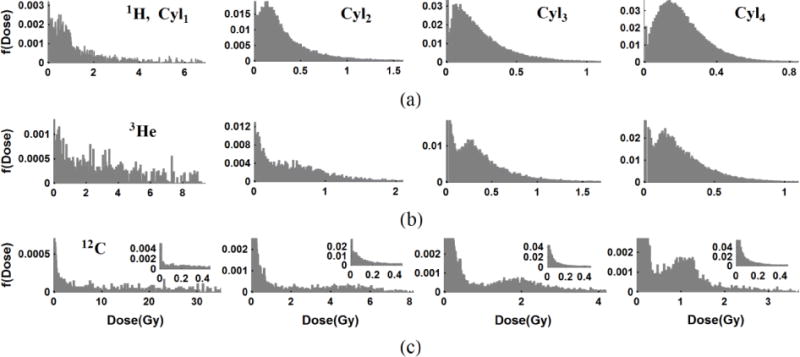
Normalized dose distribution f(Dose) at D0,F=0.2 Gy in cylinders (VCyl1, VCyl2, VCyl3, VCyl4) (column 1 to 4) for (1H, 3He, 12C) particles (row 1 to 3) sampled over generated libraries. A large percentage of volumes get no-hits by primary beam or scattered electrons. Higher dose values in the dose distribution come from either primary beam hits like in 12C in (c) or combinations of primary particles and δ-rays crossing the volumes for 1H in (a).
Table 5.
List of % of no-hits and highest 5% dose threshold values at D0,F=0.2 Gy in cylinders.
| VCyl1 | VCyl2 | VCyl3 | VCyl4 | ||
|---|---|---|---|---|---|
| % of no-hits | 1H | 78.7 | 29.2 | 10.1 | 1.4 |
| 3He | 90.4 | 59.1 | 39.0 | 17.1 | |
| 12C | 95.1 | 75.2 | 60.1 | 39.3 | |
| Highest 5% dose threshold (Gy) | 1H | 1.234 | 0.722 | 0.581 | 0.446 |
| 3He | 1.301 | 1.028 | 0.767 | 0.582 | |
| 12C | 0 | 0.731 | 1.698 | 1.209 |
3.8. Fast analytical method confirms primary dose contribution calculated by stochastic and simulation methods
There are three complementary methods to find the total mean primary dose, in equation (11) at a given beam absorbed dose or fluence. First the computationally intensive ‘simulation’ procedure in this paper provides primary particle CDDF (figures S.2 and S.3 and in tables 3 and 4). From equation (7) the is equal to using equation (3). The other two fast methods are called ‘stochastic’ and ‘analytic’ methods that are worked out for spheres. The stochastic method involves finding the dose by ED events of a stochastic track passing through the center of the sphere and taking the ratio by the theoretical value given in equation (8). The ratio makes the distinction between energy confined by the Vmicro to the total energy given to the medium by a stochastic primary beam. The kernel of the analytical approach is obtained by figure S.1(a) and the methodology of the ‘analytical’ method is introduced in equations (12–16). The Ctrack(0) is calculated for the line passing thorough the center of the beam that represents the dose confined by the Vmicro at uniform isotropic fluence. The results are listed in table 6. Because the kernel of analytical method is derived from the stochastic track simulations there is a good agreement between the two methods. The deviations in the ‘simulation’ method results from the exact value of that can be attributed to the limited number of primary hits at given number of trials. Although Ctrack(0) is not calculated for cylindrical structures the equivalence of ‘stochastic’ and ‘analytical’ methods paves the way for fast stochastic method. A stochastic beam is limited by the RBeam radius on the order of cylinder diagonal length then and CDDF as in figure S.2 can be found over a number of trials in future studies.
Table 6.
Ratio of primary dose (Ctrack(0)) at given macroscopic dose determined by three methods.
| Particle | Method | VSph1 | VSph2 | VSph3 | VSph4 |
|---|---|---|---|---|---|
| 1H, 32 MeV | Analytical | 0.7915 | 0.8291 | 0.8375 | 0.8530 |
| Stochastic | 0.7923 | 0.8358 | 0.8486 | 0.8476 | |
| Simulation | 0.8173 | 0.8478 | 0.8706 | 0.8645 | |
| 3He, 38MeV/n | Analytical | 0.7855 | 0.8219 | 0.8301 | 0.8450 |
| Stochastic | 0.7798 | 0.8270 | 0.8340 | 0.8476 | |
| Simulation | 0.7504 | 0.8324 | 0.8499 | 0.8332 | |
| 12C, 59 MeV/n | Analytical | 0.7678 | 0.8019 | 0.8097 | 0.8238 |
| Stochastic | 0.7628 | 0.8022 | 0.8123 | 0.8233 | |
| Simulation | 0.7282 | 0.8278 | 0.7731 | 0.8337 |
3.9. Cylinders as neuronal compartments and choice of segment lengths on dendrites
The spatial distribution of dose for long elongated and continuous dendrites requires a definition of volume, hence dendritic segment length at given diameter. The choice of cylinder length, aspect ratio, analysis of hit probability and dose per segment become important in interpretation of dose and radiation quality in numerical studies. Figure 9 shows an example of segmentation of dendritic branch on a pyramidal neuron. The same branch is shown with the AR of 2 and 0.5 in figure 9(b1,b2). The segment dose per hit and probability of hit at constant diameter can change 2.5 times between the two choices of segmentation in this example calculated by equations (8) and (9). A constant AR along the dendrites with varying diameter provides a dose distribution following the same normalized chord length distribution. A large AR with elongated cylinders reduces the number of total segments per neuron and may reduce the computation time. However, interpretation of figure 5(a) where most of the dose deposition events take place at H=dCyl indicate that the AR should be around one. Figure 9(c) shows the same dendritic branch with AR=1. Here segment lengths are reduced as dendritic diameters get thinner but keeping the same dendritic branch volume constant.
Figure 9.
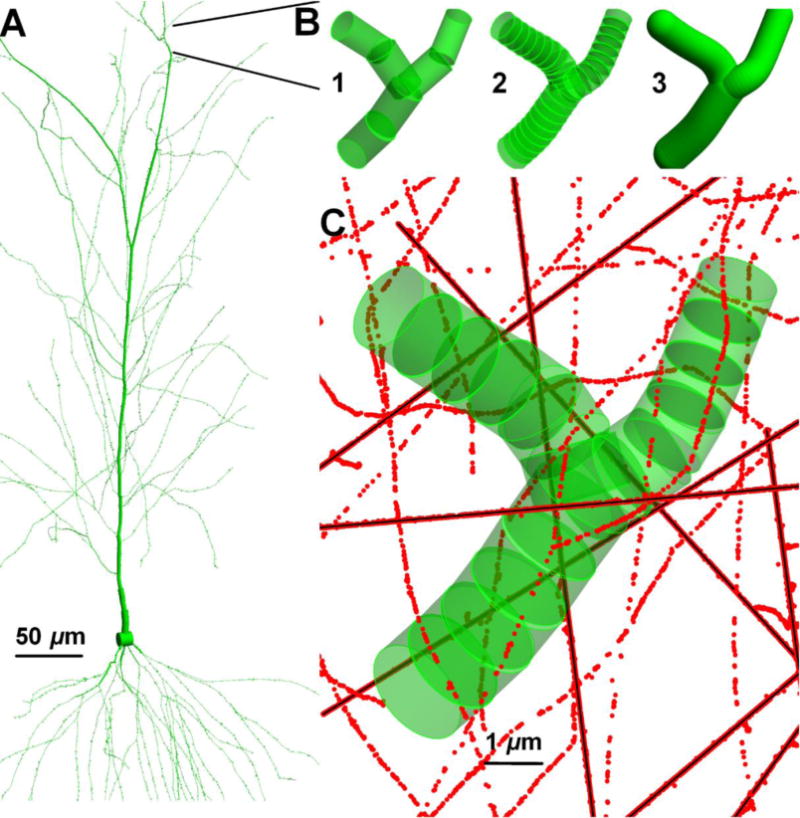
(a) A pyramidal neuron and (b) its continuous dendritic branch is segmented to different segment lengths (c) to find segment’s doses under 3He (38 MeV/n) irradiation. The segments have the aspect ratio of (0.5, 2, continuous, 1) (b1, b2, b3, c) on the panels.
4. Discussion and conclusions
Studies of the microdosimetry of spheres (Gersey et al 2002) and cylinders (Charlton et al 1985a, Ziebel et al 2008, Wroe et al 2007) have been made in the past for applications in DNA damage induction, micro-electronics damage, and for radiation detection. A key difference for studies of ED in neuron cells is the significant variability in volume dimensions to be considered. This variability along with the large computational times required for Monte-Carlo track structure simulations, especially for high energy particles, led us to investigate methods to improve computational efficiency while considering both spherical and cylindrical volumes. The chord length analysis of convex bodies was extensively studied by Kellerer 1971, 1984, 1985. Cylinders and spheres are examples of convex bodies, while large scale electronic devices (Katz et al 1997) or cellular structures (Penfold et al 2014) can be built up using these micron scale components to investigate spatial dose deposition by charged particles (Kellerer 1985; Charlton et al 1985a, 1985b; Nikjoo et al 1991). Focus on enzymes (Butts and Katz 1967), proteins (Davies 1987, Du and Gebicki 2004) and DNA (Nikjoo et al 2001) structures has been used to explain cellular damage by particle tracks of electrons, protons and heavy charged particles. An important feature of these studies is the use of a threshold in event sizes to describe damage induction, and the high ED events produced by the track core which suggest qualitative differences may occur in damage induction. Similar concepts can be used in developing models of changes to dendritic morphology.
The elongation of cylinders (either oblate or prolate) leads to deviation from an equal height and diameter (AR=1), which exaggerates the dosimetric difference with that of spheres (figure 4). A simple expression by Cauchy (equation (9)) provides the mean cross-section of convex bodies including cylinders, hence mean number of hits by primary beams at uniform isotropic fluence in equation (3). Likewise, primary track dose per hit is proportional to chord length in equation (8). The mean number of δ-ray hits in equation (4) and nearly constant mean number of secondary ED events per micron discussed in section 3.5 extend the same conclusions of mean number of hits and dose deposition per hit. By changing the aspect ratio of cylinders at a constant volume and keeping the product of mean number of hits and chord length constant, the same average macroscopic dose is obtained. Spheres always have the larger mean dose per hit and the smaller mean number of hits than the cylinders.
Computational time was a challenge in this study mainly arising from the requirement of sampling over many stochastic beams at a given RBeam. Increases in particle energy and the radial extent of track expand the number of particle beams as the square of RBeam at constant fluence. To obtain accurate statistics of the Rδ to RP ratio and probability distribution of necessitates capturing hits by δ-rays over large radial and longitudinal distances from a particles path. However, two observations in this study motivate a fast sampling procedure. First, if the ratio of Rδ to RP and production of δ-rays scale with the LET ratio of particles, then a generic value can be utilized. Second, the number of δ-ray hits as a function of impact parameter decreases by power law in figure 3(d), which is also suggested by the log-linear distribution in figure 3(c). However, the impact parameter independence of distribution leads to sampling at smaller RBeam to create the CDDF of secondary dose in figures S.2(b) and S.3(b).
Dose deposition by particles (1H, 3He, 12C) at given D0,F were investigated for interest in therapeutic implications of normal tissue damage in Hadron therapy. The ratio of total secondary dose by δ-rays to total dose deposition is defined as 1-Ctrack(0) with values for Ctrack(0) is given in table 6. Although high LET carbon ions generate 2-fold higher maximum initial energy electrons than protons, the mean dose deposition per δ-ray crossing, in tables 3 and 4 and CDDF profiles in figure S.2 and S.3 are very similar for these ions. This supports that dose deposition by the δ-rays is very similar for the particles investigated. The main difference is the number of primary particle tracks at given D0,F and their mean number of hits inversely scales with the LET values in equation (3).
The biological response to particle tracks in cellular microdosimetry can be evaluated in terms of the mean number of primary beam hit PP and threshold of biological response to primary beam dose deposition given in CDDF in figure S2.(a) and S.3(a). Responses should be governed by PP for carbon ions, at low dose, D0,F (e.g D0,F<0.2 Gy) and small Vmicro as in figure 8. The high ionization of carbon tracks and large could play a causal role in dendritic pruning. The micro-compartments under proton irradiation are hit at higher probability than 3He or 12C beams. One caveat comes from the size of stochastic ED events along the particle tracks. As the number and ED per voxel change a constant chord length can have varying distribution as shown in figure 5. The presence of high ED events on the voxel energy spectrum (e.g. >200 eV/voxel) in figure 6(d–f) could play a key role in the radiation quality dependence observed in changes in dendritic morphology (Pariahar et al 2015a, 2015b).
Stochastic simulations and numerical analyses highlighted a methodology to find primary beam and δ-ray dose depositions in micro-volumes. Three parameters are needed for statistical sampling of ED for a given Vmicro: dose distribution of primary and δ-rays per particle, and ratio of electron tracks (Rδ/RP) per particle beam. In addition, the frequency of δ-ray hits to a given Vmicro as a function of impact parameter (figure 3(d)) can be further investigated. A fast computational method to extract the CDDF of in figure S.2(a) and S.3(a) would be to place the target volume in an area were the radius is scaled by the diagonal length of Vmicro. At first, the CDDF of seems to require computational intensive sampling in a volume that scales with RBeam. However, the impact parameter independence of in Fig. 3(c,d) supports that smaller values of RBeam can be considered. Because the highest electron energies increases with the particle energy, higher energy particles of interest for space radiation studies, may have impact parameter an dependence (or CDDF) for that depends on the initial electron energies. These questions can be tested with similar Monte-Carlo simulations as considered here.
A question arises on how to segment a continuous tube-like structure like the dendrites on a neuronal tree to sample the spatial dependence of ED events. Features of dendrite arbors include branching, spanning in 3D-space, and reduction in diameter toward to tips of branches. These features suggest dendrites to be represented as cylinders in a mathematical reconstruction. We showed that the microscopic dose and probability of hit in micro-volumes at given fluence depend on the elongation of cylindrical structures. As a first approximation, a long dendritic segment can be kept as a long, constant diameter segment with large aspect ratio. Alternatively much shorter segments with slowly changing diameter and rotation in space may capture detailed 3-D features of the biological structure. The differences in ED events between a long segment volume and smaller segment volumes are the higher probability of hit and lower dose per segment to the larger volume segment. Because the diameters of dendrites are constrained by the biology of their formation and regulation, we suggest the segment lengths for modeling damage should be on the order of its diameter. In addition, having the same aspect ratio for segmentation facilitates a consistent dose prediction of dendritic branches in different neurons or neuron types that can be compared for irradiation response. Neuronal spines are protrusions from dendritic branches with variable sub-micron volumes and diffusion limited neck structures (Alp et al, 2015). Therefore, their segment sizes can be distributed as cylinders with different aspect ratios with the statistics of distributions are being confirmed by experimental observation.
Biological damage could arise from multiple hits and accumulated total dose in the same segment or a global response to uniform dose deposition along the segments of dendritic branches. For the former case, we note that changes in dendritic morphology described by changes in total dendrite length could reflect multiple pruning sites along the dendrite which contribute to observed changes in morphology (Chakraborti et al 2012, Parihar et al 2015a, 2015b). Therefore, the dendritic damage profile under low LET maybe similar to random pruning sites, while high LET radiation could lead to a pruning site distribution reflective of the particle track structure. These possibilities will be considered in future work with the methods developed here, including calculations for particles of higher kinetic energy and charge numbers such as 28Si and 56Fe.
Supplementary Material
Highlight.
Exposures to protons and heavy ions may harm patients and astronauts by altering cognition and memory
Risk assessment must consider ground based research using animal models in order to project the risk to humans
We describe methods to evaluate microscopic energy deposition in dendrites and spines that comprise neuron cells
This work supports the understanding cognitive changes caused by protons and heavy ions
Acknowledgments
This study was supported by the National Cancer Institute (1RO1CA208526-01) and the University of Nevada, Las Vegas.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alp M, Parihar VK, Limoli CL, Cucinotta FA. Irradiation of neurons with high-energy charged particles: An in silico modeling approach. PLoS Comput Biol. 2015;11:e1004428. doi: 10.1371/journal.pcbi.1004428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ascoli GA. Mobilizing the base of neuroscience data: the case of neuronal morphologies. Nature Rev Neurosci. 2006;7:318–324. doi: 10.1038/nrn1885. [DOI] [PubMed] [Google Scholar]
- Ascoli GA, Donohue DE, Halavi M. NeuroMorpho.Org: a central resource for neuronal morphologies. J Neurosci. 2007;27:9247–9251. doi: 10.1523/jneurosci.2055-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ascoli GA. Sharing neuron data: Carrots, sticks, and digital records. PLoS Biol. 2015;13(10):e1002275. doi: 10.1371/journal.pbio.1002275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azzam EI, Jay-Gerin J-P, Pain D. Ionizing radiation-induced metabolic oxidative stress and prolonged cell injury. Cancer Lett. 2012;327:48–60. doi: 10.1016/j.canlet.2011.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butts JJ, Katz R. Theory of RBE for heavy ion bombardment of dry enzymes and viruses. Radiat Res. 1967;4:855–871. doi: 10.2307/3572151. [DOI] [PubMed] [Google Scholar]
- Cacao E, Cucinotta FA. Modeling impaired hippocampal neurogenesis following radiation exposure. Radiat Res. 2016a;185:319–331. doi: 10.1667/RR14289.S1. [DOI] [PubMed] [Google Scholar]
- Cacao E, Cucinotta FA. Modeling heavy ion impairment of hippocampal neurogenesis after acute and fractionated irradiation. Radiat Res. 2016b;185 doi: 10.1667/RR14569.1. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborti A, Allen A, Allen B, Rosi S, Fike JR. Cranial irradiation alters dendritic spine density and morphology in the hippocampus. PLoS One. 2012;7:e40844. doi: 10.1371/journal.pone.0040844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlton DE, Goodhead DT, Wilson WE, Paretzke HG. Energy deposition in cylindrical volumes: (a) Protons, energy 0.3 MeV to 4.0 MeV, (b) Alpha particles, energy 1.2 MeV to 20.00 MeV. MRC Radiobio Unit Monog 85/1. Med Res Counc Radiobio Unit. 1985a Didcot, England. [Google Scholar]
- Charlton DE, Goodhead DT, Wilson WE, Paretzke HG. The deposition of energy in small cylindrical targets by high LET radiations. Radiat Prot Dosim. 1985b;13:123–125. [Google Scholar]
- Cucinotta FA, Katz R, Wilson JW, Dubey RR. Heavy ion track-structure calculations for radial dose in arbitrary materials. Washington D.C.: 1995. (NASA Technical Paper 3497). [Google Scholar]
- Cucinotta FA, Katz R, Wilson JW. Radial distribution of electron spectra from heavy ions. Radiat Environ Biophys. 1998;37:259–265. doi: 10.1007/s004110050127. [DOI] [PubMed] [Google Scholar]
- Cucinotta FA, Alp M, Sulzman FM, Wang M. Space radiation risks to the central nervous system. Life Sci Space Res. 2014;2:54–69. doi: 10.1016/j.lssr.2014.06.003. [DOI] [Google Scholar]
- Davies KJ. Protein damage and degradation by oxygen radicals. I. general aspects. J Biol Chem. 1987;262:9895–9901. [PubMed] [Google Scholar]
- Du J, Gebicki JM. Proteins are major initial cell targets of hydroxyl free radicals. Int J Biochem Cell Biol. 2004;11:2334–2343. doi: 10.1016/j.biocel.2004.05.012. [DOI] [PubMed] [Google Scholar]
- El Naqa I, Pater P, Seuntjens J. Monte Carlo role in radiobiological modelling of radiotherapy outcomes. Phys Med Biol. 2012;11:R75–97. doi: 10.1088/0031-9155/57/11/R75. [DOI] [PubMed] [Google Scholar]
- Gersey BB, Borak TB, Guetersloh SB, Zeitlin C, Miller J, Heilbronn L, Murakami T, Iwata Y. The response of a spherical tissue-equivalent proportional counter to iron particles from 200-100 MeV/nucleon. Radiat Res. 2002;157:350–360. doi: 10.1667/0033-7587(2002)157[0350:TROAST]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- Greene-Schloesser D, Robbins ME, Peiffer AM, Shaw EG, Wheeler KT, Chan MD. Radiation-induced brain injury: A review. Front Oncol 2012. 2012;2:73. doi: 10.3389/fonc.2012.00073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz R, LaBel K, Wang JJ, Cronquist B, Koga R, Penzin S, Swift G. Radiation effects on current field programmable technologies. IEEE T Nucl Sci. 1997;6:1945–1956. doi: 10.1109/23.658966. [DOI] [Google Scholar]
- Kellerer AM, Chmelevsky D. Criteria for the applicability of let. Radiat Res. 1975;63:226–234. doi: 10.2307/3574148. [DOI] [PubMed] [Google Scholar]
- Kellerer AM. Criteria for the equivalence of spherical and cylindrical proportional counters in microdosimetry. Radiat Res. 1981;2:277–286. doi: 10.2307/3575505. [DOI] [Google Scholar]
- Kellerer AM. In: Fundamentals of microdosimetry The dosimetry of ionizing radiation. Kase KE, Bjarngard BE, Attix FH, editors. Academic Press; p. 1985. [Google Scholar]
- Kubota Y, Hatada S, Kawaguchi Y. Important factors for the three-dimensional reconstruction of neuronal structures from serial ultrathin sections. Front Neural Circuits. 2009;3:4. doi: 10.3389/neuro.04.004.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langworthy JB. The chord distribution for a right circular cylinder. Naval Research Laboratory; 1988. (NRL Memorandum Report 6220). [Google Scholar]
- Mader U. Chord length distribution for circular cylinders. Radiat Res. 1980;82:454–466. doi: 10.2307/3575312. [DOI] [Google Scholar]
- Meijering E. Neuron tracing in perspective. Cytometry A. 2010;77:693–704. doi: 10.1002/cyto.a.20895. [DOI] [PubMed] [Google Scholar]
- Nikjoo H, Goodhead DT, Charlton DE, Paretzke HG. Energy deposition in small cylindrical targets by monoenergetic electrons. Int J Radiat Biol. 1991;60:739–756. doi: 10.1080/09553009114552561. [DOI] [PubMed] [Google Scholar]
- Nikjoo H, O’Neill P, Wilson WE, Goodhead DT. Computational approach for determining the spectrum of DNA damage induced by ionizing radiation. Radiat Res. 2001;156:577–583. doi: 10.1667/0033-7587(2001)156[0577:CAFDTS]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- Palmans H, Rabus H, Belchior AL, Bug MU, Galer S, et al. Future development of biologically relevant dosimetry. Br J Radiol. 2015;88(1045):20140392. doi: 10.1259/bjr.20140392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parihar VK, Limoli CL. Cranial irradiation compromises neuronal architecture in the hippocampus. Proc Natl Acad Sci USA. 2013;110:12822–12827. doi: 10.1073/pnas.1307301110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parihar VK, Allen B, Tran KK, Macaraeg TG, Chu EM, Kwok SF, Chmielewski NN, Craver BM, Baulch JE, Acharya MM, Cucinotta FA, Limoli CL. What happens to your brain on the way to Mars. Sci Adv. 2015a;1:e1400256. doi: 10.1126/sciadv.1400256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parihar VK, Pasha J, Tran KK, Craver BM, Acharya MM, Limoli CL. Persistent changes in neuronal structure and synaptic plasticity caused by proton irradiation. Brain Struct Funct. 2015b;220:1161–1171. doi: 10.1007/s00429-014-07009-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penfold SN, Brown MP, Staudacher AH, Bezak E. Monte Carlo simulations of dose distributions with necrotic tumor targeted radioimmunotherapy. Appl Radiat Isot. 2014;90:40–45. doi: 10.1016/j.apradiso.2014.03.006. [DOI] [PubMed] [Google Scholar]
- Peng H, Long F, Myers G. Automatic 3D neuron tracing using all-path pruning. Bioinformatics. 2011;27(13):i239–i247. doi: 10.1093/bioinformatics/btr237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plante I, Cucinotta FA. Ionization and excitation cross sections for the interaction of HZE particles in liquid water and application to Monte-Carlo simulation of radiation tracks. New J Phys. 2008;10:1–15. doi: 10.1088/1367-2630/10/12/125020. [DOI] [Google Scholar]
- Plante I, Cucinotta FA. Cross sections for the interactions of 1 eV – 100 MeV electrons in liquid water and application to Monte-Carlo simulation of HZE radiation tracks. New J Phys. 2009;11:1–24. doi: 10.1088/1367-2630/11/6/063047. [DOI] [Google Scholar]
- Plante I, Cucinotta FA. Energy deposition and relative frequency of hits of cylindrical nanovolume in medium irradiated by ions: Monte Carlo simulation of tracks structure. Radiat Environ Biophys. 2010;49:5–13. doi: 10.1007/s00411-009-0255-7. [DOI] [PubMed] [Google Scholar]
- Raber J, Allen AR, Sharma S, Allen B, Rosi S, Olsen RH, Davis MJ, Eiwaz M, Fike JR, Nelson GA. Effects of proton and combined proton and (56)Fe radiation on the hippocampus. Radiat Res. 2016;185:20–30. doi: 10.1667/RR14222.1. [DOI] [PubMed] [Google Scholar]
- Shirai K, Mizui T, Suzuki Y, Okamoto M, Hanamurab K, Yoshidaa Y, Hinoc M, Nodaa S, Aljahdaria WS, Chakravartid A, Shiraob T, Nakanoa T. X irradiation changes dendritic spine morphology and density through reduction of cytoskeletal proteins in mature neurons. Radiat Res. 2013;179:630–636. doi: 10.1667/RR3098.1. [DOI] [PubMed] [Google Scholar]
- Vickers GT, Brown DJ. The distribution of projected area and perimeter of convex, solid particles. Proc R Soc Lond A. 2001;457:283–306. doi: 10.1098/rspa.2000.0667. [DOI] [Google Scholar]
- Wroe A, Rosenfeld A, Reinhard M, Pisacane V, Ziegler J, Nelson M, Cucinotta F, Zaider M, Dicello J. Solid state microdosimetry with heavy ions for space applications. IEEE T Nucl Sci. 2007;54:2264–2271. doi: 10.1109/TNS.2007.910037. [DOI] [Google Scholar]
- Ziebell A, Lim WH, Reinhard MI, Cornelius I, Prokopovich DA, Siegele R, Dzurak AS, Rosenfeld AB. A cylindrical silicon-on-insulator microdosimeter: charge collection characteristics. IEEE T Nucl Sci. 2008;55:3414–3420. doi: 10.1109/TNS.2008.2004464. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


