Using the Lorenz Curve to Characterize Risk Predictiveness and Etiologic Heterogeneity

Abstract

The Lorenz curve is a graphical tool that is used widely in econometrics. It represents the spread of a probability distribution, and its traditional use has been to characterize population distributions of wealth or income, or more specifically, inequalities in wealth or income. However, its utility in public health research has not been broadly established. The purpose of this article is to explain its special usefulness for characterizing the population distribution of disease risks, and in particular for identifying the precise disease burden that can be predicted to occur in segments of the population that are known to have especially high (or low) risks, a feature that is important for evaluating the yield of screening or other disease prevention initiatives. We demonstrate that, although the Lorenz curve represents the distribution of predicted risks in a population at risk for the disease, in fact it can be estimated from a case–control study conducted in the population without the need for information on absolute risks. We explore two different estimation strategies and compare their statistical properties using simulations. The Lorenz curve is a statistical tool that deserves wider use in public health research.

Introduction

The development of risk prediction tools has been the subject of considerable research from methodologists in recent years.¹ Particular attention has been paid to the topic of prediction accuracy and to the usefulness of summary measures of prediction accuracy that can be used to compare prediction rules. The measure that is most widely used, the area under the receiver operating curve, was initially developed for diagnostic tests and is suitable for predicting a binary event. It is based on the specificity and sensitivity of the risk score, and it measures the probability that a randomly selected diseased subject has a higher predicted risk than a randomly selected non-diseased subject.² Concordance indices measure the same quantity over a follow-up period.³ To account for the fact that the onset of the disease takes time and that censoring can occur, a time-dependent area under the curve has been proposed by Heagerty.⁴ Reclassification measures have also received a lot of attention. The net reclassification index evaluates the extent to which patients are reclassified when using a new predictive rule compared to an old one, conditional on disease status.⁵ The integrated discrimination index is a related measure based on the difference in sensitivity and specificity between the two scores. Another popular type of measure to assess prediction accuracy is the error of prediction, or Brier score, which quantifies the distance between the prediction and the actual outcome.^6,7 Finally, calibration represents whether the risk predictions reflect the true risks in the population. For example, among individuals with risks in the region of p% we expect about p% to experience the predicted event. If so, the prediction rule is considered to be well calibrated.⁸

In a public health context the discriminative accuracy of a risk prediction tool is closely related to the notion of risk concentration, in that risk concentration reflects the extent to which occurrences of the disease are likely to occur in a predictable, ideally small subset of the population. Pepe and colleagues have recognized this feature of “risk predictiveness” and have proposed graphical tools that map out broad variations in risk in the population of relevance.^9–11 Our view is that the variation in risk of the disease in the population is indeed the feature of a risk prediction tool that is the most relevant from a public health perspective. However, we feel that the ideal graphical tool for representing this distribution is an old fashioned tool in statistics, the Lorenz curve.¹² The Lorenz curve has a long history of application in econometrics. We believe that it is especially useful in the context of disease prevention because it maps out what public health policy investigators need to know. That is, it tells us how much disease burden will occur in any given proportion of the population with risks above a chosen threshold. Very few investigators have made use of the Lorenz curve to illustrate public health concepts, though there have been some notable exceptions. For example, Green et al.¹³ used it to describe regional variations in the incidence of multiple sclerosis, Hickson et al.¹⁴ used the tool to characterize the representativeness of African American participants in a study of heart disease, Perini et al.¹⁵ used it to characterize the methylphenidale consumption in Brazil, Duarte et al.¹⁶ studied the distribution of malaria cases in the Brazilian Amazon, Hashemi et al.¹⁷ used it to characterize regional access to cataract surgery, and Gail¹⁸ and Petracci et al.¹⁹ have used it in evaluating breast cancer risk.

The Lorenz curve was initially developed by economists to characterize the distribution of the wealth (or income) among individuals, and it is frequently used to compare social inequalities between countries. In this context the X-axis represents the proportion of the population, ranked from those with the lowest wealth to the highest, while the Y-axis represents the cumulative distribution of total wealth. Consequently, the curve can be used to read off statistics such as, say, the top 1% of the population owns 40% of the wealth. In the context of risk prediction in public health the X-axis represents the cumulative proportion of individuals in the population at risk, ranked from the lowest risk to the highest. By analogy with the econometric context, the Y-axis is the corresponding cumulative percentage of risk. However, since disease occurrences in the population occur in proportion to risk, the Y-axis also represents the cumulative numbers of individuals predicted to contract the disease, and thus simultaneously represents the cumulative disease burden.²⁰ Consequently, one can use the curve directly to read off statistics such as, say, 60% of the cancers will occur in the 20% of the population with the highest risks. This is precisely the kind of statistic that is crucially relevant for planning screening programs or other focused disease prevention measures. These statistics, when combined with data on costs and benefits, are crucial for evaluating the cost-effectiveness of such initiatives.

The aim of this paper is to clarify the utility and relevance of the Lorenz curve in this public health context. Much of the extensive research on this topic in the econometric context of wealth or income distribution is applicable to the context of disease risk prediction.^21–24 We further demonstrate that, although the Lorenz curve represents the distribution of absolute risks in the population of interest, it can be estimated solely from the relative risk estimates obtainable from population-based case–control studies. We describe candidate estimation methods and study and compare their statistical properties using simulations. We illustrate the methods in the context of investigating the additional risk predictiveness obtained by creating separate risk prediction tools for disease sub-types that are etiologically distinct, using data from a breast cancer study where the risk predictiveness of the different sub-types is compared.

Risk predictiveness and the Lorenz curve

Definition of the Lorenz curve

Let r denote generically the disease risk of a randomly selected individual in the population and let F(r) denote the cumulative distribution of risks. Then X = F(r)defines the X-axis. The Y-axis represents the cumulative risk in the population among all individuals with risks less than or equal to r, i.e. $\mathrm{Y}=\mathrm{L}(\mathrm{r})={\mathrm{\mu }}^{-1}{\int }_0^{\mathrm{r}}\text{uf}(\mathrm{u})\text{du}$, where f (r) is the probability density of the risks and μ is the mean of the risk distribution.²¹ L(r) represents the size-biased distribution of risks that occurs when individuals are sampled in proportion to their individual risks.²⁵ This is precisely what happens when considering incident cases of disease that occur in a population. For example, if one individual has double the risk of another individual, the first one is literally twice as likely to become a case; if the risk is triple then first individual is three times as likely to become a case; and so on. It follows that when you identify all incident cases during a given time period, as in a population-based case–control study, you are in effect sampling individuals with risks from the distribution L(r), i.e. cases in a population-based case–control study have risks representative of the distribution L(r). Similarly, random sampling of controls in a population-based case–control study is akin to sampling from F(r), the distribution of risks in the population.

We note that the concept of risk is a construct that depends on the factors that are used to define it. For example, in cancer epidemiology many risk prediction tools have been developed. One of the earliest was the Gail model, used to predict the risk of breast cancer in women based on a small number of key risk factors.²⁶ One could construct a Lorenz curve corresponding to the risks predicted by the Gail model by sampling women from the population at risk, identifying their Gail risk scores, and estimating the corresponding distributions F(r) and L(r). This Lorenz curve would correspond specifically to the Gail model. However, if the model were enhanced by inclusion of new risk factors then this new risk model would have a different Lorenz curve, with a broader distribution of risks.

Summary Measures

The Lorenz curve characterizes the concentration of risk in the population. In this sense “concentration” refers to a concentration of disease occurrences in a subset of the population with the highest risks. Such “concentration” corresponds to increased variation in risks, as opposed to concentration of the risks themselves. In other words, the larger the variance of the risks, the more concentrated is the overall risk distribution. The curve can be used flexibly to determine the proportional burden of disease that will occur in a given proportion of the population with the highest predicted risks, and this can be accomplished for any such proportion. So we can determine, say, the proportion of cancers that will occur in the top 10% of the population on the basis of predicted risk, or the top 20%, and so forth. In general, these proportions will be larger for curves that are more convex. However, it is useful to have a single measure that characterizes the degree of risk concentration in the population that can be used, for example, to compare different populations or different risk prediction tools. A natural candidate is the variance, or more specifically the coefficient of variation of the risks, since the Lorenz curve is a scale-free entity. It can be shown that the coefficient of variation, and thus the risk concentration, is necessarily increased when a new informative risk factor is added to an existing model.²⁷

However, the most widely-used measure of concentration is the Gini index.²⁸ The Gini index represents twice the area between the Lorenz curve and the 45° line, scaled to range from no concentration (Gini=0) to maximum concentration (in theory Gini=1). The Gini coefficient, denoted G, is defined as $\mathrm{G}=2\left(0.5-{\int }_0^1\mathrm{L}(\mathrm{r})\text{dF}(\mathrm{r})\right)$. In our later simulations we will use both this index and the squared coefficient of variation of the risk distribution, denoted by K² = σ²/μ², where σ² is the variance of the risks, as measures of risk concentration. Estimation of these quantities will be used to evaluate the bias and accuracy of estimation techniques defined in the next section. These two indices are similar but not identical. Indeed, Lee²⁹ has shown that the Gini index is actually half of the coefficient of deviation of the risk distribution as opposed to the coefficient of variation. The numerator of the coefficient of deviation is the mean absolute difference between two randomly selected risks while the numerator of the coefficient of variation is the mean absolute difference of a randomly selected risk from the mean risk. In both cases the denominator is the mean risk.

Estimation of the Lorenz curve from case–control data

We consider the setting in which we have data from a case–control study with n controls and m cases. We assume that a risk prediction model is estimated from the cases and controls using the risk factors in the study and that this is used to estimate the individual risks of each of the cases and controls. For example, if the vector of risk factors is denoted by x and we use a conventional logistic regression then the risk predictor would be of the form exp(β̂′x), where β represents the parameters of the model and β̂ represents the parameter estimates. Unadjusted for the overall disease rate in the population these predictors simply represent the relative probability that a given individual in the study is a case versus a control, with sampling fractions proportional to m and n. However, since the Lorenz curve represents risk concentration, a standardized entity, it is only the relative values of these risk predictors that need to be employed in constructing it. Furthermore, since the Lorenz curve is a function solely of the risk distribution in the population it can be constructed solely from the estimated risks in the controls (representing the population at risk) as follows. Let r̂_i, i = 1,…, n represent the ranked risks in the controls estimated in this way. Then an empirical estimate of the Lorenz curve can be obtained using F̂(r_i) = i / n and $\widehat{\mathrm{L}}({\mathrm{r}}_{\mathrm{i}})={\sum }_{\mathrm{l}=1}^{\mathrm{i}}{\widehat{\mathrm{r}}}_{\mathrm{l}}/{\sum }_{\mathrm{l}=1}^{\mathrm{n}}{\widehat{\mathrm{r}}}_{\mathrm{l}}$. We refer to this as Method A. Note that the cases do influence this estimator through their influence in creating the risk score.

We also examine an alternative approach that makes use of the risk estimates in the cases. Let these be denoted r̃_j, j = 1,…, m. Since the Y-axis of the Lorenz curve represents the risk distribution in incident cases we can use these to estimate L(r) directly. It follows that an empirical estimate of the Lorenz curve can be constructed from the joint ranks of the cases and controls as follows: F̂(r_i) = i / n as before, while L̂(r_i) = j /m, where j satisfies the conditions r̃_j ≤ r̂_i and r̃_j+1 > r̂_i. We refer to this as Method B.

The coefficient of risk variation can be estimated directly from the predicted risks in the controls using K̂² = σ̂²/μ̂², where ${\widehat{\mathrm{\sigma }}}^2={\mathrm{n}}^{-1}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\widehat{\mathrm{r}}}_{\mathrm{i}}^2-{\widehat{\mathrm{\mu }}}^2$ and $\widehat{\mathrm{\mu }}={\mathrm{n}}^{-1}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\widehat{\mathrm{r}}}_{\mathrm{i}}$. The estimate of the Gini coefficient, which is double the area between the Lorenz curve and the 45° line, can be obtained using $\widehat{\mathrm{G}}=2{\mathrm{D}}^{-1}{\sum }_{\mathrm{d}=1}^{\mathrm{D}}\left(\widehat{\mathrm{F}}({\mathrm{r}}_{\mathrm{d}})-\widehat{\mathrm{L}}({\mathrm{r}}_{\mathrm{d}})\right)$, where d=1, …, D, indexes the distinct risk categories and D is the total number of risk categories. [In the case of a continuous risk model with no ties, D = n.] These results will of course be dependent on whether Method A or Method B is used to estimate L̂ (●).

Example

To illustrate the use of the Lorenz curve in epidemiology we use a subset of cases from the Cancer and Steroid Hormone Study for whom tumor tissue was collected for molecular analysis and analyzed for the purposes of identifying etiologically distinctive sub-types.³⁰ This collection of m=551 cases and n=2,990 controls was used recently to identify etiologically distinct subtypes of breast cancer using gene expressions in the tumors from a panel of breast cancer genes to create the subtypes.³¹ This research made use of data from a study that was approved by the institutional review board at Memorial Sloan Kettering Cancer Center under a waiver of authorization (WA0324-12).

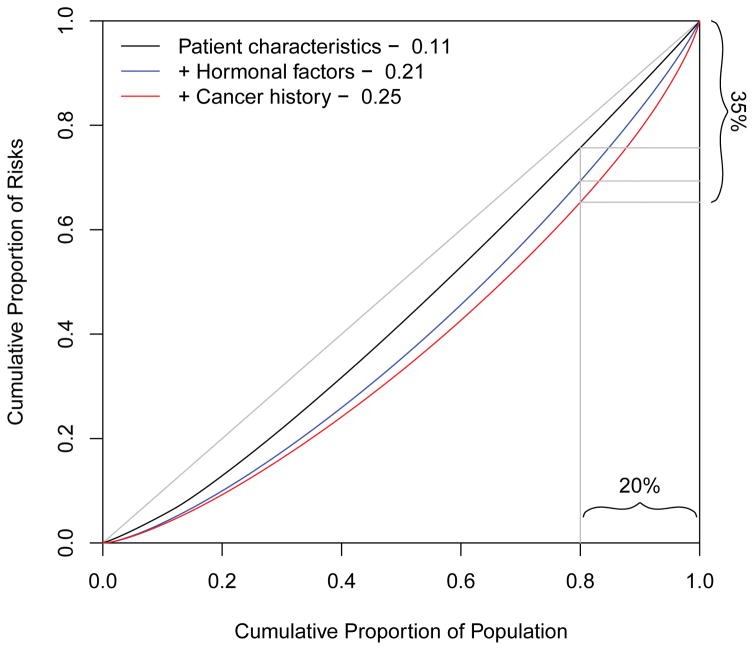
We first demonstrate the use of Lorenz curves to gauge the increases in risk concentration due to the addition of groups of risk factors sequentially to the risk prediction model. First, the risk of breast cancer for each subject was estimated by logistic regression comparing all cases and controls using age at diagnosis, pre- and post-menopausal body mass index, and race. This leads to a modest Gini coefficient of 0.11, and the Lorenz curve is displayed in black in Figure 1. On the basis of this model only 24% of cases will occur in the 20% of the population with the highest risks. We then augmented the model by including the hormonal factors age at menarche, nulliparity, number of children, age at first birth, months of breastfeeding, menopausal status, and age at menopause. The Gini index is increased to 0.21 and the corresponding blue Lorenz curve in Figure 1 indicates that 31% of the cases will occur in the top 20% of the population based on risk. Finally, when adding the information about relevant disease (prior benign breast disease) and family history of breast cancer the Gini index increases to 0.25. Using this risk prediction model 35% of the cases will occur in the 20% of the population with the highest estimated risks.

Figure 1.

Lorenz curves comparing three prediction models on the Cancer and Steroid Hormone Study cases and controls based on 551 cases and 2990 controls.

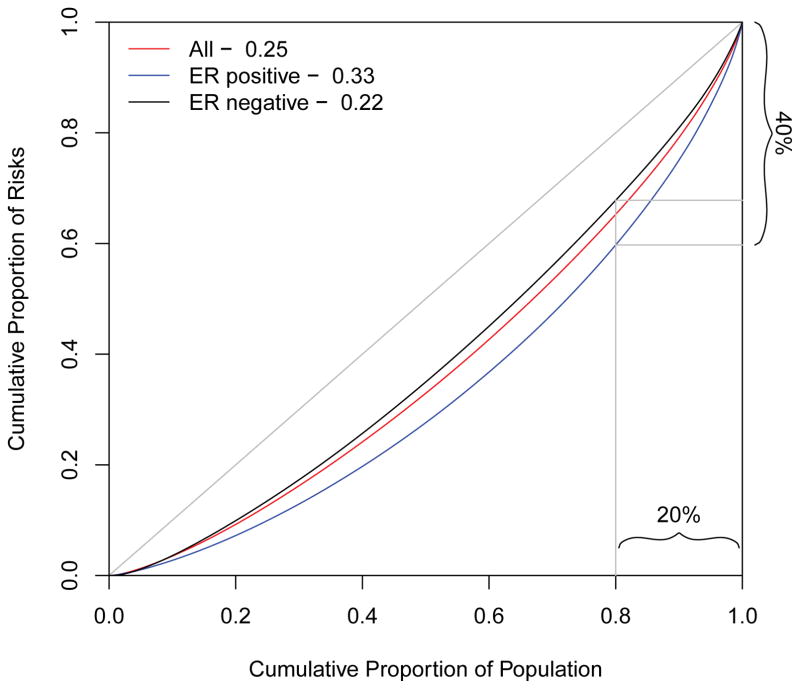
We then explored the extent to which risk concentration might be improved by defining disease sub-types with distinct risk profiles, such as those defined by estrogen receptor, progesterone receptor or human epidermal growth factor receptor 2 status in the tumor samples. We display the results for the strongest of these, estrogen receptor status. The risk prediction models for the subtypes characterized by presence or absence of estrogen receptors involved logistic regression comparing cases in the sub-type of interest (receptor positive or negative) versus all controls using the same set of risk factors as before. The results are illustrated in Figure 2. The figure demonstrates that the risk factors more accurately predict estrogen receptor positive cases, showing that 40% of estrogen receptor positive cases will occur in the top 20% of the population ranked on the basis of risk of this sub-type (blue curve). By contrast the risk factors do not improve our ability to predict estrogen receptor negative breast cancers (black curve).

Figure 2.

Lorenz curves comparing the risk predictiveness of two sub-types of breast cancer based on data from the Cancer and Steroid Hormone Study. The blue curve is based on 294 estrogen receptor positive (ER+) cases versus the 2990 controls. The black curve is based on 224 estrogen receptor negative (ER−) cases versus 2990 controls. The benchmark red curve is based on all cases and is the same one as the red curve in Figure 1.

Statistical properties / Simulations

Our first simulation was designed to confirm that the Lorenz curve can indeed be estimated from case–control data when in fact the data are generated from a pre-specified disease incidence model. We generated data from an underlying “true” model with lognormal risks, i.e. we generated a risk r = exp(x) for each subject in the population, where x was generated from a normal distribution. That is, we generated data from a population with a known log-normal risk distribution. By controlling the mean and variance of x we are able to choose the expected value for both the prevalence and the coefficient of risk variation, K. We used these sets of risks to generate datasets and to estimate the Lorenz curve and its concentration measures K² and G by both Method A and Method B. Population controls were generated by randomly sampling n values of x, while cases were sampled by generating a random value of x, including the subject as a case on the basis of a Bernoulli trial with probability of success r = exp(x), and repeating the process until m cases were successfully sampled. This process was repeated a large number of times (1000 times) to determine biases and variances. The results for Method A are shown in Table 1. The results for Method B are very similar and are available on-line in eTable 1. In the top panel (K²=0.25) the risk distribution was configured to produce a degree of concentration similar to that observed in the example from the Cancer and Steroid Hormone Study. The bottom panel represents a much higher degree of risk concentration. Absolute risks of 0.1 and 0.01 represent settings in which the disease occurrence is common and relatively rare, respectively.

Table 1.

Simulated Data Using Lognormal Risks

Cases/Controls	Gini				K2
	Truea	Mean	Standard Error	Bias	Truea	Mean	Standard Error	Bias
K2=0.25
Mean Absolute Risk = 0.1b
250/250	0.262	0.262	0.047	0.000	0.250	0.269	0.120	0.019
500/500	0.262	0.260	0.035	−0.002	0.250	0.257	0.084	0.007
1000/1000	0.262	0.262	0.024	0.000	0.250	0.255	0.057	0.005
250/2500	0.262	0.260	0.037	−0.003	0.250	0.254	0.083	0.004
500/2500	0.262	0.261	0.025	−0.001	0.250	0.254	0.057	0.004
1000/2500	0.262	0.262	0.020	0.000	0.250	0.253	0.045	0.003
Mean Absolute Risk = 0.01b
250/250	0.260	0.259	0.049	−0.001	0.250	0.264	0.147	0.014
500/500	0.260	0.263	0.036	0.003	0.250	0.264	0.086	0.014
1000/1000	0.260	0.260	0.024	0.000	0.250	0.250	0.054	0.000
250/2500	0.260	0.260	0.037	0.000	0.250	0.254	0.082	0.004
500/2500	0.260	0.261	0.027	0.001	0.250	0.254	0.060	0.004
1000/2500	0.260	0.262	0.020	0.002	0.250	0.253	0.045	0.003
K2=1
Mean Absolute Risk = 0.1b
250/250	0.445	0.446	0.046	0.002	1.000	1.072	0.536	0.072
500/500	0.445	0.442	0.034	−0.002	1.000	0.995	0.282	−0.005
1000/1000	0.445	0.443	0.024	−0.001	1.000	1.004	0.216	0.004
250/2500	0.445	0.440	0.033	−0.004	1.000	0.995	0.241	−0.005
500/2500	0.445	0.445	0.024	0.000	1.000	1.012	0.185	0.012
1000/2500	0.445	0.445	0.019	0.000	1.000	1.010	0.163	0.010
Mean Absolute Risk = 0.01b
250/250	0.443	0.442	0.047	0.000	1.000	1.030	0.464	0.030
500/500	0.443	0.441	0.033	−0.001	1.000	1.000	0.306	0.000
1000/1000	0.443	0.444	0.024	0.001	1.000	1.014	0.237	0.014
250/2500	0.443	0.445	0.031	0.003	1.000	1.026	0.242	0.026
500/2500	0.443	0.444	0.024	0.001	1.000	1.012	0.195	0.012
1000/2500	0.443	0.444	0.020	0.001	1.000	1.010	0.166	0.010

K: coefficient of variation.

^aTrue values were obtained on a sample of 10,000 controls, and thus vary a little from one sampling to another.

^bTo obtain risk distributions with these mean absolute risks we generated values of x from the following normal distributions and set the risk to r = exp(x):- N(−2.414, 0.223); N(−4.717, 0.223); N(−2.505, 0.405); N(−4.808, 0.405); N(−2.649, 0.693); N(−4.952, 0.693).

The results demonstrate that there is essentially no bias in the estimate of the Gini coefficient. The estimate of K² is modestly positively biased for the smaller sample sizes examined, although the larger biases in this setting are in part a result of the larger standard errors. Results for an intermediate risk concentration are available in eTable 1. Overall the results confirm that it is possible to estimate the Lorenz curve from case–control data, regardless of the fact that the curve represents concentration of the distribution of absolute risks.

To test the method in a setting that is a better representation of how it would be applied in practice we constructed simulations framed by the Cancer and Steroid Hormone Study dataset used in the example in the previous section. First, we used the complete set of 551 cases and 2,990 controls to develop a baseline risk prediction model. We used a logistic regression model to estimate the parameters which we assumed to be the “true” underlying risk prediction model based on β̂′x where x represents the set of risk factors and β̂ is the set of parameter estimates assumed to be the true estimates. In simulating data from this model we varied the underlying population risk by using as the risk log(r) = β̆ + β̂′x where β̆ = log(π̆)−log(π/ (1−π)), π is the sampling fraction of cases in the case–control study, i.e. 551/(551+2990), and π̆ is the population risk of disease which was varied systematically in the simulations. We used this “true” model to determine the true values of K² and G, using a sample of 10,000 controls.

We randomly selected with replacement a sample of n controls from the Cancer and Steroid Hormone Study data, with covariates x_i, i=1, …, n. To generate the cases, we first randomly selected (with replacement) a control with covariate vector x. We then calculated r = exp(β̆+β̂′x), generated a Bernoulli with probability r, and assigned x as a case if the Bernoulli was a “success”. A new control was sampled and the process continued until m cases were “successfully” accrued, with covariate vectors denoted (x̃₁, x̃₂,….x̃_m). We then performed logistic regression on (x̃₁, x̃₂,….x̃_m). versus (x₁, x₂,…, x_n). We used the parameter estimates β^* from this run to estimate risks r^* = exp(β^*′x) for each case and control and used these sets of risks to estimate the Lorenz curve, K² and G by both Method A and Method B. As before, this process was repeated a large number of times (1000 times) to determine biases and variances.

The results for Method A are presented in Table 2. As before the results for Method B are similar and are available on-line in eTable 2. As in Table 1 the biases are unaffected by the true prevalence of disease, confirming the fact that the Lorenz curve reflects the risk concentration rather than absolute risk. There is positive bias throughout, due to the fact that the prediction model is estimated from the data on which it is evaluated. However, as would be expected, bias declines as the sample size increases. Biases for K² are larger than for G, though they decrease substantially with increasing sample sizes.

Table 2.

Simulated Data from the Cancer and Steroid Hormone Study

Cases/Controls	Gini				K2
	Truea	Mean	Standard Error	Bias	Truea	Mean	Standard Error	Bias
Mean Absolute Risk = 0.1
250/250	0.256	0.307	0.043	0.051	0.254	0.415	0.214	0.160
500/500	0.256	0.280	0.033	0.024	0.254	0.325	0.103	0.071
1000/1000	0.256	0.265	0.023	0.009	0.254	0.279	0.064	0.025
250/2500	0.256	0.280	0.034	0.025	0.254	0.320	0.096	0.065
500/2500	0.256	0.269	0.024	0.014	0.254	0.288	0.063	0.033
1000/2500	0.256	0.262	0.020	0.006	0.254	0.269	0.051	0.014
Mean Absolute Risk = 0.001
250/250	0.256	0.304	0.045	0.048	0.256	0.407	0.221	0.152
500/500	0.256	0.279	0.034	0.023	0.256	0.323	0.108	0.067
1000/1000	0.256	0.267	0.025	0.011	0.256	0.285	0.067	0.029
250/2500	0.256	0.281	0.033	0.026	0.256	0.322	0.095	0.066
500/2500	0.256	0.269	0.025	0.013	0.256	0.286	0.066	0.030
1000/2500	0.256	0.261	0.019	0.006	0.256	0.268	0.049	0.013

K: coefficient of variation.

^aTrue values were obtained on a sample of 10,000 controls, and thus vary a little from one sampling to another.

Discussion

A widely used graphical tool for characterizing the accuracy of risk prediction models is the receiver operating characteristic curve. This is somewhat similar to the Lorenz curve but differs in important ways. The receiver operating characteristic curve is constructed around a binary classification, for example disease present versus disease absent, and it contrasts the sensitivity against the specificity of a classification rule or diagnostic test. By contrast, the Lorenz curve focuses on the concentration of a continuous quantity, in our case risk. The Y-axis of the Lorenz curve represents, in essence, the expected number of cases that will occur in a defined segment of the population, while the X-axis represents the total population rather than individuals who do not experience the disease. Just as for the receiver operating characteristic curve, as the size of the high risk group progressively decreases, the number of subjects who will experience the disease who are excluded from this high risk group progressively increases. By focusing on risk concentration, the Lorenz curve allows users to identify the extent to which incidences of disease will occur in subsets of the population characterized by risk. In an era in which we are increasingly able to predict risks of various diseases, and in which both the economic and morbidity costs of screening programs are hotly debated, the extent to which risk prediction models can identify segments of the population in which the preponderance of the cases will occur is one of the crucial measures for evaluating the merit of their utility. For this reason we believe that the Lorenz curve is the natural graphical tool for displaying and characterizing risk predictiveness.

We do note that risk concentration is a metric that is unrelated to absolute risk. Indeed, this independence is why we are able to estimate the Lorenz curve from retrospectively sampled case–control data. Although calibration is a very important attribute of a risk prediction tool, interestingly, estimation of the Lorenz curve is less likely to be influenced by a poorly calibrated model. That is, proportional biases in the risk prediction model will not influence the corresponding Lorenz curve, though clearly non-proportional biases in the risk predictor would lead to bias.

The Lorenz curve is an inherently population-based metric. That is, the risk concentration is dependent on the population from which the data are derived. For example, if the curve is derived from a case-cohort design using incidence density sampling it will reflect the risk concentration in the specific cohort employed. Likewise, for a population-based case–control study the curve will reflect the risk concentration in the population from which the cases and controls are sampled. The use of data from matched case–control studies will potentially influence risk concentration in that matching on a factor that influences risk effectively removes the contribution of that factor from the coefficient of risk variation and thus would correspondingly reduce the risk concentration in the Lorenz curve. To our knowledge methods for re-calibrating a Lorenz curve to eliminate the effect of matching or to translate a curve estimated on one population to a different population have not been developed and are topics for future research.

The technical message from our work is that although the Lorenz curve characterizes the distribution of absolute risks one does not need data on absolute risks to construct it. Risk concentration is a scale free entity. Thus even though risk predictions constructed from a case–control study represent relative risks (unless they are separately adjusted to population rates) the concentration of these relative risks will be the same regardless of the sampling fractions of cases and controls used in the study. Consequently we can construct the Lorenz curve using data from a case–control study. We have also shown that the parameters representing risk concentration can be estimated with modest bias provided that the sample sizes in the case–control study are not especially small, and that biases that do occur are largely due to the well-known overconfidence that results when a risk prediction rule is applied to the dataset from which it is generated, a bias that can be corrected using a validation sample.³ Such bias increases with the number of covariates examined for inclusion in the risk prediction tool and decreases with the sample size of the study.

In summary, the Lorenz curve is a simple and accessible graphical tool that provides information that is especially relevant for evaluating the potential yield of screening programs that target high-risk subsets of the population. It is a tool that should be more widely used in the public health setting.