Probe Oscillation Shear Elastography (PROSE): A High Frame-Rate Method for Two-Dimensional Ultrasound Shear Wave Elastography

Abstract

Ultrasound shear wave elastography (SWE) utilizes the propagation of induced shear waves to characterize the shear modulus of soft tissue. Many methods rely on an acoustic radiation force (ARF) “push beam” to generate shear waves. However, specialized hardware is required to generate the push beams, and the thermal stress that is placed upon the ultrasound system, transducer, and tissue by the push beams currently limits the frame-rate to about 1 Hz. These constraints have limited the implementation of ARF to high-end clinical systems. This paper presents Probe Oscillation Shear Elastography (PROSE) as an alternative method to measure tissue elasticity. PROSE generates shear waves using a harmonic mechanical vibration of an ultrasound transducer, while simultaneously detecting motion with the same transducer under pulse-echo mode. Motion of the transducer during detection produces a “strain-like” compression artifact that is coupled with the observed shear waves. A novel symmetric sampling scheme is proposed such that pulse-echo detection events are acquired when the ultrasound transducer returns to the same physical position, allowing the shear waves to be decoupled from the compression artifact. Full field-of-view (FOV) two-dimensional (2D) shear wave speed images were obtained by applying a local frequency estimation (LFE) technique, capable of generating a 2D map from a single frame of shear wave motion. The shear wave imaging frame rate of PROSE is comparable to the vibration frequency, which can be an order of magnitude higher than ARF based techniques. PROSE was able to produce smooth and accurate shear wave images from three homogeneous phantoms with different moduli, with an effective frame rate of 300Hz. An inclusion phantom study showed that increased vibration frequencies improved the accuracy of inclusion imaging, and allowed targets as small as 6.5 mm to be resolved with good contrast (contrast-to-noise ratio ≥19 dB) between the target and background.

I. INTRODUCTION

IN MEDICAL practice, physicians have long used manual palpation of soft tissues as a method to aid medical diagnosis. While effective, this is a qualitative process that is limited to superficial tissues and suffers from inter-rater variability due to the subjective nature of the technique. To address these limitations, elasticity imaging has been developed to provide non-invasive and objective quantification of the mechanical properties of tissue [1]. While many different techniques have been developed to quantify these properties [2–11], many of these techniques utilize the propagation of induced shear waves as a surrogate for, or to quantitatively estimate the shear modulus of soft tissue. Assuming soft tissues are incompressible, isotropic, linear, and elastic, the shear modulus (μ) can be related to shear wave propagation speed, c_s, by

$$\mathrm{\mu }=\mathrm{\rho }{\mathrm{c}}_{\mathrm{s}}^2,$$ (1)

where ρ is density and can be assumed to be 1000 kg/cm³ for all soft tissues [10]. This relationship allows the shear modulus to be calculated from the propagation speed of the induced shear wave.

Acoustic radiation force (ARF) based techniques have been successfully used to generate shear waves within soft tissue. This is done by utilizing an ultrasound push beam to displace soft tissue and track the propagation of the resulting shear waves in pulse-echo mode to produce quantitative estimates of tissue stiffness [2, 3, 5, 6, 8, 9, 11]. While ARF shear wave elastography (SWE) methods have proved to be a versatile tool for evaluation of the mechanical properties of tissue [12–14], this technique suffers from two major drawbacks. The first is that the high voltage push beam used to generate shear waves requires upgraded hardware, including power supplies and transmission circuits, which limits the accessibility of ARF SWE techniques to dedicated research platforms and high-end clinical systems [2, 15–17]. Secondly, the delivered push beams places thermal stress on the hardware, ultrasound transducer, and tissue, ultimately limiting the typical elastography frame-rate to about 1 Hz [18] to provide hardware cooling time and prevent tissue damage. While the low frame-rate is not prohibitive for imaging static soft tissues, it currently is not suitable to image dynamic soft tissues or for the real-time survey of large three-dimensional regions.

There are many alternatives to generate shear waves without the use of an ARF-based push beam. Twenty five years ago, Yamakoshi utilized a continuous sinusoidal vibration of a plate placed adjacent to an ultrasound transducer to generate shear waves, and used a phase based estimation technique to recover the shear wave speed [10]. More recently Kevin Parker’s group has developed a method that utilizes multiple external vibration shear wave sources to produce a “crawling wave” field that can be used to compute the shear modulus [19, 20]. However, both of these techniques require separate devices for the generation and the detection of shear waves, which increases the footprint of the measurement probe, and can cause difficulty when investigating certain tissues due to physiological constraints (e.g. liver due to rib shadowing). Transient Elastography (TE), commercialized as Fibroscan (Echosens, Paris, France), has addressed this issue by using a small single element transducer to deliver a mechanical impulse to generate a single longitudinally polarized transient shear wave into the body that can be detected by the same ultrasound transducer [8]. TE has the added advantage that the use of transient excitation avoids standing wave and other potential artifacts. As described by Sandrin [21], these longitudinally polarized shear waves arise as result of the diffraction from a source of finite size as the summed contributions of transversely polarized shear waves coming from subsources give rise to a globally, longitudinally polarized shear wave on the axis of the vibrator. In a recent paper, Catheline and Benech demonstrate from the elastodynamic Green’s function that there are longitudinal shear waves that can be detected in both the near and far field [22]. TE has been widely applied in studying liver fibrosis; however, FibroScan does not provide two-dimensional (2D) imaging and is not suited for detection of local changes in tissue elasticity. It is feasible to extend TE to 2D [23], however these methods are not capable of high frame-rate imaging as they require the generated shear wave to travel through the entire target and dissipate, before a second image can be acquired. Therefore, there is still a need for the development of a mechanically coupled shear wave device capable of producing high frame-rate 2D elastography images.

In this paper we propose Probe Oscillation Shear Wave Elastography (PROSE) as a new method, which utilizes continuous mechanical vibration of the ultrasound transducer to produce harmonic longitudinally polarized shear waves, similar to the waves generated using TE, for 2D quantitative elastography while simultaneously acquiring the resulting shear wave motion using the same transducer under pulse-echo detection mode. To accomplish this, a standard ultrasound transducer was mounted co-axially with a custom made voice-coil actuator system, allowing the transducer to vibrate in the axial direction. When the system is placed in contact with an object, the motion at the face of the transducer produces longitudinally polarized shear waves to propagate within the contacted medium, which can be observed using standard pulse-echo detection. Single frame shear wave motion was obtained using a symmetric sampling scheme and the shear wave speed image was reconstructed using the Local Frequency Estimation (LFE) processing method [24]. The efficacy of PROSE was evaluated through homogeneous and inclusion phantom studies.

II. METHODS

A. Vibration System

To generate shear wave motion, a custom vibration system was created, coaxially mounting a linear voice coil actuator (BEI Kimco Magnetics, Vista, CA) to an L11-4v linear array ultrasound transducer (Verasonics Inc., Kirkland, WA) for use with a Verasonics Vantage Ultrasound system (Verasonics Inc., Kirkland, WA). A function generator (Agilent 33250A, Agilent Technologies, Inc., Santa Clara, CA, USA) was used to generate a sinusoidal driving signal for shear wave generation. This output was connected to an amplifier (Crown D150A, Crown Audio, Inc., Elkhart, IN, USA; voltage gain: 26 dB) before being delivered to the voice-coil vibration system. To generate shear waves, the vibration system was manually held with a single hand such that the transducer was in continuous contact with the tested object. The vibration system is depicted in Fig. 1.

Fig. 1.

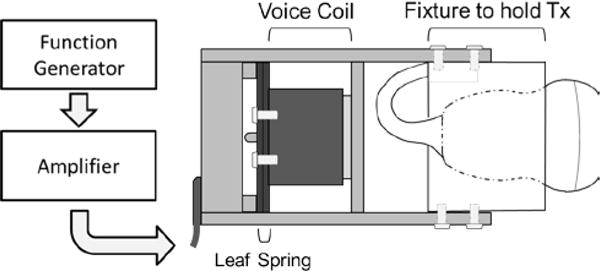
A diagram depicting the equipment used to drive the transducer (Tx) vibration system. A sinusoidal signal is output from a function generator and then amplified to drive the voice-coil actuator. The voice-coil was mechanically secured to the leaf spring and the Tx was secured to the rest of the system through a custom fixture, allowing the entire system to vibrate. Shear waves are generated by the motion of the transducer in contact with the object’s surface. Shear waves were observed using standard pulse-echo detection.

B. Symmetric Detection

The generated motion can be observed using a standard pulse-echo detection. However, the detected motion is comprised of three separate components: 1) the compressional wave generated by the harmonic vibration of the transducer, 2) the shear waves generated in the same fashion, and 3) a compression artifact caused by transducer motion relative to the imaged tissue. This compression artifact arises from transducer compression from the surface producing deformations within the object similar to deformation in quasi-static compression elastography. Fig. 2 illustrates how this effect arises when the transducer is moved by Δz between two consecutive detection events. In a non-moving reference system, the relative displacement of a single scatterer (represented by grid intersections) is greatest at the surface whereas a scatterer at the bottom will not be displaced. This leads to a depth dependent displacement profile that nonlinearly decreases with depth. If the transducer’s frame of reference is used, as would be the case during pulse-echo detection, the compression profile is small at the surface since the scatterers’ displacement is similar to that of the transducer, whereas the scatters at the bottom will show a displacement closer to the total amount the transducer was displaced (dashed line in Fig. 2c). The resulting shear wave motion observed by the transducer is contaminated by the compression profile (black line in Fig. 2c). It should be noted that with sinusoidal probe motion the magnitude of the strain profile is not static, but will oscillate as the relative displacement of individual scatters changes as the probe moves through its cycle.

Fig. 2.

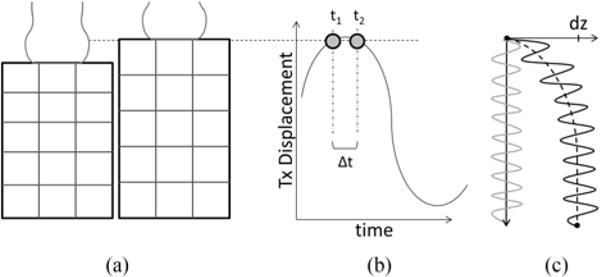
a). Compression of the transducer introduces deformation within the medium, leading to a strain-like compression profile (c, black dashed line) that contaminates the shear wave motion (c, black solid line). b) The proposed symmetric sampling scheme allows the transducer to return to the same physical location between consecutive pulse-echo detection events, suppressing the compression artifact (c, grey line).

The effects of the compressional wave can be suppressed through spatial high-pass filtering [25], because the large differences in propagation speed of the compressional and shear waves allows for clear separation of the wavelengths of the two waves. However the compression artifact is more difficult to decouple from the shear waves, and may cause complications when calculating the shear wave speed using time-of-flight (TOF) or phase gradient methods if not properly suppressed [26, 27]. Temporal filtering is unable to decouple the two effects as they both oscillate with the same frequency; and spatial filtering is ineffective as the spatial frequency content of the compression profile often overlaps with the spatial frequencies of the shear waves. While it may be possible to estimate the compression through a fitting-and-subtraction process, it is not guaranteed to be accurate in the presence of tissue heterogeneity that would arise with inclusions.

Alternatively, because the transducer’s motion is sinusoidal, a sampling scheme can be implemented such that the two consecutive pulse-echo events for motion detections are symmetrically spaced in time around the peak transducer displacement position so the transducer is at the same physical location for the two pulse-echo events. Because pulse-echo motion detection only detects relative motion between two pulse-echo events, the compression profile is automatically suppressed and only shear waves are “seen” by this symmetric detection scheme. Fig. 2 shows the symmetric detection events at t₁ and t₂ and the resulting shear wave motion detected without the compression artifact (grey line, Fig 2c). Thus, it is possible to acquire two symmetrically sampled shear wave images per cycle, one at the maximum and one at the minimum of the transducer position. To accomplish the desired detection timing, a miniature accelerometer (ADXL335, Analog Devices, Norwood, MA) was mounted on the transducer. Ultrasound detection timing was adjusted such that the detection events occurred symmetrically around the maximum and minimum transducer displacement, with the time between two sequential detection events (Δt) empirically set as 1/10^th of the vibration period.

C. Motion Detection

Coherent compounding plane wave imaging [28, 29] was used to detect the resulting motion (detection pulse center frequency 6.25 MHz). As previously established, a three angle compounding method (steering angles of −2°, 0°, and 2°) was utilized to increase the signal-to-noise-ratio (SNR) of the shear wave signal without substantially reducing the effective frame rate [30]. Because the probe is continuously moving, each steering angle will capture a slightly different image, resulting in blurring of the final compounded images. However, it has been previously established that as long as the transmission sequence is identical, causing identical blurring patterns in each of the compounded images, the underlying motion can still be successfully recovered using standard motion calculation methods [31]. The spatial pixel resolution of the image was one ultrasound wavelength (0.246 mm), and resulting field-of-view (FOV) of the investigated medium was 45.8 × 38.4 mm. Particle velocity was computed from the in-phase/quadrature (IQ) data of consecutive frames utilizing a one-dimensional autocorrelation method [32]. A three pixel spatial window was used for averaging in the autocorrelation process, and a 3 × 3 pixel spatial median filter was used to remove spurious noise from the resulting shear wave motion signal.

D. Filtering Process

Once the shear wave motion was acquired using the symmetric detection scheme and particle velocity data was obtained using the autocorrelation process. A sixth order Butterworth band-pass filter was applied to each frame to remove spatial wavelengths representing shear wave speeds outside a predetermined physiological range (cutoffs corresponding to 0.5–10 m/s). Because the shear wave propagation is primarily in the axial direction, motion propagating in the lateral direction was removed by filtering the corresponding spatial Fourier domain (k-space) components through the use of a rolled-off wedge filter [33, 34].

E. Local Shear Wave Speed Estimation

Sampling twice per period does not have the temporal resolution required to robustly estimate the shear wave speed using standard TOF methods. However, since the shear waves were harmonic in nature, LFE can be used to obtain a 2D shear wave speed image from a single frame of 2D shear wave data [24, 35, 36]. Because the LFE requires the Fourier Transform, wave motion was mirrored in the two spatial dimensions to reduce the rippling effects in k-space due to discontinuous edges in the spatial domain. The resulting images were processed using LFE to estimate the spatial wavelength at each pixel. The LFE utilized 10 frequency bands with half-octave scaling of the center frequency for each band, spanning the wavelengths corresponding to shear wave speeds of 0.5–10 m/s [24]. An additional weighting term was added to the estimation method to compensate for changes in shear wave amplitude when transitioning from materials with different stiffness [37]. Because the vibration frequency used to generate the shear waves is known, the spatial wavelength maps were converted to shear wave speed images using velocity of a shear wave in the medium,

$${\mathrm{c}}_{\mathrm{s}}={\mathrm{f}}_{\mathrm{v}}\lambda ,$$ (2)

where f_v is the known vibration frequency and λ is the measured wavelength.

F. Homogeneous Phantom Study

Three tissue-mimicking homogeneous cylindrical phantoms (Model 039, CIRS Inc., diameter 11.6 cm, height 14 cm; sound speed of 1540 m/s, ultrasound attenuation of 0.5 dB/cm/MHz) with nominal Young’s moduli (E) of 10, 25, and 45 kPa were imaged using the PROSE technique. It has been previously shown that for a perfectly elastic material the shear wave speeds can be related to Young’s modulus by,

$$\mathrm{E}\approx 3\mathrm{\mu }=3\mathrm{\rho }{\mathrm{c}}_{\mathrm{s}}^2,$$ (3)

resulting in nominal shear wave speeds of 1.83, 2.89, and 3.87 m/s for the three phantoms [2]. Because it was previously shown that pre-compression of materials can change stiffness measurements [38, 39], the transducer vibration system was manually handheld on the surface of the phantom with care taken to minimize manual compression of the phantom. The motion of the probe is on the order of millimeters, therefore, it is not expected that the vibration will substantially increase the shear modulus of the phantom through the vibration cycle. Utilizing a trigger from the Verasonics system, a 300 Hz sinusoidal signal was applied to the probe vibration system. Since the vibration system started from rest, a 150 ms warm-up period was added to ensure that the system reached steady state. Immediately following the warm-up period, the symmetric sampling scheme was initiated, allowing for continuous acquisition with a maximum effective frame-rate of twice the vibration frequency. After motion demodulation, the two resulting motion frames were processed using spatial wedge and band-pass filters, and shear wave speed images were generated using LFE. A final estimate of the shear wave speed was obtained by averaging the two images obtained at the maximum and minimum displacement.

A single rectangular region-of-interest (ROI) was used to calculate the mean and standard deviation of the shear wave speed images. For comparison five shear wave speed images were acquired with a General Electric LOGIQ E9 scanner (LE9; GE Healthcare, Wauwatosa, WI) equipped with an ARF SWE method [15]. The mean and standard deviation from the LE9 (9L, Breast settings, 1 cm diameter circular ROIs) measurements were used as a reference to compare with results of PROSE.

G. Inclusion Phantom Study

To test the resolution capabilities of PROSE, a standard stepped cylinder inclusion phantom (Model 049A, CIRS Inc., Norfolk, VA) was imaged. The nominal shear wave speed of the Type IV inclusion is 5.2 m/s and provides good contrast to the softer background material’s shear wave speed of 2.9 m/s. Since it is known that the resolution of the LFE is linked to the wavelength of the shear waves [40], the 10.4 mm Type IV inclusion was imaged at 300 Hz, 350 Hz and 400 Hz vibration frequency. A real-time B-mode imaging sequence was added to guide transducer placement and a reference B-mode image was saved just prior to the initiation of PROSE acquisitions. To evaluate the ability of PROSE to resolve inclusions of various sizes, the 6.5, 10.4, and 16.7 mm inclusions were also imaged using a 400 Hz vibration frequency. For both of the inclusion studies, circular ROIs containing the inclusions were selected based on the reference B-mode image, whereas the ROI for the background was a rectangle placed above the inclusion. Five reference measurements were acquired using the LE9 (9L, Breast settings) for each of the three inclusions, using circular ROI drawn with from the B-mode image, as well as the background (1 cm diameter circular ROI). The LE9 results were used as a reference to compare with PROSE results.

III. RESULTS

Fig. 3 shows a frame of the shear wave motion signal and the shear wave speed images obtained with PROSE from the homogeneous phantoms. The measured shear wave speed estimates were 1.74 ± 0.16 m/s, 2.43 ± 0.13 m/s, and 3.51 ± 0.19 m/s for the 10 kPa, 25 kPa and 45 kPa phantoms, respectively, compared to 1.63 ± 0.05 m/s, 2.46 ± 0.06 m/s, and 3.56 ± 0.12 m/s, respectively, using the LE9 (Fig. 4).

Fig. 3.

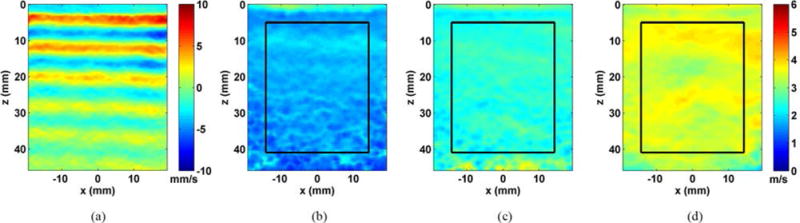
Results from evaluating the homogeneous phantoms with PROSE at 300 Hz. a) A representative shear wave motion frame from the 25 kPa phantom. b) The reconstructed shear wave speed image from the 10 kPa phantom, c) the 25 kPa phantom and d) the 45 kPa phantom.

Fig. 4.

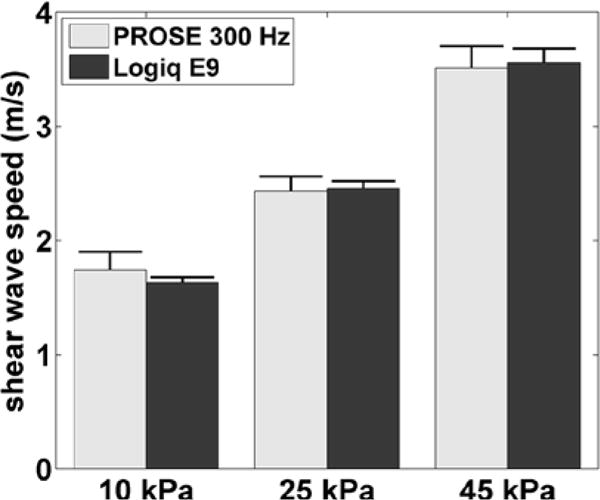
Shear wave speed measurements of the three homogeneous phantoms for PROSE at 300 Hz compared with those obtained with the LOGIQ E9. Error bars represent one standard deviation.

Fig. 5 shows the resulting shear wave speed images of the 10.4 mm inclusion with varying frequencies. Two ROIs were manually selected to evaluate the performance of PROSE. One ROI was selected using the B-mode image to determine the inclusion boundaries. A second ROI, used to measure the background, was placed above the 10.4 mm inclusion and 5 mm from the edges. The measured shear wave speeds within the inclusions were 3.63 ± 0.33 m/s, 4.26 ± 0.32 m/s, and 4.40 ± 0.47 m/s for the 300 Hz, 350 Hz, and 400 Hz acquisitions, respectively, compared to 4.59 ± 0.42 m/s using the LE9. The measured shear wave speeds in the background were 2.59 ± 0.11 m/s, 2.56 ± 0.11 m/s, and 2.50 ± 0.15 m/s for the 300 Hz, 350 Hz, and 400 Hz acquisitions, respectively, compared to 2.79 ± 0.11 m/s, using the LE9. These results and comparisons to the nominal values were reported in Table I. The contrast to noise ratio (CNR) was calculated to quantify the ability to detect the stiff inclusions,

$$\mathrm{CNR}=\frac{\left|{\mathrm{C}}_{\mathrm{I}}-{\mathrm{C}}_{\mathrm{B}}\right|}{{\mathrm{C}}_{\mathrm{b}}},$$ (4)

where C_I, and C_B are the mean shear wave speed of the inclusion and background, respectively; C_b is the standard deviation of the shear wave speed of the background. The measured CNR values were converted to decibels using 20log₁₀(CNR) and are included in Table I.

Fig. 5.

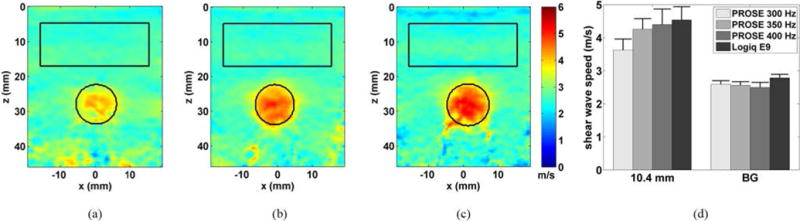
Shear wave speed images from the inclusion phantom, 10.4 mm target, for PROSE performed at a) 300 Hz, b) 350 Hz and c) 400 Hz. ROIs were drawn from B-mode images. d.) Comparison of the inclusion and background shear wave speed of PROSE with the LE9. Error bars represent one standard deviation.

TABLE 1.

Shear Wave Speed Bias and CNR of Inclusion and Background

		Inclusion (m/s) mean ± std.	Inclusion Bias from nominal (%)	Background (m/s) mean ± std.	Background Bias from nominal (%)	CNR (dB)
PROSE	16.7 mm; 400 Hz	4.85 ± 0.49	−6.08	2.60 ± 0.18	−11.3	22.1
	10.4 mm; 400 Hz	4.40 ± 0.47	−14.8	2.50 ± 0.15	−13.4	22.1
	10.4 mm; 350 Hz	4.26 ± 0.32	−17.5	2.56 ± 0.11	−11.3	23.8
	10.4 mm; 300 Hz	3.63 ± 0.33	−29.7	2.59 ± 0.11	−10.3	19.5
	6.5 mm; 400 Hz	3.70 ± 0.27	−28.3	2.55 ± 0.11	−11.7	20.4
LOGIQ E9	16.7 mm	4.86 ± 0.49	−5.85	–	–	25.5
	10.4 mm	4.59 ± 0.42	−12.1	–	–	24.3
	6.5 mm	4.17 ± 0.36	−19.3	–	–	22.0
	Background	–	–	2.79 ± 0.11	−3.49	–

Fig. 6 shows the shear wave speed images that were obtained from the stepped cylinder phantom with three different inclusion sizes. ROIs were established similarly to the previous inclusion study. The measured shear wave speeds at 400 Hz within the inclusions were 4.85 ± 0.49 m/s, 4.40 ± 0.47 m/s, and 3.70 ± 0.27 m/s for the 16.7 mm, 10.4 mm, and 6.5 mm inclusions, respectively, compared to 4.86 ± 0.49 m/s, 4.59 ± 0.42 m/s, and 4.17 ± 0.36 m/s, respectively, using the LE9. The measured shear wave speeds in the background were 2.60 ± 0.18 m/s, 2.50 ± 0.15 m/s, and 2.55 ± 0.11 m/s for the 16.7 mm, 10.4 mm and 6.5 mm inclusions, respectively, compared to 2.79 ± 0.11 m/s, using LE9. These results were summarized and compared in Fig. 7 and Table I.

Fig. 6.

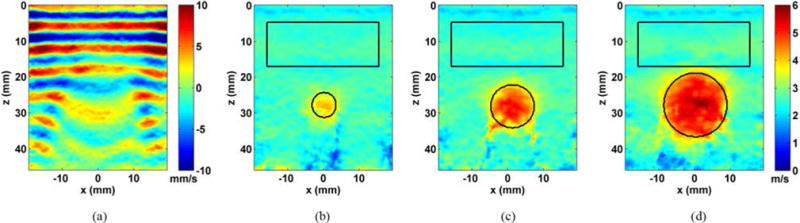
Results from evaluating the inclusion phantom with PROSE at 400 Hz. a) A representative shear wave motion frame from the 16.7 mm inclusion. b) The shear wave speed image from the 6.5 mm inclusion, c) the 10.4 mm inclusion and d) the 16.7 mm inclusion.

Fig. 7.

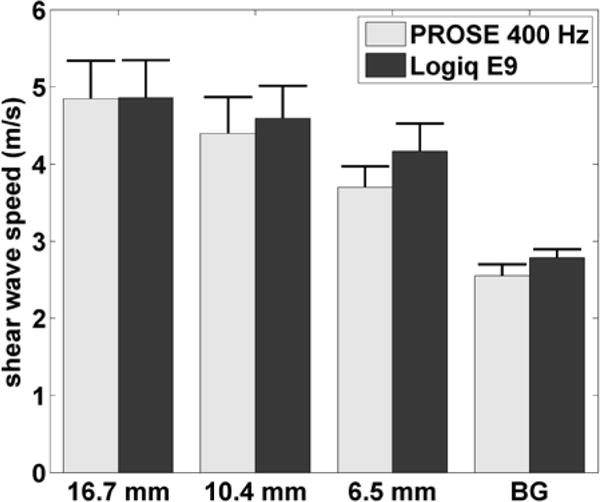
Shear wave speeds for individual inclusions and the background (BG) of the inclusion phantom for PROSE at 400 Hz and the LE9. Error bars represent one standard deviation.

IV. DISCUSSION

In this study we presented a new technique, PROSE, which is capable of simultaneously generating and detecting longitudinally polarized harmonic shear waves for 2D shear wave elastography. Shear waves were introduced through the continuous harmonic vibration of a standard transducer using a voice-coil actuator system. As opposed to ARF-based methods for generating shear waves, it was possible to use the transducer in “detect-only” mode, thus eliminating the stress imposed on the ultrasound system, transducer, and tissue by the high intensity push beams. A novel symmetric detection scheme was used to suppress the interference of compression strain and the shear wave signal detected by pulse-echo ultrasound. A single frame LFE processing technique was used to evaluate the detected motion, and allowed for a substantial increase in the shear wave imaging frame-rate compared to traditional full FOV ARF techniques.

Experiments in homogeneous phantoms and inclusion phantoms demonstrated that PROSE was able to produce 2D shear wave images with values similar to those obtained with a high-end GE LOGIQ E9 scanner. All of the homogenous phantom results showed smooth shear wave speed images with relatively small standard deviations.

The key principle behind PROSE is that symmetric sampling, across peaks or nulls of probe compression, is able to acquire two images where the compression of the material is identical but the shear wave phase differs, allowing for isolation of the shear wave signal from probe compression artifact. To ensure sampling when the compressional effects were identical, this study relied on a three-axis accelerometer to provide information of the probes trajectory. A small timing error may result in incomplete suppression of the compressional effects, which has low spatial frequency (i.e. large spatial wavelength) and thus may lead to overestimation of shear wave speed. In principle, a higher vibration frequency will require more precise timing for symmetric sampling. As an additional precaution, all shear wave fields were processed using a spatial band-pass filter designed to suppress large spatial frequencies due to incomplete removal of the compressional effects by the symmetric sampling scheme [25]. Cut points of the band-pass filter were selected based on the expected biological range of shear wave speed (0.5–10 m/s) and the vibration frequency of PROSE. In this study the time between symmetrically sampled frames (Δt) was empirically set at 1/10th the vibration period. This sets an upper limit of the imaging depth due to echo time-of-flight considerations as it is necessary to receive all echoes within the Δt window. For the highest vibration frequency used in this study (400 Hz), the Δt used is 250 microseconds. Considering 3 angle plane wave compounding, the pulse-echo time for each plane wave image is 83.3 microseconds, which corresponds to a maximal imaging depth of over 60 mm. If the motion is small enough that aliasing will not occur in the shear wave motion calculation step, increasing Δt will allow an increase in imaging depth without needing to change the number of steering angles or the vibration frequency. Conversely, if the motion was large enough for aliasing to occur, it would be necessary to reduce Δt to facilitate correct motion calculation. In this study the maximal probe motion was below 0.1 mm for all experiments and thus sufficiently small to prevent aliasing.

PROSE has the capacity for imaging inclusions. However, there are three sources of errors that must be considered. First, the propagation speed of shear waves within the inclusion may be physically modified by the boundary effects imposed by the background material. Therefore, the shear wave speed within the inclusion may no longer be solely determined by the inclusion’s material property. Secondly, the LFE algorithm ideally requires one or more wavelengths to accurately estimate the shear wave speed of inclusions [36]. The inclusions in this study have a shear wave speed of about 4.5 m/s. This corresponds to a wavelength of about 15 mm at 300 Hz and 11 mm at 400 Hz. At 300 Hz, the inclusion (diameter 10.4 mm) contains less than one shear wavelength, and therefore are biased low. At 400 Hz, the inclusion has about one wavelength and the results are much closer to that obtained by the LOGIQ E9. Finally, the LFE algorithm assumes local homogeneity, which is violated near boundaries between regions with different stiffness. This causes the shear wave speed reported by the LFE to gradually transition between regions [35], leading to elevated shear wave speeds in the background and reduced shear wave speeds inside the inclusion near the boundary. As the vibration frequency is increased, the shear wave wavelength decreases, leading to a reduced transition region and a reduction of underestimation bias for the inclusion. Figure 5d illustrates that these effects were observed experimentally.

The choice of vibration frequency has effects on PROSE imaging. Ideally, high vibration frequency is preferred because the shorter wavelength of shear waves at higher vibration frequencies is beneficial for resolving small inclusions. higher attenuation and therefore have less penetration. In this study, the vibration frequency of 300–400 Hz was chosen to image the 6.5 mm inclusion for the phantom study. It is expected that in practice, the vibration frequency can be easily adjusted and optimized for a given imaging task, thanks to the high frame rate potential of PROSE.

PROSE provides two key benefits over other ultrasound elastography techniques. The first is the increased frame-rate. Due to the symmetric sampling scheme, PROSE’s frame-rate is fundamentally linked to the vibration frequency. Given a vibration frequency of 300 Hz and PROSE’s ability to acquire and process two images every period, a maximum frame-rate of 600 Hz was achieved. However, to increase the robustness of the measurements, two sequential shear wave speed maps were averaged, reducing the effective PRF to the vibration frequency. Thus, the PRT for this study was 3.3, 2.9 and 1.7 ms for vibrations frequencies of 300, 350, and 400 Hz, respectively. This upper limit of frame rate may be higher than what is clinically necessary. This high frame rate capacity can be used to improve image signal-to-noise ratio by multi-frame averaging. Currently, the LFE processing is the limiting factor for real-time display. The current MATLAB (MathWorks Inc., Natick, MA) implementation of the LFE was able to process a single frame in less than 170 ms (2.90 GHz, Intel i5 processor, 8.00 GB RAM). However, it is expected that an optimized implementation in C/C++ with GPU will reduce the processing time by over an order of magnitude. As such, it is expected that PROSE will be able to achieve a real-time frame-rate greater than 10 Hz, and this will increase as computational technology improves. Such a frame rate will be helpful for elasticity imaging of lesions that are difficult to visualize in B-mode imaging (such as myofascial trigger points), where real-time B-mode imaging cannot be easily used to locate the lesion for elasticity imaging.

The second benefit is the method’s flexibility. PROSE relies on generating a shear wave field that originates from the surface and propagates into the target, thus, both diffraction effects as well as attenuation will need to be considered. Because the diffraction pattern is determined by probe contact and underlying material, altering the contact area may improve wave propagation. Additionally, in situations where the material is viscoelastic, attenuation will be a factor in limiting the depth of observable shear waves. There is a frequency-penetration tradeoff, because higher vibration frequencies have better spatial resolution but attenuate faster leading to shallower imaging depths. Fundamentally, PROSE can be performed using a wide range of vibration frequencies, allowing a user switching from a shallow imaging mode with good spatial resolution at high frequency to a deep tissue imaging mode by changing the driving signal. It is expected that PROSE could allow the user to change the vibration frequency on-the-fly, allowing for target specific imaging that can be rapidly adapted for each patient.

While the PROSE method has shown promising results, the technique is still limited by wave propagation effects common to all mechanical shear wave methods. As the wave field propagates away from the transducer, the waves can reflect or establish standing wave patterns, giving rise to more complex wave fields. While the LFE method is robust in handling wave fields with multiple propagation directions within the imaging plane [27, 41, 42], no 2D imaging method can account for out-of-plane wave propagation, which may bias the results [25]. Volumetric (3D) imaging of shear waves may be the fundamental solution to this issue [42]. It is expected that this problem of out-of-plane wave propagation should be alleviated when we increase the shear wave frequency, because shear waves attenuate more quickly at higher frequency, thus reducing the chance of strong reflections. Additionally, for in vivo applications, higher attenuation of shear wave and irregular boundary conditions are expected to reduce the contribution of shear wave motion from reflected and out-of-plane shear waves, further mitigating the effect and allowing a wider range of vibration frequencies to be used.

It is expected that transitioning to in vivo imaging will bring additional challenges. For example, the effective coupling of shear wave energy through different tissue layers to the target region may need further investigation. We expect that this would not be a significant problem because FibroScan can effectively deliver shear waves into deep liver regions through the muscle and fat layers. Tissues are viscoelastic, which will impose higher attenuation of shear waves and thus may reduce the penetration of PROSE for in vivo applications. Shear wave speed will be frequency dependent due to tissue viscosity. Therefore, care needs be taken when interpreting these measurements at a single frequency. Viscoelasticity, hysteresis, and nonlinear effects of tissue may cause imperfect removal of the compression artifact, even if the probe were at the exact location during symmetric sampling. It is expected that in practice these high order effects will not be prominent because the vibration amplitude of the probe is small. In addition, the band-pass filter used in this study should be able to further suppress any residual compression artifacts. Future studies are needed to further investigate the impact of these higher order effects for in vivo tissues. Another consideration for in vivo applications is the effects of physiological motion on image acquisition. Most other methods utilize time-of-flight or phase-based reconstructions, which makes them vulnerable to motion artifacts as it’s necessary to track motion through multiple frames. In contrast, PROSE utilizes a single frame of shear wave motion for LFE reconstruction, allowing for full FOV estimations to be acquired in a very short duration (0.25–0.33 ms), thus substantially reducing the window for motion artifacts.

In future work, the actuation system will be miniaturized, by replacing the signal generator and amplifier with integrated circuit counterparts. The actuator and probe adaptor should be improved to be smaller and easily attachable to a wide range of ultrasound transducers. One should be able to eliminate the motion sensor used to guide the timing of symmetric pulse-echo detection and use the sinusoidal driving signal to trigger pulse-echo detection, once the fixed phase delay between the driving signal and the actual transducer displacement is evaluated. Additionally, methods for increasing the vibration amplitude will also be explored as this may allow for increased wave penetration at higher frequencies. Finally, the current implementation only utilized a single pair of frames for the symmetric motion detection spaced by a constant Δt set at 1/10^th the vibration frequency. The effect of varying Δt was not explored. Future experiments will be conducted to optimize the selection of Δt with respect to the tissue motion, as well as exploring the use of multiple pairs of frames evenly distributed around the maximum or minimum displacement can be obtained, and results (2D map of shear wave motion or final elastography images) averaged to improve the signal-to-noise ratio. As such, it is expected that these improvements will position PROSE as an attractive low-cost, high frame-rate ultrasound elastography method.

V. CONCLUSIONS

This paper introduces PROSE as a novel high frame-rate shear wave elasticity imaging technique capable of generating 2D shear wave speed images. This was accomplished by generating shear waves through mechanical vibration of the ultrasound transducer with simultaneous motion detection. PROSE demonstrated good reconstructions of 2-D shear wave speed images in both homogeneous and inclusion phantoms compared to results obtained by the GE LE9 scanner. With further refinement of vibration hardware, PROSE may be a promising technology for real-time shear wave imaging for mid- to low-end ultrasound systems.