Quantitative Susceptibility Mapping using Structural Feature based Collaborative Reconstruction (SFCR) in the Human Brain

Abstract

The reconstruction of MR quantitative susceptibility mapping (QSM) from local phase measurements is an ill posed inverse problem and different regularization strategies incorporating a priori information extracted from magnitude and phase images have been proposed. However, the anatomy observed in magnitude and phase images does not always coincide spatially with that in susceptibility maps, which could give erroneous estimation in the reconstructed susceptibility map. In this paper, we develop a structural feature based collaborative reconstruction (SFCR) method for QSM including both magnitude and susceptibility based information. The SFCR algorithm is composed of two consecutive steps corresponding to complementary reconstruction models, each with a structural feature based l1 norm constraint and a voxel fidelity based l2 norm constraint, which allows both the structure edges and tiny features to be recovered, whereas the noise and artifacts could be reduced. In the M-step, the initial susceptibility map is reconstructed by employing a k-space based compressed sensing model incorporating magnitude prior. In the S-step, the susceptibility map is fitted in spatial domain using weighted constraints derived from the initial susceptibility map from the M-step. Simulations and in vivo human experiments at 7T MRI show that the SFCR method provides high quality susceptibility maps with improved RMSE and MSSIM. Finally, the susceptibility values of deep gray matter are analyzed in multiple head positions, with the supine position most approximate to the gold standard COSMOS result.

I. Introduction

Magnetic susceptibility is an intrinsic physical property of a material that reflects its degree of magnetization in response to an applied magnetic field. In brain imaging, tissue magnetic susceptibility contrast is dominated by tissue iron and myelin content with additional contributions from calcium under certain conditions [1]. Accurate measures of tissue susceptibility therefore may provide valuable information for the diagnosis of intracerebral bleeding and calcification and for monitoring neuro-degenerative diseases such as Parkinson’s disease, Alzheimer’s disease, multiple sclerosis, Huntington’s disease and even cognitive development in children [2–4]. Imaging tissue magnetic susceptibility with high spatial resolution has recently become possible with the development of quantitative susceptibility mapping (QSM) techniques using high field MRI [5]. In a magnetic field, ferromagnetic, paramagnetic or diamagnetic tissue components such as iron or myelin induce changes in the local magnetic field that can be measured by MR phase or frequency imaging [6], e.g. using a gradient recalled echo (GRE) sequence. However, reconstruction of the magnetic susceptibility distribution from local phase is an ill-conditioned inverse problem due to the singularity at the magic angle in the dipole convolution kernel of the susceptibility to phase transformation [7].

Different strategies have been proposed to solve this ill-conditioned problem. Thresholded K-space Division (TKD) is a direct and fast solution in the Fourier domain, which simply sets small values in the convolution kernel below a threshold to a constant when performing the inverse calculation [8], [9]. Yet, it suffers from either underestimation of the susceptibility values or streaking artifacts. Calculation of susceptibility through multiple orientations sampling (COSMOS) [10], on the other hand, employs data redundancy, i.e. phase data acquired at multiple head orientations with respect to the main magnetic field, to stabilize the QSM inverse problem. COSMOS is usually the gold standard when comparing different QSM algorithms, but acquiring multiple orientation data is unfortunately inconvenient for clinical use and acquisitions are generally limited to single orientation. To derive quantitative susceptibility maps, several regularization methods incorporating different types of a priori information have been proposed [11–13]. In the morphology enabled dipole inversion (MEDI) approach [14–16], a priori anatomical information from magnitude images is used. Combined edge information extracted from both magnitude and phase images has also been proposed as a priori information for QSM regularization [17–20], such as HEIDI. However, morphologic information obtained from either magnitude or phase does not necessarily match all the structural features seen in the susceptibility maps. Such discrepancies can introduce erroneous structure shapes in the reconstructed susceptibility maps.

In order to address this problem, we propose a structural feature based collaborative reconstruction algorithm (SFCR) for QSM. The SFCR is composed of two consecutive steps corresponding to two complementary reconstruction models. In the M(agnitude)-step, we reconstruct an initial estimate of the susceptibility map employing a regional adaptive compressed sensing model in k-space with constraints incorporating the morphological information from magnitude images. In the S(usceptibility)-step, the ultimate susceptibility map is fitted in image space with a weighted l1 norm constraint using a priori information extracted from the M-step susceptibility map. Besides, a voxel fidelity based l2 norm constraint is introduced to suppress the possible artifacts as well as prevent voxels of high SNR from under estimation. The performance of SFCR is compared with that of TKD and MEDI using both numerical simulation and in vivo human data and evaluated in terms of Root Mean Square Error (RMSE) and Mean Structure Similarity Index (MSSIM). Since QSM has the unique potential to represent the characteristics of deep gray matter and diseases related to these regions, we focus our comparison analysis on regions of interest (ROI) mainly in deep gray matter for both the simulation model and the in vivo human brain data.

II. Theory

A. QSM Theory

The normalized magnetic field shift $\delta B=\mathrm{\Delta }B/B_0$ measured in a gradient echo sequence is related to the MR image phase via $\phi =-\delta B\cdot B_0\cdot \gamma \cdot TE$, where B₀ is the main magnetic field strength, γ is the gyromagnetic ratio, and TE the echo time. Following the Maxwell’s equation, the relative field shift δB becomes an element wise multiplication between the susceptibility distribution χ and a dipole kernel in Fourier domain. Denoting the dipole kernel in the Fourier domain with $C_k(k)=\left(1/3-k_z^2/k^2\right)$, where k is the spatial frequency vector, the susceptibility map may be estimated from the measured phase map using the inverse of the kernel as

$${\chi }_k(k)=C_k{(k)}^{-1}\delta B_k(k)$$ (1)

However, this problem is ill-posed because of the zero values of C_k(k) in k-space on a double conical surface at the magic angle 54.7°. A straight forward approach is to perform a threshold based k-space division, e.g. in the TKD approach, using k-space masking to avoid noise amplification in regions where the kernel function is small [8], [9]. However, such modification of the convolution kernel leads to streaking artifacts or underestimation of the susceptibility values and certain systematic corrections [18] are needed to get a less biased quantitative estimation.

A common approach to solve ill-posed inverse problems is regularization, such as Tikhonov regularization using l2 norm [21]. In addition, regularization using l1 norm tends to promote sparsity in the solution [22]. Previously QSM studies have shown that regularization incorporating the morphological information available from magnitude images can suppress streaking artifacts, as is done in MEDI [14]. It assumes consistency of the tissue structures between the susceptibility and magnitude images obtained from the same acquisition. However, the anatomical features of T2* weighted magnitude images do not necessarily match those of susceptibility maps. Such discrepancies between the structure prior constraint used for QSM regularization and the true morphology will introduce erroneous structure shapes or artifacts in the reconstructed susceptibility maps. Therefore, technical developments to account for such difference are needed.

B. Structural Feature based Collaborative Reconstruction (SFCR) Method

In this method, we propose a collaborative reconstruction framework composed of two steps using complementary theories, each with two regularization constraints. At first we derive an initial estimation of the susceptibility map in k-space with structural features extracted from GRE magnitude images (M-step). In the subsequent collaborative S-step, we use this estimation to extract a more accurate a priori weighting matrix for estimating the final susceptibility map in spatial space.

1). M-step: Initial Reconstruction based on a Priori Magnitude Information

The susceptibility map is reconstructed using a k-space regional adaptive compressed sensing (CS) model with a regularization constraint that incorporates the morphological information extracted from magnitude images. The ill-conditioned k-space regions are treated as missing data in an under-sampled acquisition. Previous studies have shown that using compressed sensing can effectively recover the susceptibility estimation in the ill-conditioned k-space regions while suppress the streaking artifacts and noise [13]. With an a priori magnitude based regularization constraint, the initial susceptibility reconstruction is formulated as

$$\begin{array}{l}\widehat{\mathbf{\chi }}\underset{\chi }{=\text{arg}\text{min}}{\lambda }_1{\left|\right|{\mathbf{\chi }}_k(k)H-\text{diag}\left(H\right)\mathrm{F}\mathbf{\chi }\left|\right|}_2\\ +{\left|\right|P_{\mathit{mag}}\nabla \mathbf{\chi }\left|\right|}_1+{\lambda }_2{\left|\right|R_1\mathbf{\chi }\left|\right|}_2\end{array}$$ (2)

The first data fidelity item is a CS-like form, where F is a Fourier transform operator in matrix format. H is a binary mask with 1 and 0 corresponding to well-conditioned and ill-conditioned subdomains in k-space by thresholding C_k(k), and diag(H) denotes a diagonal matrix with the elements of H on its diagonal. λ₁ and λ₂ are Lagrange multipliers adjusting constraint weights. Considering that morphological inconsistencies between susceptibility and magnitude images are sparse, a sparsity regularization constraint in the spatial domain is added, where the l1 norm can be regarded as an effective substitute for the l0 norm, which is harder to solve in practice. The structural weighting matrix P_mag is derived from thresholding the gradient of magnitude image. It is a binary mask that is zero in voxels with large gradients and one for voxels with small gradients

$$\left|P_{\mathit{mag}}\right|=\sqrt{\frac{1}{3}{\displaystyle \sum _i{P}_{\mathit{mag}\_i}^2}},P_{\mathit{mag}\_i}=\{\begin{array}{c}0,\left|{\nabla }_{i}I\right|\ge {\mu }_{\mathit{mag}}\\ 1,\left|{\nabla }_{i}I\right|<{\mu }_{\mathit{mag}}\end{array},i\in \left\{x,y,z\right\}$$ (3)

where I is the three dimensional magnitude image and ∇_iI denotes its gradient in the ith dimension. μ_mag is selected according to the structure complexity and noise level in I. In the l1 norm constraint, susceptibility features corresponding to tissue edges showing strong contrast in magnitude images are expected to be emphasized, while susceptibility features corresponding to those edges showing weak contrast in magnitude are prone to be suppressed by the sparsity constraint. In the l2 norm smooth constraint, R₁ is a fidelity mask in which the value in brain tissue with high SNR is equal to zero, while it is one in case of low SNR.

2) S-step: Collaborative Reconstruction based on Susceptibility Structural Features

In the S-step, we employ a weighted l1 constraint constructed from the susceptibility map $\widehat{\mathbf{\chi }}$ obtained in the M-step to correct possible errors induced by morphology differences that exist between the magnitude and susceptibility maps

$$\mathbf{\chi }=\underset{\chi }{\text{argmin}}{\gamma }_1{\Vert W(\delta B-C\mathbf{\chi })\Vert }_2+{\Vert P_{\widehat{\mathbf{\chi }}}\nabla \mathbf{\chi }\Vert }_1+{\gamma }_2{\Vert R_2\mathbf{\chi }\Vert }_2$$ (4)

The fidelity term in S-step is evaluated in the spatial domain, complementary to the data fidelity term in k-space used in the M-step. W is a weighting matrix proportional to the signal to noise ratio reflecting the reliability of the data measured for each voxel. C is a matrix encoding the convolution with the unit dipole field C=F⁻¹C_k(k)F, where F denotes the Fourier transform. The Lagrange multipliers γ₁ and γ₂ adjust the constraint weights relative to the energy fidelity term. The structural feature weighting matrix $P_{\widehat{\mathbf{\chi }}}$ is derived from gradients of the initial susceptibility map $\widehat{\mathbf{\chi }}$ generated from the M-step with a threshold μ_sus as

$$\left|P_{\widehat{\mathbf{\chi }}}\right|=\sqrt{\frac{1}{3}{\displaystyle \sum _i{P}_{\widehat{\mathbf{\chi }}\_i}^2}},P_{\widehat{\mathbf{\chi }}\_i}=\{\begin{array}{c}0,\left|{\nabla }_i\widehat{\mathbf{\chi }}\right|\ge {\mu }_{\mathit{sus}}\\ 1,\left|{\nabla }_i\widehat{\mathbf{\chi }}\right|<{\mu }_{\mathit{sus}}\end{array},i\in \left\{x,y,z\right\}$$ (5)

In the S-step reconstruction, the l1 norm performs a weighted sparsity constraint based on structural information extracted from susceptibility maps, i.e. through its gradient strength. Thus, the susceptibility structure features are emphasized, while tiny variations are suppressed as artifacts. The reconstruction error caused by a priori information derived from magnitude image will be corrected in this step. However, using the reconstrution model with a single l1 norm constraint, the reconstructed three dimensional susceptibility maps are still prone to be contaminated by granular or chessboard artifact. Meanwhile, large and abrupt susceptibility variation may cause nonneglectable susceptibility artifacts, especially around large vessels and deep gray matter regions of substantia nigra (SN) and globus pallidus (GP), where the susceptibility artifact may obviously decrease the susceptibility from the actual value [23], [24]. Therefore, an l2 norm constraint is introduced to piecewise smooth the reconstructed susceptibility map and suppress the possible artifacts. The weighting matrix R₂ is a fidelity mask similar to R₁ mask in the M-step, where the voxel of high SNR in the initial susceptibility map is equal to zero, and the low SNR voxel is one, moreover, the voxel corresponds to the susceptibility artifact is set to be 2. Using the R₂ weighted l2 norm constraint, it can protect voxels in regions of high susceptibility from being over-smoothed, and also prevent granular or chessboard reconstruction artifacts.

C. Algorithm Implementation

The objective functions in the M-step and S-step involve a combined optimization of l1 and l2 norm constraints that is difficult to solve directly using traditional methods [25]. In order to solve this optimization model, we introduced an intermediate variable $b=\left|\right|P\nabla \mathbf{\chi }|{|}_1$, allowing the optimization to be devided into two sub-procedures: first to fix χ and solve b by using an Iterative Shrinkage Thresholding algorithm (IST) [26], [27], and then to fix b and solve χ using the Conjugate Gradient (CG) algorithm.

In the M-step, employing the intermediate variable $b=P_{\mathit{mag}}\nabla \mathbf{\chi }$, the objective function (2) can be rewritten as

$$\begin{array}{l}\widehat{\mathbf{\chi }}\underset{\chi }{=\text{arg}\min }{\lambda }_1{\left|\right|{\mathbf{\chi }}_k(k)H-\text{diag}(H)\mathrm{F}\mathbf{\chi }\left|\right|}_2+{\Vert b\Vert }_1\\ +\beta {\left|\right|b-P_{\mathit{mag}}\nabla \mathbf{\chi }\left|\right|}_2+{\lambda }_2{\left|\right|R_1\mathbf{\chi }\left|\right|}_2\end{array}$$ (6)

when β→∞, the solution to (6) approaches the solution to (2). Assuming that β is fixed, (6) can be solved in two alternating iterative optimization procedures. To compute b for a fixed χ, the subproblem in (6) becomes

$$b\underset{b}{=\text{arg}\text{min}}{\Vert b\Vert }_1+\beta {\left|\right|b-P_{\mathit{mag}}\nabla \mathbf{\chi }\left|\right|}_2$$ (7)

We solve this reweighted l1 minimization problem using the IST algorithm

$$b=\text{soft}\left(\mathbf{\chi },1/\beta \right)=max\left(P_{\mathit{mag}}\nabla \mathbf{\chi }-1/\beta ,0\right)$$ (8)

in which soft(·,1/β) is a soft thresholding function with threshold 1/β. Here the parameter β grows with the power of 2 during the iteration, which helps the IST algorithm to converge faster. To update χ with a fixed b, the approximation corresponds to

$$\begin{array}{l}\widehat{\mathbf{\chi }}=\underset{\mathrm{\chi }}{\text{arg}\min }{\lambda }_1{\left|\right|{\mathbf{\chi }}_k(k)H-\text{diag}(H)\mathrm{F}\mathbf{\chi }\left|\right|}_2\\ +{\lambda }_2{\left|\right|R_1\mathbf{\chi }\left|\right|}_2+\beta {\left|\right|b-P_{\mathit{mag}}\nabla \mathbf{\chi }\left|\right|}_2\end{array}$$ (9)

This is a quadratic programming problem and the optimal solution is achievable by setting its gradient to zero with respect to χ. We then have

$$\begin{array}{l}\left({\lambda }_1{F}^{-1}{\mathbf{H}}^T\mathbf{H}F+{\lambda }_2{\mathbf{R}}_1+\beta {\nabla }^T{\mathbf{P}}_{\mathit{mag}}^T{\mathbf{P}}_{\mathit{mag}}\nabla \right)\mathbf{\chi }\\ ={\lambda }_1{F}^{-1}{\mathbf{H}}^T{\mathbf{\chi }}_k\left(k\right)+\beta {\nabla }^T{\mathbf{P}}_{\mathit{mag}}^{T}b\end{array}$$ (10)

This function can be solved using the CG method. To demonstrate our approach, we outline below the detailed algorithm implementation for the M-step procedure.

M-step Algorithm procedure
Initialization:
a) Use the thresholded Ck(k) to get the weighting matrix H; b) Compute the a priori weighting matrix Pmag and fidelity weighting matrix R1; c) Initialize parameters β = 2, b = 0, and Lagrange multipliers λ1 and λ2; d) Set CG tolerance error η = 1×10−3 and iteration number 100; e) Preset iteration counter m and maximal iteration number M;
Iteration:
f) Calculate b with ${\mathbf{\chi }}_m$ using (8), update $b_{m+1}\leftarrow b_m$; g) Calculate χ with $b_{m+1}$ using (10), update ${\mathbf{\chi }}_{m+1}\leftarrow {\mathbf{\chi }}_m$; h) If m < M, update $\beta \leftarrow 2\beta$, return to f);  otherwise, iteration terminate and output χ.

A similar algorithm implementation can be applied to solve the optimization problem in the S-step, except for some parameter settings. The CG algorithm formulation for S-step is

$$\begin{array}{l}({\gamma }_1{\mathbf{C}}^{\mathbf{T}}{\mathbf{W}}^{\mathbf{T}}\mathbf{WC}+{\gamma }_2{R}_2+\beta {\nabla }^{\mathrm{T}}{P}_{\widehat{\mathbf{\chi }}}^{\mathrm{T}}{P}_{\widehat{\mathbf{\chi }}}\nabla )\mathbf{\chi }\\ ={\gamma }_1{\mathbf{C}}^{\mathbf{T}}{\mathbf{W}}^{\mathbf{T}}\mathbf{W}\delta \mathrm{B}+\beta {\nabla }^T{P}_{\widehat{\mathbf{\chi }}}^{\mathrm{T}}b\end{array}$$ (11)

III. Materials and Methods

Both numerical simulation and in vivo human experiment were used to evaluate the performance of the SFCR algorithm in comparison to TKD [8], [9], MEDI [14], [16] and HEIDI- like method called as HEDI in our paper [17]. The MEDI implementation used the code distributed by the original authors. For the HEIDI code is not public, we implemented HEDI using MEDI solvers with extracting gradient weighting matrix from the background field corrected GRE phase (i.e. field shift in the paper). The edge percentage was set as a constant of 30% for all methods in the experiment. The RMSE and MSSIM with respect to the gold standards (known model for the simulation and COSMOS for in vivo data) were used as quantitative performance evaluation. The MSSIM was defined as mean SSIM (Structure Similarity) [28]. The regularization parameters of all methods were optimized to minimize RMSE and maximize MSSIM for both the simulation and in vivo data. More information is in the supplementary material.

A. Numerical Brain Simulations

A 3D numerical brain phantom of size 217×181×181 was designed based on the susceptibility data used in the human brain atlas from a previous study [29]. The background area and all Cerebrospinal fluid (CSF) regions were set to have zero susceptibility. While inside the brain, the susceptibility value of all white matter regions was set to −0.03 ppm, gray matter cortex to 0.01 ppm, and the caudate nucleus (CN), globus pallidus (GP), putamen (PU), red nucleus (RN), and substantia nigra (SN) to 0.08, 0.18, 0.07, 0.12, 0.12 ppm, respectively. Normally distributed Gaussian noise with a standard deviation of 0.002 ppm was also added. In addition, a magnitude image was simulated by setting white matter, gray matter cortex and CN, GP, PU, RN, and SN to be 0.95, 1, 0.8, 0.4, 0.8, 0.5, 0.5 in normalized intensity [16] with normally distributed Gaussian noise added (standard deviation 0.005). The relative field shift δB was generated from the forward calculation in Section II.

B. In Vivo Human Brain Data Acquisition

In vivo human data were acquired at the F. M. Kirby Research Center in Kennedy Krieger Institute and Johns Hopkins University Hospital, after IRB approval and written informed consent. Five healthy male subjects (30 to 36 years old) were studied using a 7T Philips Healthcare MRI equipped with a 32-channel Novamedical head receive coil. A 3D multi-echo GRE sequence was used with field of view (FOV) 220mm×220mm×110mm, matrix size of 224×224×110, TR/TE1/ΔTE = 45/2/2ms, 9–16 echoes, SENSE factor = 2.5×2 for the phase-encode directions, flip angle = 9°, and scan duration of 5:15 min per acquisition. Fat suppression was accomplished using a water-selective ProSet 121 pulse. In vivo human brain data at multiple head orientations were acquired to calculate susceptibility maps using COSMOS [10], which was used as a gold standard for quantitative comparison of the single orientation QSM reconstruction methods and for adjusting regularization parameters. Multiple orientation data were acquired with the volunteer’s head at four positions: normal supine position, tilted to subject’s right shoulder, tilted to subject’s left shoulder and tilted to subject’s back. The rotation angle for each orientation varied randomly between 5° to 22° from the main ${\mathrm{B}}_0$ axis. Axial GRE images were positioned parallel to the AC-PC axis and perpendicular to the mid-sagittal plane, and the magnet was quickly shimmed every time the head position was changed.

C. Human Brain Data Preprocessing

For each subject, the magnitude images at the first echo of the three tilted head orientations were coregistered to that of normal supine position by rigid body linear transformation using the FSL FLIRT tool [30], [31]. The coregistration transformation matrix was then applied to all other echo times to generate the coregistered magnitude and phase images. Subsequently, all data were put in the same subject frame of reference. After that, coregistrated phase images were unwrapped using a Laplacian-based phase unwrapping algorithm [32]. To eliminate the background field caused mainly by the susceptibility variations around the air-tissue interfaces, the SHARP method [23] with a spherical convolution kernel of radius 4 mm was applied to the unwrapped phase images using our QSM toolbox. A brain mask was generated with the FSL BET tool using the magnitude image at the supine position.

D. Susceptibility Map Reconstruction

The frequency shift was calculated by least squares fitting of the linear slope of the phase as the function of TE using multiple echoes. The linear fitting of the phase over time also provides an estimate of the initial phase, which can be used to exclude some voxels those have unreliable phase measurement due to turbulent flow, partial volume effect or extremely high invoxel resonance frequency shift. We used the mean normalized GRE magnitude image at the sixth echo (TE=12ms) to generate the weighting matrix which showed appropriate tissue contrast for comparison at 7T scanner. Serving as the in vivo gold standard susceptibility reference, COSMOS based susceptibility maps were calculated with relative convergence tolerance of 10⁻⁵ using LSQR algorithm. In addition, the lateral ventricular region was selected as a reference for susceptibility quantification setting CSF to 0 ppm. Data processing was implemented in MATLAB 2014a on a windows 7 workstation with an Intel Xeon processor E5-1620, and 16GB RAM. For quantitative susceptibility analysis, we selected local regions of interest based on a QSM human brain atlas [29] for three dimensional data using LDDMM, part of the MRI Studio toolbox (X. Li, H. Jiang, S. Mori; Johns Hopkins University, http://www.mristudio.org), and then fine ROI delineations were corrected manually.

IV. Results

A. Parameter Determination

The optimal regularization parameters for MEDI and SFCR are determined by successively reconstructing susceptibility maps with different values and calculating the RMSE and MSSIM with respect to the susceptibility model and the corresponding COSMOS maps of the volunteers, respectively. The choice of λ in MEDI offers a trade-off between data fidelity and streaking artifacts. The data fidelity term in the code of MEDI toolbox is $\lambda {\Vert \mathit{W}(\delta \phi -C_{\chi })\Vert }_2$. Fig.1a–c shows that λ varies from 0 to 6000 plotted against RMSE, MSSIM and the Residual error using the simulation data. The minimal RMSE and the maximal MSSIM all achieve at λ=250 as marked, while the Residual error ${\Vert \mathit{W}(\delta \phi -C_{\chi })\Vert }_2/\sqrt{N}$ converges with increasing λ. Here, the optimal value 250 is close to the choice of 316 used in [7]. The optimal λ for the in vivo human brain data was set to be 300 in the same way.

Fig. 1.

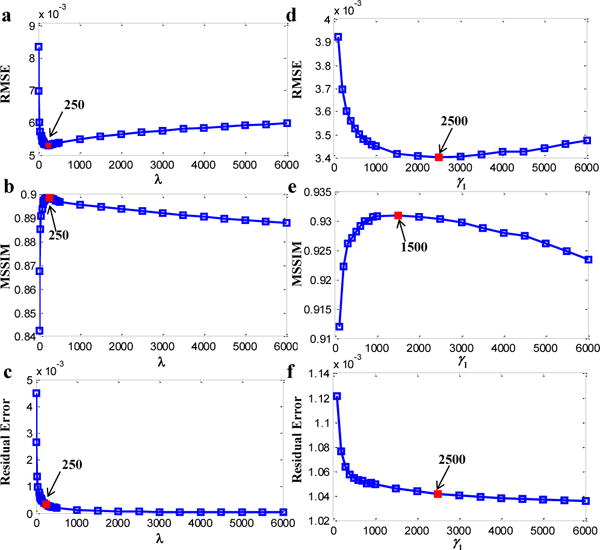
Selection of the optimal regularization parameters for MEDI (λ) and SFCR (γ₁) with respect to the RMSE, MSSIM and Residual error using the numerical simulation data. The minimal RMSE and the maximal MSSIM are in red.

In our SFCR method, the model formations of the two steps and their regularization parameters are similar. λ₁ and λ₂ are Lagrange multipliers defined in the M-step, while γ₁ and γ₂ are in the S-step. λ₁ and γ₁ adjust the weights of the data fidelity term relative to the structure a priori regularization term. An increasing λ₁ and γ₁ means to a strong constraint on the data fidelity but the streaking artifacts may not be removed clearly. On the contrast, decreasing λ₁ and γ₁ may lead to structural features missing in the reconstructed map. Since the M-step is used to generate the interim susceptibility map for extracting a priori information, while the final susceptibility map is reconstructed by the S-step, we illustrate the regularization parameter determination of γ₁ using the simulation data as an example in Fig.1d–f by setting λ₁=50, λ₂=γ₂=1 as default. We observed that the minimal RMSE and the maximal MSSIM achieve at different values, and the Residual error ${\Vert \mathit{W}(\delta B-C_{\chi })\Vert }_2/\sqrt{N}$ converges to 1.03×10⁻³. Finally, we determined γ₁=1500 for the simulation data and γ₁=2000 for the in vivo data, while setting λ₁=50 for all data.

Parameters of λ₂ and γ₂ are the Lagrange multipliers of the fidelity mask based constraint terms. A proper determination of λ₂ and γ₂ is helpful to smooth chessboard or granular artifacts and suppress susceptibility artifacts, but too large values may yield to over-smoothing or underestimation. We tested λ₂ and γ₂ in the range of 0–50 with a fixed λ₁ and γ₁, and then it was determined to be λ₂=γ₂=1 for the simulation data, and λ₂=1, γ₂=20 for the in vivo data. In the same way, we took 0.2 as the optimum threshold for C_k(k).

B. Numerical Simulation Results

The brain simulation model and the related structure weighting matrix are depicted with two typical slices in Fig.2, which mimics the condition in real human data. We can see that in Fig. 2a–b the structural features extracted from the magnitude images and the field shifts are not consistent with that from the susceptibility maps. For example, some edges in the regions pointed by the red arrows are missing in the magnitude images, while some redundant structures in the field maps are not in the true QSMs. In Fig. 2c–d, even though the initial QSM generated by the M-step do not recover the exact contrast yet, it is able to capture those missing edges and most of the edges are overlapped with the true QSM.

Fig. 2.

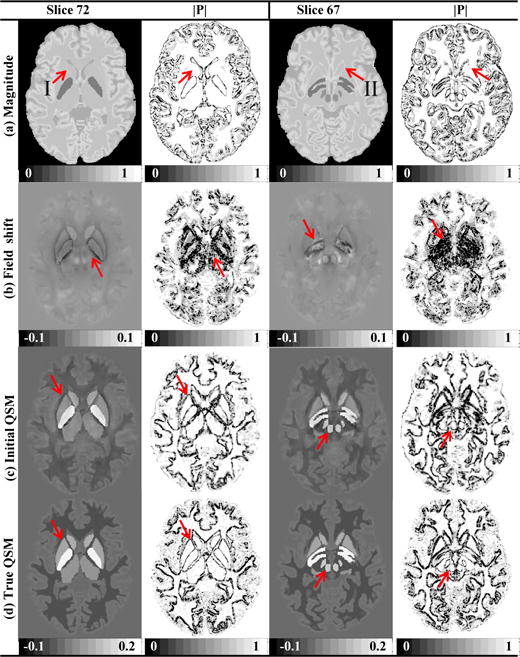
Numerical human brain simulation data and comparisons on their corresponding a priori weighting matrices of (a) magnitude images, (b) field shifts, (c) initial QSMs in M-step, and (d) true QSMs (in ppm). Red arrows in (a) indicate regions of susceptibility structures absent in the magnitude image, and red arrows in (b) indicate structures nonexistent in QSM. Red arrows in (c-d) demonstrate the structure consistency between the initial QSM and true QSM.

In Fig. 3, the reconstructed susceptibility maps of the brain model generated by the TKD, MEDI, HEDI and SFCR methods are compared on two different slices accompanied with their error maps relative to the true QSM. Local regions over the deep gray matter are zoomed to show more details, and two line profiles across the local regions are plotted for improved illustration of the edges. For the results of TKD, the maps are corrupted by serious streaking artifacts and significant overestimation or underestimation in several regions (as seen in the error maps). The MEDI and HEDI results although with improvement on the streaking artifacts suppression over TKD, still have discernible structure related errors easy to observe in the error maps. In Fig.3e–f, the profiles of the simulation are piecewise constant. However, the susceptibility values of TKD fluctuate around the true values. The contrast decrease in profiles of MEDI (arrows I and II) is caused by the missing edges marked in Fig. 2a. The noise in the HEDI result as arrows pointed is due to redundant structures in the field map shown in Fig. 2b. Finally, the susceptibility maps calculated by SFCR achieve a reconstruction with excellent image contrast, precise estimation and no streaking artifacts as shown in their error maps and zooming views, where the number of remaining structural features is seldom and the errors are close to zero. Table I quantitatively evaluates the reconstruction performance of these methods in Fig. 3 in terms of their RMSE (left column) and MSSIM (right column). The results of MEDI and HEDI are better than TKD, but SFCR method further improves the reconstruction accuracy. The computation time of the simulation data was 229s for MEDI and 198s for SFCR.

Fig. 3.

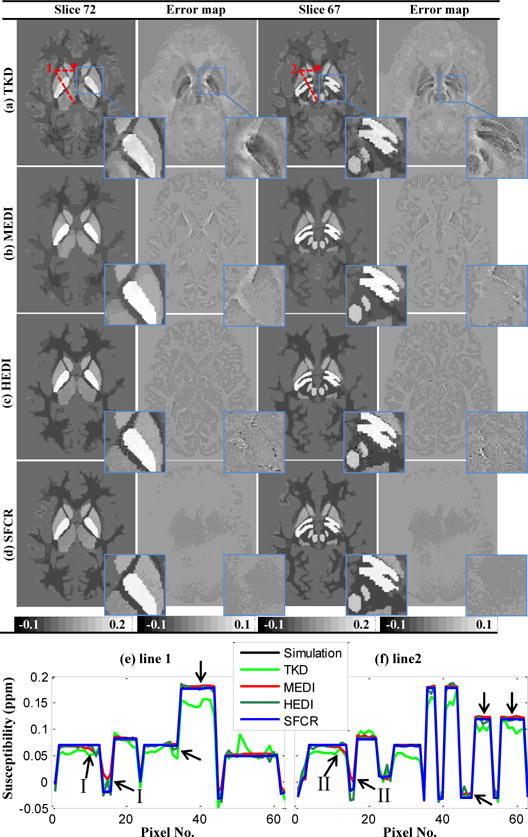
Comparison on susceptibility maps reconstructed by TKD (a), MEDI (b), HEDI (c) and SFCR (d) of the simulation data of two slices and their error maps with zoomed views in blue rectangles. The error maps of MEDI and HEDI present obvious residual structures, while there is no noticeable error in SFCR results. (e-f) susceptibility profiles of line 1 and line 2 with • denoting the starting point, where arrows indicate profile differences of MEDI and HEDI.

Table I.

Reconstruction performances in terms of RMSE (left column, ppm) and MSSIM (right column) for simulation data in Fig. 3.

Method	TKD		MEDI		HEDI		SFCR
Slice 72	0.0081	0.7812	0.0053	0.8987	0.0048	0.9081	0.0035	0.9314
Slice 67	0.0076	0.7893	0.0051	0.9056	0.0045	0.9124	0.0034	0.9362

C. In Vivo Human Brain Results

Two slices of a human subject are shown in Fig. 4 together with the corresponding a priori weighting matrices. We can observe that the obvious tissue edges between white matter, gray matter and blood vessels in the susceptibility maps do not always correspond to those in the magnitude image or the field shift, which is especially clear in the structure weighting matrix. For instance, the interfaces around the PU and CN derived from the susceptibility map of slice 35 are not fully represented in the magnitude images (red arrows in Fig.4a), while the edge information extracted from the field shift encompasses an area that is larger than the susceptibility map, e.g. the region pointed by red arrows in slice 23 in Fig.4b. However, the weighting matrices extracted from the initial QSM in the M-step are almost consistent to the COSMOS. Thus, it is the best way to employ the susceptibility map to derive the structural feature weighting matrix.

Fig. 4. In vivo.

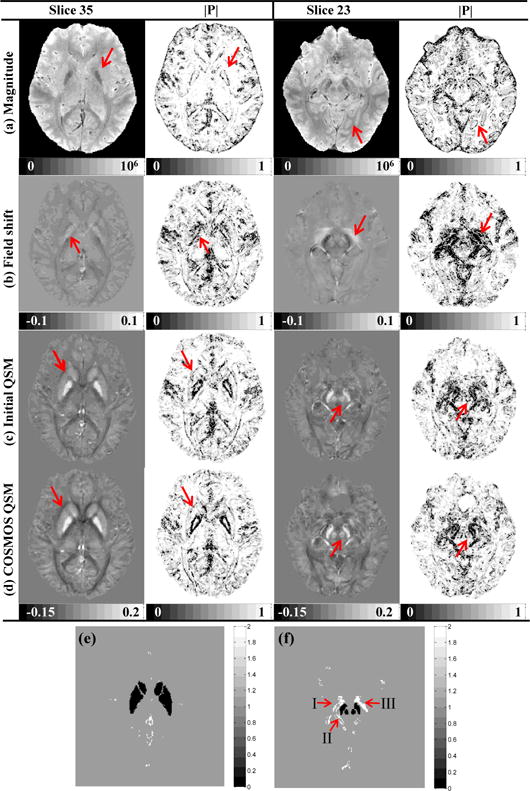
human brain data and comparisons on their corresponding a priori weighting matrices of (a) magnitude images, (b) field shifts, (c) initial QSMs in M-step, and (d) COSMOS QSMs (in ppm). Weighting matrices extracted from the initial QSM is almost consistent to the COSMOS, but there are obvious structural differences in magnitude and field maps as pointed by arrows. (e-f) the fidelity mask R₂ to deal with the effect of unreliable phase data.

Since we know venous blood is rich of deoxygenated hemoglobin, their high magnetic susceptibilities induce local magnetic field inhomogeneity. Even after background removing, the subsequent field map still exhibits unreliable data around regions of the interpeduncular vein (I), basal vein (II), crus cerebri and SN pars reticulate (III) [23]. Even in the COSMOS result, we can see the effect of this kind of susceptibility artifact around interpeduncular vein in the zoomed view, where the value of white matter is smaller than −0.1ppm. The fidelity mask R₂ is used to suppress such artifacts, where the voxels affected by serious susceptibility artifacts are extracted by thresholding the three dimensional gradient of the susceptibility map $\widehat{\mathbf{\chi }}$ with threshold 0.2 ppm. In slice 35, the artifacts distribute mainly around the great cerebral vein, while for slice 23 the artifacts locate primarily over the SN as shown in Fig. 4e–f.

In Fig.5, susceptibility maps of an in vivo human brain in supine position generated by TKD, MEDI, HEDI and SFCR are compared to the COSMOS reconstruction. TKD again is unable to reconstruct the map without streaking artifacts that is more visible in the error maps, where the GP is clearly underestimated. The over-smoothing in the reconstructed maps of MEDI prohibits identification of subtle susceptibility variations. As a consequence, the GP, CN and PU appear homogenous. In addition, voxels over SN and RN are accompanied with granular artifacts as shown in the zooming views. The results of HEDI are suffered from the redundant structures especially for slice 23, in which the susceptibility contrast cannot be well recovered like MEDI as show in Fig.5f with arrow indication. However, the results of SFCR have little artifacts and also have a good performance in preserving the fine structures, such as tiny blood vessels and tissue subtle variations appearing in the COSMOS map. Compared with other methods, the profiles of SFCR are generally closest to those of COSMOS without apparent deviation. With the fidelity mask based constraint, SFCR method is able to suppress the susceptibility artifacts along the veins (regions I-III) without decreasing the contrast, leading to best performance over the SN and RN in the midbrain. Table II summarizes the reconstruction performance of all methods for in vivo human brain data. The results of SFCR are apparently better than the other methods. Computation time for the single orientation method was 216s for MEDI and 182s for SFCR. More detail is in the supplementary material.

Fig. 5.

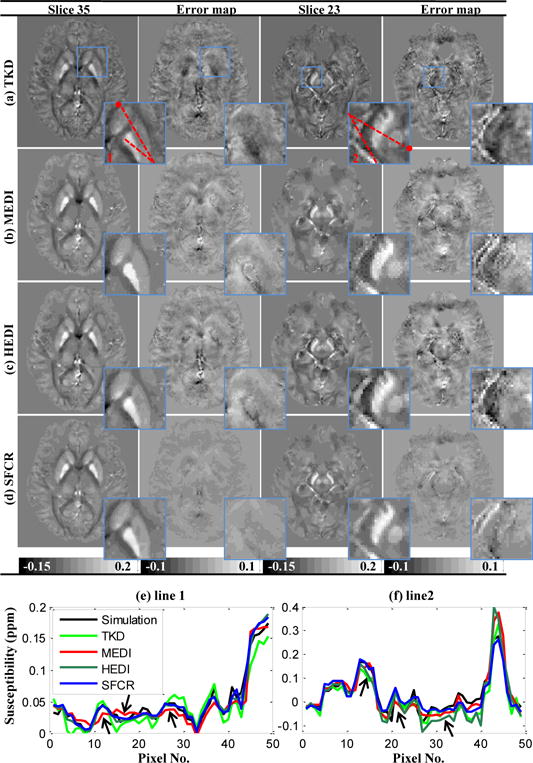
Comparison on susceptibility maps reconstructed by TKD (a), MEDI (b), HEDI (c) and SFCR (d) of an in vivo human brain data with two slices and their error maps with zoomed views in blue rectangles. (e-f) susceptibility profiles of line 1 and line 2 with • denoting the starting point, where arrows indicate profile differences of MEDI and HEDI.

Table II.

Reconstruction performances in terms of RMSE (left column, ppm) and MSSIM (right column) for human brain in Fig. 5.

Method	TKD		MEDI		HEDI		SFCR
Slice 35	0.0116	0.6963	0.0097	0.8317	0.0091	0.8397	0.0076	0.8650
Slice 23	0.0126	0.6762	0.0110	0.8152	0.0102	0.8306	0.0085	0.8467

Fig. 6 presents SFCR calculated susceptibility maps of four different head orientations in a human subject together with SSIM maps referenced to the COSMOS, where tilting angles of each orientation are noted in the term of (x, y, z) angles in degree in the figure heading. It is observed that fine structures, including small vessels, cerebral gyrus and tiny textures of the gray matter and white matter are reconstructed well and consistent in location in all positions. As expected, the susceptibility maps are similar to each other, but also exhibit distinguishable orientation dependence in regions with high fiber density [33–35], such as the posterior limb of the internal capsule, the splenium of corpus callosum and posterior thalamic radiation, which are clearly visible in SSIM maps (voxels in green and blue colors). More interestingly, there is an asymmetry between left and right hemispheres in the head positions of right and left. Besides the susceptibility intensity difference for GP, the volume of the right GP in the right position and the volume of the left GP in the left position are increased. These types of orientation variations are also observed in the region of SN. Meanwhile, the susceptibility intensities of SN in the left and right hemispheres are almost symmetric in the supine and back positions, but the intensity of back position is lower than the supine.

Fig. 6.

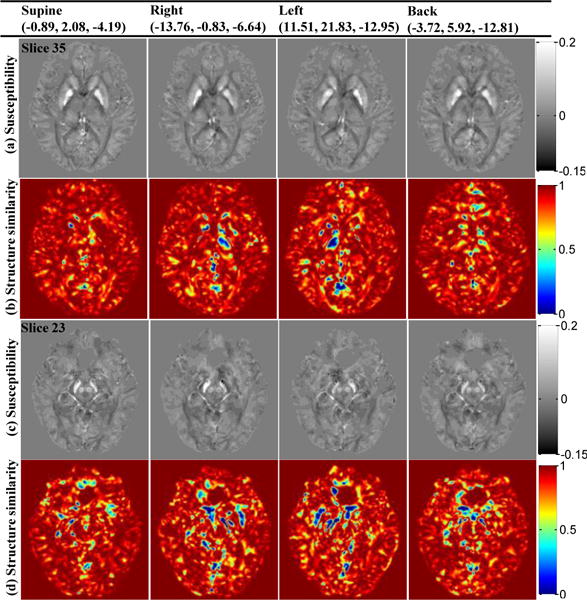
Susceptibility maps similarity and orientation dependence in four head orientations reconstructed by SFCR with their SSIM maps referenced to the COSMOS results. Tilting angles of each orientation are noted in the term of (x, y, z) angles in degree in the figure heading.

In Fig. 7 the mean susceptibility (MS) values and their standard deviations of five ROIs in the deep gray matter are compared between four orientations reconstructed by SFCR and COSMOS for the same subject in Fig. 6. The ROI contours are shown in axial, coronal and sagittal views. We find that the MS values of CN and PU in four orientations are almost equal to COSMOS, while the MS values of GP, SN and RN present obvious orientation related differences. The susceptibility values of RN in supine and back position are larger than the left and right position. The susceptibility values for GP and SN in right, left and back position are lower than the supine position and COSMOS result. The susceptibility standard deviations of all four positions are comparable to that of the COSMOS, with those of SN and GP larger than PU, RN and CN. In all, the measured susceptibility of deep gray matter in supine position is the largest of four orientations and closest to COSMOS. This result is consistent with the results in Fig. 6.

Fig. 7.

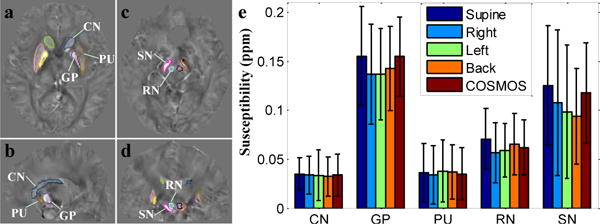
(a–d) ROI contours of three dimensional volumes; (e) bar graph compares the mean susceptibilities and standard deviations of ROIs in deep gray matter between four orientations reconstructed by SFCR and COSMOS, with supine position is the closest to COSMOS.

Fig. 8 shows a linear regression comparison between MEDI and SFCR at different head orientations over COSMOS using the susceptibility values of ROIs in deep gray matter together with corpus callosum (CC) and thalamus (TA). The MS is the average over five healthy subjects. The inter-subject MS values measured in CC, TA, CN and PU are similar in four positions for both MEDI and SFCR, but values of RN, SN and GP show orientation related differences, especially SN in the back position noticeably decreased. Among four orientations, the MS values in the supine position are closest to those found by COSMOS approach. Although the correlation coefficients r for all methods are close to 1 with p values and the intercepts close to zero, the slope of SFCR in the supine position is 0.95, significantly improved with respect to 0.79 of TKD, 0.87 of MEDI, and 0.89 of HEDI. This result on multiple subjects is coincident with the observations in the single human subject shown in Fig. 6 and Fig. 7. Table III summarizes the MS values of the selected ROIs of every subject in the supine position of SFCR (top row) and COSMOS results (bottom row). The average over the five subjects is the same with p=0.99, showing no significant group difference.

Fig. 8.

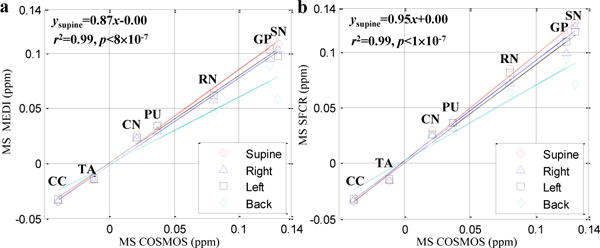
Correlation of inter-subject averaged susceptibility values (MS) measured in the selected brain regions using MEDI (a) and SFCR (b) methods with those using COSMOS. The line regression parameters of the supine position are noted on the top left of each figure.

Table III.

Susceptibility values (ppm) of five human subjects in selected deep gray matter regions using the SFCR method (top row) at supine position in comparison to COSMOS method (bottom row).

Subject	CN	GP	PU	RN	SN
1	0.028±0.019	0.096±0.027	0.013±0.021	0.073±0.017	0.117±0.049
	0.024±0.018	0.109±0.030	0.010±0.015	0.066±0.012	0.111±0.041
2	0.021±0.015	0.130±0.036	0.047±0.019	0.089±0.021	0.113±0.035
	0.017±0.016	0.129±0.030	0.061±0.021	0.092±0.023	0.120±0.020
3	0.033±0.014	0.083±0.031	0.043±0.030	0.047±0.035	0.129±0.033
	0.027±0.015	0.094±0.032	0.045±0.036	0.058±0.029	0.153±0.028
4	0.024±0.016	0.126±0.048	0.023±0.019	0.057±0.028	0.148±0.052
	0.019±0.021	0.127±0.043	0.022±0.020	0.053±0.022	0.133±0.044
5	0.026±0.017	0.151±0.044	0.043±0.031	0.130±0.034	0.139±0.055
	0.017±0.015	0.158±0.035	0.046±0.030	0.133±0.026	0.133±0.052
MS±SD	0.026±0.004	0.117±0.027	0.034±0.015	0.079±0.033	0.129±0.015
	0.021±0.004	0.124±0.021	0.037±0.018	0.080±0.030	0.130±0.014

Note: susceptibility values are in the format of mean ± standard deviation in the ROI volumes of each subject, except MS±SD denoting the inter-subject average and standard deviation of the five subjects.

V. Discussion and Conclusion

The main challenge for accurate QSM reconstruction is accurate reconstruction of quantitative susceptibility values, including artifact reduction, preservation of subtle susceptibility variations, and minimizing noise amplification. As a direct inverse method with no regularization, TKD induces streaking artifacts and suffers from underestimation of susceptibilities and severe noise amplification. In MEDI, a weighted l1 norm constraint based on a priori derived from the magnitude image is used to reduce streaking artifacts in the susceptibility maps [14], [15]. A modified nonlinear MEDI method has also been proposed in which phase noise and unwrapping errors can be properly accounted for [16]. Even though MEDI gives a better estimation than TKD, unexpected aliasing is induced by morphological inconsistencies existing between the magnitude and susceptibility images as demonstrated in Fig. 2 and 4. To overcome this problem, some researchers obtain the edge a priori from both magnitude and phase data, but extracting structure priori from the phase data has shortcomings similar to those of the magnitude image.

For improving the QSM quality, two strategies are presented in the HEIDI [17]: applying different solution strategies in three different sub-domains of the Fourier space; combining magnitude with phase image to determine a priori information about the susceptibility distribution. A priori smoothness information ${\mathrm{W}}_j$ was obtained by combining three binary masks using point-wise multiplication as ${\mathrm{W}}_j=W_j^{\nabla \phi }·W_j^{\mathrm{\Delta }\phi }·W_j^{\nabla m}$, where $W_j^{\nabla \phi }$ and $W_j^{\mathrm{\Delta }\phi }$ are defined by thresholding the gradient and laplacian of the background-field corrected GRE phase, and $W_j^{\nabla m}$ is derived by thresholding the GRE magnitude image. In this way, ${\mathrm{W}}_j$ is similar to the mask of most zero values, which is the gradient of phase image $W_j^{\nabla \phi }$ in practice. Although the background field was eliminated from the unwrapped phase image, there are still some unreliable phase data in the regions with high susceptibility variations, e.g. the straight sinus, internal cerebral vein, superior cerebral vein, interpeduncular vein, and basal vein in the in vivo human brain. The authors said that voxels with unreliable phase value were identified with an empirically established absolute value greater than π/8 [18], and then were set to zero in the processed phase data. Therefore, the structure features in the unreliable phase region are not able to be represented in ${\mathrm{W}}_j$. The reconstruction quality of HEIDI is also dominated by subdomains dividing parameters (t_ill, t_well, t_trans) and inherent artifacts associated with the reconstruction of three sub-domains. Practical choice of the domain definition parameters principally depends on the accuracy of the a priori information, the amount of noise in phase data, and the performance of the denoising algorithm. HEIDI employed a simple unregularized algorithm for reconstructing the well-conditioned sub-domain to illustrate that streaking artifacts can be reduced without regularization in the well posed subdomain. However, they also said in the Discussion section that the QSM problem is often underdetermined inside and adjacent to lesions requiring a priori information also for the inversion of the well posed subdomain. A MEDI-like approach with prior information on critical spatial regions instead of the unregularized algorithm used in HEIDI should be a promising approach [17]. Based on our above analysis, we implemented HEDI instead by extracting gradient from the field shift map with MEDI solver in the experiment.

In our method, we apply a collaborative reconstruction framework composed of two-step procedures, one using the compressed sensing model in k-space and the other using a weighted fidelity item in the spatial domain. Since a priori structural information based on the initial susceptibility map is believed to be better, a susceptibility structure based a priori term in the S-step is introduced. As shown in Fig. 3 and 5, the experimental results for MEDI and HEDI usually exhibit over smoothing in local regions accompanied with obvious artifacts and noise, which are caused by missing edges in the magnitude image or redundant structures in the field map shown in Fig. 2 and 4. When we use the intermediate estimation of the susceptibility to constitute the weighting matrix, the reconstruction errors caused by morphology differences are corrected, and it shows improvement over these previous approaches. The structure regularization constraint is used mainly to preserve structure edges in the susceptibility map. However, such a reconstruction model is not stable enough to achieve an accurate solution without considering other artifacts.

The susceptibility artifact around the abrupt susceptibility change could cause unreliable phase data, which may affect the susceptibility value in the reconstruction if we have no special solution to deal with it, for instance around the regions of veins. In general, there is a trade-off between the artifact suppression and structure preservation. The large γ₁ determines a high restriction on data fidelity but a relative loose restriction on artifacts, while a small γ₁ enforces to suppress the artifact but prone to be over smoothing or decrease the contrast. However, the map of in vivo human brain contains a lot of fine structure features. In that case, the regularization parameters should not be set too small only for suppressing artifacts but regardless of the over smoothing problem. Thus, we introduce another constraint term into the reconstruction model based on a fidelity mask R₂, which is generated by thresholding the three dimensional gradient of the susceptibility maps obtained in the M-step. For the noticeable susceptibility artifacts around the regions of large vessels in Fig. 5, The constraint term based on fidelity mask can effectively reduce this susceptibility artifacts, while protect high SNR voxels from underestimation. In this way, we can facilitate the artifacts suppression while preserving the structure features with no need to set γ₁ too small. As experimentally demonstrated, the combination of the structure regularization constraint and a fidelity based constraint allowed both the structure edges and tiny features to be well recovered, whereas the noise and artifacts could be effectively reduced. More detail is in the supplementary material with a comparison on γ₂=0 and 20 to demonstrate the different roles of the two constraint terms.

The choice of Lagrange multipliers depend on the scale of each l1 or l2 norms in the reconstruction model, i.e. the scale of δB and χ, noise and artifact level, and structure complexity in the map. We think it’s best to determine the regularization parameters separately for different data, which is searching the optimal value of the regularization parameters in a proper range employing the L-curve method with respect to the evaluation metric. So we set different regularization parameters for MEDI and our methods in the simulation and in vivo experiment. However, if the susceptibility distributions are similar or once the imaging acquisition protocol for a specific organ is established, the same regularization parameters can be applied across subjects due to the similarity in the imaging content and noise level. Hence, we observed that the regularization parameters for the simulation data and the in vivo data are close for both methods. In Fig. 1, when regularization parameters λ and γ₁ vary from their optimal values to 6000, the variations of the evaluation metrics of MEDI are larger than SFCR method. Therefore, our method also enables a more stable solution. Even if imaging acquisition protocol is different, it is not necessary to search the optimal values of the Lagrange multipliers in a wide range employing the L-curve method, but fine tunings are appreciative.

The thresholds of P_mag and $P_{\widehat{\mathbf{\chi }}}$ should be proportional to the structure complexity in the map, so it can be a definite value for a specific organ. H is a binary mask by thresholding C_k(k), where we took 0.2 as the threshold by experimental test, which is similar to other related papers using TKD in the scale of 0.15–0.25 [8], [9]. Such a range of variation will have no effect on the final result of our method. Thus, these three threshold parameters can be treated as constants in the human brain QSM. As we know, the shape and intensity of the susceptibility artifact depend on local anatomic relationships, field strength, difference in susceptibilities, echo time as well as bandwidth (or readout gradient strength and direction). In the published papers [14], [16], [18], [29], the susceptibility scale of venous blood is [0.25, 0.3] ppm, with deep gray matter range of [0.03, 0.2] ppm and white matter range of [−0.03, −0.05] ppm using CSF as reference. In the experiment, we found there are obvious susceptibility artifacts around the veins and GP arising from abrupt susceptibility difference, despite background removing to the preprocessed phase image by SHARP. Therefore, we apply 0.2 ppm to thresholding the three dimensional gradient of the susceptibility map $\widehat{\mathbf{\chi }}$ to extract the voxels affected by serious susceptibility artifacts for the fidelity mask R₂. This threshold could be a constant in the human brain QSM. However, there may be other adaptive way to detect the unreliable phase or susceptibility artifact, which is one focus of our ongoing work.

In the implementation, susceptibility initialization using the M-step is obtained at the second iteration, while the consecutive S-step iteration usually converges in less than eight iterations. Since each step contains a minimization model that combines an energy fidelity item with l1 norm and l2 norm constraints, it cannot be solved by a single CG algorithm directly. The model solution of our method is separated into two sub-procedures by employing the IST algorithm and CG algorithm. As a fast algorithm, IST takes advantage of solving the optimization problem containing the l1 norm constraint with favorable iteration convergence speed, which enables the computation time of SFCR a bit faster than MEDI. In Reference [22], Bilgic proposed a fast l1-regularized QSM and shared the matlab code on his homepage. Once the regularization parameters are determined, the run time of the split Bregman QSM is 138s for the numerical simulation data, 127s for the in vivo human brain data in our computer, which is a little faster than SFCR (about 180s). The computation speed of SFCR could be improved when incorporating split-Bregman or ADMM techniques or parallel computing.

At present, it is well recognized that the susceptibility anisotropy in white matter originates predominantly from the organized anisotropic lipid molecules in myelin [36], [37]. The susceptibility values of in vivo human brain data at multiple orientations in Fig. 6 show that the white matter anisotropy is in the range of 0.01–0.03 ppm, which is consistent with the conclusion in [34]. However, there is a noticeable susceptibility intensity difference related to the head orientation around the GP and posterior limb of the internal capsule, also over interpeduncular vein and the splenium of the corpus callosum in Fig. 6, and near the areas between the vein and SN especially an asymmetry between left and right hemispheres in the head position of right and left. At the same time, the susceptibility maps of the right and left positions differ more than those of the supine and back positions as compared to COSMOS results. We think this phenomenon is a consequence of susceptibility artifacts, and not due to intrinsic orientation anisotropy in gray matter. In the supine and back position, left and right hemispheres are nearly symmetric with respect to the main magnetic field B₀, but this kind of symmetry is changed in the right and left head position. Such kind of asymmetry relative to the main field may consequently give different susceptibility artifacts in QSM reconstruction especially in and around those areas with abrupt susceptibility variations. Usually the susceptibility variation is much steeper over GP and SN than CN and PU, it may induce more artifacts. Thus, we can understand that, among the selected regions, the orientation difference on the GP, SN and RN was more obvious than the CN and PU in Fig. 7 and 8.

Of the four different acquisition directions we tested, the susceptibilities measured using the supine position are most similar to the COSMOS results. For the five volunteers, no statistically significant difference was found between the supine susceptibilities and their corresponding COSMOS values as shown in Fig. 8 and Table III. The reason might be the supine position is the closest to the center of the four head orientations acquired for COSMOS, and also due to the fact that all acquisitions were registered to the supine position data in order to compute the COSMOS map. Therefore, when head rotation is not practical, such as in clinical application, it is best to study subjects in the supine position, which fortunately is the most comfortable position. In addition, it should be noticed that even though we used COSMOS as the standard for comparing different single orientation QSM methods, COSMOS assumes that tissue magnetic susceptibility is isotropic and thus is unable to reflect susceptibility anisotropy. Instead it averages out the orientation dependence, which is kind of equivalent to taking the mean susceptibility values at different head orientations.