Random subsets of structured deterministic frames have MANOVA spectra

Significance

A frame (overcomplete set of vectors) represents an analog coding scheme. Deterministic frame constructions offer useful codes for communication and signal processing tasks. When the coded signal only uses a random subset of the frame vectors (for example, in compressed sensing), the coding quality is determined by the typical covariances within subsets of frame vectors. We provide a method to calculate functions of these typical covariances, which predict specific performance measures of the corresponding coding scheme. Our method uses a universality property: for many well-known deterministic and random frames, typical covariances within subsets of frame vectors do not depend on the frame and are described by the MANOVA (multivariate ANOVA) ensemble, a classical object in statistics and random matrix theory.

Abstract

We draw a random subset of $k$ rows from a frame with $n$ rows (vectors) and $m$ columns (dimensions), where $k$ and $m$ are proportional to $n$. For a variety of important deterministic equiangular tight frames (ETFs) and tight non-ETFs, we consider the distribution of singular values of the $k$-subset matrix. We observe that, for large $n$, they can be precisely described by a known probability distribution—Wachter’s MANOVA (multivariate ANOVA) spectral distribution, a phenomenon that was previously known only for two types of random frames. In terms of convergence to this limit, the $k$-subset matrix from all of these frames is shown to be empirically indistinguishable from the classical MANOVA (Jacobi) random matrix ensemble. Thus, empirically, the MANOVA ensemble offers a universal description of the spectra of randomly selected $k$ subframes, even those taken from deterministic frames. The same universality phenomena is shown to hold for notable random frames as well. This description enables exact calculations of properties of solutions for systems of linear equations based on a random choice of $k$ frame vectors of $n$ possible vectors and has a variety of implications for erasure coding, compressed sensing, and sparse recovery. When the aspect ratio $m/n$ is small, the MANOVA spectrum tends to the well-known Marčenko–Pastur distribution of the singular values of a Gaussian matrix, in agreement with previous work on highly redundant frames. Our results are empirical, but they are exhaustive, precise, and fully reproducible.

Consider a frame ${\{{𝐱}_i\}}_{i=1}^n\subset {ℝ}^m$ or ${ℂ}^m$, and stack the vectors as rows to obtain the $n$-by-$m$ frame matrix $X$. Assume that ${||{𝐱}_i||}_2=1$ (deterministic frames) or ${lim}_{n\to \mathrm{\infty }}\parallel {𝐱}_i\parallel =1$ almost surely (random frames). This paper studies properties of a random subframe ${\{{𝐱}_i\}}_{i\in K}$, where $K$ is chosen uniformly at random from $[n]=\{1,\dots ,n\}$ and $|K|=k\le n$. We let $X_K$ denote the $k$-by-$m$ submatrix of $X$ created by picking only the rows ${\{{𝐱}_i\}}_{i\in K}$; call this object a typical $k$ submatrix of $X$. We consider a collection of well-known deterministic frames, listed in Table 1, which we denote by $\mathcal{X}$. Most of the frames in $\mathcal{X}$ are equiangular tight frames (ETFs), and some are near-ETFs.

Table 1.

Frames under study

Label	Name	$ℝ$ or $ℂ$	Natural $\gamma$	Tight frame	Equiangular	Refs.
Deterministic frames
DSS	Difference set spectrum	$ℂ$		Yes	Yes	36
GF	Grassmannian frame	$ℂ$	$1/2$	Yes	Yes	37, corollary 2.6b
RealPF	Real Paley’s construction	$ℝ$	$1/2$	Yes	Yes	37, corollary 2.6a
ComplexPF	Complex Paley’s construction	$ℂ$	$1/2$	Yes	Yes	38
Alltop	Quadratic Phase Chirp	$ℂ$	$1/L$	Yes	No	26, equation S4
SS	Spikes and Sines	$ℂ$	$1/2$	Yes	No	6
SH	Spikes and Hadamard	$ℝ$	$1/2$	Yes	No	6
Random frames
HAAR	Unitary Haar frame	$ℂ$		Yes	No	3, 4
RealHAAR	Orthogonal Haar frame	$ℝ$		Yes	No	4
RandDFT	Random Fourier transform	$ℂ$		Yes	No	3
RandDCT	Random Cosine transform	$ℝ$		Yes	No

This paper suggests that, for a frame in $\mathcal{X}$, it is possible to calculate quantities of the form ${𝔼}_K\mathrm{\Psi }(\lambda (G_K))$, where $\lambda (G_K)=({\lambda }_1(G_K),\mathrm{\dots },{\lambda }_k(G_K))$ is the vector of eigenvalues of the $k$-by-$k$ Gram matrix $G_K=X_K{X}_K^{\prime }$ and $\mathrm{\Psi }$ is a functional of these eigenvalues. As discussed below, such quantities are of considerable interest in various applications where frames are used across a variety of domains, including compressed sensing, sparse recovery, and erasure coding.

We present a simple and explicit formula for calculating ${𝔼}_K\mathrm{\Psi }(\lambda (G_K))$ for a given frame in $\mathcal{X}$ and a given spectral functional $\mathrm{\Psi }$. Specifically, for the case $k\le m$,

$${𝔼}_K\mathrm{\Psi }(\lambda (G_K))\approx \mathrm{\Psi }\left(f_{\beta ,\gamma }^{MANOVA}\right),$$

where $\beta =k/m$, $\gamma =m/n$, and $f_{\beta ,\gamma }^{MANOVA}$ is the density of Wachter’s classical multivariate ANOVA limiting distribution (1), which we denote here by MANOVA$(\beta ,\gamma )$. The fluctuations about this approximate value are given exactly by

$${𝔼}_K{|\mathrm{\Psi }(\lambda (G_K))-\mathrm{\Psi }\left(f_{\beta ,\gamma }^{MANOVA}\right)|}^2=C{n}^{-b}{\log }^{-a}(n).$$ [1]

Although the constant $C$ may depend on the frame, the exponents $a$ and $b$ are universal and depend only on $\mathrm{\Psi }$ and the aspect ratios $\beta$ and $\gamma$. Evidently, the precision of the MANOVA-based approximation is good, is known, and improves as $m$ and $k$ both grow proportionally to $n$.

Eq. 1 is based on a far-reaching universality hypothesis. For all frames in $\mathcal{X}$ as well as well-known random frames also listed in Table 1, we find that the spectrum of the typical $k$-submatrix ensemble is indistinguishable from that of the classical MANOVA (Jacobi) random matrix ensemble (2) of the same size. (Interestingly, it will be shown that, for deterministic ETFs, this indistinguishability holds in a stronger sense than for deterministic non-ETFs.) This universality is not asymptotic and concerns finite $n$-by-$m$ frames. However, it does imply that the spectrum of the typical $k$-submatrix ensemble converges to a universal limiting distribution, which is none other than Wachter’s MANOVA$(\beta ,\gamma )$ limiting distribution (1). It also implies that the universal exponents $a$ and $b$ in Eq. 1 are previously unknown, universal quantities corresponding to the classical MANOVA (Jacobi) random matrix ensemble.

This brief announcement tests Eq. 1 and the underlying universality hypothesis by conducting substantial computer experiments, in which a large number of random $k$ submatrices are generated. We study a large variety of deterministic frames, both real and complex. In addition to the universal object (the MANOVA ensemble) itself, we study difference set spectrum (DSS) frames, Grassmannian frame (GF), real Paley (RealPF) frames, complex Paley (ComplexPF) frames, quadratic phase chirp (Alltop) frames, Spikes and Sines (SS) frames, and Spikes and Hadamard (SH) frames.

We report compelling empirical evidence, systematically documented and analyzed, which fully supports the universality hypothesis and Eq. 1. Our results are empirical, but they are exhaustive, precise, and reproducible, and they meet the best standards of empirical science.

For this purpose, we develop a natural framework for empirically testing such hypotheses regarding limiting distribution and convergence rates of random matrix ensembles. Before turning to deterministic frames, we validate our framework on well-known random frames, including real orthogonal Haar frames, complex unitary Haar frames, real random Cosine frames, and complex random Fourier frames. Interestingly, rigorous proofs that identify the MANOVA distribution as the limiting spectral distribution of typical $k$ submatrices can be found in the literature for two of these random frames, namely the random Fourier frame (3) and the unitary Haar frame (4).

Motivation

Frames can be viewed as an analog counterpart for digital coding. They provide overcomplete representation of signals, adding redundancy and increasing immunity to noise. Indeed, they are used in many branches of science and engineering for stable signal representation as well as error and erasure correction.

Let $\lambda (G)$ denote the vector of nonzero eigenvalues of $G=X\prime X$, and let ${\lambda }_{max}(G)$ and ${\lambda }_{min}(G)$ denote its maximum and minimum, respectively. Frames were traditionally designed to achieve frame bounds ${\lambda }_{min}(G)$ as high as possible [${\lambda }_{max}(G)$ as low as possible]. Alternatively, they were designed to minimize mutual coherence (5, 6), the maximal pairwise correlation between any two frame vectors.

In the passing decade, it has become apparent that neither frame bounds (a global criterion) nor coherence (a local pairwise criterion) are sufficient to explain various phenomena related to overcomplete representations and that one should also look at collective behavior of $k$ frame vectors from the frame, $2\le k\le n$. Although different applications focus on different properties of the submatrix $G_K$, most of these properties can be expressed as a function of $\lambda (G_K)$ and even just an average of a scalar function of the eigenvalues. Here are a few notable examples.

Restricted Isometry Property.

Recovery of any $k/2$-sparse signal $𝐯\in {ℝ}^n$ from its linear measurement $F\prime 𝐯$ using ${\mathrm{\ell }}_1$ minimization is guaranteed if the spectral radius of $G_K-I$ [restricted isometry property (RIP)], namely

$${\mathrm{\Psi }}_{RIP}(\lambda (G_K))=\max \{{\lambda }_{max}(G_K)-1,1-{\lambda }_{min}(G_K)\},$$ [2]

is uniformly bounded by some $\delta <0.4531$ on all $K\subset [n]$ (7–9).

Statistical RIP.

Numerous authors have studied a relaxation of the RIP condition suggested in ref. 10. Define

$${\mathrm{\Psi }}_{StRIP,\delta }(\lambda (G_K))=\{\begin{array}{cc}1\hspace{1em}\hfill & {\mathrm{\Psi }}_{RIP}(\lambda (G_K))\le \delta \hfill \\ 0\hspace{1em}\hfill & \text{otherwise}\hfill \end{array}.$$ [3]

Then, ${𝔼}_K{\mathrm{\Psi }}_{StRIP,\delta }(\lambda (G_K))$ is the probability that the RIP condition with bound $\delta$ holds when $X$ acts on a signal supported on a random set of $k$ coordinates.

Analog Coding of a Source with Erasures.

In ref. 11, two of us considered a typical erasure pattern of $n-k$ random samples known at the transmitter but not known at the receiver. The rate distortion function of the coding scheme suggested in ref. 11 is determined by ${𝔼}_K\log (\beta {\mathrm{\Psi }}_{AC}(\lambda (G_K)))$, with

$${\mathrm{\Psi }}_{AC}(\lambda (G_K))=\frac{\frac{1}{k}\text{tr}[{(G_K)}^{-1}]}{{\left(\frac{1}{k}\text{tr}[G_K]\right)}^{-1}},$$ [4]

[i.e., ${\mathrm{\Psi }}_{AC}(\lambda (G_K))$ is the arithmetic-to-harmonic means ratio of the eigenvalues (the arithmetic mean is $1$ because of the normalization of frames)]. This quantity is the signal amplification responsible for the excess rate of the suggested coding scheme. Note that $\beta$ here is the inverse of $\beta$ defined in ref. 11.

Shannon Transform.

The quantity

$${\mathrm{\Psi }}_{Shannon}(\lambda (G_K))={\displaystyle \frac{1}{k}}\log (det(I+\alpha G_K))={\displaystyle \frac{1}{k}}\text{tr}(\log (I+\alpha G_K)),$$ [5]

which was suggested in ref. 12, measures the capacity of a linear Gaussian erasure channel. Specifically, it assumes $y=XX\prime x+z$ (where $x$ and $y$ are the channel input and output) followed by $n-k$ random erasures. The quantity $\alpha$ in Eq. 5 is the signal-to-noise ratio $SNR=\alpha \ge 0$.

In this paper, we focus on typical case performance criteria [those that seek to optimize ${𝔼}_K\mathrm{\Psi }(\lambda (G_K))$ over random choice of $K$] rather than worse case performance criteria [those that seek to optimize ${\max }_{K\subset [n]}\mathrm{\Psi }(\lambda (G_K))$, such as RIP]. For the remainder of this paper, $K\subset [n]$ will denote a uniformly distributed random subset of size $k$. Importantly, $k$ should be allowed to be large, even as large as $m$.

For a given $\mathrm{\Psi }$, one would like to design frames that optimize ${𝔼}_K\mathrm{\Psi }(\lambda (G_K))$. This optimization turns out to be a difficult task; in fact, it is not even known how to calculate ${𝔼}_K\mathrm{\Psi }(\lambda (G_K))$ for a given frame $X$. Indeed, to calculate this quantity, one effectively has to average $\mathrm{\Psi }$ over the spectrum $\lambda (G_K)$ for all $\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)$ subsets $K\subset [n]$. It is of little surprise to the information theorist that the first frame designs, for which performance was formally bounded (and still not calculated exactly), consisted of random vectors (8, 13–17).

Random Frames

When the frame is random, namely when $X$ is drawn from some ensemble of random matrices, each $k$ submatrix $X_K$ is also a random matrix. Given a specific $\mathrm{\Psi }$, rather than seeking to bound ${𝔼}_K\mathrm{\Psi }(\lambda (G_K))$ for specific $n$ and $m$, it can be extremely rewarding to study the limit of $\mathrm{\Psi }(\lambda (G_K))$ as the frame sizes $n$ and $m$ grow. The reason is that tools from random matrix theory become available, which allow exact asymptotic calculation of $\lambda (G_K)$ and $\mathrm{\Psi }(\lambda (G_K))$, and also because their limiting values are usually very close to their corresponding values for finite $n$ and $m$, even for low values of $n$.

Let us consider then a sequence of dimensions $m_n$ with $m_n/n={\gamma }_n\to \gamma$ and a sequence of random frame matrices $X^{(n)}\subset {ℝ}^{n\times m_n}$ or ${ℂ}^{n\times m_n}$. To characterize the collective behavior of $k$ submatrices, we choose a sequence $k_n$ with $k_n/m_n={\beta }_n\to \beta$ and look at the spectrum $\lambda (G_{K_n})$ of the random matrix $X_{K_n}$ as $n\to \mathrm{\infty }$, where $K_n\subset [n]$ is a randomly chosen subset with $|K_n|=k_n$. Here and below, to avoid cumbersome notation, we omit the subscript $n$ and write $m$, $k$, and $K$ for $m_n$, $k_n$, and $K_n$.

A mainstay of random matrix theory is the celebrated convergence of the empirical spectral distribution of random matrices, drawn from a certain ensemble, to a limiting spectral distribution corresponding to that ensemble. Such convergence has indeed been established for three random frames:

1. Gaussian i.i.d. Frame.

Let $X_{normal}^{(n)}$ have i.i.d. (independent and identically distributed) normal entries with mean zero and variance $1/m$. The empirical distribution of $\lambda (G_K)$ famously converges, almost surely in distribution, to the Marčenko–Pastur density (18) with parameter $\beta$:

$$f_{\beta }^{MP}(x)=\frac{\sqrt{(x-{\lambda }_{-}^{MP})({\lambda }_{+}^{MP}-x)}}{2\beta \pi x}\cdot I_{({\lambda }_{-}^{MP},{\lambda }_{+}^{MP})}(x),$$ [6]

supported on $[{\lambda }_{-}^{MP},{\lambda }_{+}^{MP}]$, where ${\lambda }_{\pm }^{MP}={(1\pm \sqrt{\beta })}^2$. Moreover, almost surely ${\lambda }_{max}(G_{normal}^{(n)})\to {\lambda }_{+}$ and ${\lambda }_{min}(G_{normal}^{(n)})\to {\lambda }_{-}$; in other words, the maximal and minimal empirical eigenvalues converge almost surely to the edges of the support of the limiting spectral distribution (19).

2. Random Fourier Frame.

Consider the random Fourier frame, in which the $m_n$ columns of $X_{Fourier}^{(n)}$ are drawn uniformly at random from the columns of the $n$-by-$n$ discrete Fourier transform (DFT) matrix (normalized such that the absolute value of matrix entries is $1/\sqrt{m}$). Farrell (3) has proved that the empirical distribution of $\lambda (G_K)$ converges, almost surely in distribution, as $n\to \mathrm{\infty }$ and $m$ and $k$ grow proportionally to $n$ to the so-called MANOVA limiting distribution, which we now describe briefly.

The classical MANOVA$(n,m,k,\mathcal{F})$ ensemble,* with $\mathcal{F}\in \{ℝ,ℂ\}$, is the distribution of the random matrix

$$\frac{n}{m}{(AA\prime +BB\prime )}^{-\frac{1}{2}}BB\prime {(AA\prime +BB\prime )}^{-\frac{1}{2}},$$ [7]

where $A_{k\times (n-m)},B_{k\times m}$ are random standard Gaussian i.i.d. matrices with entries in $\mathcal{F}$. Wachter (1) discovered that, as $k/m\to \beta \le 1$ and $m/n\to \gamma$, the empirical spectral distribution of the MANOVA$(n,m,k,ℝ)$ ensemble converges, almost surely in distribution, to the so-called MANOVA$(\beta ,\gamma )$ limiting spectral distribution,^† with density that is given by

$$f_{\beta ,\gamma }^{MANOVA}(x)=\frac{\sqrt{(x-r_{-})(r_{+}-x)}}{2\beta \pi x(1-\gamma x)}\cdot I_{(r_{-},r_{+})}(x)+{\left(1+\frac{1}{\beta }-\frac{1}{\beta \gamma }\right)}^{+}\cdot \delta \left(x-\frac{1}{\gamma }\right),$$ [8]

where ${(x)}^{+}=\max (0,x)$. The limiting MANOVA distribution is compactly supported on $[r_{-},r_{+}]$ with

$$r_{\pm }={(\sqrt{\beta (1-\gamma )}\pm \sqrt{1-\beta \gamma })}^2.$$ [9]

The same holds for the MANOVA$(n,m,k,ℂ)$ ensemble.

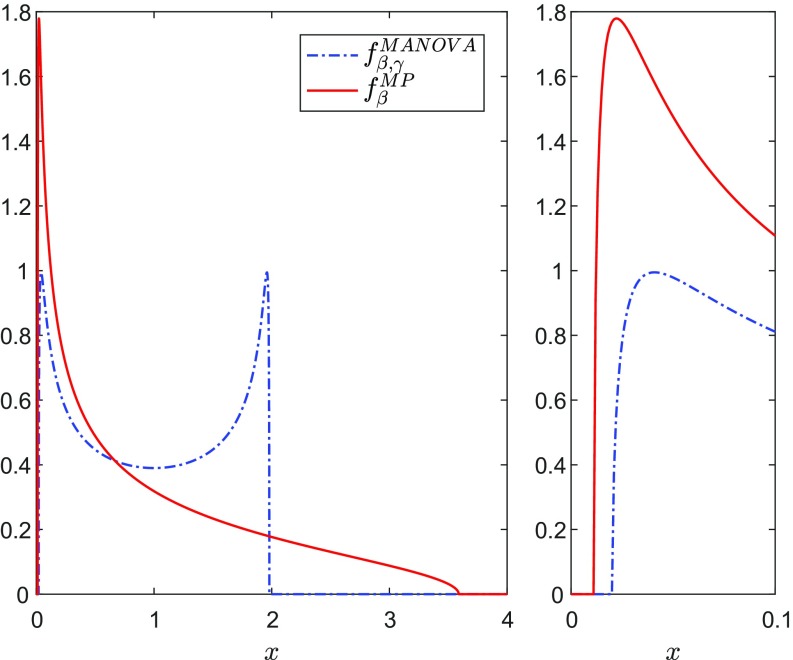
Note that the support of the MANOVA$(\beta ,\gamma )$ distribution is smaller than that of the corresponding Marčenko–Pastur law for the same aspect ratios. Fig. 1 shows these two densities for $\beta =0.8$ and $\gamma =0.5$. Nevertheless, as the MANOVA dimension ratio becomes small, its distribution tends to the Marčenko–Pastur distribution (Eq. 6) [i.e., $f_{\beta ,\gamma }^{MANOVA}(x)\to f_{\beta }^{MP}(x)$ as $\gamma \to 0$]. Thus, a highly redundant random Fourier frame behaves like a Gaussian i.i.d. frame.

Fig. 1.

Limiting MANOVA ($\beta =0.8,\gamma =0.5$) and Marčenko–Pastur ($\beta =0.8$) density functions. (Left) Density on the interval $x\in [\mathrm{0,4}]$. (Right) Zoom in on the interval $x\in [\mathrm{0,0.1}]$.

3. Unitary Haar Frame.

Let $X_{haar}^{(n)}$ consist of the first $m$ columns of a Haar-distributed $n$-by-$n$ unitary matrix normalized by $\sqrt{n/m}$ (the Haar distribution being the uniform distribution over the group of $n$-by-$n$ unitary matrices). Edelman and Sutton (4) proved that the empirical spectral distribution of $\lambda (G_K$) also converges, almost surely in distribution, to the MANOVA limiting spectral distribution (refs. 1 and 3, closing remarks).

The maximal and minimal eigenvalues of a matrix from the MANOVA$(n,m,k,\mathcal{F})$ ensemble ($\mathcal{F}\in \{ℝ,ℂ\}$) are known to converge almost surely to $r_{+}$ and $r_{-}$, respectively (20). Although we are not aware of any parallel results for the random Fourier and Haar frames, the empirical evidence in this paper shows that it must be the case.

These random matrix phenomena have practical significance for evaluations of functions of the form $\mathrm{\Psi }(\lambda (G_K))$, such as those mentioned above. The functions ${\mathrm{\Psi }}_{AC}$ and ${\mathrm{\Psi }}_{Shannon}$, for example, are called linear spectral statistics in ref. 21, namely functions of $\lambda (G_K)$ that may be written as an integral of a scalar function against the empirical measure of $\lambda (G_K)$. Convergence of the empirical distribution of $\lambda (G_K^{(n)})$ to the limiting MANOVA distribution with density $f_{\beta ,\gamma }^{MANOVA}$ implies

$$\begin{array}{c}\underset{n\to \mathrm{\infty }}{lim}{\mathrm{\Psi }}_{AC}(\lambda (G_{K_n}^{(n)}))=\int \frac{1}{x}{f}_{\beta ,\gamma }^{MANOVA}(x)dx\\ \underset{n\to \mathrm{\infty }}{lim}{\mathrm{\Psi }}_{Shannon}(\lambda (G_{K_n}^{(n)}))=\int \log (1+\alpha x)f_{\beta ,\gamma }^{MANOVA}(x)dx\end{array}$$ [10]

for both the random Fourier and Haar frames; the integrals on the right-hand side may be evaluated explicitly. Similarly, convergence of ${\lambda }_{max}(G_K)$ and ${\lambda }_{min}(G_K)$ to $r_{+}$ and $r_{-}$ implies, for example, that

$$\underset{n\to \mathrm{\infty }}{lim}{\mathrm{\Psi }}_{RIP}(\lambda (G_K^{(n)}))=\max (r_{+}-1,1-r_{-}).$$ [11]

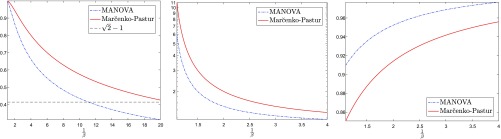
To show why such calculations are significant, we note that Eqs. 10 and 11 immediately allow us to compare the Gaussian i.i.d. frame with the random Fourier and Haar frames in terms of their limiting value of functions of interest. Fig. 2 compares the limiting value of ${\mathrm{\Psi }}_{RIP}$, ${\mathrm{\Psi }}_{AC}$, and ${\mathrm{\Psi }}_{Shannon}$ over varying values of $\beta ={lim}_{n\to \mathrm{\infty }}k/m$. The plots clearly show that frames with a typical $k$ submatrix that exhibits a MANOVA spectrum are superior to frames with a typical $k$ submatrix that exhibits a Marčenko–Pastur spectrum across the performance measures.

Fig. 2.

Comparison of limiting values of ${𝔼}_K\mathrm{\Psi }(\lambda (G_K))$ for the three functions $\mathrm{\Psi }$ discussed in Motivation between the Marčenko–Pastur limiting distribution and the MANOVA distribution. (Left) ${\mathrm{\Psi }}_{RIP}$ (lower is better). (Center) ${\mathrm{\Psi }}_{AC}$ (lower is better). (Right) ${\mathrm{\Psi }}_{Shannon}$ (higher is better).

Deterministic Frames: Universality Hypothesis

Deterministic frames, namely frames with design that involves no randomness, have so far eluded this kind of asymptotically exact analysis. Although there are results regarding RIP (22, 23) and statistical RIP (10, 24, 25), for example, of deterministic frame designs, they are mostly focused on highly redundant frames ($\gamma \to 0$) and the wide submatrix ($\beta \to 0$) case, where the spectrum tends to the Marčenko–Pastur distribution. Furthermore, nothing analogous, say, to the precise comparisons of Fig. 2 exists in the literature to the best of our knowledge. Specifically, no results analogous to Eqs. 10 and 11 are known for deterministic frames, let alone the associated convergence rates, if any.

To subject deterministic frames to an asymptotic analysis, we shift our focus from a single frame $X$ to a family of deterministic frames $\{X^{(n)}\}$ created by a common construction. The frame matrix $X^{(n)}$ is $n$-by-$m$. Each frame family determines allowable subsequences $(n,m)$; to simplify notation, we leave the subsequence implicit and index the frame sequence simply by $n$. The frame family also determines the aspect ratio limit $\gamma ={lim}_{n\to \mathrm{\infty }}m/n$. In what follows, we also fix a sequence $k$ with $\beta ={lim}_{n\to \mathrm{\infty }}k/m$ and let $K\subset [n]$ denote a uniformly distributed random subset.

Frames Under Study.

The different frames that we studied are listed in Table 1 in a manner inspired by ref. 26. In addition to our deterministic frames of interest (the set $\mathcal{X}$), Table 1 also contains two examples of random frames (real and complex variants for each) for validation and convergence analysis purposes.

Functionals Under Study.

We studied the functionals ${\mathrm{\Psi }}_{StRIP}$ from Eq. 3, ${\mathrm{\Psi }}_{AC}$ from Eq. 4, and ${\mathrm{\Psi }}_{Shannon}$ from Eq. 5. In addition, we studied the maximal and minimal eigenvalues of $G_K$ and its condition number:

$$\begin{array}{c}{\mathrm{\Psi }}_{max}(\lambda (G_K))={\lambda }_{max}(G_K)\\ {\mathrm{\Psi }}_{min}(\lambda (G_K))={\lambda }_{min}(G_K)\\ {\mathrm{\Psi }}_{cond}(\lambda (G_K))=\frac{{\lambda }_{max}(G_K)}{{\lambda }_{min}(G_K)}.\end{array}$$

Measuring the Rate of Convergence.

To quantify the rate of convergence of the entire spectrum of the $k$-by-$m$ matrix $X_K$, which is a $k$ submatrix of an $n$-by-$m$ frame matrix $X$, to a limiting distribution, we let $F[X_K]$ denote the empirical cumulative distribution function (CDF) of $\lambda (G_K)$ and $F_{\beta ,\gamma }^{MANOVA}(x)={\int }_{r_{-}}^x{f}_{\beta ,\gamma }^{MANOVA}(z)dz$ denote the CDF of the MANOVA$(\beta ,\gamma )$ limiting distribution. The quantity

$${\mathrm{\Delta }}_{KS}(X_K)={||F[X_K]-F_{{\beta }_n,{\gamma }_n}^{MANOVA}||}_{KS},$$

where $\left|\right|\cdot |{|}_{KS}$ is the Kolmogorov–Smirnov (KS) distance between CDFs, measures the distance to the hypothesized limit. Here, ${\beta }_n=k/m$ and ${\gamma }_n=m/n$ are the actual aspect ratios for the matrix $X_K$ at hand. As a baseline, we use ${\mathrm{\Delta }}_{KS}(Y_{n,m,k,\mathcal{F}})$, where $Y_{n,m,k,\mathcal{F}}$ is a matrix from the MANOVA$(n,m,k,\mathcal{F})$ ensemble, with $\mathcal{F}=ℝ$ if $X_K$ is real and $\mathcal{F}=ℂ$ if $X_K$ is complex. Fig. 3 illustrates the KS distance between an empirical CDF and the limiting MANOVA CDF.

Fig. 3.

KS distance of random DFT subframe: $\beta =0.8$, $\gamma =0.5$, and $n=100$.

Similarly, to quantify the rate of convergence of a functional $\mathrm{\Psi }$, the quantity

$${\mathrm{\Delta }}_{\mathrm{\Psi }}(X_K;n,m,k)=|\mathrm{\Psi }(\lambda (G_K))-\mathrm{\Psi }(f_{{\beta }_n,{\gamma }_n}^{MANOVA})|$$

is the distance between the measured value of $\mathrm{\Psi }$ on a given $k$ submatrix $X_K$ and its hypothesized limiting value. For a baseline, we can use ${\mathrm{\Delta }}_{\mathrm{\Psi }}(Y_{n,m,k,\mathcal{F}})$, with $\mathcal{F}=ℝ$ if $X_K$ is real and $\mathcal{F}=ℂ$ if $X_K$ is complex. For linear spectral functionals, like ${\mathrm{\Psi }}_{AC}$ and ${\mathrm{\Psi }}_{Shannon}$, which may be written as $\mathrm{\Psi }(\lambda (G_K))=\int \psi dF[X_K]$ for some kernel $\psi$, we have $\mathrm{\Psi }(f_{\beta ,\gamma }^{MANOVA})=\int \psi d{F}_{\beta ,\gamma }^{MANOVA}$. For ${\mathrm{\Psi }}_{RIP}$ that depends on ${\lambda }_{max}(G_K)$ and ${\lambda }_{min}(G_K)$, we have ${\mathrm{\Psi }}_{RIP}(f_{\beta ,\gamma }^{MANOVA})=\max \{r_{+}-1,1-r_{-}\}$.

Universality Hypothesis.

The contributions of this paper are based on the following assertions on the typical $k$-submatrix ensemble $X_K$ corresponding to a frame family $X^{(n)}$. This family may be random or deterministic, real or complex.

H1. Existence of a Limiting Spectral Distribution.

The empirical spectral distribution of $X_K^{(n)}$, namely the distribution of $\lambda (G_K^{(n)})$, converges, as $n\to \mathrm{\infty }$, to a compactly supported limiting distribution; furthermore, ${\lambda }_{max}(G_K^{(n)})$ and ${\lambda }_{min}(G_K^{(n)})$ converge to the edges of that compact support.

H2. Universality of the Limiting Spectral Distribution.

The limiting spectral distribution of $X_K^{(n)}$ is the MANOVA$(\beta ,\gamma )$ distribution (1) with density that is shown in Eq. 8. Also, ${\lambda }_{max}(G_K^{(n)})\to r_{+}$ and ${\lambda }_{min}(G_K^{(n)})\to r_{-}$, where $r_{\pm }$ is given by Eq. 9.

H3. Exact Power Law Rate of Convergence for the Entire Spectrum.

The spectrum of $X_K^{(n)}$ converges to the limiting MANOVA$(\beta ,\gamma )$ distribution

$${\left({𝔼}_{K_n}\left({\mathrm{\Delta }}_{KS}(X_K^{(n)})\right)\right)}^2\searrow 0,$$

and in fact, its fluctuations are given by the law

$$Va{r}_K({\mathrm{\Delta }}_{KS}(X_K^{(n)}))=C{n}^{-2b}$$ [12]

for some constants $C,b$, which may depend on the frame family.

H4. Universality of the Rate of Convergence for the Entire Spectrum of ETFs.

For an ETF family, the exponent $b$ in Eq. 12 is universal and does not depend on the frame. Furthermore, Eq. 12 also holds, with the same universal exponent, replacing $G_K^{(n)}$ with a same-sized matrix from the MANOVA$(n,m,k,\mathcal{F})$ distribution defined in Eq. 7 with $\mathcal{F}=ℝ$ if $X^{(n)}$ is a real frame family and $\mathcal{F}=ℂ$ if $X^{(n)}$ is a complex frame family. In other words, the universal exponent $b$ for ETFs is a property of the MANOVA (Jacobi) random matrix ensemble.

H5. Exact Power Law Rate of Convergence for Functionals.

For a “nice” functional $\mathrm{\Psi }$, the value of $\mathrm{\Psi }(\lambda (G_K^{(n)}))$ converges to $\mathrm{\Psi }(f_{\beta ,\gamma }^{MANOVA})$ according to the law

$${𝔼}_K({\mathrm{\Delta }}_{\mathrm{\Psi }}{(X_K^{(n)})}^2)=C{n}^{-b}{\log }^{-a}(n)$$ [13]

for some constants $C,b,a$.

H6. Universality of the Rate of Convergence for Functionals.

Although the constant $C$ in Eq. 13 may depend on the frame, the exponents $a,b$ are universal. Eq. 13 also holds, with the same universal exponents, replacing $G_K^{(n)}$ with a same-sized matrix from the MANOVA$(n,m,k,\mathcal{F})$ ensemble defined in Eq. 7, with $\mathcal{F}=ℝ$ if $X^{(n)}$ is a real frame family and $\mathcal{F}=ℂ$ if $X^{(n)}$ is a complex frame family. In other words, the universal exponents $a,b$ are a property of the MANOVA (Jacobi) random matrix ensemble.

Nonstandard Aspect Ratio $𝜷\mathbf{>}\mathbf{1}$.

Although the classical MANOVA ensemble and limiting density are not defined for $\beta >1$, in our case, it is certainly possible to sample $k>m$ vectors from the $n$ possible frame vectors, resulting in a situation with $\beta >1$. In this situation, the hypotheses above require slight modifications. Specifically, the limiting spectral distribution of $X_K^{(n)}$ for $\beta >1$ is

$$\left(1-\frac{1}{\beta }\right)\delta (x)+f_{\beta ,\gamma }^{MANOVA}(x),$$ [14]

where $f_{\beta ,\gamma }^{MANOVA}(x)$ is the function (no longer a density) defined in Eq. 8. The rate of convergence of the distribution of nonzero eigenvalues to the limiting density $1/\beta f_{1/\beta ,\beta \gamma }^{MANOVA}(1/\beta x)=\beta f_{\beta ,\gamma }^{MANOVA}(x)$ is compared with the baseline $\beta \cdot Y_{n,k,m,\mathcal{F}}$, where $Y_{n,k,m,\mathcal{F}}$ is a matrix from the MANOVA$(n,k,m,\mathcal{F})$ ensemble (i.e., with reversed order of $k$ and $m$).

Methods

The software that we developed has been permanently deposited in the data and code supplement (https://purl.stanford.edu/qg138qm8653). Because many of the deterministic frames under study are only defined for $\gamma =0.5$, we primarily studied the aspect ratios $(\gamma =0.5,\beta )$ with $\beta \in \{0.3,0.5,0.6,0.7,0.8,0.9\}$. In addition, we inspected all frames under study that are defined for the aspect ratios $(\gamma =0.25,\beta =0.6)$ and $(\gamma =0.25,\beta =0.8)$ (all random frames as well as DSS and Alltop). We also studied nonstandard aspect ratios $\beta >1$ as described in SI Appendix (https://purl.stanford.edu/qg138qm8653). For deterministic frames, $n$ took allowed values in the ranges $(240,2,000)$, $(2^5,2^{12})$ for Grassmannian and SH frames, and $(600,4,000)$ for DSS frame with $\gamma =0.25$. For random frames and MANOVA ensemble, we used dense grid of values in the range $(240,2,000)$. Hypothesis testing as discussed below was based on a subset of these values, where $n\ge 1,000$. For each of the frame families under study and each value of $\beta$ and $\gamma$ under study, we selected a sequence $(n,m,k)$. The values $n$ and $m$ were selected so that $m/n$ will be as close as possible to $\gamma$; however, because of different aspect ratio constraints by the different frames, occasionally, we had $m/n$ close but not equal to $\gamma$. We then determined $k$, such that $k/m$ will be as close as possible to $\beta$. For each $n$, we generated a single $n$-by-$m$ frame matrix $X^{(n)}$. We then produced $T$ independent samples from the uniform distribution on $k_n$ subsets, $K[1],\mathrm{\dots },K[T]\subset [n]$, and generated their corresponding $k$ submatrices $X_{K[i]}^{(n)}$ ($1\le i\le T$). Importantly, all of these are submatrices of the same frame matrix $X^{(n)}$. We calculated ${\overline{\mathrm{\Delta }}}_{KS}^{Var}(X_K^{(n)})={\overline{{\mathrm{\Delta }}^2}}_{KS}(X_K^{(n)})-{\overline{\mathrm{\Delta }}}_{KS}^2(X_K^{(n)})$, the empirical variance of ${\mathrm{\Delta }}_{KS}(X_{K[i]}^{(n)})$, and ${\overline{{\mathrm{\Delta }}^2}}_{KS}(X_K^{(n)})$, the average value of ${\mathrm{\Delta }}_{KS}^2(X_{K[i]}^{(n)})$ on $1\le i\le T$ as a Monte Carlo approximation to the left-hand side of Eq. 12, variance and MSE (mean square error), respectively. For each of the functionals under study, we also calculated ${\overline{{\mathrm{\Delta }}^2}}_{\mathrm{\Psi }}(X_{K[i]}^{(n)})$, the average value of ${\mathrm{\Delta }}_{\mathrm{\Psi }}^2(X_{K[i]}^{(n)})$ on $1\le i\le T$, as a Monte Carlo approximation to the left-hand size of Eq. 13.

Separately, for each triplet ($n$, $m$, $k$) and $\mathcal{F}\in \left\{ℝ\mathit{,}ℂ\right\}$, we have performed $T$ independent draws from the MANOVA$(n,m,k,\mathcal{F})$ ensembles [7] and calculated analogous quantities ${\overline{\mathrm{\Delta }}}_{KS}^{Var}(Y_{n,m,k,\mathcal{F}})$, ${\overline{{\mathrm{\Delta }}^2}}_{KS}(Y_{n,m,k,\mathcal{F}})$, and ${\overline{{\mathrm{\Delta }}^2}}_{\mathrm{\Psi }}(Y_{n,m,k,\mathcal{F}})$.

Test 1: Testing H1–H4.

For each of the frames under study and each value of $(\beta ,\gamma )$, we computed the KS distance for $T={10}^4$ submatrices and performed simple linear regression of $-1/2\log \left({\overline{\mathrm{\Delta }}}_{KS}^{Var}(X_K^{(n)})\right)$ on $\log (n)$ with an intercept. We obtained the estimated linear coefficient $\widehat{b}$ as an estimate for the exponent $b$ and its SE $\sigma (\widehat{b})$. Similarly, we regressed $-1/2\log \left({\overline{\mathrm{\Delta }}}_{KS}^{Var}(Y_{n,m,k,\mathcal{F}})\right)$ on $\log (n)$ to obtain ${\widehat{b}}_{MANOVA}$ and $\sigma ({\widehat{b}}_{MANOVA})$. We performed Student’s t test to test the null hypotheses $b=b_{MANOVA}$ using the test statistic

$$t=\frac{\widehat{b}-b_{MANOVA}}{\sqrt{\sigma {(\widehat{b})}^2+\sigma {({\widehat{b}}_{MANOVA})}^2}}.$$

Under the null hypothesis, the test statistic is distributed $t_{(N+N_{MANOVA}-4)}$, where $N$ and $N_{MANOVA}$ are the numbers of different values of $n$ for which we have collected the data for a frame and the MANOVA ensemble, respectively. We report the $R^2$ of the linear fit, the slope coefficient $\widehat{b}$ and its SE, and the P value of the above t test. We next regressed $-\log \left({\overline{{\mathrm{\Delta }}^2}}_{KS}\right)$ on $\log (n)$. Because ${\overline{{\mathrm{\Delta }}^2}}_{KS}={\left({\overline{\mathrm{\Delta }}}_{KS}\right)}^2+{\overline{\mathrm{\Delta }}}_{KS}^{Var}$, a linear fit verifies that ${\left({\overline{\mathrm{\Delta }}}_{KS}\right)}^2\searrow 0$.

Test 2: Testing H5–H6.

For each of the frames under study, each of the functionals $\mathrm{\Psi }$ under study, and each value of $(\beta ,\gamma )$, we computed the empirical value of the functionals on $T={10}^3$ submatrices. We first performed linear regression of $-\log \left({\overline{{\mathrm{\Delta }}^2}}_{\mathrm{\Psi }}(Y_{n,m,k,\mathcal{F}})\right)$ on $\log (n)$ and $\log (\log (n))$ with an intercept for $\mathcal{F}\in \left\{ℝ,ℂ\right\}$. Let $a_0$ denote the fitted coefficient for $\log (n)$, and let $b_0$ denote the fitted coefficient for $\log (\log (n))$. This step was based on triplets $(n,m,k)$, yielding accurate aspect ratios in the range $240\le n\le 2,000$. We then performed simple linear regression of $-\log \left({\overline{{\mathrm{\Delta }}^2}}_{\mathrm{\Psi }}(X_K^{(n)};n,m,k)\right)$ on $\log (n)+(a_0/b_0)\cdot \log (\log (n))$. The estimated linear regression coefficient $\widehat{b}$ is the estimate for the exponent $b$ in Eq. 13, and $\sigma (\widehat{b})$ is its SE. We used $\widehat{b}\cdot (a_0/b_0)$ as an estimate for the exponent $a$ in Eq. 13. We proceeded as above to test the null hypothesis $b=b_0$. We report the $R^2$ of the linear fit, the slope coefficient $\widehat{b}$ and its SE, and the P value of the test above.

Computing.

To allow the number of Monte Carlo samples to be as large as $T={10}^4$ and $n$ to be as large as $2,000$, we used a large Matlab cluster running on Amazon Web Services. We used 32 logical core machines with 240 GB RAM (random access memory) each, which were running several hundred hours in total. The code that we executed has been deposited (https://purl.stanford.edu/qg138qm8653); it may easily be executed for smaller values of $T$ and $n$ on smaller machines.

Results

The raw results obtained in our experiments as well as the analysis results of each experiment have been deposited with their generating code (https://purl.stanford.edu/qg138qm8653).

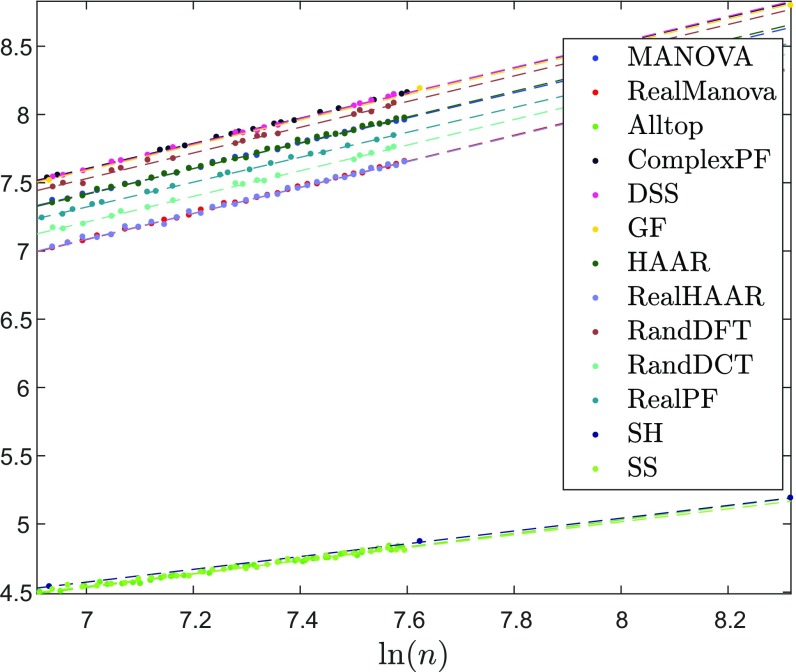
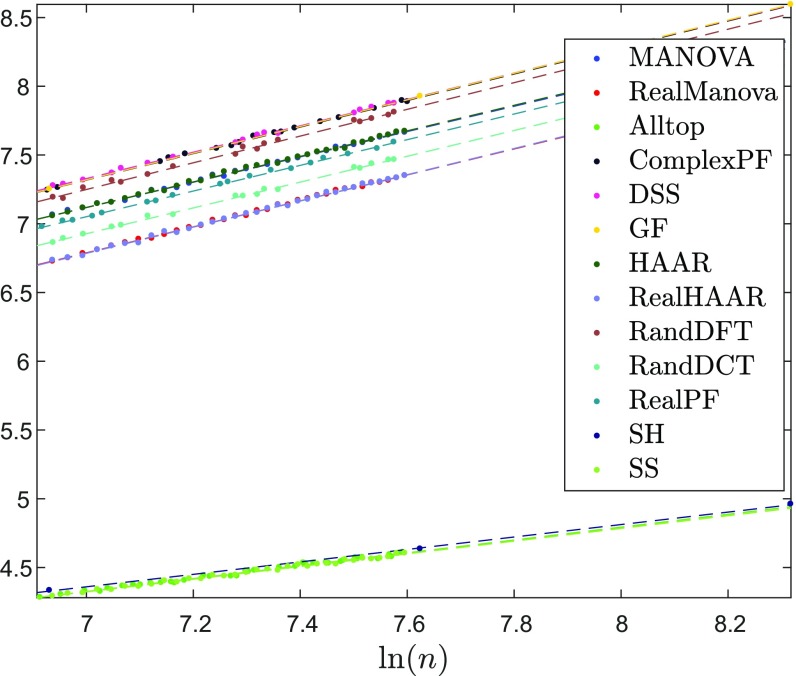
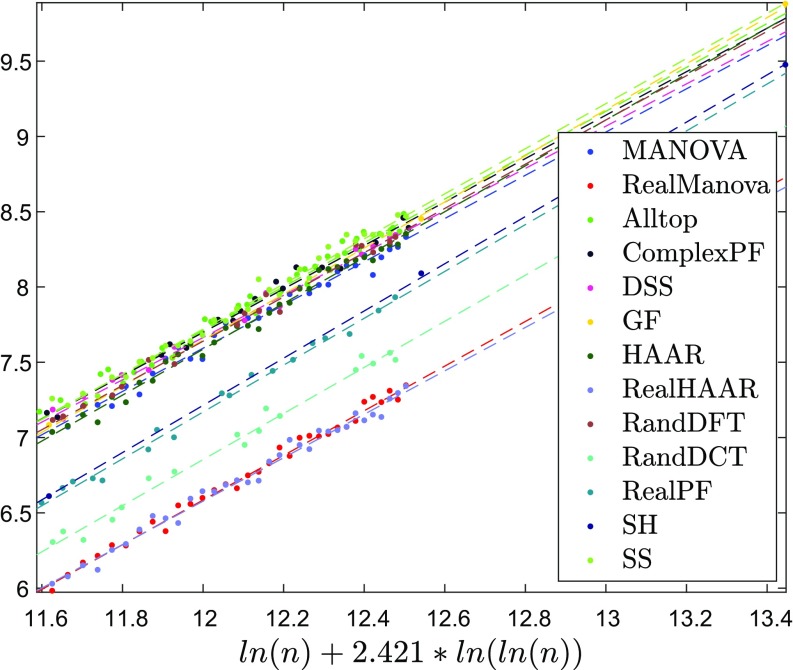
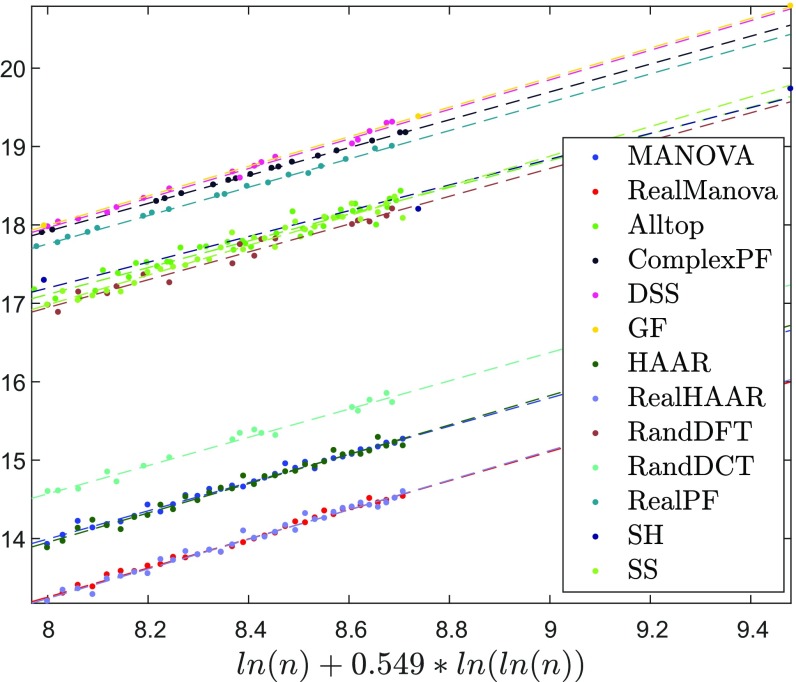
For space considerations, the full documentation of our results is deferred to SI Appendix (https://purl.stanford.edu/qg138qm8653). To offer a few examples, Fig. 4 and Table 2 show the linear fit to ${\overline{\mathrm{\Delta }}}_{KS}^{Var}$ for $(\gamma =0.5,\beta =0.8)$. Fig. 5 shows the linear fit to ${\overline{\mathrm{\Delta }}}_{KS}^{Var}$ for a different value of $\beta$, namely $(\gamma =0.5,\beta =0.6)$. Fig. 6 shows the linear fit to ${\overline{\mathrm{\Delta }}}_{{\mathrm{\Psi }}_{AC}}$ for $(\gamma =0.5,\beta =0.8)$. Fig. 7 and Table 3 show the linear fit to ${\overline{\mathrm{\Delta }}}_{{\mathrm{\Psi }}_{Shannon}}$ for $(\gamma =0.5,\beta =0.8)$. Similar figures and tables for the other values $(\gamma ,\beta )$, in particular, $(\beta =0.3,\gamma =0.5)$, $(\beta =0.5,\gamma =0.5)$, $(\beta =0.7,\gamma =0.5)$, $(\beta =0.9,\gamma =0.5)$, $(\beta =0.6,\gamma =0.25)$, and $(\beta =0.8,\gamma =0.25)$, are deferred to SI Appendix. Note that, in all coefficient tables, both those shown here and those deferred to SI Appendix, the upper boxes show complex frames (with t test comparison with the complex MANOVA ensemble of the same size denoted “MANOVA”), and the bottom boxes show real frames (with t test comparison with the real MANOVA ensemble of the same size denoted “RealMANOVA”). In each box, the top rows are deterministic frames, and the bottom rows are random frames. Furthermore, note that, in plots for test 2, the horizontal axis is slightly different for real and complex frames, because the preliminary step described above was performed separately for real and complex frames. In the interest of space, we plot all frames over the horizontal axis calculated for complex frames.

Fig. 4.

Test 1 for $\gamma =0.5$ and $\beta =0.8$. The plot shows $-1/2\hspace{0.17em}\ln Va{r}_K({\mathrm{\Delta }}_{KS}(X_K^{(n)}))$ over $\ln (n)$.

Table 2.

Results of test 1 for $𝜸=0.5$ and $𝜷=0.8$

Frame	$R^2$	$\widehat{b}$	$SE(\widehat{b})$	P value $b=b_{MANOVA}$
MANOVA	0.99828	0.92505	0.00690	1
DSS	0.99858	0.93652	0.00911	0.32089
GF	0.99921	0.92474	0.02608	0.99082
ComplexPF	0.99950	0.92454	0.00535	0.95390
Alltop	0.98906	0.49660	0.00883	9.4651e-47
SS	0.98767	0.47354	0.00950	5.8136e-45
HAAR	0.99736	0.94421	0.00873	0.09019
RandDFT	0.99544	0.94127	0.01644	0.36788
RealMANOVA	0.99873	0.95610	0.00613	1
RealPF	0.99871	0.91244	0.00821	9.7174e-05
SH	0.99989	0.46822	0.00492	6.3109e-35
RealHAAR	0.99596	0.94456	0.01081	0.35675
RandDCT	0.99773	0.93859	0.01156	0.18737

Fig. 5.

Test 1 for $\gamma =0.5$ and $\beta =0.6$. The plot shows $-1/2\hspace{0.17em}\ln Va{r}_K({\mathrm{\Delta }}_{KS}(X_K^{(n)}))$ over $\ln (n)$.

Fig. 6.

Test 2 for ${\mathrm{\Psi }}_{AC}$, $\gamma =0.5$, and $\beta =0.8$. The plot shows $-\ln \hspace{0.17em}{𝔼}_K({\mathrm{\Delta }}_{\mathrm{\Psi }}{(X_K^{(n)})}^2)$.

Fig. 7.

Test 2 for ${\mathrm{\Psi }}_{Shannon}$, $\gamma =0.5$, and $\beta =0.8$. The plot shows $-\ln \hspace{0.17em}{𝔼}_K({\mathrm{\Delta }}_{\mathrm{\Psi }}{(X_K^{(n)})}^2)$.

Table 3.

Results of test 2 for ${𝚿}_{Shannon}$, $𝜸=0.5$, and $𝜷=0.8$

Frame	$R^2$	$\widehat{b}$	$SE(\widehat{b})$	P value $b=b_{MANOVA}$
MANOVA	0.98721	1.79936	0.03678	1
DSS	0.99110	1.88674	0.04615	0.14551
GF	0.99997	1.88548	0.01073	0.03161
ComplexPF	0.99977	1.77783	0.00701	0.56808
Alltop	0.93841	1.70618	0.07388	0.26297
SS	0.95539	1.89501	0.07355	0.24922
HAAR	0.97971	1.87082	0.04836	0.24400
RandDFT	0.96928	1.77454	0.08157	0.78270
RealMANOVA	0.99202	2.05451	0.03309	1
RealPF	0.99834	2.00345	0.02045	0.19576
SH	0.97850	1.81297	0.26874	0.37904
RealHAAR	0.98287	2.09078	0.04958	0.54503
RandDCT	0.98364	1.99663	0.06648	0.43977

Validation on Random Frames.

Although our primary interest was in deterministic frames, we included in the frames under study random frames. For the complex Haar frame and random Fourier frame, convergence of the empirical CDF of the spectrum to the limiting MANOVA$(\beta ,\gamma )$ distribution has been proved in refs. 3 and 4. To our surprise, not only was our framework validated on the four random frames under study, in the sense of asymptotic empirical spectral distribution, but also, all universality hypotheses H1–H6 were accepted (not rejected at the 0.001 significance level, with very few exceptions).

Test Results on Deterministic Frames.

A tabular summary of our results, per hypothesis and per frame under study, is included for convenience in SI Appendix. Universality hypotheses H1–H3 were accepted on all deterministic frames. For H1 and H2, convergence of the empirical spectral distribution to the MANOVA$(\beta ,\gamma )$ limit has been observed in all cases. For H3, the linear fit in all cases was excellent with $R^2>0.99$ without exception, confirming the power law in Eq. 12 and the polynomial decrease of ${\overline{{\mathrm{\Delta }}^2}}_{KS}$ with $n$. Universality hypothesis H4 was accepted (not rejected) for deterministic ETFs at the 0.001 significance level, with few exceptions (Table 2; full results and a summary table are in SI Appendix); it was rejected for deterministic non-ETFs. For $\gamma =0.25$, hypothesis H4 has also been accepted for the Alltop frame (SI Appendix). Universality hypothesis H5 was accepted for all deterministic frames, with excellent linear fits ($R^2>0.97$ without exception), confirming the power law in Eq. 13. Universality hypothesis H6 was accepted (not rejected) at the 0.001 significance level (and even 0.05 with few exceptions) for all deterministic frames. For the reader’s convenience, Table 4 summarizes the universal exponents for convergence of the entire spectrum (H4) and the universal exponents for convergence of the functionals under study (H6) for $(\beta ,\gamma )=(0.8,0.5)$. The framework developed in this paper readily allows tabulation of these universal exponents for any value of $(\beta ,\gamma )$. We have observed that the universal exponents are slightly sensitive to the random seed. However, exact evaluation of this variability requires very significant computational resources and is beyond our scope. Similarly, some sensitivity of the P values to random seed has been observed.

Table 4.

Summary of universal exponents for convergence: $\gamma =0.5$, $\beta =0.8$, and $({𝚿}_S={𝚿}_{Shannon})$

Frame	$b_{spectrum}$	$b_{{\mathrm{\Psi }}_{RIP}}$	$a_{{\mathrm{\Psi }}_{RIP}}$	$b_{{\mathrm{\Psi }}_{AC}}$	$a_{{\mathrm{\Psi }}_{AC}}$	$b_{{\mathrm{\Psi }}_S}$	$a_{{\mathrm{\Psi }}_S}$	$b_{{\mathrm{\Psi }}_{max}}$	$a_{{\mathrm{\Psi }}_{max}}$	$b_{{\mathrm{\Psi }}_{min}}$	$a_{{\mathrm{\Psi }}_{min}}$	$b_{{\mathrm{\Psi }}_{cond}}$	$a_{{\mathrm{\Psi }}_{cond}}$
MANOVA	0.93	1.15	2.21	1.44	3.48	1.80	0.99	1.13	2.48	1.00	3.09	1.87	−4.55
DSS	0.94	1.14	2.18	1.40	3.40	1.89	1.04	1.10	2.41	1.00	3.11	1.87	−4.56
GF	0.92	1.17	2.23	1.53	3.70	1.89	1.03	1.13	2.48	1.04	3.22	1.95	−4.76
ComplexPF	0.92	1.13	2.17	1.44	3.49	1.78	0.98	1.10	2.41	1.00	3.12	1.87	−4.56
Alltop	0.50	1.14	2.18	1.46	3.53	1.71	0.94	1.11	2.42	1.01	3.13	1.86	−4.54
SS	0.47	1.11	2.13	1.50	3.63	1.90	1.04	1.08	2.36	0.98	3.06	1.83	−4.47
HAAR	0.94	1.10	2.11	1.52	3.69	1.87	1.03	1.09	2.37	1.01	3.13	1.88	−4.59
RandDFT	0.94	1.21	2.32	1.47	3.56	1.77	0.97	1.11	2.42	1.03	3.18	1.93	−4.70
RealMANOVA	0.96	0.87	3.58	1.26	5.21	1.27	5.26	0.90	3.73	0.87	3.58	0.77	3.17
RealPF	0.91	0.92	3.82	1.32	5.46	1.24	5.12	0.94	3.88	0.94	3.88	0.81	3.36
SH	0.47	0.93	3.82	1.34	5.53	1.14	4.71	0.93	3.82	0.93	3.82	0.85	3.51
RealHAAR	0.94	0.86	3.54	1.23	5.07	1.29	5.35	0.89	3.68	0.90	3.73	0.79	3.28
RandDCT	0.94	0.99	4.08	1.30	5.38	1.24	5.10	0.94	3.89	0.95	3.93	0.82	3.40

Reproducibility Advisory.

All of the figures and tables in this paper, including those in SI Appendix, are fully reproducible from our raw results and code deposited in the data and code supplement (https://purl.stanford.edu/qg138qm8653).

Discussion

The Hypotheses.

Our universality hypotheses may be surprising in several aspects. First, the frames examined were designed to minimize frame bounds and worse case pairwise correlations. Still, it seems that they perform well when the performance criterion is based on spectrum of the typical selection of $k$ frame vectors. Second, under the universality hypotheses, all of these deterministic frames perform exactly as well as random frame designs, such as the random Fourier frame. Inasmuch as frames are continuous codes, we find deterministic codes matching the performance of random codes. Third, the hypotheses suggest an extremely broad universality property: many different ensembles of random matrices asymptotically exhibit the limiting MANOVA spectrum.

All of the deterministic frames under study satisfy the universality hypotheses (with hypothesis H4 satisfied only for ETFs). This finding should not give the impression that any deterministic frame satisfies these hypotheses! First, the empirical measures of an arbitrary sequence of frames rarely converge (thus violating hypothesis H1). Second, even if they converge, a too simplistic frame design often leads to concentration of the lower edge of the empirical spectrum near zero, resulting in a non-MANOVA spectrum and poor performance. For example, if the frame is sparse, say, consisting of some $m$ columns of the $n$-by-$n$ identity matrix, then a fraction $(n-m)/n$ of the singular values of a typical submatrix is exactly zero.

The frames under study are all ETFs or near-ETFs, all with favorable frame properties. To make this point, we have included in SI Appendix (https://purl.stanford.edu/qg138qm8653) study of a low-pass frame, in which the Fourier frequencies included in the frame are the lowest ones. This construction is in contrast with the clever choice of frequencies leading to the DSS frame. Indeed, the low-pass frame does not have appealing frame properties. It is quite obvious from the results in SI Appendix as well as the results regarding the closely related random Vandermonde ensemble (27) that such frames do not satisfy any of the universality hypotheses H2–H6.

We note that convergence rates of the form Eqs. 12 and 13 are known for other classical random matrix ensembles (28–31).

We further note that hypotheses H1–H4 do not imply hypotheses H5 and H6. Even if the empirical CDF converges in the KS metric to the limiting MANOVA$(\beta ,\gamma )$ distribution, functionals that are not continuous in the KS metric do not necessarily converge, and moreover, no uniform rate of convergence is a priori implied.

Our Contributions.

This paper presents a simple method for approximate computation (with known and good approximation error) of spectral functionals of $k$-submatrix ensemble for a variety of random and deterministic frames using Eq. 1. Our results make it possible to tabulate these approximate values, creating a useful resource for scientists. As an example, we include Table 5, a lookup table for the value of the functional ${\mathrm{\Psi }}_{AC}$ on the DSS deterministic frame family, listing by values of $n$ and $k$ the asymptotic (approximate) value calculated analytically from the limiting $f_{\beta ,\gamma }^{MANOVA}$ distribution, and the standard approximation error.

Table 5.

Root mean square error $𝚿(f_{\beta ,\gamma }^{MANOVA})\pm \sqrt{{\mathrm{\Delta }}_{𝚿}{(X_K^{(n)})}^2}$ for ${\mathrm{\Psi }}_{AC}$ and DSS frame, $m\mathbf{=}(n-1)/2$ and $k\mathbf{=}\beta \cdot m$

$n$	1,031	1,151	1,291	1,451	1,571	1,811	1,951
$\beta =0.8$	3 $\pm$ 0.0281	3 $\pm$ 0.0253	3 $\pm$ 0.0227	3 $\pm$ 0.0204	3 $\pm$ 0.0189	3 $\pm$ 0.0166	3 $\pm$ 0.0155
$\beta =0.6$	1.75 $\pm$ 0.0073	1.75 $\pm$ 0.0065	1.75 $\pm$ 0.0058	1.75 $\pm$ 0.0051	1.75 $\pm$ 0.0048	1.75 $\pm$ 0.0041	1.75 $\pm$ 0.0038

To this end, we developed a systematic empirical framework, which allows validation of Eq. 1 and discovery of the exponents there. Our work is fully reproducible, and our framework is available (along with the rest of our results and code) in the code and data supplement (https://purl.stanford.edu/qg138qm8653). In addition, our results provide overwhelming empirical evidence for a number of phenomena.

• i)The typical $k$-submatrix ensemble of deterministic frames is an object of interest. Although there is absolutely no randomness involved in the submatrix $X_K$ of a deterministic frame (other than the choice of subset $K$), the typical $k$ submatrix seems to be an ensemble in its own right, with properties so far attributed only to random matrix ensembles—including a universal, compactly supported limiting spectral distribution and convergence of the maximal (minimal) singular value to the upper (lower) edges of the limiting distribution.
• ii)MANOVA$(\beta ,\gamma )$ as a universal limiting spectral distribution. Wachter’s MANOVA$(\beta ,\gamma )$ distribution is the limiting spectral distribution of $\lambda (G_K)$ as $k/m\to \beta$ and $m/n\to \gamma$ for the typical $k$-submatrix ensemble of deterministic frames (including difference set, Grassmannian, real Paley, complex Paley, quadratic chirp, SS, and SH). The same is true for real random frames—random cosine transform and random Haar.
• iii)Convergence of the edge spectrum. For all of the deterministic frames above as well as the random frames (random cosine, random Fourier, complex Haar, and real Haar), the maximal and minimal eigenvalues of the $k$-typical submatrix ensemble converge to the support edges of the MANOVA$(\beta ,\gamma )$ limiting distribution. The convergence follows a universal power law rate.
• iv)A definite power law rate of convergence for the entire spectrum of the MANOVA$(n,m,k,\mathcal{F})$ ensemble to its MANOVA$(\beta ,\gamma )$ limit, with different exponents in the real and complex cases.
• v)Universality of the power law exponents for the entire spectrum. The complex deterministic ETFs (difference set, Grassmannian, and complex Paley) share the power law exponents with the MANOVA$(n,m,k,ℂ)$ ensemble. The same is true for the complex random frames (random Fourier and complex Haar). The complex tight nonequiangular Alltop frame, which can be constructed for various aspect ratios, also shares the power law exponents with the MANOVA$(n,m,k,ℂ)$ ensemble for $\gamma <0.5$. The real deterministic ETF (real Paley) shares the exponent with the MANOVA$(n,m,k,ℝ)$. The same is true for real random frames (random cosine and real Haar). All non-ETFs under study, with $\gamma =0.5$, share different power law exponents (slower convergence).
• vi)A definite power law rate of convergence for functionals, including ${\mathrm{\Psi }}_{StRIP}$, ${\mathrm{\Psi }}_{AC}$, and ${\mathrm{\Psi }}_{Shannon}$.
• vii)Universality of the power law exponents for functionals. For practically all frames under study, both random and deterministic, the power law exponents for functionals agree with those of the MANOVA$(n,m,k,ℝ)$ (real frames) and MANOVA$(n,m,k,ℂ)$ (complex frames).

Intercepts.

Our results showed a surprising categorization of the deterministic and random frames under study according to the constant $C$ in Eq. 12 or equivalently, according to the intercept (vertical shift) in the linear regression on $\log (n)$. Figs. 4 and 5 clearly show that the regression lines, while having identical slopes (as predicated by hypothesis H3), are grouped according to their intercepts into the following seven categories: complex MANOVA ensemble and complex Haar (Manova and HAAR); real MANOVA ensemble and real Haar (RealManova and RealHAAR); complex ETFs (DSS, GF, and ComplexPF); non-ETFs (SS, SH, and Alltop); real ETF (RealPF); complex random Fourier (RandDFT); and real random Fourier (RandDCT).

Interestingly, intercepts of all complex frames are larger (meaning that the linear coefficient $C$ in Eq. 12 is smaller) than those of all real frames. Also, the less randomness exists in the frame, the higher the intercept: intercepts of deterministic ETFs are higher than those of random Fourier and random cosine, which are in turn, higher than those of Haar frames and the MANOVA ensembles.

Related Work.

Farrell (3) has conjectured that the phenomenon of convergence of the spectrum of typical $k$ submatrices to the limiting MANOVA distribution is indeed much broader and extends beyond the partial Fourier frame that he considered. A related empirical study was conducted by Monajemi et al. (26). In it, the authors considered the so-called sparsity-undersampling phase transition in compressed sensing. This asymptotic quantity poses a performance criterion for frames that interacts with the typical $k$ submatrix $X_K$ in a manner possibly more complicated than the spectrum $\lambda (G_K)$. The authors investigated various deterministic frames, most of which are studied in this paper, and brought empirical evidence that the phase transition for each of these deterministic frames is identical to the phase transition of Gaussian frames. Gurevich and Hadani (24) proposed certain deterministic frame construction and effectively proved that the empirical spectral distribution of their typical $k$ submatrix converges to a semicircle, assuming $k=m^{1-\epsilon }$, a scaling relation different from the one considered here. The work in refs. 32 and 33 also considered deterministic frame designs, chirp sensing codes, and binary linear codes, with a random sampling. In their design, the aspect ratios are large (e.g., in ref. 32, $m\sim k^2$ and $n\sim m^2$), and therefore, the spectrum converges to the Marčenko–Pastur distribution. Tropp (34) provided bounds for ${\lambda }_{max}(G_K)$ and ${\lambda }_{min}(G_K)$ when $X$ is a general dictionary. Collins (35) has shown that the spectrum of a matrix model deriving from random projections has the same eigenvalue distribution of the MANOVA ensemble in finite $n$. Wachter (1) used a connection between the MANOVA ensemble and submatrices of Haar matrices to derive the asymptotic spectral distribution MANOVA$(\beta ,\gamma )$.

Conclusions

We have observed a surprising universality property for the $k$-submatrix ensemble corresponding to various well-known deterministic frames as well as well-known random frames. The MANOVA ensemble and the MANOVA limiting distribution emerge as key objects in the study of frames, both random and deterministic, in the context of sparse signals and erasure channels. We hope that our findings will invite rigorous mathematical study of these fascinating phenomena.

In any frame where our universality hypotheses hold (including all of the frames under study here), Fig. 2 correctly describes the limiting values of $f_{RIP}$, $f_{AC}$, and $f_{Shannon}$ and shows that codes based on deterministic frames (involving no randomness and allowing fast implementations) are better across performance measures than i.i.d. random codes.

The empirical framework that we proposed in this paper may be easily applied to new frame families $X^{(n)}$ and new functionals $\mathrm{\Psi }$, extending our results further and mapping the frontiers of the universality property. In any frame family and for any functional where our universality hypotheses hold, we have proposed a simple, effective method for calculating quantities of the form ${𝔼}_K\mathrm{\Psi }\left(\lambda \left(G_K\right)\right)$ to known approximation, which improves polynomially with $n$.