Significance
Closed-shell metal–metal bonds are experimentally and theoretically substantiated as bona fide polar-covalent/ligand-unassisted/ground-state Cu(I)–Au(I) d10–d10 bonds. Counterintuitively, replacing some of the gold content with copper leads to stronger metal–metal bonding (despite the lesser relativistic effects in Cu vs. Au) and higher phosphorescence quantum efficiency [despite much lower spin-orbit coupling constants (ξSOC) for 3d vs. 5d orbitals]. The former results are attributed to greater orbital mixing between (n+1)s/p orbitals of one metal with filled nd10 orbitals of the other metal in the heterometallic vs. homometallic system, whereas the near-unity photoluminescence quantum yields and higher extinction coefficients in mixed-metal (Au/Cu) heterometallic vs. homometallic systems are attributed to symmetry reduction. The latter results are promising for enabling societally useful technologies (e.g., Ir-/rare-earth-free LEDs).
Keywords: heterobimetallic complexes, Cu(I)–Au(I) complexes, d10–d10 metal–metal bonds, near-unity photoluminescence quantum yields, OLED/LED materials
Abstract
Outer-shell s0/p0 orbital mixing with d10 orbitals and symmetry reduction upon cupriphication of cyclic trinuclear trigonal-planar gold(I) complexes are found to sensitize ground-state Cu(I)–Au(I) covalent bonds and near-unity phosphorescence quantum yields. Heterobimetallic Au4Cu2 {[Au4(μ-C2,N3-EtIm)4Cu2(µ-3,5-(CF3)2Pz)2], (4a)}, Au2Cu {[Au2(μ-C2,N3-BzIm)2Cu(µ-3,5-(CF3)2Pz)], (1) and [Au2(μ-C2,N3-MeIm)2Cu(µ-3,5-(CF3)2Pz)], (3a)}, AuCu2 {[Au(μ-C2,N3-MeIm)Cu2(µ-3,5-(CF3)2Pz)2], (3b) and [Au(μ-C2,N3-EtIm)Cu2(µ-3,5-(CF3)2Pz)2], (4b)} and stacked Au3/Cu3 {[Au(μ-C2,N3-BzIm)]3[Cu(µ-3,5-(CF3)2Pz)]3, (2)} form upon reacting Au3 {[Au(μ-C2,N3-(N-R)Im)]3 ((N-R)Im = imidazolate; R = benzyl/methyl/ethyl = BzIm/MeIm/EtIm)} with Cu3 {[Cu(μ-3,5-(CF3)2Pz)]3 (3,5-(CF3)2Pz = 3,5-bis(trifluoromethyl)pyrazolate)}. The crystal structures of 1 and 3a reveal stair-step infinite chains whereby adjacent dimer-of-trimer units are noncovalently packed via two Au(I)⋯Cu(I) metallophilic interactions, whereas 4a exhibits a hexanuclear cluster structure wherein two monomer-of-trimer units are linked by a genuine d10–d10 polar-covalent bond with ligand-unassisted Cu(I)–Au(I) distances of 2.8750(8) Å each—the shortest such an intermolecular distance ever reported between any two d10 centers so as to deem it a “metal–metal bond” vis-à-vis “metallophilic interaction.” Density-functional calculations estimate 35–43 kcal/mol binding energy, akin to typical M–M single-bond energies. Congruently, FTIR spectra of 4a show multiple far-IR bands within 65–200 cm−1, assignable to vCu-Au as validated by both the Harvey–Gray method of crystallographic-distance-to-force-constant correlation and dispersive density functional theory computations. Notably, the heterobimetallic complexes herein exhibit photophysical properties that are favorable to those for their homometallic congeners, due to threefold-to-twofold symmetry reduction, resulting in cuprophilic sensitization in extinction coefficient and solid-state photoluminescence quantum yields approaching unity (ΦPL = 0.90–0.97 vs. 0–0.83 for Au3 and Cu3 precursors), which bodes well for potential future utilization in inorganic and/or organic LED applications.
On the eve of the 10th anniversary of Cotton’s passing we recall seminal, inspiring work by Cotton et al. (1) that had addressed
the question raised by many compounds in which short metal-metal distances might be taken to imply the existence of M-M bonds…, the answer depending on the degree of participation of outer (s,p) valence orbitals…. Although the metal-metal distances are short (Cu-Cu = 2.497(2) and Ag-Ag = 2.705(1) Å), we conclude that there is little or no direct metal-metal bonding.
Here, we show that outer 4s/p (CuI) and 6s/p (AuI) orbitals can admix with the respective valence 3d and 5d orbitals to sensitize a bona fide polar-covalent metal–metal bond between two d10 centers manifest by two rather short, 2.8750(8) Å, Cu(I)–Au(I) bonds without any ligand-bite-size assistance. The reduced symmetry in this family of complexes is also shown to impart higher extinction coefficients and phosphorescence quantum yields than those attained by the parent homometallic precursor complexes.
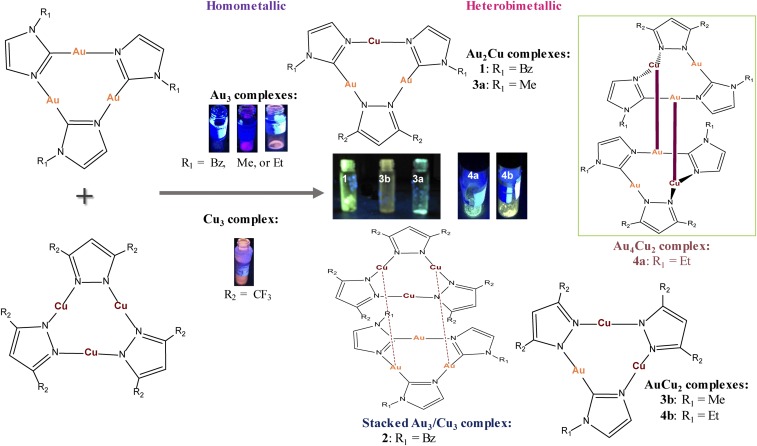
Heterometallic complexes are remarkable molecules owing to their unique catalytic and optoelectronic properties (2, 3). Heterometallic species involving coinage metals have received immense attention owing to their fascinating structural and photophysical properties, including polar–metallophilic interactions and stimulus-responsive luminescence (3–9). Notable examples include Balch’s luminescent Ir–Au–Ir chains (4), Fackler’s luminescence-thermochromic AgIAuI-pyrazolates (7), Catalano’s Au–Cu (8), and Laguna’s Au–Tl vapochromic sensors (9). Herein, we report the synthesis of unprecedented heterobimetallic Au(I)/Cu(I) complexes (Fig. 1) with a thorough discussion of their unusual structural and photophysical properties.
Fig. 1.
Synthesis and solid-state luminescence of heterobimetallic and stacked multinuclear complexes from homometallic precursors. The stacked complex does not exhibit detectable luminescence at room temperature.
Results and Discussion
Synthetic Chemistry.
Reactions of π-basic [Au(μ-C2,N3-BzIm)]3, [Au(μ-C2,N3-EtIm)]3, or [Au(μ-C2,N3-MeIm)]3 with π-acidic [Cu(μ-3,5-(CF3)2Pz)]3 in dichloromethane under ambient conditions attain new heterobimetallic complexes; see Fig. 1 and the following balanced equations:
| [1] |
| [2] |
| [3a] |
| [3b] |
| [4a] |
| [4b] |
Products 1, 3a, 3b, 4a, and 4b are heterobimetallic complexes, whereas 2 is a π-acid/π-base Au3/Cu3 stacked complex. Either [Au(μ-C2,N3-MeIm)]3 or [Au(μ-C2,N3-EtIm)]3 reacted with [Cu(μ-3,5-(CF3)2Pz)]3 in a 2:1 or 1:2 stoichiometric ratio to afford 3a, 4a, 3b, or 4b, respectively, whereas 2:1 and 1:2 reactions of [Au(μ-C2,N3-BzIm)]3 and [Cu(μ-3,5-(CF3)2Pz)]3 yielded 1 and 2, respectively; see SI Appendix for details. Formation of 2 suggests that the first step in the other reactions potentially entails a π-acid/π-base stacked intermediate preceding stable heterobimetallic products according to the concept of hard and soft acids and bases proposed by Pearson in 1973 (10). Therefore, Cu(I)—being the harder acid in the heterobimetallic products—is always coordinately bonded through nitrogen, whereas imidazolates ligate to Au(I) via their C-donor atoms. Moreover, the hypothesis of an initial π-acid/π-base interaction followed by a ligand exchange mechanism is supported by previous studies on the reactivity of Ag3/Au3 complexes (7), providing fundamentally similar evidence. Hence, the heterobimetallic Au(I)/Cu(I) complexes herein are successfully synthesized in high yields by mixing the homometallic Au3 and Cu3 precursors that, after a likely π-acid/π-base intermediate, rearrange to the heterobimetallic complexes as a consequence of the lability of Au–N and Cu–N bonds and the stability of Au–C bonds. Crystals of 1, 3a, and 4a show bright-green photoluminescence vs. yellow for 3b and 4b (Fig. 1), with no detectable luminescence for stacked complex 2 at room temperature (bright yellow at 77 K; SI Appendix, Fig. S9).
Crystal Structures.
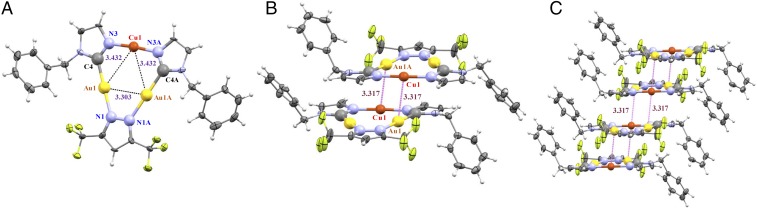
Figs. 2–4 illustrate the crystal structures for 1, 3a, and 4a and SI Appendix, Table S1 summarizes the corresponding structural parameters. The heterobimetallic complexes 1, 3a, and 4a crystallize in orthorhombic, monoclinic, and triclinic crystal systems with space groups Pbcn, C2/c, and P-1, respectively (SI Appendix, Table S1). The crystal structure of 3a is disordered in metal centers and N-methylimidazolate ligands sharing position, whereas no disorder is found for 1 or 4a.
Fig. 2.
(A) ORTEP plot for the crystal structure for one molecule of complex 1. (B) Dimer-of-trimer formation found in the stacking of 1. (C) Fragment of crystal packing of 1 along the b axis.
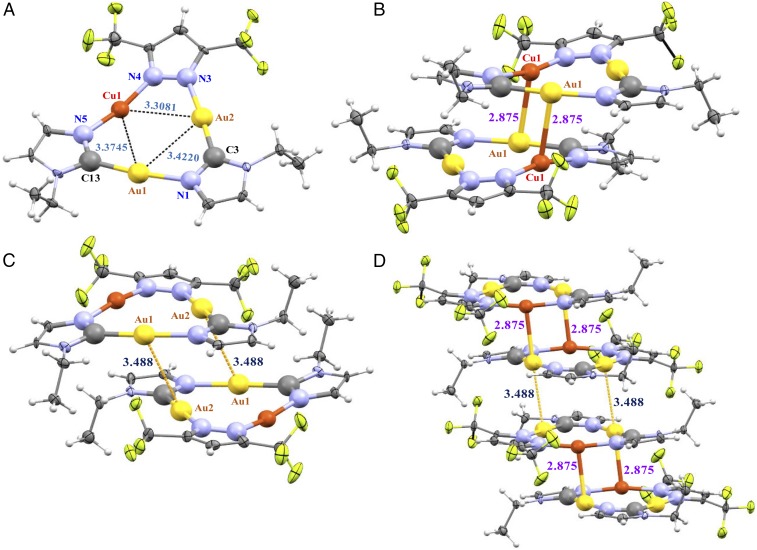
Fig. 4.
(A) ORTEP plot for the crystal structure for half the molecule, representing each monomer-of-trimer unit, of complex 4a. (B) Crystal structure for one full molecule of complex 4a. (C) A fragment of the crystal packing along the a axis. (D) Extended crystal packing of 4a molecules along the a axis.
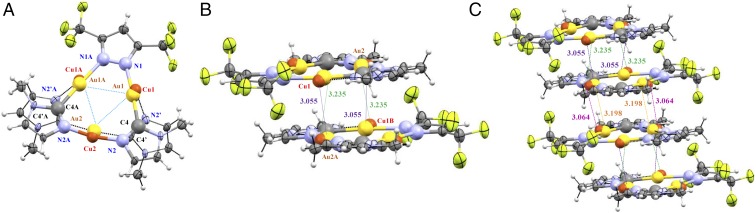
Units of 1 and 3a are crystallographically packed such that (C–Au–N, N–Cu–N) angles slightly deviate from linearity, attaining [177.6(5)°, 175.7(7)°] in 1 and [175.4(4)°, 168.1(1)°–171.1(1)°] in 3a—the range/uncertainty/untrustworthiness in the latter due to disorder. Likewise, the Au–C bond and the Au–N bond distances in 3a are slightly shorter than those found in 1, whereas the Cu–N bond lengths are extremely long compared with those obtained for 1 (SI Appendix, Table S1). Compared with those reported for the starting homometallic complexes [Au(μ-C2,N3-BzIm)]3 and [Cu(µ-3,5-(CF3)2Pz)]3 (11, 12), the bond angles around Au atoms are longer whereas those around Cu atoms are shorter in 1 and 3a. In the context of noncovalent metallophilic interactions in 1, two intermolecular Au⋯Cu contacts (3.317 Å) link cyclotrimer molecules, forming extended stacks (Fig. 2B). Next-neighbor dimer-of-trimer units form a Cu2Au4 metal framework that adopts a chair-like configuration with two equal intertrimer Cu⋯Au separations (Fig. 2C). Similarly, there are four intermolecular Au⋯Cu contacts for each molecule in 3a (Fig. 3B), two interactions above and two below each molecule. This allows extended-chain formation in a staircase motif of dimer-of-trimer units in a chair-like configuration (Fig. 3C) with intertrimer separations in 1 and 3a significantly shorter than the intratrimer Cu⋯Au distances (Figs. 2A and 3A). The packing herein for 1 or 3a —notwithstanding the latter’s disorder—is similar to that in [Au-C,N-(ethoxy)(p-tolyl)carbeniate]3 or [Au(μ-3,5-(CF3)2Pz)]3 (13).
Fig. 3.
(A) ORTEP plot for the crystal structure for one molecule of complex 3a. (B) Dimer-of-trimer formation found in the stacking of 3a. (C) Crystal packing of complex 3a along the c axis.
Covalent d10–d10 Metal–Metal Bonding.
The specific situation for 4a merits a multifaceted discussion of structural, spectral, and computational data analyses to scrutinize its possible 3d10–5d10 polar-covalent metal–metal bonds.
Crystallographic considerations.
The principal piece of evidence to validate such a bond is the presence of a ligand-unassisted short distance of 2.8750(8) Å between the two crystallographically equivalent Cu(1) atoms with their next-neighbor two crystallographically congruent Au(1) atoms in the adjacent cyclotrimers, as shown in the crystal structure of compound 4a (Fig. 4 B and D). This is the shortest intermolecular distance ever reported between any two d10 centers so as to deem it a “metal–metal bond” vis-à-vis “metallophilic interaction.” The affinity of copper to gold is manifest by a rather significant underdeviation from linearity in the N(4)-Cu(1)-N(5) angles of 167.5(2)° in the two adjacent cyclotrimers to effect attractive shortening of the two Cu(1)–Au(1) ligand-unassisted covalent bonds (Fig. 4B and SI Appendix, Table S2). This is exactly opposite to the situation in Cotton’s work on M2(form)2 systems (M = Cu(I) or Ag(I); form = N,N′-di-p-formamidinate) whereby the N(1)-Cu-N(2) or N(1)-Ag-N(2) angles of 185.5° and 191.2°, respectively, overdeviated from linearity to effect repulsive elongation of Cu⋯Cu or Ag⋯Ag ligand-assisted noncovalent bonds/interactions beyond what the bite size allows with linear bonds (1). The situation here represents a greater affinity of copper to gold than it does gold to copper, given the smaller deviation from linearity in the C(13)-Au(1)-N(1) angle of 173.4(2)° and C(3)-Au(2)-N(3) angle of 176.4(2)° than the aforementioned deviation in the bond angles around Cu atoms. The attractive deviation from linearity can be used to substantiate the involvement of the 3dπ-5dπ component of the Cu(I)–Au(I) (or d10–d10) bonding claimed herein for the Cu(1)–Au(1) ligand-unassisted polar-covalent bonds in 4a crystals—in addition to the 3dσ–5dσ component—in the same manner by which Cotton et al. (1) have justified the opposite repulsive deviation to imply the lack of involvement of ndπ orbitals in M–M bonding in favor of M–L π-bonding in M2(form)2 species. Additional theoretical insights for 3dσ–5dσ/3dπ–5dπ/3dδ-5dδ bonding are addressed based on dispersive density functional theory (DFT) computations (discussed below). To end this crystallographic argument, however, we consider the quintuple M–M bond by Power and coworkers (14) for trigonal Cr(I) d5 centers and the related less-than-quintuple M–M bonds in trigonal paddlewheels of non-d5 systems recently reviewed by Murillo (15) in terms of the role of symmetry reduction in increasing the M–M bond order (16). In a similar manner, the symmetry reduction from an idealized D∞h to C2v in the coordination sphere of especially the Cu1 atom in 4a crystals renders stronger mixing of 3dσ/π/δ orbitals with the corresponding 5dσ/π/δ orbitals of the Au1 atom in the next-neighbor molecule at the expense of mixing with the orbitals of the two pyrazolate ligands or the Au2 and Au1 atoms in the same molecule. Additionally, there is significant deviation from planarity of the Cu and Au atoms with respect to the centroid plain defined by the four N and two C atoms of the Im and Pz ligands in each monomer-of-trimer unit (Fig. 4A). To quantify the deviation from planarity experienced by the Cu1 atom, we define three independent centroids. Centroid 1 (c1) is calculated between C3 and N1; centroid c2 corresponds to the plane defined by Au1, Au2, C3, C13, N1, N3, N4, and N5; and centroid c3 is located between N4 and N5. The angle between the three centroids is 178.123(10)°, whereas the angle between c1, c2, and Cu1 is 173.012(19)°. The nearly 5° deviation from approximate linearity, together with a rather significant 0.204-Å separation between c3 and Cu1, both offer further crystallographic support for the position of Cu1 to be clearly out of the primary plane of the cluster, hence making it available to bond with the Au1 atom of the adjacent cyclotrimer. The deviation from planarity and linearity no longer keeps Cu(I) and Au(I) as linear, two-coordinate centers but, indeed, closer to three-coordinate trigonal-planar and T-shaped centers, respectively—akin to metal geometries in bona fide covalent M–M bonds [e.g., as found in Au(II)–Au(II) bonds in square planar d9 systems] (16).
The pertinent situation herein is somewhat akin to three other literature systems with varying degrees of similarity in M–M′ distances found in complex 4a. The first analogy—albeit less extensively—is with respect to the rather strong Pt(II)–Tl(III) polar-covalent bonding in Tl[(NC)5Pt-Tl(CN)n]n− complexes discovered by Glaser and coworkers (17) to attain exceptionally short distances of 2.60(1), 2.62(1), and 2.64(1) Å for n = 1–3, respectively. The electronegativity gradient and corresponding orbital mismatch between the Pt(II) and Tl(III) centers lead to a much greater shortening of the M–M′ distances than those allowed by the summed van der Waals radii in the former situation 3.68 Å for Pt(II)–Tl(III) and 3.06 Å for Cu(I)–Au(I) (18, 19). A closer example in terms of “softness”/electrostatic compatibility exists vs. the Tl(I)–Pt(0) polar covalent bonding for [Pt(PPh2py)3Tl]X complexes, which led to Tl–Pt bond distances of 2.8888(5) and 2.8653(4) Å with X = NO3− and C2H3O2−, respectively (20). At the other extreme, we can consider the system AgAu(MTP)2 (MTP, diphenylmethylenethiophosphinate) described as an Ag(I)⋯Au(I) heterobimetallic argento-aurophilic interaction (as opposed to polar-covalent bonding) type, with a distance of 2.9124(13) Å (21). This ligand-assisted Ag(I)⋯Au(I) intramolecular distance is longer than the ligand-unassisted Cu(I)–Au(I) intermolecular distance in 4a and, likewise, the attractive deviation from linearity is less extensive for the M⋯M′ centers (171.71(13)° for S1-Ag-S1A and 179.1(6)° for C1-Au-C1A in AgAu(MTP)2 vs. 167.5(2)° for N5-Cu1-N4 and 173.4(2)° for C13-Au1-N1 in 4a). The analogous ligand-unassisted intermolecular argento-aurophilic interaction in AgAu(MTP)2 is much weaker at 3.635 Å [i.e., >0.75 Å longer than the polar-covalent intertrimer bond distance of 2.8750(8) Å in 4a].
In terms of literature comparisons with relevant homometallic M⋯M metallophilic and/or M–M covalent bonding systems, we consider the two most direct precedents: cyclotrimeric Au(I)-imidazolate and Cu(I)-pyrazolate analogs of the systems herein. Although the former compound was studied for decades (22, 23), the crystal structure of [Au(μ-C2,N3-BzIm)]3 was only recently published; it exhibited a semiprismatic conformation with one long (3.558 Å) and two short (3.346 Å) intertrimer distances to manifest its strong aurophilic interactions (11). The copper precursor for 1–4 has been studied by Dias et al. (24) and revealed rather long Cu(I)⋯Cu(I) cuprophilic separations of 3.813 and 3.987 Å. Expanding to include cyclotrimers with other bridging ligands, the strongest intertrimer metallophilic interactions are manifest by two Au(I)–carbeniate complexes: the hexagonal polymorph of [Au3(MeN = COMe)3] (25) and a recent modification thereof, [Au3(MeN = COnBu)3] (26), which exhibited strongly connected extended chains with three intertrimer aurophilic interactions of ca. 3.34 Å and 3.44 Å, respectively. A significantly shorter Au⋯Au separation of ca. 3.22 Å was exhibited by triclinic [Au3(MeN = COMe)3] that nonetheless represented weaker aurophilic interaction vs. its hexagonal polymorph (27). Even with partial oxidation via organic electron acceptors, some of the aforementioned cyclotrimers exhibited shortened Au⋯Au intertrimer distances that nevertheless remained >3.15 Å (22, 23), which are still much longer than the two 2.8750(8) Å “intertrimer” CuI–AuI bonds in 4a herein. Likewise, the Cu(I) precursor for 1–4 herein exhibits colossal shortening of Cu⋯Cu intertrimer and interplanar separations by ca. 0.56 Å and 0.65 Å, respectively, upon photoexcitation; nevertheless, the resulting separations remained too long to be deemed a metal–metal bond (28). Bona fide single bonds exist upon full oxidation to Au(II) to attain ligand-assisted separations of 2.4752(9) Å (21), whereas more rare ligand-unassisted versions with ca. 2.49–2.64 Å have been described and validated theoretically by Xiong and Pyykkö (29). The two 2.8750(8)-Å intertrimer Cu(I)–Au(I) separations in 4a herein are each within the range of the longest such Au(II)–Au(II) single bonds and other conventional, well-established systems (i.e., 2.96–2.99 Å known for Mo–Mo and W–W single bonds from their nd-σ2 electronic configuration) (30).
Vibrational spectral considerations.
SI Appendix, Fig. S1 shows the IR spectrum of a neat solid powder of 4a in the far-IR region. The strong, broad main bands at ca. 470 and 270 cm−1 are assignable to vM-L (vCu-N; vAu-C; vAu-N) and δL-M-L/M-L-L (δN-Cu-N; δC-Au-N; δCu-N-C; δAu-C-N; δCu-N-N; δAu-N-C; etc.) vibrations, respectively, because this is the general spectral region for M–L bond vibrations (31–33); animation of our DFT simulations on 4a models substantiated both these assignments. We have scrutinized the bands at <200 cm−1 to evaluate whether they exhibit significant vCu-Au contribution based on the Harvey–Gray method of correlating the crystallographic M–M distance to the corresponding force constant (33), as well as based on DFT simulations (discussed below). The IR spectrum of 4a shown in SI Appendix, Fig. S1 entails multiple bands within 65–200 cm−1 that are potentially assignable to vCu-Au vibrations within the rectangular Cu1-Au1′⋯Au1-Cu1′ cluster (primes designate the adjacent trimer). The general pattern of such far-IR bands, comprising doublets each of which has a stronger and weaker component, is consistent with a group theory analysis for a D2h symmetry of such a tetranuclear metal cluster rectangle, which entails one IR-allowed (B2u) and one IR-forbidden (B1g) vCu-Au band; the “forbidden” B1g band gains intensity due to the symmetry reduction from D2h when one considers the rest of the hexanuclear dimer-of-trimer molecule besides the rectangular cluster. Using the Harvey–Gray method (33), the crystallographic Cu1-Au1′ distance of 2.8750(8) Å gives rise to a force constant of 0.8287 mdyn/Å or 82.87 N/m, which corresponds to a vCu-Au value of 171.0 cm−1—in very good agreement with the band at 173.6 cm−1 in the experimental spectrum of the neat solid of 4a in SI Appendix, Fig. S1 and the computational data shown in Fig. 5. This estimation corresponds to our modification of the Harvey–Gray method by using the Woodruff formula for 4d-4d vM-M homometallic vibrations—given the absence of such correlations for 3d-5d vM-M′ or any heterometallic vibrations—on the premise that the average or reduced mass is similar between the two types of bonds; obviously, we have used the accurate reduced mass for the Cu-Au bond (33). (Indeed, this reduced mass falls well within the range of reduced masses of the diatomic species used in the 4d-4d vM-M homometallic correlation.) We attempted to investigate the effect of clustering on the calculated position of the vCu-Au band by making a correlation between two Cu–Au reduced masses separated by the crystallographic intratrimer separation of 3.3745(7) Å. Unfortunately, the pertinent Woodruff formula is not applicable at such long separations. However, clustering further decreases the reduced mass so as to increase vCu-Au, whereas the large separation between the two Cu–Au intertrimer bonds should decrease the vCu-Au frequency. We settle to considering the problem associated with the 171.0-cm−1 Woodruff formula prediction vs. the corresponding 173.6-cm−1 closest experimental band for 4a to be between two orthogonal Cu–Au intertrimer polar-covalent bonds separated by noncovalent Cu⋯Au cupro-aurophilic intratrimer interactions. The broadness of the relevant experimental band in SI Appendix, Fig. S1 (spanning the 150- to 212-cm−1 range) coupled with the “estimation” nature of the Harvey–Gray method (31–33), the two aforementioned opposing factors for the clustering effect, and temperature effects (given the IR spectrum is gathered at ambient temperature vs. 100 K for the crystal structure), all are factors that beg for theoretical strengthening of this assignment.
Fig. 5.
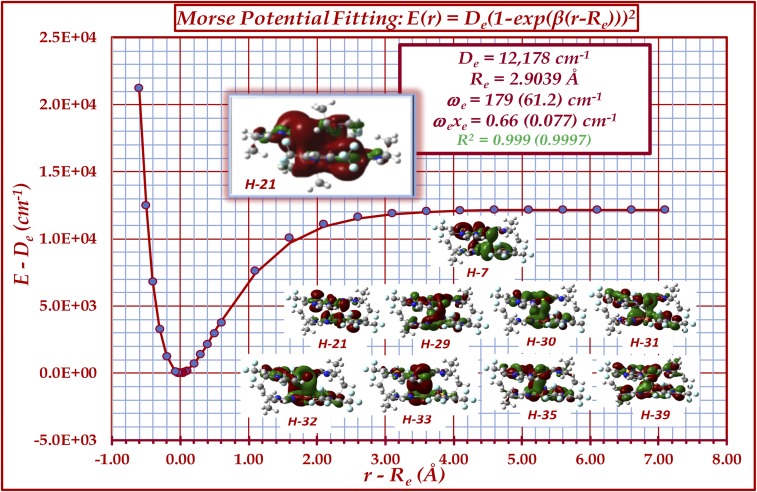
Potential energy surface plot upon varying only the vertical intertrimer separation in the optimized structure of a full {[Au2(μ-C2,N3-EtIm)2Cu(µ-3,5-(CF3)2Pz)]}2 hexanuclear dimer-of-trimer model of 4a. Bonding and spectroscopic constants are given with main vs. (parenthesized) ωe and ωexe values given based on the reduced masses of CuAu atoms vs. (entire molecule). Also shown are the Kohn–Sham contours of the nine Cu–Au strongly bonding molecular orbitals in the full 4a molecule (isodensity = 0.01 for the zoomed-out H-21 and 0.02 for all others). Orbital notation describes the relative energy (e.g., H-35 = the occupied molecular orbital that lies 35th in energy below the HOMO). See SI Appendix for a more comprehensive illustration of molecular orbitals.
Theoretical considerations.
Dispersive DFT computations using Truhlar’s M06 “desert island” functional (34, 35), which we have demonstrated its ability to describe both weak metallophilic d10–d10 interactions and chemisorption interactions in our previous collaborative work (36), is used to substantiate the polar-covalent bonding in 4a. The computed structure shown in SI Appendix, Fig. S2 is, overall, in good agreement with the experimental structural data shown in Fig. 4 and SI Appendix, Table S2. This is so not only for the coordination sphere of the Cu(I) and Au(I) centers but also for the two pertinent Cu(I)–Au(I) intertrimer bonds, which have been attained with an excellent qualitative and reasonable quantitative agreement with the crystal structure (2.9039 Å vs. 2.8750(8) Å). In addition to the bond distance, the large deviation from linearity in the N–Cu–N bond angle was also reproduced reasonably well (within 3.5°, 171.0° vs. 167.5(2)°) and likewise for the N–Au–C bonds that are engaged in the Cu–Au bond [within 0.6°, 172.8° vs. 173.4(2)°], which is significantly greater than the deviation from linearity for the other N–Au–C bonds that are not engaged in the Cu–Au bond [within 0.2°, 176.7° vs. 176.4(2)°].
The M06/CEP-31G(d) (34–38) density-functional computations, quite conservatively given the aforementioned merely qualitative agreement with the structural bonding parameters, estimate the Cu(I)–Au(I) bond energy in 4a as ca. 30–35 kcal/mol. We have derived this binding energy by two methodologies: (i) full optimization of the hexanuclear dimer-of-trimer model to attain the structure in SI Appendix, Fig. S2 and (ii) potential energy surface (PES) scan calculations. Method i gives rise to −31.5 kcal/mol, whereas method ii attains −34.8 kcal/mol or De = 12,178 cm−1 (Fig. 5). Further analysis of the PES by fitting it to a Morse function attains a stretching frequency for the vertical motion, presumed as intertrimer symmetric vCu-Au, of 179 cm−1. Indeed, the underdescription of the Cu(I)–Au(I) polar-covalent bonding in 4a surmised from the crystallographic arguments in the previous paragraph leads us to speculate that the computed De and vCu-Au values from the PES analysis in Fig. 5 is a lower limit. If we were to assign the experimental vCu-Au value as the stronger 198.6 cm−1 peak (IR-allowed B2u) instead of the weaker 173.6 cm−1 shoulder (IR-forbidden B1g) in SI Appendix, Fig. S2, then we would estimate the experimental De as ca. 15,000 cm−1 or 43 kcal/mol, given the quadratic relationship between the stretching frequency and De. The longer DFT-computed Re vs. experiment and the aforementioned limitations of DFT methods are also consistent with this assignment of higher vCu-Au and De values. Regardless of this “adjustment,” such values of 12,000–15,000 cm−1 or 34–43 kcal/mol are commensurate with the bond energies of bona fide single M–M covalent bonds such as those in Cotton’s classical d1–d1 or d9–d9 ground-state species (30), or those calculated by Xiong and Pyykkö (29) [15,000–17,000 cm−1 via GGA/TZ2P (SR-ZORA) ADF calculations], and excimeric group 12 ligand-free neutral metallic dimers [De values of ca. 8,000–10,000 cm−1 via CCSD(T)/complete basis set limit for their phosphorescent 3∑+ state] (39, 40). The aforementioned calculated vCu-Au of ∼179 cm−1 is insensitive to three approaches: (i) the one used in Fig. 5 whereby the Morse potential is assembled for the symmetric vertical intertrimer vibration using an “effective reduced mass” corresponding to only the Cu and Au atoms (akin to the insensitivity of vC = C in a diene such as cyclobutadiene or 1,5-cyclooctadiene vs. ethylene, considering the reduced mass of the two cyclotrimer molecules gives rise to ∼61 cm−1, which also accounts for the experimental peak at ∼65 cm−1 in SI Appendix, Fig. S1); (ii) another set of scan calculations whereby we varied only the out-of-plane Cu–Au distance in the proximity of the optimized geometry by displacing both Cu and Au atoms of each intermolecular bond equally, which attains a pure vCu-Au of 182 cm−1 via Dunham analysis (41), very similar to the value from approach i and, indeed, identical—within 0.1 cm−1—to the value obtained by subjecting selected Fig. 5 data near the potential minimum to the same Dunham analysis for approach i instead of fitting the entire dataset to a Morse potential (see in the SI Appendix, Table S3 for additional details); and (iii) a third set of scan calculations whereby we varied only the out-of-plane Cu–Au distance in near the optimized geometry by displacing only the Cu atom of each intermolecular bond to approach a stagnant Au atom in the next molecule, which attains an asymmetric vCu-Au of 173 cm−1 via Dunham analysis, again very similar to the frequency from both approaches i and ii.
Additional theoretical considerations must be accounted for besides the computational validation of the short Re and high vCu-Au and De values to ascertain the polar covalency of the Cu–Au bonds in the crystal structure of 4a. Although the covalency of a d10–d10 “bond” is counterintuitive, the discrepancy in electronegativity between not only the Au+ and Cu+ atomic ions but also the heavily fluorinated 3,5-(CF3)2Pz− and alkylated EtIm− ligands bonded to them, respectively, greatly alters the otherwise perfectly matched energies of nd and (n+1)s/p orbitals between two identical metal atoms. SI Appendix, Schemes S1 and S2 show that this leads to important distinctions between polar vs. nonpolar covalent M–M bonds. Two manifestations of this distinction are exhibited even by the simple Cu(I)–Au(I) ligand-free or “naked” model, namely, (i) the (n+1)s/p orbital mixing is more likely to occur as one between the 6s/p orbitals of Au(I) with the 3d orbitals of Cu(I) instead of 4s/p(Cu)/5d(Au) orbital mixing, and (ii) the δ bond, which is generally accepted to be the “weakest link” in Cotton’s M–M bonding scheme, so much so that δ orbitals are often described as nonbonding molecular orbitals (30), is greatly strengthened such that the δ* orbital is no longer the first antibonding orbital and the δ-δ* orbital splitting (0.664 eV) is almost on par with the π-π* splitting (0.761 eV), as illustrated in SI Appendix, Scheme S1. This situation is akin to that for π(n)p bonding orbitals becoming lower in energy than σ(n)p bonding orbitals in the bonding scheme of heteronuclear vs. homonuclear diatomics of main-group elements due to greater (n)p/(n)s orbital mixing in the former, as postulated in typical inorganic chemistry textbooks (42). Such influences of polar covalency are magnified in ligand-containing models of 4a, including the full {[Au4(μ-C2,N3-EtIm)4Cu2(µ-3,5-(CF3)2Pz)2]} hexanuclear dimer-of-trimer model and the [Au2(μ-C2,N3-EtIm)2Cu2(µ-3,5-(CF3)2Pz)2] tetranuclear cluster model of interconnected corner units (SI Appendix, Scheme S2). As a consequence, the antibonding dz2-dz2 σ* in Cotton’s M–M bonding scheme becomes a nonbonding orbital when one considers, as a second step, the interaction of this molecular orbital with the (n+1)s/pz atomic orbital of the second atom. As a result, the formal bond order becomes 1 instead of 0 in the resulting heterobimetallic molecule. The Kohn–Sham frontier molecular orbital contours of the two-aforementioned ligand-containing models of 4a clearly bear out this formalism. SI Appendix, Fig. S3 show that although all six Cu–Au bonding molecular orbitals demonstrate a rather unmistakable strongly bonding character based on both the strong electron density in bonding regions and their rather low relative energy below the HOMO, the other occupied molecular orbitals with strong metal contributions include a significant number of either nonbonding (i.e., HOMO-1 and HOMO-16) or only weakly antibonding (i.e., HOMO-9 and HOMO-15) orbitals of the [Au2(μ-C2,N3-EtIm)2Cu2(µ-3,5-(CF3)2Pz)2] tetranuclear cluster model. The same conclusion holds true for the full {[Au4(μ-C2,N3-EtIm)4Cu2(µ-3,5-(CF3)2Pz)2]} hexanuclear dimer-of-trimer model, indeed to a greater extent, as manifest by the strongly bonding nature of nine occupied molecular orbitals that exhibit such a clear Cu–Au bonding character (insets in Fig. 5) vs. only three exhibiting a clear Cu–Au antibonding character among frontier molecular orbitals that are occupied and exhibit strong metal contribution (see SI Appendix for a more comprehensive illustration of molecular orbitals for both the full {[Au4(μ-C2,N3-EtIm)4Cu2(µ-3,5-(CF3)2Pz)2]} hexanuclear dimer-of-trimer model—SI Appendix, Figs. S4 and S6—and the [Au2(μ-C2,N3-EtIm)2Cu2(µ-3,5-(CF3)2Pz)2] tetranuclear cluster model—SI Appendix, Figs. S3 and S5). The Cu–Au bonding formalism in the full hexanuclear dimer-of-trimer model of 4a involves initial metal–metal bonding within a monomer-of-trimer that leads to equally occupied bonding and antibonding orbitals with a formal 0 bond order, as a first step. Upon intertrimer Cu–Au bonding in the hexanuclear dimer-of-trimer as a second step, however, one needs to consider two factors: (i) the interaction of the two “corner units” considered hitherto for the [Au2(μ-C2,N3-EtIm)2Cu2(µ-3,5-(CF3)2Pz)2] tetranuclear cluster model, which generates six Cu–Au bonding orbitals (SI Appendix, Fig. S3); and (ii) crystal field theory considerations dictate stronger intratrimer interactions for dxy and dx2-y2 orbitals as well as, albeit to a lesser extent, dz2 orbitals of the two Au(I) and one Cu(I) atoms in the trigonal-planar monomer-of-trimer model to initially form three δ bonding orbitals and three δ* antibonding orbitals. The latter approach the (n+1) shell such that they become subject to more energy-favorable orbital mixing upon the intertrimer interactions in the hexanuclear dimer-of-trimer, hence reversing their bonding characters to become bonding with respect to the intertrimer Cu–Au bonds pertinent herein for 4a. Although this formalism justifies the presence of nine Cu–Au strongly bonding molecular orbitals shown in insets in Fig. 5 and SI Appendix, Figs. S4 and S6, additional rigorous theoretical scrutiny (bond order calculation schemes, breakdown of bonding forces via projections, corresponding orbitals, constrained variations, etc.) is warranted.
Photophysical Studies.
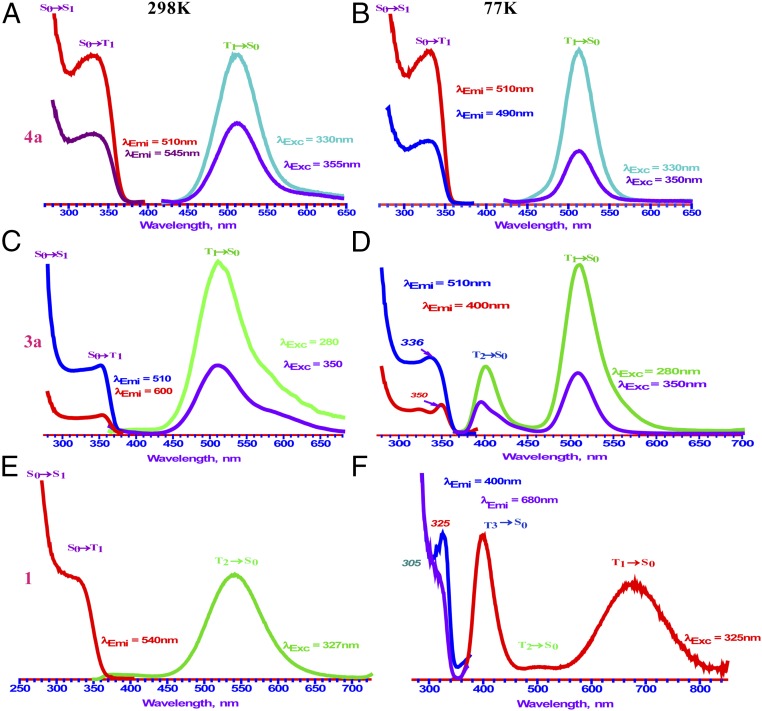
Table 1 summarizes the photophysical data for homometallic and heterobimetallic complexes studied and Figs. 6 and 7 and SI Appendix, Figs. S7–S11 compile the detailed electronic spectra. The spectral profiles are relatively simple for 4a crystalline powder (Fig. 6), showing a single emission in the green region with a peak maximum at 510 nm for the broad, unstructured band and a single excitation feature at 330 nm that is independent of temperature or excitation wavelength. These are assignable to T1→S0 phosphorescence emission and S0→T1 spin-forbidden excitation, respectively, whereas the rise in the blue edge of the excitation spectrum is the S0→S1 spin-allowed absorption given the microsecond lifetimes (6–7 μs) and the higher-energy solution absorption at λmax ≤ 300 nm (Table 1 and SI Appendix, Fig. S7). This assignment gives rise to a genuine Stokes’ shift of 10,700 cm−1, suggesting a large excited-state distortion of a dodecanuclear tetramer-of-trimer unit whereby the aurophilic interactions undergo excimeric contraction of Au(I)⋯Au(I) distances from 3.488 Å to significantly shorter distances. If the excited-state distortion were due to the contraction of the polar-covalent Cu(I)–Au(I) bond instead, a much smaller Stokes’ shift than the >1.3 eV value would be expected, because it is hard to envision such a bond shortening way beyond 2.8750(8) Å, as supported by Coppens and coworkers’ studies (28).
Table 1.
Summary of photophysical parameters for homometallic and heterobimetallic complexes in this study
| Complex | ε, M−1⋅cm−1 | ΦPL, % | τ, μs |
| [Au (μ-C2, N3-MeIm)]3 | 4,800 | 56.88 ± 3.58 | 11.5 (298 K) 34.6 and 15.4 (77 K) |
| Au (μ-C2, N3-BzIm)]3 | 7,880 | N/A | N/A |
| [Cu(μ-3,5-(CF3)2Pz)]3 | 2,600 | 82.17 ± 0.16 | N/A |
| [Au2(μ-C2,N3-BzIm)2Cu(µ-3,5-(CF3)2Pz)] (1) | 11,560 | 85.16 ± 1.57 | 12.2 (298 K) 47.0 and 38.3 (77 K) |
| [Au2(μ-C2,N3-MeIm)2Cu(µ-3,5-(CF3)2Pz)] (3a) | 20,590 | 97.13 ± 0.80 | 12.3 (298 K) 10.8 and 11.2 (77 K) |
| [Au(μ-C2,N3-MeIm)Cu2(µ-3,5-(CF3)2Pz)2] (3b) | 2,850 | 17.51 ± 0.25 | 26.2 and 4.88 (298 K) and 179.7 and 95.7 (77 K) |
| {Au(μ-C2,N3-BzIm)}3{Cu(µ-3,5-(CF3)2Pz)}3 (2) | N/A | N/A | 61.5 and 22.5 (77 K) |
| [Au4(μ-C2,N3-EtIm)4Cu2(µ-3,5-(CF3)2Pz)2] (4a) | 17,260 | 90.31 ± 0.70 | 6.92 (298 K) and 6.57 (77 K) |
| [Au(μ-C2,N3-EtIm)]3 | 3,950 | N/A | 11.8 (298 K) and 59.8 (77 K) |
ε , extinction coefficient at 268 nm for dilute (ca. 0.1 μM) solutions; ΦPL, photoluminescence quantum yield in the solid-state powder form; and τ, photoluminescence lifetime at the characteristic λmax. Some entries are designated with “N/A” for “not applicable” because the emission is too weak to measure its lifetime or quantum yield, or the extinction coefficient could not be measured in solution due to lack of solubility.
Fig. 6.
Steady-state photoluminescence spectra for a crystalline powder sample of 4a (A and B), 3a (C and D), and 1 (E and F) at 298 K (Left) and 77 K (Right).
Fig. 7.
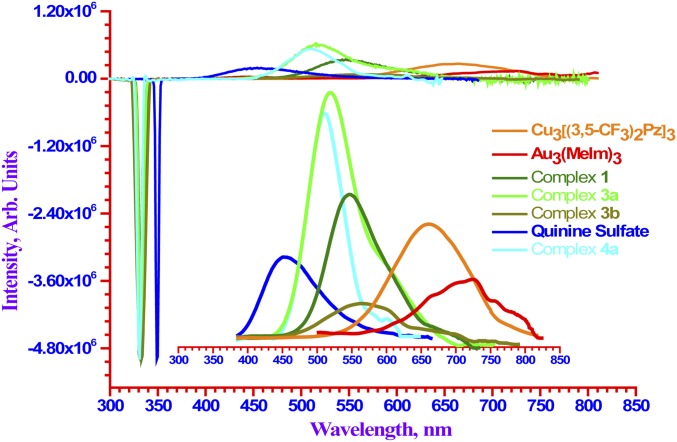
Emission (peaks) and excitation (valleys) spectra used in absolute photoluminescence quantum yield (Φ) calculations, shown normalized at the excitation wavelength for each sample to facilitate visual comparisons of Φ based on relative emission intensities (zoomed in the inset).
The photoluminescence spectra of complexes 3a and 1 show multiple temperature/excitation-dependent emission bands (Fig. 6). Also, the large intensity difference in excitation spectra in 3a (λex ∼ 350 nm and λex < 300 nm; e.g., λex = 280 nm) and 1 (λex ∼ 325 nm and λex < 300 nm; e.g., λex = 280 nm) indicates the involvement of spin-forbidden (S0→T1) and spin-allowed (S0→S1) transitions. The 298-K lower-energy emission of 3a (λmax = 510 nm, T1→S0) undergoes thermal broadening at 77 K and an additional higher-energy band (λmax = 400 nm, T2→S0) appears. This T2 band disappears at room temperature via internal conversion process to the T1 state, given the lifetime data in microseconds regime for both bands, which are metal-centered excimeric in nature without a clear vibronic structure (43). Similarly, the emission spectra of complex 1 at 298 K (λmax = 540 nm, T2→S0) becomes dual emission bands at 77 K (λmax = 680 nm, T1→S0; 400 nm, T3→S0) through either modest compression of Au(I)⋯Cu(I) intertrimer distances across the entire stack of chains leading to a higher-energy T3 band or by a strong compression of Au(I)⋯Cu(I) intertrimer distances, leading to a lower-energy T1 band as described in our previous work (25). The benzyl groups in complex 1 provide a steric effect that could cause an increase in Cu⋯Au intermolecular distances, which explains the slight increase in the Stokes’ shift for the 540-nm green-emission band at 298 K for this complex compared with the corresponding green emission that appears at 510 nm in the methyl imidazolate analog complex 3a.
The luminescence data for complexes 3b and 2 are shown in Table 1 and SI Appendix, Figs. S8 and S9. The solids of both 3b and 2 have a low-energy excitation with λmax = 330 nm and 325 nm, respectively. The emission profile for 3b at 298 K shows a band with λmax = 575 nm, which red-shifts to 600 nm at 77 K. Complex 2 shows an emission band with λmax = 575 nm at 77 K. Both 3b and 2 exhibit long lifetimes (in microseconds) with significantly large Stokes’ shifts, suggesting excimeric excited states with contracted intertrimer M⋯M distances vs. the corresponding ground state.
Fig. 7 shows absolute ΦPL spectral data acquired for solid samples and the standard reference material quinine sulfate (1 N sulfuric acid/ethanol solution, ΦPL of 55%) (44–47). The heterobimetallic complexes 1 (∼85%), 3a (∼97%), and 4a (∼90%) exhibit extremely high quantum yields (Table 1), which is supported by the temperature-independent emission intensity (SI Appendix, Fig. S11) and lifetimes of 4a and 3a. We believe that these higher quantum yields are bestowed by the lowered symmetry from D3h (homometallic) to C2v (heterobimetallic) upon Cu–Au interaction/bond formation, leading to enhanced extinction coefficients in solution (SI Appendix, Fig. S7) and sensitized ΦPL in the solid state at the molecular and supramolecular levels, respectively.
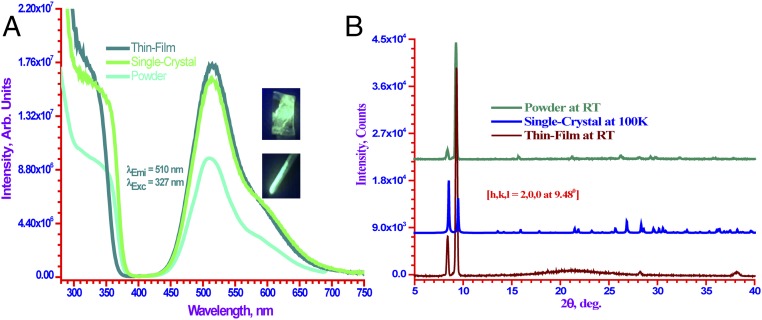
Finally, we have subjected three representative high-quantum-yield complexes analyzed in this work to a screening study aimed to assess their possible use in optoelectronic devices such as organic LEDs (OLEDs). The heterobimetallic (3a and 4a) and homometallic ([Cu(μ-3,5-(CF3)2Pz)]3) complexes have demonstrated their processability into OLED functional thin-film forms by thermal evaporation (vacuum sublimation) and/or solution drop-casting with photoluminescence spectra nearly identical to those for single crystal and/or microcrystalline powder forms of the same material, as illustrated in Fig. 8A for 3a (the highest-PLQY material) and in SI Appendix, Figs. S11 and S12 for [Cu(μ-3,5-(CF3)2Pz)]3 and 4a, respectively. Thin-film and powder X-ray diffraction (XRD) analysis confirms that the polymorphic form in the single crystals is sustained, given the overall similarity in the XRD patterns for all three solid forms of each of these three high-PLQY materials, as shown in Fig. 8B and SI Appendix, Figs. S13 and S14. As illustrated in Fig. 8B for 3a, the diffraction pattern from a single crystal (middle pattern) shows a theoretical dataset assuming randomly oriented crystallites/particles, and hence all possible peaks are present—representing different hkl faces. In the powder (Fig. 8B, top pattern) or thin-film (Fig. 8B, bottom pattern) diffraction patterns, some peaks are enhanced or diminished due to preferred orientation. The crystallites are usually more oriented in their preferred direction when a thin film is deposited, as represented by the most enhanced peak at around 9.48° for 3a with an hkl face of (2,0,0), whereby the broad peak (hump) at around 21° is from the amorphous glass substrate. These findings are encouraging for pursuing the use of the high-quantum-yield solid materials in this work for high-efficiency phosphorescent Ir-free OLED device architectures as well as down-conversion phosphors for inorganic LEDs to replace rare earth-based phosphor materials.
Fig. 8.
(A) Demonstration of processability into OLED functional thin-film form and the indifference of the photoluminescence spectra thereof vs. powder and single-crystal forms for 3a. (B) XRD pattern of a powder sample on glass substrate (Top), simulated single-crystal powder XRD pattern (Middle), and XRD pattern of a drop-casted thin film (Bottom) for 3a.
Conclusions and Prospects
In conclusion, a synthetic method for the preparation of stable heterobimetallic Au4Cu2, Au2Cu, Cu2Au, and stacked Au3/Cu3 complexes is hereby documented and discussed. Crystallographic, far-IR, and dispersive DFT data have been profusely discussed and reinforce the formation of a bona fide polar-covalent bond between Cu(I) and Au(I) atoms of the {[Au4(μ-C2,N3-EtIm)4Cu2(µ-3,5-(CF3)2Pz)2]} hexanuclear dimer-of-trimer 4a, whereas the analogous [Au2(μ-C2,N3-BzIm)2Cu(µ-3,5-(CF3)2Pz)] (1) and [Au2(μ-C2,N3-MeIm)2Cu(µ-3,5-(CF3)2Pz)] (3a) species are found to exhibit cupro-aurophilic as opposed to aurophilic or cuprophilic noncovalent metal⋯metal interactions. The reaction mechanism occurring is not completely understood but it likely proceeds via π-acid/π-base interactions—a well-known chemistry for this type of complexes. The reduced symmetry in the Au2Cu compounds has been demonstrated to attain greater extinction coefficient in solution and higher solid-state photoluminescence quantum yield than those for the homometallic complexes, indeed approaching unity for 3a and 4a, which opens promising applications of such materials in OLEDs as light-emitting layers and/or inorganic LEDs as down-conversion phosphors.
Materials and Methods
The photoluminescence measurements were carried out with a PTI Quanta Master Model QM-4 scanning spectrofluorometer. OLED thin films were prepared via both vacuum sublimation by using a 12-source Trovato Model 300C vacuum deposition system and drop-casting. Geometry optimization and single-point calculations were performed using the Gaussian 09 suite of programs. Single crystal structural data analysis and refinement was done by using Bruker APEX2, SAINT, SADABS, and SHELXTL (Bruker AXS Inc.) as well as the CrysAlisPro (version 1.171.39.7f) software system and AutoChem 2.1 software system in conjunction with Olex2 1.2 (Rigaku Corp.) (48–50). The experimental details and computational methods are provided in SI Appendix.
Representative Synthetic Procedure of the Heterobimetallic Au4Cu2 Complex, 4a.
One mole of [Au(μ-C2,N3-EtIm)]3 and 0.5 mol of [Cu(µ-3,5-(CF3)2Pz)]3 were dissolved in dichloromethane, separately. The latter solution was transferred into the solution containing the gold metallocycle and a white precipitate formed. The resulting suspension was stirred for 2 h then filtered and washed with hexane twice. Yellowish-white single crystals were obtained by slow evaporation of a warm dichloromethane solution.
Supporting Information.
The details of the synthesis, characterization, crystal refinement, and computational methodology, and other electronic spectral, crystallographic, and computational results are available in SI Appendix. Additional crystallographic results are included in Datasets S1–S3.
Supplementary Material
Acknowledgments
M.A.O. thanks Harry B. Gray, Pierre D. Harvey, Donald G. Truhlar, Pekka Pyykkö, Paul S. Bagus, John P. Fackler, Jr., and Thomas R. Cundari for helpful discussions. M.A.O. gratefully acknowledges support to his group’s contributions by Robert A. Welch Foundation Grant B-1542 and NSF Grant CHE-1413641 and its corresponding international supplement CHE-1545934 for the collaboration with R.G. and A.-M.M.R. and Grant CHE-1531468 for support of the UNT-Chemistry high performance computing facility. This work was also supported by a Fondi di Ateneo per la Ricerca grant from University of Camerino and the Consortium Inter-universities for the Research on Chemistry of Metals with Biological Systems (R.G. and A.B.) and the Scientific Research Support Fund of the Ministry of Higher Education and Scientific Research in Jordan (A.-M.M.R. and M.A.O.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1700890114/-/DCSupplemental.
References
- 1.Cotton FA, Feng X, Matusz M, Poli R. Experimental and theoretical studies of the copper(I) and silver(I) dinuclear N,N′-di-p-tolylformamidinato complexes. J Am Chem Soc. 1988;110:7077–7083. [Google Scholar]
- 2.Cooper BG, Napoline JW, Thomas CM. Catalytic applications of early/late heterobimetallic complexes. Catal Rev Sci Eng. 2012;54:1–40. [Google Scholar]
- 3.Fernández EJ, Laguna A, López-de-Luzuriaga JM. Gold-heterometal complexes. Evolution of a new class of luminescent materials. Dalton Trans. 2007;20:1969–1981. doi: 10.1039/b702838p. [DOI] [PubMed] [Google Scholar]
- 4.Balch AL, Nagle JK, Oram DE, Reedy PE., Jr Oxidative additions and luminescence involving iridium-gold-iridium chains formed by binding of gold(I) to the metallamacrocycle Ir2Cl2(CO)2[μ-Ph2PCH2As(Ph)CH2PPh2]2. J Am Chem Soc. 1988;110:454–462. [Google Scholar]
- 5.Fernández EJ, et al. [Au2Tl2(C6Cl5)4]·(CH3)2CO: A luminescent loosely bound butterfly cluster with a Tl(I)—Tl(I) interaction. J Am Chem Soc. 2002;124:5942–5943. doi: 10.1021/ja017240e. [DOI] [PubMed] [Google Scholar]
- 6.Fernández EJ, et al. A family of Au—Tl loosely bound butterfly clusters. Inorg Chem. 2005;44:6012–6018. doi: 10.1021/ic050060b. [DOI] [PubMed] [Google Scholar]
- 7.Mohamed AA, Galassi R, Papa F, Burini A, Fackler JP., Jr Gold (I) and silver (I) mixed-metal trinuclear complexes: Dimeric products from the reaction of gold(I) carbeniates or benzylimidazolates with silver(I) 3,5,-diphenylpyrazolate. Inorg Chem. 2006;45:7770–7776. doi: 10.1021/ic060792j. [DOI] [PubMed] [Google Scholar]
- 8.Strasser CE, Catalano VJ. “On-off” Au(I)·Cu(I) interactions in a Au(NHC)2 luminescent vapochromatic sensor. J Am Chem Soc. 2010;132:10009–10011. doi: 10.1021/ja104585q. [DOI] [PubMed] [Google Scholar]
- 9.Fernández EJ, et al. {Tl[Au(C6Cl5)2]}n: A vapochromic complex. J Am Chem Soc. 2003;125:2022–2023. doi: 10.1021/ja028734u. [DOI] [PubMed] [Google Scholar]
- 10.Pearson RG, editor. Hard and Soft Acids and Bases. Dowden, Hutchinson & Ross; Stroudsburg, PA: 1973. [Google Scholar]
- 11.Elbjeirami O, Rashdan MD, Nesterov V, Rawashdeh-Omary MA. Structure and luminescence properties of a well-known macrometallocyclic trinuclear Au(I) complex and its adduct with a perfluorinated fluorophore showing cooperative anisotropic supramolecular interactions. Dalton Trans. 2010;39:9465–9468. doi: 10.1039/c0dt00736f. [DOI] [PubMed] [Google Scholar]
- 12.Dias HVR, Polach SA, Wang Z. Coinage metal complexes of 3,5-bis(trifluoromethyl)pyrazolate ligand: Synthesis and characterization of {[3,5-(CF3)2Pz]Cu}3 and {[3,5-(CF3)2Pz]Ag}3. J Fluor Chem. 2000;103:163–169. [Google Scholar]
- 13.Bonati F, Burini A, Pietroni BR, Bovio B. Reactions of C-imidazolyllithium derivatives with group Ib compounds: Tris[μ-(1-alkylimidazolato-N3,C2)]tri-gold(I) and -silver(I). Crystal structure of bis(1-benzylimidazolin-2-yliden)gold(I) chloride. J Organomet Chem. 1989;375:147–160. [Google Scholar]
- 14.Nguyen T, et al. Synthesis of a stable compound with fivefold bonding between two chromium(I) centers. Science. 2005;310:844–847. doi: 10.1126/science.1116789. [DOI] [PubMed] [Google Scholar]
- 15.Murillo CA. The δ bond and trigonal paddlewheels before the dawn of the quintuple bond. Comments Inorg Chem. 2015;32:39–58. [Google Scholar]
- 16.Irwin MD, Abdou E, Mohamed AA, Fackler JP., Jr Synthesis and x-ray structures of silver and gold guanidinate-like complexes. A Au(II) complex with a 2.47 Å Au—Au distance. Chem Commun (Camb) 2003;23:2882–2883. doi: 10.1039/b309724m. [DOI] [PubMed] [Google Scholar]
- 17.Jaliehvand F, et al. New class of oligonuclear platinum-thallium compounds with a dirst metal-metal bond. 5. Structure determination of heterodimetallic cyano complexes in aqueous solution by EXAFS and vibrational spectroscopy. Inorg Chem. 2001;40:3889–3899. doi: 10.1021/ic010055h. [DOI] [PubMed] [Google Scholar]
- 18.Bondi A. Van der Waals volumes and radii. J Phys Chem. 1964;68:441–451. [Google Scholar]
- 19.Hu S-Z, Zhou Z-H, Robertson BE. Consistent approaches to van der Waals radii for the metallic elements. Z Kristallogr. 2009;224:375–383. [Google Scholar]
- 20.Catalano VJ, Bennett BL, Muratidis S, Noll BC. Unsupported Pt(0)-Tl(I) bonds in the simple [Pt(PPh2Py)3Tl]+ complexes. J Am Chem Soc. 2001;123:173–174. doi: 10.1021/ja0055054. [DOI] [PubMed] [Google Scholar]
- 21.Rawashdeh-Omary MA, Omary MA, Fackler JP., Jr Argento–aurophilic bonding in organosulfur complexes. The molecular and electronic structures of the heterobimetallic complex AgAu(MTP)2. Inorg Chim Acta. 2002;334:376–384. [Google Scholar]
- 22.Burini A, Mohamed AA, Fackler JP., Jr Cyclic trinuclear gold(I) compounds: Synthesis, structures and supramolecular acid-base π-stacks. Comments Inorg Chem. 2003;24:253–280. [Google Scholar]
- 23.Omary MA, Mohamed AA, Rawashdeh-Omary MA, Fackler JP., Jr Photophysics of supramolecular binary stacks consisting of electron-rich trinuclear Au(I) complexes and organic electrophiles. Coord Chem Rev. 2005;249:1372–1381. [Google Scholar]
- 24.Dias HVR, et al. Brightly phosphorescent trinuclear copper(I) complexes of pyrazolates: Substituent effects on the supramolecular structure and photophysics. J Am Chem Soc. 2005;127:7489–7501. doi: 10.1021/ja0427146. [DOI] [PubMed] [Google Scholar]
- 25.Vickery JC, Olmstead M, Fung EY, Balch AL. Solvent-stimulated luminescence from the supramolecular aggregation of a trinuclear gold(I) complex that displays extensive intermolecular Au⋯Au interactions. Angew Chem Int Ed Engl. 1997;36:1179–1181. [Google Scholar]
- 26.McDougald RN, Jr, et al. Molecular and electronic structure of cyclic trinuclear gold(I) carbeniate complexes: Insight for structure/luminescence/conductivity relationships. Inorg Chem. 2014;53:7485–7499. doi: 10.1021/ic500808q. [DOI] [PubMed] [Google Scholar]
- 27.White-Morris R, Olmstead M, Attar S, Balch AL. Intermolecular interactions in polymorphs of trinuclear gold(I) complexes: Insight into the solvoluminescence of AuI3(MeN=COMe)3. Inorg Chem. 2005;44:5021–5029. doi: 10.1021/ic050381n. [DOI] [PubMed] [Google Scholar]
- 28.Vorontsov II, et al. Shedding light on the structure of a photo-induced transient excimer by time-resolved diffraction. Phys Rev Lett. 2005;94:193003. doi: 10.1103/PhysRevLett.94.193003. [DOI] [PubMed] [Google Scholar]
- 29.Xiong X-G, Pyykkö P. Unbridged Au(II)—Au(II) bonds are theoretically allowed. Chem Commun (Camb) 2013;49:2103–2105. doi: 10.1039/c2cc37875b. [DOI] [PubMed] [Google Scholar]
- 30.Cotton FA, Walton RA. Multiple Bonds Between Metal Atoms. Wiley; New York: 1982. [Google Scholar]
- 31.Omary MA, Webb TR, Assefa Z, Shankle GE, Patterson HH. Crystal structure, electronic structure, and temperature-dependent Raman spectra of Tl[Ag(CN)2]: Evidence for ligand-unsupported argentophilic interactions. Inorg Chem. 1998;37:1380–1386. doi: 10.1021/ic970694l. [DOI] [PubMed] [Google Scholar]
- 32.Chadwick BM, Frankiss SG. Vibrational spectra and structures of some dicyanoaurate(I) complexes. J Mol Struct. 1976;31:1–9. [Google Scholar]
- 33.Harvey PD, Gray HB. Low-lying singlet and triplet electronic excited states of binuclear (d10-d10) palladium(0) and platinum(0) complexes. J Am Chem Soc. 1988;110:2145–2147. [Google Scholar]
- 34.Zhao Y, Truhlar DG. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor Chem Acc. 2008;120:215–241. [Google Scholar]
- 35.Zhao Y, Truhlar DG. Density functionals with broad applicability in chemistry. Acc Chem Res. 2008;41:157–167. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
- 36.Galassi R, et al. Solventless supramolecular chemistry via vapor diffusion of volatile small molecules upon a new trinuclear silver(I)-nitrated pyrazolate macrometallocyclic solid: An experimental/theoretical investigation of the dipole/quadrupole chemisorption phenomena. Inorg Chem. 2013;52:14124–14137. doi: 10.1021/ic401948p. [DOI] [PubMed] [Google Scholar]
- 37.Cundari TR, Stevens WJ. Effective core potential methods for the lanthanides. J Chem Phys. 1993;98:55555–55565. [Google Scholar]
- 38.McDonald RS, Patterson P, Rodwell J, Whalley A. Intramolecular nucleophilic participation by the thiol group during amide hydrolysis. Part 2. The imidazole catalysis dilemma. Can J Chem. 1992;70:62–67. [Google Scholar]
- 39.Determan JJ, Omary MA, Wilson AK. Modeling the photophysics of Zn and Cd monomers, metallophilic dimers, and covalent excimers. J Phys Chem A. 2011;115:374–382. doi: 10.1021/jp108384s. [DOI] [PubMed] [Google Scholar]
- 40.Omary MA, Sinha P, Bagus PS, Wilson AK. Electronic structure of mercury oligomers and exciplexes: Models for long-range/multi-center bonding in phosphorescent transition metal compounds. J Phys Chem A. 2005;109:690–702. doi: 10.1021/jp045143c. [DOI] [PubMed] [Google Scholar]
- 41.Dunham JL. The energy levels of a rotating vibrator. Phys Rev. 1932;41:721–731. [Google Scholar]
- 42.Miessler GL, Fischer PJ, Tarr DA. Inorganic Chemistry. Prentice Hall; Upper Saddle River, NJ: 2014. [Google Scholar]
- 43.Omary MA, et al. Metal effect on the supramolecular structure, photophysics, and acid-base character of trinuclear pyrazolato coinage metal complexes. Inorg Chem. 2005;44:8200–8210. doi: 10.1021/ic0508730. [DOI] [PubMed] [Google Scholar]
- 44.Kawamura Y, Sasabe H, Adachi C. Simple accurate system for measuring absolute photoluminescence quantum efficiency in organic solid-state thin films. Jpn J Appl Phys. 2004;43:7729–7730. [Google Scholar]
- 45.Turro NJ. Modern Molecular Photochemistry. Benjamin/Cummings; Menlo Park, CA: 1978. [Google Scholar]
- 46.Wang Q, et al. Doping-free organic light-emitting diodes with very high power efficiency, simple device structure, and superior spectral performance. Adv Funct Mater. 2014;24:4746–4752. [Google Scholar]
- 47.Wang Q, et al. Exciton and polaron quenching in doping-free phosphorescent organic light-emitting diodes from a Pt(II)-based fast phosphor. Adv Funct Mater. 2013;23:5420–5428. [Google Scholar]
- 48.Sheldrick GM. Crystal structure refinement with SHELXL. Acta Crystallogr C Struct Chem. 2015;71:3–8. doi: 10.1107/S2053229614024218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sheldrick GM. A short history of SHELX. Acta Crystallogr A. 2008;64:112–122. doi: 10.1107/S0108767307043930. [DOI] [PubMed] [Google Scholar]
- 50.Spek AL. Structure validation in chemical crystallography. Acta Crystallogr Sect D Biol Crystallogr. 2009;65:148–155. doi: 10.1107/S090744490804362X. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.