All-angle negative refraction of highly squeezed plasmon and phonon polaritons in graphene–boron nitride heterostructures

Significance

Realizing negative refraction of highly squeezed polaritons is an important step toward the active manipulation of light at the extreme nanoscale. To realize negative refraction, an effective means to tailor the coupling of different polaritons is absolutely necessary yet undeveloped. Here, we predict a viable way to flip the sign of group velocities of hybrid plasmon–phonon–polaritons in graphene–boron nitride (BN) heterostructures. The polaritonic strong coupling enables the all-angle negative refraction phenomena between highly squeezed graphene’s plasmons, BN’s phonon polaritons, and their hybrid polaritons. Due to the combined advantages of tunability, low loss, and ultrahigh confinement provided by these polaritons, graphene–BN heterostructures thus provide fundamental tools to explore the manipulation of light at the extreme nanoscale.

Abstract

A fundamental building block for nanophotonics is the ability to achieve negative refraction of polaritons, because this could enable the demonstration of many unique nanoscale applications such as deep-subwavelength imaging, superlens, and novel guiding. However, to achieve negative refraction of highly squeezed polaritons, such as plasmon polaritons in graphene and phonon polaritons in boron nitride (BN) with their wavelengths squeezed by a factor over 100, requires the ability to flip the sign of their group velocity at will, which is challenging. Here we reveal that the strong coupling between plasmon and phonon polaritons in graphene–BN heterostructures can be used to flip the sign of the group velocity of the resulting hybrid (plasmon–phonon–polariton) modes. We predict all-angle negative refraction between plasmon and phonon polaritons and, even more surprisingly, between hybrid graphene plasmons and between hybrid phonon polaritons. Graphene–BN heterostructures thus provide a versatile platform for the design of nanometasurfaces and nanoimaging elements.

Polaritons with high spatial confinement, such as plasmon polaritons in graphene (1–5) and phonon polaritons in a thin hexagonal boron nitride (BN) slab (6–15), enable control over the propagation of light at the extreme nanoscale, due to their in-plane polaritonic wavelength that can be squeezed by a factor over 100. Henceforth we use the term squeezing factor (or confinement factor) to define the ratio between the wavelength in free space and the in-plane polaritonic wavelength. The combination of tunability, low losses, and ultraconfinement (1, 2, 8, 10, 11, 15) makes them superior alternatives to conventional metal plasmons and highly appealing for nanophotonic applications (3–5, 10–13, 15). Their extreme spatial confinement, however, also limits our ability to tailor their dispersion relations.

Unlike the case of 2D plasmons, the coupling between metal plasmons in a metal–dielectric–metal structure dramatically changes their dispersion relation and can even flip the sign of their group velocities (16, 17). This has led to exciting applications by tailoring the in-plane plasmonic refraction, giving flexibility in controlling the energy flow of light. Specifically, by flipping the sign of the group velocity of metal plasmons, plasmonic negative refraction has been predicted (16) and demonstrated (17). The negative refraction has also been extensively explored in metamaterials, metasurfaces, and photonic crystals (18–26), but they become experimentally very challenging to realize when dealing with polaritons with high squeezing factors. In contrast to metal plasmons, the group velocity of graphene plasmons (2, 11, 27) and all other 2D plasmons (28–32) is always positive, including that in graphene-based multilayer structures (33). This has made the in-plane negative refraction for highly squeezed 2D plasmon polaritons seem impossible to achieve.

Contrary to 2D plasmons, the group velocity of phonon polaritons in a BN slab is negative (positive) in BN’s first (second) reststrahlen band (8, 10, 11), as was recently observed experimentally (9, 12). However, like 2D plasmons, the control of the group velocities of these phonon polaritons remains difficult due to their high spatial confinement (6, 7, 9, 12, 13). Moreover, although recent works have demonstrated that the dispersion relations of graphene plasmons and BN’s phonon polaritons in a graphene–BN heterostructure can be modified through plasmon–phonon–polariton hybridization (6, 10, 11, 14), the ability to flip the sign of the group velocity of these strongly squeezed hybrid polaritons has not been observed or predicted so far.

In this work, we predict that using the strong coupling between graphene plasmon and BN’s phonon polaritons in graphene–BN heterostructures provides an unprecedented control over their dispersion relations and can even flip the signs of their group velocities within BN’s first reststrahlen band. Using realistic material losses in graphene–BN heterostructures, we demonstrate theoretically all-angle in-plane polaritonic negative refraction between graphene plasmon and BN’s phonon polariton. And even more surprisingly, we predict negative refraction between two kinds of graphene plasmons and between two kinds of BN’s phonon polaritons, where the squeezing factors of these polaritons are all larger than 100. Unlike conventional all-angle negative refraction of metal plasmons that are restricted to work at a given fixed frequency (16), the working frequency of the all-angle polaritonic negative refraction demonstrated here can be flexibly tunable within BN’s first reststrahlen band, due to the tunability of the chemical potential in graphene.

Results

To highlight the underlying physics, we begin by studying the in-plane negative refraction between the graphene plasmon and BN’s phonon polariton within BN’s first reststrahlen band (i.e., 22.3–24.6 THz), as shown in Fig. 1. In the heterostructure (Fig. 1A), the left air–graphene–substrate region supports plasmon polaritons, and the right air–BN–substrate region supports phonon polaritons. These polaritons propagate in the x–y plane, and there is an interface along the y direction. In this work, the random phase approximation (RPA) (2, 27, 34) is used to characterize graphene’s surface conductivity. A conservative electron mobility of 10,000 cm²⋅V⁻¹⋅s⁻¹ is assumed in graphene. Realistic losses in both graphene and BN are considered. To maintain the relatively low propagation loss of these highly squeezed polaritons, we consider lossless dielectrics as substrates, for example germanium (35, 36) with a relative permittivity of ${\epsilon }_r=16$ at the frequency of interest. We note that although SiO₂ and SiC (36) are popular substrates for graphene and BN devices, they are lossy within BN’s first reststrahlen band. In addition, the choice of bulk BN as the substrate is also not beneficial because the mode of graphene plasmons will disappear within BN’s first reststrahlen band (11), as can be seen in Fig. S1.

Fig. 1.

In-plane negative refraction between plasmon polaritons in graphene and phonon polaritons in a BN slab. (A) Schematic structure, along with the $E_z$-field distribution of plasmon and phonon polaritons. The chemical potential of graphene is ${\mu }_c=0.2$ eV and the thickness of BN is 20 nm. (B) Dispersion relation of phonon polaritons. It is an instructive way to visualize the dispersion of these polaritons via a false-color plot of $\left|Im\left(r_p\right)\right|,$ where $r_p$ is the reflection coefficient of p-polarized waves for the right region in A. This is because these polaritons are the singularity poles in the coefficient of $r_p.$ The yellow line is the dispersion of plasmon polaritons for the left region in A. The highlighted blue circle is the crossing point between the dispersion lines of plasmon and phonon polaritons. The red dashed lower and upper lines correspond to the transverse optical (TO) and longitudinal optical (LO) frequencies, respectively. The Fermi velocity is $v_F=c/300.$ (C) $E_z$-field distribution excited by a dipole source at 22.96 THz. The yellow dashed line indicates the interface between left and right regions.

Fig. S1.

Dispersion of graphene plasmons in structure of air–graphene–BN. The chemical potential of graphene is ${\mu }_c=0.35$ eV.

Fig. 1B shows the dispersion of graphene plasmons and BN’s phonon polaritons. For clarity, below we discuss the direction of the group velocity $\partial \omega /\partial q$ of these polaritons and/or the direction of their power flow with respect to the direction of their phase velocity $\omega /q;$ when the sign of the group velocity is defined as positive, the group velocity and the phase velocity are in the same direction; when the sign of the group velocity is defined as negative, the group velocity and the phase velocity are in the opposite direction. The group velocity of graphene plasmons is positive whereas that of BN’s phonon polaritons is negative in Fig. 1B. The direction of the group velocity is determined by the direction of the total power flow, which can be quantitatively described (Power Flow Calculation for calculation details). To gain an intuitive understanding of the group velocity of these polaritons, one should analyze the direction of their total power flow. For graphene plasmons, the power flow is positive in the surrounding dielectrics and is negligible within graphene due to graphene’s infinitesimal thickness, rendering the group velocity of graphene plasmons to be positive. For BN’s phonon polaritons, because BN is a type-I hyperbolic material (${\epsilon }_x={\epsilon }_y>0,$ ${\epsilon }_z<0$) within the first reststrahlen band (7, 12), the power flow is negative inside BN. Moreover, there is more power flow inside BN than that outside BN, rendering the group velocity of BN’s phonon polaritons to be negative.

The in-plane negative refraction between graphene plasmon and BN’s phonon polariton can happen because of their opposite signs of group velocities and approximately the same squeezing factors within BN’s first reststrahlen band. We can choose a working frequency such that the wavevectors of these polaritons are equal, such as the blue solid point [$Re\left(q\right)=94\times {10}^6$ m⁻¹ at 22.96 THz] in Fig. 1B. Therefore, the effective phase indexes of these polaritons at this specific point are matched in magnitude. Equally as important, this phase-index matching further enables the in-plane negative refraction at all angles of incidence (16, 22).

As shown in Fig. 1C, we numerically demonstrate the all-angle in-plane negative refraction between graphene plasmons and BN’s phonon polaritons at 22.96 THz, using the finite-element method (the commercial software COMSOL Multiphysics). Graphene plasmons are excited by a dipole source in the left region and couple to BN’s phonon polaritons at the interface. Because the signs of the group velocities of polaritons in the left and right regions are opposite, we get negative refraction in the plane where these polaritons propagate (i.e., the x–y plane). More generally, this indicates that the negative refraction happens in a plane parallel to the graphene plane, which is thus denoted as in-plane negative refraction. This in-plane negative refraction happens even when the configuration has different thicknesses on the two sides of the interface. Moreover, an image is formed in the right region, which computationally validates the all-angle negative refraction. In this system, the ratio $\left|\frac{Re\left(q\right)}{Im\left(q\right)}\right|,$ as the dimensionless figure of merit for propagation damping (11), is equal to 15 for graphene plasmons and 23 for BN’s phonon polaritons. This indicates relatively low propagation losses for these polaritons (11), which facilitates future experimental verifications and applications. In Fig. 1C, the squeezing factor $\frac{Re\left(q\right)}{\omega /c}=195$ indicates that compared with the wavelength in free space, the polaritonic wavelength is squeezed by a factor of 195. We note that the imaging mechanism here is not a perfect image recovery. This is because there is reflection at the interface due to the modal-profile mismatch ($E_z$ profiles in Fig. 1A) between plasmon and phonon polaritons, and the losses [i.e., $Im\left(q\right)$] in the left and right regions are different in Fig. 1C. To suppress the reflection, one way is to maximize the mode overlap between the incident and transmitted mode profiles at the discontinuous interface (16). Note that although the reflection at the interface can affect the transmission, the field intensity of polaritons in the region of transmission also largely depends on their propagation loss. Therefore, a complete optimization of the field intensity in the region of transmission should consider both reflection and the propagation loss of polaritons (more discussion in Optimization of the Field Intensity in the Region of Transmission and Figs. S2–S4). In addition to the situation considered above, we also consider a structure where graphene exists in both the left and the right regions (which may be easier to fabricate) and demonstrate the all-angle in-plane negative refraction between graphene plasmons and BN’s phonon polaritons (Fig. S5).

Fig. S2.

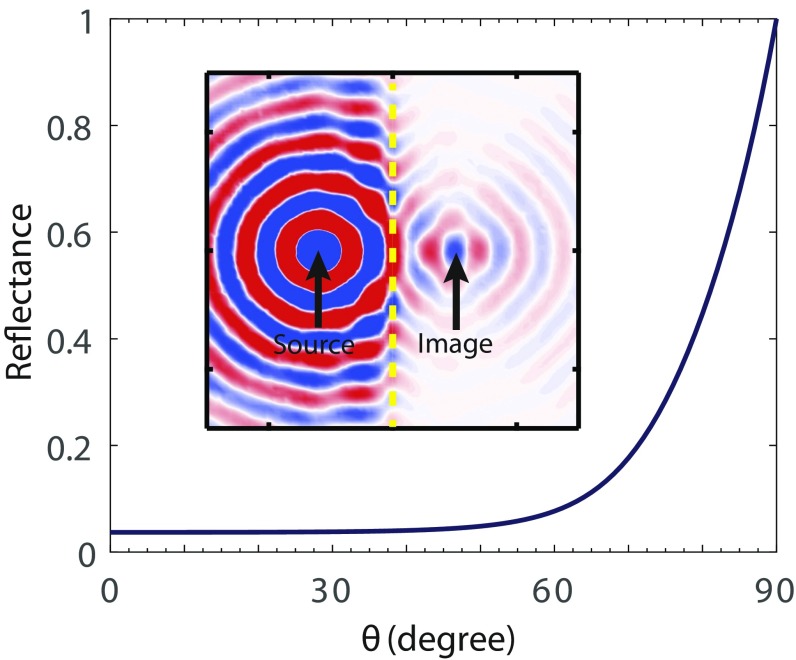
Reflectance at the discontinuous interface between air–graphene–substrate and air–BN–substrate estimated from a simplified model. All setups are the same as those in Fig. 1C. Inset is from Fig. 1C.

Fig. S4.

All-angle negative refraction between graphene plasmons and BN’s phonon polaritons at the frequency of the phase-index–matched crossing point. The frequency, the chemical potential of graphene, and the thickness of BN are denoted in each plot. (A) All setups are the same as those in Fig. 1C. The thickness of BN is 20 nm and the chemical potential of graphene is 0.2 eV. (B) The thickness of BN in A is decreased to 5 nm. (C) The chemical potential of graphene in A is increased to 0.4 eV. The wavevector $Re\left(q\right)$ is (A) $94\times {10}^6$ m⁻¹, (B) $100\times {10}^6$ m⁻¹, and (C) $60\times {10}^6$ m⁻¹, respectively. To compare the field intensity in the region of transmission, the distance of the dipole source from the interface (denoted as the yellow dashed line) in C is 94/60 times that in A. The ratio $\left|\frac{Re\left(q\right)}{Im\left(q\right)}\right|,$ which characterizes the propagation loss, is equal to (A) 15, (B) 15, and (C) 47 for graphene plasmons and is equal to (A) 23, (B) 20, and (C) 28 for BN’s phonon polaritons, respectively.

Fig. S5.

In-plane negative refraction between ultraconfined graphene plasmon and phonon–polariton-like type-I hybridized polariton. (A) Schematic structure, along with the $E_z$-field distribution of plasmon and phonon polaritons. The chemical potential of graphene is ${\mu }_c=0.2$ eV and the thickness of BN is 50 nm. (B) Dispersion of hybridized plasmon–phonon–polaritons for the right region in A. The yellow line is the dispersion of graphene plasmons for the left region in A. For the phase-index–matched blue crossing point, we have $Re\left(q\right)=50.8\times {10}^6$ m⁻¹ at 23.17 THz and $\frac{Re\left(q\right)}{\omega /c}=104;$ $\left|\frac{Re\left(q\right)}{Im\left(q\right)}\right|$ is equal to 23 and 15 for plasmon and phonon polaritons in the left and right regions, respectively. (C) $E_z$-field distribution excited by a dipole source at 23.17 THz.

Whereas the negative refractions between the graphene plasmon and BN’s phonon polariton in Fig. 1 are quite expected because of their opposite group velocity signs in BN’s first reststrahlen band, we also found two completely unexpected types of negative refractions occurring in these systems. We show how negative refraction can occur between two kinds of hybrid graphene plasmons (Fig. 2) or between two kinds of hybrid phonon polaritons (Fig. 3).

Fig. 2.

In-plane negative refraction between graphene plasmons and plasmon–polariton-like type-I hybrid polaritons. (A) Schematic structure. The thickness of BN is 25 nm and the chemical potential of graphene in the left region is ${\mu }_{c2}=0.15$ eV. (B–E) Evolution of the dispersion of type-I hybrid plasmon–phonon–polaritons for the right region in A under different values for the chemical potential, ${\mu }_{c1}.$ The yellow line in D is the dispersion of graphene plasmons for the left region in A. (F) Dispersion of air–graphene–substrate–graphene–substrate, where the structure is the same as that in D except for the replacement of BN with substrate. (G) $E_z$-field distribution of negative refraction. The incident and refracted polaritonic modes are highlighted by a blue solid point in D at 23.32 THz. The incident angle is 45° and the power flow direction is marked by the yellow arrows.

Fig. 3.

In-plane negative refraction between BN’s phonon polaritons and phonon–polariton-like type-II hybrid polaritons. (A) Schematic structure. The thickness of BN in the left region is $d_2=7$ nm and the chemical potential of graphene is ${\mu }_c=0.3$ eV. (B–E) Evolution of the dispersion of type-II hybrid plasmon–phonon–polaritons for the right region in A under different thicknesses of the BN slab, $d_1.$ The green line in D is the dispersion of BN’s phonon polaritons (shown in F). (F) Dispersion of air–BN–substrate, where the structure is the same as in the left region in A. (G) $E_z$-field distribution of negative refraction. The incident and refracted polaritonic modes are highlighted by a blue solid circle in D at 23.94 THz. The incident angle is 30° and the power flow direction is marked by the yellow arrows.

Below we show the strong coupling between graphene plasmons and BN’s phonon polaritons can flip the signs of the group velocities of the hybrid plasmon–phonon–polaritons in graphene–BN heterostructures, as shown in Figs. 2 and 3. There are two different types of polaritonic dispersion lines in graphene–BN heterostructures. For the first type, there is always a part of the dispersion line existing outside BN’s first reststrahlen band, whereas the other part of the dispersion line can exist inside BN’s first reststrahlen band, which is more plasmon–polariton-like; below, we thus refer to this type of mode as the type-I hybrid polariton. For the second type, the dispersion line exists only within BN’s first reststrahlen band, which is more phonon–polariton-like; below, we refer to this type of mode as the type-II hybrid polariton.

Fig. 2 demonstrates the all-angle in-plane negative refraction between the graphene plasmon and the type-I hybrid polariton. Because the type-I hybrid polariton is more plasmon–polariton-like, one can refer to this type of refraction as the negative refraction between two kinds of graphene plasmons. In Fig. 2A, the left air–graphene–substrate region supports graphene plasmons, and the right air–graphene–BN–graphene–substrate region supports type-I hybrid plasmon–phonon–polaritons. Here we choose the lossless polycrystalline chemical-vapor deposition (CVD) diamond (36–38) with a relative permittivity of ${\epsilon }_r=5.6$ as the substrate, because the synthetic diamond is lossless at the frequency of interest and is also readily available (37, 38).

Fig. 2 B–E shows the evolution of the dispersion of type-I hybrid polaritons in the right region at different chemical potentials. When the chemical potential of two graphene layers is low (Fig. 2B), the group velocity of type-I hybrid polaritons is positive. When we increase the chemical potential (${\mu }_{\text{c}}\ge 0.25$ eV in Fig. 2 C–E), part of the dispersion relation within BN’s first reststrahlen band exhibits a negative group velocity. This twisting of the dispersion of type-I hybrid polaritons can again be intuitively understood via the power flow calculation. In graphene–BN heterostructures, the power flow is negative inside BN and more power can flow inside BN than outside BN. For example, for the blue crossing point between the dispersion lines of the graphene plasmon and the type-I hybrid polariton in Fig. 2D, the ratio between the power flow inside BN ($P_{inBN}$) and that outside BN ($P_{outBN}$) is $\frac{P_{inBN}}{P_{outBN}}=-11.$ The domination of the power flow in BN renders the group velocity of type-I hybrid polaritons to be negative. As a comparison, Fig. 2F shows the dispersion of graphene plasmons in a structure without BN, where the group velocity stays positive.

Importantly, due to the tunability of the chemical potential in graphene, the phase-index–matched crossing points in Figs. 1 and 2 are dynamically controllable within BN’s first reststrahlen band. For example, when the chemical potential of graphene in the left region of Fig. 1A changes from 0.1 eV to 0.6 eV, the frequency of the phase-index–matched crossing point in Fig. 1B varies from 22.77 THz to 23.58 THz; when the chemical potential of graphene in the left region of Fig. 2A changes from 0.05 eV to 0.25 eV, the frequency of the phase-index–matched crossing points in Fig. 2D varies from 22.94 THz to 23.49 THz. Moreover, because the negative group velocity of the type-I hybrid polaritons can be realized in a wide range of chemical potential (${\mu }_{\text{c}}\ge 0.25$ eV) in the right region of Fig. 2A, we can also tune the frequency of the phase-index–matched crossing point by changing the chemical potential in the right region of Fig. 2A. The different chemical potentials of graphene in the left and right regions in Fig. 2 may be achieved by following the methods proposed in ref. 1. These above advantages offer the possibility for tunable in-plane polaritonic negative refraction, which is desirable for many nanophotonic applications. As an example, we show that for the phase-index–matched crossing point at 23.32 THz in Fig. 2D, $Re\left(q\right)=66.8\times {10}^6$ m⁻¹, the squeezing factor $\frac{Re\left(q\right)}{\omega /c}=137,$ and $\left|\frac{Re\left(q\right)}{Im\left(q\right)}\right|$ is equal to 14 and 20 for the graphene plasmon and the type-I hybrid polariton, respectively. We numerically verify the in-plane negative refraction between graphene plasmons and type-I hybrid polaritons at 23.32 THz in Fig. 2G, where type-I hybrid polaritons are incident from the right region at an angle of 45° (there is no specific requirement on the incident angle; see more discussion of the setup in Negative Refraction Between Highly Squeezed Polaritons and Fig. S6).

Fig. S6.

Dispersion of plasmon–polariton-like type-I hybrid polaritons within BN’s first reststrahlen band. The structure of air–graphene–BN–graphene–substrate is the same as that in the right region of Fig. 2A, where the chemical potential ${\mu }_{\text{c}}$ of graphene is labeled in the key. These four dispersion lines are extracted from the dispersion lines of type-I hybrid polaritons in Fig. 2 B–E. When ${\mu }_{\text{c}}=0.35$ eV (${\mu }_{\text{c}}=0.45$ eV), there are two type-I hybrid polaritonic modes at 23.3 THz, denoted as R₁ and R₂ (L₁ and L₂), respectively. The sign of the group velocity of modes R₁ and L₁ is positive, whereas the sign of the group velocity of modes R₂ and L₂ is negative.

Fig. 3 demonstrates the all-angle in-plane negative refraction between BN’s phonon polaritons and type-II hybrid polaritons. Because the type-II hybrid polariton is more phonon–polariton-like, we refer to this type of refraction as the negative refraction between two kinds of phonon polaritons. In Fig. 3A, the left air–BN–substrate region supports phonon polaritons, and the right air–BN–graphene–substrate region supports type-II hybrid polaritons. Fig. 3 B–E shows the modification of the sign of the group velocity for type-II hybrid polaritons by changing the thickness of BN in the right region. When BN is thick (Fig. 3B), the group velocity of type-II hybrid polaritons is negative. When we decrease the thickness of BN, part of the dispersion line exhibits a positive group velocity (Fig. 3 C–E). We use the power flow calculation to explain this dispersion twisting. The power flow is positive outside BN, and for small enough BN thicknesses, more power can flow outside BN than inside BN, flipping the group velocity to be positive. Here we use the blue crossing point between the dispersion lines of BN’s phonon polariton and the type-II hybrid polariton in Fig. 3D as an example. The ratio between the power flow inside and outside BN is $\frac{P_{inBN}}{P_{outBN}}=-\mathrm{0.4.}$ Such a power flow distribution renders the group velocity of type-II hybrid polaritons to be positive. Because the BN slab behaves like a waveguide, we can also see that the number of the type-II hybrid polariton modes decreases when the thickness of BN decreases. As a comparison, Fig. 3F shows the dispersion of BN’s phonon polaritons in a structure without graphene, where the group velocity remains negative.

At the phase-index–matched crossing point at 23.94 THz in Fig. 3D, we have $Re\left(q\right)=77.4\times {10}^6$ m⁻¹ and the squeezing factor $\frac{Re\left(q\right)}{\omega /c}=154;$ $\left|\frac{Re\left(q\right)}{Im\left(q\right)}\right|$ is equal to 21 and 9 for BN’s phonon polariton and the type-II hybrid polariton, respectively. We numerically verify the in-plane negative refraction between BN’s phonon polaritons and type-II hybrid polaritons in Fig. 3G, where type-II hybrid polaritons are incident from the right region at an angle of 30° (the incident angle is arbitrarily chosen; see more discussion of the setup in Negative Refraction Between Highly Squeezed Polaritons).

Power Flow Calculation

In addition, by setting $A_{+}=C_{-}=0$ in Eq. S3 and enforcing the boundary conditions above, we can obtain the transverse electric and magnetic field distributions of the eigenmode of these ultraconfined polaritons. We can further use the transverse field distributions of these polaritonic eigenmodes to calculate their power flow in each region. Because the time-averaged Poynting’s vector (power flow density) is $\langle \overline{S}(\overline{r},t)\rangle =\frac{1}{2}Re\{\overline{E}\times \overline{H}\ast \},$ one can obtain the in-plane power time-averaged Poynting’s vector (parallel to the x–y plane) as $\langle S_{\text{in}-\text{plane}}(\overline{r},t)\rangle =\frac{1}{2}Re\{-E_{z}H\ast \}.$ The integration of $\langle S_{\text{in}-\text{plane}}(\overline{r},t)\rangle$ with respect to $z$ then gives the power flow of these polaritons in different regions.

In the above power flow calculation, the in-plane wavevector is assumed to be in the x direction (with $\overline{H}=\widehat{y}{H}_y;$ Eq. S3). Nevertheless, these formulas are applicable for cases where the in-plane wavevector is not in the x direction (with $\overline{H}=\widehat{x}{H}_x+\widehat{y}{H}_y$). This way, we can also use the above power flow calculation to analyze the energy flow along the y direction, such as that in Figs. 1C, 2G, and 3G. When the signs of the group velocity of polaritons in the left and right regions are opposite in Figs. 1C, 2G, and 3G, the polaritonic negative refraction will happen. This is because the power flows in the left and right regions in the y direction (parallel to the interface) are opposite. Note that the negative refraction is irrelevant to the power flow in the x direction (normal to the interface), which is always the same in the left and right regions.

Optimization of the Field Intensity in the Region of Transmission

Note that although the reflection at the discontinuous interface can affect the transmission, the field intensity of polaritons in the region of transmission also largely depends on their propagation loss. Therefore, a complete optimization of the field intensity in the region of transmission should consider both reflection and the propagation loss.

Regarding the reflection, it is widely accepted that the overlap of mode profiles can be used to estimate the reflectance qualitatively (16, 52, 53). In general, the larger the mode overlap is, the less the reflectance. However, the exact closed-form reflectance at a discontinuous interface cannot be analytically calculated with Maxwell’s equations. A rough estimation of the reflectance can be done by simply extracting the effective refractive indexes (as $n=\omega /q$) and effective impedances (as $\eta =\frac{{\displaystyle \int }{E}_{z}dz}{{\displaystyle \int }Hdz}$) for the incident, reflected, and transmitted polaritonic eigenmodes as plane waves, when the scattering loss at the interface is neglected. As shown in Fig. S2, the reflectance is negligible (nonnegligible) at small (large) incident angles. This is consistent with the simulation field pattern in Fig. 1C (or in Fig. S2, Inset), where interference wrinkles show up only at large angles.

To suppress the reflection, one way is to maximize the mode overlap between the incident and transmitted mode profiles at the interface (16), such as changing the BN’s thickness or the chemical potential of graphene. In Fig. S3, we show that the mode overlap can indeed be increased by decreasing the BN’s thickness, for the case studied in Fig. 1C. This indicates that the reflectance at the interface should be suppressed by using a thinner BN slab.

Fig. S3.

Eigenmode profile of the magnetic field for (A and B) graphene plasmons and (C and D) BN’s phonon polaritons at the frequency of the phase-index–matched crossing point. All parameters in A and C are the same as those in Fig. 1C, where the thickness of BN is 20 nm and the frequency is 22.96 THz. In B and D, the thickness of BN is decreased to 5 nm and the phase-index–matched frequency is shifted to 23.99 THz, whereas the other setups are the same as those in A and C. The mode profiles of graphene plasmons and BN’s phonon polaritons are well matched only within the substrate region. The mode mismatch in the region above the substrate can be decreased by decreasing the thickness of BN.

Practically, one needs to consider both mode overlap and polaritonic propagation loss to evaluate the quality of imaging. We implemented COMSOL simulations to discuss the impact from BN’s thicknesses and chemical potentials of graphene, as shown in Fig. S4. Compared with the initial geometry (Fig. S4A), the field intensity in the region of transmission is not enhanced through using a thinner BN slab (Fig. S4B). Although the mode overlap should be enhanced with thinner BN (Fig. S3), larger propagation loss reduces the image quality in the region of transmission (Fig. S4B). On the other hand, increasing the chemical potential of graphene can lower the propagation loss of polaritons. Fig. S4 A and C shows that the field intensity in the region of transmission is enhanced by increasing the chemical potential of graphene, although there is still significant reflection for large incident angles in Fig. S4C. Note that here we assume the electron mobility in graphene, which characterizes the material loss, is constant. In practice, the increase of chemical potential might decrease the electron mobility (especially when achieved by chemical doping) and can lead to larger propagation loss of polaritons.

In summary, we find that reducing the BN thickness can improve the mode overlap (better transmission) at the cost of larger propagation loss, whereas increasing the chemical potential of graphene can reduce the propagation loss. For future experiments, optimizations should be taken into account and trade-offs should be considered for specific geometries and experimental conditions.

Negative Refraction Between Highly Squeezed Polaritons

We demonstrate an alternative structure that can enable the all-angle in-plane negative refraction between highly squeezed plasmon and phonon polaritons, as shown in Fig. S5. Different from Fig. 1, here graphene exists in both the left and right regions, which may simplify the fabrication process of the structure.

At the working frequency in Fig. 2G (Fig. 3G), there is only one polariton mode in the left region, whereas there are two (three) polariton modes in the right region in Fig. 2G (Fig. 3G), where the signs of these group velocities are different (see dispersions in Figs. 2D and 3D). When the polariton is incident from the left region in Fig. 2G (Fig. 3G), there can be double (triple) refraction at the interface, including the negative and positive refractions, making the analysis rather complicated. This indicates that the all-angle negative refraction shown in Figs. 2 and 3 is not suitable for the dipole source imaging. Therefore, to guarantee the negative refraction only between two specific modes in the left and right regions, it is required to input the chosen polariton mode from the right region. This way, along with the phase-index–matching condition, the negative refraction between the two specific modes in the left and right regions can happen at any incident angle [i.e., (0°, 90°)] in Figs. 2G and 3G. As a demonstration of concept, the chosen polariton is incident from the right region at an angle of 45° in Fig. 2G and 30° in Fig. 3G, respectively.

In Fig. 1C, we demonstrate the negative refraction between graphene plasmon and the lowest-order mode of BN’s phonon polariton only at 22.96 THz. However, as shown in Fig. 1B, the phase-index–matching point can also occur at different frequencies, between graphene plasmons and the high-order modes of BN’s phonon polaritons. Therefore, the all-angle in-plane negative refraction between graphene plasmon and the higher-order mode of BN’s phonon polariton is also possible. However, this in-plane negative refraction is not suitable for the dipole source imaging. Meanwhile, to guarantee the negative refraction only between two specific modes in the left and right regions, it is required to input the chosen polariton mode from the right region. The reason is the same as in the above discussion for Figs. 2G and 3G.

We also checked the refraction in the structure of air–graphene–BN–graphene–substrate (same as the right region in Fig. 2A), where the left and right regions have the same structure but may have different chemical potentials in graphene. It turns out that this structure is not suitable for the demonstration of the all-angle negative refraction between plasmon–polariton-like type-I hybrid polaritons. This is because for this structure, the dispersion lines of type-I hybrid polaritons with different chemical potentials in graphene do not have a phase-index–matched crossing point within BN’s first reststrahlen band, as shown in Fig. S6. Note that to realize the all-angle negative refraction, the signs of the group velocity of the two type-I polaritonic modes at the crossing point should be opposite. However, there might be double or multiple refraction between type-I hybrid polaritons in this structure, among which one is the negative refraction. For example, as shown in Fig. S6, a chemical potential of 0.35 eV (0.45 eV) of graphene in the right (left) region yields two modes of type-I hybrid polaritons with different signs of the group velocity at 23.3 THz. The existence of both positive and negative dispersion will give rise to double refraction (including positive refraction and negative refraction) at 23.3 THz.

Discussion

It is worthy to note that the all-angle negative refraction shown in Figs. 2 and 3 is not suitable for dipole source imaging. This is because in the right region of the heterostructure, there are multiple hybrid plasmon–phonon–polariton modes with different wavevectors existing at the same working frequency (see dispersions in Figs. 2D and 3D). When a dipole source is used, there will be unavoidable excitation of other hybrid polariton modes in the right region, which will blur the formation of an image.

Other types of negative refractions have been described in previous works, including the negative refraction of electrons (39–41). Other studies have shown plasmonic (42–44) and optical (45, 46) negative refraction in 3D bulk media made of graphene-based periodic structures. Negative refraction of light propagating through a single layer of graphene was first observed in ref. 47. However, most of these electromagnetic refractions occurred out of the graphene plane and not in plane, therefore without taking advantage of the high spatial confinement and strong coupling of 2D polariton modes that are critical in this work. One viable way to experimentally verify the in-plane negative refraction of these highly squeezed polaritons is to apply the method of the direct geometric visualization of negative refraction (17).

In conclusion, we reveal a viable way to flip the sign of group velocities of hybrid plasmon–phonon–polaritons in graphene–BN heterostructures, by using the strong coupling between graphene plasmons and BN’s phonon polaritons. This enables the flexible control of the in-plane refraction of highly squeezed polaritons, which is of fundamental importance for the manipulation of light at the nanoscale. Our full-wave simulations verify that all-angle in-plane negative refraction can be realized between graphene plasmons, BN’s phonon polaritons, and their hybrid polaritons in graphene–BN heterostructures. Moreover, the working frequency of these all-angle negative refractions can be flexibly tunable within BN’s first reststrahlen band through changing the chemical potential of graphene. Due to the combined advantages of tunability, low loss, and superior spatial confinement provided by these polaritons on the platform of graphene–BN heterostructures, we expect many other actively tunable polaritonic effects to be explored and used for the design of advanced polaritonic devices such as metasurfaces and superlenses.

Materials and Methods

The finite-element simulation is implemented via the frequency domain simulation in COMSOL. Graphene in the COMSOL simulation is modeled by a surface, where conditions for discontinuities in the electromagnetic fields are satisfied by taking into account the surface conductivity. This ensures high calculation accuracy, compared with the volumetric permittivity of an ultrathin graphene slab that is often considered (1). The surface conductivity of the surface is calculated by RPA. The meshing resolution in the vicinity of graphene and BN is 1 nm in the z direction. In Fig. 1, a z-polarized dipole source is placed in the left region and 20 nm above the structure to excite the plasmon polaritons. Fig. 1C is obtained at 20 nm below the BN–substrate interface. The phenomenon of negative refraction in Fig. 1C is pronounced, regardless of the vertical position of the dipole source. In Figs. 2 and 3, a mode source is launched from the right side of the structure to excite the specific mode of interest. Figs. 2G and 3G are obtained at 15 nm below and 2.5 nm above the BN–substrate interface, respectively.

Graphene’s Surface Conductivity and BN’s Permittivity

In this work, we use RPA to model the surface conductivity of graphene. RPA takes the nonlocal response into consideration (2, 27, 34), and can be fully described by the following set of equations:

$${\sigma }_{s,RPA}\left(q,\omega \right)=-i\omega {\chi }_{\tau }(q,\omega )$$ [S1a]

$${\chi }_{\tau }\left(q,\omega \right)=\frac{(1+i/\omega \tau )\chi (q,\omega +i/\tau )}{1+(i/\omega \tau )\chi (q,\omega +i/\tau )/\chi (q,0)}$$ [S1b]

$$\chi \left(q,\omega \right)=\frac{e^2}{2{\pi }^2\hslash q^2}{\displaystyle \int }{d}^2\overline{q}\prime {\displaystyle \sum }_{s,s\prime =\pm }\left[1+ss\prime \frac{\overline{q}\prime \cdot |\overline{q}+\overline{q}\prime |}{q\prime |\overline{q}+\overline{q}\prime |}\right]\frac{f_d\left(s\prime \hslash v_F\left|\overline{q}+\overline{q}\prime \right|\right)-f_d\left(s\hslash v_{F}q\prime \right)}{\omega +v_F\left(sq\prime -s\prime \left|\overline{q}+\overline{q}\prime \right|\right)+i{0}^{+}}.$$ [S1c]

In the above, $f_d\left(E\right)={(e^{\left(E-{\mu }_c\right)/k_{B}T}+1)}^{-1}$ is the Fermi–Dirac distribution function, ${\mu }_c$ is the chemical potential, $q$ is the in-plane wavevector, $\tau$ is the relaxation time that characterizes the loss in graphene, the Fermi velocity $v_F=1\times {10}^6$ m/s, and $k_B$ is the Boltzmann constant. When the temperature $\text{T}=0$ K, we have $f_d\left(E\right)=\theta \left({\mu }_c-E\right),$ where $\theta \left({\mu }_c-E\right)$ is a step function. Eq. S1c at $\text{T}=0$ K has an analytical expression

$$\chi \left(q,\omega \right)=\frac{e^2}{4\pi \hslash }\left[\frac{8k_F}{q^2{v}_F}+\frac{\left[G\left(-{\mathrm{\Delta }}_{-}\right)-i\pi \right]\theta \left(-{\mathrm{\Delta }}_{-}-1\right)+G\left({\mathrm{\Delta }}_{-}\right)\theta \left({\mathrm{\Delta }}_{-}+1\right)-\left[G\left({\mathrm{\Delta }}_{+}\right)-i\pi \right]}{\sqrt{{\omega }^2-v_F^2{q}^2}}\right],$$ [S1d]

where $G\left(z\right)=z\sqrt{z^2-1}-\text{log}\left(z+\sqrt{z^2-1}\right)$ and ${\mathrm{\Delta }}_{\pm }=\frac{\hslash \omega \pm 2{\mu }_c}{\hslash v_{F}q}.$ The square root in $G\left(z\right)$ is chosen to yield a positive imaginary part when $\left|z\right|<1$ and is chosen to yield a positive real part when $\left|z\right|>1$ (34). The range of the imaginary part of the logarithm is chosen to be $\left(-\pi ,\pi \right]$ (2, 34). In addition, we have

$$\chi \left(q,0\right)=\frac{e^2}{2\pi \hslash v_{F}q}\left\{\frac{4k_F}{q}-\theta (1-x)\left[x\sqrt{1-x^2}-co{s}^{-1}x\right]\right\},$$ [S1e]

where $x=2k_F/q.$ The nonlocal RPA is calculated by using these formulas in this work. Because our working frequency within BN’s first reststrahlen band (∼22.3–24.6 THz) is below that of the optical phonon branch of graphene, $\hslash \mathrm{\omega }\approx 0.2$ eV (∼48 THz), the relaxation time of graphene can be theoretically estimated from the electron mobility (denoted as $\mu$); i.e., $\tau ={\mu }_c\mu /\left(e{v}_F^2\right)$ (27). In this work, a conservative electron mobility of 10,000 cm²⋅V⁻¹⋅s⁻¹ is assumed in graphene (48). In addition, because our working frequency (∼22.3–24.6 THz) is much smaller than the corresponding frequency ($\ge 36$ THz) of the Fermi energy (${\mu }_c\ge 0.15$ eV) in this work, graphene’s surface conductivities at $\text{T}=0$ K and $\text{T}=300$ K have trivial difference. Therefore, the temperature will have trivial influence on the phenomena of the in-plane polaritonic negative refraction demonstrated in this work.

Hexagonal BN is an anisotropic material, and its relative permittivity can be characterized by a diagonal tensor, i.e., $[{\epsilon }_x,{\epsilon }_y,{\epsilon }_z],$ where ${\epsilon }_x={\epsilon }_y\ne {\epsilon }_z.$ Here, we use the experimental data (11, 49) to characterize the relative permittivity of BN; i.e.,

$${\epsilon }_l\left(\omega \right)={\epsilon }_l\left(\infty \right)+s_{v,l}\frac{{\omega }_{v.l}^2}{{\omega }_{v.l}^2-i{\gamma }_{v,l}\omega -{\omega }^2},\hspace{1em}l=x,y,z.$$ [S2]

For the in-plane direction ($x\hspace{0.17em}\text{or}\hspace{0.17em}y$), we have ${\epsilon }_l\left(\infty \right)=4.87,$ the real-valued constant $s_{v,l}=1.83$ (dimensionless coupling factor), the normal frequency of vibration $\hslash {\omega }_{v,l}=170.1$ meV, and the amplitude decay rate $\hslash {\gamma }_{v,l}=0.87$ meV (11, 49). For the out-of-plane direction ($z$), we have ${\epsilon }_l\left(\infty \right)=2.95,$ $s_{v,l}=0.61,$ $\hslash {\omega }_{v,l}=92.5$ meV, and $\hslash {\gamma }_{v,l}=0.25$ meV (11, 49). As discussed in ref. 11, because the nonlocal effect should appear only once $q$ is comparable to the reciprocal lattice vector, a regime that is two orders of magnitude away from our discussed cases, it is reasonable to neglect the nonlocal effect in the permittivity of BN.

Dispersion of Hybridized Plasmon–Phonon–Polaritons

In this section, we analytically derive the formulas that govern the basic properties of hybridized plasmon–phonon–polaritons in graphene–BN heterostructures within the framework of macroscopic electromagnetic theory (50). We use the air–graphene–BN–graphene–substrate structure to illustrate our calculation method. We assume the first and second graphene layers to be located at the two interfaces (i.e., the planes of $z=0$ and $z=d$) between region 1 ($z<0,$ air), region 2 ($0<z<d,$ BN), and region 3 ($z>d,$ substrate), where $d$ is the thickness of the BN slab. For TM (p-polarized) waves, one can set the magnetic fields in each region (50) as

$${\overline{H}}_1=\widehat{y}{e}^{iqx}(A_{+}{e}^{+i{k}_{1z}z}+A_{-}{e}^{-i{k}_{1z}z})$$ [S3a]

$${\overline{H}}_2=\widehat{y}{e}^{iqx}(B_{+}{e}^{+i{k}_{2z}z}+B_{-}{e}^{-i{k}_{2z}z})$$ [S3b]

$${\overline{H}}_3=\widehat{y}{e}^{iqx}(C_{+}{e}^{+i{k}_{3z}z}+C_{-}{e}^{+i{k}_{3z}z}).$$ [S3c]

The corresponding electric fields in each region can be obtained by using $\left(\widehat{x}q+\widehat{x}{k}_z\right)\times \overline{H}=-\mathrm{\omega }\overline{\overline{\epsilon }}\overline{E}.$ In the above, $k_{z1}=\sqrt{\frac{{\omega }^2}{c^2}{\epsilon }_{r1}-q^2},$ $k_{z2}=\sqrt{\frac{{\omega }^2}{c^2}{\epsilon }_x-q^2\frac{{\epsilon }_x}{{\epsilon }_z}},$ and $k_{z3}=\sqrt{\frac{{\omega }^2}{c^2}{\epsilon }_{r3}-q^2}$ are the wavevector components perpendicular to the interface; ${\epsilon }_{r1}$ and ${\epsilon }_{r3}$ are the relative permittivity of regions 1 and 3, respectively. The relation between parameters $A_{\pm }-C_{\pm }$ can be solved by matching the boundary conditions at the two interfaces. By letting the surface normal $\widehat{n}=-\widehat{z},$ we have $\widehat{n}\times \left({\overline{E}}_1-{\overline{E}}_2\right)=0$ and $\widehat{n}\times \left({\overline{H}}_1-{\overline{H}}_2\right)=\widehat{x}{\sigma }_{s1}{E}_{x1}$ at $z=0,$ and we have $\widehat{n}\times \left({\overline{E}}_2-{\overline{E}}_3\right)=0$ and $\widehat{n}\times \left({\overline{H}}_2-{\overline{H}}_3\right)=\widehat{x}{\sigma }_{s2}{E}_{x2}$ at $z=d.$ Here we denote the surface conductivity of the first and second graphene layers to be ${\sigma }_{s1}$ and ${\sigma }_{s2},$ respectively.

By enforcing these boundary conditions, we obtain $\frac{C_{+}}{C_{-}}={\stackrel{\sim }{R}}_{32}$ when the electromagnetic wave is incident from region 3; i.e.,

$${\stackrel{\sim }{R}}_{32}=R_{32}+\frac{T_{32}{R}_{21}{T}_{23}{e}^{+i2k_{z2}d}}{1-R_{21}{R}_{23}{e}^{+i2k_{z2}d}}.$$ [S4]

In the above, we have $R_{32}=\frac{1+\frac{{\sigma }_{s2}}{\omega {\epsilon }_0}\frac{k_{z2}}{{\epsilon }_x}-\frac{k_{z2}/{\epsilon }_x}{k_{z3}/{\epsilon }_{r3}}}{1+\frac{{\sigma }_{s2}}{\omega {\epsilon }_0}\frac{k_{z2}}{{\epsilon }_x}+\frac{k_{z2}/{\epsilon }_x}{k_{z3}/{\epsilon }_{r3}}},$ $R_{23}=\frac{1+\frac{{\sigma }_{s2}}{\omega {\epsilon }_0}\frac{k_{z3}}{{\epsilon }_{r3}}-\frac{k_{z3}/{\epsilon }_{r3}}{k_{z2}/{\epsilon }_x}}{1+\frac{{\sigma }_{s2}}{\omega {\epsilon }_0}\frac{k_{z3}}{{\epsilon }_{r3}}+\frac{k_{z3}/{\epsilon }_{r3}}{k_{z2}/{\epsilon }_x}},$ $R_{21}=\frac{1+\frac{{\sigma }_{s1}}{\omega {\epsilon }_0}\frac{k_{z1}}{{\epsilon }_{r1}}-\frac{k_{z1}/{\epsilon }_{r1}}{k_{z2}/{\epsilon }_x}}{1+\frac{{\sigma }_{s1}}{\omega {\epsilon }_0}\frac{k_{z1}}{{\epsilon }_{r1}}+\frac{k_{z1}/{\epsilon }_{r1}}{k_{z2}/{\epsilon }_x}},$ $T_{32}=\frac{2}{1+\frac{{\sigma }_{s2}}{\omega {\epsilon }_0}\frac{k_{z2}}{{\epsilon }_x}+\frac{k_{z2}/{\epsilon }_x}{k_{z3}/{\epsilon }_{r3}}},$ and $T_{23}=\frac{2}{1+\frac{{\sigma }_{s2}}{\omega {\epsilon }_0}\frac{k_{z3}}{{\epsilon }_{r3}}+\frac{k_{z3}/{\epsilon }_{r3}}{k_{z2}/{\epsilon }_x}},$ where ${\epsilon }_0$ is the permittivity of free space.

In the main text, we denote $r_p={\stackrel{\sim }{R}}_{32}.$ Because the modes of hybridized plasmons–phonon–polaritons are the singularity poles in the coefficient of $r_p,$ it is an instructive way to visualize the dispersion of these hybridized plasmons–phonon–polaritons via a false-color plot of $\left|Im\left(r_p\right)\right|$ as a function of $q$ and $\omega$ (8).

When setting ${\sigma }_{s1}=0$ in Eq. S4, one can solve the dispersion of hybridized plasmon–phonon-polaritons in the structure of air–BN–graphene–substrate. When setting ${\sigma }_{s1}={\sigma }_{s2}=0$ in Eq. S4, one can solve the dispersion of phonon polaritons in the structure of air–BN–substrate. When setting ${\sigma }_{s1}=0$ and ${\epsilon }_x={\epsilon }_z={\epsilon }_{r1}$ in Eq. S4, one can solve the dispersion of plasmon polaritons in the structure of air–graphene–substrate; i.e., $\frac{k_{z1}}{{\epsilon }_{r1}}+\frac{k_{z3}}{{\epsilon }_{r3}}+\frac{{\sigma }_{s2}}{\omega {\epsilon }_0}\frac{k_{z1}}{{\epsilon }_{r1}}\frac{k_{z3}}{{\epsilon }_{r3}}=0.$

Choice of the Substrate

When one selects the bulk BN to be the substrate of graphene, the mode of graphene plasmons within BN’s first reststrahlen band will disappear, as shown in Fig. S1. It has been reported that a silicon (Si) substrate can locally modify the π-orbital network of the graphene layer, resulting from the covalent bonding between the carbon (C) atoms and the surface Si atoms (51). This will inevitably increase the optical losses in graphene. Due to the above facts, both bulk BN and Si are not considered as the potential substrate in this work.

To maintain the relatively low propagation loss of the highly squeezed polaritons, we consider lossless dielectrics as substrates, such as germanium (Ge) in Figs. 1 and 3 and diamond in Fig. 2. The Ge and diamond have already been widely investigated as potential substrates for graphene (35, 37, 38).