Age of Jupiter inferred from the distinct genetics and formation times of meteorites

Significance

Jupiter is the most massive planet of the Solar System and its presence had an immense effect on the dynamics of the solar accretion disk. Knowing the age of Jupiter, therefore, is key for understanding how the Solar System evolved toward its present-day architecture. However, although models predict that Jupiter formed relatively early, until now, its formation has never been dated. Here we show through isotope analyses of meteorites that Jupiter’s solid core formed within only ∼1 My after the start of Solar System history, making it the oldest planet. Through its rapid formation, Jupiter acted as an effective barrier against inward transport of material across the disk, potentially explaining why our Solar System lacks any super-Earths.

Abstract

The age of Jupiter, the largest planet in our Solar System, is still unknown. Gas-giant planet formation likely involved the growth of large solid cores, followed by the accumulation of gas onto these cores. Thus, the gas-giant cores must have formed before dissipation of the solar nebula, which likely occurred within less than 10 My after Solar System formation. Although such rapid accretion of the gas-giant cores has successfully been modeled, until now it has not been possible to date their formation. Here, using molybdenum and tungsten isotope measurements on iron meteorites, we demonstrate that meteorites derive from two genetically distinct nebular reservoirs that coexisted and remained spatially separated between ∼1 My and ∼3–4 My after Solar System formation. The most plausible mechanism for this efficient separation is the formation of Jupiter, opening a gap in the disk and preventing the exchange of material between the two reservoirs. As such, our results indicate that Jupiter’s core grew to ∼20 Earth masses within <1 My, followed by a more protracted growth to ∼50 Earth masses until at least ∼3–4 My after Solar System formation. Thus, Jupiter is the oldest planet of the Solar System, and its solid core formed well before the solar nebula gas dissipated, consistent with the core accretion model for giant planet formation.

The formation of gas-giant planets such as Jupiter and Saturn is thought to have involved the growth of large solid cores of ∼10–20 Earth masses (M_E), followed by the accumulation of gas onto these cores (1, 2). Thus, the gas-giant cores must have formed before dissipation of the solar nebula—the gaseous circumstellar disk surrounding the young Sun—which likely occurred between 1 My and 10 My after Solar System formation (3). Although such rapid accretion of the gas-giant cores has successfully been modeled (1, 2, 4), until now it has not been possible to actually date their formation. Here we show that the growth of Jupiter can be dated using the distinct genetic heritage and formation times of meteorites.

Most meteorites derive from small bodies located in the main asteroid belt between Mars and Jupiter. Originally these bodies probably formed at a much wider range of heliocentric distances, as suggested by the distinct chemical and isotopic compositions of meteorites (5–8) and by dynamical models indicating that the gravitational influence of the gas giants led to scattering of small bodies into the asteroid belt (9, 10). Information on the initial formation location of meteorite parent bodies within the solar accretion disk can be obtained from nucleosynthetic isotope anomalies in meteorites. These anomalies arise through the heterogeneous distribution of isotopically anomalous presolar components and vary as a function of heliocentric distance (6, 11). For instance, Cr, Ti, and Mo isotope anomalies (6–8, 12) reveal a fundamental dichotomy in the genetic heritage of meteorites, distinguishing between “noncarbonaceous” and “carbonaceous” meteorite reservoirs (11). This distinction may reflect either a temporal change in disk composition or the separation of materials accreted inside [noncarbonaceous (NC) meteorites] and outside [carbonaceous (CC) meteorites] the orbit of Jupiter (11–14). If the latter is correct, then the age of Jupiter can be determined by assessing the formation time and longevity of the NC and CC meteorite reservoirs. However, it is currently not known when these two reservoirs formed and whether and for how long they remained isolated from each other.

To address these issues and to ultimately determine the timescale of Jupiter’s formation, we obtained W and Mo isotopic data for iron meteorites (Materials and Methods, SI Materials and Methods, Fig. S1, and Tables S1–S4). These samples are fragments of the metallic cores from some of the earliest-formed planetesimals (15), making them ideal samples to search for the effects of giant planet formation on the dynamics of the early Solar System. Previous W isotope studies on iron meteorites have focused on the major groups (i.e., IIAB, IID, IIIAB, IVA, and IVB) and on determining the timescales and processes of core formation in these bodies (15). Here we extend these studies by examining a larger set of iron meteorite groups (i.e., IC, IIC, IID, IIF, IIIE, and IIIF), for which we determined the timing of core formation using the ¹⁸²Hf–¹⁸²W chronometer (half-life = 8.9 My), as well as nucleosynthetic Mo isotopic signatures, which enables us to link these irons to either the NC or the CC meteorites.

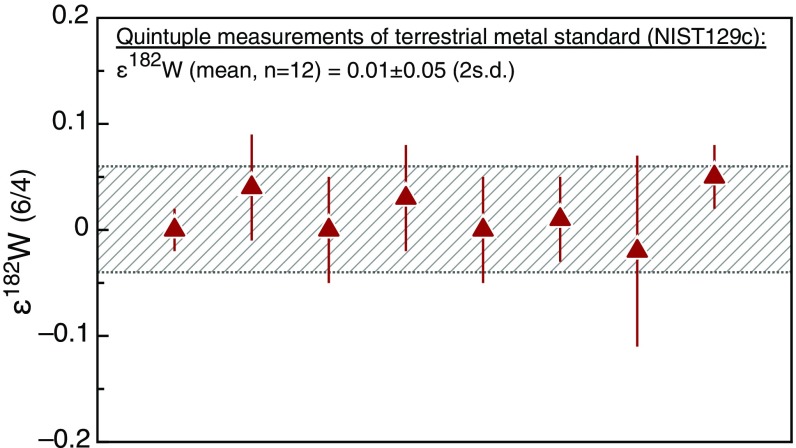
Fig. S1.

ε¹⁸²W results for the terrestrial metal standard (NIST129c) analyzed in this study. Each data point represents a quintuple measurement of a standard that was processed through the full chemical separation and error bars denote 95% confidence limits of the five solution replicate measurements. Hatched area shows the SD (2 SD) of the replicate quintuple measurements.

Table S1.

Tungsten isotope compositions of terrestrial metal standard NIST129c determined by MC-ICPMS

Standard ID	ε182W (6/3)meas.*, ±2 SE	ε182W (6/4)meas.*, ±2 SE	ε183W (6/4)meas.*, ±2 SE	ε184W (6/3)meas.*, ±2 SE
S04	0.07 ± 0.04	0.03 ± 0.04	−0.03 ± 0.04	0.02 ± 0.03
S04	0.04 ± 0.04	−0.01 ± 0.04	−0.04 ± 0.03	0.03 ± 0.02
S04	−0.04 ± 0.04	−0.06 ± 0.04	−0.02 ± 0.03	0.01 ± 0.02
S04	0.00 ± 0.04	0.02 ± 0.04	0.01 ± 0.04	−0.01 ± 0.02
S04	−0.01 ± 0.08	−0.02 ± 0.09	−0.01 ± 0.07	0.00 ± 0.05
S04	−0.04 ± 0.08	−0.02 ± 0.09	0.01 ± 0.08	−0.01 ± 0.05
S04	0.03 ± 0.07	0.08 ± 0.08	0.04 ± 0.06	−0.02 ± 0.04
S04	0.02 ± 0.09	0.05 ± 0.09	0.02 ± 0.07	−0.01 ± 0.05
S04	0.09 ± 0.07	0.06 ± 0.09	−0.02 ± 0.07	0.01 ± 0.05
S04	−0.01 ± 0.08	−0.03 ± 0.08	−0.01 ± 0.07	0.01 ± 0.05
S04	−0.02 ± 0.07	−0.01 ± 0.08	0.01 ± 0.07	−0.01 ± 0.05
S04	0.02 ± 0.07	−0.01 ± 0.08	−0.03 ± 0.06	0.02 ± 0.04
S04	−0.01 ± 0.07	−0.09 ± 0.08	−0.06 ± 0.06	0.04 ± 0.04
S04	0.05 ± 0.07	0.00 ± 0.08	−0.04 ± 0.07	0.03 ± 0.04
S04	0.06 ± 0.07	0.01 ± 0.08	−0.04 ± 0.06	0.03 ± 0.04
S04	−0.03 ± 0.07	0.05 ± 0.08	0.06 ± 0.06	−0.04 ± 0.04
S04	0.02 ± 0.07	0.05 ± 0.09	0.03 ± 0.07	−0.02 ± 0.05
T07	−0.01 ± 0.06	0.02 ± 0.06	0.03 ± 0.06	−0.02 ± 0.04
T07	−0.01 ± 0.06	−0.01 ± 0.07	0.00 ± 0.06	0.00 ± 0.04
T07	0.06 ± 0.06	0.04 ± 0.07	−0.01 ± 0.06	0.01 ± 0.04
T07	0.08 ± 0.07	0.07 ± 0.06	−0.01 ± 0.06	0.01 ± 0.04
T07	0.18 ± 0.06	0.08 ± 0.07	−0.07 ± 0.06	0.05 ± 0.04
Z08	0.04 ± 0.05	0.05 ± 0.06	0.01 ± 0.05	0.00 ± 0.04
Z08	0.08 ± 0.05	−0.05 ± 0.06	−0.09 ± 0.05	0.06 ± 0.03
Z08	0.06 ± 0.05	0.02 ± 0.06	−0.03 ± 0.05	0.02 ± 0.03
Z08	−0.01 ± 0.05	0.00 ± 0.06	0.00 ± 0.05	0.00 ± 0.03
Z08	0.09 ± 0.05	0.08 ± 0.06	−0.01 ± 0.05	0.00 ± 0.03
Z08	0.10 ± 0.05	0.02 ± 0.06	−0.06 ± 0.05	0.04 ± 0.03
Z08	0.03 ± 0.06	0.08 ± 0.05	0.04 ± 0.05	−0.03 ± 0.04
Z08	−0.04 ± 0.05	−0.09 ± 0.06	−0.04 ± 0.05	0.02 ± 0.03
Z08	0.00 ± 0.05	−0.10 ± 0.06	−0.07 ± 0.05	0.05 ± 0.03
AG04	0.01 ± 0.07	0.01 ± 0.07	0.00 ± 0.07	0.00 ± 0.04
AG04	0.07 ± 0.08	0.00 ± 0.07	−0.05 ± 0.07	0.03 ± 0.04
AG04	0.15 ± 0.06	0.06 ± 0.08	−0.07 ± 0.07	0.05 ± 0.04
AG04	0.02 ± 0.07	0.10 ± 0.07	0.06 ± 0.07	−0.04 ± 0.04
AG04	0.00 ± 0.07	0.00 ± 0.07	0.00 ± 0.07	0.00 ± 0.04
SG	0.02 ± 0.05	0.00 ± 0.07	−0.01 ± 0.05	0.01 ± 0.03
SG	0.01 ± 0.05	−0.01 ± 0.07	−0.01 ± 0.05	0.01 ± 0.03
SG	−0.02 ± 0.05	−0.05 ± 0.07	−0.02 ± 0.05	0.01 ± 0.03
SG	−0.05 ± 0.05	0.03 ± 0.08	0.06 ± 0.05	−0.04 ± 0.03
SG	0.02 ± 0.05	0.02 ± 0.07	0.00 ± 0.05	0.00 ± 0.03
BW09	0.02 ± 0.06	−0.07 ± 0.07	−0.07 ± 0.05	0.04 ± 0.03
BW09	0.03 ± 0.06	0.02 ± 0.07	−0.01 ± 0.05	0.00 ± 0.03
BW09	0.10 ± 0.06	0.02 ± 0.08	−0.06 ± 0.05	0.04 ± 0.03
BW09	0.12 ± 0.06	0.02 ± 0.08	−0.07 ± 0.05	0.05 ± 0.03
BW09	0.08 ± 0.08	0.04 ± 0.08	−0.03 ± 0.06	0.02 ± 0.04
CF10	0.15 ± 0.06	−0.03 ± 0.06	−0.13 ± 0.05	0.09 ± 0.03
CF10	0.06 ± 0.06	−0.01 ± 0.07	−0.05 ± 0.06	0.03 ± 0.04
CC10	0.11 ± 0.06	0.04 ± 0.06	−0.05 ± 0.07	0.03 ± 0.04
CC10	−0.02 ± 0.05	0.06 ± 0.06	0.06 ± 0.05	−0.04 ± 0.04
CC10	0.06 ± 0.05	0.07 ± 0.06	0.01 ± 0.06	0.00 ± 0.04
CC10	0.06 ± 0.05	0.02 ± 0.06	−0.03 ± 0.06	0.02 ± 0.04
Mean, n = 53
±2 SD	0.04 ± 0.11	0.01 ± 0.09	−0.02 ± 0.08	0.01 ± 0.05
±95% conf. limit	0.04 ± 0.01	0.01 ± 0.01	−0.02 ± 0.01	0.01 ± 0.01

Uncertainties represent 2 SE obtained from within-run statistics.

^*Internally normalized to ¹⁸⁶W/¹⁸³W = 1.98594 or to ¹⁸⁶W/¹⁸⁴W = 0.92767.

Table S4.

Molybdenum isotope compositions of iron meteorites analyzed by MC-ICPMS

Meteorite Group	Collection, no.	ID	N	ε92Mo, ±95% conf.	ε94Mo, ±95% conf.	ε95Mo, ±95% conf.	ε97Mo, ±95% conf.	ε100Mo, ±95% conf.
IC iron meteorites
Chihuahua City	BM 1959, 1011	BW01	8	0.96 ± 0.12	0.86 ± 0.08	0.34 ± 0.07	0.20 ± 0.08	0.27 ± 0.13
Murnpeowie	BM 2005, M179	BW02	8	1.16 ± 0.20	1.11 ± 0.20	0.41 ± 0.05	0.27 ± 0.05	0.37 ± 0.08
IIC iron meteorites
Kumerina	BM 1938, 220	BW03	8	2.91 ± 0.28	2.34 ± 0.18	1.50 ± 0.08	0.79 ± 0.10	0.92 ± 0.09
Wiley	BM 1959, 914	BW04	8	4.14 ± 0.22	3.39 ± 0.13	2.19 ± 0.11	1.19 ± 0.11	1.54 ± 0.14
Ballinoo	ME 980	CJ01	8	2.76 ± 0.13	2.19 ± 0.10	1.60 ± 0.09	0.89 ± 0.09	1.01 ± 0.10
IID iron meteorites
Bridgewater	ME 1895	BT02	7	1.63 ± 0.10	1.16 ± 0.16	0.96 ± 0.15	0.51 ± 0.12	0.67 ± 0.17
IIF iron meteorites
Monahans	BM 1959, 910	CC01	8	1.50 ± 0.21	1.11 ± 0.13	0.94 ± 0.08	0.50 ± 0.08	0.63 ± 0.13
IIIE iron meteorites
Kokstad	ME 1015	BW05	8	0.98 ± 0.17	0.86 ± 0.14	0.33 ± 0.13	0.26 ± 0.09	0.28 ± 0.08
Colonia Obreira	ME 2871	BW06	8	1.03 ± 1.36	0.97 ± 0.16	0.35 ± 0.09	0.25 ± 0.14	0.35 ± 0.12
Staunton	BM 1955, M239	BW07	8	1.02 ± 0.16	0.95 ± 0.10	0.41 ± 0.11	0.30 ± 0.08	0.39 ± 0.11
Paneth's iron	BM 2005, M199	BW08	8	1.09 ± 0.15	0.93 ± 0.20	0.42 ± 0.07	0.35 ± 0.05	0.37 ± 0.12
IIIF iron meteorites
Klamath Falls	ME 2789	CC02	8	1.70 ± 0.18	1.20 ± 0.18	0.98 ± 0.06	0.56 ± 0.11	0.62 ± 0.09
Clark County	BM 1959, 949	CC03	6	1.45 ± 0.23	1.20 ± 0.17	1.00 ± 0.06	0.54 ± 0.04	0.59 ± 0.23

Instrumental mass bias was corrected using the exponential law by internal normalization to ⁹⁸Mo/⁹⁶Mo = 1.453173. N, number of solution replicates. The uncertainties reported for measured εⁱMo values of samples (subscript “meas.”) represent the 95% conf. limits of the mean [i.e., according to (SD × t_0.95,N−1)/√N].

SI Materials and Methods

Samples and Chemical Separation of W, Pt, and Mo.

For this study we selected 16 samples covering five different rare iron meteorite groups (IC, IIC, IIF, IIIE, and IIIF; Tables S2–S4). We targeted these samples because some of them (e.g., IIC iron meteorites) show ¹⁵N signatures suggestive of an outer Solar System origin (38, 39). These iron meteorite samples, therefore, are prime candidates for differentiated bodies that might have accreted beyond Jupiter. In addition, we also analyzed 3 IID iron meteorites that complement the Pt-W isotope dataset for IID iron meteorites obtained previously (36). Samples (∼0.2–1.5 g) were cut using a diamond saw, polished with abrasives (SiC), and ultrasonically cleaned in ethanol to remove any saw marks and adhering dust. To remove any terrestrial contamination, the samples were then mildly leached in 6 M HCl (plus trace HNO₃) on a hotplate at ∼90 °C for ∼10 min. The iron meteorites were digested in 20 mL concentrated HNO₃–HCl (2:1) on a hotplate at 130 °C for at least 24 h. Upon complete digestion the sample solutions were split into a fraction for W and Mo (∼90%) and for Pt (∼10%) isotope analysis.

Table S2.

Platinum isotope compositions of metal samples determined by MC-ICPMS

Sample Group	Collection, no.	N	Normalized to 196Pt/195Pt			Normalized to 198Pt/195Pt
			ε192Pt, ±2 SD	ε194Pt, ±2 SD	ε198Pt, ±2 SD	ε192Pt, ±2 SD	ε194Pt, ±2 SD	ε196Pt, ±2 SD
IC iron meteorites
Chihuahua City	BM 1959, 1011	1	0.76 ± 1.30	0.24 ± 0.13	−0.20 ± 0.22	0.50 ± 1.30	0.17 ± 0.11	0.07 ± 0.07
Murnpeowie	BM 2005, M179	2	5.11 ± 1.30	0.88 ± 0.13	−1.15 ± 0.22	3.95 ± 1.30	0.50 ± 0.11	0.38 ± 0.07
Murnpeowie (replicate)	BM 2005, M179	4	3.11 ± 1.02	0.55 ± 0.14	−0.76 ± 0.16	2.34 ± 1.05	0.29 ± 0.11	0.26 ± 0.05
Arispe	Münster	6	14.30 ± 0.29	0.84 ± 0.04	−1.04 ± 0.09	13.33 ± 0.27	0.52 ± 0.03	0.35 ± 0.03
Arispe (replicate)	Münster	6	13.81 ± 0.22	0.80 ± 0.06	−1.03 ± 0.12	12.89 ± 0.36	0.48 ± 0.04	0.32 ± 0.04
Bendego	USNM #351	2	1.01 ± 1.30	0.90 ± 0.13	−1.55 ± 0.22	−0.57 ± 1.30	0.38 ± 0.11	0.52 ± 0.07
Arispe	ME 1011	3	14.97 ± 1.30	1.08 ± 0.13	−1.25 ± 0.22	13.69 ± 1.30	0.67 ± 0.11	0.42 ± 0.07
Bendego	ME 6	3	2.52 ± 1.30	0.80 ± 0.13	−1.42 ± 0.22	1.08 ± 1.30	0.32 ± 0.11	0.47 ± 0.07
IIC iron meteorites
Kumerina	BM 1938, 220	2	0.94 ± 1.30	0.21 ± 0.13	−0.13 ± 0.22	0.80 ± 1.30	0.17 ± 0.11	0.04 ± 0.07
Kumerina (replicate)	BM 1938, 220	3	−0.08 ± 1.30	0.01 ± 0.13	0.07 ± 0.22	−0.02 ± 1.30	0.04 ± 0.11	−0.02 ± 0.07
Wiley	BM 1959, 914	4	0.69 ± 1.12	0.15 ± 0.01	−0.14 ± 0.21	0.55 ± 1.34	0.12 ± 0.05	0.05 ± 0.07
Wiley (replicate)	BM 1959, 914	5	0.81 ± 0.65	0.19 ± 0.09	−0.25 ± 0.18	0.58 ± 0.65	0.11 ± 0.06	0.08 ± 0.06
Ballinoo	ME 980	3	−0.44 ± 1.30	0.06 ± 0.13	0.04 ± 0.22	−0.37 ± 1.30	0.08 ± 0.11	−0.01 ± 0.07
IID iron meteorites
Bridgewater	ME 1895	5	0.70 ± 0.90	0.00 ± 0.09	0.04 ± 0.05	0.80 ± 0.90	0.02 ± 0.08	−0.01 ± 0.02
N’Kandhla	BM 1921, 17	5	0.65 ± 0.29	0.03 ± 0.09	−0.03 ± 0.16	0.64 ± 0.23	0.03 ± 0.05	0.01 ± 0.05
Richa	BM 1966, 55	4	1.28 ± 0.26	−0.01 ± 0.05	0.06 ± 0.11	1.36 ± 0.30	0.01 ± 0.07	−0.02 ± 0.04
IIF iron meteorites
Monahans	BM 1959, 910	4	1.10 ± 0.87	0.22 ± 0.07	−0.21 ± 0.12	0.91 ± 0.90	0.15 ± 0.05	0.07 ± 0.04
Monahans (replicate)	BM 1959, 910	2	1.67 ± 1.30	0.17 ± 0.13	−0.23 ± 0.22	1.43 ± 1.30	0.09 ± 0.11	0.08 ± 0.07
IIIE iron meteorites
Willow Creek	Münster	1	0.95 ± 1.30	0.27 ± 0.13	−0.40 ± 0.22	0.55 ± 1.30	0.14 ± 0.11	0.13 ± 0.07
Kokstad	ME 1015	1	2.74 ± 1.30	0.74 ± 0.13	−1.05 ± 0.22	1.62 ± 1.30	0.38 ± 0.11	0.35 ± 0.07
Kokstad (replicate)	ME 1015	2	1.62 ± 1.30	0.57 ± 0.13	−0.77 ± 0.22	0.82 ± 1.30	0.29 ± 0.11	0.26 ± 0.07
Colonia Obrera	ME 2871	1	0.14 ± 1.30	0.07 ± 0.13	0.03 ± 0.22	0.17 ± 1.30	0.06 ± 0.11	−0.01 ± 0.07
Colonia Obrera (replicate)	ME 2871	1	−0.17 ± 1.30	0.10 ± 0.13	−0.09 ± 0.22	−0.30 ± 1.30	0.08 ± 0.11	0.03 ± 0.07
Staunton	BM 1955, M239	1	−0.10 ± 1.30	0.17 ± 0.13	0.22 ± 0.22	−0.17 ± 1.30	0.15 ± 0.11	−0.07 ± 0.07
Staunton (replicate)	BM 1955, M239	2	−0.16 ± 1.30	0.14 ± 0.13	−0.16 ± 0.22	−0.28 ± 1.30	0.08 ± 0.11	0.05 ± 0.07
Paneth’s Iron	BM 2005, M199	2	0.55 ± 1.30	0.19 ± 0.13	−0.26 ± 0.22	0.26 ± 1.30	0.12 ± 0.11	0.09 ± 0.07
IIIF iron meteorites
Klamath Falls	ME 2789	1	0.98 ± 1.30	0.09 ± 0.13	−0.18 ± 0.22	0.39 ± 1.30	0.06 ± 0.11	0.06 ± 0.07
Klamath Falls (replicate)	ME 2789	1	0.97 ± 1.30	0.12 ± 0.13	0.02 ± 0.22	0.99 ± 1.30	0.13 ± 0.11	−0.01 ± 0.07
Clark County	BM 1959, 949	4	2.88 ± 0.99	0.11 ± 0.11	−0.08 ± 0.22	2.81 ± 0.78	0.08 ± 0.06	0.03 ± 0.07
Clark County (replicate)	BM 1959, 949	2	3.79 ± 1.30	0.27 ± 0.13	−0.29 ± 0.22	3.54 ± 1.30	0.17 ± 0.11	0.10 ± 0.07
Terrestrial metal standard
NIST129c #1		2	0.51 ± 1.30	0.10 ± 0.13	−0.15 ± 0.22	0.38 ± 1.30	0.08 ± 0.11	0.05 ± 0.07
NIST129c #2		7	0.66 ± 0.24	0.07 ± 0.10	−0.07 ± 0.10	0.58 ± 0.25	0.04 ± 0.07	0.02 ± 0.03
NIST129c #3		1	0.36 ± 1.30	0.02 ± 0.13	−0.08 ± 0.22	0.28 ± 1.30	−0.01 ± 0.11	0.03 ± 0.07
NIST129c #4		4	0.99 ± 1.23	0.04 ± 0.11	0.02 ± 0.15	0.97 ± 1.31	0.04 ± 0.08	−0.01 ± 0.05

Instrumental mass fractionation was corrected using the exponential law by internal normalization to ¹⁹⁸Pt/¹⁹⁵Pt = 0.2145 or to ¹⁹⁶Pt/¹⁹⁵Pt = 0.7464. N, number of solution replicates. The uncertainties reported for εⁱPt values of samples, in the case n < 4, represent the 2 SD (n = 63) obtained from repeated analyses of the terrestrial standard NIST129c (15): [±1.3 for ε¹⁹²Pt (6/5), ±0.13 for ε¹⁹⁴Pt (6/5), ±0.22 for ε¹⁹⁸Pt (6/5), ±1.3 for ε¹⁹²Pt (8/5), ±0.11 for ε¹⁹⁴Pt (8/5), ±0.07 for ε¹⁹⁶Pt (8/5)] or in the case n > 4, the 95% conf. limits of the mean [i.e., according to (SD × t_0.95,N−1)/√N].

The chemical separation of Pt followed previously published procedures (36) and is based on the techniques initially described in ref. 40. Tungsten and Mo were sequentially separated from the sample matrix using anion exchange chromatography (4 mL Biorad AG1X8, 200–400 mesh) (41), where W was eluted using 15 mL 6 M HCl–1 M HF, followed by Mo using 10 mL 3 M HNO₃. The W cuts from the first column were further purified using a cleanup anion chromatography step, which essentially is a miniaturized version of the first column with only 1 mL resin (41). To obtain Mo cuts with sufficiently low Ru/Mo and Zr/Mo, the Mo cuts from the first column were further purified using two additional ion chromatography steps, using Eichrom TRU resin (6). Total yields after the chemical separation were ∼70–100% for W, ∼70% for Pt, and ∼70% for Mo. Total procedural blanks were <200 pg for W, <100 pg for Pt, and <1,000 pg for Mo. These blank amounts are inconsequential because of the large amount of each element analyzed (∼250 ng W, ∼100–400 ng Pt, and ∼500–800 ng Mo).

Mass Spectrometry.

The W, Pt, and Mo isotope compositions were measured on a ThermoScientific Neptune Plus MC-ICPMS in the Institut für Planetologie at the University of Münster. The analytical methods for high-precision W, Pt, and Mo isotope analyses were largely based on previously reported procedures (12, 15, 36). Samples and standards for W, Pt, and Mo isotope measurements were introduced into the mass spectrometer, using ESI or Teledyne Cetac C-flow self-aspirating PFA nebulizers (∼50–60 μL/min) connected to a Teledyne Cetac Aridus II desolvator system. For W, the measurements were performed in low-resolution mode, using Jet sampler and X-skimmer cones. All four major W isotopes (¹⁸²W, ¹⁸³W, ¹⁸⁴W, and ¹⁸⁶W) were measured simultaneously. Total ion beams of ∼2–3 ×10⁻¹⁰ were obtained for ∼30-ppb W standard solutions at an uptake rate of ∼60 μL/min. Electronic baselines were obtained before each sample measurement by deflecting the beam using the electrostatic analyzer for 60 s and then subtracted from sample signal intensities. A single W isotope measurement comprised 200 cycles of 4.2 s integration time each. Small isobaric interferences from ¹⁸⁴Os and ¹⁸⁶Os on W isotope ratios were corrected by monitoring interference-free ¹⁸⁸Os and were generally much smaller than ∼5 ppm on ¹⁸²W/¹⁸⁴W. Instrumental mass bias was corrected by internal normalization to either ¹⁸⁶W/¹⁸³W = 1.9859 (denoted “6/3”) or ¹⁸⁶W/¹⁸⁴W = 0.92767 (denoted “6/4”), using the exponential law. The W isotope analyses of samples were bracketed by measurements of terrestrial solution standards (Alfa Aesar; batch 22312), whose concentrations matched those of the sample solutions to within ∼10–20%.

For Pt, the measurements were performed in low-resolution mode, using standard Ni sampler and (H) skimmer cones. Total ion beams of ∼2–4 ×10⁻¹⁰ were obtained for ∼200-ppb Pt standard solutions at uptake rates of ∼50–60 μL/min. Five Pt isotopes (¹⁹²Pt, ¹⁹⁴Pt, ¹⁹⁵Pt, ¹⁹⁶Pt, and ¹⁹⁸Pt) were measured simultaneously, and each measurement comprised a 60-s electronic baseline measurement followed by 100 isotope ratio measurements of 4.2 s integration time each. Instrumental mass bias was corrected by internally normalizing to either ¹⁹⁶Pt/¹⁹⁵Pt = 0.7464 (denoted “6/5”) or ¹⁹⁸Pt/¹⁹⁵Pt = 0.2145 (denoted “8/5”), using the exponential law. All Pt isotope data are reported in εⁱPt, as the parts per 10⁴ deviation in ⁱPt/^jPt relative to the terrestrial bracketing solution standard analyses.

The Mo isotope compositions of iron meteorites were performed in low-resolution mode, using standard Ni sampler and (H) skimmer cones. Total ion beams of ∼1.1 ×10⁻¹⁰ were obtained for ∼100-ppb Mo standard solutions at an uptake rate of ∼50 μL/min. Six Mo isotopes (⁹²Mo, ⁹⁴Mo, ⁹⁵Mo, ⁹⁶Mo, ⁹⁸Mo, and ¹⁰⁰Mo) were measured simultaneously, and each measurement consisted of 40 on-peak baseline measurements of 4.2 s each, followed by 100 isotope ratio measurements of 8.4 s integration time each. Although the measurement solutions generally had very low ⁹¹Zr/⁹⁶Mo (<0.00005) and ⁹⁹Ru/⁹⁶Mo (<0.00001), potential isobaric interferences from remaining Zr and Ru were corrected for by monitoring interference-free ⁹¹Zr and ⁹⁹Ru. The magnitude of these corrections was generally <0.2 ε-units on εⁱMo. Only a few measurement solutions had larger Zr/Mo (i.e., up to ⁹¹Zr/⁹⁶Mo ∼ 0.002 for Wiley), resulting in larger interference corrections (up to ∼10–20 εⁱMo units). Nevertheless, measurements of Mo solution standards with admixed Zr and Ru demonstrate up to Zr inference corrections of ∼25 ε on εⁱMo yield accurate results (12). Instrumental mass bias was corrected by internal normalization to ⁹⁸Mo/⁹⁶Mo = 1.453173 (denoted “8/6”), using the exponential law. The W, Pt, and Mo isotope data are reported as ε-unit (i.e., parts per 10⁴) deviation relative to the isotopic ratios measured for terrestrial bracketing solution standards. The reported εⁱW, εⁱPt, and εⁱMo values for samples (Tables S2–S4) represent the mean of pooled solution replicates (n = 1–8) together with their associated external uncertainties.

Accuracy and Reproducibility of W, Pt, and Mo Isotope Measurements.

The accuracy and precision of the W, Pt, and Mo isotope measurements were assessed through analyses of terrestrial standards that were processed and analyzed alongside the iron meteorites (Tables S1 and S2 and Fig. S1). These analyses followed our well-established routines for high-precision W, Pt, and Mo measurements by MC-ICPMS (6, 12, 15, 36). Previous high-precision W isotope studies using MC-ICPMS observed very small excesses in ε¹⁸²W (6/3) and ε¹⁸⁴W (6/3) and corresponding deficits in ε¹⁸³W (6/4) for processed terrestrial standards, most likely caused by a nuclear field shift effect induced during incomplete redissolution of W in Savillex beakers (36, 41–47). The magnitude of the analytical ¹⁸³W effect varies among different studies and typically is between –0.1 and –0.2 ε¹⁸³W (41–43, 46). In the present study, we were able to minimize this effect by repeated dry downs of the samples with HClO₄ following each step of ion exchange separation of W. The repeated analyses of eight different digestions of the NIST129c metal standard processed this way yielded a mean ε¹⁸³W of –0.03 ± 0.03 (95% conf. interval, n = 8, Table S1 and Fig. S2); the mean ε¹⁸²W (6/3) of the NIST129c analyses is +0.05 ± 0.03 (95% conf. interval, n = 8), consistent with a small analytical ¹⁸³W effect for which we expect ε¹⁸²W (6/3) ∼ 1.5 × ε¹⁸³W (6/4). Thus, the average magnitude of this ¹⁸³W effect is significantly smaller than in previous studies and does not compromise the conclusions drawn from the ε¹⁸³W data. Finally, we underline that this analytical effect occurs only for normalizations involving ¹⁸³W. For this reason, the ε¹⁸²W (6/4) values—the normalization generally used for chronological interpretation—are not compromised by this effect.

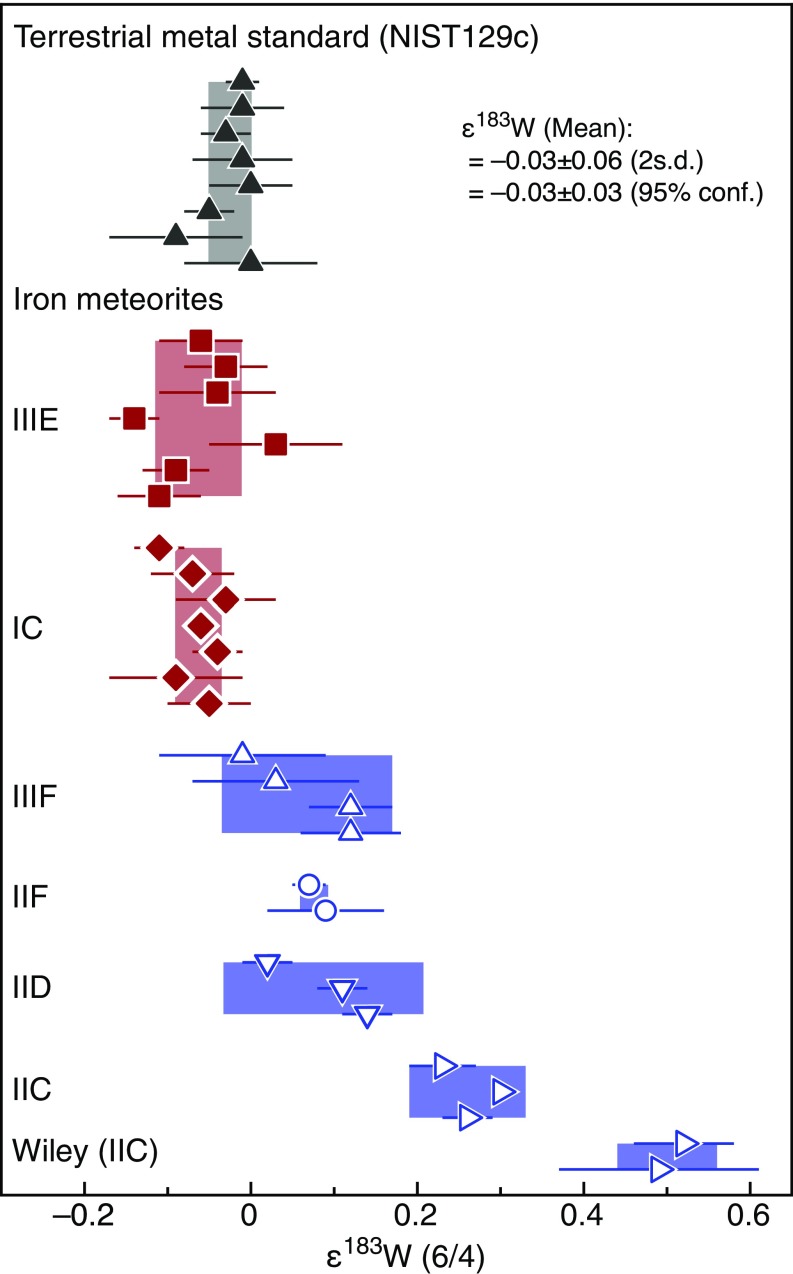
Fig. S2.

Measured ε¹⁸³W of iron meteorites analyzed in this study. Also shown are results for the terrestrial metal standard (NIST129c) analyzed alongside the iron meteorites. Error bars denote external uncertainties of quintuple measurements (95% conf. limit). Shaded areas show group mean values and their associated external uncertainties (95% conf. limit).

CC and NC Iron Meteorites

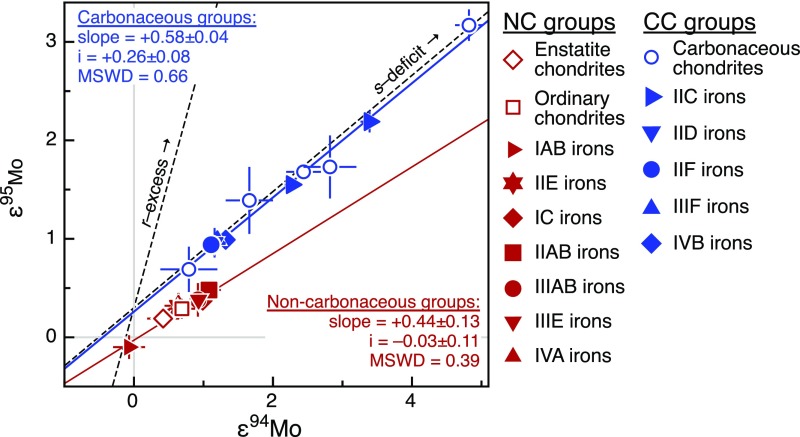
The Mo isotopic data reveal variable nucleosynthetic anomalies in iron meteorites (Fig. 1). Consistent with prior studies (6), we find that these anomalies predominantly reflect the heterogeneous distribution of a presolar carrier enriched in Mo nuclides produced in the slow neutron capture process (s-process) of nucleosynthesis (Fig. 1). However, in a plot of ε⁹⁵Mo vs. ε⁹⁴Mo (the parts per 10,000 deviations of ⁹⁵Mo/⁹⁶Mo and ⁹⁴Mo/⁹⁶Mo from terrestrial standard values), the iron meteorites fall onto two distinct s-process mixing lines. Whereas most of the newly investigated irons (IIC, IID, IIF, and IIIF) plot on an s-process mixing line together with carbonaceous chondrites, most of the previously studied irons as well as the IC and IIIE irons plot on another s-process mixing line together with ordinary chondrites, enstatite chondrites, and the Earth’s mantle (εⁱMo = 0) (Fig. 1). Thus, several iron meteorite groups (IIC, IID, IIF, IIIF, and IVB) belong to the CC meteorites, whereas several other groups (IC, IIAB, IIIAB, IIIE, and IVA) belong to the NC meteorites (Fig. 1).

Fig. 1.

Molybdenum isotope dichotomy of iron meteorite groups. Iron meteorites and chondrites define two distinct trends in ε⁹⁵Mo vs. ε⁹⁴Mo space, separating a CC (blue symbols) from a NC reservoir (red symbols). Note that the two regressions (solid lines) through the iron meteorite and chondrites from NC and CC reservoirs yield significantly different ε⁹⁵Mo intercept values. Error bars denote 95% conf. limits on group mean values. Also shown are s-process and r-process mixing lines (dashed lines), plotted at an ordinate ε⁹⁵Mo of +0.3 and calculated using the Mo isotopic composition of presolar SiC grains (37), representing s-process Mo and the corresponding r-process residuals. Note that other Mo isotopes show consistent systematics (Fig. S5). Data for IC, IIC, IID, IIF, IIIF, and IIIE iron meteorites are from this study and data for chondrites and other iron meteorite groups are from ref. 6.

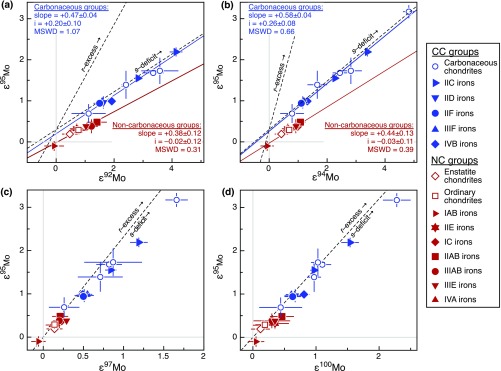
Fig. S5.

Molybdenum isotope systematics of iron meteorites. (A) In ε⁹⁵Mo vs. ε⁹²Mo space different iron meteorites and chondrites define two distinct trends, separating a CC (blue symbols) from a NC reservoir (red symbols). Regressions through the iron meteorite and chondrite data of the two reservoirs are shown as solid lines. Data are from this study and from ref. 6. Error bars denote external uncertainties (95% conf. limits) on group mean values. The variations within the CC and the NC reservoirs are due to s-process heterogeneity and the offset of the two lines by the homogeneous addition of r-process Mo to the CC reservoir. Also shown are s-process and r-process mixing lines (dashed), plotted at an ordinate ε⁹⁵Mo of +0.3 and calculated using the Mo isotopic composition of presolar SiC grains (37), representing s-process Mo and the corresponding r-process residuals. (B) Same as A but in ε⁹⁵Mo vs. ε⁹⁴Mo space. (C) In ε⁹⁵Mo vs. ε⁹⁷Mo space, the two reservoirs cannot be discriminated from each other, because r- and s-process mixing lines define identical trajectories. Nevertheless, even in this space, the data are consistent with an addition of r-process material to the CC reservoir relative to the NC reservoir. For instance, the IIF overlap with the IIAB irons in their ε⁹²Mo and ε⁹⁴Mo compositions, but not in ε⁹⁵Mo. (D) Same as C but for ε⁹⁵Mo vs. ε¹⁰⁰Mo.

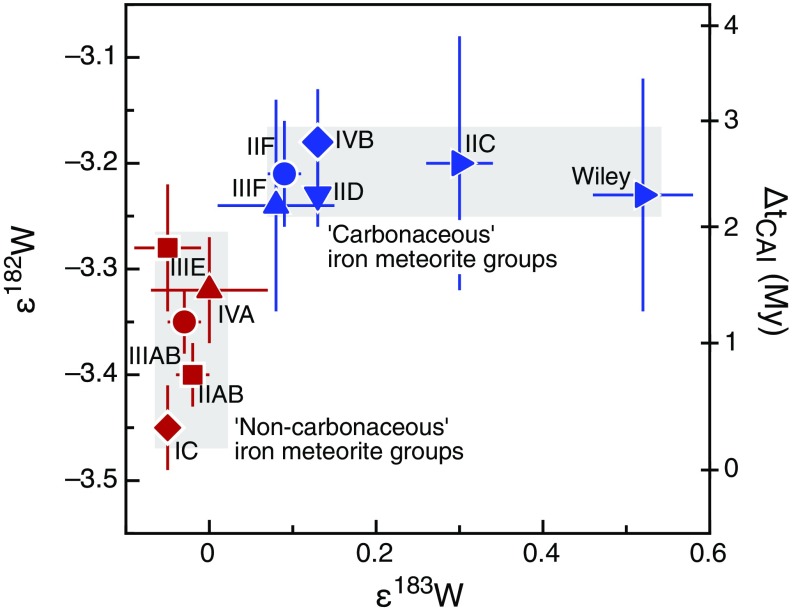
A similar genetic dichotomy is seen for W isotopes, which for iron meteorites reveal two distinct clusters of ε¹⁸²W and ε¹⁸³W (the parts per 10,000 deviations of ¹⁸²W/¹⁸⁴W and ¹⁸³W/¹⁸⁴W from terrestrial standard values). The NC irons have ε¹⁸²W values between approximately –3.4 and –3.3 and no nucleosynthetic W isotope anomalies (i.e., ε¹⁸³W ∼ 0), whereas the CC irons have ε¹⁸²W values of around –3.2 and show nucleosynthetic ε¹⁸³W excesses (Fig. 2, Fig. S2, and Table S5). Note that the ε¹⁸²W values of each group were corrected for the effects of cosmic ray exposure (Figs. S3 and S4 and Table S5), using Pt isotopes as the neutron dosimeter (15). In addition, for the iron groups showing ¹⁸³W anomalies, the ε¹⁸²W values were corrected for nucleosynthetic ε¹⁸²W variations, by using correlated ε¹⁸²W–ε¹⁸³W variations induced by nucleosynthetic isotope heterogeneities (15) (SI Text for details).

Fig. 2.

Tungsten isotope dichotomy of iron meteorite groups. Error bars denote 95% conf. intervals on group mean values. ε¹⁸²W signatures were corrected for effects of nucleosynthetic heterogeneity and secondary neutron capture (SI Text). Plotted on the right ordinate axis are two-stage Hf-W model ages of core formation (SI Text for details). See Fig. 1 for symbol legend.

Table S5.

Preexposure ε¹⁸²W, ε¹⁸³W, and Hf-W model ages of iron meteorite groups

Iron Meteorite Group	N	ε182Wpreexposure, 95% conf.	ε183W, ±95% conf.	ΔtCAI *, My, ±2σ
NC reservoir
IC	5	−3.45 ± 0.04	−0.05 ± 0.02	0.3 ± 0.5
IIAB	8	−3.40 ± 0.03	−0.02 ± 0.02	0.8 ± 0.5
IIIAB	13	−3.35 ± 0.03	−0.03 ± 0.02	1.2 ± 0.5
IIIE	5	−3.28 ± 0.06	−0.05 ± 0.04	1.8 ± 0.7
IVA	6	−3.32 ± 0.05	0.00 ± 0.07	1.5 ± 0.6
CC reservoir
IIC	2	−3.20 ± 0.12	0.30 ± 0.04	2.6 ± 1.3
Wiley (IIC)	1	−3.23 ± 0.11	0.52 ± 0.06	2.3 ± 1.2
IID	12	−3.23 ± 0.04	0.13 ± 0.01	2.3 ± 0.6
IIF	1	−3.21 ± 0.05	0.09 ± 0.02	2.5 ± 0.7
IIIF	2	−3.24 ± 0.10	0.08 ± 0.07	2.2 ± 1.1
IVB	14	−3.18 ± 0.05	0.13 ± 0.02	2.8 ± 0.7

^*Two-stage Hf-W model age of core formation (in million years), given relative to the time of CAI formation.

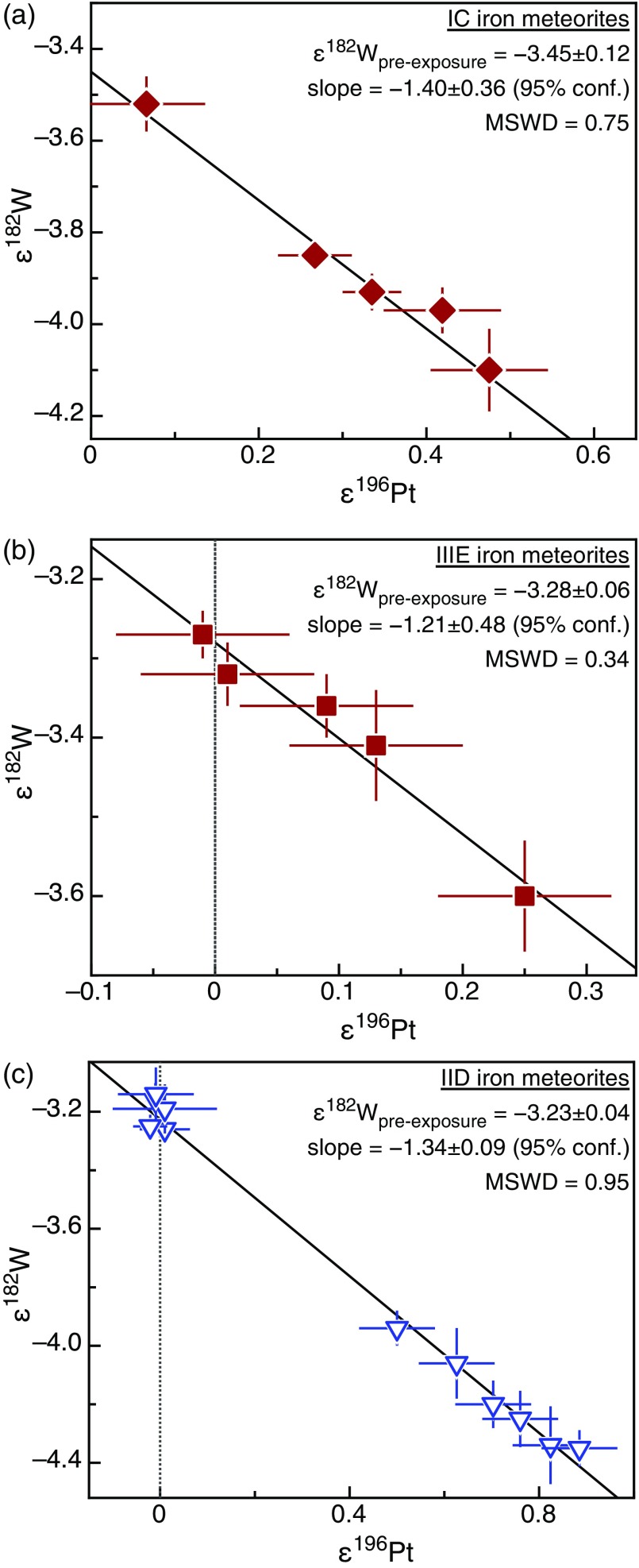
Fig. S3.

(A–C) Neutron capture-induced ε¹⁸²W vs. ε¹⁹⁶Pt correlations for the (A) IC, (B) IIIE, and (C) IID iron meteorite groups analyzed in this study. Solid lines are best-fit regressions through the data with their 95% confidence envelopes (dashed lines) and preexposure ε¹⁸²W intersecting the ordinate at ε¹⁹⁶Pt = 0. Error bars of the data points represent external uncertainties (2 SD for Pt and 95% confidence for W). Small downward corrections for nucleosynthetic heterogeneity were made to the IID data points (Materials and Methods).

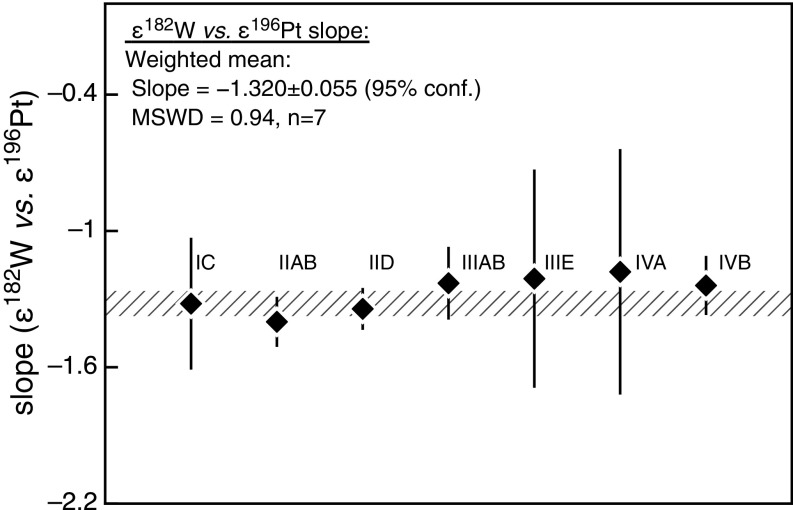
Fig. S4.

Regression-derived ε¹⁸²W vs. ε¹⁹⁶Pt slopes obtained from neutron capture-induced ε¹⁸²W–ε¹⁹⁶Pt correlations defined by different iron meteorite groups. The solid gray line shows the weighted average slope for the investigated iron meteorite groups (n = 7) and the hatched area shows the associated uncertainty (95% conf. limit).

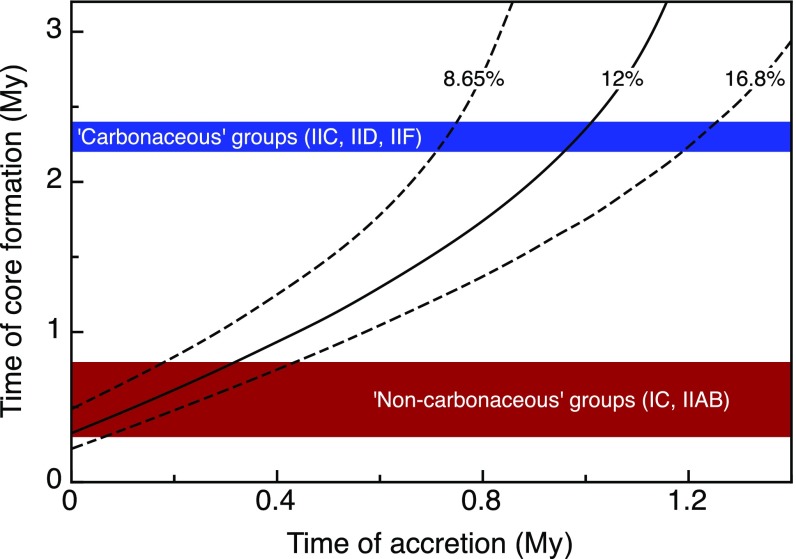
As variable ε¹⁸²W values in iron meteorites reflect different times of Hf/W fractionation during metal–silicate separation on their parent bodies (15–17), the higher ε¹⁸²W of the CC irons indicates a later time of core formation (Table S5), at ∼2.2 My to ∼2.8 My, compared with the NC irons, at ∼0.3 My to ∼1.8 My after the start of Solar System history [as defined by the formation of Ca-Al–rich inclusions (CAI)]. A prior study has shown that ε¹⁸²W differences between different groups of iron meteorites could be due to distinct melting temperatures during core formation, reflecting the different S contents and hence liquidus temperatures of the cores (15). However, the NC and CC reservoirs both include iron meteorite groups with similar volatile element concentrations and, hence, presumably similar S contents. Thus, different melting temperatures of the NC and CC parent bodies cannot be the cause of the observed ε¹⁸²W dichotomy. Instead, the difference in core formation times is most easily explained by different accretion times of the CC and NC iron meteorite parent bodies. Thermal modeling of bodies internally heated by ²⁶Al decay (SI Text) shows that the NC iron meteorite parent bodies probably accreted within <0.4 My after CAI formation, whereas the CC iron meteorite parent bodies accreted slightly later, at ${0.9}_{\mathrm{-}0.2}^{\mathrm{+}0.4}$ My after CAI formation (Fig. 3). Taken together, the Mo and W isotopic data thus indicate that accretion of CC and NC iron meteorite parent bodies occurred not only in genetically distinct nebular regions, but also at different times (Figs. 2 and 3).

Fig. 3.

Relation between the time of accretion and core formation on iron meteorite parent bodies. Curves show thermal modeling results quantifying the relation between the time of core formation and the time of parent body accretion (SI Text), for different Al concentrations of the bulk parent bodies (for 8.65 wt%, 12 wt%, and 16.8 wt% Al). Colored areas show the observed core formation ages of NC iron meteorite parent bodies and CC parent bodies.

Coexistence and Spatial Separation of CC and NC Meteorite Reservoirs

The distinct genetic heritage and accretion times of iron meteorite parent bodies make it possible to constrain the formation time and longevity of the NC and CC nebular reservoirs. Accretion of CC iron meteorite parent bodies at ∼1 My after CAI formation implies that by this time, the NC and CC reservoirs were already separated. The distinction between the NC and CC reservoirs most likely reflects the addition of presolar material enriched in r-process nuclides to the solar nebula region from which the CC meteorites derive (12). Given that all CC meteorites plot on a single s-process mixing line with a constant offset compared with the NC line (Fig. 1), they all have the same r-process excess relative to the NC meteorites. Consequently, this r-process component must have been added to and homogeneously distributed within the CC reservoir before the first CC bodies formed. The ¹⁸²W data for the CC irons, therefore, indicate that this addition of material and, hence, the formation of the CC reservoir occurred within ∼1 My of Solar System formation.

A key constraint from our results is that the accretion of ordinary chondrite parent bodies in the NC reservoir (i.e., at ∼2 My) (18) occurred after the accretion of iron meteorite parent bodies in the CC reservoir (at ∼1 My). Thus, the existence of the NC and CC reservoirs cannot simply reflect a compositional change of the solar nebula over time. Instead, the CC and NC nebular reservoirs must have existed contemporaneously and remained spatially separated within the solar circumstellar disk. The timespan over which this separation persisted can be inferred by considering the accretion times of the youngest meteorite parent bodies in each reservoir. This is because in the ε⁹⁵Mo–ε⁹⁴Mo diagram (Fig. 1), no meteorites plot between the CC and NC lines, meaning that the NC and CC reservoirs cannot have mixed but instead must have remained isolated from each other until parent body accretion in the NC and CC reservoirs terminated. As accretion of chondrite parent bodies occurred at ∼2 My after CAI formation in the NC reservoir (ordinary chondrites) and until ∼3–4 My in the CC reservoir (CC chondrites) (18–20), this means that the NC and CC reservoirs must have remained isolated from each other from <1 My until at least ∼3–4 My after CAI formation. This prolonged spatial separation of the NC and CC reservoirs cannot simply reflect a large distance between these reservoirs within the disk, because the rapid speed of grain drift in the disk would have facilitated efficient mixing on much shorter timescales (21, 22). One way to avoid the inward drift of material would be the rapid accumulation of these grains into planetesimals. However, this also cannot explain the efficient separation of the NC and CC reservoirs, because in both reservoirs planetesimal accretion occurred concurrently for several million years. Consequently, the precursor dust of planetesimals in both reservoirs must have been present for this period and, therefore, cannot have been locked up in earlier-formed planetesimals.

The most plausible mechanism to efficiently separate two disk reservoirs for an extended period is the accretion of a giant planet in between them, generating a gap within the disk and inhibiting the inward drift of dust grains (13, 23, 24) (Fig. 4). Being the largest and nearest gas-giant planet, Jupiter is the most likely candidate for separating the NC and CC reservoirs. As the Earth is part of the NC reservoir, this implies that the CC reservoir was initially located outside Jupiter’s orbit, meaning that CC bodies originally derive from the outer Solar System. Because the CC meteorites include some iron meteorites, one important implication of our data is that early and rapid formation of differentiated planetesimals was possible not only in the innermost terrestrial planet region (25), but also farther out in the disk.

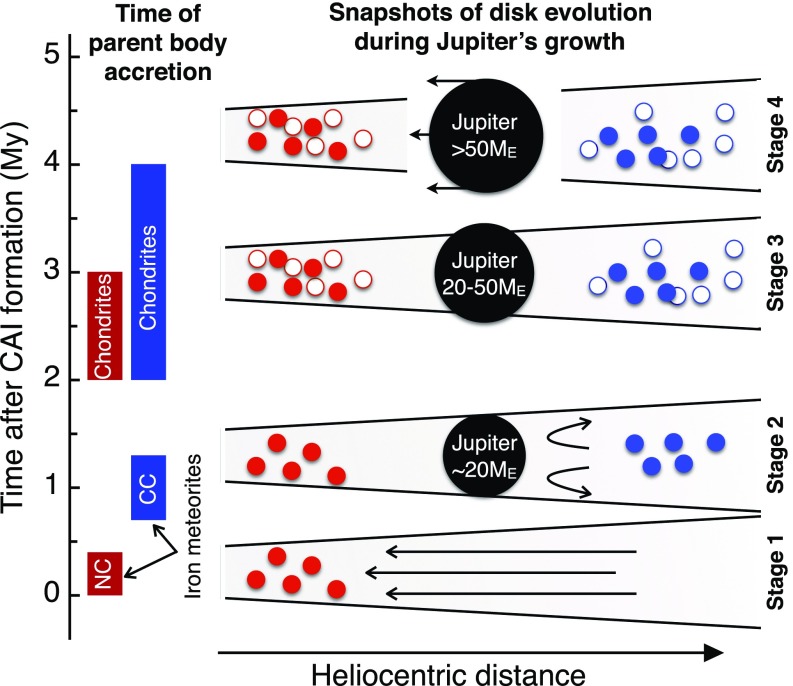
Fig. 4.

Four snapshots of Jupiter’s growth in the solar circumstellar disk. At stage 1, within <0.4 My after CAI, the NC iron meteorite parent bodies (red solid symbols) accreted in a continuous gas disk characterized by inward drag of solids. At stage 2, around ∼1 My after CAI, iron meteorite parent bodies of the CC reservoir (blue solid symbols) had accreted and Jupiter had already grown to ∼20 M_E, preventing any inward drag of solids (24). At stage 3, from ∼2 My to ∼4 My after CAI, Jupiter grew further through gas accretion onto its core. Moreover, the ordinary chondrite parent bodies (red open symbols) accreted in the NC reservoir and CC chondrite parent bodies (blue open symbols) in the CC reservoir. At stage 4, after ∼3–4 My after CAI, Jupiter had grown to ∼50 M_E and had opened a gap in the disk (13, 23, 24), likely resulting in the inward migration of Jupiter. Solid boxes (Left) show the accretion ages of iron meteorite and chondrite parent bodies in the NC and CC reservoirs (see CC and NC Iron Meteorites).

The formation of Jupiter between the NC and CC reservoirs not only provides a mechanism for efficiently separating these two reservoirs for an extended period, but also provides a means for the later transport of CC bodies into the inner Solar System. This is necessary because although the NC and CC bodies initially formed in spatially distinct areas of the disk, at the present day they both reside in the main asteroid belt. This is a natural outcome of the growth of Jupiter, which ultimately leads to scattering of bodies from beyond Jupiter’s orbit (i.e., CC bodies) into the inner Solar System, either during an inward-then-outward migration of Jupiter (10, 23) or during runaway growth of Jupiter on a fixed orbit (26). Thus, the presence of Jupiter between the NC and CC reservoirs provides the most plausible mechanism to account for both (i) the prolonged spatial separation of these reservoirs and (ii) the co-occurrence of NC and CC bodies in the present-day asteroid belt.

Growth History of Jupiter

With the assumption that the prolonged spatial separation of the NC and CC reservoirs reflects the formation of Jupiter in between these reservoirs, the distinct timescales for the accretion of NC and CC meteorite parent bodies make it possible to date the formation of Jupiter. The growth of Jupiter beyond a certain mass would have inhibited the inward drift of particles (13, 24), and once it grew further, Jupiter ultimately would have generated a gap within the disk (23). In particular, theoretical studies suggest that the inward drift of particles stopped once Jupiter’s core had grown to about 20 M_E (24), while a gap formed once Jupiter reached approximately 50 M_E (13, 23, 27). Thus, because the r-process material that was added to the CC reservoir did not infiltrate the coexisting yet spatially separated NC reservoir, this implies that at the time the r-process material was added, Jupiter already had a size of >20 M_E. Furthermore, because this material must have been added and homogenized before the first planetesimals formed within the CC reservoir at ∼1 My after CAI formation, these results mandate that Jupiter reached a size of >20 M_E within ∼1 My of Solar System formation (Fig. 4). This early formation of (proto-)Jupiter is consistent with the rapid growth of Jupiter’s core predicted in theoretical models (1, 4), regardless of whether pebble accretion (28, 29) or hierarchical growth models (30, 31) are assumed.

Once Jupiter reached a mass of 50 M_E, which happens via gas accretion onto its solid core, a gap opened in the disk (13, 23, 24, 27), followed by scattering of bodies from beyond Jupiter’s orbit (i.e., CC bodies) into the inner Solar System (10, 23, 26). Our results show that this scattering of CC bodies and, hence, Jupiter’s outward migration or runaway growth cannot have started before ∼3–4 My after CAI formation. This is because CC chondrite parent bodies continued to form until at least ∼3–4 My after CAI formation (18–20). As these chondrites plot on the CC line in Mo isotope space (Fig. 1), they must have formed before the scattering of CC meteorites into the inner Solar System and, hence, before the CC meteorite parent bodies joined the NC parent bodies in the asteroid belt. Accordingly, these data indicate that Jupiter reached ∼50 M_E later than ∼3–4 My after CAI formation. This is consistent with theoretical predictions that the rapid growth of Jupiter’s core to ∼20 M_E was followed by a more protracted stage of gas and solid accretion to several tens of Earth’s masses (1, 32, 33) before runaway gas accretion led to Jupiter’s final mass (∼318 M_E). Thus, our results are in good agreement with the timing and sequence of events predicted in the core accretion model for the formation of Jupiter (1). One important implication of this result is that, because Jupiter acted as a barrier against inward transport of solids across the disk, the inner Solar System remained relatively mass deficient, possibly explaining its lack of any “super-Earths” (34, 35).

Materials and Methods

For this study we selected a total of 19 samples covering six different rare iron meteorite groups (IC, IIC, IID, IIF, IIIE, and IIIF). This sample set complements the iron meteorites from major groups (IIAB, IID, IIIAB, IVA, and IVB) whose W, Pt, and Mo isotope compositions had previously been analyzed (6, 15). After digestion of the iron meteorites in concentrated HNO₃–HCl (2:1), the sample solutions were split into a fraction for W and Mo (∼90%) and for Pt (∼10%) isotope analysis. The chemical separation of W, Pt, and Mo was accomplished using ion exchange chromatography following previously published procedures (6, 12, 15, 36). The W, Pt, and Mo isotope compositions were measured on a ThermoScientific Neptune Plus MC-ICPMS in the Institut für Planetologie at the University of Münster (12, 15, 36) (SI Materials and Methods for details). Instrumental mass bias was corrected by internally normalizing to ¹⁸⁶W/¹⁸⁴W = 0.92767, ¹⁹⁸Pt/¹⁹⁵Pt = 0.2145, and ⁹⁸Mo/⁹⁶Mo = 1.453173, using the exponential law. The W, Pt, and Mo isotope data are reported as ε-unit (i.e., parts per 10⁴) deviation relative to the isotopic ratios measured for terrestrial bracketing solution standards. The reported εⁱW, εⁱPt, and εⁱMo values for samples (Tables S1–S4) represent the mean of pooled solution replicates (n = 1–8) together with their associated uncertainties [2 SD or 95% confidence (conf.) interval].

SI Text

Quantifying Nucleosynthetic and Cosmogenic W Isotope Variations.

Determining the timescales of core formation in iron meteorite parent bodies using their ¹⁸²W compositions requires the prior quantification of any cosmogenic and nucleosynthetic ¹⁸²W variations in the investigated sample suite. Cosmogenic W isotope variations result from secondary neutron capture effects induced during cosmic ray exposure; these effects lead to downward shifts of ε¹⁸²W without affecting ε¹⁸³W (or ε¹⁸⁴W) (17, 48, 49). Consequently, the correction for cosmogenic ε¹⁸²W effects requires the use of an independent in situ neutron dosimeter, such as Pt or Os isotopes (see below). Nucleosynthetic W isotope anomalies, on the other hand, arise from the heterogeneous distribution of s- and r-process components and result in correlated ε¹⁸²W–ε¹⁸³W (6/4) and ε¹⁸²W–ε¹⁸⁴W (6/3) variations (44, 50–52). Thus, the magnitude of nucleosynthetic ε¹⁸²W variations can be quantified using the ε¹⁸³W compositions determined for each group of irons (below). Note that variations in ε¹⁸³W (or ε¹⁸⁴W) are solely of nucleosynthetic origin (neutron capture-induced variations of the ¹⁸³W/¹⁸⁴W ratio cancel out by mass bias correction to a fixed ¹⁸⁶W/¹⁸⁴W or ¹⁸⁶W/¹⁸³W), and so a reliable correction for nucleosynthetic W isotope anomalies is possible even for strongly irradiated samples.

Nucleosynthetic W isotope anomalies.

The iron meteorites analyzed in the present study show a significant range in their ¹⁸³W compositions with measured ε¹⁸³W values between about –0.14 and +0.52 (Table S3 and Fig. S2). This range is larger than the scatter observed for the ε¹⁸³W measurements of the terrestrial metal standard NIST129c, indicating that some of the meteorites have resolved ε¹⁸³W anomalies. In particular, the positive ε¹⁸³W observed for several samples cannot be caused by the analytical ¹⁸³W effect (above), which can only produce negative ε¹⁸³W. The IC and IIIE iron meteorites exhibit similar scatter in ε¹⁸³W to the NIST129c standard (Fig. S2) and, when normalized to the mean ε¹⁸³W of the NIST129c analyses, have mean ε¹⁸³W values of −0.05 ± 0.02 (IC irons) and −0.05 ± 0.04 (IIIE irons). Thus, these two groups of irons do not show evidence for any significant nucleosynthetic ε¹⁸³W anomalies, in agreement with the absence of such anomalies in the IIAB, IIIAB, and IVA iron meteorite groups (15). In contrast, resolved ε¹⁸³W excesses relative to the terrestrial standards (Alfa Aesar; NIST129c) are observed for the IIC, IID, and IIF irons analyzed in the present study (Fig. S2). Similar ε¹⁸³W excesses have previously been reported for IVB (+0.13 ± 0.02) and IID (+0.12 ± 0.02) irons (note that the three IID irons analyzed here exhibit similar ε¹⁸³W excesses to those found previously) (36, 52, 53). The IIIF irons probably also show a similar ε¹⁸³W excess, but this value is not resolved at present. Whereas the IID, IIF, and IVB (and possibly the IIIF) irons all exhibit similar ε¹⁸³W ∼ +0.12, the IIC irons show the largest ε¹⁸³W excesses yet observed for iron meteorites. Whereas Kumerina and Ballinoo exhibit uniform ε¹⁸³W excesses of +0.30 ± 0.04, Wiley shows a distinctly higher ε¹⁸³W of +0.54 ± 0.06 (Fig. S2). The difference between these two values is larger than the scatter observed for the NIST129c analyses and thus indicates nucleosynthetic W isotope heterogeneity among different members of the IIC group. Therefore, Wiley probably derives from a distinct parent body from that of Kumerina and Ballinoo. Taken together, the ¹⁸³W systematics reveal a dichotomy between iron meteorite groups showing a nucleosynthetic W isotope anomaly (IIC, IID, IIF, IIIF, and IVB) and those lacking such a signature (IC, IIAB, IIIAB, IIIE, and IVA).

Table S3.

Tungsten isotope compositions of iron meteorites determined by MC-ICPMS

Meteorite Group	Collection, no.	ID	N	Normalized to 186W/183W				Normalized to 186W/184W
				ε182Wmeas., ±95% conf.	ε184Wmeas., ±95% conf.	ε182Wcorr.*, ±95% conf	ε184Wcorr.*, ±95% conf.	ε182Wmeas., ±95% conf.	ε183Wmeas., ±95% conf.	ε183Wcorr.*, ±95% conf.
IC iron meteorites
Chihuahua City	BM 1959, 1011	BW01	6	−3.36 ± 0.03	0.08 ± 0.02	−3.40 ± 0.03	0.06 ± 0.02	−3.52 ± 0.06	−0.11 ± 0.03	−0.10 ± 0.04
Murnpeowie	BM 2005, M179	BW02	6	−3.77 ± 0.06	0.05 ± 0.03	−3.81 ± 0.06	0.04 ± 0.03	−3.87 ± 0.02	−0.07 ± 0.05	−0.05 ± 0.05
Murnpeowie (replicate)	BM 2005, M179	CJ02	5	−3.80 ± 0.04	0.02 ± 0.04	−3.84 ± 0.04	0.01 ± 0.04	−3.84 ± 0.04	−0.03 ± 0.06	−0.01 ± 0.06
Arispe	Münster	A1	5	−3.87 ± 0.05	0.04 ± 0.01	−3.91 ± 0.06	0.03 ± 0.02	−3.93 ± 0.03	−0.06 ± 0.02	−0.04 ± 0.02
Arispe (replicate)	Münster	A2	5	−3.85 ± 0.04	0.02 ± 0.02	−3.89 ± 0.05	0.01 ± 0.02	−3.92 ± 0.04	−0.04 ± 0.03	−0.02 ± 0.03
Arispe	ME 1011	J-AC06	6	−3.86 ± 0.08	0.06 ± 0.06	−3.90 ± 0.08	0.04 ± 0.06	−3.97 ± 0.05	−0.09 ± 0.08	−0.07 ± 0.09
Bendego	ME 6	J-AC07	6	−4.03 ± 0.12	0.03 ± 0.03	−4.07 ± 0.13	0.02 ± 0.03	−4.10 ± 0.09	−0.05 ± 0.05	−0.03 ± 0.05
IIC iron meteorites
Kumerina	BM 1938, 220	BW03	6	−3.12 ± 0.06	−0.15 ± 0.03	−3.16 ± 0.06	−0.16 ± 0.03	−2.82 ± 0.05	0.23 ± 0.04	0.25 ± 0.04
Kumerina (replicate)	BM 1938, 220	CC06	6	−3.15 ± 0.03	−0.20 ± 0.01	−3.19 ± 0.03	−0.21 ± 0.01	−2.76 ± 0.03	0.30 ± 0.01	0.32 ± 0.01
Wiley	BM 1959, 914	BW04	6	−3.28 ± 0.05	−0.34 ± 0.04	−3.32 ± 0.05	−0.35 ± 0.04	−2.59 ± 0.04	0.52 ± 0.06	0.53 ± 0.06
Wiley (replicate)	BM 1959, 914	CC07	5	−3.21 ± 0.08	−0.32 ± 0.08	−3.25 ± 0.08	−0.34 ± 0.08	−2.56 ± 0.10	0.49 ± 0.12	0.51 ± 0.12
Ballinoo	ME 980	CJ01	5	−3.15 ± 0.06	−0.17 ± 0.02	−3.18 ± 0.06	−0.18 ± 0.02	−2.80 ± 0.06	0.26 ± 0.03	0.28 ± 0.03
IID iron meteorites
Bridgewater	ME 1895	BT02	5	−3.01 ± 0.03	−0.01 ± 0.02	−3.04 ± 0.04	−0.03 ± 0.02	−2.98 ± 0.06	0.02 ± 0.03	0.04 ± 0.03
N'Kandhla	BM 1921, 17	CC08	6	−3.22 ± 0.03	−0.07 ± 0.02	−3.26 ± 0.04	−0.08 ± 0.02	−3.08 ± 0.02	0.11 ± 0.03	0.12 ± 0.03
Richa	BM 1966, 55	CC09	6	−3.25 ± 0.04	−0.09 ± 0.02	−3.29 ± 0.04	−0.10 ± 0.02	−3.07 ± 0.04	0.14 ± 0.03	0.15 ± 0.04
IIF iron meteorites
Monahans	BM 1959, 910	CC01	6	−3.26 ± 0.04	−0.04 ± 0.01	−3.30 ± 0.04	−0.06 ± 0.01	−3.17 ± 0.03	0.07 ± 0.02	0.09 ± 0.02
Monahans (replicate)	BM 1959, 910	CJ06	5	−3.29 ± 0.05	−0.06 ± 0.04	−3.32 ± 0.05	−0.07 ± 0.04	−3.17 ± 0.08	0.09 ± 0.07	0.10 ± 0.07
IIIE iron meteorites
Willow Creek	Münster	NK	5	−3.33 ± 0.05	0.04 ± 0.03	−3.37 ± 0.05	0.03 ± 0.03	−3.41 ± 0.07	−0.06 ± 0.05	−0.04 ± 0.05
Kokstad	ME 1015	BW05	5	−3.56 ± 0.04	0.02 ± 0.04	−3.60 ± 0.04	0.01 ± 0.04	−3.60 ± 0.05	−0.03 ± 0.05	−0.01 ± 0.05
Kokstad (replicate)	ME 1015	CJ08	5	−3.55 ± 0.04	0.03 ± 0.04	−3.59 ± 0.04	0.02 ± 0.04	−3.61 ± 0.09	−0.04 ± 0.07	−0.02 ± 0.07
Colonia Obrera	ME 2871	BW06	5	−3.14 ± 0.02	0.09 ± 0.02	−3.17 ± 0.03	0.08 ± 0.02	−3.33 ± 0.04	−0.14 ± 0.03	−0.12 ± 0.04
Colonia Obrera (replicate)	ME 2871	CJ05	5	−3.35 ± 0.09	−0.02 ± 0.05	−3.39 ± 0.09	−0.03 ± 0.05	−3.31 ± 0.04	0.03 ± 0.08	0.05 ± 0.08
Staunton	BM 1955, M239	BW07	5	−3.15 ± 0.07	0.06 ± 0.03	−3.18 ± 0.07	0.05 ± 0.03	−3.27 ± 0.03	−0.09 ± 0.04	−0.07 ± 0.04
Paneth's Iron	BM 2005, M199	BW08	6	−3.22 ± 0.06	0.07 ± 0.03	−3.26 ± 0.07	0.06 ± 0.03	−3.36 ± 0.04	−0.11 ± 0.05	−0.09 ± 0.05
IIIF iron meteorites
Klamath Falls	ME 2789	CC02	3	−3.14 ± 0.12	0.00 ± 0.06	−3.18 ± 0.12	−0.01 ± 0.06	−3.15 ± 0.10	−0.01 ± 0.10	0.01 ± 0.10
Klamath Falls (replicate)	ME 2789	CJ03	2	−3.20 ± 0.12	−0.02 ± 0.06	−3.23 ± 0.12	−0.03 ± 0.06	−3.15 ± 0.10	0.03 ± 0.10	0.05 ± 0.10
Clark County	BM 1959, 949	CC03	6	−3.35 ± 0.08	−0.08 ± 0.04	−3.39 ± 0.08	−0.09 ± 0.04	−3.19 ± 0.08	0.12 ± 0.05	0.14 ± 0.06
Clark County (replicate)	BM 1959, 949	CJ04	5	−3.40 ± 0.07	−0.08 ± 0.04	−3.43 ± 0.07	−0.09 ± 0.04	−3.23 ± 0.06	0.12 ± 0.06	0.14 ± 0.06

For W, instrumental mass fractionation was corrected using the exponential law by internal normalization to ¹⁸⁶W/¹⁸³W = 1.98594 or to ¹⁸⁶W/¹⁸⁴W = 0.92767. N, number of solution replicates. The uncertainties reported for measured εⁱW values of samples (subscript “meas.”) represent the 2 SD obtained from repeated analyses of the terrestrial standard NIST129c (Table S1) in the case n < 4 or, in the case n > 4, the 95% conf. limits of the mean [i.e., according to (SD × t_0.95,N−1)/√N].

^*Corrected for a small analytical mass-independent effect on ¹⁸³W by normalizing to the average εⁱW values obtained for the terrestrial metal standard NIST129c (Table S1). The added uncertainty induced by this correction was propagated into the reported uncertainties for measured εⁱW values.

The effect of nucleosynthetic W isotope heterogeneity on ε¹⁸²W can be quantified using the ε¹⁸³W of a sample and the empirically defined linear relations between nucleosynthetic ε¹⁸²W and ε¹⁸³W (or ε¹⁸⁴W) variations (36, 41, 51). Using W isotope data for bulk CAI yields a ε¹⁸²W (6/4) vs. ε¹⁸³W (6/4) slope of +1.41 ± 0.05 (95% conf. interval) for data internally normalized to ¹⁸⁶W/¹⁸⁴W and a shallower ε¹⁸²W (6/3) vs. ε¹⁸⁴W (6/3) slope of −0.11 ± 0.05 for ¹⁸⁶W/¹⁸³W normalized data (44). These slopes are in excellent agreement with those obtained for leachates of CC chondrites (51, 54). Based on nucleosynthetic W isotope anomalies in Allende chondrules and matrix, slightly different slopes of ε¹⁸²W (6/4) vs. ε¹⁸³W (6/4) = +1.25 ± 0.06 and ε¹⁸²W (6/3) vs. ε¹⁸⁴W (6/3) = +0.12 ± 0.07 were obtained (50). However, the ε¹⁸³W anomalies observed for the samples investigated in the present study are so small that these differences in slopes are inconsequential for the correction of measured ε¹⁸²W values. Here, we corrected the measured ε¹⁸²W values of the IIC, IID, IIF, and IIIF meteorites, using the mean ε¹⁸³W for each group and the empirical ε¹⁸²W vs. ε¹⁸ⁱW slopes obtained from the CAI data. This procedure yields downward corrections on ε¹⁸²W of ∼0.2–0.7 for the ¹⁸⁶W/¹⁸⁴W-normalized data and of <0.04 ε¹⁸²W for the ¹⁸⁶W/¹⁸³W-normalized data. Using the slopes from ref. 50 instead results in corrected ε¹⁸²W values that are only ∼0.01–0.07 ε-units higher, that is, essentially within uncertainty.

Neutron capture effects and preexposure ε¹⁸²W.

Recent studies have shown that corrections for secondary neutron capture-induced ε¹⁸²W variations are possible using Pt (15, 36, 53) and Os isotopes (53, 55) as in situ neutron dosimeters. Here we use the same approach as in refs. 15 and 36 and determine “preexposure” ε¹⁸²W values (i.e., ε¹⁸²W unaffected by neutron capture) for each group of iron meteorites from the intercepts of empirical neutron capture-induced ε¹⁸²W vs. ε¹⁹⁶Pt correlation lines. Using this method, the preexposure ε¹⁸²W values for the five major iron meteorite groups (IIAB, IID, IIIAB, IVA, and IVB) were determined in a previous study (15) (Table S5). In the present study, we obtained similar empirical ε¹⁸²W vs. ε¹⁹⁶Pt correlations for the IC and IIIE groups (Fig. S3), yielding preexposure ε¹⁸²W of −3.45 ± 0.12 (95% conf. interval, n = 5) for the IC irons and −3.28 ± 0.06 (n = 5) for the IIIE irons. For the IID irons, we previously obtained a preexposure ε¹⁸²W of –3.18 ± 0.11 (15, 36). Based on combined Os and W measurements of Carbo a lower preexposure ε¹⁸²W of −3.57 ± 0.21 was reported subsequently (56). However, as Carbo is a strongly irradiated iron meteorite, this lower preexposure ε¹⁸²W relied on a large extrapolation, resulting in a rather large uncertainty on ε¹⁸²W. Here we extended the Pt-W isotope dataset of the IID irons, using samples from Bridgewater, N’Kandhla, and Riches. All newly analyzed IID irons have relatively elevated ε¹⁸²W coupled with small or negligible ε¹⁹⁶Pt anomalies (Fig. S3). Together, all investigated IID iron meteorites show a well-defined ε¹⁸²W–ε¹⁹⁶Pt correlation with a precise preexposure ε¹⁸²W of −3.23 ± 0.04 (95% conf. interval, n = 12).

As most of the rare iron meteorite groups comprise only a few meteorites, obtaining reliable ε¹⁸²W vs. ε¹⁹⁶Pt correlations to constrain their preexposure ε¹⁸²W is not always possible. Thus, for the IIC, IIF, and IIIF groups, for which we analyzed only two or three samples, the measured ε¹⁸²W of each sample was corrected individually using its measured ε¹⁹⁶Pt and the mean ε¹⁸²W vs. ε¹⁹⁶Pt slope obtained from the other iron meteorite groups. This approach is valid because the ε¹⁸²W vs. ε¹⁹⁶Pt slopes of the major iron meteorite groups are indistinguishable from each other (Fig. S4), resulting in a precisely defined mean ε¹⁸²W vs. ε¹⁹⁶Pt slope of 1.320 ± 0.055 (95% conf. interval, n = 7). Hence, the preexposure ε¹⁸²W of an individual sample can be determined using the following equation:

$${\mathrm{\epsilon }}^{182}{\mathrm{W}}_{\mathrm{preexposure}}={\mathrm{\epsilon }}^{182}{\mathrm{W}}_{\text{measured}}-{\mathrm{\epsilon }}^{196}\mathrm{P}{\mathrm{t}}_{\text{measured}}\mathrm{\times }\left(-1.320\mathrm{\pm }0.055\right).$$ [S1]

Using this equation, we calculated preexposure ε¹⁸²W values for every sample of the iron meteorite groups investigated here, resulting in average preexposure ε¹⁸²W values of –3.45 ± 0.04 (95% conf. interval) for the IC irons, −3.20 ± 0.12 for the IIC irons, −3.23 ± 0.03 for the IID irons, −3.21 ± 0.05 for the IIF irons, –3.27 ± 0.04 for the IIIE irons, and −3.24 ± 0.10 for the IIIF irons (Table S5). For the IC, IID, and IIIE groups, these preexposure ε¹⁸²W values are in excellent agreement with those obtained using the empirical Pt-W isotope correlations for these groups (Fig. S3), demonstrating that these two correction methods lead to consistent results.

Hf-W Model Ages of Core Formation.

The preexposure ε¹⁸²W values can be used to calculate Hf-W model ages for each group of iron meteorites. These ages provide the time of a single event of Hf/W fractionation from a reservoir with chondritic ¹⁸⁰Hf/¹⁸⁴W, which in case of the iron meteorites presumably occurred by metal–silicate separation during core formation. The model age is calculated using the relation

$$\mathrm{\Delta }t=-\frac{1}{\mathrm{\lambda }}\ln \left[\frac{{\left({\mathrm{\epsilon }}^{182}\mathrm{W}\right)}_{\text{Sample}}-{\left({\mathrm{\epsilon }}^{182}\mathrm{W}\right)}_{\text{Chondrites}}}{{\left({\mathrm{\epsilon }}^{182}\mathrm{W}\right)}_{\text{SSI}}-{\left({\mathrm{\epsilon }}^{182}\mathrm{W}\right)}_{\text{Chondrites}}}\right],$$ [S2]

where (ε¹⁸²W)_Sample represents the preexposure ε¹⁸²W of any iron meteorite group, ε¹⁸²W_chondrites is the composition of carbonaceous chondrites (−1.91 ± 0.08) (57), ε¹⁸²W_SSI is the Solar System initial of –3.49 ± 0.07 as obtained from CAI (44), and λ is the decay constant of ¹⁸²Hf of 0.078 ± 0.002 My⁻¹ (2σ) (58). The distinct preexposure ε¹⁸²W values obtained for the iron meteorite groups from this study (IC, IIC, IID, IIF, IIIE, and IIIF) yield a range of Hf-W model ages from ∼0.3 My to ∼2.8 My after CAI formation (Table S5), consistent with the range of ages determined previously for the major iron meteorite groups (IIAB, IIIAB, IVA, and IVB) (15). Nevertheless, the CC iron meteorite groups exhibit on average younger Hf-W model ages of ∼2.2–2.8 My after CAI formation than the NC groups (∼0.3–1.8 My).

Thermal Model.

To quantify the relationship between the timing of accretion and core formation, we modeled the thermal evolution of bodies internally heated by ²⁶Al decay (15). This model assumes single-stage core formation at a given temperature, but this assumption is not always valid, especially for volatile-depleted, S-poor bodies (15). In such bodies (e.g., IIIF, IVA, and IVB), silicate melt extraction probably preceded the melting of a significant portion of the Fe metal and also removed most of the heat-producing ²⁶Al from the mantle (59). Thus, heating slowed down considerably following silicate melt extraction, making it difficult to reliably estimate the timing of final metal melting and core formation in these volatile-depleted, S-poor bodies. In contrast, in volatile- and S-rich bodies, most of the Fe metal was already molten at the time of silicate melt extraction, meaning that the separation of silicate and metal melts probably occurred at about the same time. Thus, for modeling the thermal evolution of volatile-rich bodies, the effect of ²⁶Al removal during silicate melt extraction is inconsequential for estimating the relation between time of core formation and time of parent body accretion. For this reason, any difference in accretion time between CC and NC iron meteorite parent bodies is most easily assessed using the most volatile-rich groups (i.e., NC groups IC and IIAB vs. CC groups IIC, IID, and IIF).

The thermal model used here assumes instantaneous accretion and calculates the temperature vs. time relations for an undifferentiated spherical planetary body that is heated by ²⁶Al decay following accretion. The model accounts for heat production by radioactive decay and for heat loss by conduction. The temperatures were evaluated at half the radius (i.e., r = 20 km) of the body. We note that, because bodies essentially heat up isothermally (59, 60), evaluating the temperature at a different radius yields identical results. The parameters used for the thermal model are parent body radius R = 40 km, thermal conductivity K = 2.1 Wm⁻¹⋅K⁻¹ (60), thermal diffusivity κ = 5.0 × 10⁻⁷ m²⋅s⁻¹, Solar System initial ²⁶Al/²⁷Al = 5.25 × 10⁻⁵, heat production A = Al concentration × (²⁶Al/²⁷Al) Wm⁻³, decay constant of ²⁶Al = 9.83 × 10⁻⁷ y⁻¹ (61), density of planetesimal ρ = 3.2 gcm⁻³, emissivity h = 1.0 m⁻¹, and the assumed ambient temperature T₀ = 250 K (60). The largest uncertainty on the modeling results comes from the assumed Al concentration of the bulk parent bodies. Here we assumed an Al concentration of 12 wt %, which is equivalent to the mean Al concentration of CC chondrites (62). Nevertheless, using different Al concentrations (i.e., as low as 8.65 wt% for CI chondrites or as high as 16.8 wt % for CV chondrites) results in inferred accretion ages that are different by only <0.2 My for NC parent bodies and by <0.4 My for CC parent bodies (Fig. 3).

Silicate melt fractions of 40–60% are necessary for an efficient separation of metal and silicate melts (59, 63, 64), and such high-melt fractions would be reached only at temperatures of ∼1,600 K to ∼1,700 K (64). For volatile- (and S-)rich bodies (i.e., IC, IIAB, IIC, IID, and IIF), this temperature is similar to the liquidus temperature of the core (the IIAB core contains ∼17 wt% S, corresponding to a liquidus temperature of ∼1,600 K), meaning that in these bodies the entire core segregated in a single instant. For the thermal model used here we thus assume that core formation in the volatile-rich iron meteorite parent bodies occurred at ∼1,600 K. However, even if the temperature of core formation was as low as ∼1,400 K—i.e., the silicate solidus and hence the lowest possible core formation temperature—this would yield inferred accretion ages that are within <0.1 My of those obtained when assuming a temperature of 1,600 K.

The modeling results show that the Hf-W model ages for core formation of ∼0.3–0.7 My obtained for some of the NC iron meteorite parent bodies (IC and IIAB) are consistent with very early accretion within less than ∼0.4 My after Solar System formation (Fig. 3). In contrast, the younger Hf-W ages of the CC iron meteorite groups (IIC, IID, and IIF) indicate that their parent bodies accreted significantly later, at ${0.9}_{-0.2}^{+0.4}$ My after Solar System formation. Although the accretion ages of volatile-poor iron meteorite parent bodies are more uncertain, the significantly higher ε¹⁸²W of volatile-poor CC groups (IIIF and IVB) over the NC groups (IVA) is fully consistent with the difference in accretion ages inferred from the more volatile-rich iron meteorite groups. Thus, we conclude that iron meteorite parent bodies in the NC reservoir accreted within ∼0.4 My after CAI formation and those in the CC reservoir slightly later, at ${0.9}_{-0.2}^{+0.4}$ My after CAI formation.