Interface-induced multiferroism by design in complex oxide superlattices

Significance

Developments in synthesis and characterizing artificially structured materials have greatly advanced the possibility to explore new states of matter in material science. Recent discoveries show that new quantum states can be achieved at heterointerfaces with various electric and mechanical boundary conditions. It remains an open question of how to design ultrathin layers with properties inaccessible in bulk phases that are amenable to technological applications. In this work, we grow heterostructures with extremely high-quality interfaces shown by state-of-the-art atomically resolved electron microscopy and spectroscopy. This combination allows us to identify an interface-induced structure that stabilizes ferromagnetism. Coupled with theory, we provide a conceptually useful recipe to design low-dimensional materials with unique functionalities, in line with the loop “make, measure, model.”

Abstract

Interfaces between materials present unique opportunities for the discovery of intriguing quantum phenomena. Here, we explore the possibility that, in the case of superlattices, if one of the layers is made ultrathin, unexpected properties can be induced between the two bracketing interfaces. We pursue this objective by combining advanced growth and characterization techniques with theoretical calculations. Using prototype La_2/3Sr_1/3MnO₃ (LSMO)/BaTiO₃ (BTO) superlattices, we observe a structural evolution in the LSMO layers as a function of thickness. Atomic-resolution EM and spectroscopy reveal an unusual polar structure phase in ultrathin LSMO at a critical thickness caused by interfacing with the adjacent BTO layers, which is confirmed by first principles calculations. Most important is the fact that this polar phase is accompanied by reemergent ferromagnetism, making this system a potential candidate for ultrathin ferroelectrics with ferromagnetic ordering. Monte Carlo simulations illustrate the important role of spin–lattice coupling in LSMO. These results open up a conceptually intriguing recipe for developing functional ultrathin materials via interface-induced spin–lattice coupling.

Interface physics has emerged as one of the most popular methods to discover unique phenomena caused by broken symmetry (1–6). In transition metal oxide (TMO) interfaces, the different electronic, magnetic, lattice, and orbital properties of two adjoined materials lead to fascinating properties that are often radically different from those of the two component bulk materials (7–10). It would seem that we are on the verge of being able to design (11) or engineer (12) the properties of interfaces.

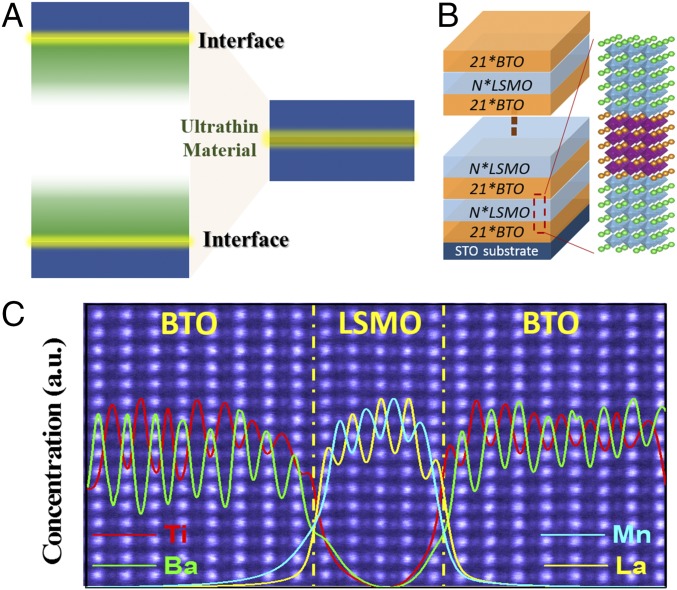
Although the behavior of individual interfaces has been widely investigated, how two or more interfaces behave within superlattices (SLs) remains an interesting and open topic (13, 14). As shown in Fig. 1A, when two interfaces are geometrically close enough, they can drastically alter the properties of the material in between because of proximity effects. Unlike layered compounds, such as Fe-based superconductors and cuprates, which have pronounced 2D properties, most perovskites with the chemical formula ABO₃ exhibit drastic decreases in their functionalities under reduced dimensionality (i.e., ultrathin materials). This property has hindered the exploration and development of active low-dimensional materials (15, 16). Therefore, exploring ultrathin materials confined by two interfaces is a rational approach to see whether interfacial effects can be exploited to achieve desired functionalities.

Fig. 1.

Designing ultrathin materials via interfaces. (A) When two interfaces are geometrically close enough, the confinement effect of two interfaces can lead to unexpected properties in the ultrathin films in between. (B) Stacking order of BTO/LSMO SLs. (C) HADDF STEM image and EELS elemental profiles extracted from La M (yellow), Ba M (green), Mn L (blue), and Ti L (red) edges for BTO/4uc-LSMO/BTO (n = 4) SL taken along [110] zone axis direction, showing sharp interfaces with minor intermixing. The dashed yellow lines mark the interfaces. For all of the STEM images, the STO substrate is located at the right side.

In this work, we present an example of using the structural phase change induced by two adjacent interfaces as a route to design ultrathin TMOs. We choose two materials with distinct properties: BaTiO₃ (BTO), which in its bulk form, is polar ferroelectric, and La_2/3Sr_1/3MnO₃ (LSMO), which in its bulk form, is nonpolar/tilt ferromagnetic. The two materials form magnetic/electric interfaces by means of SLs. By fixing the BTO thickness and reducing the LSMO layer from thick to ultrathin, we directly observed a structural phase transition from bulk nonpolar to unconventional polar in LSMO. Interestingly, this structural transition is accompanied by an unusual reemergence and stabilization of ferromagnetism when the LSMO is four-unit cells (u.c.) thick, making it a potential candidate for ultrathin multiferroics with ferromagnetic order. Our findings suggest a conceptually useful recipe to develop functional ultrathin materials via an interface-induced structure–property relationship.

SLs with a stacking order of BTO₂₁/(LSMO_N/BTO₂₁)_M were grown on SrTiO₃ (100) (STO) substrates (Fig. 1B) with LSMO thickness N ranging from 32 to 2 u.c.; N × M = 40 for N ≤ 20 and M = 1 for n = 32. Each building block consists of an N-u.c.-thick LSMO layer sandwiched with 21-u.c.-thick ferroelectric BTO to ensure no direct interaction between adjacent LSMO layers. Both BTO and LSMO exhibit excellent 2D layer by layer growth mode (detailed growth information can be found in Methods and SI Appendix) (17).

We performed X-ray diffraction (XRD) measurements, and the results are shown in SI Appendix, Fig. S2. SI Appendix, Fig. S2 A and B shows the θ − 2θ XRD scans for (BTO₂₁/LSMO₄)₁₀ on SrTiO₃ through the (001)_pc, (002)_pc, and (003)_pc peaks of the BTO, LSMO, and STO, where pc indicates pseudocubic indices. In all cases, SL reflections and Laue fringes confirm film uniformity. Rocking curves around the (002) BTO film reflection show a slight broadening, suggesting slight relaxation from the substrate, which is expected given the film thickness (SI Appendix, Fig. S2C). A previous report observed that BTO films begin to relax from STO substrate beyond a critical thickness of ∼4 nm (18). In all of our SLs, the BTO thickness is much thicker than this critical thickness, and therefore, structural relaxation is expected. Indeed, our reciprocal space mapping data show that the SL layers are relaxed from the STO substrate but coherent epitaxial strain between the BTO and LSMO layers is maintained (SI Appendix, Fig. S2D).

To examine the interface quality, we use atomically resolved scanning transmission electron microscopy (STEM) combined with electron energy loss spectroscopy (EELS). We chose three samples with LSMO thickness N of 32, 10, and 4, aiming at revealing the interfacial effect with reduced dimensionality. Fig. 1C shows the high-angle annular dark-field (HAADF) image of n = 4-u.c. film, including EELS elemental spatial profiles for La, Ba, Mn, and Ti (n = 10- and 32-u.c. films data in SI Appendix, Figs. S3 and S4). The interfaces are coherent. The composition profile reveals the stacking sequence to be BaO-TiO₂-LaSrO-MnO₂ at the left-side interface and MnO₂-LaSrO-TiO₂-BaO at the right side [i.e., LSMO is terminated with an (La/Sr)O layer at both interfaces and sandwiched by BTO terminated with TiO₂]. This result suggests that, in LSMO layers, a self-organized termination conversion occurred from MnO₂ to (La,Sr)O during growth. Although the nature of termination conversion requires additional understanding, our results suggest that, in BTO/LSMO SLs, (La,Sr)O termination is energetically favorable.

An important issue in interface physics is the level of chemical intermixing and diffusion at the interface, which can be severe in oxide heterostructures. Detailed analysis of the EELS elemental profiles in Fig. 1C illustrates that chemical intermixing is mostly confined within one u.c. in both the BTO and the LSMO at the interface (i.e., the intermixing mostly exists between the adjacent TiO₂ and MnO₂ layers). Qualitative analysis shows that, within the layer, only 5–20% of Ti atoms diffuse to the adjacent MnO₂ layer for n = 4- and 10-u.c. (50% for n = 32 u.c.) samples, further confirming the high interface quality. Therefore, the sharp interfaces suggest that all three films are dominated by the intrinsic properties of LSMO and BTO. Note that such sharp interfaces serve as a prerequisite to study the interfacial effects in ultrathin thicknesses.

Magnetic/electric interfaces have been extensively studied as a promising means of exploring the interplay between electricity and magnetism (19–24). Indeed, large electrostatic and electrochemical effects across the interface have been observed to modulate magnetism (25–29). However, structurally, the two materials belong to distinct phases: BTO exhibits a polar phase, where metal and oxygen ions displace against one another, whereas LSMO exhibits a nonpolar antiferrodistortive (AFD) phase, where oxygen octahedrons have tilts (30, 31). One would expect that such structural conflict can be radically magnified when reducing the LSMO thickness into the ultrathin regime, where two adjacent BTO/LSMO interfaces are geometrically close.

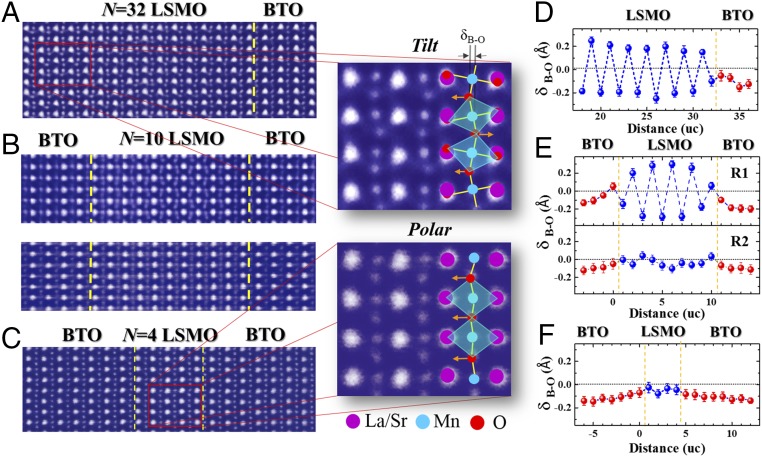
To examine the structure evolution, we performed high-resolution annular bright-field (ABF) STEM imaging to directly image the metal-oxygen octahedron (MnO₆) in all three films. In Fig. 2, the MnO₆ distortions in the [110] orientation are imaged. These images can resolve the layer by layer evolution of octahedron modulation in all three films. To distinguish tilt and polar distortions, we define the quantities δ_Mn-O and δ_Ti-O as the relative displacements of oxygen with respect to the B-site position as shown in Fig. 2. The tilt distortion is represented by the alternating sign of δ_Mn-O along both in-plane and out-of-plane directions, whereas polar distortion is represented by the same sign of δ_Mn-O. Because of the cross-sectional nature of STEM images, the rotational distortion cannot be directly visualized. We note that BTO is very stiff against oxygen octahedron rotation (32), and therefore an interface with BTO tends to suppress oxygen octahedron rotational distortions.

Fig. 2.

Structural evolution of BTO/LSMO SLs. Intensity-inversed ABF STEM image of BTO/LSMO SL with (A) n = 32, (B) n = 10, and (C) n = 4 u.c. taken along [110] direction. Enlarged images show the MnO₆ octahedral AFD tilt in A and Mn-O polar displacements in C for LSMO film, with the atomic model superimposed. (D–F) Metal cation–oxygen displacements (δ_B-O; B = Mn, Ti) as a function of distance measured from the ABF STEM image. The δ_B-O values were obtained by averaging alternatingly over 30 u.c. along the interface direction. The dashed yellow lines mark the position of interfaces, and the TiO₂ plane at the left-side interface was set as x = 0.

In the n = 32-u.c. film (Fig. 2 A and D), the LSMO layers show bulk-like AFD tilt distortions as evidenced by the alternating sign of oxygen buckling δ_Mn-O both along neighboring layers and within each individual layer. BTO layers, however, exhibit typical Ti-O polar displacement (the same sign of buckling along each directions), reflecting their ferroelectric nature.

In the n = 10-u.c. film, there exists two distinct octahedral distortion regions as seen in the STEM images that we captured (Fig. 2 B and E). Both regions are AFD. They share a similarity in that the MnO₆ layer near both BTO interfaces becomes nearly undistorted with δ_Mn-O close to zero, deviating from the layers away from the interface. The difference is that region 1 has larger MnO₆ distortion corresponding to smaller δ_Mn-O, whereas region 2 has smaller MnO₆ distortion with larger δ_Mn-O. These observations indicate the structural phase separation on the order of nanometer in the n = 10 film, consistent with the phase separation scenario previously reported in thin LSMO films (33). The nature of electronic behavior of the two regions is under additional investigation.

The most striking observation occurs in the n = 4-u.c. film as shown in Fig. 2 C and F. Although BTO still retains its Ti-O polar displacement δ_Ti-O, the Mn-O bond in LSMO follows the same polar structure, because δ_Mn-O has the same sign in all four layers. This feature suggests a complete structure change in n = 4 LSMO through interfacing with BTO, with a structure transition from conventional AFD to an unconventional polar phase.

These data reveal the interesting role of structure correlation at interfaces under reduced dimensionality. It shows the competition between intrinsic AFD tilt distortions in LSMO and the polar distortive interaction from BTO via interfacial coherency (34–37). In the n = 32-u.c. LSMO film, two BTO/LSMO interfaces are far away, whereby the BTO structure has little effect on LSMO by only reducing the tilt octahedral distortion right at the interface layer to maintain structure coherency. When the distance between the two interfaces was reduced to 10 u.c., the polar structure of BTO at both sides of the LSMO influences and competes with the intrinsic LSMO structure, resulting in a phase-separated state with two sets of MnO₆ distortion. In the n = 4 film, intriguingly, the effect from the two interfaces is strong enough to overcome the intrinsic AFD tilt phase in LSMO and drives LSMO into a polar phase, suggesting the importance of structural effects induced by two adjacent interfaces on ultrathin materials. We note that, near the BTO/LSMO interfaces in Fig. 2, the Ti-O displacement amplitude is strongly suppressed, which can help to reduce the depolarization field from the BTO films.

More importantly, Fig. 2C suggests that we successfully translate a polar distortion from BTO to ultrathin LSMO, showing that it is possible to achieve robust polar structure in ultrathin TMOs. Our observation is in line with the observed polarization of dielectric STO in BTO/STO and PbTiO₃/SrTiO₃ SLs (38–42). Further reducing the ultrathin film thickness is expected to enhance the polar distortion in ultrathin films. In summation, our data in Fig. 2 show that structural correlation through interfaces is one of the dominant factors in governing the properties of ultrathin materials. Future experiments are endeavoring to switch the polarization direction by applying an electric field, aiming at achieving active ferroelectricity in ultrathin LSMO films.

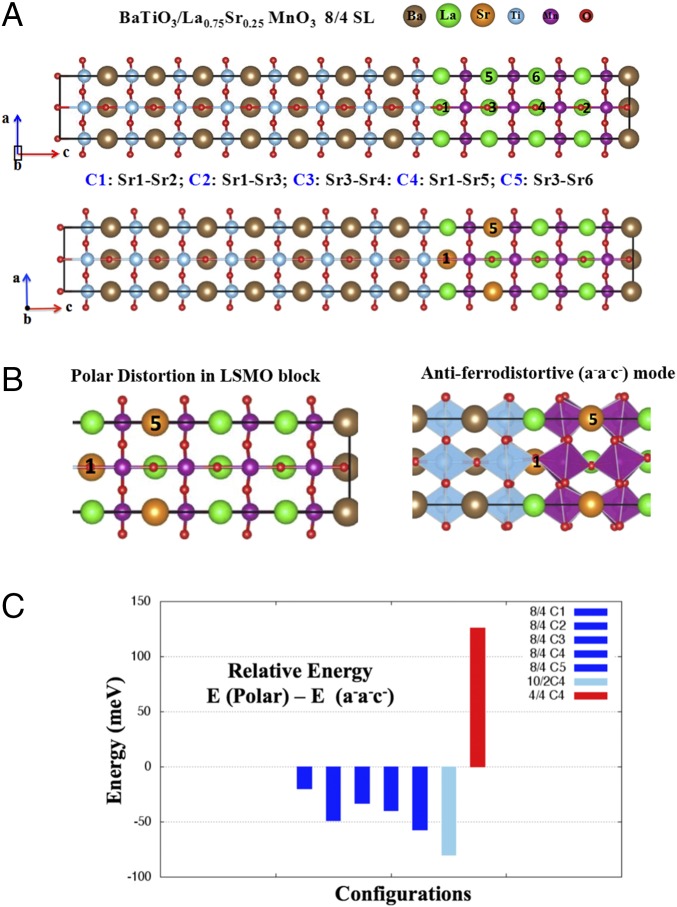
Our observation of a polar mode in ultrathin LSMO is supported by first principles calculations. We have performed density functional theory (DFT) calculations on three different BTO/LSMO SLs: (i) 4/4 u.c., (ii) 8/4 u.c. (as shown in Fig. 3A), and (iii) 10/2 u.c. The concentrations of Sr are 25% in 4/4 and 8/4 SLs and 33% in 10/2 SLs. The experimental concentration is 33%.

Fig. 3.

Structures from DFT calculations. (A) Possible configurations of La/Sr arrangements. C1 (Sr1–Sr2): two Sr atoms both at the BTO/LSO interface far from each other. C2 (Sr2–Sr1): two Sr atoms are at the interface at nearest neighbor (NN) columnar positions. C3 (Sr3–Sr4): two Sr atoms are in the core at NN columnar position. C4 (Sr1–Sr5): two Sr atoms are at NN rock salt positions at the interface. C5 (Sr3–Sr6): two Sr atoms are at NN rock salt position at the core. C4 configuration is found to have the lowest energy among all other configurations that have been considered for 8/4 SL. In the case of 4/4 SL, C4 configuration has been considered for comparison. Optimized structure of 8/4 SL shows suppression of a⁻a⁻c⁻ distortion and presence of Q^LSMO_Polar mode. (B) Illustration of competing distortions considered in LSMO block [i.e., Q^LSMO_Polar] and antiferrodistortive (a⁻a⁻c⁻) mode and (C) relative stability between competing polar and AFD (a⁻a⁻c⁻) modes [i.e., E (Polar) − E (a⁻a⁻c⁻)].

The supercell was constructed by starting with experimentally determined lattice parameters followed by a relaxation of both the supercell parameters and the internal degrees of freedom. We start with the experimentally determined c-axis lattice parameter (SI Appendix) to model the BTO layers (u.c. c axis = 4.16 Å) and the LSMO layers (u.c. c axis = 3.93 Å). For the a-axis lattice parameter, we use bulk cubic BTO (u.c. a axis = 5.645, rotated $\sqrt{2}\hspace{0.17em}a\hspace{0.17em}\times \hspace{0.17em}\sqrt{2\hspace{0.17em}}\hspace{0.17em}a$). In each of the model SLs, we have incorporated a tetragonal polar structure in the BTO layers as observed. For the LSMO layers, we performed calculations with either a polar distortion (Q^LSMO_Polar) for an 8/4 SL or an AFD a⁻a⁻c⁻ distortion (Q_AFD) as in bulk LSMO as illustrated in Fig. 3B. The relaxation of the supercell is discussed further in Methods. In each case, the system was allowed to relax until the force on each atom converged to 0.02 eV/Å. We assumed ferromagnetic ordering as determined by the experimental data (see below), with the goal of accounting for the appearance of polar displacements.

The initial configurations are illustrated in Fig. 3A. In the case of the 8/4 SL for the LSMO block, we constructed five different configurations considering five different relative positions of La/Sr, where two Sr atoms are always at different layers as illustrated in Fig. 3A. Here, configurations C1–C3 represent columnar arrangements of two Sr atoms, whereas configurations C4 and C5 represent nearest neighbor rock salt ordering of two Sr atoms (Fig. 3A has a detailed description).

The main results are summarized as follows. (i) Considering an 8/4 SL, when we compare total energies, we find that Q^LSMO_Polar has a lower total energy than the Q_AFD (a⁻a⁻c⁻) pattern (Fig. 3 B and C). No distortions or tilts are induced, in agreement with the experimental data. The same is true for a 10/2 SL but is not true for a 4/4 SL. (ii) La/Sr configurations considered here do not change the relative energy landscape. We found that configuration C4 has the lowest energy among the other configurations, which indicates that Sr atoms prefer to substitute La at the interface in a nearest neighbor rock salt arrangement. The net result is that, when the LSMO layer is ultrathin, it is polar and free of octahedral tilts as observed.

We further note that, in the case of the 8/4 SL for the C4 configuration, the two nonequivalent average O-Mn-O bond distances along the c axis are found to be 2.02 and 1.84 Å, respectively, which shows strong off-centering of Mn ions from the center of the O cage. A similar result is found for the 10/2 SL. These results show explicitly the presence of the observed polar mode in accord with the experimental data. These results also support our idea that, when two interfaces are close enough, a structural transition occurs to govern the property of the ultrathin material between them. We note that, because of computational challenges, smaller SLs are used, but they captured the essential trend in the experiments. We also expect similar experimental observations with the SL periodicities used in calculations.

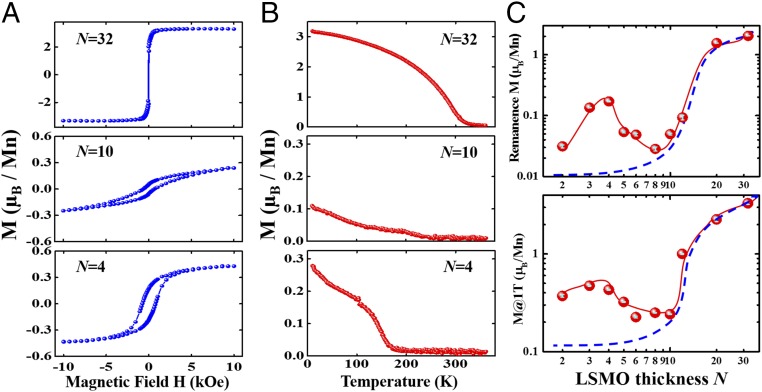
We then further examine the magnetic properties of these SLs. Magnetism in ultrathin ferromagnetic manganite films has been extensively studied. Although mechanisms, such as orbital reconstruction, oxygen vacancies, epitaxial strain, and interlayer correlations, have been shown to be important (43–46), it is widely recognized that, when the thickness of ferromagnetic films is reduced, the magnetization is monotonically suppressed (45–48). We measured the magnetic properties of the same three samples in Fig. 2. As shown in Fig. 4 A and B, the n = 32 film shows a normal paramagnetic to ferromagnetic transition above room temperature and strong ferromagnetism at 10 K. In contrast, the n = 10 film shows strongly quenched magnetization with no clear Curie transition. Interestingly, in the n = 4 film, a clear paramagnetic to ferromagnetic transition is restored with a Tc ∼ 172 K along with a clear ferromagnetic hysteresis M vs. H curve at 10 K. Such observations indicate an unusual magnetic behavior of LSMO under reduced thickness.

Fig. 4.

Unusual magnetic response of LSMO under reduced dimensionality of BTO/LSMO SLs. (A) M vs. H at zero field cooling and (B) M vs. T at 1,000 Oe curves for n = 32, 10, and 4 samples in Fig. 2. (C) Remanence magnetization and magnetization at 1 T as a function of LSMO thickness N at 10 K extracted from SI Appendix, Fig. S6. Error bar is embedded in cyan, which is typically two orders of magnitude smaller than the signal. Red curves are for eye guidance only. Blue dashed lines are for eye guidance only, indicating the monotonic decrease of magnetization in normal circumstances.

We subsequently examined the magnetic properties in these SLs by reducing the LSMO-layer thickness systematically. Contrary to expectations, both remanence and saturation magnetic moments show nonmonotonic behavior with reducing LSMO thickness as shown in Fig. 4C (SI Appendix, Figs. S6–S8). All of our samples are carefully aligned parallel to the magnetic field, and our magnetic data are of high quality, with an error bar that is two orders of magnitude smaller than the signal. When reducing the LSMO thickness from n = 32 u.c., the magnetic moments are strongly suppressed, as expected, to a minimum around 6–8 u.c. with very weak ferromagnetic signals. They then reemerge in the ultrathin regime at 3–4 u.c. with strong ferromagnetic character. This magnetic anomaly is further evidenced by magnetization vs. temperature curves that show strongly quenched ferromagnetism down to 6–8 u.c. and clear paramagnetic-to-ferromagnetic transition at 3–4 u.c. The transport data are also shown in SI Appendix, Fig. S9. The n = 32 film shows metallic behavior below 327K, whereas the n = 10 and 4 films show insulating behavior. This observed trend of metal to insulator character with reducing N is consistent with previous reports (43–46). The mechanisms of such behavior can be attributed to localization, reduced dimensionality, orbital reconstruction, and phase separation under reduced film thickness, although the exact nature is still under hot debate.

These results suggest that we have achieved an insulating and unusual polar ultrathin LSMO film with reemergent and stable ferromagnetism, which has the potential to become an ultrathin ferroelectric with ferromagnetic ordering, a state that rarely exists in nature. This finding is particularly attractive: because of the chemical bonding, the polar phase usually occurs in nonmagnetic perovskites (30, 31, 49, 50). With recent development of new mechanisms for achieving coexisting ferroelectricity and ferromagnetism (51, 52), our results provide a useful path for how to achieve ferroelectric ferromagnets via interface-induced structural transition in the ultrathin limit (15, 16, 53, 54). We also note that, although controlling interfacial properties via interface octahedral modulation has been a hotly studied subject recently (54–56), our findings push this concept much further by using a structural phase change to realize ultrathin films with unique functional properties.

Our observations also indicate that the structural change induced by interfaces can be the dominant mechanism in magnetic/electric interfaces, thus modulating the intrinsic spin–lattice coupling behavior in ultrathin TMOs. This finding is in clear contrast with previous observations that charge modulation governs the interface and controls the magnetism in TMOs (25–29). To clarify this issue, we carefully examine the valence states of Mn and Ti.

There seems to be a consensus that, when interfaced with ferroelectric films, the valence of Mn in LSMO is prone to exhibit deviations from its nominal values (25, 28, 29, 57, 58), and this valence change was considered as the origin of magnetic modulation (25, 28, 59, 60). To verify possible mechanisms, we extracted the Mn and Ti valence states from EELS (61) for all three films, and the results are summarized in Fig. 5. The EELS fine structures of the Mn L and O K edges were collected with atomic-layer precision to study the Mn oxidation state in the LSMO films. The intensity ratio between the L₃ and L₂ edges was used to determine Mn oxidation states, which is further confirmed by the results measured from the fine structure in the O K edge for accurate determination (SI Appendix, Figs. S10 and S11). Moreover, the Mn L and O K edges from the nominal LSMO sample were used as a reference for Mn^+3.33. As shown in Fig. 5, for all three films, Mn oxidation states across the LSMO film are slightly lower than the nominal value of +3.33. The valence state of Mn ions shows a variation between +3.10 and +3.25 for the n = 32-u.c. film, +3.13 and +3.30 for the n = 10-u.c. film, and +3.10 and +3.17 for the n = 4-u.c. film. This result suggests that there is no appreciable difference in the valence state with varying LSMO thickness.

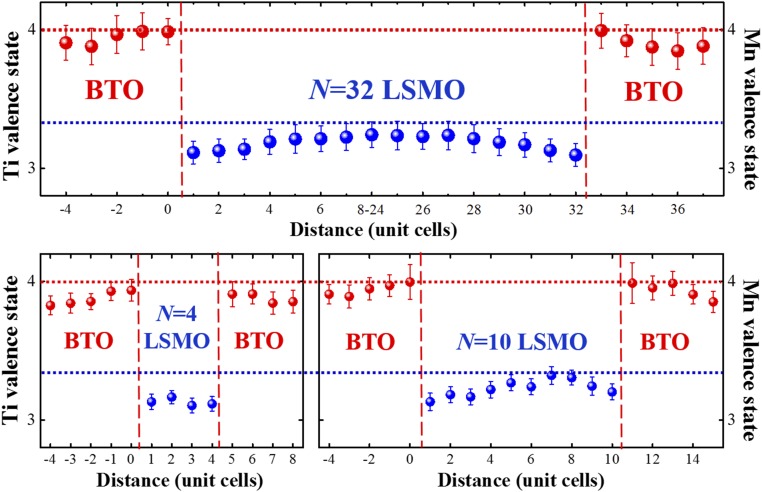
Fig. 5.

Layer by layer resolved Mn and Ti valence states for BTO/LSMO SL with n = 4, 10, and 32 u.c. The red and blue dashed lines indicate nominal Mn +3.33 and Ti +4.0, respectively. The oxidation states of Ti and Mn ions for all three films show similar variation across the interface.

The reduction of Mn valence when interfaced with ferroelectric materials has been widely observed in the literature (22, 25, 26). Although we did not observe appreciable valence variation in Fig. 5, there is still a possibility that the change of electronic valence is a major cause of the observed magnetic anomaly in the ultrathin region. Electrostatic doping is regarded as one of the major driving forces for magnetic/electric coupling (25–28, 59, 60, 62, 63). The electric field from ferroelectric materials creates hole depletion in LSMO on one side of the interface and accumulation on the other side, effectively tuning the valence of Mn and magnetization (64). This effect would cause the Mn valence to increase on one side of the interface relative to nominal value and decrease on the other side, which contradicts our observations for all three films.

Ferroelectric screening effects by oxygen vacancies have been recently observed to govern the valence state of Mn at interfaces (29). Indeed, oxygen vacancies can act as electron dopants and lower the Mn valence (65). If this scenario were the case in our films, the n = 4-u.c. film should present more oxygen vacancies than the n = 10-u.c. film, because Mn has slightly lower valence. This mechanism would cause more quenched ferromagnetism in the n = 4-u.c. film (66). This scenario certainly is inconsistent with our observed reemergent ferromagnetism in this film.

We further examined the valence state of Ti in BTO (SI Appendix, Fig. S12). As shown in Fig. 5, for all three films, the features are identical. The Ti away from the interface has a valence state of +3.9, which suggests about 1.67% oxygen deficiency in BTO. At the interface, the valence increases to +4.0, suggesting a small amount of effective charge transfer from Mn (65). The fact that the value and the tendency of Ti valences are nearly identical for all three films rules out the possibility that Ti valences play any major role in the observed magnetic anomaly in the ultrathin film region. We note that both the valence drop of Mn near the interface caused by charge redistribution or oxygen vacancies and the small charge transfer to Ti can serve to compensate the depolarization field in BTO films.

We also investigated the lattice constant change induced by substrate piezoelectric and interface coherency effects (67–69). As shown in SI Appendix, Fig. S5, BTO shows a c-axis lattice constant of about 4.16 Å. Both n = 4- and n = 10-u.c. LSMO show the same averaged c-axis lattice constants of 3.93 Å. This result suggests that the lattice effect is not responsible for our abnormal magnetic behavior at low thickness in LSMO.

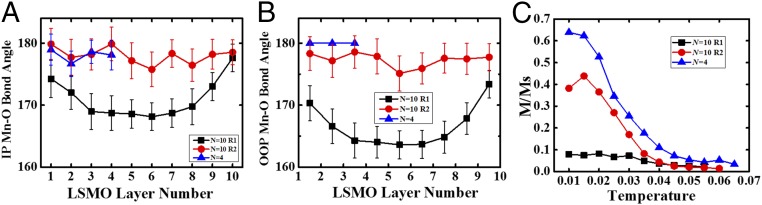
To establish a qualitative understanding of the observed phenomena, we performed a Monte Carlo simulation on the double-exchange model, including the structural distortion. The structural difference in Fig. 2 results in different bond angles in LSMO, which can directly alter the magnetism (64). Here, we focus on n = 4 and 10 u.c., where the magnetic anomaly occurs. As shown before, the Mn-O-Mn bond angles are significantly modified, whereas the Mn-O bond lengths are nearly identical. To keep the physics simple and clear, here the bond angle effects caused by both double exchange and superexchange are considered (more details are in SI Appendix). Because the valence in both films shows no appreciable change, we fix the same valence state to see the effect of lattice distortion. The bond angles for n = 4 u.c. and two regions in n = 10 u.c. are calculated from Fig. 2 and shown in Fig. 6 A and B (SI Appendix). By adopting the experimental bond angles, the 4- and 10-layer systems are simulated for comparison.

Fig. 6.

Calculated Mn-O bond angle and temperature-dependent magnetization per Mn obtained from Monte Carlo simulation of the double-exchange model. (A) In-plane (IP) and (B) out-of-plane (OOP) Mn-O bond angle for n = 10- (two regions) and n = 4-u.c. LSMO films. (C) By adopting the bond angles shown in A and B, the double-exchange model can simulate the magnetization (M) as a function of temperature (in units of the double-exchange hopping t0 ∼ 0.5 eV). It is clear that (i) the 4-layer LSMO shows the most prominent ferromagnetism, (ii) the ferromagnetism in the second case of the 10-layer LSMO is almost quenched, and (iii) the first case of 10-layer LSMO shows suppressed ferromagnetism, weaker than the 4-layer but stronger than the second case. Thus, the phase-separated 10-layer LSMO shows spatially contrasting magnetization. Ms, the saturated magnetization.

As shown in Fig. 6C, the simulation indeed shows that the n = 4-u.c. SL displays strong ferromagnetism, with prominent magnetization and higher Curie temperature. In contrast, the n = 10-u.c. case shows divergent magnetic behavior with two configurations of bond angles. Region 1 with smaller lattice distortions (larger bond angles) shows relatively stronger ferromagnetic tendency, whereas the ferromagnetism in region 2 (with smaller bond angles) is almost fully quenched. Both regions have weaker ferromagnetism than the n = 4-u.c. film. These results show that the change in Mn-O-Mn bond angles effectively tunes the exchange coefficients and bandwidth in LSMO and is, therefore, responsible for magnetization, which is consistent with previous work (36). In short, the experimentally observed bond angle modulation can indeed significantly change the magnetic properties of manganite few layers, consistent with both theoretical calculations and experimental observations. These results show the important role of spin–lattice coupling in complex oxide heterostructures, especially in ultrathin regions.

Our results above make use of a conceptually intriguing recipe of using a structural phase change induced by adjacent interfaces for the design of ultrathin film properties that are not present in the bulk material. Such an approach can be easily generalized to a broad range of correlated materials to explore their properties. One can control the desired structure of the ultrathin materials by fabricating heterojunctions using materials with known structural properties. Such structural transition can lead to ultrathin materials with intriguing magnetic/electronic properties through modulating its intrinsic spin–lattice coupling and other coupling effects. We expect our findings to have a broad impact on future design and application in nanoelectronics using ultrathin materials.

Methods

Thin Film Growth, XRD, and Magnetic Measurements.

The BTO₂₁/(LSMO_N/BTO₂₁)_M SLs were grown on SrTiO₃ (100) single-crystal substrates using stoichiometric targets of BTO and LSMO by pulsed laser deposition. The substrates were treated for 30 s in buffered hydrogen fluoride and annealed at 950 °C in 0.1 MPa oxygen atmosphere. During growth, the substrate temperature was held at 700 °C with laser energy density ∼1 J cm⁻². BTO was grown at 5 Hz, 10 mtorr, with growth rate of 0.02 layer per pulse, and LSMO was grown at 3 Hz, 80 mtorr oxygen with growth rate of 0.007 layer per pulse, both mixed with 1% ozone. Reflection high-energy electron diffraction was used during growth to monitor oscillations and surface quality. After growth, samples were cooled down to room temperature at 100 mtorr oxygen/ozone atmosphere. XRD mappings were performed on a PanAlytical X’Pert thin film diffractometer with Cu Kα−1 radiation with a single-crystal monochromator. Magnetic measurements are performed in a Quantum Design Magnetic Property Measurement System from 10 to 360 K by using the reciprocating sample option with the sensitivity of 5 × 10⁻⁹ EMU.

STEM and EELS Observation.

Cross-sectional transmission EM samples were thinned down to 30 nm by a focused ion beam with Ga⁺ ion milling followed with Ar+ ion milling. All of the samples were studied under a double aberration-corrected 200-kV JEOL ARM equipped with a dual energy loss spectrometer. The atomic structure of the film was studied by atomic-resolution HAADF and ABF STEM imaging. The annular detection angles for HAADF images were 50–133 and 11–23 mrad for ABF images. To determine the individual cation–oxygen displacements across the interface with a precision of a few picometers, we used the Gaussian fitting method to locate individual atomic positions.

The STEM conditions were optimized for EELS with a probe size of ∼0.9 Å, a convergence semiangle of 20 mrad, and collection semiangle of 88 mrad. Line-scanning EELS were obtained across the interface with a step size of 0.12 Å and a dwell time of 0.05 s per pixel. A dispersion of the 0.25 eV per channel was selected to simultaneously collect the Ti-L, O-K, Mn-L, La-L, and Ba-L edges with an energy resolution of 0.75 eV. To correct the intrinsic shift of energy of the electron beam, the zero-loss peak was collected simultaneously in the EELS line-scanning process. The absolute energy was calibrated carefully with the simultaneously acquired zero-loss peak. The EEL spectra were background-subtracted with a power law function, and multiple scattering was corrected by deconvolution. The EELS elemental profiles were obtained by integrating the Ba-M_4,5, La-M_4,5, Mn-L_2,3, and Ti-L_2,3 edges.

Double-Exchange Model and Monte Carlo Simulation.

The standard two-orbital double-exchange model has been proven to be successful to give a realistic description of manganites (64). A recent study also simulated the bond angle-dependent magnetism of LaMnO₃ ultrathin films sandwiched in SrTiO₃ layers, which gave a successful explanation of experimental observation (36). The conventional coefficients are adopted according to previous studies to give a proper description to La_1-xSr_xMnO₃ (36, 70, 71). Then, the effects of Mn-O-Mn bending bonds to both the double exchange and superexchange have been taken into account (36). More details on modeling and simulation can be found in SI Appendix.

First Principles DFT Calculation.

First principles calculations were carried out using DFT (72) with projector-augmented wave potentials (73) using the Perdew-Burke-Ernzerhof (PBE) exchange correlation functional (74) as implemented in the Vienna ab initio simulation package (73). The total energy and Hellman–Feynman forces were converged to 1 μeV and 0.02 eV/Å, respectively. All calculations were performed with a 450-eV energy cutoff and a Γ-centered 4 × 4 × 2 k-point mesh. We have considered the $\sqrt{2}\hspace{0.17em}\hspace{0.17em}a\hspace{0.17em}\times \hspace{0.17em}\sqrt{2\hspace{0.17em}}\hspace{0.17em}b\hspace{0.17em}\times \hspace{0.17em}12c$ supercell of the pseudocubic u.c. The system contains a total of 120 atoms. Here, we started with a and b as the in-plane lattice constants with bulk BTO values (a = 3.992 Å) and experimentally determined c-axis lattice parameters (SI Appendix), where the u.c. c axis = 4.16 Å for BTO and the LSMO layers u.c. c axis = 3.93 Å. For the 8/4 BTO/LSMO SL with 12 total u.c., the c axis has been obtained as 8 (u.c) $\times$ 4.16 + 4 (u.c.) $\times$ 3.93 = 49.0 Å. Similarly, the c axes for 10/2 and 4/4 SLs of the supercell turn out to be 49.46 and 32.36 Å, respectively. After constructing the supercell, both lattice parameters and also internal atomic positions are allowed to relax. The lattice parameter of the lowest energy structure for the 8/4 SL is 3.95 Å, whereas for 10/2 and 4/4, the values are 3.98 and 3.93 Å, respectively. This result is in line with the experimental data that the in-plane lattice is relaxed from the STO substrate. The out-of-plane parameter is found to be within 2% of the experimental value. DFT calculations were carried out without a Hubbard U, which has been previously shown to be adequate for total energies in Mn oxides (75).