Abstract
Most predictive models and scores of graft survival in renal transplantation include factors known before transplant or at the end of the first year. They cannot be updated thereafter, even in patients developing donor-specific anti-HLA antibodies and acute rejection.We developed a conditional and adjustable score for prediction of graft failure (AdGFS) up to 10 years post-transplantation in 664 kidney transplant patients. AdGFS was externally validated and calibrated in 896 kidney transplant patients.The final model included five baseline factors (pretransplant non donor-specific anti-HLA antibodies, donor age, serum creatinine measured at 1 year, longitudinal serum creatinine clusters during the first year, proteinuria measured at 1 year), and two predictors updated over time (de novo donor-specific anti-HLA antibodies and first acute rejection). AdGFS was able to stratify patients into four risk-groups, at different post-transplantation times. It showed good discrimination (time-dependent ROC curve at ten years: 0.83 (CI95% 0.76–0.89).
Introduction
Scoring systems that predict survival outcome after kidney transplantation can help physicians improve risk stratification among recipients and make the best therapeutic decision for a patient who develops de novo donor-specific anti-human leucocyte antigen (HLA) antibody (DSA). Serum creatinine (Scr) and estimated glomerular filtration rate (GFR) are not sufficiently reliable predictors for long-term risk of graft loss or patient death [1]. In the last decade, predictive models of graft survival based on large panels of data collected in the donor [2], in the recipient before transplantation [3], and/or in the first year post-transplantation [4,5] have been proposed. A limitation of these models is that they do not take into account the onset of adverse events over time, which modify graft outcome. In particular, these models never consider the impact of the development of de novo (dn)DSA beyond one year post-transplantation on graft outcome, although this has been demonstrated to be strongly associated with graft loss through antibody-mediated rejections [6,7]. All the studies focusing on the impact of the development of de novo DSA on graft outcome have concluded that post–transplant DSA monitoring could improve prediction of individual risk for kidney allograft loss [5,8]. The previously proposed tools were globally validated in patient cohorts but they often lost their predictive power in small patient subgroups with specific risks of graft failure, i.e. the patients who need them most.
Development of a graft failure risk score is most often based on Cox’s proportional hazards models (eventually with time-dependent covariates) to identify predictive risk factors [4,9,10] Random survival forest (RSF) modeling is an alternative non-parametric method based on an ensemble tree method for the analysis of right censored survival data [11]. RSF was found able to identify complex interactions among multiple variables and performed better than traditional cox proportional hazard model [12]. Other advantages of RSF are (i) insensitivity to noise brought by missing values or error data [11] and (ii) inclusion of an internal validation process [11]. Thus, RSF has been used in several risk models in cardiology [13] and oncology [14,15]. A conditional scoring system may be more appropriate than the addition of weights as derived from Cox model if the impact of a risk factor is different, whether or not it is associated with other factors. Finally, a prognostic tool that can be updated with comorbidity onset may be more powerful [16].
The objective of the present study was to build (using RSF) and validate a new conditional risk-scoring system of graft failure up to ten years post-transplantation, taking into account onset of emerging risks over time such as development of dnDSA. Our score highlights the impact of renal function during the first year and the evolution of the risk of graft loss with the onset of dnDSA and acute rejection.
Methods
This study adheres to the Declaration of Istanbul.
Database
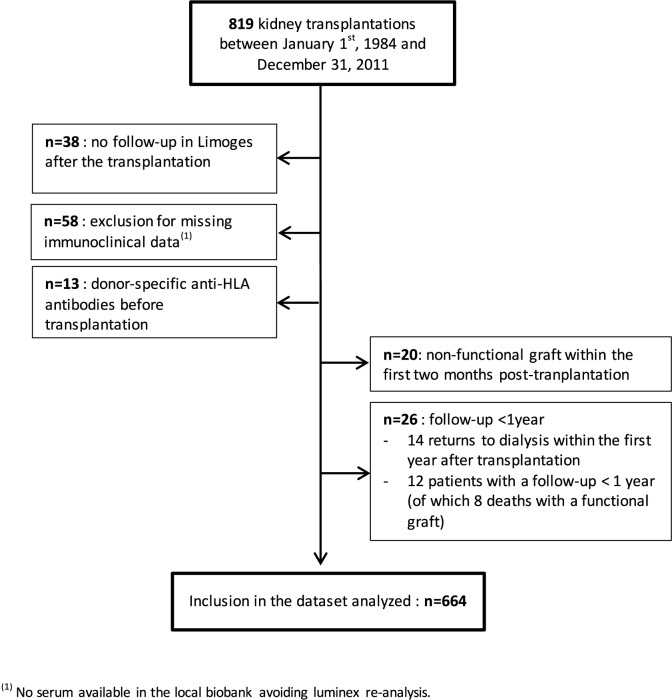
Of the 819 transplantations performed at the University Hospital of Limoges (France) between december 1984 and december 2011, 664 were included in the primary cohort (development database). A flow-chart showing patient selection is shown in Fig 1. All 664 transplants studied came from heart-beating deceased donors and had a follow-up of at least one year after transplantation. The maintenance immunosuppressive regimen consisted mainly of one calcineurin inhibitor (cyclosporine or, since 2001, tacrolimus) associated with azathioprine (until 1996) or mycophenolate mofetil (after 1996) and corticosteroids (generally stopped between 3 and 6 months post-transplantation). All patients received induction therapy. Patient outcome was known for each patient at the date of the last follow-up. Death was considered as a censored event when the recipient died with a functioning graft. When graft function was not known on the exact date of death, the date of the last biological assessment before death was then considered as the censoring time. Usually, graft function was recorded a few days before death. When patients died because of graft loss, death was considered as a graft failure.
Fig 1. Flowchart showing selection of renal transplant patients.
Donor, recipient and graft characteristics were collected from the CRISTAL register (from the French public agency “Agence de la Biomédecine”). Samples for immunological analysis were available in the local biobank, declared to the Ministry of Health (N° DC-2010-1074). At the time of transplantation, DNA was systematically extracted from the cells of the spleen or lymph node of the donor. DNA (storage 4°C) and cells (storage nitrogen) were preserved for each donor. Sera of the patients were systematically preserved at -20°C.
The study database was approved by the French Informatics and Liberty National Commission (CNIL, registration number 1795293).
Anti-HLA antibodies screening
Anti-HLA-A, -B, -C, -DP, -DQ, -DR antibodies were screened and identified using Luminex® solid-phase assay (One Lambda LABScreen assays) in samples collected before transplantation and routinely after transplantation (three, six, twelve months, once every year thereafter, and whenever clinically indicated). Results were expressed as median fluorescence intensity (MFI). MFI >1000 was considered positive. All sera tested using the Complement Dependent Cytotoxicity method prior to the availability of Luminex® technology in our center (2007), were re-analyzed using Luminex®. As DQ, DP and C HLA typing was not previously systematically performed in our center, a molecular DNA typing of donor and recipient was performed in case of detection by Luminex® of an anti-HLA-C, -DQ or -DP antibody during the survey. This procedure allowed to determine the specificity (donor-specific or non donor-specific) of the anti-HLA antibody and to avoid bias in the determination of DSA. DSA diagnosis prior to renal transplantation was an exclusion criterion for transplantation in our center. Patients in whom the Luminex® reanalysis identified presence of DSA before transplantation (n = 13) were excluded from the database studied.
Cluster analysis of serum creatinine over the first year post-transplantation
Homogeneous subgroups of trajectories of serum creatinine measured within the first year post-transplantation were identified by a clustering method based on k-means, specifically designed to analyze longitudinal data and implemented in the ‘kml’ R-package (version 1.1.3) [17]. This method does not require any assumption regarding the shape of the serum creatinine-time curves, contrary to model-based methods which fit the trajectories with a specific model (e.g. linear, polynomial or exponential). The optimal number of clusters was selected using the statistical criterion proposed by Calinski and Harabasz [18].
Identification of factors predictive of graft survival
The impact of the following variables was investigated on graft survival: (i) donor characteristics (age, cause of death—cardiac, stroke or traumatic injuries-); (ii) recipient demographic variables (age at time of transplantation, gender); (iii) transplantation characteristics [time period of transplantation (i.e. 1984–1993, 1994–2003 or 2004–2011), cold ischemia time, previous kidney transplantation(s)]; (iv) immunological variables (HLA-A, HLA-B and HLA-DR mismatches, pre-transplant anti-HLA antibodies, source of anti-HLA alloimmunization (i.e. previous transplantation, pregnancy, blood transfusion), occurrence of de novo donor-specific and/or non-donor-specific anti-HLA antibodies (dnDSA and dnNDSA, respectively) with the date of the first diagnosis; (v) biological variables [repeated measurements of serum creatinine (μM) over the first year post-transplantation, proteinuria (g/L) at one year post-transplantation]; (vi) clinical variables (initial renal disease, date of first acute rejection diagnosis, date of return to dialysis, date of end of follow-up); and (vii) immunosuppressive drugs administered. Patient ethnicity was not recorded since it is not authorized by French law.
RSF analysis was performed to select and rank the most predictive covariates of graft failure using the date of transplantation as time origin [11]. RSF was implemented in the ‘randomForestSRC’ R-package (version 2.0.0). Briefly, a RSF was generated by creating 1000 trees, each tree built on a randomly selected bootstrap sample (using 63% of the original data) using a randomly selected subset of covariates. Each bootstrap sample excluded, on average, 37% of the data, which were reserved for a test set called “out-of-bag” data (OOB). RSF evaluated the change in prediction error attributable to each covariate. The prediction error (i.e. the percentage of patients misclassified) was assessed with the Harrell’s concordance index (Harrell’s c-index) using OOB data [19]. The c-index was computed using an OOB set constructed with the 1000 OOB datasets provided by the 1000 bootstrap samples used in growing the forest. The OOB prediction error is defined as 1 minus Harrell’s c-index [11]. The prediction error ranges between 0 and 1, where a value of 0.5 corresponds to a prediction no better than random guessing and a value of 0 reflects perfect accuracy. The parameter “nsplit” used to specify random splitting was fixed at 3. The predictive performance of the studied variables was evaluated by their “variable importance” (VIMP), calculated by RSF. VIMP measures the change in prediction error for a forest grown with or without this variable.
Variables selection was successively done by (1) fitting data by RSF and ranking all available variables and (2) iteratively fitting RSF by removing at each iteration a variable from the bottom of the positive variable importance ranking list. The minimal combination of variables leading to the smallest “out-of-bag” prediction error rate, assessed by the Harrell’s c-index, was selected.
A conditional survival tree [20] was subsequently drawn from the whole original dataset, using the most predictive variables selected from RSF [‘party’ (version 1.0–21) R-package].
Prediction of graft failure
Score calculations were derived from both the VIMP sourced from the final RSF model and the conditional survival tree. The weight of each variable (i.e. each risk factor) was based on the ratio between its VIMP and the VIMP of the last predictive variable retained. A same value of weight was allocated for variables split at the same tree-depth in the conditional survival tree. The weighted risk score was calculated by adding the weights of the different risk factors within each branch of the conditional survival tree. This strategy led to a score for each patient subgroup identified at each terminal node of the conditional survival tree. Time-dependent receiver operating characteristic (ROC) curves with area under the curve (AUC) for censored survival data were used to evaluate the discrimination of the developed score. Additional weights were attributed for variables not selected in the conditional survival tree but highly associated with graft survival in the RSF analysis, provided their inclusion improved the ROC AUC. The weight of a factor could be increased if it allowed maximization of the ROC AUC at ten years post-transplantation. The predictive performance of the developed score was evaluated by time-dependent sensitivity, specificity, positive predictive value (PPV) and negative predictive value (NPV) with their standard error, all estimated at several cutpoints, i.e. for different threshold score values and for different times after transplantation. Therefore, ‘timeROC’ (version 0.2) R package was employed using the Kaplan-Meier estimator of the censoring distribution. Baseline (i.e. including variables available at one year post-transplantation) and adjusted (i.e. adding variables collected after one year post-transplantation) scores were also compared using time-dependent ROC AUC.
External validation
External validation of the developed score was performed in patients transplanted between 2002 and 2010 in two independent French transplantation centers (CHU Tours n = 706; CHU Poitiers n = 190). As in the development cohort, patients with pre-transplant DSA were excluded. All anti-HLA antibodies screenings were performed using Luminex®. The validation database (Astre database) was approved by the CNIL (Authorization number DR-2012-518).
Validation procedure included: recalculation of the Scr clusters considering the external database only, calculation of the individual scores using the developed scoring system, determination of the time-dependent ROC AUC at ten years post-transplantation and calibration based on Hosmer-Lemeshow goodness-of-fit test adapted for survival data [21]. The calibration evaluation consisted in comparing numbers of patients with graft failure expected and observed in the validation cohort using the calculation of the numbers of events based on Kaplan-Meier survival estimates which was by proposed by D’Agostino-Nam [22]. In a first step, the number of graft failures observed in the validation cohort in different time-intervals ([0–2[, [2–4[, [4–6[, [6–8[, [8–10] years after transplantation) were calculated for each risk group as the product ni(1-KMi(t)) where KMi is the Kaplan-Meier survival estimate at a fixed time t for groupi and ni the number of observations in groupi. The survival probabilities expected in the validation cohort were calculated using the Kaplan-Meier estimates obtained in the development cohort. With this test, the p value has to be higher than 0.05.
Statistical analyses
The study used a conditional approach to determine a patient risk-stratification with several (>2) levels of risk of graft failure. An estimated 616 patients were needed for a power of 80% and a two-sided significance level of 5%. Based on published data and expert opinion, we assumed (i) a 10-years free graft failure survival of 82% in the studied population of renal transplant patients and (ii) that kidney function one year after the transplantation and occurrence of de novo DSA over time will be major discriminant parameters to classify the patients in the different risk levels. We hypothesized that 25% of the studied patients would have an impaired renal function one year after transplantation (i.e a serum creatinine concentration higher than 1.8 mg/dL (160 μmol/L) [1]) resulting in 10-years free graft failure survival being decreased to 70%. In agreement with Wiebe et al. [23] we hypothesized cumulative incidence of de novo DSA of 15% resulting in a 10-years free graft failure survival decreased to 60% and to 40% in the groups with a serum creatinine concentration lower than 160 μmol/L and higher than 160 μmol/L, respectively. Acute rejection being a known major risk factor of graft failure in patients with DSA [24], we considered that around 33% of the patients with DSA would have developed acute rejection and that their graft survival would be reduced to 25%.
Comparison between categorical data was done using the Pearson chi-square test or the exact Fisher test. Normally distributed data were analyzed by Anova and the parametric t-test, whereas nonparametric tests (Kruskall-Wallis and Mann–Whitney tests respectively) were used otherwise. Kaplan-Meier analysis was used to assess graft survival (graft loss, i.e. return to dialysis). Graft survival in different patient subgroups was compared using the log rank test.
Statistical analyses were performed with MedCalc for Windows, version 14.10.2. (MedCalc Software, Ostend, Belgium) and R version 2.15.1 (www.R-project.org). The R packages are freely available through the Comprehensive R Archive Network distribution system (http://cran.r-project.org).
Results
Development database
The characteristics of the studied kidney transplants are listed in Table 1.
Table 1. Kidney transplant characteristics of the development and validation databases.
| Development Database (n = 664) |
Validation Database (n = 896) |
||
|---|---|---|---|
| Tours | Poitiers | ||
| Total number of transplants | 664 | 706 | 190 |
| Duration of follow-up (years) | 6.4 (± 3.3) | 7.4 (± 2.3) | 7.9 (± 1.2) |
| Functional renal grafts at 10 years post-transplantation | 202 (30.4%) | 171 (24.2%) | 31 (16.3%) |
| Recipient gender (M/F) | 405/259 | NA | NA |
| Recipient age (years) | 49 (± 14) (15–77)* |
NA | NA |
| Donor age (years) | 44 (± 16) | 51 (± 17) | 48 (± 15) |
| HLA A Mismatch | 1.2 (± 0.7) | NA | NA |
| HLA B Mismatch | 1.5 (± 0.6) | NA | NA |
| HLA DR Mismatch | 1.2 (± 0.7) | NA | NA |
| First transplantation | 608 (91.6%) | NA | NA |
| Pretransplant NDSA | 105 (15.8%) | 151 (21.4%) | 34 (17.9%) |
| Serum creatinine at M12 (μM) | 139 (± 71) | 136 (± 49) | 131 (± 40) |
| Proteinuria at M12 (g/L) | 0.18 (± 0.50) | 0.19 (± 0.45) | |
| Proteinuria at M12 (g/24h) | 0.63 (± 1.96) | 0.37 (± 0.80) | |
| Return to dialysis | 69 (10.4%) | 116 (16.4%) | 22 (11.6%) |
| Death with a functional graft (censured data) | 60 (9.0%) | NA | NA |
| de novo NDSA | 142 (21.3%) | NA | NA |
| Median (range) time to onset (years) | 3.02 (0.02–10) | ||
| de novo DSA | 62 (9.3%) | 113 (16%) | 41 (21.6%) |
| Median (range) time to onset (years) | 3.92 (0.02–9.83) | 2.94 (0.79–5.04) | 3.12 (1.95–5.1) |
| Patients with onset of dnDSA in the first year after transplantation | 11 (17.7%) | 35 (31.0%) | 7 (16.7%) |
| First acute rejection episode | 137 (20.6%) | 219 (31%) | 48 (25.3%) |
| Median (range) time to onset (years) | 0.26 (0.01–9.27) | 0.15 (0.04–0.35) | 0.25 (0.03–0.40) |
Data are n (%), mean (± SD) or median (range)
*4 patients under the age of 18 years (3 of them aged 17 years)
DSA = donor-specific anti-HLA antibodies. NDSA = non-donor-specific anti-HLA antibodies. M12 = month 12 post-transplantation. NA Not Appropriate
During the whole study period, 137 patients have been treated for a first acute rejection among them 122 (89%) were biopsy proven. One hundred nine first rejections occurred during the first year post-transplantation. Borderline rejection was evidenced in 36 patients and T-Cell mediated rejection (TCMR) in 105 patients, Antibody-mediated rejection (ABMR) in 14 patients and mixed (ABMR + TCMR) in three patients. Only two patients displayed ABMR criteria on a biopsy done before the definition of ABMR in the Banff classification.
During follow-up, dnDSA were present in 62 patients. The median time to dnDSA diagnosis was significantly lower in patients who exhibited pretransplant NDSA than in patients who did not (1.42 vs 4.87 years, p = 0.0012). Sixty-four percent of patients with dnDSA (n = 39) had class II antigens, 34% (n = 21) had class I and 2% (n = 2) had both class I and II antigens. Nearly all patients who developed dnDSA after transplantation had previously (n = 19) or concomitantly (n = 36) developed dnNDSA. Except for one patient who presented dnDSA transiently (i.e., detected at 1.6 years after transplantation and absent at subsequent screenings), DSA remained persistent at all screenings following the first detection. Thirteen patients with dnDSA returned to dialysis, including six within the year following the diagnosis of dnDSA (median 1.04 years, range: 0.03–4.46). Eleven out the 17 patients with ABMR on histology had developed dnDSA.
Scr profiles over the first year post-transplantation were best partitioned in three clusters (Fig 2). Graft survival after transplantation was significantly different in these three subgroups (p<0.0001) (Fig 2). The percentage of donors over 60 years of age increased from cluster A to C (29 [7.7%], 57 [23.4%], and 19 [44.2%], respectively, p<0.0001). The mean cold ischemia time was significantly higher in cluster C than in clusters A and B, p = 0.034). No cold ischemia time lower than 12 hours was observed in cluster C.
Fig 2. Serum creatinine clusters.
(A) Mean trajectories of serum creatinine resulting from k-means for the longitudinal data clustering method superposed with individual profiles over the first 12 months post-transplantation. (B) Kaplan-Meier estimates (±95% confidence intervals) of graft survival according to the first-year creatinine profile cluster. The free graft failure survival was significantly associated with clusters (log-rank test, p<0.0001).
Identification of factors predictive of graft survival after the first year post-transplantation
The classification of the variables according to their out-of-bag importance in the full RSF model is illustrated in the Fig 3. The best model was obtained using the log rank splitting rule with 1000 trees with a Harrell’s Concordance error rate of 21% (standard deviation 0.2%) (Fig 3). This final model included five baseline variables (pretransplant NDSA, donor age, Scr measured at 12 months post-transplantation (ScrM12), Scr clusters, proteinuria measured at M12 (ProtM12)), and two predictors which could be updated during the follow-up of the graft (onset of dnDSA and first acute rejection whatever the time of onset after transplantation).
Fig 3. Out-of-bag data variable importance values obtained by random survival forest analysis.
(A) full model and (B) final model. The log-rank splitting rule was used.
The partial plots of graft survival, predicted in the RSF analysis using the retained continuous variables (after adjusting for all other predictors) showed decreased survival when donor age exceeds 60 years, and very steep survival curves when ScrM12 >150 μM, so that small increments in ScrM12 would result in large survival declines (Fig 4).
Fig 4. Partial plots for the continuous variables retained in the random survival forest analysis as predictors of graft failure.
The vertical axis represents the predicted survival at 10 years for a given predictor, after adjusting for all other predictors. Points indicate partial values and dashed lines are ±2 standard error bars.
Adjustable graft failure score (AdGFS) for prediction of graft survival
A scoring system was constructed using conditional survival tree analysis, with nodes corresponding to the variables selected in the final RSF model. The tree identified height terminal nodes, corresponding to height patient subgroups (Fig 5). The hierarchical order of the variables in predicting graft survival provided by the conditional survival tree was in accordance with the variable ranks obtained by RSF analysis.
Fig 5. Conditional inference tree applied for graft survival with predicted Kaplan-Meier curves in the terminal nodes.
The tree was obtained using recursive partitioning for censored response in a conditional inference framework implemented in ‘party’ R-package.
Our scoring system, named AdGFS (Adjustable Graft Failure Score), is shown in Fig 6. AdGFS outperformed the baseline score including predictors available at one year after transplantation (time-dependent ROC AUC at ten years: 0.83 (CI95% 0.76–0.89) vs 0.75 (CI95% 0.68–0.82), p = 0.0075). Taking into account onset of dnDSA and first acute rejection developed over time, after one year post-transplantation improved survival prediction beyond 5 years post-transplantation (p = 0.0244).
Fig 6. Scoring system for computing AdGFS values.
ScrM12 = serum creatinine at 12 months post-transplantation. ProtM12 = proteinuria at 12 months post-transplantation. Scr = serum creatinine. dnDSA = de novo donor-specific anti-HLA antibodies. NDSA = non donor-specific anti-HLA antibodies.
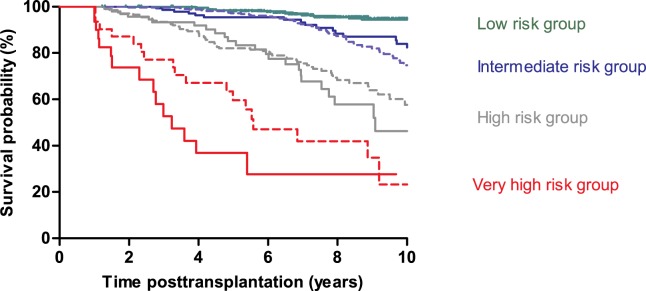
AdGFS values are reported for each patient subgroup in Fig 5. Table 2 presents, for the different cutpoints of AdGFS values, the performance characteristics of graft survival prediction at different post-transplantation times. For example, a patient with low score (AdGFS = 2) has a probability of graft survival up to 10 years post-transplantation of approximately 94.5% (NPV). Onset dnDSA during the follow-up increased the score value (adjusted score = 6) and led to a probability of graft loss of 64.9% at 8 years and 83.6% at 10 years post-transplantation (PPV) (Table 2). Probabilities of graft survival lower than 20% (PPV > 80%) at ten years post-transplantation were obtained for score values of 6 and more. Risk groups were defined according to the AdGFS value: low risk (0), intermediate risk (2–4), high risk (6–8), and very high risk (10–12). Ten years graft survival was significantly different between these four risk groups (p< 0.0001) (Fig 7).
Table 2. Performance characteristics of adjustable graft failure score (AdGFS) for cutpoints 0, 2, 4, 6, 8, 10 and for different times over 10 years post-transplantation.
| Cutoff point (c) | Number of positive tests (>c) | Number of negative tests (≤c) | Censored post-transplantation time (years) | Se (se_Se)% | Sp (se_Sp)% | PPV (se_PPV) % | NPV (se_NPV)% |
|---|---|---|---|---|---|---|---|
| 0 | 292 | 365 | 2 | 100 (0) | 59.7 (2.1) | 4.3 (1.3) | 100 (0) |
| 299 | 358 | 4 | 95.7 (4.2) | 60.9 (2.3) | 11.1 (2.1) | 99.6 (0.4) | |
| 303 | 354 | 6 | 85.7 (5.9) | 66.2 (2.6) | 17.9 (2.9) | 98.1 (0.8) | |
| 309 | 348 | 8 | 80.7 (5.5) | 69.2 (2.9) | 29.1 (3.8) | 95.8 (1.4) | |
| 314 | 343 | 10 | 79.4 (5.4) | 72.5 (3.2) | 35.9 (4.5) | 94.8 (1.5) | |
| 2 | 264 | 393 | 2 | 100 (0) | 63.2 (2.1) | 4.6 (1.4) | 100 (0) |
| 271 | 386 | 4 | 91.9 (5.5) | 64.6 (2.3) | 11.7 (2.3) | 99.3 (0.5) | |
| 275 | 382 | 6 | 83.3 (6.2) | 68.5 (2.5) | 18.5 (3.0) | 97.9 (0.9) | |
| 282 | 375 | 8 | 79.3 (5.6) | 69.9 (2.9) | 29.2 (3.9) | 95.5 (1.4) | |
| 288 | 369 | 10 | 78.3 (5.4) | 73.1 (3.2) | 36.0 (4.5) | 94.5 (1.5) | |
| 4 | 120 | 537 | 2 | 100 (0) | 85.4 (1.5) | 11.0 (3.2) | 100 (0) |
| 122 | 535 | 4 | 75.7 (8.6) | 87.0 (1.6) | 23.0 (4.6) | 98.5 (0.6) | |
| 125 | 532 | 6 | 70.6 (7.4) | 91.0 (1.6) | 40.2 (6.2) | 97.3 (0.8) | |
| 130 | 527 | 8 | 58.5 (6.7) | 95.0 (1.4) | 64.9 (7.4) | 93.6 (1.4) | |
| 134 | 523 | 10 | 53.7 (6.5) | 97.7 (1.0) | 83.6 (7.2) | 91.6 (1.6) | |
| 6 | 62 | 595 | 2 | 90.9 (8.7) | 93.3 (1.1) | 19.8 (5.7) | 99.8 (0.2) |
| 62 | 595 | 4 | 68.2 (9.2) | 94.3 (1.1) | 37.9 (7.2) | 98.3 (0.6) | |
| 62 | 595 | 6 | 56.6 (8.0) | 96.0 (1.1) | 55.2 (8.4) | 96.2 (1.0) | |
| 62 | 595 | 8 | 39.4 (6.4) | 97.7 (1.0) | 73.0 (9.0) | 91.1 (1.6) | |
| 62 | 595 | 10 | 33.1 (5.7) | 98.4 (0.9) | 80.7 (9.5) | 88.4 (1.9) | |
| 8 | 31 | 626 | 2 | 62.8 (14.7) | 97.5 (0.7) | 31.1 (10.0) | 99.3 (0.4) |
| 31 | 626 | 4 | 50.4 (9.7) | 98.4 (0.6) | 62.6 (10.9) | 97.4 (0.7) | |
| 31 | 626 | 6 | 34.2 (7.5) | 99.1 (0.5) | 77.6 (11.0) | 94.6 (1.1) | |
| 31 | 626 | 8 | 19.9 (4.9) | 99.6 (0.4) | 89.1 (10.0) | 88.8 (1.7) | |
| 31 | 626 | 10 | 16.7 (4.2) | 100.0 (0.0) | 100 (0) | 86.1 (1.9) | |
| 10 | 9 | 648 | 2 | 17.6 (11.4) | 99.1 (0.4) | 26.2 (16.2) | 98.5 (0.5) |
| 9 | 648 | 4 | 26.5 (8.7) | 100 (0) | 100 (0) | 96.3 (0.8) | |
| 9 | 648 | 6 | 16.3 (5.8) | 100 (0) | 100 (0) | 93.3 (1.2) | |
| 9 | 648 | 8 | 9.5 (3.5) | 100 (0) | 100 (0) | 87.5 (1.7) | |
| 9 | 648 | 10 | 7.9 (3.0) | 100 (0) | 100 (0) | 84.9 (1.9) |
Time post-transplantation was defined as the duration between the date of transplantation and the time point where graft failure prediction was made. The test was considered as positive when AdGFS score > cutpoint and negative when score was ≤ cutpoint. Time dependent sensitivity (Se), Specificity (Sp) Positive Predictive Value (PPV) and Negative Predictive Value (NPV) were computed with standard error (se) at the six given cutpoints: 0 and 2, 4, 6, 8, 10 for different censored post-transplantation times. AdGFS could be calculated in 657 patients, 7 patients were secondarily excluded due to missing data.
Fig 7. Comparison of Kaplan-Meier graft survival curves for the four risk groups namely low-, intermediate-, high-, and very high- risk of graft loss in the development dataset (solid lines) and in the external validation dataset (dashed lines).
Patients were partitioned according to the calculated score value: low risk (0), intermediate risk (2 or 4), high risk (6 or 8), and very high risk (10 or 12). Graft survival in the development and validation datasets did not differ within each of the four risk groups.
External validation of AdGFS
Table 1 reports the characteristics of the patients. Graft survival within each risk group was similar in the development and external validation datasets (Fig 7). The accuracy of the score at predicting graft failure remained high in the validation dataset, with a time-dependent ROC AUC of 0.79 (CI 95% 0.74–0.84) at ten years after transplantation. Results of calibration evaluation of AdGFS in the external dataset were good: observed numbers of patients with graft failure were close to the expected numbers using the AdGFS risk groups ((χ2 = 2.39, p = 0.30) (Table 3).
Table 3. Goodness-of-fit test for external validation of the AdGFS score.
| Risk group | Number of patients with graft failure | Number of patients without graft failure | ||
|---|---|---|---|---|
| Observed | Expected | Observed | Expected | |
| Low (0) | 14 | 14.9 | 314 | 313.1 |
| Intermediate (2 or 4) | 47 | 53.8 | 286 | 279.2 |
| High (6 or 8) | 57 | 58.3 | 146 | 144.7 |
| Very high (10 or 12) | 18 | 14.8 | 14 | 17.2 |
Data refers to the number of patients. Chi-squared = 2.39 (p = 0.30) with 2 degrees of freedom. The number of patients with graft failure expected in the validation cohort for the four different risk groups was calculated using the Kaplan-Meier survival estimates obtained in the development cohort.
Discussion
In the present work, we developed and externally validated a conditional and adjustable predictive score (named AdGFS) of long-term kidney graft failure including pre-transplantation, early post-transplantation predictors and two factors collected all along the patients’ follow-up: onset of dnDSA and first acute rejection episodes. All the items included in the score are available everywhere in the day-to-day clinical surveillance of the patients. This score can be calculated from one year post-transplantation and updated all along the evolution of the graft depending on the occurrence of dnDSA and acute rejection. The calibration and discrimination of this score were good in large cohorts of patients treated with the current standard of care.
All previously published scores are computed using only individual factors known before the end of the first year post-transplantation. They are never updated, even if the patient’s prognosis is altered. The performance of these scores is usually evaluated with respect to shorter term graft survival and at a single time point [3–5,10,25]. In this study, we used the non-parametric RSF method which has several advantages compared to regression approaches among which it does not test the goodness of fit of data to a hypothesis, but seeks a model that explains the data [26].
Most of the baseline predictors selected for the calculation of AdGFS, are well-accepted graft failure risk factors [3,4,9,10,27]. Renal function in the first year post-transplantation was found to be predictive of graft survival at 3, 5 [28,29] and 8 years post-transplantation [4]. Proteinuria has also recently been associated with graft failure in a cohort of 1518 patients [30]. The cut-off points for Scr and proteinuria defined in order to maximize time-dependent ROC AUC, are in accordance with previously published values [30]. Comparison between a score calculated with the baseline parameters included in AdGFS (i.e. the variables collected up to one year post-transplantation) and AdGFS (i.e. adding variables collected after one year post-transplantation) demonstrated the added value of taking into account follow-up data beyond one year post-transplantation.
The present study confirmed the deleterious role of donor age and its link with Scr [2,31]. Donor age above 60 years was retained in different donor quality scoring systems [32] and was also associated with graft outcome after acute ABMR [33]. In the present study, two other baseline predictors were identified: Scr cluster and pretransplant NDSA. Longitudinal Scr clusters, assessing the Scr time-profiles along the first year, have never been used before in predictive model of graft failure. Clustering adds information to the use of single or repeated measurement(s) of biological or clinical markers. Herein, it revealed patient subgroups with homogenous Scr time-profiles. This approach is in line with FDA guidance to better differentiate phenotypes of patients (http://www.fda.gov/downloads/Drugs/GuidanceComplianceregulatoryInformation/Guidances/UCM458485.pdf). For future studies, we propose a graphical tool dedicated to allocating new patients in the clusters (S1 Fig).
No previously proposed score takes into account onset of dnDSA beyond one year post-transplantation and their impact on graft survival [5,6,34,35]. Our study, finding a cumulative incidence of 9.3% of dnDSA and a 24% rate of graft failure at 3 years after the onset of dnDSA, is in accordance with previous studies showing a 5-year post-transplantation cumulative incidence of dnDSA from 5.5 to 20% [6,23], a 7 to 9% risk of graft failure in the first year after the occurrence of dnDSA, and up to 24% of patients with chronic ABMR and renal failure within 3 years post-DSA [6,24].
AdGFS is the first score to include new-onset dnDSA to predict graft survival. The inclusion of dnDSA requires an adjustable approach since they may appear at any time. AdGFS can be updated during patient follow-up in case of dnDSA or acute rejection. DnDSA’s pathogenicity depends on their association with acute rejection, as previously found by Cooper and colleagues [36]. Taking into account dnDSA improved survival prediction beyond 5 years post-transplantation in accordance with published works highlighting that graft loss attributable to dnDSA occurs several years after their onset [24].
Other factors classically reported to be associated with graft failure [4,27,32,37], such as HLA mismatches, cold ischemia, recipient gender, and immunosuppressive treatments, were not retained in the score because they did not allow a decrease in the error rate in the RSF analysis, and they did not improve the time-dependent ROC AUC. This was explained by their significant association with the retained variables (e.g increased cold ischemia time was associated with Scr clusters).
Contrary to published scores, AdGFS predicted graft failure at different post-transplantation times up to ten years and stratified the patients into four risk groups. Kasiske and colleagues [9] evaluated only the 5 year risk of graft failure and the discriminatory ability of their scores remained modest as highlighted by the authors. In the Kidney Transplant Failure Score, graft failure was evaluated at 8 years post-transplantation and patients were stratified into only two groups [4]. The good results of our external validation in a population different with regards to time of transplantation and standard-of-care supported the robustness of AdGFS.
Assessment of the individual patient’s risk of transplant failure throughout the time after transplantation may be a decisive tool to select the optimal care strategy for the patient. For instance, in the high risk group, specific treatments for dnDSA might be questionable regarding the balance between the probability of maintaining a functioning graft and the side effects associated to these treatments.
The main strength of this study lies in the long follow-up and careful monitoring of anti-HLA antibodies using a Luminex® solid-phase assay, even for patients grafted before the year 2000. The database is one of the largest in which the impact of dnDSA was analyzed. Our study has some limitations. It included fewer patients than some previously published cohorts and was validated (i) beyond one year of transplantation, (ii) in deceased donors’ grafts, and (iii) in patients without DSA at the time of transplantation. Thereby, AdGFS can be cannot be calculated before one year post-transplantation neither in case of living donor nor in patients with DSA before transplantation.
In conclusion, we propose an adjustable score for risk stratification of graft failure at different post-transplantation times. AdGFS showed good discrimination and could be more useful than scores ignoring onset of dnDSA, for decisions regarding more or less intensive surveillance and treatment of the patients.
Supporting information
Supplementary individuals can be allocated to a cluster using a graphical approach in which the individual serum creatinine values obtained at each visit are superimposed to the 10th-90th percentiles interval of serum creatinine values obtained in the three clusters for the same times. Examples of predicted cluster for three different patients are shown.
(EPS)
Acknowledgments
The authors would like to thank Dr Mireille Drouet and Dr Hélène Pauthier and the HLA laboratory of Limoges (University hospital) for their technical assistance, Zeinab Daher Abdi and Fathia Mouzarine for collecting the data. The authors thank David P. Figgitt PhD, Content Ed Net, for providing editorial assistance.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
The Astre database was funded by Roche, Astellas and Sanofi. The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Kaplan B, Schold J, Meier-Kriesche H- U. Poor predictive value of serum creatinine for renal allograft loss. Am J Transplant Off J Am Soc Transplant Am Soc Transpl Surg. 2003;3: 1560–1565. [DOI] [PubMed] [Google Scholar]
- 2.Nyberg SL, Matas AJ, Kremers WK, Thostenson JD, Larson TS, Prieto M, et al. Improved scoring system to assess adult donors for cadaver renal transplantation. Am J Transplant Off J Am Soc Transplant Am Soc Transpl Surg. 2003;3: 715–721. [DOI] [PubMed] [Google Scholar]
- 3.Brown TS, Elster EA, Stevens K, Graybill JC, Gillern S, Phinney S, et al. Bayesian modeling of pretransplant variables accurately predicts kidney graft survival. Am J Nephrol. 2012;36: 561–569. doi: 10.1159/000345552 [DOI] [PubMed] [Google Scholar]
- 4.Foucher Y, Daguin P, Akl A, Kessler M, Ladrière M, Legendre C, et al. A clinical scoring system highly predictive of long-term kidney graft survival. Kidney Int. 2010;78: 1288–1294. doi: 10.1038/ki.2010.232 [DOI] [PubMed] [Google Scholar]
- 5.Gonzales MM, Bentall A, Kremers WK, Stegall MD, Borrows R. Predicting Individual Renal Allograft Outcomes Using Risk Models with 1-Year Surveillance Biopsy and Alloantibody Data. J Am Soc Nephrol JASN. 2016; doi: 10.1681/ASN.2015070811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hourmant M, Cesbron-Gautier A, Terasaki PI, Mizutani K, Moreau A, Meurette A, et al. Frequency and clinical implications of development of donor-specific and non-donor-specific HLA antibodies after kidney transplantation. J Am Soc Nephrol JASN. 2005;16: 2804–2812. doi: 10.1681/ASN.2004121130 [DOI] [PubMed] [Google Scholar]
- 7.Lefaucheur C, Loupy A, Vernerey D, Duong-Van-Huyen J- P, Suberbielle C, Anglicheau D, et al. Antibody-mediated vascular rejection of kidney allografts: a population-based study. Lancet Lond Engl. 2013;381: 313–319. doi: 10.1016/S0140-6736(12)61265-3 [DOI] [PubMed] [Google Scholar]
- 8.Viglietti D, Loupy A, Vernerey D, Bentlejewski C, Gosset C, Aubert O, et al. Value of Donor-Specific Anti-HLA Antibody Monitoring and Characterization for Risk Stratification of Kidney Allograft Loss. J Am Soc Nephrol JASN. 2017;28: 702–715. doi: 10.1681/ASN.2016030368 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kasiske BL, Israni AK, Snyder JJ, Skeans MA, Peng Y, Weinhandl ED. A simple tool to predict outcomes after kidney transplant. Am J Kidney Dis Off J Natl Kidney Found. 2010;56: 947–960. doi: 10.1053/j.ajkd.2010.06.020 [DOI] [PubMed] [Google Scholar]
- 10.Shabir S, Halimi J-M, Cherukuri A, Ball S, Ferro C, Lipkin G, et al. Predicting 5-year risk of kidney transplant failure: a prediction instrument using data available at 1 year posttransplantation. Am J Kidney Dis Off J Natl Kidney Found. 2014;63: 643–651. doi: 10.1053/j.ajkd.2013.10.059 [DOI] [PubMed] [Google Scholar]
- 11.Ishwaran H, Kogalur UB, Blackstone EH, Lauer MS. Random survival forests. Ann Appl Stat. 2008;2: 841–860. [Google Scholar]
- 12.Miao F, Cai Y-P, Zhang Y-X, Li Y, Zhang Y-T. Risk Prediction of One-Year Mortality in Patients with Cardiac Arrhythmias Using Random Survival Forest. Comput Math Methods Med. 2015;2015: 303250 doi: 10.1155/2015/303250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hsich E, Gorodeski EZ, Blackstone EH, Ishwaran H, Lauer MS. Identifying important risk factors for survival in patient with systolic heart failure using random survival forests. Circ Cardiovasc Qual Outcomes. 2011;4: 39–45. doi: 10.1161/CIRCOUTCOMES.110.939371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ishwaran H, Blackstone EH, Apperson-Hansen C, Rice TW. A novel approach to cancer staging: application to esophageal cancer. Biostat Oxf Engl. 2009;10: 603–620. doi: 10.1093/biostatistics/kxp016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Datema FR, Moya A, Krause P, Bäck T, Willmes L, Langeveld T, et al. Novel head and neck cancer survival analysis approach: random survival forests versus Cox proportional hazards regression. Head Neck. 2012;34: 50–58. doi: 10.1002/hed.21698 [DOI] [PubMed] [Google Scholar]
- 16.Sène M, Taylor JM, Dignam JJ, Jacqmin-Gadda H, Proust-Lima C. Individualized dynamic prediction of prostate cancer recurrence with and without the initiation of a second treatment: Development and validation. Stat Methods Med Res. 2014; doi: 10.1177/0962280214535763 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Genolini C, Falissard B. KmL: a package to cluster longitudinal data. Comput Methods Programs Biomed. 2011;104: e112–121. doi: 10.1016/j.cmpb.2011.05.008 [DOI] [PubMed] [Google Scholar]
- 18.Calinski T, Harabasz J. A dendrite method for cluster analysis. Commun Stat. 1974;3: 1–27. [Google Scholar]
- 19.Harrell FE, Califf RM, Pryor DB, Lee KL, Rosati RA. Evaluating the yield of medical tests. JAMA. 1982;247: 2543–2546. [PubMed] [Google Scholar]
- 20.Hothorn T, Hornik K, Zeileis A. Unbiased recursive partitioning: a conditional inference framework. J Comput Graph Stat. 2006;15: 651–674. [Google Scholar]
- 21.Leteurtre S, Martinot A, Duhamel A, Proulx F, Grandbastien B, Cotting J, et al. Validation of the paediatric logistic organ dysfunction (PELOD) score: prospective, observational, multicentre study. Lancet Lond Engl. 2003;362: 192–197. doi: 10.1016/S0140-6736(03)13908-6 [DOI] [PubMed] [Google Scholar]
- 22.D’Agostino RB, Nam B-H. Evaluation of the performance of survival analysis models: discrimination and calibration measure. Handbook of Statistics, Survival Methods. 2004. pp. 1–25. [Google Scholar]
- 23.Wiebe C, Gibson IW, Blydt-Hansen TD, Karpinski M, Ho J, Storsley LJ, et al. Evolution and clinical pathologic correlations of de novo donor-specific HLA antibody post kidney transplant. Am J Transplant Off J Am Soc Transplant Am Soc Transpl Surg. 2012;12: 1157–1167. doi: 10.1111/j.1600-6143.2012.04013.x [DOI] [PubMed] [Google Scholar]
- 24.Everly MJ, Rebellato LM, Haisch CE, Ozawa M, Parker K, Briley KP, et al. Incidence and impact of de novo donor-specific alloantibody in primary renal allografts. Transplantation. 2013;95: 410–417. doi: 10.1097/TP.0b013e31827d62e3 [DOI] [PubMed] [Google Scholar]
- 25.Kasiske BL, Andany MA, Hernández D, Silkensen J, Rabb H, McClean J, et al. Comparing methods for monitoring serum creatinine to predict late renal allograft failure. Am J Kidney Dis Off J Natl Kidney Found. 2001;38: 1065–1073. doi: 10.1053/ajkd.2001.28605 [DOI] [PubMed] [Google Scholar]
- 26.Dietrich S, Floegel A, Troll M, Kühn T, Rathmann W, Peters A, et al. Random Survival Forest in practice: a method for modelling complex metabolomics data in time to event analysis. Int J Epidemiol. 2016; doi: 10.1093/ije/dyw145 [DOI] [PubMed] [Google Scholar]
- 27.Moore J, He X, Shabir S, Hanvesakul R, Benavente D, Cockwell P, et al. Development and evaluation of a composite risk score to predict kidney transplant failure. Am J Kidney Dis Off J Natl Kidney Found. 2011;57: 744–751. doi: 10.1053/j.ajkd.2010.12.017 [DOI] [PubMed] [Google Scholar]
- 28.Hariharan S, McBride MA, Cherikh WS, Tolleris CB, Bresnahan BA, Johnson CP. Post-transplant renal function in the first year predicts long-term kidney transplant survival. Kidney Int. 2002;62: 311–318. doi: 10.1046/j.1523-1755.2002.00424.x [DOI] [PubMed] [Google Scholar]
- 29.First MR. Renal function as a predictor of long-term graft survival in renal transplant patients. Nephrol Dial Transplant Off Publ Eur Dial Transpl Assoc—Eur Ren Assoc. 2003;18 Suppl 1: i3–6. [DOI] [PubMed] [Google Scholar]
- 30.Naesens M, Lerut E, Emonds M-P, Herelixka A, Evenepoel P, Claes K, et al. Proteinuria as a Noninvasive Marker for Renal Allograft Histology and Failure: An Observational Cohort Study. J Am Soc Nephrol JASN. 2016;27: 281–292. doi: 10.1681/ASN.2015010062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Irish WD, McCollum DA, Tesi RJ, Owen AB, Brennan DC, Bailly JE, et al. Nomogram for predicting the likelihood of delayed graft function in adult cadaveric renal transplant recipients. J Am Soc Nephrol JASN. 2003;14: 2967–2974. [DOI] [PubMed] [Google Scholar]
- 32.Aubert O, Kamar N, Vernerey D, Viglietti D, Martinez F, Duong-Van-Huyen J-P, et al. Long term outcomes of transplantation using kidneys from expanded criteria donors: prospective, population based cohort study. BMJ. 2015;351: h3557 doi: 10.1136/bmj.h3557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Loupy A, Lefaucheur C, Vernerey D, Chang J, Hidalgo LG, Beuscart T, et al. Molecular microscope strategy to improve risk stratification in early antibody-mediated kidney allograft rejection. J Am Soc Nephrol JASN. 2014;25: 2267–2277. doi: 10.1681/ASN.2013111149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lachmann N, Terasaki PI, Budde K, Liefeldt L, Kahl A, Reinke P, et al. Anti-human leukocyte antigen and donor-specific antibodies detected by luminex posttransplant serve as biomarkers for chronic rejection of renal allografts. Transplantation. 2009;87: 1505–1513. doi: 10.1097/TP.0b013e3181a44206 [DOI] [PubMed] [Google Scholar]
- 35.Lefaucheur C, Loupy A, Hill GS, Andrade J, Nochy D, Antoine C, et al. Preexisting donor-specific HLA antibodies predict outcome in kidney transplantation. J Am Soc Nephrol JASN. 2010;21: 1398–1406. doi: 10.1681/ASN.2009101065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cooper JE, Gralla J, Cagle L, Goldberg R, Chan L, Wiseman AC. Inferior kidney allograft outcomes in patients with de novo donor-specific antibodies are due to acute rejection episodes. Transplantation. 2011;91: 1103–1109. doi: 10.1097/TP.0b013e3182139da1 [DOI] [PubMed] [Google Scholar]
- 37.Debout A, Foucher Y, Trébern-Launay K, Legendre C, Kreis H, Mourad G, et al. Each additional hour of cold ischemia time significantly increases the risk of graft failure and mortality following renal transplantation. Kidney Int. 2015;87: 343–349. doi: 10.1038/ki.2014.304 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary individuals can be allocated to a cluster using a graphical approach in which the individual serum creatinine values obtained at each visit are superimposed to the 10th-90th percentiles interval of serum creatinine values obtained in the three clusters for the same times. Examples of predicted cluster for three different patients are shown.
(EPS)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.