Model Averaging with AIC Weights for Hypothesis Testing of Hormesis at Low Doses

Abstract

For many dose–response studies, large samples are not available. Particularly, when the outcome of interest is binary rather than continuous, a large sample size is required to provide evidence for hormesis at low doses. In a small or moderate sample, we can gain statistical power by the use of a parametric model. It is an efficient approach when it is correctly specified, but it can be misleading otherwise. This research is motivated by the fact that data points at high experimental doses have too much contribution in the hypothesis testing when a parametric model is misspecified. In dose–response analyses, to account for model uncertainty and to reduce the impact of model misspecification, averaging multiple models have been widely discussed in the literature. In this article, we propose to average semiparametric models when we test for hormesis at low doses. We show the different characteristics of averaging parametric models and averaging semiparametric models by simulation. We apply the proposed method to real data, and we show that P values from averaged semiparametric models are more credible than P values from averaged parametric methods. When the true dose–response relationship does not follow a parametric assumption, the proposed method can be an alternative robust approach.

Introduction

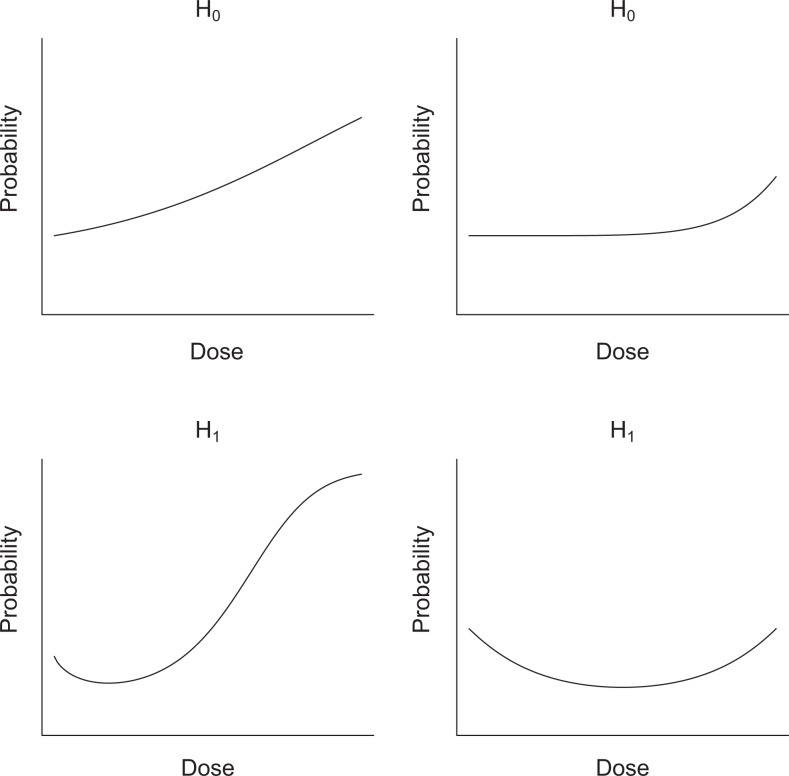
In toxicology, hormesis is known to be a biphasic dose–response relationship with a stimulatory response at low doses and an inhibitory response at high doses.^1,2 In this article, we focus on statistical hypothesis testing for hormesis when the outcome of interest is binary. The null hypothesis is the absence of hormesis denoted by H ₀, and the alternative hypothesis is the presence of hormesis denoted by H ₁. For illustration, 2 models for H ₀ and 2 models for H ₁ are shown in Figure 1.

Figure 1.

Dose–response relationships. The top figures show 2 hypothetical monotonic dose–response relationships (null hypothesis, denoted by H ₀), and the bottom figures show 2 hypothetical hormetic dose–response relationships (alternative hypothesis, denoted by H ₁).

Mathematically speaking, we do not have a sign change in the slope of a dose–response curve at low doses when H ₀ is true. The slope is entirely positive at low doses (top left in the figure), or the zero slope (ie, flat line) becomes a positive slope after passing some threshold dose point (top right in the figure). On the other hand, we have 1 sign change in the slope at low doses when H ₁ is true. The starting slope is negative, and the slope becomes positive at some dose point (bottom left and bottom right in the figure). When H ₀ is true, for a given significance level α, we want the probability of rejecting H ₀ to be at α or below. When H ₁ is true, we want the statistical power as high as possible.

We can increase the statistical power by increasing the number of experimental doses and/or the sample size inside the hormetic range. In such a case, various statistical methods are available including polynomial, fractional polynomial modeling, splines, and nonparametric smoothing techniques.³ However, having such an ideal experimental design is not always possible in practice. Although we prefer statistical methods that require weak assumptions, we need to borrow a parametric assumption to gain statistical power in small-sample studies. Several useful parametric models used in dose–response assessments are equipped in Benchmark Dose Model software.⁴ These models can be modified to quadratic or other alternative forms in order to model a nonmonotonic dose–response relationship.^5-7 A parametric model yields a high statistical power when it is correctly specified, but it can lead to a very low statistical power when it is misspecified. The loss of statistical power due to model misspecification will be shown in this study. There are 2 main reasons. First, the observed data points cannot be adequately modeled by the parametric structure.³ Second, in the case of model misspecification, data points at high doses make situations even worse because they have too much contribution in the parameter estimation. Such data points are called high-leverage points.⁸

We have 2 aims in this article. First, we explicitly address the impact of model misspecification and high-leverage points in parametric modeling when we perform hypothesis testing for hormesis at significance level α. Second, we propose averaging multiple semiparametric models using the weights calculated by Akaike information criterion (AIC).⁹ In both frequentist and Bayesian frameworks, model averaging methods have been widely discussed in cancer risk assessments, particularly for the estimation of benchmark dose. Model averaging allows us to reduce the impact of model misspecification and to account for model uncertainty.^7,10-13 In this article, we present the simulation study to compare parametric methods and the proposed semiparametric method. For illustration, we apply the methods to some data discussed in Calabrese and Baldwin¹⁴ which seem to show evidence for hormesis at various degrees. In the application, we show that P values calculated from parametric models can be misleading, and P values calculated from the semiparametric method better match with observed dose–response trend.

Statistical Methods

In this section, we review a logistic regression model in “Logistic Regression Model” subsection We base our discussion on the logistic model among many parametric models because of its popularity, and the same discussion can be carried out for another form of parameterization. We briefly review the model averaging method based on the AIC in “Model Averaging in Parametric Models (L3 and L4)” subsection. We then discuss the application of model averaging to semiparametric models in “Application of Model Averaging to Semiparametric Models” subsection. More mathematical detail is included in the Appendix.

The following notation is used in the section. Let x_j ≥ 0 denote the jth fixed experimental dose for j = 1,…, J, where J is the total number of experimental doses. Without loss of generality, let x ₁ = 0 be the control dose and x ₁ < x ₂ <…< x_J. Let Y_ij denote the binary random variable, where Y_ij = 1 if the ith experimental unit treated at dose x_j shows a toxic outcome and Y_ij = 0 otherwise. Let π_j denote the unknown probability of observing Y_ij = 1 (ie, the probability of observing a toxic outcome at does x_j). Let n_j denote the number of experimental units observed at dose x_j, and let N = Σ_j n_j denote the total sample size for the experiment.

Logistic Regression Model

To model a potential “J-shaped” dose–response relationship, a logistic regression model with the quadratic term

$$\text{log}\left(\frac{{\text{π}}_j}{1-{\text{π}}_j}\right)={\beta }_0+{\beta }_1{x}_j+{\beta }_2{x}_j^2$$

is briefly discussed by May and Bigelow.³ They considered the log dose, but it is not an important distinction in our discussion. Throughout the article, the logistic regression model is referred to as the L3 model, where L3 stands for the logistic regression model with 3 parameters β₀, β₁, and β₂. The quadratic term allows a hormetic dose–response curve at low doses, and similar parameterizations are discussed by Bogen⁶ and Kim et al⁷ using different link functions. In the quadratic form, hypothesis testing for hormesis is simply formulated as H ₀: β₁ ≥ 0 versus H ₁: β₁ < 0. In a large sample, we can make inference for β₁ based on the maximum likelihood estimator for β₁, but we usually do not observe such a large sample size particularly inside the hormetic range in practice.³ In this article, we base our inference on bootstrapping to approximate the sampling distribution of the maximum likelihood estimator for β₁.¹⁵ Our focus is on the consequence of wrong implementation of this model.

The L3 model is an efficient statistical strategy when it is correctly specified. On the other hand, when the model is misspecified, it can lead us to a misleading result even in a large sample. Under model misspecification, observations made at high experimental doses have too much contribution in the estimation of β₁ (known as high-leverage points), and it can significantly decrease statistical power. Motivated by a power transformation described by Tukey transformation,¹⁶ the L3 model can be modified as

$$\text{log}\left(\frac{{\text{π}}_j}{1-{\text{π}}_j}\right)={\beta }_0+{\beta }_1{(x_j)}^{{\beta }_3}+{\beta }_2{(x_j^2)}^{{\beta }_3}$$

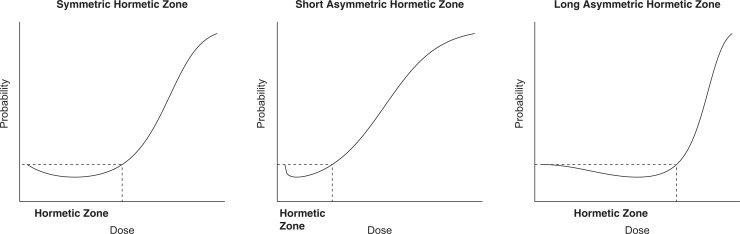
where β₃ > 0. This parameterization is referred to as the L4 model, where L4 stands for the logistic regression with 4 parameters β₀, β₁, β₂, and β₃. A similar parameterization was discussed by Kim et al.¹⁷ Compared to the L3 model, the L4 model is more flexible while it maintains the same form of hypothesis testing H ₀: β₁ ≥ 0 versus H ₁: β₁ < 0. As shown in Figure 2, the L3 model is limited to a symmetric hormetic zone only (figure on the left), and the L4 model is able to generate an asymmetric hormetic zone by adding the power parameter β₃ (figures in the middle and on the right). Note that the L3 model is a special case of the L4 model when β₃ = 1.

Figure 2.

Hormetic dose–response relationships generated by the logistic regression models. The left figure is the L3 model with β ₀ = −1.5, β ₁ = −5, and β ₂ = 10, the middle figure is the L4 model with β ₀ = −1.5, β ₁ = −5, β ₂ = 10, and β ₃ = 0.5, and the right figure is the L4 model with β ₀ = −1.5, β ₁ = −5, β ₂ = 10, and β ₃ = 2.

Model Averaging in Parametric Models (L3 and L4)

The advantage of the L3 model is efficiency (high statistical power) when the true hormetic zone is symmetric and the true dose–response relationship follows the quadratic form. The disadvantage is a loss of statistical power when the model is misspecified. It is also sensitive to high-leverage points. The impact of model misspecification and high-leverage points can be increased particularly when the experiment is poorly designed. On the other hand, the advantage of the L4 model is flexibility, and it can maintain relatively high statistical power when the true hormetic zone is asymmetric. The disadvantage of L4 is a loss of statistical power due to overparameterization when the true hormetic dose–response relationship can be adequately modeled by the L3 model. To compromise the characteristics of L3 and L4, we may consider the model averaging method based on the AIC.⁹ The method of AIC model averaging is often used to account for model uncertainty and to reduce the impact of model misspecification when a single model is used for inference.^10,18,19

Let w _L3 and w _L4 denote the AIC weight calculated from the observed data, where w _L3 + w _L3 = 1 (see Appendix). When a fitted model has a higher value of the likelihood function than the other fitted model, it receives a higher weight. In addition, it penalizes an additional model parameter to balance between goodness of fit and overparameterization. When we have 2 bootstrap distributions from L3 and L4, we can consider a mixture distribution according the AIC weights. Since both L3 and L4 determine hormesis by the sign of β₁, we can perform the hypothesis testing H ₀: β₁ ≥ 0 versus H ₁: β₁ < 0 based on the mixture distribution of estimated β₁. At significance level α = .05, we reject H ₀ in favor of H ₁ when the (1 − α)th quantile of the distribution is below 0. Throughout the discussion, this model averaging method is referred to as MA_P (model averaging with the parameter models). When H ₀ is true, the type I error rate under MA_A is fairly close to the minimum of the type I error rate under L3 and the type I error rate under L4 (see Appendix and Simulation Result).

Averaging β₁ in L3 and β₁ in L4 is a meaningless procedure when our goal is parameter estimation. However, our goal is hypothesis testing not parameter estimation. Though β₁ in L3 and β₁ in L4 have different meanings, both β₁ < 0 in L3 and β₁ < 0 in L4 have the same meaning (presence of hormesis) in the context of our hypothesis testing. Under each model using bootstrapping, we may seek evidence for β₁ < 0 through the bootstrap distribution of estimated β₁. Therefore, when a mixture bootstrap distribution of estimated β₁ is mostly negative (regardless of magnitude), it may be regarded as evidence for hormesis.

Application of Model Averaging to Semiparametric Models

Recall that we let π_j denote the probability of a toxic outcome at dose x_j. In general, we need evidence for π₁ > π₂ to reject H ₀ in favor of H ₁. In this section, we introduce a proposed model averaging method which does not require a link function between the probability of a toxic outcome and the dose.

Let M ₁ denote the saturated model with J free parameters, π₁, π₂,…, π_J, so each π_j is estimated by the observed proportion at dose x_j. Let M ₂ denote a model with J − 1 free parameters by the condition π₂ = π₃, so π₂ is estimated by the observed proportion at the 2 doses x ₂ and x ₃. Let M ₃ denote a model with J − 2 free parameters by the condition π₂ = π₃ = π₄, so π₂ is estimated by the observed proportion at the 3 doses x ₂, x ₃, and x ₄. Using general notation, let M_k denote the model with J − k + 1 free parameters such that π₂ =…= π_{k +1}. We consider up to M_{J −2} and obtain the AIC-weights w ₁,…, w_{J −2} by maximizing the log-likelihood function (see Appendix for detail). When we have more experimental units inside the hormetic range, the model averaging will become more robust regardless of the values of x ₁,…, x_J because the model structure depends on the order x ₁,…, x_J and estimated π₁,…, π_J. It does not assume a particular shape of dose–response curve.

For each M_k, we can obtain the bootstrap distribution of estimated π₁ − π₂, then we test for hypothesis testing H ₀: π₁ − π₂ ≤ 0 versus H ₁: π₁ − π₂ > 0 based on the mixture of the J − 2 bootstrap distributions weighted by the AIC weights. At significance level α, we reject H ₀ in favor of H ₁ when the αth quantile of the mixture distribution exceeds 0. Throughout the discussion, this model averaging method is referred to as MA_SP (model averaging with semiparametric models).

Results

In this section, we compare the operating characteristics of the 4 aforementioned models: L3, L4, MA_P, and MA_SP. We consider 16 simulation scenarios with 5 scenarios under H ₀ and 11 scenarios under H ₁ (see Simulation Design). We summarize the simulation results by the probability of rejecting H ₀ under each scenario and for each model (see Simulation Result). Then, we apply the 4 models to the data discussed in Calabrese and Baldwin¹⁴ which provided some degree of evidence for hormesis at low doses (see Application).

Simulation Design

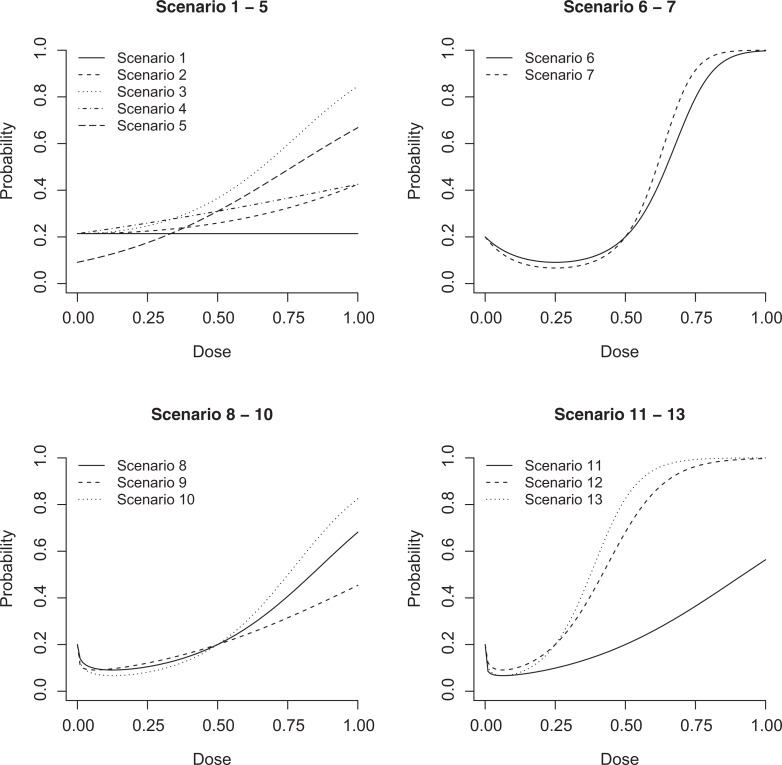
To control noise in the simulation, for all 16 scenarios, we assumed J = 6 experimental doses geometrically spaced as x ₁ = 0, x ₂ = 0.0625, x ₃ = 0.125, x ₄ = 0.25, x ₅ = 0.5, and x ₆ = 1, and we assumed n_j = 50 for each dose group so that N = 300 is the total sample size. For the case of H ₀, we generated data under the logistic models L₃ or L₄ (scenarios 1-5). For the case of H ₁, we generated data under L₃ (scenarios 6 and 7), L₄ (scenarios 8-13) and neither (scenarios 14-16).

The scenarios under the parametric structures are shown in Figure 3 (scenarios 1-13). For these parametric scenarios, the parameter values are presented in Table 1. For scenarios 14 to 16, we broke the parametric structures, so both L3 and L4 are misspecified models in the 3 scenarios. We made pointwise assumptions π₁ = 0.2, π₂ = 0.09, π₃ = 0.1, π₄ = 0.2, π₅ = 0.4, and π₆ = 0.6 in scenario 14; 0.2, 0.09, 0.07, 0.2, 0.4, and 0.6 in scenario 15, respectively; and 0.2, 0.07, 0.08, 0.2, 0.4, and 0.6 in scenario 16, respectively. Each scenario was simulated 1000 times, and 2000 bootstrap samples were used per simulated sample. We fixed the significance level at α = .05, and the probability of rejecting H ₀ was recorded for each method under each scenario.

Figure 3.

Simulation scenarios generated by the logistic models (scenarios 1-13). The parameter values are provided in Table 1.

Table 1.

Parameter Values for Scenarios 1 to 13 Under the Logistic Model.

Scenario	1	2	3	4	5	6	7	8	9	10	11	12	13
β0	−1.3	−1.3	−1.3	−1.3	−2.3	−1.39	−1.39	−1.39	−1.39	−1.39	−1.39	−1.39	−1.39
β1	0	0	0	0	0	−7.33	−10.02	−5.18	−4.62	−7.09	−6.31	−7.33	−10.02
β2	0	1	3	1	3	14.66	20.04	7.33	5.82	10.02	7.95	14.66	20.04
β3	0	1	1	.5	.5	1	1	.5	.33	.5	.33	.5	.5

Simulation Result

Table 2 provides the simulation results. When H ₀ was true in scenarios 1 to 5, the L3 model violated α = .05 in some scenarios at mild degree, and the L4 model violated α = .05 at serious degree in scenario 2. The estimated type I error probability was .082 which is difficult to believe that it just happened by chance for 1000 replications of the scenario. In each scenario, the model averaging method MA_P rejected H ₀ with a probability between the resulting probabilities in L3 and L4 with an anticipated result. The model averaging method MA_SP obeyed α = .05 in the 5 null scenarios.

Table 2.

Simulation Results, the Probability of Rejecting H ₀ Based on 1000 Simulated Data per Scenario.^a

Scenario	True Model	L3	L4	MAP	MASP
1	L3/L4	.055	.044	.042	.044
2	L3/L4	.056	.082	.061	.037
3	L3/L4	.019	.029	.018	.020
4	L3/L4	.066	.038	.043	.025
5	L3/L4	.000	.003	.000	.019
6	L3	.984	.764	.894	.279
7	L3	.998	.845	.948	.400
8	L4	.277	.570	.467	.474
9	L4	.135	.474	.327	.470
10	L4	.387	.706	.641	.673
11	L4	.145	.635	.517	.689
12	L4	.318	.525	.446	.475
13	L4	.453	.768	.660	.670
14	–	.000	.180	.107	.438
15	–	.000	.200	.144	.580
16	–	.000	.268	.200	.666

^aL3 represents logistic regression model with the 3 parameters β₀, β₁, and β₂; L4, logistic regression model with the 4 parameters β₀, β₁, β₂, and β₃; MA_P, model averaging with the parametric models L3 and L4; MA_SP, model averaging with the semiparametric models.

In scenarios 6 and 7, when H ₁ was true under the L3 model, the L4 model led to slightly lower statistical powers than the L3 model due to overparameterization. The MA_P model yielded statistical power between the results in M3 and M4 as anticipated. On the other hand, the MA_SP yielded substantially lower statistical powers in the 2 scenarios. When the true dose–response curve is generated under the simple L3 model, the L3 model outperformed which is not surprising.

In scenarios 8 to 13, when H ₁ was true under the L4 model, the L3 model could not tolerate model misspecification by showing substantially lower statistical powers due to the inflexibility. The L4 model mostly showed outperformance because the scenarios belong to its own parameterization. In these 6 scenarios, the MA_SP model was consistently more powerful than the MA_p model despite the contribution of the true L4 model to MA_P. In scenarios 9 to 11, the MA_SP model showed comparable results to the results from the true L4 model.

We now turn our focus on scenarios 14, 15, and 16. Recall that these 3 scenarios did not belong to any of L3, L4, MA_P, and MA_SP. The M3 model could not reject H ₀ even once, the L4 model showed statistical powers of .180, .200, and .268, respectively, and the MA_P model showed statistical powers of .107, .144, and .200, respectively. On the other hand, the MA_SP showed statistical powers of .438, .580, and .666, respectively.

The take-home message is clear. The parametric L3 and L4 models sometimes showed outperformance within their own parameterizations (statistical power of .984 and .998 from L3 in scenarios 6 and 7, respectively; statistical power of .570, .474, .706, .525, and .768 from L4 in scenarios 8, 9, 10, 12 and 13, respectively; see Table 2), but they performed poorly when the truth was not under the model (statistical power of 0 from L3 in scenarios 14, 15, and 16; statistical power of .180, .200, and .268 from L4 in scenarios 14, 15, and 16 which are less than one half when compared to .438, .580, and .666 from MA_SP in the respective scenarios; see Table 2). This is a general phenomenon in statistics. On the other hand, the MA_SP model was relatively less sensitive, and the model averaging among the semiparametric model (MA_SP) showed greater statistical power than the model averaging among the parametric models (MA_P) in the scenarios except when L3 was the true model (see scenarios 8-16 in Table 2).

Application

In this section, we apply the 4 models (L3, L4, MA_P, and MA_SP) to some of binary data discussed in Calabrese and Baldwin¹⁴ and compare P values from the 4 models.

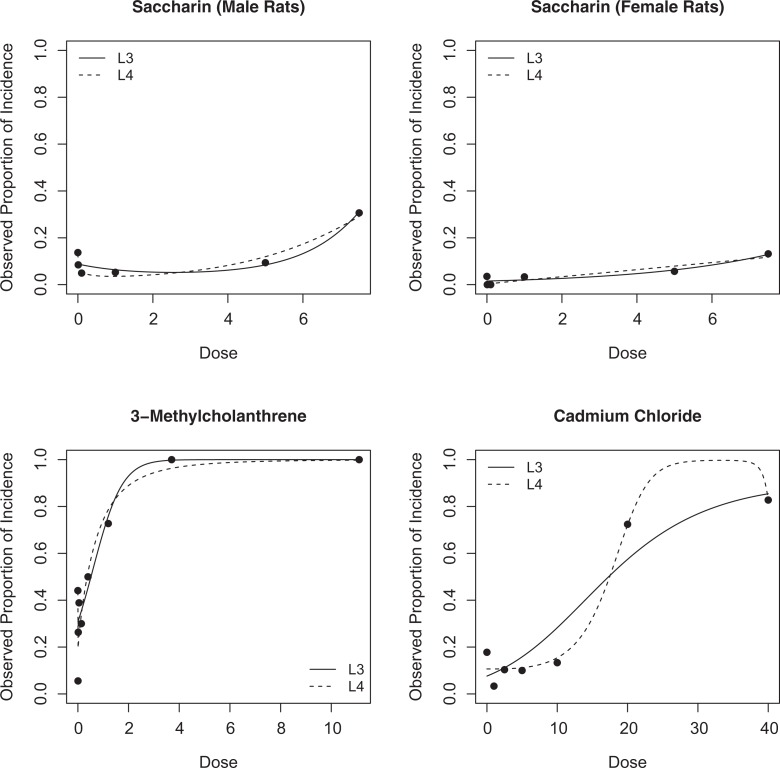
Calabrese and Baldwin¹⁴ discussed the effects of saccharin on hyperplasia of the urinary bladder. The 6 experimental doses were 0, .01, .1, 1, 5, and 7.5 (% in diets). The respective observed proportions of tumor incidence were 10/73 (14%), 6/71 (8%), 4/81 (5%), 4/76 (5%), 6/64 (9%), and 19/62 (31%) for male rats (see the top left panel in Figure 4). When we implemented the L3, L4, MA_P, and MA_SP models, the respective P values were .042, .027, .034, and .059, respectively. This is one of the cases when the parametric models adequately described the dose–response relationships, and the MA_SP model could not achieve the significance level α = .05. At the same experimental doses, the respective observed proportions of incidence were 3/85 (4%), 0/81 (0%), 0/81 (0%), 3/90 (3%), 5/88 (6%), and 10/76 (13%) for female rats (see the top right panel in Figure 4). When we implemented the L3, L4, MA_P, and MA_SP models, the respective P values were .811, .070, .207, and .014, respectively. As shown in the figure (the top right panel), the data points in the observed range are not symmetric, so the L3 model was not able to model the observed nonmonotonic dose–response relationship adequately.

Figure 4.

Fitted dose–response curves under the L3 and L4 models using the maximum likelihood estimates.

Calabrese and Baldwin¹⁴ also discussed the effect of 3-Methylcholanthrene on pulmonary tumors in female rats. The 9 experimental doses were 0, .005, .015, .046, .137, .4, 1.2, 3.7, and 11.1 (μg). The observed proportions of tumor incidence were 15/34 (44%), 1/18 (6%), 5/19 (26%), 7/18 (39%), 6/20 (30%), 12/24 (50%), 8/11 (73%), 10/10 (100%), and 11/11 (100%), respectively (see the bottom left panel in Figure 4). Compared to the previous data set (effect of saccharin on urinary bladder), it has a smaller total sample size but a larger number of experimental doses. The L3, L4, MA_P, and MA_SP models yielded P values of .869, .070, .224, and .003, respectively. As shown in Figure 4 (the bottom left panel), the L3 model was not flexible enough to describe the observed data, and the L4 model was quite flexible to follow the observed nonmonotonic trend though it did not achieve statistical significance. Under the MA_SP model, the data served as significance evidence for hormesis with a P value .003 < α = .05.

As a final example, the same paper¹⁴ discussed the effect of cadmium chloride on testicular tumors. From the 7 experimental doses 0, 1, 2.5, 5, 10, 20, and 40 (µmol/kg), the observed proportions of incidence were 8/45 (17.8%), 1/30 (3.3%), 3/29 (10.3%), 3/30 (10.0%), 4/30 (13.3%), 21/29 (72.4%), and 24/29 (82.8%), respectively (see the bottom right panel in Figure 4). Despite the strong hormetic trend, P values from L3, L4, MA_P, and MA_SP were .99, .64, .65, and .06, respectively, and they seem to be influenced by the 2 data pints at the high doses 20 and 40 μmol/kg. The P values from the parametric methods (L3, L4, and MA_P) do not seem credible, and the P value from averaging the semiparametric models seems more credible based on the observed trend before modeling. In the figure (the bottom right panel), the L3 model was not able to model the asymmetric hormetic trend, and the flexibility of the L4 model was used to chase the 2 data points at the high experimental doses rather than the data points at low doses. An interesting issue with the L4 model is discussed in the following section.

Discussion

The focus of this article is not to argue the existence of hormesis for a particular carcinogen. Our focus is a valid hypothesis testing for a hormetic effect at low doses. We presented the different characteristics of averaging parametric models and averaging semiparametric models. In conclusion, when the true hormetic relationship is under the simple L3 model, the parametric approach MA_P (and individual L3 and L4) outperformed the semiparametric approach MA_SP, which is not surprising. On the other hand, when we compare the 2 averaging methods, MA_SP outperformed MA_P when the true hormetic relationship is nonparametric and even when the truth is generated under the parametric L4 model. It is also shown that the parametric approaches cannot tolerate model misspecification for the hypothesis testing. To this end, when the truth does not follow a parametric form, MA_SP can be useful for more robust and higher statistical power.

In large sample studies with many experimental doses in a hormetic range, a nonparametric method can be a more reasonable approach because it can disconnect information between doses inside a hormetic range and higher doses. May and Bigelow³ discussed the practical challenges due to insufficient sample sizes and a lack of experimental doses (missing a potential hormetic range). In small sample studies, borrowing mathematical structure (ie, parametric models) to gain efficiency seems inevitable. As discussed in “Results,” however, it sometimes gives us a misleading result not simply due to a lack of evidence but due to model misspecification and high-leverage data points (recall the low statistical power from L3, L4, and MA_P in scenarios 14-16 in Table 2). Motivated by this fact, we considered averaging semiparametric models (MA_SP) with AIC weights to test for a hormetic effect at low doses. When we implemented to real data, calculated P values from MA_SP made more sense than P values from L3, L4, and MA_P particularly in the last applied example in “Application” (cadmium chloride on testicular tumors).

In the simulation study, we showed pros and cons of the parametric methods (L3, L4, and MA_P) and of the semiparametric method (MA_SP). Under the correctly specified parametric form, the statistical power from L3 was highest among the 4 methods as shown in scenarios 6 and 7 in Table 2, and MA_P outperformed MA_SP in the 2 scenarios generated by L3. Under the wrong parametric form, we lost statistical power substantially as shown in scenarios 14 to 16 (zero statistical power from L3 in Table 2). We observed that MA_SP outperformed MS_P in the 3 scenarios generated outside of L3 or L4. Even when the true scenario was generated by L4, MA_SP could yield higher statistical power than MA_P as shown in scenarios 8 to 13 (see Table 2). In practice, we cannot guarantee that observed outcomes (which are based on the unknown true dose–response relationship) will follow a parametric model as seen in the cadmium chloride data, and it is not under our control. Instead, the proposed model averaging method with semiparametric models does not require the parametric form, and we learned that it is relatively less sensitive to the shape of observed dose–response trend.

For the L4 model, we refitted the cadmium chloride data with the restriction 0 < β₃ < 1. The restricted parameterization yielded a P value lower than α = .05 by adequately modeling the asymmetric hormetic zone. However, when we ran a simulation study under the null scenarios, it violated the significance level α = .05 seriously. In other words, the restricted parameterization tended to favor H ₁ too often when H ₀ is true. Additionally, we implemented the nonparametric regression method discussed in Hall and Heckman²⁰ in the simulation study. The advantage of a nonparametric method is insensitivity to data points at high doses, but it yielded lower statistical powers than MA_SP in all of the alternative scenarios (generally below .2). We also studied other methods among others. We modified the test statistic in Baraud et al,²¹ which is more appropriate for the binomial data (ie, difference in the 2 probabilities, comparing the control group and the lowest nonzero dose group). It tended to be too conservative, and it did not seem appropriate for a sparse experimental doses. Similarly, we tested an umbrella shape at low doses (decreasing then increasing) using the additive constrained regression.²² Due to the small number of dose groups, the model fitted the data exactly, and it inflated the type I error rate in null scenarios. A nonparametric method is often useful for a large sample study, but 50 experimental units per dose group with 6 experimental units do not seem sufficiently large particularly for binary outcomes.

To further study L3, L4, MA_P, and MA_SP for increased sample sizes (fixing the experimental doses), we manipulated the cadmium chloride data by doubling the sample size while maintaining the observed proportions, that is 16/90 (17.8%), 2/60 (3.3%), 6/58 (10.3%), 6/60 (10.0%), 8/60 (13.3%), 42/58 (72.4%), and 48/58 (82.8%). Recall the P values were .99, .64, .65, and .06 for L3, L4, MA_P, and MA_SP, respectively, before the manipulation (see Application). After the manipulation, the P values changed to .999, .727, .727, and .006 for L3, L4, MA_P, and MA_SP, respectively. When we multiplied the sample size by 10, that is 80/450 (17.8%), 10/300 (3.3%), 30/290 (10.3%), 30/300 (10.0%), 40/300 (13.3%), 210/290 (72.4%), and 240/290 (82.8%), the P values were close to 1, .943, .943, and close to 0 for L3, L4, MA_P, and MA_SP, respectively. Then, we tested an additional simulation scenario under the assumptions (1) π₁ = .178, π₂ = .033, π₃ = .103, π₄ = .100, π₅ = .133, π₆ = .724, and π₇ = .828 and (2) n ₁ = 450, n ₂ = 300, n ₃ = 290, n ₄ = 300, n ₅ = 300, n ₆ = 290, and n ₇ = 290. The resulting statistical powers were near 0, .005, .005, and near 1 for L3, L4, MA_P, and MA_SP, respectively. The results illustrate the impact of model misspecification even with large data under the parametric methods when we test for hormesis.

The Generic Hockey Stick model proposed by Bogen⁶ is a parametric model with the enhanced polynomial flexibility and the link function used in the linearized multistage model.²³ In sparse data, it may have the advantage of utilizing 3 parameters to allow greater flexibility than the L3 models considered in this study. However, the Fisher expected information tells us that the parameter estimation still heavily depends on high data points when we use a polynomial predictor. In practice, high-response data are removed when (1) they are irrelevant to low-dose inference and (2) they severely deviate from an assumed parametric model. We concern about too few data points after removing the data points, and it may increase the type I error rate under the null scenario. It is our future study.

Based on the simulation study, we have thought that averaging L4 and MA_SP can balance the sensitivity (when the observed data points can be approximated by the assumed parametric structure) and the robustness (when they do not follow the assumed parametric structure). It is our current research direction.

Appendix

Model Averaging of L3 and L4

Let y_ij = 1 if we observe the ith experimental unit treated by dose x_j showed a toxic outcome (and y_ij = 0 otherwise) for i = 1,…, n_j and j = 1,…, J (see Model Averaging in Parametric Models [L3 and L4] subsection). Let π_j denote the probability of observing a toxic event at dose x_j which is unknown for j = 1,…, J. Given the data, the log-likelihood function is

$$l={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{i=1}^{n_j}\left(y_{ij}\text{log}({\text{π}}_j)+(1-y_{ij})\text{log}(1-{\text{π}}_j)\right)}}$$

The L3 model assumes

$${\text{π}}_j=\frac{e^{{\beta }_0+{\beta }_1{x}_j+{\beta }_2{x}_j^2}}{1+e^{{\beta }_0+{\beta }_1{x}_j+{\beta }_2{x}_j^2}}$$

so l is a function of β₀, β₁, and β₂, denoted by l_L3(β₀, β₁, β₂). The L4 model assumes

$${\text{π}}_j=\frac{e^{{\beta }_0+{\beta }_1{x}_j^{{\beta }_3}+{\beta }_2{x}_j^{2{\beta }_3}}}{1+e^{{\beta }_0+{\beta }_1{x}_j^{{\beta }_3}+{\beta }_2{x}_j^{2{\beta }_3}}}$$

so l is a function of β₀, β₁, β₂, and β₃, denoted by l_L4(β₀, β₁, β₂, β₃). Let ${\widehat{l}}_{L3}$ denote the maximized l_L3(β₀, β₁, β₂) with respect to (β₀, β₁, β₂), and let ${\widehat{l}}_{L4}$ denote the maximized l_L4(β₀, β₁, β₂, β₃) with respect to (β₀, β₁, β₂, β₃). The AIC of the L3 model is defined as ${\text{AIC}}_{L3}=-2{\widehat{l}}_{L3}+2p=-2{\widehat{l}}_{L3}+6$ because the model has p = 3 parameters. The AIC of the L4 model is defined as ${\text{AIC}}_{L4}=-2{\widehat{l}}_{L4}+2p=-2{\widehat{l}}_{L3}+8$ because it has p = 4 parameters. Then the AIC weight of the L3 model and of the L4 model is

$$w_{L3}=\frac{e^{-0.5{\text{AIC}}_{L3}}}{e^{-0.5{\text{AIC}}_{L3}}+e^{-0.5{\text{AIC}}_{L4}}},w_{L4}=\frac{e^{-0.5{\text{AIC}}_{L4}}}{e^{-0.5{\text{AIC}}_{L3}}+e^{-0.5{\text{AIC}}_{L4}}},$$

respectively.

Type I Error Rate Under MA_P

Assume the null hypothesis H ₀ is true (see Model Averaging in Parametric Models [L3 and L4] subsection). Let B denote the number of bootstrap samples. Let w be a number between 0 and 1 (ie, AIC weight). Let p ₃ denote the proportion of bootstrap estimates such that ${\hat{\beta }}_1>0$ under the L3 model. Consider a significance level α = .05. In this case, under the L3 model, we reject H ₀ in favor of H ₁ when B × p ₃ < .05 × B. Similarly, let p ₄ denote the proportion of bootstrap estimates such that ${\hat{\beta }}_1>0$ under the L4 model. Under the L4 model, we reject H ₀ in favor of H ₁ when B × p ₄ < .05 × B. Now, consider a mixture bootstrap distribution of estimated β₁ (ie, averaging the 2 bootstrap distributions from L3 and L4). If L3 is weighted by w and L4 is weighted by 1 − w, we reject H ₀ in favor of H ₁ when B [w × p ₃ + (1 − w) × p ₄] < .05 × B under the model averaging MA_P. Now let R ₃, R ₄, and R _MA denote the event that H ₀ is rejected under L3, L4, and MA_P, respectively. We consider the 4 cases. If R₃ ∩ R₄ occurs, it implies R _MA (case 1). If $R_3\cap R_4^C$ occurs (ie, H ₀ is rejected under L3 but not under L4), it is inconclusive (case 2). If $R_3^C\cap R_4$ occurs, it is inconclusive (case 3). If $R_3^C\cap R_4^C$ occurs, it implies $R_{\text{MA}}^C$. To this end,

$$\begin{array}{ll}P(R_{MA})\hfill & \le P(R_3\cap R_4)+P(R_3\cap R_4^C)+P(R_3^C\cap R_4)\hfill \\ \hfill & =P(R_3)+P(R_3^C\cap R_4)\hfill \end{array}$$

and

$$\begin{array}{ll}P(R_{MA})\hfill & \le P(R_3\cap R_4)+P(R_3\cap R_4^C)+P(R_3^C\cap R_4)\hfill \\ \hfill & =P(R_4)+P(R_3\cap R_4^C)\hfill \end{array}$$

In other words, the type I error rate under MA_P has the upper bound

$$P(R_{\text{MA}})\le \text{min}\left\{P(R_3)+P(R_3^C\cap R_4),\hspace{0.17em}P(R_4)+P(R_3\cap R_4^C)\right\}$$

If we observe an unusual original sample against H ₀, both the probability of R ₃ and the probability of R ₄ increase, so $P(R_3^C\cap R_4)$ and $P(R_3\cap R_4^C)$ are fairly small. To this end, the type I error rate under MA_P cannot be too far away from a range between the type I error rate under L3 and under L4. In the simulation study (“Simulation Result” and Table 2), we observe that P(R _MA) is close to the minimum of P(R ₃) and P(R ₄) under the null scenarios (scenarios 1-5).

Model Averaging of M₁,…, M_J−2

Assuming model M_k, for k = 1,…, J − 2, the log-likelihood function is given by (see Application of Model Averaging to Semiparametric Models subsection)

$$l_k({\text{π}}_1,\mathrm{...},{\text{π}}_J)={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{i=1}^{n_j}\left(y_{ij}\text{log}({\text{π}}_j)+(1-y_{ij})\text{log}(1-{\text{π}}_j)\right)}}$$

with the restriction π₂ =…= π_{k +1}.

• For model M ₁, it is the saturated model, so the maximum ${\widehat{l}}_1$ can be achieved by letting π_j = Σ_i y_ij/n_j, the observed proportion of toxic outcomes at dose x_j.

• For model M ₂ with the restriction π₂ = π₃, the maximum ${\widehat{l}}_2$ can be achieved by letting π_j = Σ_i y_ij/n_j for j not being equal to 2 or 3 and π₂ = π₃ = (Σ_i y_i2 + Σ_i y_{i 3})/(n₂ + n ₃) which is the pooled estimation.

• For model M ₃, with the restriction π₂ = π₃ = π₄, the maximum ${\widehat{l}}_3$ can be achieved by letting π_j = Σ_i y_ij/n_j for j not being equal to 2, 3, or 4 and π₂ = π₃ = π₄ = (Σ_i y_i2 + Σ_i y_{i 3} + Σ_i y_{i 4})/(n₂ + n ₃ + n ₄).

• This pattern continued up to M_{J − 2}, where J is the number of fixed experimental doses.

The AIC of model M_k is ${\text{AIC}}_k=-2{\widehat{l}}_k+2p_k$, where p_k = J − k + 1 is the number of free parameters in the model. Then the AIC weight of M_k is given by

$$w_k=\frac{e^{-0.5{\text{AIC}}_k}}{e^{-0.5{\text{AIC}}_1}+\dots +e^{-0.5{\text{AIC}}_{J-2}}}$$