Variations in normal color vision. VI. Factors underlying individual differences in hue scaling and their implications for models of color appearance

Abstract

Observers with normal color vision vary widely in their judgments of color appearance, such as the specific spectral stimuli they perceive as pure or unique hues. We examined the basis of these individual differences by using factor analysis to examine the variations in hue-scaling functions from both new and previously published data. Observers reported the perceived proportion of red, green, blue or yellow in chromatic stimuli sampling angles at fixed intervals within the LM and S cone-opponent plane. These proportions were converted to hue angles in a perceptual-opponent space defined by red vs. green and blue vs. yellow axes. Factors were then extracted from the correlation matrix using PCA and Varimax rotation. These analyses revealed that inter-observer differences depend on seven or more narrowly-tuned factors. Moreover, although the task required observers to decompose the stimuli into four primary colors, there was no evidence for factors corresponding to these four primaries, or for opponent relationships between primaries. Perceptions of “redness” in orange, red, and purple, for instance, involved separate factors rather than one shared process for red. This pattern was compared to factor analyses of Monte Carlo simulations of the individual differences in scaling predicted by variations in standard opponent mechanisms, such as their spectral tuning or relative sensitivity. The observed factor pattern is inconsistent with these models and thus with conventional accounts of color appearance based on the Hering primaries. Instead, our analysis points to a perceptual representation of color in terms of multiple mechanisms or decision rules that each influence the perception of only a relatively narrow range of hues, potentially consistent with a population code for color suggested by cortical physiology.

1. Introduction

Conventional explanations of human color vision are dominated by two fundamental theories. One describes the initial absorption of light by the three classes of cones (trichromacy), and the second the subsequent processing of the cone signals within opponent mechanisms that represent color in terms of red-green, blue-yellow, and black-white dimensions (opponent processing) [e.g. (Hurvich & Jameson, 1957)]. The spectral sensitivities of the opponent processes were first characterized by hue-cancelation experiments, in which the intensity of a fixed primary hue (e.g. red) was added to null the opponent color (e.g. green) in the stimulus (Hurvich & Jameson, 1955). Subsequently, Jameson and Hurvich also developed a hue-scaling task, in which observers directly judged the strength of the chromatic responses by reporting the proportion of each primary in the stimulus (e.g. the proportion of red and yellow perceived in an orange hue) (Jameson & Hurvich, 1959). Both techniques supported many of the basic premises of opponent-process theory (Hering, 1964): that all hues can be described as a combination of two of the four hue primaries; that red and green, and blue and yellow, are mutually exclusive sensations; and that the four Hering primaries appear pure or unique in that they cannot as easily be perceived as a mixture of other hues (e.g. seeing red as a combination of orange and purple). Both cancellation and hue-scaling experiments have also been widely used to quantify the opponent processes under a variety of conditions, including how color varies with the parameters of the stimulus (e.g. (Abramov & Gordon, 2005, Abramov, Gordon & Chan, 1991, Jameson & Hurvich, 1956) or as a function of eccentricity (e.g. (Boynton, Schafer & Neun, 1964, Hibino, 1992). The spectral sensitivities of the red-green and blue-yellow processes can be modeled in terms of the cone sensitivities, thus showing how the cone signals are combined to form the opponent channels (De Valois & De Valois, 1993, Wooten & Werner, 1979, Wuerger, Atkinson & Cropper, 2005). Such analyses led to a standard two-stage model of color vision [e.g. (Hurvich & Jameson, 1957)] where hue percepts arise directly from the responses in the underlying red-green and blue-yellow mechanisms.

However, while this scheme remains a dominant account of color perception, the neural substrate predicted by opponent-process theory remains elusive. The spectral sensitivities of the primary cell types in the retina and geniculate do not have the tuning required to account for the stimuli that appear unique or pure (De Valois, Abramov & Jacobs, 1966, Derrington, Krauskopf & Lennie, 1984). Moreover, color tuning in the visual cortex appears too variable to be consistent with only two discrete chromatic dimensions (Kuriki, Sun, Ueno, Tanaka & Cheng, 2015, Lennie, Krauskopf & Sclar, 1990, Shapley & Hawken, 2011, Xiao, Wang & Felleman, 2003, Zaidi, Marshall, Thoen & Conway, 2014). Such results have led to suggestions that cells with the appropriate responses may arise later in the system and that chromatic representations undergo transformations at multiple stages, with the neural organization mediating color appearance arising at later stages (Brouwer & Heeger, 2009, De Valois & De Valois, 1993, Stoughton & Conway, 2008). It has also led to proposals that color percepts may be mediated by specialized neural pathways that arise as early as the retina (Schmidt, Neitz & Neitz, 2014). The failure to find a clear neural basis for red-green and blue-yellow responses has also raised the possibility that these percepts do not reflect special states in the brain but rather special characteristics of the environment. For example, the blue-yellow axis falls close to the daylight locus, and thus might correspond to a learned property of the world (Lee, 1990, Mollon, 2006, Panorgias, Kulikowski, Parry, McKeefry & Murray, 2012, Shepard, 1992). By this account, the perceptual null implied by unique hues need not reflect a null in the corresponding neural response, for the percept could in principle be tied to an arbitrary pattern of neural activity (Mollon & Jordan, 1997). However, many still hold that the phenomenal experience of color revealed by tasks like hue scaling ultimately depends on neural processes that directly signal pure hue sensations, and that these processes signal only a small number of sensations corresponding to red-green and blue-yellow qualia.

In the present study we explored the mechanisms of color appearance by analyzing individual differences in hue-scaling functions, using the methods of factor analysis to extract the underlying dimensions of variation in hue-scaling judgments. Factor analysis is a standard statistical technique for identifying the latent variables or factors contributing to variations in a set of measurements or observed variables, based on the correlations among the observed variables. For example, an individual who reports a higher than average proportion of red at a particular chromaticity is more likely to report more red in nearby chromaticities. Thus, the measurements for these stimuli will covary, presumably because they both depend on the influence of a common process. Factor analytic techniques have been widely used to explore properties of the visual system [e.g.; (de-Wit & Wagemans, 2016, Jones, 1948, Peterzell, 2016, Thurstone, 1944, Wilmer, 2008)], and in particular, to examine the mechanisms of color vision and chromatic processing (Burt, 1946, Dobkins, Gunther & Peterzell, 2000, Gunther & Dobkins, 2003, Peterzell, Chang & Teller, 2000, Peterzell & Teller, 2000, Pickford, 1946, Webster & MacLeod, 1988). In some cases this approach can provide precise quantitative information about the mechanisms and how they vary across individuals. For example, individual differences in color matching result from several well-characterized processes that influence spectral sensitivity, including the densities of inert screening pigments and the absorption spectra of the photopigments, and factor analysis can be used to identify and parcel out these different sources of sensitivity variation and specify their relative contributions to color matching as well as their values for individual observers (MacLeod & Webster, 1988, Webster & MacLeod, 1988). In many other cases we know much less about the processes limiting perception and performance. However, factor analysis can still provide a valuable tool for constraining the possible models of these processes.

Here we used factor analysis to explore the basis for inter-observer variations in hue scaling. We reasoned that if these scaling functions did reflect the activity of two processes signaling red-green and blue-yellow sensations, then these processes should be evident in the patterns of variation revealed by the factor analysis. That is, the analysis should reveal a small set of general factors corresponding to the opponent primaries. To test this, we analyzed two datasets, one from a previous study that measured hue scaling functions for 59 observers (Malkoc, Kay & Webster, 2005), and a second that was collected for the present study. The latter was added to provide a finer sampling of both the stimulus set and the scaled responses, and because we were also interested in relating the percepts of the observers (as measured by the scaling) to measurements of how they verbally labeled the hues. We report the relationship between hue scaling and color naming in the accompanying paper (Emery, Volbrecht, Peterzell & Webster, submitted). Here we focus on the hue scaling functions and how they differ across observers, and what those differences imply about the visual representation of color.

2. Materials and Methods

2.1 Participants

The participants included 26 graduate and undergraduate students from the University of Nevada, Reno ranging from ages 18 to 47. A 27^th observer was excluded based on the high variability of their settings. Sixteen of the observers were female. Undergraduate students were provided extra credit in exchange for their participation. All observers had normal color vision as assessed by the Cambridge Colour Test, as well as a contrast threshold task, and all had normal or corrected-to-normal visual acuity. Each observer participated with informed consent, and all procedures followed protocols approved by the University of Nevada, Reno's Institutional Review Board, and were conducted in accordance with the

2.2 Stimuli

Stimuli were presented on a SONY Multiscan 500PS Trinitron CRT monitor controlled with a Cambridge Research Systems ViSaGe Stimulus Generator, providing 12-bit resolution per gun. The monitor was calibrated with a Photo Research PR 655 spectroradiometer with gun outputs linearized with a gamma correction. The stimuli had a constant luminance of 20 cd/m² and were shown on an 11.3 by 8.5 gray background that had the same luminance as the test stimuli and the chromaticity of Illuminant C (CIE 1931 x,y = 0.31, 0.316). Luminance was based on photometric measurements and thus stimuli were not adjusted to be equiluminant for individual observers. The test chromaticities were based on a variant of the MacLeod-Boynton (MacLeod & Boynton, 1979) chromaticity diagram, scaled based on previous studies (Webster, Miyahara, Malkoc & Raker, 2000) to roughly equate sensitivity along the L vs. M and S vs. LM axes:

$$\begin{array}{cc}\hfill \mathrm{LvsM}& ={({\mathrm{l}}_{\mathrm{mb}}-0.6568)}^{\ast }2754\hfill \\ \hfill \mathrm{SvsLM}& ={({\mathrm{s}}_{\mathrm{mb}}-0.01825)}^{\ast }4099\hfill \end{array}$$

LvsM and SvsLM are the chromatic contrasts along the cardinal axes, and l_mb and s_mb are the l and s (or r and b) coordinates in the MacLeod-Boynton space. The contrasts are relative to the chosen achromatic point in the space (0.6568, 0.01825, the MacLeod-Boynton coordinates for illuminant C), and are scaled to roughly reflect equivalent multiples of threshold.

Stimuli within this space were defined by a vector with a direction corresponding to the chromatic angle, and a length corresponding to chromatic contrast. Contrast was fixed at a value of 60, and stimulus angle was varied in 10-deg steps to define 36 test chromaticities. These chromaticities were shown foveally in 2-deg uniform squares pulsing for 500 ms, with 1-s intervals of the gray background between each pulse. The same stimulus was repeated until the observer recorded their setting. Observers viewed the display binocularly from a distance of 200 centimeters in an otherwise dark room.

2.3 Hue scaling

The hue-scaling task involved judging each hue as a relative percentage of red, green, blue or yellow, by using a handheld keypad to vary the percentages displayed for each primary at the bottom of the screen. Values could be varied in increments of 5% and were restricted such that for each hue the sum of the percentages had to total 100%, and percentages could not be assigned to both red and green or both blue and yellow at the same time (Abramov et al., 1991). The percentages were converted into a corresponding angle within a perceptual red-green (0-180 degrees) versus blue-yellow (90-270 degrees) opponent space:

$$\text{hue angle}={\tan }^{-1}[(\text{blue}-\text{yellow})∕(\text{red}-\text{green})].$$

For example, if an observer responded that a stimulus appeared 50% red and 50% blue, then the corresponding hue angle was 45 deg. Note that throughout the paper the term stimulus angle refers to the physical stimulus in terms of its angle within the LM vs S chromatic plane and hue angle denotes the observer's response in terms of the angle within the red-green vs. blue-yellow perceptual color space. An advantage of the hue angle is that it allows the scaling functions to be represented by a single dependent measure. A second advantage is that the conversion to an angle tends to normalize for the variance differences inherent in proportions, obviating the need for corrections such as the arcsine transform (Warton & Hui, 2011).

2.4 Procedure

Observers participated in three sessions each lasting less than 1 hr. The first session involved assessments of color vision, measurements of contrast thresholds, and measurements of color naming. (The latter is discussed in the accompanying paper, Emery et al. submitted) The remaining two sessions each involved scaling the hue of each stimulus two times, for a total of four measurements. Results are based on the analysis of the hue angles averaged across the four repeated settings. The first scaling session included practice trials prior to the start of the actual experiment. These trials consisted of making settings for six hue angles spanning the color space in 60-deg steps. The observer then adapted for two min to the background before scaling the complete stimulus set. The stimulus angles were shown in random order and each continued to pulse until the observer pressed a key to accept his/her setting. The duration for each setting could thus vary and was not recorded. After the last setting, an intermission was provided during which the screen remained gray. The observer then initiated the start of the second set of trials when s/he was ready.

3. Results

3.1 Hue scaling

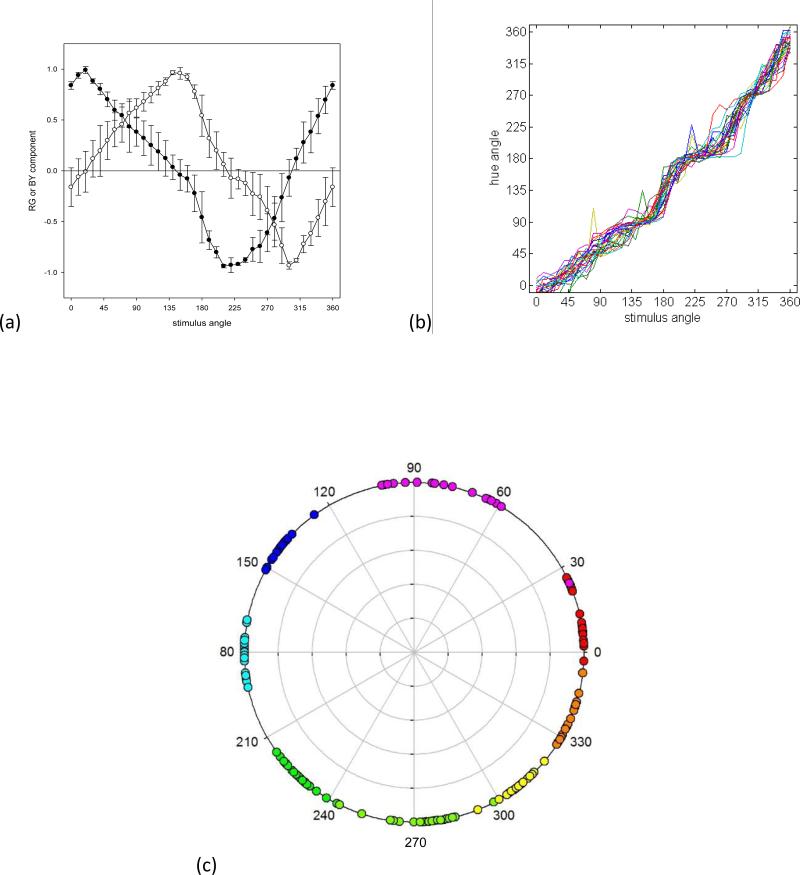
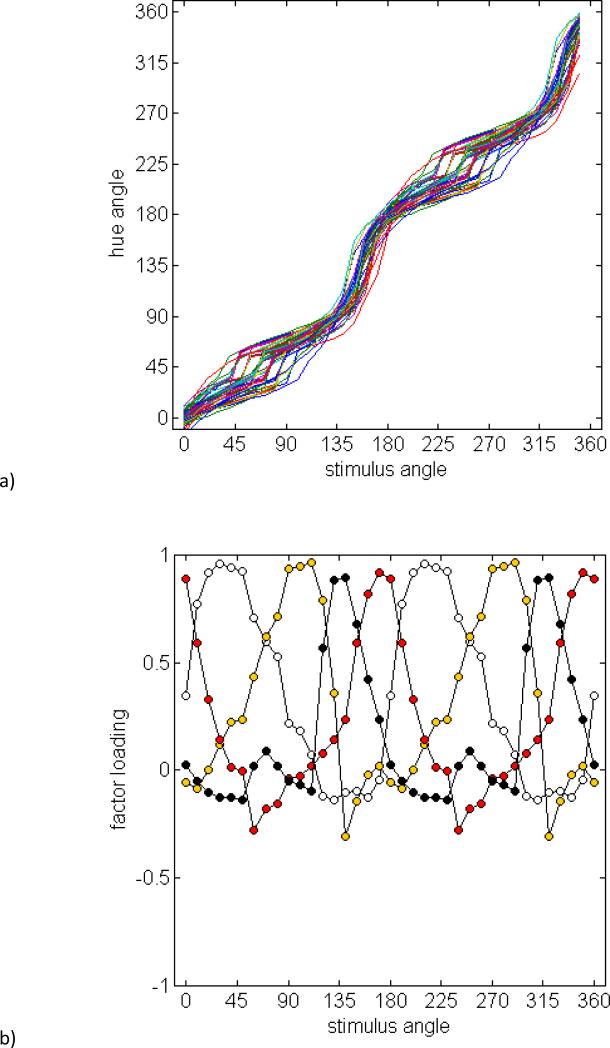
Figure 1a plots the mean hue-scaling functions for the 27 observers. These functions are based on the cosine (red-green) and sine (blue-yellow) of the hue angle (Figure 1b) and thus reflect the putative red-green and blue-yellow responses rather than the raw rated proportion of red, green, blue or yellow in the stimulus. To visualize the relationship between the hue angles and stimulus angles, Figure 1c plots the stimulus angles corresponding to the four unique hues or four binary hues. These were estimated by fitting an 8^th-order polynomial to each observer's scaling function (to reduce variations owing to noise), and then calculating the values of the fitted function for hue angles at 45 deg intervals. The loci of the hues replicate several previously reported properties of color appearance (Krauskopf, Williams & Heeley, 1982, Malkoc et al., 2005, Webster et al., 2000, Wuerger et al., 2005). First, the average blue and yellow values (137 and 308 deg) are roughly complementary and nearly equidistant from the two cardinal axes. In contrast, red and green do not lie along a common axis in the cone-opponent space (averaging 13 and 227 deg). The loci for three of the binary hues (purple, blue-green, and yellow-green) tend to cluster along the cardinal axes. Thus, the blue-green boundary tends to separate S-cone increments from decrements, while the purple and yellow-green loci tend to separate +L(−M) from −L(+M) deviations from the neutral background. The exception is the binary color orange, which is not aligned to one of the cardinal axes. Instead, the final cardinal-axis pole is closer to the average value for unique red.

Figure 1.

a) Mean chromatic response functions estimated from the hue scaling functions for the 26 observers (new data set). Filled symbols plot the estimated chromatic response functions for red (positive) and green (negative); unfilled symbols plot the functions for blue (positive) or yellow (negative). Error bars correspond to the standard deviation of the settings across observers. b) Individual settings for the perceptual hue angles, based on converting the scaling responses to the corresponding angle in the RG vs BY perceptual space. c) Stimulus angles corresponding to the loci of unique or binary hues for each observer.

Another feature of the hue loci is that they vary markedly across individual observers, with an average standard deviation of 14 deg. Such individual differences are a prominent characteristic of the unique hues (Kuehni, 2004). Overall, variance was greatest in the purplish region of the color space. However, the range of loci was similar for the unique versus binary hues, such that the overall variance did not differ between them (F(1,95)=1.22, p =.17). Finally, these variations were largely uncorrelated across the different color categories. For example, Table 1 shows the correlation matrix for the unique and binary hues. When corrected for multiple comparisons, the only pairs to show a statistically significant relationship were green with yellow-green and orange with red (Table 1).

Table 1.

Correlations between the stimulus angles for the unique and binary hues (new data set). Shaded cells show siginificant correlatiations after correction for multiple comparisons.

	red	purple	blue	blue-green	green	yellow-green	yellow	orange
red	1	.210	.056	−.195	−.228	−.279	.008	.631*
purple		1	.587	−.040	−.190	−.113	−.265	−.023
blue			1	.477	.064	−.002	.209	.257
blue-green				1	.117	−.438	.015	.296
green					1	.634*	.359	−.222
yellow-grn						1	.584	−.313
yellow							1	.472
orange								1

3.2 Factor analysis

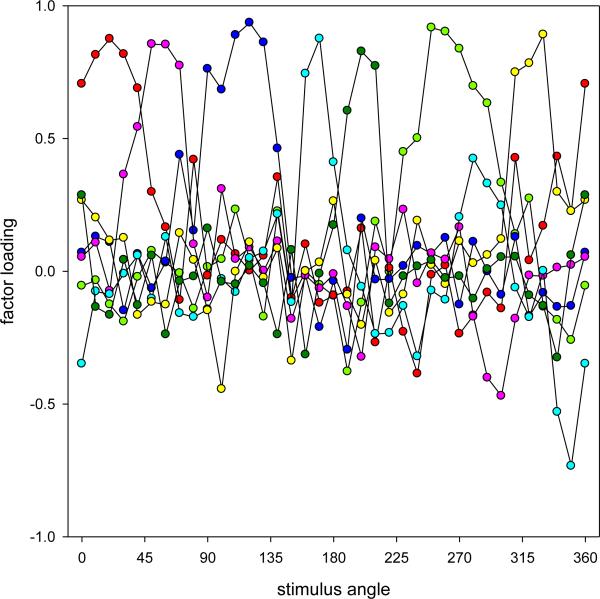
As noted, factor analysis is a widely-used dimension-reduction technique that seeks to identify the underlying sources of variation in a set of observations. A typical analysis involves multiple steps, each with various options (Costello & Osborne, 2005). The factors were computed from the correlation matrix and initially extracted with principal component analysis (a technique closely related to conventional factor analysis, which differs in that the variance is not partitioned into shared and unique components; the correlation matrix for the data was not positive definite, precluding standard factor analysis). The extracted factors are represented by their factor loadings, which specify the correlation between the factor and each variable. The square of the factor loading thus gives the proportion of variance in the variable attributable to the factor. PCA extracts components in decreasing order of the total variance each accounts for, and with the factors orthogonal to each other. The total variance is given by the eigenvalue, or the sum of the squared loadings. A second major step in factor analysis is to rotate these components with the goal of creating a simpler structure or pattern of loadings, or to identify more meaningful or interpretable factors (e.g, in terms of the nature of their influence on the variables). We used the standard Varimax rotation which again constrains the factors to be independent, but which repartitions the variance between them in order to maximize the variance in the loadings within each factor (thus favoring solutions in which the loadings tend to be either very high or very low). This seeks a sparser structure in which the variations in each variable are primarily associated with only one of the factors (and so that the number of near-zero loadings is maximized). Note that the polarity of the loadings is arbitrary, since negative or positive loadings could correspond to either more or less of the underlying process (e.g. more or less red in the scaling). A final issue is with regard to the number of factors. Generally there must be as many factors as variables to represent all of the variance, but only some of these are assumed to account for real variations as opposed to noise. A common practice is to use a scree plot of the ordered eigenvalues to search for a sudden drop in the variance accounted for, or to limit the number of factors to those that account for at least the equivalent of one of the observed variables (an eigenvalue of 1). However, in this case we departed from standard procedures by taking advantage of the fact that our variables were defined by metrical variations in the stimulus dimension. The number of factors to extract was determined by examining their loadings to identify the factors that exhibited systematic tuning, or specifically, moderate to high loadings on two or more adjacent variables. This non-random pattern is indicative of “real” structure in the data rather than random noise, so that the factors with systematic loadings are likely to correspond to meaningful variations in the settings, and is an approach that has been applied previously and often in factor analyses of continuous stimulus dimensions in visual data [e.g. (Dobkins et al., 2000, Gunther & Dobkins, 2003, Peterzell et al., 2000, Peterzell & Teller, 2000, Peterzell, Werner & Kaplan, 1993, Peterzell, Werner & Kaplan, 1995, Webster & MacLeod, 1988)]. While we did not impose a specific criterion, we note that the factors retained for the hue scaling (Figure 2) all had adjacent loadings of 0.6 or higher.

Figure 2.

Factor loadings for the hue scaling functions (new data set). Curves show the loadings for the seven systematic factors following Varimax rotation.

Figure 2 plots the loadings for seven of the first eight extracted factors, which all met the criterion for systematic variation. Together, these accounted for 77.4 percent of the total variance. Each of these factors has high positive loadings for a relatively narrow range of contiguous stimulus angles. Thus the underlying factors are largely monopolar and band-limited, and appear to more or less uniformly tile the color space, with each accounting for the variations only over a narrow range of stimulus angles. The general pattern remained similar when we excluded two observers who exhibited the highest variability (more than 1.5 times the average standard deviation) in their repeated settings. Factors obtained for an oblique rotation (Direct Oblimin) were also similar, with little correlation evident among the factors. This supports the use of Varimax as the appropriate criterion for the rotation. Thus the analysis suggests that individual differences in the scaling depend on multiple sources (i.e. factors) that vary independently and which each influence settings only over a restricted range of chromatic angles (i.e. high loadings on a small number of neighboring angles). Finally, we also added variables in the analysis corresponding to the observer's gender, age, and relative sensitivity (as measured by preliminary contrast thresholds). However, none of these observer variables were systematically related to the hue scaling.

3.3 Factor analysis of the Malkoc et al. hue scaling data

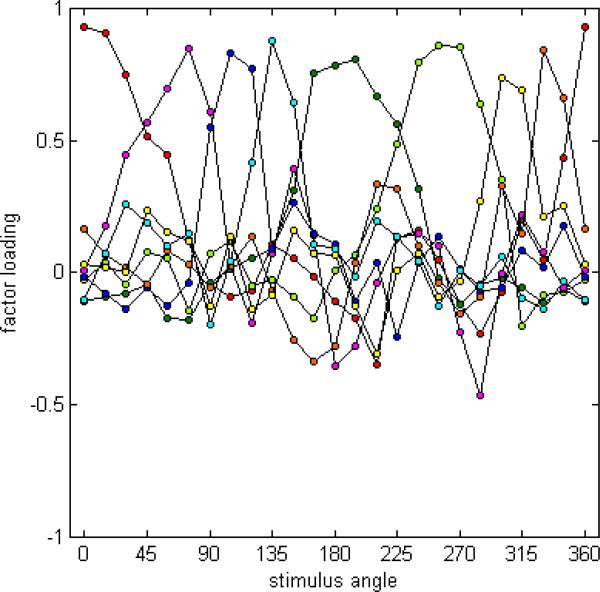
To verify this pattern of results, we performed a similar analysis of the hue-scaling functions measured by Malkoc et al. (2005) for 59 observers. The isoluminant stimuli from this study fell in intervals of 15 deg rather than 10 deg, and the color proportions were reported by pressing buttons for each primary hue rather than entering an actual percentage (e.g. 3 red presses and 2 yellow for an orange hue that appeared composed of roughly 60% red). Again, their data exhibited the same general pattern of results as described above for the settings collected in the present study, though the range of the hue loci were substantially more variable. Malkoc et al. did not perform a factor analysis of their data; however, they did examine the correlations in the scaled responses for their stimulus angles, and noted that only nearby chromatic stimuli showed significant correlations. Thus their analysis presaged many of the results and conclusions reported above from the factor analyses.

For the factor analysis with Malkoc et al.'s (2005) data, we excluded one observer who exhibited highly variable hue angles. The analysis of the remaining 58 observers revealed eight factors with systematic loadings, which accounted for 84% of the variability in the data. The loadings for these eight factors following Varimax rotation are shown in Figure 3. The factor loadings for an oblique rotation were again similar, with little correlation evident among the factors. As in the preceding analysis, the factors appear to more or less uniformly tile the color space, with each influencing a narrow range of angles.

Figure 3.

Factor loadings for the hue scaling functions of Malkoc et al. (2005). Plotted are the eight factors showing systematic loadings following Varimax rotation.

3.4 Predicted factor loadings from Monte Carlo simulations of models

In this section we compare the observed pattern of factor loadings to the loadings predicted from alternative accounts of color appearance. While there are various specific models of the mechanisms of color appearance, our aim was to evaluate more qualitative predictions for different classes of models, particularly with regard to the number and nature of the processes mediating color appearance. We first show that conventional models of opponency are inconsistent with the factor pattern from this and Malkoc et al.'s (2005) studies, and then propose different variants on these models that could give rise to the general pattern of results observed.

3.4.1. Pre-opponent sensitivity differences

Before considering models of color appearance, we note that color-normal observers vary widely in the cone spectral sensitivities because of factors arising early in the eye. These include differences in: 1) the densities of the inert screening pigments (lens and macular pigment), 2) the optical densities and spectral peaks of the cone photopigments, and 3) the relative numbers of different cone classes (Asano, Fairchild & Blonde, 2016, Hofer, Carroll, Neitz, Neitz & Williams, 2005, Webster & MacLeod, 1988). These differences have large effects on chromatic sensitivity and color matching, and have in some cases been associated with individual differences in color appearance (Hibino, 1992, Jordan & Mollon, 1995, Schmidt et al., 2014, Welbourne, Thompson, Wade & Morland, 2013). However, color perception mostly compensates for these spectral sensitivity differences (Webster, 2015a), such that achromatic loci or unique hues show very little dependence on factors such as lens (Delahunt, Webster, Ma & Werner, 2004, Schefrin & Werner, 1990, Werner & Schefrin, 1993) or macular pigment density (Webster, Halen, Meyers, Winkler & Werner, 2010, Webster & Leonard, 2008), or cone ratios (Brainard, Roorda, Yamauchi, Calderone, Metha, Neitz, Neitz, Williams & Jacobs, 2000). Moreover, because these factors tend to impact fairly broad regions of the visible spectrum, their predicted influences span a wide range of hues, and cannot readily account for the frequent finding that variations in the different unique hues are independent (Webster et al., 2000). Thus we ignore these differences in the following analyses and focus instead on how color might be represented in mechanisms that are already normalized to discount for much of the inherent spectral sensitivity differences among observers.

3.4.2 Opponent Processes

As noted, color-opponent theory is based on the premise that hue sensations are directly mediated by responses in two opponent channels that signal red vs. green or blue vs. yellow sensations. The simplest accounts of these channels are that they are formed by different linear combinations of the cone signals, with spectral sensitivities anchored by the loci of the unique hues. For our analyses the specific sensitivities are not critical. To very roughly approximate the unique hues, we defined the channels as:

blue-yellow = S – L+M; which varies as a cosine of the stimulus angle with peak response along the 90-270 deg axis and a null (unique red and green), along the 0-180 axis, and

red-green = L – M+S; which peaks along the 45-225 deg axis and has a null (unique blue and yellow) along the 135-315 deg axis

These modal channels might vary across individuals in various ways, thereby differentially affecting the variance in the hue scaling at different stimulus angles.

Predicted factor loadings

One way we examined these potential variations was to directly calculate predicted factor loadings for a given source of variation. The square of the factor loading represents the proportion of variance owing to a given factor. Predicted loadings can thus be generated by comparing the variation in the settings produced by changes in the factor, relative to the total observed variation (Webster & MacLeod, 1988):

$${\alpha }_{\mathrm{ji}}={\sigma }_{\mathrm{x}}(\partial {\mathrm{p}}_{\mathrm{s}}∕\partial {\mathrm{x}}_{\mathrm{i}})∕{\sigma }_{\mathrm{j}}$$

where α_ji is the predicted loading of factor i for stimulus angle j, and σ_j is the observed standard deviation of the settings. The predicted standard deviation is given by the variation in the level of the factor (σ_x) times the change in the setting (∂p_s) for a unit change in the factor (∂x_i).

Monte Carlo Simulations

As a second approach, we also simulated hue-scaling functions for a set of observers who varied in specified ways, and then factor analyzed the simulated data set. Monte Carlo simulations have also been used in various studies to generate predicted factors (Peterzell et al., 1993, Peterzell et al., 1995, Sekuler, Wilson & Owsley, 1984). The first approach has the advantage that the pattern of predictions for a single factor can be directly visualized, while the second better illustrates the impact of the factor on the hue scaling, and also allows the predictions to be extracted and rotated in the same way as the observed measurements.

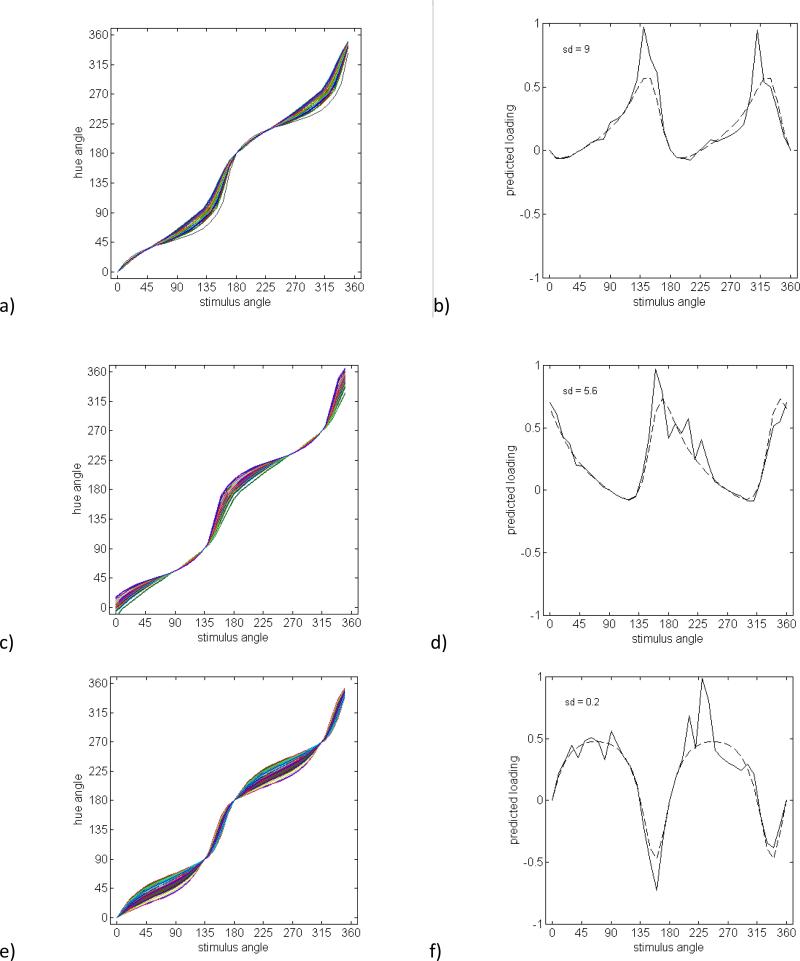
Figure 4 shows the pattern of loadings for several potential sources of variation in the opponent mechanisms. For this analysis, we constructed predicted factors based both on the variability in the individual items, σ_j (in order to incorporate the actual structure in the data); and also held σ_j constant and equal to the average standard deviation (so that the structure owing to the predicted factors is more clearly illustrated). Each figure plots both sets of predictions. The first two sources of inter-observer variation we considered correspond to changing the weightings of the cone inputs, which rotates the preferred color axes of the opponent mechanisms. For the red-green mechanism, the loadings correspond to a standard deviation of 9 deg in the preferred axis, a value chosen to produce maximum loadings close to 1 (Figures 4a and 4b). (An alternative would be to vary the standard deviation to try to find the best fit to the observed loadings. However, as we argue for all of the predictions in this section, the predicted pattern of loadings is unlike any of the observed factors.) For blue-yellow, the factor shown is based on a standard deviation of 5.6 (Figures 4c and 4d). Note that a higher variance for either of these factors would be outside the range implied by the variations in the observed measurements. Not surprisingly, both variations produce a broad and bimodal pattern of loadings, since the red and green (or blue and yellow) sensitivities covary. Observers might also vary in the relative sensitivity of the red-green and blue-yellow channels. This effect is shown in Figures 4e and 4f for a standard deviation of 20% in the relative sensitivity. Again the loadings are broad and bimodal, and in this case also bipolar, because variations in relative sensitivity lead to both postive and negative correlations across different pairs of variables.

Figure 4.

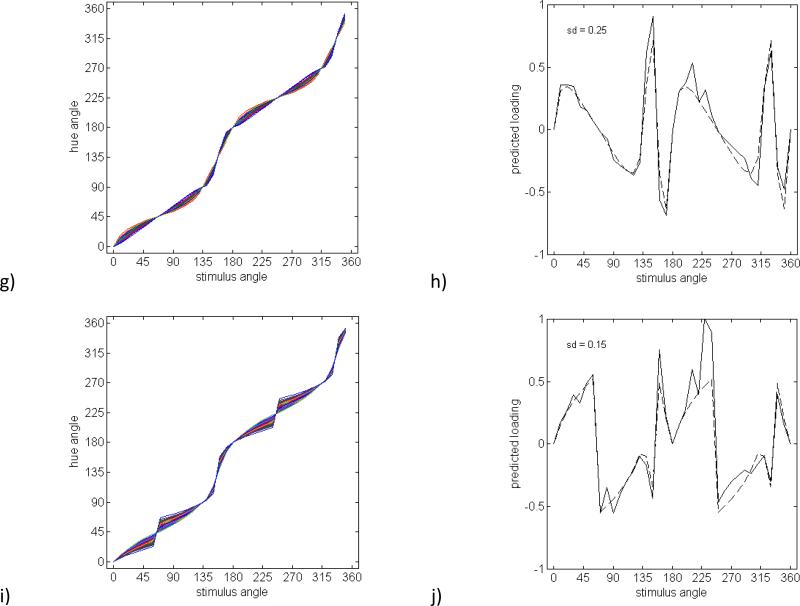
Simulated hue scaling functions and individual factors with loadings predicted based on the individual standard deviations at each stimulus angle (solid lines) or a constant standard deviation equal to the average across all stimulus angles (dashed lines). a) Hue scaling functions for a group of observers differing in the locus of the red-green axis and b) a factor with loadings estimated directly from variation across observers in the locus of the red-green axis (SD = 9°). c) Hue scaling functions and d) predicted factor loadings based on variation across observers in the locus of the blue-yellow mechanism (SD = 5.6°). e) Hue scaling functions and f) factor loadings predicted for variations in the relative sensitivity of the red-green and blue-yellow mechanisms (SD = 20%). g) Hue scaling functions and h) a factor loadings predicted from varyiations in the degree of nonlinearity in the contrast response of the red-green and blue-yellow opponent mechanisms. The nonlinearity is modeled as a cosine tuning function rasied to different exponenents (SD = 0.25). i) Hue scaling functions and j) a factor loadings predicted for a group of observers differing in the magnitude of categorical bias in their responses (SD = 0.15).

The final two examples illustrate potential nonlinearities in the opponent responses, which have been explored in a variety of studies of color appearance (Ayama, Nakatsue & Kaiser, 1987, Burns, Elsner, Pokorny & Smith, 1984, Larimer, Krantz & Cicerone, 1975, Mizokami, Werner, Crognale & Webster, 2006). We did not attempt to quantitively model the specific nonlinearities revealed by these studies, but instead considered two generic types of nonlinear responses. One way a nonlinearity could manifest is in the response functions for the mechanisms. In Figures 4g and h this was simulated by raising the cosine tuning to different exponents to broaden or narrow the tuning (with the same exponents applied to red-green and blue-yellow) (De Valois, De Valois & Mahon, 2000). The predicted factor is based on a standard deviation of 0.25 and predicts large effects on any stimulus angles that are not aligned to the unique or binary axes. A second potential nonlinearity that has been a focus of several studies could be in the degree of categorical coding, such that observers give more weight to the dominant hue component when judging the proportions (Regier & Kay, 2009). Following Webster and Kay (Webster & Kay, 2012), we modeled this as a relative weighting of the pure categorical response [the unique hue angle of the dominant component (Θ_c)], and the linear response (Θ_l):

$${\Theta }_{\mathrm{pred}}=\mathrm{b}{\Theta }_{\mathrm{c}}+(1-\mathrm{b}){\Theta }_{\mathrm{l}}$$

Figures 4i and 4j show the predictions for a standard deviation of 0.15 in the value for the bias (b) [somewhat weaker than the the biases estimated by Webster and Kay (2012) for the Malkoc et al. (2005) hue-scaling functions]. As with the response nonlinearity, the bias systematically alters all hues between the unique and binary axes and thus again leads to a broad pattern of loadings.

Figure 5 shows Monte Carlo simulations of the hue-scaling functions when the five hypothetical sources of variation shown in Figure 4 were all included. This produced four extracted factors (Figure 5b), presumably because the separate nonlinearities were absorbed by a single factor. The loadings for each of these factors remain bimodal and thus are incompatible with the multiple unimodal factors derived from the observed data. Thus, a conventional model based on opponent red-green and blue-yellow mechanisms, along with plausible ways these mechanisms might vary, provides a poor account of the hue scaling.

Figure 5.

a) Simulations of hue scaling functions for observers varying in five factors corresponding to the tuning and relative sensitivity of the two opponent mechanisms, nonlinearities in the contrast response, and categorical biases. b) Factor loadings based on a factor analysis of the simulated dataset.

3.4.3 Models based on independent, monopolar hue mechanisms

Four independent, monopolar hue mechanisms

In fact, this failure of the opponent model was already evident from the relative independence of the unique hues, as described above. Several lines of evidence suggest that red and green, and blue and yellow, are instead encoded by separate mechanisms. For example, the red and green responses show partial independence with adaptation (Krauskopf et al., 1982), the size of a peripheral “perceptive” field at which saturation stabilizes differs for the four unique hues (Abramov & Gordon, 1994), and as noted, opposite unique hues are often not complementary colors, and thus do not reflect opposite cone combinations (Webster et al., 2000, Wuerger et al., 2005). The splitting of the opponent axis has also been argued on theoretical grounds (MacLeod, 2003), and as well on physiological grounds in that cortical cells have low spontaneous activity and therefore cannot signal opposite responses (excitation and inhibition) as readily as retinal or geniculate cells (De Valois & De Valois, 1993). Such observations have led several authors to propose that cortical color coding is mediated by four hue mechanisms rather than the two opponent channels (e.g. (Abramov & Gordon, 1994, De Valois & De Valois, 1993). Some have also reported the existence of “forbidden colors” (i.e., reddish-green, bluish-yellow), and concluded that opponency is “soft wired” and can be disabled such that four chromatic processes operate independently (Billock, Gleason & Tsou, 2001).

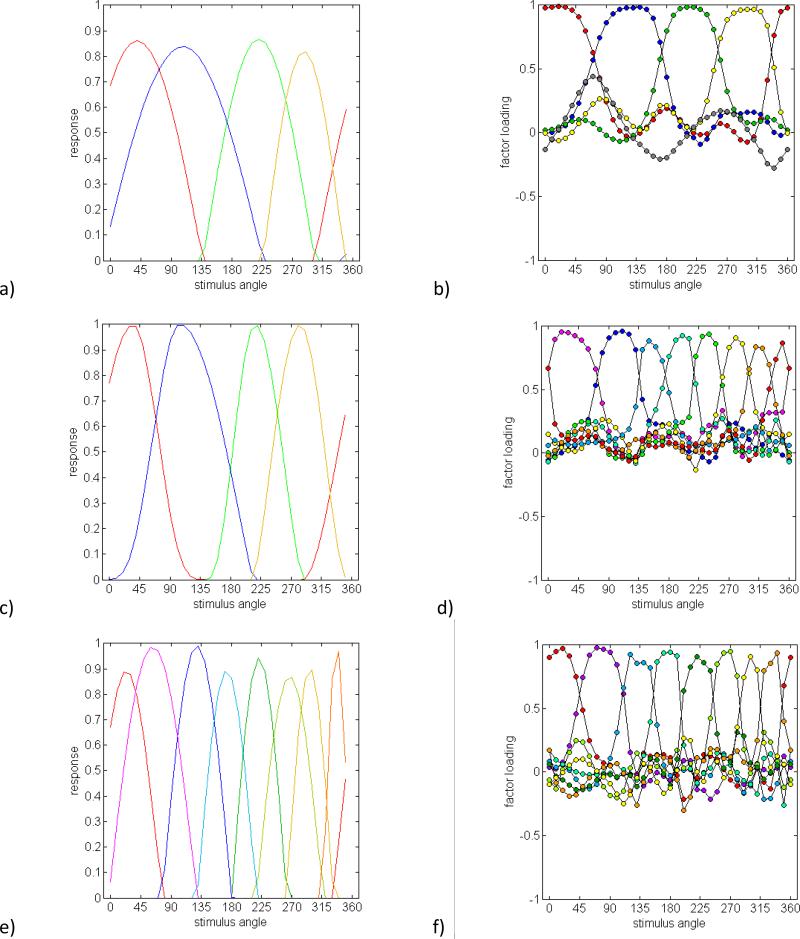
To evaluate this class of models, we generated predictions based on a set of monopolar hue mechanisms, in which each hue (e.g. red or green) was signaled by a different underlying channel. Note that simply splitting a linear red-green opponent mechanism into two half-rectified responses (as suggested in some models of cortical color coding) does not on its own solve the problem that the two poles vary independently, for in this case the two opponent responses remain yoked. A further problem is that for linear mechanisms, sensitivity again varies as the cosine of the preferred stimulus angle, and thus falls to zero in the plane orthogonal to the preferred axis. If red and green are modeled in this way and allowed to vary independently, then this creates some chromatic directions where both mechanisms respond and some where neither does. In actual measurements, the opponent hue pairs together fill the color space, but do so asymmetrically, so that for example more stimulus angles are perceived as blue than yellow (De Valois, De Valois, Switkes & Mahon, 1997). We therefore simulated a case where the hue mechanisms were each allowed to vary over arbitrary arcs of the color circle and in which the opponent pair fully spanned the space while remaining mutually exclusive. For this, each mechanism was modeled as a half-rectified cosine with a frequency scaled so that the response fell to zero at the bounding unique hues, and with a phase equidistant from the two unique hues. For example, the green mechanism ranged from unique blue to unique yellow and peaked midway between. The loci of the four unique hues varied independently across the simulated observers, and the sensitivity of each mechanism also varied randomly over a 20% range. An example of these hue mechanisms is shown in Figure 6a. The perceived hue was assumed to correspond to the relative responses across the set of channels. Thus, this model was similar to the opponent-channel model in assuming that the perception of red directly reflected the activity of an underlying “red” mechanism, but differed in that the spectral sensitivities of the hue mechanisms were more tailored to capture the asymmetries in the observed measurements, and thus less to a specific mechanistic basis for these sensitivities based on their cone inputs.

Figure 6.

Factor loadings predicted by unipolar hue mechanisms. a) Sensivitivities of independent red, green, blue and yellow mechanisms that vary their bandwidth and relative sensitvity, and b) predicted factor loadings based on the simulated variations. c) and d) Sensitivities and predicted loadings for mechanisms with varying bandwidths and asymmetric tuning functions. e) and f) Sensitivities and predicted loadings for eight independent hue mechanisms.

Figure 6b plots the predicted factor loadings for a simulated set of 50 observers. Four of these factors reflect the variations in each primary hue. They are now unimodal like the observed loadings, but are again broadly tuned and thus inconsistent with the observed pattern. The fifth factor (open symbols) corresponds to the variations in relative sensitivity and is also unlike the empirical factors.

Four independent, monopolar hue mechanisms, with local nonlinearities

There are again various ways these hue mechanisms might vary that could potentially increase the dimensions of inter-observer variation in the hue scaling. Global nonlinearities, of the type considered above, again predicted factor loadings that were too broad to replicate the observed factor pattern. However, another possibility we explored were local nonlinearities in the response functions. This was simulated by allowing the tuning functions on either side of the peak sensitivity to vary independently. Figures 6c and 6d show that this manipulation, combined with variations in the mechanism peaks, now generates a pattern of multiple factors reminiscent of the observations. While these asymmetric tuning curves might better emulate how the hue-scaling functions differ, it is not obvious how they could arise from simple nonlinearities in the neural responses (e.g. in the form of a transducer function following the linear filter). However, local variations might also occur if observers apply different rules, e.g. in the categorical biases they exhibit, for different subsets of colors (Komarova & Jameson, 2013).

Eight independent, monopolar hue mechanisms

As an alternative, we next considered an elaborated model with eight hue mechanisms, corresponding to the four unique hues and the four binary hues. The responses in each were again coded as a half-rectified cosine that fell to zero at the adjacent bounding hues. Thus in this case the red mechanism varied from the blue-red to the yellow-red category boundaries correspondng to “unique” purple and orange. One possible rule for combining these channels to form the red-green and and blue-yellow components would be to sum the channel responses weighted by each mechanism's contribution to a given hue. For example, red sensations might correspond to the sum of the red, purple and orange mechanisms that all signal redness but in different proportions. However, this effectively reintroduces a broad bandwidth for each component hue, leading to broad factors that again fail to predict the data

A second pooling rule we evaluated was to treat each of the eight colors as a pure category (corresponding to hue angles at 45 deg intervals in the perceptual color space). The hue angle of any stimulus could then be estimated from the pooled and normalized responses across the eight mechanisms:

$$\Sigma \left({{\mathrm{a}}_{\mathrm{i}}}^{\ast }{\mathrm{r}}_{\mathrm{i}}\right)∕\Sigma {\mathrm{r}}_{\mathrm{i}}$$

where a_i is the hue angle signaled by the ith mechanism and r_i is the response of the mechanism. This results in only the two nearest mechanisms contributing to each hue response, and leads to a set of eight narrowly tuned factors that again capture the general characteristics of the observed loadings. By this account, rather than the four primary hue dimensions of Hering, at least eight distinct hue mechanisms are necessary to explain the variability in hue scaling. Moreover, this account suggests that even though these eight hues can be conceptually decomposed into the opponent dimensions, the “redness” present in orange or purple is in fact a different and independent attribute of the representation.

3.4.4 Population coding (continuum of channels)

The final model we explored abandoned the idea that specific hues are directly signaled by an underyling mechanism, and was instead based on a population code for color. In this case information about color might be represented by the responses within an effectively continuous distribution of channels, each tuned to a different angle within the LM vs S chromatic plane, but none of which necessarily generates a specific sensation. Instead, different hues correspond to different responses within the population, such as the mode or peak of the response distribution. Thus by this account there are no explicit “hue” mechanisms (such as an underlying “red” channel whose response signals redness). Rather, hues are coded as different patterns in the population response, similar to how different spatial orientations might be represented by a continuum of channels tuned to different orientations. Individual differences could reflect how these channels are interpreted or labeled, so that two observers assign different percepts to the channel responses.

The specific question, then, is “how many independently-variable labels or assignments observers might make; or in other words, how many distinct ‘primaries’ observers might use to represent the continuum of hues. If there were only a small number, such as the four unique hues, then these should anchor the interpretation of intermediate hues – as graded variations in the primary responses - and the influence of these anchors should span broad regions of the hue circle. Alternatively, if observers variably assign hue percepts to many different chromatic directions, then there should be many anchors each with a narrowly circumscribed influence on the appearance of neighboring directions. Thus we asked how many anchors are needed to be consistent with the number and chromatic bandwidth of the observed factors.

To assess this, we did not consider the underlying channels (since similar effects could be explained by few or many channels depending on how the channel responses are coded), but instead simply modeled the hue scaling curves, again asking how many points of independent variation are required to approximate the observed factors. Curves were generated by anchoring them relative to the mean unique hue settings for the group, with the unique hues for each individual again generated from random normal deviates. Intermediate hues were based on a spline interpolation between the anchors, with the only restriction that the interpolated values increased monotonically (so that predicted hue percepts varied progressively around the color circle).

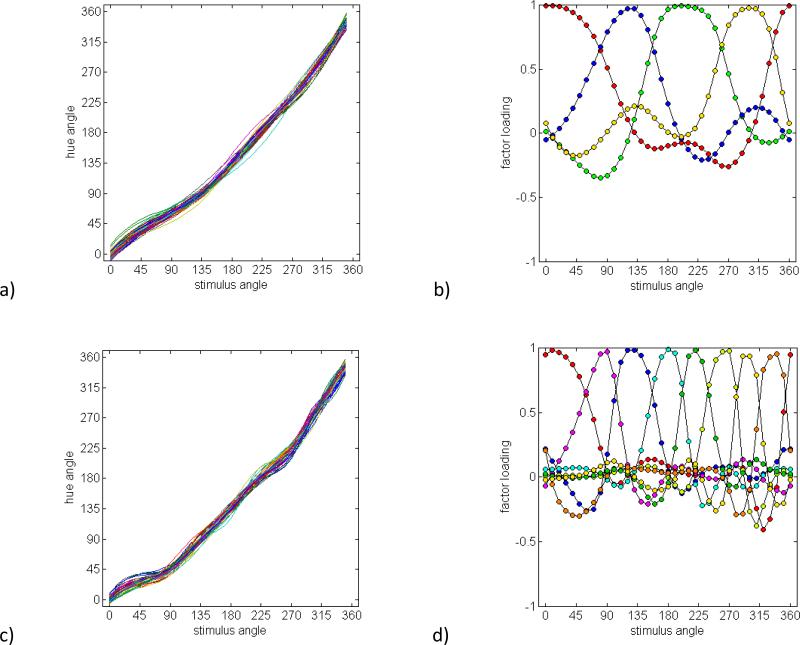
Models based on 4-, 8-, and 16 independently-varying anchors

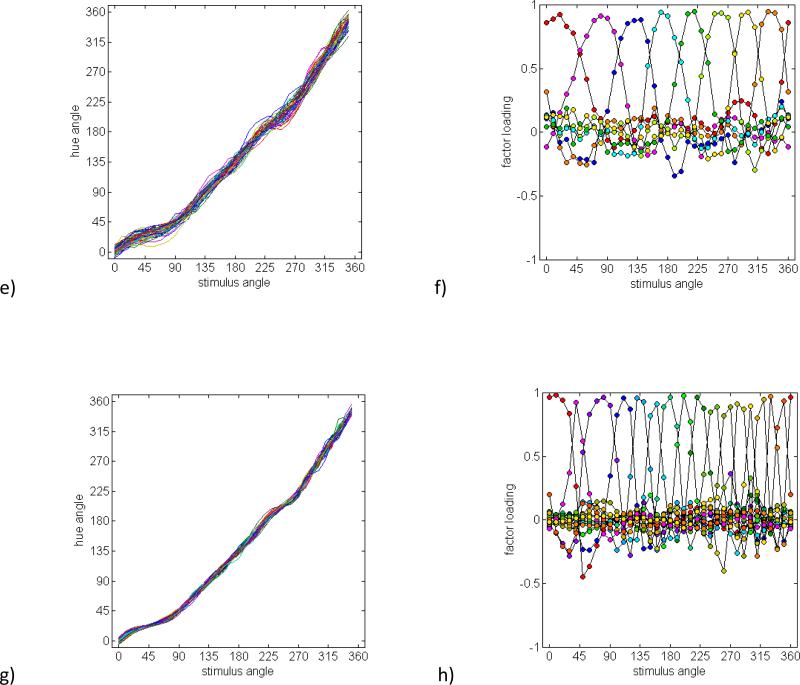
Figure 7a shows the hue scaling curves for 50 simulated observers who were defined by the differences in the loci of the four unique hues, while Figure 7b shows the resulting factor pattern. Not surprisingly, the four variable anchors give rise to four broadly tuned factors which are again too broad to account for the observed loadings. In Figures 7c and 7d, we added four additional individually-varying anchors, with mean values close to the observed binary hues. As in the hue mechanism model with added binary mechanisms, this again results in eight factors that approximate the number and bandwidths of the observed loadings. The predicted factors exhibit weak negative tails that are not readily evident in the observed pattern. However, when a modest degree of noise is added to the predicted curves to simulate measurement error, these tails are largely obscured, leaving narrow, unimodal factors spanning the stimulus angles (Figures 7e and 7f). This analysis illustrates that within-observer noise may have obscured more subtle features of the derived factors, but leaves intact the essential characteristic of multiple, narrowly factors. Finally, Figures 7g and 7h show the curves and loadings based on sixteen independently varying anchors. These were created by adding eight further anchors intermediate to adjacent unique and binary hues. Here the sixteen factors are now too narrowly tuned to predict the observed loadings. Thus like the preceding model, the present analysis is consistent with partitioning hues into roughly eight underlying dimensions that can vary across individuals.

Figure 7.

Predicted scaling functions and factors based on a population code for color with varying anchors corresponding to the stimulus angles associated with different hues. a) and b) Simulated scaling functions and factor loadings based on four variable anchors centered on the four primary hues. c) and d) Predictions for eight anchors corresponding to the focal angles for the unique or binary hues. e) and f) Eight anchors with added measurement noise. g) and h) Sixteen anchored hues.

On the one hand, demonstrating that n sources of variations lead to n factors may seem trivial and obvious, and the present analysis is more an exercise in regenerating the observed variations than predicting them. However, this simulation is nevertheless useful for interpreting the pattern of observed loadings from the perspective of a multichannel code for color, in which the percepts need not be directly tied to the responses of mechanisms that are themselves labeled for specific hue sensations. Within this putative code, the labeling of the responses is not so finely graded that the hue at each measured stimulus angle varies independently, but is again much more narrowly tuned than predicted by an anchoring associated only with the primary hues. Thus, like the explicit hue mechanisms, this analysis points to multiple chromatic mechanisms or decision rules that nevertheless provide only a fairly coarse partitioning of hue.

4. Discussion

To summarize, our results reveal that differences in how color-normal observers scale the hues of chromatic stimuli depend on a surprisingly large number of narrowly-tuned factors, demonstrating that the appearance of different circumscribed regions of the color circle are free to vary independently across observers. The basic pattern of multiple factors was confirmed across two studies of hue scaling involving different participants and procedures. We have shown that this multiple-factor pattern is inconsistent with conventional models of canonical color-opponent processes, including models where the opposing poles of these processes are allowed to vary independently. These findings instead reinforce the independence of adjacent hue categories suggested by previous studies showing that the loci of the unique and binary hues are largely uncorrelated across observers, so that the stimuli an observer selects as pure red and blue fail to predict what they describe as purple (Malkoc et al., 2005). However, this independence is particularly striking in the hue-scaling task, because this task explicitly requires observers to decompose the purple into its red and blue components, and thus might be expected to more readily tap into putative processes signaling these components. Thus, an important implication of the multiple observed factors is that different processes appear to operate for different stimuli that contain these components. That is, the varying tinges of red perceived in different hues may have different origins. In turn, this suggests that there may not be a small set of monolithic hue signals mediating color sensations, and in particular, our results reveal little evidence for an influence on hue scaling of any broadly-tuned mechanisms such the Hering opponent-processes or the cone-opponent cardinal mechanisms of precortical color coding.

As noted, it may be possible to salvage an account of color experience based on the four Hering primaries by allowing for local nonlinearities in hue responses. These could reflect not only early nonlinearities but also “higher-level” processes such as the influence of language or categorical biases that might differentially impact different colors (Komarova & Jameson, 2013). Yet an alternative is that different hues are constrained by different processes, such that orange and red and purple are each intrinsically free to vary. As we showed, one way this could arise is if different hues are each explicitly coded by different mechanisms, whose sensitivities could vary across observers. Alternatively, the sensitivities could in principle be the same, but observers might differ in how they interpret the patterns of activity across the channels, again such that the labeling can vary for multiple hues and not just the four opponent primaries. The latter case does not require multiple underlying channels for color. That is, individuals could vary in how they “read out” the varying levels of activity even within a pair of mechanisms, for example tuned to the retinogeniculate cardinal axes. For example, two observers might differ in how they scale “orange” hues just because they assign different interpretations to the relative activity of the cardinal mechanisms. However, several lines of evidence point to the presence of multiple higher-order mechanisms in the cortical coding of color (though this evidence has not always gone unchallenged (Eskew, 2009)). This includes psychophysical studies demonstrating that sensitivity and appearance cannot be accounted for by a small number of separable mechanisms (e.g. (Krauskopf, 1999)); masking and adaptation effects that are selective for multiple chromatic directions (Gegenfurtner & Kiper, 1992, Krauskopf, Williams, Mandler & Brown, 1986, Webster & Mollon, 1994); and single-cell and neuroimaging studies revealing neural tuning along a variety of chromatic axes dimensions (Kuriki et al., 2015, Lennie et al., 1990, Shapley & Hawken, 2011, Xiao et al., 2003, Zaidi et al., 2014). A further theoretical rationale for encoding color by multiple mechanisms is that this representation is already evident for other stimulus attributes such as spatial orientation (Hubel & Wiesel, 1968) or motion-direction (Maunsell & Van Essen, 1983) or motor control (Georgopoulos, Schwartz & Kettner, 1986), which like color could be fully specificed by only a small number of channels tuned to the cardinal dimensions (e.g. horizontal and vertical) but which instead appear to be represented by populations of cells tuned to many different directions. There are several advantages of this population coding, including noise reduction and allowing cells with broadly-tuned sensitivities to represent very fine differences in the stimulus. It seems plausible that the visual system would exploit similar coding strategies for representing different properties of the world, including color (Clifford, 2002, Webster, 2015b, Zaidi et al., 2014).

A multiple-channel representation of this kind poses fundamental challenges for opponent color theory, for if there are more than three distinctly tuned mechanisms encoding the chromatic plane, then there are no chromatic directions that isolate a single channel (Webster & Mollon, 1994). Thus the notion that unique hues reflect the undiluted responses of an underlying color process is difficult to reconcile with a distributed representation of color. As noted in the Introduction, the uniqueness of the unique hues has also been challenged on several other grounds, including that neural mechanisms with the tuning required to directly mediate the unique hues have yet to be identified. Moreover, the primacy of the unique hues has been questioned in studies showing that these hues are no less variable than binary hues (Bosten & Lawrance-Owen, 2014, Malkoc et al., 2005), and may be surprisingly variable depending on the instructions given to the observer (Bosten & Boehm, 2014).

In many cases the evidence for multiple higher-order color mechanisms rests on measurements of chromatic sensitivity or visual performance, or in tasks not directly related to color appearance (Eskew, 2009, Krauskopf, 1999). This raises the possibility that these studies are tapping into processes or pathways that are not directly involved in suprathreshold color perception, and thus might still allow for the canonical red-green and blue-yellow processes in the case of color appearance. Adaptation to chromatic contrast results in selective response changes that overtly alter color appearance, and thus must directly influence the pathways and processes mediating color percepts (Webster & Mollon, 1994). However these results have been attributed not only to multiple adaptable channels but also to changes in the tuning of a small number of mechanisms (Atick, Li & Redlich, 1993, Zaidi & Shapiro, 1993).

Moreover, it remains possible that these multiple mechanisms occur at intermediate cortical stages, and that their responses are subsequently synthesized to form explicit red-green and blue-yellow responses. While the present results cannot exclude this possibility, they do reveal the influence of multiple processes on a task that explicitly involves judgments of color appearance and that are operational under a fixed state of adaptation.

Again, we considered two possible accounts of the hue scaling in terms of multiple mechanisms. One preserved the basic notion that hue percepts are directly generated by the responses in channels labeled for specific hues, but included channels for the intermediate hues in addition to the unique hues. The second was a more generic representation, in which the hue percepts could be related in more or less arbitrary ways to the underlying population activity. Importantly, in both accounts the basis for the unique hues are very different from conventional opponent theory. Instead of corresponding to a null in the channel responses, both predict that the stimuli we experience as “pure” hues occur at peaks in the channel responses, and are not more or less special than the peaks that occur for intermediate hues.

The observed variability in the hue scaling constrains the number of degrees of freedom in this multiple-channel structure to roughly 8 dimensions. The basis for this level of partitioning remains uncertain, and could reflect the bandwidths of the underlying mechanisms or the decision rules for how they are pooled and interpreted. However, it is noteworthy that eight dimensions is roughly the number required to include hues which observers can readily distinguish and classify as separate categories (i.e. both the unique hues red, green, blue, and yellow, and the binary hues orange, purple, blue-green, and yellow-green) while not so fine as to distinguish among different shades within a category (e.g. variants of orange). This suggests the possibility that the partitioning is linked to how observers label hues, an issue we explore in the accompanying paper (Emery et al., submitted).

An obvious concern with either of these accounts is that in hue scaling observers do appear able to extract the red-green and blue-yellow sensations present in different colors. How is this possible if, as we argue, the colors they perceive are not simply the sum of these sensations? There are several possible answers to this question. First, we note that the ability to dissect the percepts in terms of some dimensions does not require that those dimensions are explicitly represented. For example, a line tilted 30 deg can easily be “seen” to have a definite vertical and horizontal extent without directly experiencing these projected components. In fact, according to opponent-process theory, hues like orange and purple are only implicitly represented by their red and yellow or blue components. However, in the same way, it is possible that the red in orange or purple is only implicitly available. A further argument for the classic opponent mechanisms is that red cannot as easily be perceptually decomposed into orange and purple. Yet this asymmetry may again be like asking how well one can perceive the 30 deg component of a horizontal edge.

A second answer to this concern is to note that the representation of color is (for most humans) necessarily trichromatic, because of the limitations imposed by the number of cone classes. As a result, three perceptual dimensions are sufficient to preserve all of the information available in the cones. There may be no advantage to deploying a higher-order perceptual representation of color, where, for example, orange bears no phenomenal relationship to red. Conversely, there are large potential advantages to coding this relationship, for it allows the representation to signal information about the relative similarity of different spectral stimuli. Thus coding all hues in terms of red-green and blue-yellow dimensions that can be associated across different stimuli may relfect a powerful perceptual strategy, even if it reveals little about the underlying architecture by which it is implemented. Our results support a growing number of studies in suggesting that this architecture may rest on many underlying mechanisms, in which no hue sensations are unique or have a superordinate status. The significance of the opponent axes may therefore be what they reveal about the perceptual organization of color rather than the neural underpinnings of this organization.