Abstract
Ag5Pb2O6 has attracted attentions due to its novel nearly-free-electron superconductivity, but its electronic structure and orbital character of the Cooper-pair electrons remain controversial. Here, we present a method utilizing core-level photoemission to show that Pb 6s electrons dominate near the Fermi level. We observe a strongly asymmetric Pb 4 f 7/2 core-level spectrum, while a Ag 3d 5/2 spectrum is well explained by two symmetric peaks. The asymmetry in the Pb 4 f 7/2 spectrum originates from the local attractive interaction between conducting Pb 6s electrons and a Pb 4 f 7/2 core hole, which implies a dominant Pb 6s contribution to the metallic conduction. In addition, the observed Pb 4 f 7/2 spectrum is not explained by the well-known Doniach-Šunjić lineshape for a simple metal. The spectrum is successfully generated by employing a Pb 6s partial density of states from local density approximation calculations, thus confirming the Pb 6s dominant character and free-electron-like density of states of Ag5Pb2O6.
Introduction
Since the discovery of the high-temperature superconducting cuprate1, two-dimensional layered oxide superconductors have become a central research subject in condensed matter physics2. Ag5Pb2O6 was recently added to the list. Figure 1 shows its layered crystal structure, in which the PbO3 honeycomb layer is sandwiched between two types of Ag layers. Despite its low T c of 52.4 mK3, the material has attracted attentions because of its nearly-free-electron nature in the normal metallic phase4, 5. Typical nearly-free-electron materials, such as alkali and noble metals, do not exhibit superconductivity at ambient pressure, except Li, which has an extremely low T c of 0.4 mK6. Therefore, Ag5Pb2O6 has been considered an ideal model system for investigating superconductivity without the effects of the complicated electronic structure.
Figure 1.
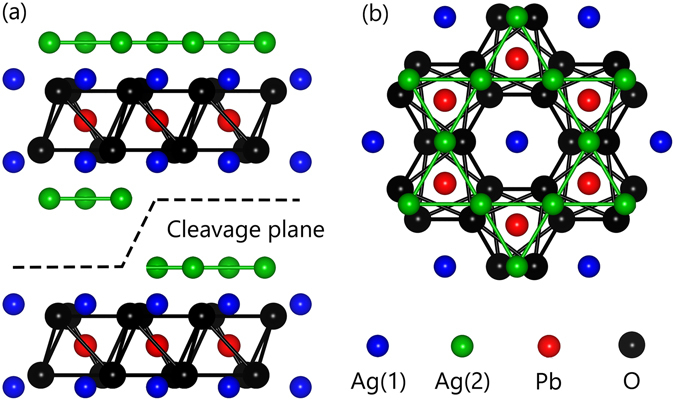
(a) Side view and (b) top view of the crystal structure of Ag5Pb2O6. Green, blue, red, and black spheres represent Ag(1), Ag(2), Pb, and O ions, respectively. Two possible cleavage planes with Ag(1) and Ag(2) terminations are shown as a dashed line.
For superconductors, understanding which electrons will participate in Cooper pairing is important. However, the conduction-state formation of Ag5Pb2O6 remains controversial. Assuming the formal valencies of Ag, Pb, and O ions of +1, +4, and −2, respectively, the material should have one excess electron per chemical formula, which will contribute to free-electron-like conduction. A simple look at the crystal structure suggests that the excess electron may belong to the Ag layers. An earlier extended Hückel tight-binding study also suggested that only the Ag 5s orbital contributes to the conduction of the material7. In contrast, a recent theoretical study using local density approximation (LDA) suggested a different electronic structure, wherein a Pb 6s orbital hybridized with O 2p orbitals crosses the Fermi level (E F), forming a nearly-free-electron band4.
Several experimental studies have attempted to understand the valence state of this material. Some bond length analyses were performed but provided contradicting results regarding the distinction between Ag-dominant8, 9 and Pb-dominant10 characters, while de Haas-van Alphen measurements5 demonstrated a nearly-free-electron Fermi surface and indirectly supported the validity of the LDA scenario4. The only direct experimental evidence was from X-ray absorption spectroscopy (XAS), which suggested that the conduction electrons may be formed by the Pb 6s orbital10. However, the absorption edge in the XAS was not sharp enough to provide decisive experimental evidence.
Valence-band photoemission measurements have served as an ideal tool for identifying the orbital character because they can directly probe valence bands of a solid. Each orbital has a distinct photon-energy dependence in photoionization cross sections11. By varying the incident photon energies, photoemission spectra can be tuned to obtain the orbital-selective partial density of states (DOS) of valence bands12. However, in case of Ag5Pb2O6, the photon-energy dependence of photoionization cross sections of Ag 5s and Pb 6s orbitals are quite similar11. Therefore, investigating the orbital characters of Ag5Pb2O6 using valence-band photoemission is difficult.
Here, we present an alternative approach that utilizes core-level photoemission to investigate the element-specific orbital characters of the conduction electrons in Ag5Pb2O6. We show that the detailed core-level lineshape, especially its asymmetry, is strongly influenced by the Coulomb interaction between a core hole and conduction electrons. We observe strong asymmetry in a Pb 4 f 7/2 core-level spectrum, while a Ag 3d 5/2 spectrum is nearly symmetric. This difference implies that the Pb 6s conduction electrons are dominant near E F. We also demonstrate that the asymmetry of the core-level spectrum can be understood quantitatively based on the Mahan-Nozières-DeDominicis (MND) theory13–15. The Pb 4 f 7/2 spectrum of Ag5Pb2O6 cannot be explained by the Doniach-Šunjić (DŠ) lineshape16, which has been widely used to explain the core-level spectra of many metallic materials. By entering a realistic DOS of the Pb 6s orbital4 into the MND model, we can successfully explain the lineshape quantitatively. Our fit results support the LDA results; i.e., Ag5Pb2O6 has a free-electron-like electronic structure but with a narrow bandwidth.
Results and Discussion
The Ag 3d 5/2 and Pb 4 f 7/2 core-level spectra of Ag5Pb2O6 are shown in Fig. 2(a) and (b), respectively. Both spectra are fitted by symmetric Lorentzian peaks convoluted by a Gaussian after subtracting Shirley backgrounds17. Red lines in Fig. 2 represent the results of the fitting. To verify any surface contributions, we measured core-level spectra at takeoff angles of 0° and 60°. At 60°, the effective probing depth should be half that of 0°. Thus, in the spectrum with a 60° takeoff angle, a surface peak should be much more intense than the bulk peaks. However, as shown in the insets of Fig. 2, the spectral differences between the 0° and 60° spectra are negligible, which confirms the absence of surface-state contributions.
Figure 2.
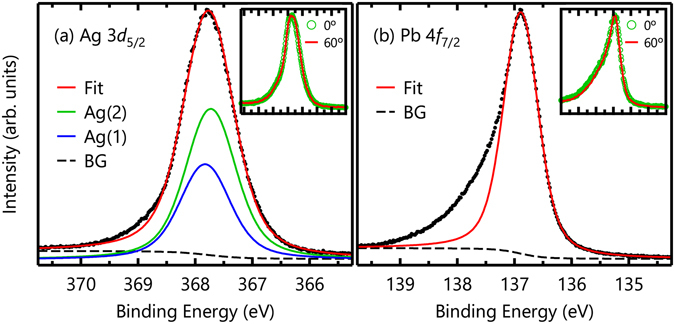
(a) Ag 3d 5/2 and (b) Pb 4 f 7/2 core-level spectra of Ag5Pb2O6. Red lines represent results fitted by symmetric Lorentzian peaks. The insets show the takeoff-angle dependence in each spectrum. The negligible differences imply that there are no surface states in either spectra.
As shown in Fig. 2(a), Ag 3d 5/2 core-level spectrum can be well described by two symmetric peaks with a Lorentzian full-width at half-maximum (FWHM) of 0.274 eV18, which we attribute to two crystallographic Ag sites: Ag(1) and Ag(2) as schematically displayed in Fig. 1. The intensity ratio between these two peaks can be determined using the emission depth distribution function19. To evaluate the function, We calculated the inelastic mean free path using the TPP-2M equation20 embedded in the NIST Electron Inelastic-Mean-Free-Path Database (https://www.nist.gov/srd/nist-standard-reference-database-71). Using the value of 4.93 Å for the inelastic mean free path, we evaluated the emission depth distribution function. With a calculated ratio of Ag(1): Ag(2) = 1: 1.58, we could obtain a good fit as shown in Fig. 3(a). The small discrepancy between the experimental and fit results may be due to the imperfection of the sample surface. Conversely, the Pb 4 f 7/2 core-level spectrum cannot be explained by a single symmetric peak, leaving a large amount of spectral weight at high binding energies as shown in Fig. 2(b).
Figure 3.
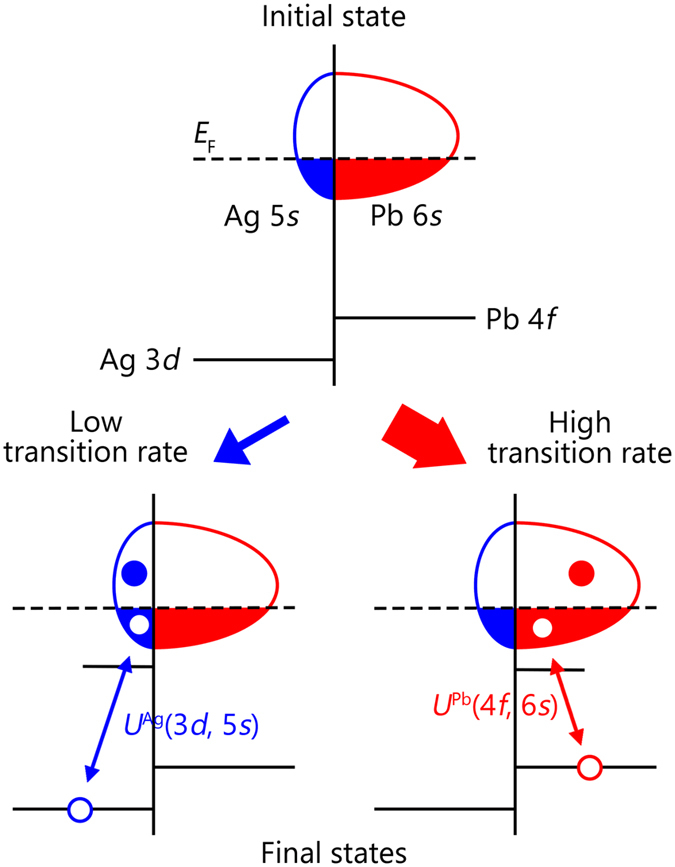
Schematic diagram of core-level photoemission in Ag5Pb2O6. A Pb-dominant character is assumed for the conduction electrons in the diagram. A Coulomb interaction between a Pb core hole and Pb conduction electrons generates electron-hole pairs in the E F-crossing band.
The strong asymmetry of the Pb 4 f 7/2 spectrum should be directly related to dominant Pb 6s partial DOS near the E F. Figure 3 schematically shows the core-level photoemission processes in Ag5Pb2O6. Local Coulomb interaction by a core photohole will scatter conduction electrons, thus exciting electron-hole pairs in a E F-crossing band. Due to the local attractive core-hole potential, an impurity-like state appears below the bottom of the valence band. The energies of the final states with electron-hole pair excitations are higher than that of the lowest energy state, resulting in a large spectral weight at a high binding energy and an asymmetric core-level lineshape. In Ag5Pb2O6, we observed that a Ag 3d 5/2 spectrum is nearly symmetric, indicating few excitations at the Ag 5s conduction band. In contrast, the Pb 4 f 7/2 core-level spectrum is highly asymmetric, which implies that many electron-hole pairs are excited at the Pb 6s conduction band as shown in Fig. 3. Therefore, the main character of the conduction electrons in Ag5Pb2O6 should be the Pb 6s electrons.
The asymmetric core-level lineshape in a metal can be understood based on the MND theory13–15, in which a local Coulomb potential due to a core hole scatters conduction electrons. The model Hamiltonian is given by
| 1 |
where is an conduction-electron creation (annihilation) operator, h †(h) a core-hole creation (annihilation) operator, ε k a conduction-electron energy with a momentum k, ε h a core-hole energy, and N the number of lattice sites considered in the model. U is an attractive on-site Coulomb interaction between conduction electrons and a core hole. Without U, the core-level spectrum should have a simple Lorentzian lineshape, whose half width at half-maximum γ reflects a core-hole lifetime. By turning on U, electron-hole pairs can be excited across the E F, resulting in an asymmetric lineshape. Thus, a quantitative analysis of an asymmetric spectral function A(ω) can provide us with important information regarding conduction bands, such as U and DOS near the E F.
In the MND theory, if a conduction-band has a flat DOS with an infinite energy range, A(ω) can be expressed in a closed form, which yields the well-known DŠ lineshape16:
| 2 |
where Γ(x) is the gamma function and α is an asymmetry parameter. This simple spectral function greatly reduces a numerical cost compared to the general MND model. When α = 0, the lineshape is just a symmetric Lorentzian of half-width γ. According to the MND theory, α is approximately given by U 2 ρ 2(E F) at the weak-coupling limit, where ρ(ε) is the conduction-band DOS16. Because of the strong locality of U, the strength of asymmetry α should be related to an element-specific partial DOS. Note that the DŠ lineshape has been quite successful at describing core-level spectra from numerous metals, such as noble21 and simple22, 23 metals.
However, the measured Pb 4 f 7/2 spectrum is not explained by the simple DŠ lineshape. Figure 4 shows several trial fits of the Pb 4 f 7/2 core-level spectrum wherein the value of α using Eq. (2) is varied. When α is small, the large asymmetry cannot be explained. Conversely, large α values render large tails at higher binding energies. The inset of Fig. 4 shows a Pb 4 f 7/2 core-level spectrum of the Pb metal from ref. 24, which is well explained by the DŠ lineshape with α = 0.11, unlike the case of Ag5 Pb2 O6. This discrepancy may be ascribed to the assumption of the flat, broad conduction-band DOS used to obtain the DŠ lineshape. A similar discrepancy in the DŠ lineshape behavior has also been reported in narrow d-band metals such as Pd and Pt21.
Figure 4.
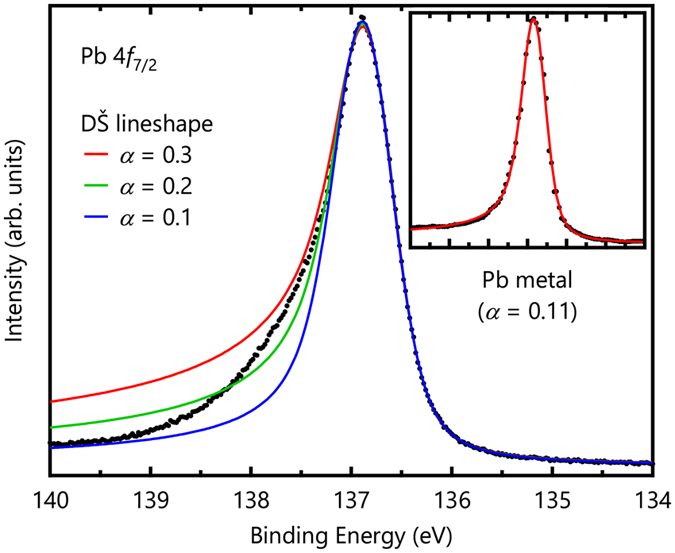
Pb 4 f 7/2 core-level spectrum and fitting results of the DŠ lineshape with several values. The inset shows a Pb 4 f 7/2 core-level spectrum of a Pb metal from ref. 24, which is well explained by the DŠ lineshape with α = 0.11.
To explain the asymmetric lineshape at a quantitative level, we adopted a theoretical approach reported by Davis and Feldkamp25, 26. The model reads
| 3 |
where is a creation (annihilation) operator of a conduction electron with an energy ε. Here, is given by
| 4 |
After the creation of a core hole, a final one-electron eigenstate ϕ n with an energy eigenvalue ω n is given by a unitary transformation S n(ε) of the initial eigenstate ψ ε: i.e.
| 5 |
After discretizing the energy for numerical calculations, a final many-body state Φα is given by a product of L eigenstates: , with an energy of , while its spectral intensity is given by |<Φα|ΦG>|2, where ΦG corresponds to the initial many-body ground state with the lowest occupied L eigenstates. Note that |<Φα|ΦG>|2 corresponds to the square of a determinant of an order-L matrix whose elements are S n(ε). When ρ(ε) is given, we can easily calculate S n(ε) and its associated spectral intensity. Then, the spectral function A(ω) is given by the total sum of spectral contributions of the N C L final states.
To explain our Pb 4 f 7/2 spectrum, we calculated the spectral function by employing the realistic Pb 6s partial DOS from LDA calculations4. An experimental DOS from valence-band photoemission would not be useful, because it is difficult to extract the contribution from Ag and Pb from the partial DOS of E F-crossing bands by varying the incident phonon energy as mentioned earlier. Moreover, the photoemission spectrum does not provide information above E F. Instead, we employed the Pb 6s partial DOS from LDA calculations as shown in the inset of Fig. 5. According to the MND theory, completely filled or empty conduction bands are not responsible for the asymmetric lineshape, because there is a finite energy gap for electron-hole pair excitations, and their spectral contributions are negligible compared with those from excitations in E F-crossing bands. To calculate a Pb 4 f 7/2 core-level spectrum, we used the partial DOS from −1.27 to 1.72 eV (the gray shaded region in the inset of Fig. 5), which corresponds to the minimum or maximum of the E F-crossing band, respectively4. In our calculations, final states with one or two electron-hole pair creations are considered to have a total spectral weight larger than 0.999.
Figure 5.
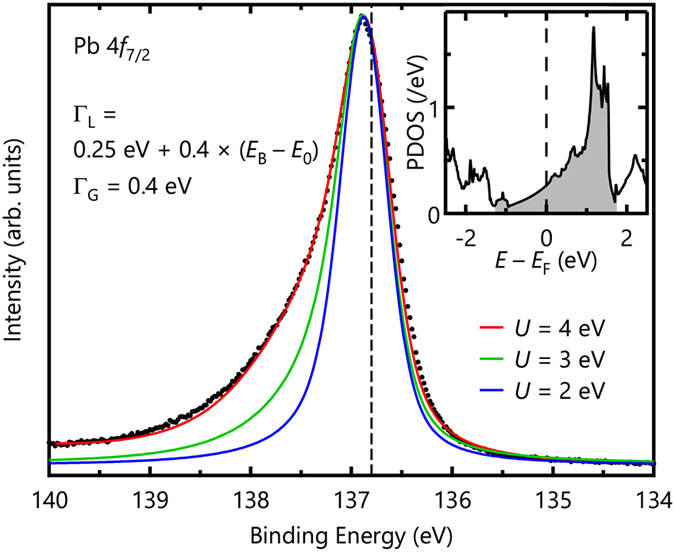
Pb 4 f 7/2 core-level spectrum and fitting results of MND-model calculations with the Pb 6s partial DOS. The spectrum is well explained with U = 4 eV. The dashed line represents the lowest binding energy of 136.8 eV. The inset shows the Pb 6s partial DOS from LDA calculations, and the gray shaded region was considered in our calculations.
The observed Pb 4 f 7/2 spectrum is quantitatively well explained by the MND calculations as shown in Fig. 5. To compare it with the experimental spectrum, we convoluted them using a Lorentzian and a Gaussian functions. For the Lorentzian broadening, we used ΓL = 0.25 eV + 0.4 × (E B − E 0) (FWHM), where the first (second) term corresponds to a lifetime for the core hole (electron-hole pair). E 0 is the lowest binding energy in the calculations. The E 0 value was set to 136.8 eV for the Pb 4 f 7/2 spectrum as represented by the dashed line in Fig. 5. To account for the extrinsic broadening, we also included a Gaussian broadening with ΓG = 0.4 eV (FWHM) in the calculations. The calculated spectrum with U = 4 eV reproduced the observed Pb 4 f 7/2 spectrum quite well. The lineshape of the high-binding-energy tail is strongly governed by the shape of DOS27. Therefore, the success of our MND calculations supports the validity of the LDA calculations4, which suggested the Pb 6s character of charge carriers and the free-electron-like electronic structure.
For comparison, we also depict calculation results with U = 2 and 3 eV in Fig. 5. The figure clearly shows that the asymmetries of the calculated spectra are quite sensitive to the values of U. Since the asymmetry parameter is approximately given by U 2 ρ 2(E F) in the DŠ lineshape16, asymmetry in a core-level spectrum is a good indicator of an element-specific contribution to metallic behavior at similar values of U. According to Hartree-Fock calculations for atomic orbitals using Cowan’s code28, the average values of bare Coulomb interaction U 0 between a core hole and conduction electrons for Ag 3d-5s and Pb 4f-6s electrons are
| 6 |
and
| 7 |
respectively, where F 0, G 2, and G 3 are Slater integrals29. These values of the bare interactions are considerably reduced due to the screening by conduction electrons. Using the relation between the screened Coulomb interaction U and a polarization P, U = U 0/(1 − PU 0)30, we can estimate the value of U Ag(3d, 5s) to be 3.7 eV from U Pb(4f, 6s) = 4 eV, assuming the same polarization for each core hole. Those values are so similar that we can expect a highly asymmetric lineshape for the Ag 3 d 5/2 spectrum, in contrast to the real one. Thus, we can conclude that the Ag 5s partial DOS at E F should be much smaller than that of Pb 6s.
Conclusion
We settled the controversy surrounding the element-specific orbital character of Ag5Pb2O6 by measuring its core-level photoemission spectra. The dominant Pb 6s character was confirmed based on the strong asymmetry of a Pb 4 f core-level spectrum and MND-model calculations. Our approach using core-level photoemission can be applied to investigate the conduction state of other compound materials, where valence-band photoemission is difficult to apply. Moreover, the failure of the DŠ lineshape indicates that, in general, we should use the more realistic DOS to explain the core-level lineshape of materials.
Methods
We synthesized Ag5Pb2O6 single crystals using a previously reported self-flux method31. First, we mixed 6N-AgNO3 (Sigma-Aldrich) and 5N-Pb(NO3)2 (Sigma-Aldrich) powders thoroughly and placed the mixture into an alumina crucible. We initially heated the mixture in air to 90° C and maintained that temperature for 3 hours. Then, we heated it at 405° C for 4 days. We varied the ratio between AgNO3 and Pb(NO3)2 to obtain large crystals with a hexagonal stick shape. The size of the largest crystal is about 0.2 × 0.2 × 2 mm3. We used the X-ray diffraction technique to confirm the crystal structure of the synthesized crystal. The diffraction pattern indicated that there was no secondary phase. We also confirmed the stoichiometry between Ag and Pb ions via the energy dispersive X-ray spectroscopy.
We performed core-level photoemission experiments at the Beamline 4A1 of Pohang Light Source. The single crystal was cleaved and measured at 50 K under a vacuum of 3 × 10−11 Torr. Possible cleavage planes are the Ag(1) and Ag(2) terminations as displayed in Fig. 1(a). To achieve the best energy resolution, we used photon energies of 480 eV for the Ag 3d 5/2 level and 280 eV for the Pb 4 f 7/2 level. We determined the binding energy with reference to the 4 f 7/2 core-level peak of polycrystalline gold electrically connected to the sample. All measured spectra were reproducible for three samples.
Acknowledgements
We thank T. Oguchi for providing the electronic-structure data of Ag5Pb2O6. We also acknowledge the experimental support provided by H.K. Yoo and C.-T.Kuo. This work was supported by the Institute for Basic Science (IBS) in Korea (Grant No. IBS-R009-D1, IBS-R009-G2), and grants from the National Research Foundation of Korea (NRF) (2012M2B2A4029470, 2017R1C1B2004927). Experiments at PLS-II were supported in part by MSIP and POSTECH.
Author Contributions
S.S. and H.-D.K. conceived and designed the work. K.D.L., C.J.W., and N.J.H. synthesized Ag5Pb2O6 single crystals. S.S., J.S.O., H.-D.K., and B.-G.P. carried out the core-level photoemission experiments. Fitting and analyses were conducted by S.S. and H.-D.K. The research was carried out with guidance from M.H., Y.J.C., C.K., H.-D.K., and T.W.N. S.S., H.-D.K., and T.W.N. co-wrote the manuscript. All authors discussed the work and reviewed the manuscript.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Hyeong-Do Kim, Email: hdkim6612@postech.ac.kr.
Tae Won Noh, Email: twnoh@snu.ac.kr.
References
- 1.Bednorz JG, Müller KA. Possible high Tc superconductivity in the Ba-La-Cu-O system. Zeitschrift für Physik B Condensed Matter. 1986;64:189–193. doi: 10.1007/BF01303701. [DOI] [Google Scholar]
- 2.Basov DN, Timusk T. Electrodynamics of high-Tc superconductors. Review of Modern Physics. 2005;77:721–779. doi: 10.1103/RevModPhys.77.721. [DOI] [Google Scholar]
- 3.Yonezawa S, Maeno Y. Type-I superconductivity of the layered silver oxide Ag5Pb2O6. Physical Review B. 2005;72:180504. doi: 10.1103/PhysRevB.72.180504. [DOI] [Google Scholar]
- 4.Oguchi T. Electronic band structure and Fermi surface of Ag5Pb2O6. Physical Review B. 2005;72:245105. doi: 10.1103/PhysRevB.72.245105. [DOI] [Google Scholar]
- 5.Sutherland M, Mann PDA, Bergemann C, Yonezawa S, Maeno Y. Nearly free electrons in the layered oxide superconductor Ag5Pb2O6. Physical Review Letters. 2006;96:097008. doi: 10.1103/PhysRevLett.96.097008. [DOI] [PubMed] [Google Scholar]
- 6.Tuoriniemi J, et al. Superconductivity in lithium below 0.4 millikelvin at ambient pressure. Nature. 2007;447:187–189. doi: 10.1038/nature05820. [DOI] [PubMed] [Google Scholar]
- 7.Brennan TD, Burdett JK. Electronic structure of Ag5Pb2O6. Inorganic Chemistry. 1994;33:4794–4799. doi: 10.1021/ic00099a033. [DOI] [Google Scholar]
- 8.Bystrom A, Evers L. The crystal structures of Ag2PbO2and Ag5Pb2O6. Acta Chemica Scandinavica. 1950;4:613–627. doi: 10.3891/acta.chem.scand.04-0613. [DOI] [Google Scholar]
- 9.Dickens B. The bondings in Ag2 PbO2 and Ag5Pb2O6. Journal of Inorganic and Nuclear. Chemistry. 1966;28:2793–2799. [Google Scholar]
- 10.YoShii K, et al. Neutron diffraction and X-ray absorption study of Ag5Pb2O6. Journal of Inorganic and Nuclear Chemistry. 2007;180:377–381. [Google Scholar]
- 11.Yeh JJ, Lindau I. Atomic subshell photoionization cross sections and asymmetry parameters. Atomic Data and Nuclear Data Tables. 1985;32:1–155. doi: 10.1016/0092-640X(85)90016-6. [DOI] [Google Scholar]
- 12.Im HJ, et al. Direct observation of dispersive kondo resonance peaks in a heavy-fermion system. Physical Review Letters. 2008;100:176402. doi: 10.1103/PhysRevLett.100.176402. [DOI] [PubMed] [Google Scholar]
- 13.Mahan GD. Excitons in degenerate semiconductors. Physical Review. 1967;153:882–889. doi: 10.1103/PhysRev.153.882. [DOI] [Google Scholar]
- 14.Nozières P, DeDominicis CT. Singularities in the X-ray absorption and emission of metals. III. one-body theory exact solution. Physical Review. 1969;178:1097–1107. doi: 10.1103/PhysRev.178.1097. [DOI] [Google Scholar]
- 15.Ohtaka K, Tanabe Y. Theory of the soft-X-ray edge problem in simple metals: historical survey and recent developments. Review of Modern Physics. 1990;62:929–991. doi: 10.1103/RevModPhys.62.929. [DOI] [Google Scholar]
- 16.Doniach S, Šunjić M. Many-electron singularity in X-ray photoemission and X-ray line spectra from metals. Journal of Physics C: Solid State Physics. 1969;3:285–291. doi: 10.1088/0022-3719/3/2/010. [DOI] [Google Scholar]
- 17.Shirley DA. High-resolution X-ray photoemission spectrum of the valence bands of gold. Physical Review. 1972;5:4709–4714. doi: 10.1103/PhysRevB.5.4709. [DOI] [Google Scholar]
- 18.Citrin PH, Wertheim GK, Baer Y. Surface-atom X-ray photoemission from clean metals: Cu, Ag, and Au. Physical Review B. 1983;27:3160–3175. doi: 10.1103/PhysRevB.27.3160. [DOI] [Google Scholar]
- 19.Hüfner, S. Photoelectron Spectroscopy (Springer-Verlag Berlin Heidelberg, 2003).
- 20.Tanuma S, Powell CJ, Penn DR. Calculations of electron inelastic mean free paths. V. data for 14 organic compounds over the 50–2000 eV range. Surface and Interface Analysis. 1994;21:165–176. doi: 10.1002/sia.740210302. [DOI] [Google Scholar]
- 21.Hüfner S, Wertheim GK. Core-line asymmetries in the X-ray-photoemission spectra of metals. Physical Review B. 1975;11:678–683. doi: 10.1103/PhysRevB.11.678. [DOI] [Google Scholar]
- 22.Citrin PH, Wertheim GK, Baer Y. Many-electron effects in core-level X-ray and electron spectroscopies from Na, Mg, and Al. Physical Review Letters. 1975;35:885–888. doi: 10.1103/PhysRevLett.35.885. [DOI] [Google Scholar]
- 23.Baer Y, Citrin PH, Wertheim GK. X-ray photoemission from lithium: An explanation of its X-ray edge. Physical Review Letters. 1975;37:49–52. doi: 10.1103/PhysRevLett.37.49. [DOI] [Google Scholar]
- 24.Nyholm R, Berndtsson A, Mårtensson N. Core level binding energies for the elements Hf to Bi (z = 72–83) Journal of Physics C: Solid State Physics. 1980;13:1091–1096. doi: 10.1088/0022-3719/13/36/009. [DOI] [Google Scholar]
- 25.Davis LC, Feldkamp LA. Effect of electron correlations on photoemission from narrow-band metals. Journal of Applied Physics. 1979;50:1944–1949. doi: 10.1063/1.327119. [DOI] [Google Scholar]
- 26.Davis LC. Photoemission from transition metals and their compounds. Journal of Applied Physics. 1985;59:25–63. doi: 10.1063/1.336323. [DOI] [Google Scholar]
- 27.Wertheim GK, Walker LR. Many-body effects in transition metals: role of the density of states. Journal of Physics F: Metal Physics. 1976;6:2297–2306. doi: 10.1088/0305-4608/6/12/015. [DOI] [Google Scholar]
- 28.Cowan, R. D. The Theory of Atomic Structure and Spectra (University of California Press, 1981).
- 29.Slater JC. The theory of complex spectra. Physical Review. 1929;34:1293–1322. doi: 10.1103/PhysRev.34.1293. [DOI] [Google Scholar]
- 30.Fetter, A. L. & Walecka, J. D. Quantum Theory of Many-Particle Systems (McGraw-Hill Book Company, 2003).
- 31.Yonezawa S, Maeno Y. Nonlinear temperature dependence of resistivity in single cyrstal Ag5Pb2O6. Physical Review B. 2004;70:184523. doi: 10.1103/PhysRevB.70.184523. [DOI] [Google Scholar]


