Methods to determine limit of detection and limit of quantification in quantitative real-time PCR (qPCR)

Abstract

Quantitative Real-Time Polymerase Chain Reaction, better known as qPCR, is the most sensitive and specific technique we have for the detection of nucleic acids. Even though it has been around for more than 30 years and is preferred in research applications, it has yet to win broad acceptance in routine practice. This requires a means to unambiguously assess the performance of specific qPCR analyses. Here we present methods to determine the limit of detection (LoD) and the limit of quantification (LoQ) as applicable to qPCR. These are based on standard statistical methods as recommended by regulatory bodies adapted to qPCR and complemented with a novel approach to estimate the precision of LoD.

1. Introduction

Arguably among the most critical performance parameters for a diagnostic procedure are those related to the minimum amount of target that can be detected and quantified [11]. The parameters describing those properties are known as the limit of detection “LoD” and the limit of quantification “LoQ”. Their definitions vary slightly among regulatory bodies and standards organizations [1]. The Clinical Laboratory Standards Institute (www.clsi.org), for example, defines LoD as “the lowest amount of analyte (measurand) in a sample that can be detected with (stated) probability, although perhaps not quantified as an exact value” [2]. In many clinical laboratories and diagnostic applications, LoD is used interchangeably to “sensitivity”, “analytical sensitivity” and “detection limit.” This may, however, be confusing as “sensitivity” is also used in other ways. For example, in some applications “sensitivity” refers to the slope of the calibration curve, which is the definition used by the International Union of Pure and Applied Chemistry (IUPAC). CLSI defines LoQ as “the lowest amount of measurand in a sample that can be quantitatively determined with {stated} acceptable precision and stated, acceptable accuracy, under stated experimental conditions” [2]. An alternative LoQ based on clinical sensitivity and specificity has been proposed for diagnostic purposes [17].

Definitions by CLSI

LoD = the lowest amount of analyte (measurand) in a sample that can be detected with (stated) probability, although perhaps not quantified as an exact value.

LoQ = the lowest amount of measurand in a sample that can be quantitatively determined with {stated} acceptable precision and stated, acceptable accuracy, under stated experimental conditions

By far most measuring techniques generate a signal response that is proportional to the amount of measurand present. For example, measured absorption is proportional to the concentration of the measurand as predicted by the Beer-Lambert law. Linear measurements typically generate a background signal that is observed in the absence of measurand and must be subtracted from the measured values. This background signal limits the sensitivity of the measurement and is used to estimate LoD [3]. Working at 95% confidence, the limit of blank “LoB” is:

$$LoB=mea{n}_{blank}+1.645\times {\sigma }_{blank}$$ (1)

where σ is the standard deviation, and

$$LoD=LoB+1.645\times {\sigma }_{lowconcentrationsample}$$ (2)

This is also the recommended estimates in the CLSI guideline EP17 [2]. The σ in Eqs. (1) and (2) refers to the true standard deviation, while SD refers to estimated standard deviation from experiments. Replacing σ for SD requires also replacing 1.645 for the corresponding t-value, which depends on the degree of freedom and, hence, the number of replicates performed).

The above equations assume response is linear and data are normal distributed in linear scale. Small deviations from normal distribution when estimating SD have been discussed [12] but in qPCR, not even the response is linear. The measured Cq values are proportional to the log base 2 (log₂) of the concentration of the measurand (or the number of target molecules present), which is a logarithmic response. This has dramatic implications on the analysis and interpretation of the data [4]. For example, no Cq value is obtained when a negative sample is measured, as the response never reaches the threshold line, and the standard deviation (SD) cannot be calculated for any set that includes negative samples. Hence, it is not possible to estimate LoD and LoQ by the standard procedures above. A further complication is that estimating confidence intervals assumes normal distribution. While linear data often are normally distributed in linear scale, qPCR data show normal distribution in logarithmic scale, further disqualifying the conventional approaches. To estimate LoD in qPCR one needs to revert to the definition of LoD In this paper we present the procedure to experimentally determine LoD based on sample replicates and also a novel method to estimate the confidence of the LoD. We also present the procedure to estimate LoQ of a qPCR system.

2. Materials and methods

The qPCR method used as an example to assess performance was ValidPrime [5], which is a optimized probe-based assay targeting a highly conserved, non-transcribed locus present in exactly one copy per haploid human genome. The test material was human genomic DNA (CAT# CHG50, TATAA Biocenter) calibrated against the National Institute of standards and technology (NIST) Human DNA Quantitation Standard (SRM 2372). A 2-fold dilution series was prepared covering the range 1 to 2048 molecules per reaction volume. Each standard sample was analyzed in 64 replicates, except for the most diluted sample, which was analyzed in 128 replicates. Grubb's test [13] was used to identify nine outliers that were removed, leaving 759 data points for the analysis.

In the qPCR reaction, TATAA Probe GrandMaster Mix L-Rox was used and the final concentration of the ValidPrime assay in the reaction was 200 nM of a FAM-labeled probe and 400 nM of each primer. The IntelliQube*1 (LGC Douglas Scientific) was used for all sample and master mix dispensing, thermal cycling, and real-time fluorescence detection, utilizing 1.6 μl reaction volumes. The 2-step qPCR protocol included a 1 min enzyme activation step at 95 °C, followed by 50 cycles of 10 s at 95 °C and 30 s at 60 °C. An auto-baselining method was used when plotting the amplification curves. Cq values were calculated with the IntelliQube software by manually setting a threshold line in the region of exponential amplification across all the amplification plots.

Cq data from the IntelliQube were preprocessed and analyzed using GenEx (MultiD analyses AB).

Coefficient of variation was calculated as:

$$\sqrt{\mathrm{ex}{p}^{{\left(SD\left(\ln \left(conc\right)\right)\right)}^2}-1}$$ (3)

assuming log-normal distribution of replicate concentrations [6]. This follows from the fact that if the stochastic variable X has lognormal distribution, then by definition ln(X) is normally distributed with, say, mean μ and standard deviation σ. The distribution function of X is then given by

$$F\left(x\right)=P\left(X<x\right)=P\left(\ln X<\ln x\right)=P\left(\frac{\ln X-\mu }{\sigma }<\frac{\ln x-\mu }{\sigma }\right)=\Phi \left(\frac{\ln x-\mu }{\sigma }\right)$$ (4)

where Φ is the distribution function of the standardized normal distribution. The probability density function of X is readily obtained as $F^{\prime }\left(x\right)$ from which the mean $e^{\mu +{\sigma }^2/2}$ and variance $\left(e^{{\sigma }^2}-1\right)e^{2\mu +{\sigma }^2}$ of X are straightforwardly obtained by integration. The coefficient of variation is defined as the ratio between the standard deviation and the mean, i.e., the coefficient of variation of X becomes $\sqrt{e^{{\sigma }^2}-1}$.

Cq values were measured at p different concentrations, c_i, i = 1, …, p, with n replicas at each concentration. For simplicity of presentation n is kept constant. The data analysis below is straightforward to generalize to the case where there are different of number of replicas for different concentrations. The resulting Cq values are arranged in a data matrix ${\left(Cq\right)}_{i,j}$ i = 1, …, p j = 1, …, n and an indicator function

$$I_{i,j}=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill ifC{q}_{i,j}<C_o\hfill \\ \hfill 0\hfill & \hfill ifC{q}_{i,j}>C_o\hfill \end{array}\right)$$ (5)

where C_o is a user specified cut-off value. Let $z_{i={\sum }_{j=1}^n{I}_{i,j}}$ be the number of detected values at concentration c_i. The logistic regression model assumes that the observed z_i is binomially distributed, $Bin\left(n,f_i\right)$, with

$$f_i=\frac{1}{1+e^{-{\beta }_0-{\beta }_1{x}_i}}$$ (6)

where x_i denotes log₂c_i. The two unknown parameters β₀ and β₁ are approximated by maximum likelihood (ML) estimation. The likelihood function is

$$L=\coprod _{i=1}^p\left(\begin{array}{c}\hfill z_i\hfill \\ \hfill n\hfill \end{array}\right)f_i^{z_i}{\left(1-f_i\right)}^{n-z_i}=\left(\coprod _{i=1}^p\left(\begin{array}{c}\hfill z_i\hfill \\ \hfill n\hfill \end{array}\right)\right)e^{{\beta }_0{y}_1+{\beta }_1{y}_2-\phi }$$ (7)

where $y_1={\sum }_{i=1}^p{z}_i$ and $y_2={\sum }_{i=1}^p{z}_i{x}_i$ and $\phi ={\sum }_{i=1}^{p}n\ln \left(1+e^{{\beta }_0+{\beta }_1{x}_i}\right)$. Setting the derivatives of L with respect to β₀ and β₁ to zero gives the system of equations for the ML estimate,

$$\begin{array}{l}{y}_1-\sum _{i=1}^p\frac{n}{1+e^{-{\beta }_0-{\beta }_1{x}_i}}=0\hfill \\ y_2-\sum _{i=1}^p\frac{n{x}_i}{1+e^{-{\beta }_0-{\beta }_1{x}_i}}=0\hfill \end{array}$$ (9)

This non-linear system of equations is solved by GenEx 6 [11], using a quasi-Newton method. The ML solution will be denoted by ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$. The logistic regression curve is obtained by plotting

$$\hat{t}=\frac{1}{1+{\text{e}}^{-{\hat{\beta }}_0-{\hat{\beta }}_1\text{x}}}$$ (10)

versus x = log₂c. The hat-notation indicates that $\hat{t}$ is the ML estimate of the exact $t=\frac{1}{1+{\text{e}}^{-{\beta }_0-{\beta }_1\text{x}}}$. The observed values y₁ and y₂ can be considered as samples from a stochastic variable (Y₁,Y₂) with distribution function ∼e^{β₀y₁+β₁y₂−φ}. The moments of (Y₁,Y₂) are obtained in terms of partial derivatives of φ with respect to β₀ and β₁, by differentiating the normalization condition

$$1=\int C{e}^{{\beta }_0{y}_1+{\beta }_1{y}_2-\phi }d{y}_{1}d{y}_2$$ (11)

with respect to β₀ and β₁. C is here a normalization constant. The ML estimate ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$ and hence, the quantity of interest $\hat{t}$, can be interpreted as samples from stochastic variables that depend on (Y₁, Y₂) through the ML equations. The standard error for $\hat{t}$ Is given by

$$\hat{\sigma }={\left(\sum _{i,j}\frac{\partial t}{\partial y_i}\frac{{\partial }^2\phi }{\partial {\beta }_i\partial {\beta }_j}\frac{\partial t}{\partial y_j}\right)}^{1/2}$$ (12)

In this formula, and in the formulas below we use the convention the limits of the summations are 0 and 1 for all indexes, and that the expression is evaluated at the ML estimated parameters ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$.

The standard 1–2α confidence interval $\hat{t}\mp z_{\alpha }\hat{\sigma }$, where z_αis a percentile of the normal distribution, approximates the exact confidence interval with accuracy $O\left(n^{-1/2}\right)$ as the sample size n grows. The parametric bootstrap confidence intervals (Efron [7], Diciccio and Efron [8]) improve on the standard intervals by taking into account higher moments in the normal approximation. There are several variants of bootstrap confidence intervals, but they all approximate the exact confidence interval with accuracy $O\left(n^{-1}\right)$. GenEx implements the ABCq confidence intervals described in Diciccio and Efron 1982. ABC stands for Approximate Bootstrap Confidence interval, and the q subscript indicates quadratic form. The formula for the ABCq confidence interval is

$$\left[\hat{t}-q_{\alpha -}\hat{\sigma },\hat{t}+q_{\alpha +}\hat{\sigma }\right]$$ (13)

where

$$q_{\alpha +}=\lambda +c_q{\lambda }^2\text{and}\lambda =\frac{z_0+z_{\alpha }}{{\left(1-a\left(z_0+z_{\alpha }\right)\right)}^2}$$ (14)

The expression for q_α− is similar but with z_α is replaced by −z_α. The three parameters a, c_q, and z₀ are defined as follows. The acceleration,

$$a=\frac{1}{6{\hat{\sigma }}^3}\sum _{i,j,k}\frac{{\partial }^3\phi }{\partial {\beta }_i\partial {\beta }_j\partial {\beta }_k}\frac{\partial t}{\partial y_i}\frac{\partial t}{\partial y_j}\frac{\partial t}{\partial y_k}$$ (15)

where the limits of summation are 0 to 1 for all indexes. The derivatives are evaluated at the ML estimated values ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$. The quadratic coefficient

$$c_q=\frac{1}{2{\hat{\sigma }}^3}\sum _{i,j,k,l}\frac{{\partial }^2\phi }{\partial {\beta }_i\partial {\beta }_k}\frac{{\partial }^2\phi }{\partial {\beta }_j\partial {\beta }_l}\frac{{\partial }^{2}t}{\partial y_i\partial y_j}\frac{\partial t}{\partial y_k}\frac{\partial t}{\partial y_l}$$ (16)

And the bias correction

$$z_0={\Phi }^{-1}\left(2\Phi \left(\text{a}\right)\Phi \left(-\hat{\gamma }\right)\right)$$ (17)

where Φ is the distribution function of the standardized normal distribution. The parameter $\hat{\gamma }$ is defined by

$$\hat{\gamma }=\frac{\hat{b}}{\hat{\sigma }}-c_q\text{,}$$ (18)

where the bias estimate is

$$\hat{b}=\frac{1}{2}\sum _{i,j}\frac{{\partial }^2\phi }{\partial {\beta }_i\partial {\beta }_j}\frac{{\partial }^{2}t}{\partial y_i\partial y_j}$$ (19)

Efron [7], [8] makes repeated use of the formula

$$\sum _j{v}_j\frac{\partial f}{\partial x_j}=\frac{d}{dh}f\left(x_0+h{v}_{0,}{x}_1+h{v}_1\right){|}_{h=0}$$ (20)

to rewrite parts of the expressions for a, c_q, and $\hat{b}$ as directional derivatives. Approximating the directional derivative by numerical differentiation is computationally efficient and avoids the possibly lengthy expressions obtained by performing the differentiation exactly.

3. Results

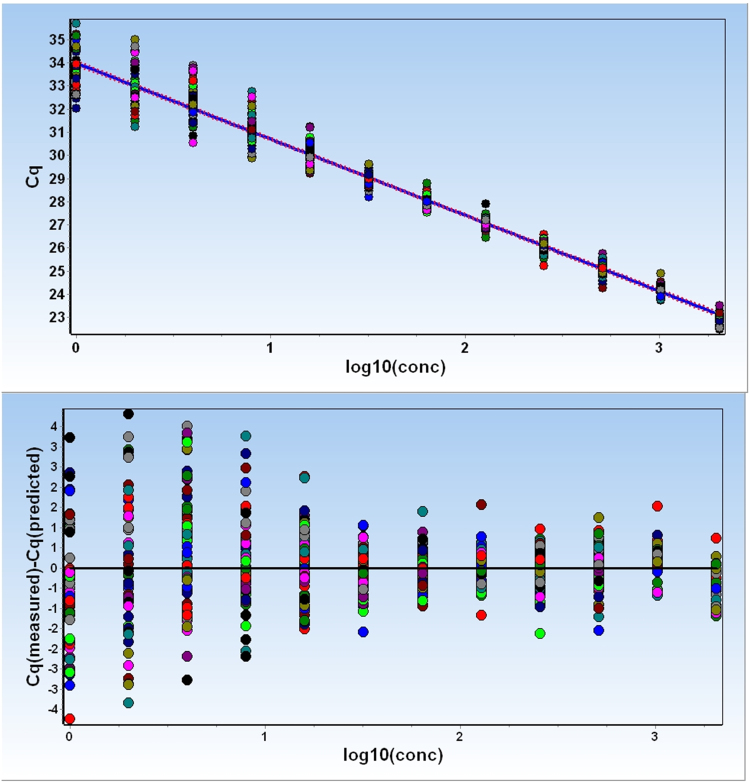
Starting from a calibrated human genome sample (NIST SRM 2372), a 2-fold dilution series of standard samples was prepared covering the range 1–2048 molecules per reaction volume. Each standard sample was analyzed in 64 replicates, except for the most diluted sample, which was analyzed in 128 replicates. Grubb's test identified nine outliers leaving 759 data points for analysis. Fig. 1 plots the measured Cq values versus the expected amounts of molecules per sample (top). The data are fitted to a straight line, which, however, is only to guide the eye, as the low concentration samples are outside the linear range of the qPCR standard curve. Fig. 1 also shows the measured Cq values in a residual plot relative to the fitted straight line (bottom). The plots show how the spread of replicates increases with decreasing amount of target. This is expected due to sampling noise. As the expected number of target copies decreases, the variation across replicates increases. Although other factors also contribute to variation across replicates [14], sampling noise, which can be modeled by the Poisson distribution, is expected to dominate at very low copy numbers [15], [16]. In Fig. 1 it is also seen that the low concentrated samples deviate from the straight line by having somewhat lower Cq values than expected. This bias is due to some of the replicate samples being negative (“non-detect”) and not considered in the plots, resulting in an apparent lower average Cq.

Fig. 1.

Standards dilution series. Top: 2-fold serial dilution of a calibrated human genomic DNA sample covering the range from 1 to 2048 target molecules on average per sample. Each sample was analyzed in 64 replicates, except for the most diluted sample, which was analyzed in 128 replicates, using the ValidPrime qPCR assay. Bottom: Residual plot of the positive reads.

4. Limit of detection

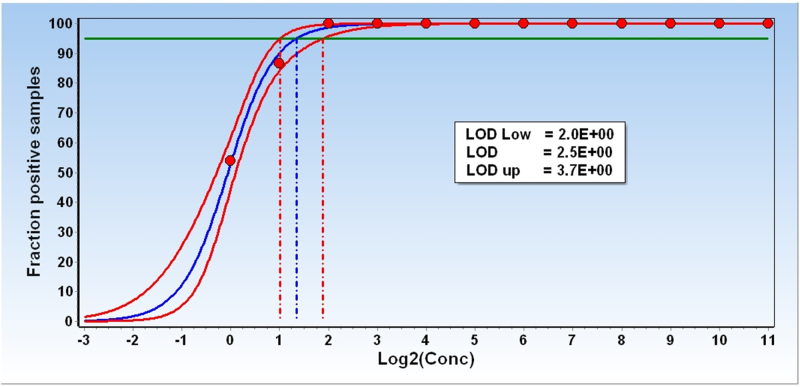
LoD for qPCR methods can be estimated from analysis of replicate standard curves [10]. From the definition of LoD follows that working at 95% confidence, LoD is the measurand concentration that produces at least 95% positive replicates. Under error free conditions, when only sampling noise would contribute to replicate variation, LoD at 95% confidence is 3 molecules [9]. For most real samples, LoD is also affected by noise contributed to by sampling, extraction, reverse transcription, and qPCR, and may be substantially higher. Fig. 2 plots the fractions of positive replicates versus the number of target molecules per sample for the ValidPrime/gDNA data. From visual inspection, the LoD at 95% confidence is between 2 and 4 target molecules. Fitting the data with the sigmoidal function:

$$y_i=\frac{1}{1+e^{-\alpha -\beta \log \left(c_i\right)}}\text{,}$$ (21)

allows for interpolation, which gives LoD = 2.5 target molecules. This is even slightly below to the theoretical limit caused by sampling noise. The precision of the estimate can be obtained by resampling of the data (Fig. 2):

$$LoD(with95\%confidence\mathrm{int}erval)=2.0\le 2.5\le 3.7$$

Fig. 2.

Limit of detection. Fractions of positive reads obtained with the ValidPrime assay when analyzing samples containing from 1 to 2048 target molecules on average per sample. The measured fractions are fitted to a sigmoidal curve for the estimation of LoD (solid line). At 95% confidence LoD is 2.5 target molecules. Resampling of the data with recurrence (dashed line) allows estimating the 95% confidence interval for the LoD = 2.0 ≤ 2.5 ≤ 3.7 (intersections of the horizontal line at 0.95 and the three sigmoidal curves).

The confidence interval encompasses the theoretical LoD of 3 molecules.

5. Limit of quantification

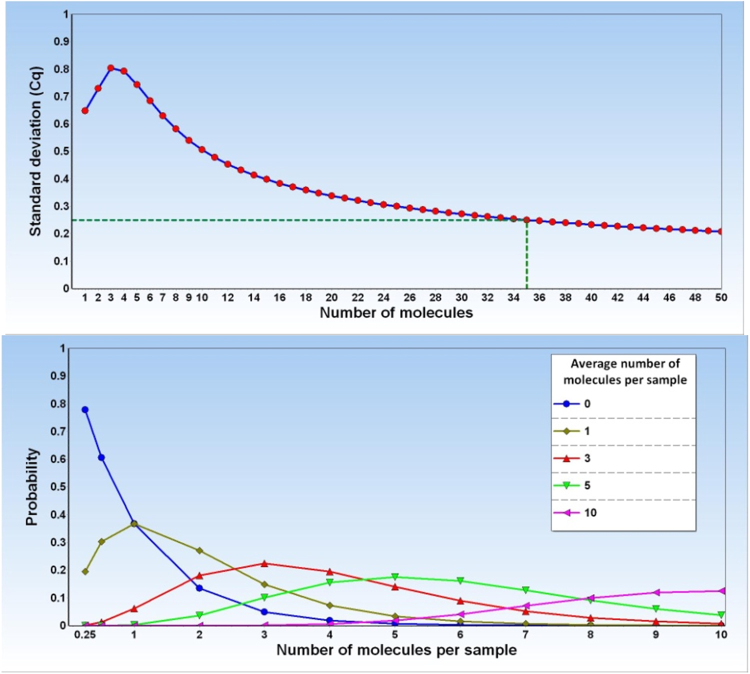
The LoQ can also be estimated from the replicate standard curves. This is done by calculating the SD for the responses of the replicate samples at the different concentrations. SD of the data can be calculated in either log (Cq values) or linear scale (relative quantities) and does not assume any particular distribution. In each case, SD reflects the average difference of the measured values to the mean in the same scale. In contrary to SD, calculation of the confidence interval assumes normal distribution. For normally distributed data, 68% of the measured values are expected to be within the mean ± 1 SD, and 95% within the mean ± 2 SD. SD is expected to increase with decreasing target concentration due to sampling noise, which alone produces an SD of 0.25 cycles when the average number of target molecules per analyzed aliquot is 35 (Fig. 3). In practice, other factors such as losses due to adsorption to surfaces, decreasing reaction yields at lower concentrations, less efficient reactions, etc., contribute to the error. Calculating SD of the qPCR data in logarithmic scale, i.e., on the Cq values, has the advantage that data usually are normal distributed and confidence intervals are readily calculated. However, for comparison with other measurement techniques the SD should be converted into linear scale and expressed in percentage of the mean, which is known as the relative standard deviation or the coefficient of variation (CV = 100 × SD/mean) which leads to the following expression for the coefficient of variation:

$$C{V}_{\ln }=\sqrt{{\left(1+E\right)}^{{\left(SD\left(Cq\right)\right)}^2*\ln \left(1+E\right)}-1}$$ (22)

where CV_ln is the coefficient of variation for log-normal distributed data as expected for concentrations measured in replicates with qPCR, having a qPCR efficiency: E, and standard deviation of replicate Cq-values: SD(Cq).

Fig. 3.

SD due to sampling ambiguity. Contribution to the standard deviation from sampling ambiguity modeled by the Poisson distribution. Left graph: distribution of target molecules across aliquots from containers with different concentrations modeled by the Poisson distribution. Right graph: SD of Cq values of replicates assuming sampling error only that can be modeled by the Poisson distribution. A container concentration of 35 target molecules on average per aliquot produces SD = 0.25 cycles.

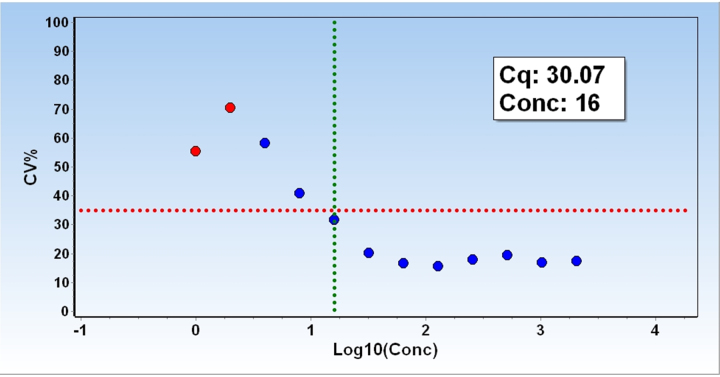
Fig. 4 shows the CV for the human gDNA samples assayed by ValidPrime as a function of the expected number of target molecules in the standard samples. CV increases with decreasing target concentration as expected due to increasing sampling noise and other factors. As target concentration decreases some of the replicate samples starts to be negative (“non-detect”). These concentrations are per definition below the LoQ, and are indicated in red in Fig. 4. There is also a bias toward lower values in the calculated SD, as the non-detect samples cannot be considered.

Fig. 4.

Limit of Quantification. Coefficient of variation (CV = 100 × SD/mean) of the back-calculated concentrations of the human genome replicate samples analyzed with the ValidPrime assays. Horizontal red dashed line indicates CV = 35% and vertical green dashed line indicates the lowest concentration of samples with a CV below 35%. Red symbols indicate presence of negative (“non-detect”) samples among the replicates. Those are ignored when calculating SD, resulting in a bias toward lower SD values.

There is no general guidance specifying acceptable threshold value of LoQ. What may be reasonable varies from case to case and depends on the complexity of the samples and the required precision in any decisions being supported by the test. At TATAA Biocenter, unless we have other guidance, we specify LoQ as the lowest concentration where replicates show a CV ≤ 35% on back calculated concentrations. Using the ValidPrime method to analyze human gDNA, we find that the lowest amount of gDNA that produces replicates with a CV ≤ 35% is 16 molecules. Hence, LoQ of the ValidPrime method as applied here is 16 molecules.

6. Discussion

The accuracy of LoD and LoQ estimates depends primarily on the concentration increments between the standard samples, while the precision depends primarily on the number of replicates. In fact, LoQ estimates are restricted to those target concentrations/amounts that were contained in the standard sample. In our example the LoQ is 16 molecules, or perhaps less as this satisfies the CV ≤ 35% criteria, but it does not reach 8 molecules, which was the amount of target molecules in the next diluted standard sample. We currently have no reliable means to interpolate the CV versus target amount data to obtain an estimate of LoQ that would be in between 8 and 16 molecules. The number of replicates performed of each standard sample determines the precision in the SD and CV estimates. If these are poor, because of low number of replicates, the LoQ criteria can accidentally be met at a different concentration leading to an erroneous estimate. Occasionally CV rises to over the set threshold (35% in our case) at a certain target amount, then drops to below this threshold at a lower target amount and then rises again. Such fluctuations are due to imprecision in the estimated CV's usually due to too low a number of replicates. In those cases, LoQ should be taken as the lowest target amount higher than any concentration with a CV exceeding the set threshold. In addition to the criteria above, LoQ can never be lower than LoD. Should experiments give such an estimate, LoQ should be reported equal to LoD.

In our ValidPrime/gDNA example, LoD is less than 4 target molecules but does not reach 2, as the standard samples containing in average 4 target molecules have a positive call rate above 95%, while the standard samples containing in average 2 target molecules have a positive call rate below 95%. By interpolating the measured call rates as a function of the average number of target molecules, we obtain a more precise estimate of LoD. For the ValidPrime/gDNA we estimate LoD by interpolation to 2.5 molecules. This is close to the expected LoD at a 95% positive call rate of 3 molecules predicted by the Poisson distribution describing sampling noise, suggesting that other contributions to noise for the ValidPrime/gDNA qPCR analysis are negligible.

If sufficient number of replicates at each standard's concentration is available, the confidence interval of the LoD estimate can be obtained by resampling of the data with recurrence. A fairly high number of replicates, often at least 20, at each concentration are needed to get convergence. The LoD confidence interval is asymmetric, with a smaller range toward lower target concentrations. For the ValidPrime method analyzing human gDNA, the LoD for 95% positive call rate estimated with a 95% confidence range was: LoD = 2.0 ≤ 2.5 ≤ 3.7 molecules.

The concentration range covered by the standard samples has very low impact on the estimated LoD and LoQ. For the LoQ estimate, only the lowest target amount with a CV below the set threshold and the highest target amount with a CV above the set threshold are used. The initial rough LoD estimate is also based on only two samples: the sample with the lowest target amount that produces positive reads at a rate above the set criteria (typically 95%) and the sample with highest target amount that produces positive reads at a rate below the set criteria. A more precise estimate of LoD can be obtained by interpolating the measured positive rates taking into account more standard samples. But even in this case only a small number of standard samples is considered, as only those that produce fractional positive rates (i.e., above 0 and below 100%) contribute appreciably to the fitting. Therefore, from a practical point of view and cost performance, it is better to narrow the target concentration range of the standards to just cover the expected LoD and LoQ and increase the number of replicates to improve precision. In practice, LoD and LoQ are not known ahead of the experiment. A pragmatic approach is then to obtain an initial rough estimate of LoD and LoQ, perhaps as part of the regular standard curve that is measured when establishing any new method to estimate the PCR efficiency, repeatability and dynamic range, and then in a second experiment narrow down the concentration range and increase the number of replicates for more precise estimates of LoD and LoQ.

Handled by Jim Huggett