Abstract
Reducing radiation dose in dual energy computed tomography (DECT) is highly desirable but it may lead to excessive noise in the filtered backprojection (FBP) reconstructed DECT images, which can inevitably increase the diagnostic uncertainty. To obtain clinically acceptable DECT images from low-mAs acquisitions, in this work we develop a novel scheme based on measurement of DECT data. In this scheme, inspired by the success of edge-preserving non-local means (NLM) filtering in CT imaging and the intrinsic characteristics underlying DECT images, i.e., global correlation and non-local similarity, an averaged image induced NLM-based (aviNLM) regularization is incorporated into the penalized weighted least-squares (PWLS) framework. Specifically, the presented NLM-based regularization is designed by averaging the acquired DECT images, which takes the image similarity within the two energies into consideration. In addition, the weighted least-squares term takes into account DECT data-dependent variance. For simplicity, the presented scheme was termed as “PWLS-aviNLM”. The performance of the presented PWLS-aviNLM algorithm was validated and evaluated on digital phantom, physical phantom and patient data. The extensive experiments validated that the presented PWLS-aviNLM algorithm outperforms the FBP, PWLS-TV and PWLS-NLM algorithms quantitatively. More importantly, it delivers the best qualitative results with the finest details and the fewest noise-induced artifacts, due to the aviNLM regularization learned fromDECT images. This study demonstrated the feasibility and efficacy of the presented PWLS-aviNLM algorithm to improve the DECT reconstruction and resulting material decomposition.
1. Introduction
Dual-energy computed tomography (DECT) scans the object using different energy spectra, which can be regarded as one of the most exciting evolving fields in radiology (Alvarez et al 1976, Noh et al 2009). Comparing to standard CT, or single-energy CT, DECT can take advantage of energy-specific attenuation coefficients to obtain material- and energy- selective images, which has led to a wide range of clinical applications, such as the automatic bone removal (Johnson et al 2007) and assessment of myocardial blood supply (Ruzsics et al 2009). Therefore, the DECT can provide more clinical information on the object than standard CT. Moreover, X-ray exposure to patients may generate healthy risks, so minimizing the exposure risk has been one of the major endeavors in current DECT study. However, reducing radiation dose may lead to excessive noise in the filtered backprojection (FBP) reconstructed DECT images if no adequate treatments in the reconstruction. Besides, in DECT imaging the material-selective images can be separated from two sets of measurements by solving an inverse problem. However, a generic problem of the direct inversion process is that the resulting images will suffer from severe noise-induced artifacts. Therefore, the purpose of this study is to propose an iterative approach to suppress noise effects and improve DECT images quality.
Up to now, many considerable efforts to suppress noise-induced artifacts in DECT images and material-decomposed images have been reported (Rutherford et al 1976, Kalender et al 1988, Warp et al 2003, Leng et al 2011, Zeng et al 2016a, Niu et al 2014, Clark et al 2014, Dong et al 2014, Sukovic et al 2000, Petrongolo et al 2015, Zhang et al 2014, Long et al 2014, Zhang et al 2016a, Zhang et al 2016b, Szczykutowicz et al 2011, Liu et al 2016). Among them, projection or image domain denoising approaches were proposed to improve low-dose DECT images quality (Rutherford et al 1976, Kalender et al 1988, Warp et al 2003, Leng et al 2011, Zeng et al 2016a, Niu et al 2014, Clark et al 2014). Recently, Zeng et al (2016a) developed a non-local means (NLM)-based filter for low-dose DECT imaging wherein the fillter operation considers the image similarity within DECT images. Although these approaches can suppress the noise to some extent, they often result in spatial resolution loss because the noise in DECT images does not obey a uniform distribution. By better modeling the projection data and the image geometry in the DECT imaging, statistical iterative reconstruction (SIR) algorithms have shown to be more robust than FBP algorithm in regard to the presence of noise-induced artifacts (Dong et al 2014, Sukovic et al 2000, Petrongolo et al 2015, Zhang et al 2014, Long et al 2014, Zhang et al 2016a, Szczykutowicz et al 2011, Liu et al 2016). Based on the maximum a posterior (MAP) estimation criteria, the SIR algorithms can be mathematically formulated with a cost function. In general, the cost function has two terms: a data-fidelity term considering the measurement statistics and a regularization term evaluating which degree the objective image fulfills the prior information. Specifically, the data-fidelity term which is a critical component of SIR algorithms models the consistency between the objective DECT images and measurements. And the regularization term has been proven to be effective in DECT images reconstruction. Therefore, designing effective regularization term to reflect the image priors is at the core of DECT images reconstruction. One classic family of the regularization term is based on total variation (TV) model, which does take into consideration the information that the DECT images are blocky and discontinuous and measure the discontinuities in the objective data (Dong et al 2014, Zhang et al 2016a, Szczykutowicz et al 2011). These regularizations are generally defined to work in a small local neighborhood. For example, Szczykutowicz et al. proposed a prior image constrained compressed sensing (PICCS) algorithm for DECT reconstruction by incorporating a prior image (averaging over FBP images reconstructed from different energies) into the reconstruction procedure (Szczykutowicz et al 2011). Moreover, Liu et al (2016) designed a material reconstruction model with nonlocal total variation (NLTV) regularization to improve the reconstructed material images quality, e.g. contrast-to-noise ratio and spatial resolution. Although these TV-based regularizations have been widely used in DECT images reconstruction, they usually smear out image details and cannot deal well with fine structures. Moreover, motion between DECT images can be an important issue in the case of slow-kV p based DECT system, which could result in that the PICCS approaches do not work effectively (Leng et al 2011).
Another established family is based on nonlocal means (NLM) based model, which has been widely used in low-dose CT image reconstruction (Zeng et al 2016a, Zhang et al 2014a, Ma et al 2012a). For instance, Ma et al (2012a) proposed a prior-image induced NLM-based regularization for low-dose cerebral perfusion CT reconstruction wherein the regularization utilized the redundant prior information within the NLM-based framework. Inspired by the success of Ma’s work and the intrinsic characteristics underlying DECT images, i.e., global correlation and non-local similarity, in this study, we propose a penalized weighted least-squares (PWLS) criteria incorporating the NLM-based regularization. Specifically, the weighted least-squares term takes into account DECT data-dependent variance and the NLM-based regularization utilizes the redundant information from an average image wherein the average image is generated from all of the images reconstructed in all energy domain. Our contributions can be summarized as follows: First, the aviNLM regularization fully takes global correlation and non-local similarity underlying the DECT images, which can characterize the priors of desired DECT images in the reconstruction framework. Second, under the one-step-late framework, the steepest descent scheme was designed to optimize the objective function to achieve clinically acceptable DECT images from low-mAs acquisitions. Experiments on digital phantom, physical phantom and patient data show that the presented PWLS-aviNLM approach can achieve remarkable gains in various aspects.
The remaining parts of this paper are organized as follows. In section 2, we describe the DECT imaging model, the presented aviNLM prior and the associated PWLS-aviNLM image reconstruction algorithm. Section 3 validates the performance of our proposed reconstruction method using digital phantom, physical phantom and clinical data. Finally, the discussion and conclusion are given in section 4.
2. Methods and materials
2.1. SIR framework for low-dose DECT
In this study, the DECT measurements at distinct projections are assumed to be conditionally independent. And under the assumption of monochromatic X-ray generation, the DECT measurements can be approximately expressed as discrete linear system:
| (1) |
where denotes the obtained DECT sinogram data after the system calibration and logarithm transformation to form ray-sums, and is the desired reconstructed DECT images, where ‘T’ denotes the matrix transpose. M in Eq. (1) represents the joint system matrix, which can be expressed as follows:
| (2) |
where is the identity matrix with the size of . denotes the Kronecker product. The operator H denotes system matrix with the size of , where I is the number of detector bins and J is the number of energy-specific image voxels to be reconstructed. is typically calculated as the path length of projection ray i with energy-specific voxel j. The goal of DECT images reconstruction is to estimate the desired DECT images U to enable image-based material decomposition.
In our study, it is the objective to reconstruct DECT images by solving the following optimization problem within PWLS criterion:
| (3) |
where is a hyper-parameter vector to balance the data-fidelity term and regularization term. Assuming the ray-sum measurements among all the bins are statistically independent, is the inverse covariance of measurements Y, which can be expressed as follows:
| (4) |
where is the variance of high-energy sinogram data and is the variance of low-energy sinogram data . According to our previous studies (Ma et al 2012b), the projection data after the calibration and log-transformation follow approximately a Gaussian distribution with an associated relationship between the data sample mean and variance, which can be expressed as follows (Ma et al 2012b) :
| (5) |
where represents the incident X-ray intensity at high- or low- energy, and is the mean of sinogram data at bin i at high- or low- energy and is the background electronic noise variance.
2.2. aviNLM regularization
It is noted that the regularization term in Eq. (3) plays a critical role for successful DECT images reconstruction and the DECT image are structurally similar implying global correlation underlying the DECT images. In this paper, according to our previous studies (Ma et al 2012a, Zhang et al 2014a, Zhang et al 2014b, Zhang et al 2014c), we propose an averaged image induced NLM-based (aviNLM) regularization, which fully takes global correlation and non-local similarity underlying the DECT images and is defined as follows:
| (6) |
where denotes a non-quadratic function and can be chosen as (Bouman et al 1993). In this study, p is set to be for all the experiments. represents an average image induced NLM filter and is described as follows (Zeng et al 2016a) :
| (7) |
where represents the search window in the image volume which is produced by averaging the DECT images. The weighting coefficients can be written as follows
| (8) |
where denotes the patch centered at the pixel i in the energy-specific image and denotes the patch centered at the pixel j in the averaged image . The notation denotes a Gaussian-weighted Euclidean distance metric between two similar patches (Buades et al 2005). The parameter d represents smoothing factor controlling the decay of the exponential function as well as the weighting coefficient. According to our previous work (Ma et al 2012a), C is local compensation factor accounting for local intensity changes, which can be expressed as follows:
| (9) |
where denotes the expected value or mean of the intensity in the patch-window V.
In summary, the objective function in Eq. (3) can be rewritten as:
| (10) |
2.3. Implementation of the PWLS-aviNLM algorithm
Because the weighting coefficients in Eq. (8) are actually determined by the desired DECT images and the aviNLM regularization term is nonlinear, it is difficult to effectively optimize the objective function in Eq. (10) with general optimization algorithms. To address this issue, similar to our previous works (Ma et al 2012a, Zhang et al 2014b), we now consider that an empirical one-step-late (OSL) scheme can be used to optimize the objective function in Eq. (10) which contains four main following steps:
Prior estimation. Given the current estimation where n denotes the iterative index and the averaged image , the aviNLM filter in Eq. (7) is first performed between Un and , and then the regularization term is calculated in Eq. (6).
- Steepest descent optimization. For minimizing the objective function of the PWLS-aviNLM algorithm, a steepest descent optimization algorithm is utilized to yield new image estimation, i.e. , which can be described as follows:
where denotes the gradient step-size and can be determined adaptively as follows (Sullivan et al 1991) :(11)
where , wherein Z denotes the normalizing factor of the aviNLM filter for each voxel in Eq. (7), and . In the implementation, as , let .(12) Cycle update. Update using the aforementioned step until stop criteria is satisfied.
2.4. Parameters selection
2.4.1. Selection of aviNLM filter parameters
It is not a trivial task to determine the optimal aviNLM filter parameter. In this work, these parameters were empirically set through extensive experiments by quantitative measures and visual inspection. We found that a search-window and patch-window are adequate for suppressing noise-induced artifacts while retaining computational efficiency, and wherein denotes the standard deviation of . denotes the size of the search window , and is a free scalar parameter and is determined by experiments.
2.4.2. Selection of hyper-parameter
The hyper-parameter vector is used to balance the data fidelity and regularization terms. Optimizing them is a difficult task in CT image reconstruction. In this study, the hyper-parameter is tuned manually to achieve a good compromise between a low noise level and a high level of detail.
2.4.3. Selection of the stop criterion
The iterative process is finished if particular convergence criterion is satisfied for a relatively stable solution. In this study, 50 iterations are usually sufficient for a stable result with sufficient stability for the presented PWLS-aviNLM algorithm.
2.5. Experimental data acquisition
To evaluate the performance of the presented PWLS-aviNLM algorithm for low dose DECT image reconstruction, a digital 4D extended cardiac-torso (XCAT) phantom (Fig. 1(a)), a physical clock phantom (Fig. 1(b)) and clinical DECT data were utilized in the study.
Figure 1.
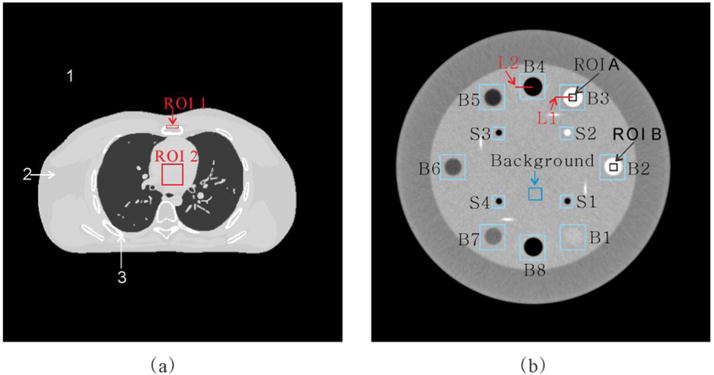
The digital XCAT phantom (a), physical clock phantom (b) for DECT experiments and detail information of the physical clock phantom in (b).
2.5.1. XCAT phantom study
The digital XCAT phantom (Fig. 1(a)) study was conducted to assess the presented PWLS-aviNLM algorithm performance. The XCAT phantom in this study consists of three different materials mimicking air, soft tissue and bone, with the issues and materials defined in Table 2. A geometry similar to mono-energetic fan-beam CT scanner model with a circle orbit is used and the related scan geometry parameters are listed in Table 3. Similar to the work (Le et al 2010, Shikhaliev 2005, Zeng et al 2015), for energy-specific noise-free sinogram data , then noisy transmission measurements at each bin was generated according to the statistical model :
| (13) |
where denotes the energy-specific incident X-ray intensity and is set to be and for high- and low -energy cases (i.e., 140 kVp, and 80 kVp), respectively. denotes the electronic background noise variance and is set to be 11(Ma et al 2012b).
Table 2.
Material types of the sub-regions in the phantom as shown in Fig. 1(a).
| Material | Density( ) | |
|---|---|---|
| 1 | Air | 0.00 |
| 2 | Average of soft tissue | 1.00 |
| 3 | Bone | 1.50 |
Table 3.
The comparison of scan geometry parameters for different experiments.
| Parameters | XCAT phantom study | Physical phantom study | Clinical data study |
|---|---|---|---|
| Projection views | 1160 | 984 | 984 |
| ChannelsPerView (bin) | 672 | 672 | 888 |
| DetectorBinSpace (mm) | 1.85 | 0.75 | 1.00 |
| DistanceSourceToDetector (mm) | 1361.20 | 1183.00 | 946.74 |
| DistanceSourceToCenter (mm) | 615.18 | 645.00 | 538.52 |
| SliceThickness (mm) | 0.625 | 3.000 | 0.625 |
2.5.2. Physical phantom study
In this study, the physical phantom (Fig. 1(b)) data were collected on a commercial CT scanner with two different tube potentials (90 and 120 kVp) at two noise level (282 and 56 mGs), respectively. Specifically, the detail scan protocols are listed in Table 4. A representative slice was specifically selected from the image volume to evaluate the presented PWLS-aviNLM algorithm. The phantom consists of a circular water background with the diameter of 15 cm, and eight large circular inserts, with detail information summarized in Table 5. In the study, the projection data were simulated by projecting the image into its sinogram domain with Siddon’s ray algorithm (Siddon 1985).
Table 4.
The detail scan protocol for the physical phantom.
| 120 kVp | 90 kVp | |||
|---|---|---|---|---|
|
| ||||
| Normal-Dose | Low-Dose | Normal-Dose | Low-Dose | |
| Exposure time (ms) | 1776 | 1776 | 1776 | 1776 |
| Tube current (mA) | 282 | 56 | 282 | 56 |
| CTDIvol (mGy) | 53.1 | 10.6 | 24.1 | 4.8 |
| Noise level ( ) | 0.012 | 1.682 | 0.034 | 2.328 |
Table 5.
Detail information for the inserts in the physical phantom.
| Material | Fomula | Gravity | Inserts |
|---|---|---|---|
| Acrylic | [C5H8O2] | 1.147 | B1 |
| DelrinTM | – | 1.368 | B2 |
| Teflon | [CF2] | 1.868 | B3,S2 |
| Air | N:0.78;O:0.21;Ar:0.01 | 0.000 | B4,B8,S1,S3,S4 |
| PMP | [C6H12(CH2)] | 0.858 | B5 |
| LDPE | [C2H4] | 0.945 | B6 |
| Polystyrece | [C8H8] | 0.998 | B7 |
To demonstrate the performance of the presented PWLS-aviNLM algorithm for low-dose DECT image reconstruction. The related scan geometry parameters are listed in Table 3. In the study, the DECT images at low noise level are selected as normal dose images which are served as ground truth.
2.5.3. Clinical data study
The clinical study was approved by the institutional review board, and written informed consent was obtained from the volunteer patient with coronary atherosclerotic plaques. The patient was scanned by the GE Discovery CT750 HD scanner with 600 mA and 281 ms (CTDIvol: 11.55 mGy). The related scan geometry parameters are listed in Table 3. The virtual monochromatic spectral (VMS) images were generated using the GE commercial software at 10 keV monochromatic energy level increments from 40–140 keV. In the study, the VMS images at 60 keV and 100 keV specifically selected as the DECT images. The low-dose DECT sinogram data were acquired using the similar simulation method in the study (Zeng et al 2015).
2.6. Performance evaluation
2.6.1. Noise reduction performance
To quantitatively evaluate the noise reduction performance of the presented PWLS-aviNLM algorithm, two metrics were utilized: (1) the peak signal-to-noise ratio (PSNR); and (2) the normalized mean square error (NMSE) :
| (14) |
| (15) |
where and represent the intensity value at the pixel k in the image μ and the ideal image , respectively. K denotes the number of image pixels, and represents the maximum intensity value of the ideal phantom image.
2.6.2. Modulation transfer function measure
In this study, to measure the spatial resolution of the DECT images reconstructed by the different algorithms, the modulation transfer function (MTF) in introduced. For the MTF computation, an edge spread function (ESF) was first obtained along the profile at one direction on the inserts (B3 and B4) in Fig. 1(b). The ESF was resampled using linear interpolation. The resampled ESF was averaged across multiple ESF realizations (measured at 3, 6, 9, and 12 o’clock positions) to yield the ensemble ESF aiming to reduce noise in ESF. Then, a line spread function (LSF) was estimate from the derivation of the ensemble ESF. The MTF could be obtained by applying the Fourier transformation of the LSF (Richard et al 2012).
2.6.3. Feature similarity index measure
To further quantify the improved accuracy obtained by the presented PWLS-aviNLM algorithm, the feature similarity (FSIM) index is employed. It is reported that the FSIM is a novel human-perception based metric with range of values from 0 to 1, which means a higher value indicating a better similarity between the estimated and reference DECT images (Zhang et al 2011).
2.7. Comparison methods
To evaluate the performance of the presented PWLS-aviNLM algorithm, the FBP algorithm with the ramp filter, the PWLS-TV algorithm and the PWLS-NLM algorithm were adopted for comparison. Specifically, the objective function of the PWLS-TV and PWLS-NLM algorithms can be written as follows:
| (16) |
For the PWLS-TV algorithm, the TV regularization term can be written as follows:
| (17) |
In addition, for the PWLS-NLM algorithm, the NLM regularization term can be written as follows:
| (18) |
For the two compared SIR algorithms, the penalty parameters are also tuned manually to achieve a good compromise between a low noise level and a high level of detail, and the iterative processes are finished when the results achieve the particular convergence criterion. Specifically, the selection for the NLM filter parameters (search-window , patch-window and scalar parameter h) for PWLS-NLM algorithm is similar to the PWLS-aviNLM algorithm introduced above.
3. Results
3.1. The XCAT phantom study
Fig. 2 shows the XCAT DECT images reconstructed by the different algorithms. The first column shows the digital phantom images, which were used as the ground truth images for comparison. The second column shows the low-dose DECT images reconstructed by the FBP algorithm, and severe noise-induced artifacts are presented. The last three columns show the low-dose DECT images reconstructed by the PWLS-TV, PWLS-NLM, and presented PWLS-aviNLM algorithms. It can be seen that the results from the SIR methods have noticeable gains relative to those from the standard FBP algorithm in terms of noise-induced artifact suppression. Some visibly obvious artifacts still exist in the PWLS-TV and PWLS-NLM reconstructed DECT images while the artifacts are basically eliminated in the PWLS-aviNLM reconstructed DECT images. To visualize the results in a better manner, the zoomed images of one selected region of interest (ROI) as indicated by the red rectangles are displayed in Fig. 3. The results further illustrate the gains obtained by the presented PWLS-aviNLM algorithm.
Figure 2.
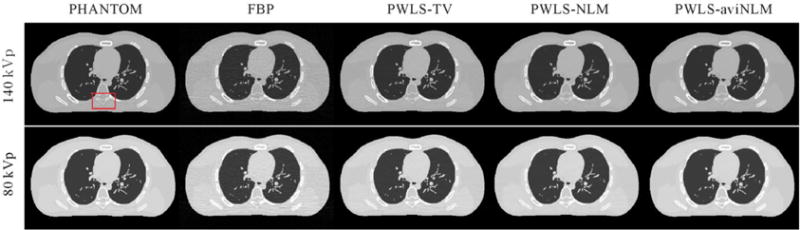
The XCAT DECT images reconstructed by the different algorithms. All the images are displayed in the same window.
Figure 3.

One zoomed region indicated by the red rectangle in Fig. 2. All the images are displayed in the same window.
Table 6 lists the PSNR and NMSE measurements of the DECT images reconstructed by four different algorithms. As expected, all the SIR algorithms exhibit significant gains over the FBP method in terms of the two measurements. Moreover, the presented PWLS-aviNLM algorithm yields an average of more than 10%, and 50% gains over the PWLS-TV and PWLS-NLM algorithms in terms of the PSNR and NMSE measurements on the DECT images, respectively. This can evidently demonstrate that the presented PWLS-aviNLM algorithm work best in noise-induced artifacts suppression among the four algorithms. In addition, Table 7 summarizes the FSIM scores of the DECT reconstructed images. We have the following observations: (1) All SIR algorithms yield better indices than the FBP algorithm in all the cases, implying that the SIR algorithms have a great potential to suppress noise-induced artifacts. (2) The presented PWLS-aviNLM algorithm has the highest FSIM scores in all the cases, indicating the high quality of the presented PWLS-aviNLM reconstructed DECT images. This is also consistent with our observations in visualization-based evaluation performed above. Therefore, the quantitative measurements illustrate that the presented PWLS-aviNLM algorithm has the best overall DECT image quality among all the algorithms.
Table 6.
The PSNR and NMSE measurements of the DECT images reconstructed by the different algorithms.
| Methods | 80kVp | 140kVp | ||
|---|---|---|---|---|
|
| ||||
| PSNR | NMSE(×10−3) | PSNR | NMSE(×10−3) | |
| FBP | 33.32 | 5.5 | 33.54 | 4.1 |
| PWLS-TV | 35.96 | 3.0 | 36.54 | 2.1 |
| PWLS-NLM | 35.23 | 3.6 | 35.19 | 2.8 |
| PWLS-aviNLM | 39.41 | 1.4 | 39.36 | 1.1 |
Table 7.
The FSIM measurements of the DECT images reconstructed by the different algorithms.
| FBP | PWLS-TV | PWLS-NLM | PWLS-aviNLM | |
|---|---|---|---|---|
| 80 kVp | 0.9643 | 0.9897 | 0.9875 | 0.9986 |
| 140kVp | 0.9726 | 0.9987 | 0.9985 | 0.9989 |
Fig. 4 shows the decomposed images of basis materials from the different algorithms wherein the bone and soft tissue were chosen as the basis materials (Soft tissue: Breast Tissue ICRU-44, 1.00 ; Bone: B-100 Bone-Equivalent Plastic, 1.50 ). In this study, the decomposed images of the basis materials are calculated from the DECT images via a direct inverse method (Heismann et al 2012). It can be seen that the noise level of the presented PWLS-aviNLM decomposed images is lowest, followed by the PWLS-NLM and PWLS-TV decomposed images wherein artifacts can be still observed. Moreover, Fig. 5 shows the mean and standard deviations (SD) values of the selected ROIs (i.e., ROI 1, and ROI 2) as indicated by the squares in Fig. 1(a) for the selective algorithms. From the results, it can be seen that the FBP algorithm has the greatest SD values in all the material, and generally the values decreases gradually from the PWLS-TV, PWLS-NLM, to the presented PWLS-aviNLM algorithm, indicating that the high quality PWLS-aviNLM reconstruction leads to excellent material decomposition results.
Figure 4.
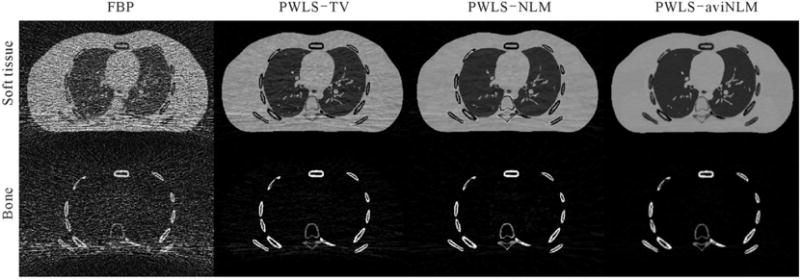
The material decomposition results from the XCAT phantom study. All the basic material images are displayed in the same window.
Figure 5.
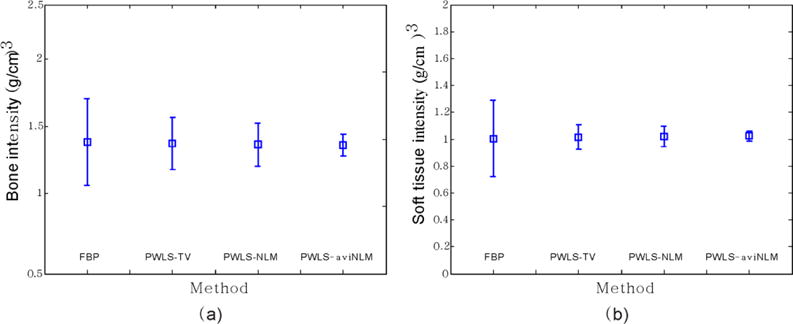
The comparison of basis material concentration obtained by the different algorithms. (a) Decomposed bone concentration as a function of the different algorithms. (b) Decomposed soft tissue concentration as a function of the different algorithms. The bone and soft tissue concentration during the simulation were 1.50 and 1.00 . The error bars represent the SD.
3.1. Physical phantom stud
Fig. 6 shows the physical phantom images reconstructed from low-dose DE projections by the different algorithms. As visualized in the figure, the low-dose DECT images reconstructed by the FBP algorithm suffer from severe noise-induced artifacts. Meanwhile, the SIR algorithms outperform FBP algorithm in terms of noise-induced artifacts suppression and the presented PWLS-aviNLM algorithm yields DECT images with superior quality, as shown in the zoomed-in ROIs indicated by the red boxes. Moreover, two ROIs (ROI A and ROI B) indicated by the boxes in Fig. 1(b) are selected to measure the contrast-to-noise ratio (CNR), which was used to estimate the detectability of objects within reconstructed images. The corresponding results are listed in Table 8. From the results, it can be observed that the presented PWLS-aviNLM algorithm can yield higher CNR values than the other three algorithms in all cases, which suggests the improvements dedicated by the presented PWLS-aviNLM algorithm.
Figure 6.

The physical phantom images reconstructed by the different algorithms from the DECT projection data. All the images are displayed in the same window.
Table 8.
The CNR measurements of the physical phantom images reconstructed by the different algorithms.
| Methods | 90 kVp | 120 kVp | ||
|---|---|---|---|---|
|
| ||||
| ROIA | ROIB | ROIA | ROIB | |
| FBP | 6.1735 | 2.4076 | 7.6481 | 2.7716 |
| PWLS-TV | 9.4489 | 6.6737 | 11.2703 | 7.3962 |
| PWLS-NLM | 8.3524 | 5.1791 | 10.0140 | 6.5013 |
| PWLS-aviNLM | 10.8970 | 9.3684 | 12.3086 | 9.7798 |
Fig. 7 shows the horizontal profiles through the centers of the inserts (B3 and B5) in the reconstructed DECT images. It can be observed that the presented PWLS-aviNLM algorithm generally appeared to produce profiles close to the ground truth as seen in the magnified views. The prior information from average image helps better adapt to the edge variation compared to other three algorithms. Moreover, Fig. 8 shows the MTFs obtained by the PWLS-TV, PWLS-NLM, and presented PWLS-aviNLM algorithms in both high and low contrast level from reconstructed DECT images. It can be observed that the PWLS-aviNLM algorithm can yield a better spatial resolution than the other two algorithms. The spatial resolution evaluations demonstrated that the presented PWLS-aviNLM algorithm can yield higher low-contrast detestability and noticeable edge-preservation in comparison with the other three algorithms.
Figure 7.
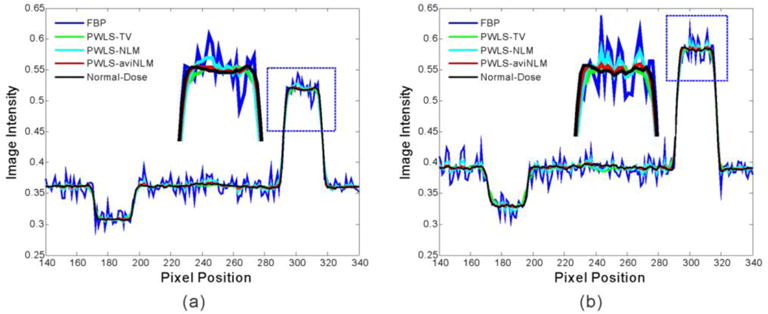
The horizontal profiles through the center of the teflon insert (B3) and the PMP insert (B5) in the reconstructed DECT images. (a) the profile of the 120 kVp; and (b) the profile of the 90kVp.
Figure 8.
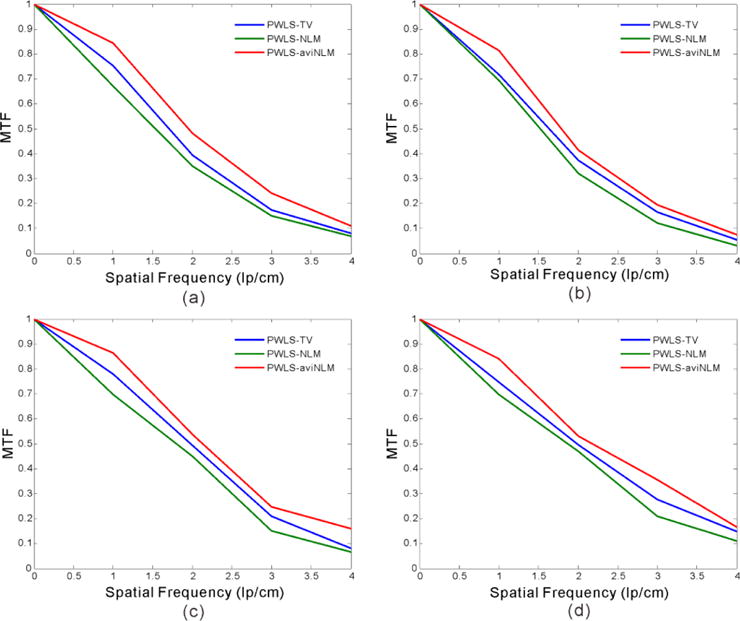
MTF curves obtained from the different algorithms at (a) 120 kVp in high contrast level (B3); (b) 120 kVp in low contrast level (B4); and (c) 90 kVp in high contrast level (B3) and (d) 90 kVp in low contrast level (B4).
Fig. 9 shows the material decomposition images by the different algorithms. In this study, the material decomposition images are yielded via a direct inverse method (Heismann et al 2012). From the results, it can be seen that the presented PWLS-aviNLM algorithm can provide the most accurate water and Teflon component among the four algorithms. In addition, it can be observed that some cupping artifacts occur in the basic material images, especially in the “water” images, which may be mainly caused by the beam hardening effects. To further quantitatively evaluate the decomposition results, the mean and SD values of ROI A in the decomposed Teflon images are computed and the corresponding results are depicted in Table 9.
Figure 9.
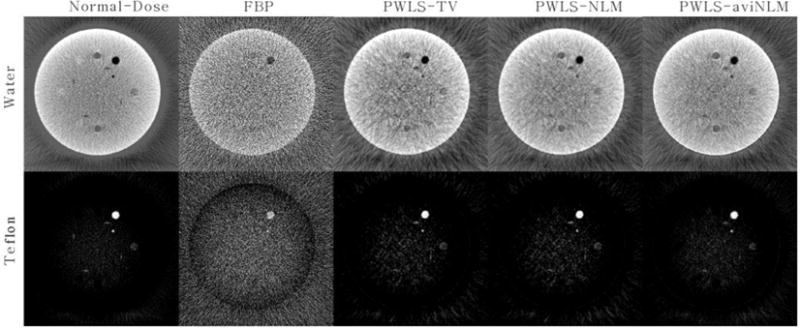
The material decomposition results from physical phantom study. All the basic material images are displayed in the same window.
Table 9.
The mean±SD measurements of ROI A in Fig. 1(b).
| FBP | PWLS-TV | PWLS-NLM | PWLS-aviNLM | Normal-Dose |
|---|---|---|---|---|
| 1.80±1.95 | 1.82±0.31 | 1.82±0.32 | 1.83±0.27 | 1.82±0.26 |
3.3. Clinical patient study
Fig. 10 shows the reconstructed images by the FBP, PWLS-TV, PWLS-NLM, and presented PWLS-aviNLM algorithms from low-dose DECT projection data. It can be seen that the three SIR algorithms have noticeable gains relative to the FBP algorithm in terms of the noise-induced artifacts suppression. From the zoom-in views of the detailed regions, it can also be seen that the presented PWLS-aviNLM algorithm outperforms the other two SIR algorithms on the fine structures reconstruction.
Figure 10.
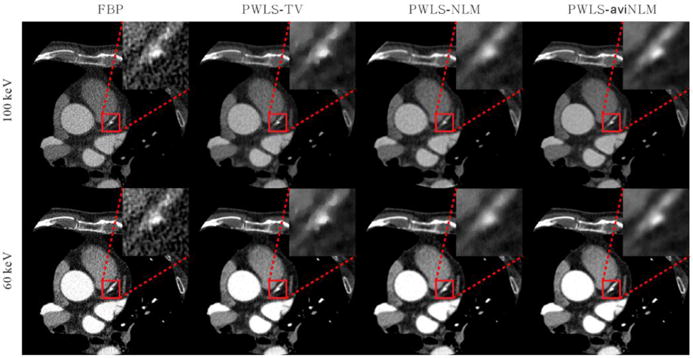
The patient data images reconstructed by the different algorithms. All the images are displayed in the same window.
Fig. 11 shows the VMS images generated from the DECT images reconstructed by different algorithms. Moreover, the zoomed images of the ROI indicated by red box are also displayed. From the results, it can be observed that the presented PWLS-aviNLM algorithm can yield the noticeable gains over the other three algorithms in terms of noise suppression and detail preservation of coronary atherosclerotic plaques in the VMS image.
Figure 11.
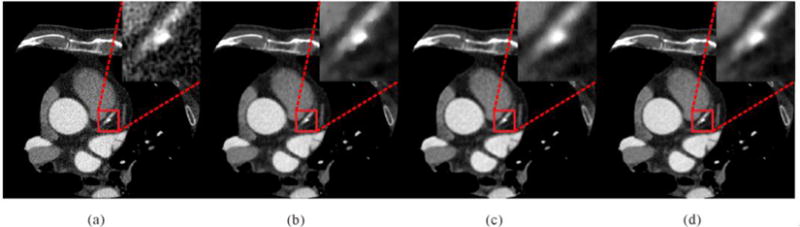
The VMS images (70 keV) generated from DECT images reconstructed by the different algorithms. (a) is from the FBP algorithm, (b) is from the PWLS-TV algorithm, (c) is from the PWLS-NLM algorithm, and (d) is from the presented PWLS-aviNLM algorithm. All the images are displayed in the same window.
To qualitatively evaluate the performances of the presented PWLS-aviNLM algorithm in a subjective manner, three radiologists with at least five years of experience in CT imaging were asked to score the VMS images in terms of noise reduction (NR), artifact suppression (AS), edge preservation (EP) and overall image quality (IQ). The four VMS images reconstructed by the different algorithms were displayed on the screen randomly, so it was a completely blind procedure for the radiologists. The scoring was done from 0 (worst) to 10 (best), and the corresponding scores are listed in Table 10. From the results, it can be seen that the presented PWLS-aviNLM algorithm can yield the highest scores among all the algorithms, indicating that the presented PWLS-aviNLM algorithm can generate high-quality VMS images. The results are consistent with the previous observations in both the XCAT phantom and physical phantom studies.
Table 10.
Subjective scores of the VMS images from the different algorithms.
| Methods | Radiologist 1
|
Radiologist 2
|
Radiologist 3
|
Summed Score
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NR | AS | EP | IQ | NR | AS | EP | IQ | NR | AS | EP | IQ | NR | AS | EP | IQ | |
| FBP | 1 | 2 | 5 | 2 | 3 | 3 | 5 | 3 | 5 | 5 | 5 | 5 | 9 | 10 | 15 | 10 |
| PWLS-TV | 4 | 3 | 5 | 4 | 7 | 6 | 4 | 5 | 6 | 6 | 5 | 6 | 17 | 15 | 14 | 15 |
| PWLS-NLM | 4 | 4 | 5 | 5 | 6 | 6 | 5 | 5 | 5 | 6 | 6 | 6 | 15 | 16 | 16 | 16 |
| PWLS-aviNLM | 7 | 8 | 6 | 6 | 8 | 8 | 6 | 7 | 7 | 7 | 6 | 7 | 22 | 23 | 18 | 20 |
4. Discussion
In this study, we proposed an iterative approach wherein an average image induced edge-preserving regularization is incorporated into the PWLS DECT reconstruction framework to reduce noise-induced artifacts in low dose DECT images. Specifically, the presented aviNLM regularization utilizes the redundancy information existing in the DECT data for it is reported that the measured DECT data both have geometrical self-similarities and are highly correlated between the two energies and the inter-image similarity is important prior knowledge for DECT images reconstruction. The experiments were conducted with the digital XCAT phantom, physical phantom and clinical patient data. The preliminary results presented in Section 3 demonstrated that the gains from the presented PWLS-aviNLM algorithm are remarkable compared with those from the PWLS-TV algorithm and PWLS-NLM in terms of qualitative and quantitative measurements. It is noted that the difference of the pixel value in the from that in the energy-specific image or could cause a slight loss of contrast in the component coefficient images.
There are ways in which the performance of the presented PWLS-aviNLM algorithm should be improved. One of these ways, as we have discussed previous in the paper, is to determine the algorithm parameters, namely the search-window, the patch-window, the control parameter and the hyper-parameter. Based on our previous studies (Ma et al 2012a, Zhang et al 2014b), the size of search-window and patch-window that are set in a reasonable range do not have noticeable effect on the resultant DECT images quality and the control parameter is set according to the scalar parameter that is determined by experiments. In addition, the determination of hyper-parameter is tuned manually to achieve a good tradeoff between noise and resolution in all the cases. It should be noted that the question, what a “good tradeoff” is, depends strongly on the task-specific cases and the preference of the observer. Thus, optimized parameters would be an interesting topic in the future study. Another way is that the mismatch between the DECT images should be taken into consideration. Although most DECT systems acquire the DECT data simultaneously in which tissue deformation is of minimal concern, somewhat motion effects may occur in the case of slow kVp switching (Zeng et al 2016a). Therefore, to obtain accurate material-specific images, some general motion correction procedures can be incorporated into the PWLS-aviNLM algorithm framework to mitigate the effects in the case of slow-kVp scanning. This can be another topic in our future research plan
In conclusion, we have developed a PWLS-aviNLM algorithmfor low-dose DECT image reconstruction. In the clinic, the presented PWLS-aviNLM algorithm can be stretched into various applications, such as photon-counting CT imaging (Zhang et al 2016a, Zeng et al 2016b, Yu et al 2016), 4D CT/CBCT imaging (Dang et al 2016), and perfusion imaging (Fang et al 2015, Zeng et al 2016c), where redundant information can be observed among image data. Also, the aviNLM-based idea could be possibly used to solve the metal artifacts reduction problem (i.e., degraded projection that might be truncated due to strong attenuation or streak artifacts around metallic objects), because the vast body of external knowledge can be globally searched in the domain of the already acquired medical CT images.
Table 1.
Abbreviations and acronyms.
| Acronym | Full Name | Acronym | Full Name |
|---|---|---|---|
| aviNLM | averaged image induced NLM-based | AS | artifact suppression |
| CDPE | polyethylene | CNR | contrast-to-noise ratio |
| DECT | dual energy computed tomography | EP | edge preservation |
| ESF | edge spread function | FBP | filtered backprojection |
| FSIM | feature similarity | IQ | image quality |
| LDPE | polyethylene | LSF | line spread function |
| MAP | maximum a posterior | MTF | modulation transfer function |
| NMSE | normalized mean square error | NLM | non-local means |
| NR | noise reduction | NLTV | nonlocal total variation |
| OSL | one-step-late | PICCS | prior image constrained compressed sensing |
| PMP | polymethylpentene | PSNR | peak signal-to-noise ratio |
| PWLS | penalized weighted least-squares | ROI | region of interest |
| SIR | statistical iterative reconstruction | TV | total variation |
| VMS | virtual monochromatic spectral | XCAT | extended cardiac-torso |
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant Nos. 81371544, 61571214, and 81501466, the Guangdong Natural Science Foundation under Grant Nos. 2015A030313271, and 2015A030310018, the Science and Technology Program of Guangdong, China under Grant No. 2015B020233008, the Science and Technology Program of Guangzhou, China under Grant No. 201510010039, the China Postdoctoral Science Foundation funded project under Grants Nos. 2016M602489 and 2016M602488, and the Scientific Research Foundation of Southern Medical University, Guangzhou, China under Grant No. CX2015N002. ZL was partially supported by the National Institutes of Health under Grant Nos. R01 CA143111 and R01 CA206171.
References
- Alvarez RE, Macovski A. Energy-selective reconstructions in X-ray computerised tomography. Phys Med Biol. 1976;21:733–744. doi: 10.1088/0031-9155/21/5/002. [DOI] [PubMed] [Google Scholar]
- Bouman C, Sauer K. A generalized Gaussian image model for edge-preserving MAP estimation. IEEE Trans Image Process. 1993;2:296–310. doi: 10.1109/83.236536. [DOI] [PubMed] [Google Scholar]
- Buades A, Coll B, Morel MJ. A review of image denoising algorithms, with a new one. Multiscale Model Simul. 2005;4:490–530. [Google Scholar]
- Clark DP, Badea CT. Spectral diffusion: an algorithm for robust material decomposition of spectral CT data. Phys Med Biol. 2014;59:6445–6466. doi: 10.1088/0031-9155/59/21/6445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong X, Niu T, Zhu L. Combined iterative reconstruction and image-domain decomposition for dual energy CT using total-variation regularization. Med Phys. 2014;41:051909(9pp.). doi: 10.1118/1.4870375. [DOI] [PubMed] [Google Scholar]
- Dang J, Yin F, You T, Dai C, Chen D, Wang J. Simultaneous 4D-CBCT reconstruction with sliding motion constraint. Med Phys. 2016;43:5453–5463. doi: 10.1118/1.4959998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang R, Zhang S, Chen T, Sanelli P. Robust low-dose CT perfusion deconvolution via tensor 439 total-variation regularization. IEEE Trans Med Imaging. 2015;34:1533–1548. doi: 10.1109/TMI.2015.2405015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heismann BJ, Schmidt BT, Flohr T. Spectral Computed Tomography. SPIE press; 2012. [Google Scholar]
- Johnson TR, Krauss B, Sedlmair M, Grasruck M, Bruder H, Morhard D, Fink C, Weckbach S, Lenhard M, Schmidt B, Flohr T, Reiser MF, Becker CR. Material differentiation by dual energy CT: initial experience. Eur Radiol. 2007;17:1510–1517. doi: 10.1007/s00330-006-0517-6. [DOI] [PubMed] [Google Scholar]
- Kalender WA, Klotz E, Kostaridou L. An algorithm for noise suppression in dual energy CT material density images. IEEE Trans Med Imaging. 1988;7:218–224. doi: 10.1109/42.7785. [DOI] [PubMed] [Google Scholar]
- Leng S, Yu L, Wang J, Fletcher JG, Mistretta CA, McCollough CH. Noise reduction in spectral CT: Reducing dose and breaking the trade-off between image noise and energy bin selection. Med Phys. 2011;38:4946–4957. doi: 10.1118/1.3609097. [DOI] [PubMed] [Google Scholar]
- Long Y, Fessler JA. Multi-material decomposition using statistical image Reconstruction for spectral CT. IEEE Trans Med Imaging. 2014;33:1614–1626. doi: 10.1109/TMI.2014.2320284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Huy Q, Molloi S. Least squares parameter estimation methods for material decomposition with energy discriminating detectors. Med Phys. 2011;38:245–255. doi: 10.1118/1.3525840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Ding H, Molloi S, Zhang X, Gao H. TICMR: Total Image Constrained Material Reconstruction via nonlocal total variation regularization for spectral CT. IEEE Trans Med Imaging. 2016;35:2578–2586. doi: 10.1109/TMI.2016.2587661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Ma J, Gao H, Huang Y, Liang J, Feng ZQ, Chen W. Iterative image reconstruction for cerebral perfusion CT using a pre-contrast scan induced edge-preserving prior. Phys Med Biol. 2012a;57:7519–7542. doi: 10.1088/0031-9155/57/22/7519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang Ma J, Fan Z, Liu Y, Huang Y, Chen JW, Lu H. Variance analysis of x-ray CT sinograms in the presence of electronic noise background. Med Phys. 2012b;39:4051–4065. doi: 10.1118/1.4722751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu T, Dong X, Petrongolo M, Zhu L. Iterative image-domain decomposition for dual-energy CT. Med Phys. 2014;41041901:463. doi: 10.1118/1.4866386. [DOI] [PubMed] [Google Scholar]
- Noh J, Fessler JA, Kinahan PE. Statistical sinogram restoration in dual-energy CT for PET attenuation correction. IEEE Trans Med Imaging. 2009;28:1688–1702. doi: 10.1109/TMI.2009.2018283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrongolo M, Zhu L. Noise suppression for dual-energy CT through entropy minimization. IEEE Trans Med Imaging. 2015;34:2286–2297. doi: 10.1109/TMI.2015.2429000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruzsics B, Schwarz F, Schoepf UJ, Lee YS, Bastarrika G, Chiaramida SA, Costello P, Zwerner PL. Comparison of dual-energy computed tomography of the heart with single photon emission computed tomography for assessment of coronary artery stenosis and of the myocardial blood supply. Am J Cardiol. 2009;104:318–326. doi: 10.1016/j.amjcard.2009.03.051. [DOI] [PubMed] [Google Scholar]
- Rutherford RA, Pullan BR, Isherwood I. Measurement of effective atomic number and electron density using an EMI scanner. Neuroradiology. 1976;11:15–21. doi: 10.1007/BF00327253. [DOI] [PubMed] [Google Scholar]
- Richard S, Husarik DB, Yadava G, Murphy SN, Samei E. Towards task-based assessment of CT performance: System and object MTF across different reconstruction algorithms. Med Phys. 2012;39:4115–4122. doi: 10.1118/1.4725171. [DOI] [PubMed] [Google Scholar]
- Sukovic P, Clinthorne NH. Penalized weighted least-squares image reconstruction for dual energy X-ray transmission tomography. IEEE Trans Med Imaging. 2000;19:1075–1081. doi: 10.1109/42.896783. [DOI] [PubMed] [Google Scholar]
- Szczykutowicz TP, Chen GH. Dual energy CT using slow kVp switching acquisition and prior image constrained compressed sensing. Phy Med Biol. 2011;55:6411–6429. doi: 10.1088/0031-9155/55/21/005. [DOI] [PubMed] [Google Scholar]
- Sullivan B, Chang HC. A generalized Landweber iteration for ill-conditioned signal restoration. Proc IEEE Acoustics, Speech, and Signal Processing. 1991;3:1729–1732. [Google Scholar]
- Shikhaliev PM. Beam hardening artefacts in computed tomography with photon counting, charge integrating and energy weighting detectors: a simulation study. Phys Med Biol. 2005;50:5813–5827. doi: 10.1088/0031-9155/50/24/004. [DOI] [PubMed] [Google Scholar]
- Siddon RL. Fast calculation of the exact radiological path of a three-dimensional CT array. Med Phys. 1985;12:252–255. doi: 10.1118/1.595715. [DOI] [PubMed] [Google Scholar]
- Warp RJ, Dobbins JT. Quantitative evaluation of noise reduction strategies in dual-energy imaging. Med Phys. 2003;30:190–198. doi: 10.1118/1.1538232. [DOI] [PubMed] [Google Scholar]
- Yu Z, Leng S, Li Z, McCollough CH. Spectral prior image constrained compressed sensing (spectral PICCS) for photon-counting computed tomography. Phys Med Biol. 2016;61:6707–6732. doi: 10.1088/0031-9155/61/18/6707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Thibault JB, Bouman CA, Sauer KD, Hsieh J. 2014 Model-based iterative reconstruction for dual-energy X-Ray CT using a joint quadratic likelihood model. IEEE Trans Med Imaging. 33:117–134. 492. doi: 10.1109/TMI.2013.2282370. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Xi Y, Song Q, Cong W, Zhou J, Wang G. Spectral CT reconstruction with image sparsity and spectral mean. IEEE Trans Comput Imaging. 2016a:P 1–1. doi: 10.1109/TCI.2016.2609414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Han H, Liang Z, Hu Y, Liu Y, Moore W, Ma J, Lu H. Extracting information from previous full-dose CT scan for knowledge-based Bayesian reconstruction of current low-dose CT images. IEEE Trans Med Imaging. 2016b;35:860–870. doi: 10.1109/TMI.2015.2498148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Huang J, Ma J, Bian Z, Feng Q, Lu H, Liang Z, Chen W. Iterative reconstruction for X-Ray computed tomography using prior-image induced nonlocal regularization. IEEE Trans Biomed Eng. 2014a;61:2367–2378. 500. doi: 10.1109/TBME.2013.2287244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Ma J, Wang J, Liu Y, Lu H, Liang Z. Statistical image reconstruction for low-dose CT using nonlocal means-based regularization. Comput Med Imaging Graph. 2014b;38:423–435. doi: 10.1016/j.compmedimag.2014.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Han H, Wang J, Ma J, Liu Y, Moore W, Liang Z. Deriving adaptive MRF coefficients from previous normal-dose CT scan for low-dose image reconstruction via penalized weighted least-squares minimization. Med Phys. 2014c;41:041916(14pp.). doi: 10.1118/1.4869160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Zhang L, Mou X, Zhang D. FSIM: a feature similarity index for image quality assessment. IEEE Trans Image Process. 2011;20:2378–2386. doi: 10.1109/TIP.2011.2109730. [DOI] [PubMed] [Google Scholar]
- Zeng D, Huang J, Bian Z, Niu S, Zhang H, Feng Q, Liang Z, Ma J. A simple low-dose X-Ray CT simulation from high-dose scan. IEEE Trans Nucl Sci. 2015;62:2226–2233. doi: 10.1109/TNS.2015.2467219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng D, Huang J, Zhang H, Bian Z, Niu S, Zhang Z, Feng Q, Chen W, Ma J. Spectral CT image restoration via an average image-induced nonlocal means filter. IEEE Trans Biomed Eng. 2016a;63:1044–1057. doi: 10.1109/TBME.2015.2476371. [DOI] [PubMed] [Google Scholar]
- Zeng D, Gao Y, Huang J, Bian Z, Zhang H, Lu L, Ma J. Penalized weighted least-squares approach for multienergy computed tomography image reconstruction via structure tensor total variation regularization. Comput Med Imaging Graph. 2016b;53:19–29. doi: 10.1016/j.compmedimag.2016.07.002. [DOI] [PubMed] [Google Scholar]
- Zeng D, Zhang X, Bian Z, Huang J, Zhang H, Lu L, Lyu W, Zhang J, Feng Q, Chen W, Ma J. Cerebral perfusion computed tomography deconvolution via structure tensor total variation regularization. Med Phys. 2016c;43:2091–2107. doi: 10.1118/1.4944866. [DOI] [PubMed] [Google Scholar]


