Reanalysis reveals flaws in the original phylogenomic evidence for two ancestral whole-genome duplications in plants.
Keywords: Plant polyploidy, whole genome duplication, molecular dating, BEAST, r8s, Phylogenomics, Genome evolution
Abstract
Whole-genome duplications (WGDs) or polyploidy events have been studied extensively in plants. In a now widely cited paper, Jiao et al. presented evidence for two ancient, ancestral plant WGDs predating the origin of flowering and seed plants, respectively. This finding was based primarily on a bimodal age distribution of gene duplication events obtained from molecular dating of almost 800 phylogenetic gene trees. We reanalyzed the phylogenomic data of Jiao et al. and found that the strong bimodality of the age distribution may be the result of technical and methodological issues and may hence not be a “true” signal of two WGD events. By using a state-of-the-art molecular dating algorithm, we demonstrate that the reported bimodal age distribution is not robust and should be interpreted with caution. Thus, there exists little evidence for two ancient WGDs in plants from phylogenomic dating.
INTRODUCTION
Whole-genome duplications (WGDs) have played important roles during land plant evolution. There is overwhelming evidence that all eudicots share an ancient WGD event (1), termed γ, and some evidence that most monocots share one ancient WGD event as well (2), termed τ. Many plant lineages have also undergone more recent polyploidy events (3, 4). In addition, using a phylogenomic approach, Jiao et al. (5) reported ancient genome duplications in plants that occurred before the divergence of monocots and eudicots. The study presented three major lines of evidence to support the conclusion of two ancient WGDs: one shared by all extant angiosperms and an even older one shared by all extant seed plants.
First, Jiao et al. (5) analyzed almost 800 gene trees that contained patterns of ancient gene duplications and found these duplications to fall mainly into two sets. Gene duplications in the first set occurred in the common ancestor of seed plants (53% of all gene duplications), and gene duplications in the other set occurred in the common ancestor of angiosperms (44%). Only a few of all identified gene duplications seemed to have occurred after the divergence of basal angiosperms (3%). Notably, this analysis indicated only the general evolutionary time frame within which any of the gene duplications in the two sets may have occurred, that is, sometime between the divergence of lycophytes and the divergence of gymnosperms and sometime between the divergence of gymnosperms and the divergence of angiosperms, respectively. These data are not necessarily indicative of polyploidy events because they do not contain any information on whether the gene duplications clustered in time during these two long intervals of ~100 million years or more each. Accordingly, Jiao et al. (5) stated that “several mechanisms could explain the […] patterns of gene duplication revealed in the gene trees, including WGD or multiple segmental or chromosomal duplications” (5). Any combination of these mechanisms would also be a possibility. Second, enrichment of functional categories that are known to be retained after WGDs was prominent in the ~800 gene trees (5). Although this provides circumstantial support for WGD, it certainly does not allow one to distinguish between one, two, or more WGD events.
Finally, Jiao et al. (5) performed molecular dating of the ~800 gene trees to analyze whether these ancient gene duplications had occurred simultaneously. The gene trees were calibrated by assigning age constraints to certain nodes that correspond to known evolutionary events. The study used age constraints of 400 to 450 million years ago (Ma) for the split of bryophytes and tracheophytes (designated as the AL node), exactly 400 Ma for the split of lycophytes and euphyllophytes (PL node), 125 to 150 Ma for the split of monocots (M) and eudicots (E) (ME node), and a maximum of 125 Ma for the split of rosids within eudicots (RO node) (Fig. 1); at most, one of each of these nodes in a tree was calibrated. Using these calibration dates, the ages of nodes representing ancestral gene duplications (situated between the PL and ME nodes) were estimated by molecular clock algorithms. Jiao et al. (5) found a strongly bimodal distribution of gene duplication ages with two separate peaks at about 319 and 192 Ma. This clustering of the estimated ages of gene duplications conclusively provided strong support for two ancient WGD events, indicating a WGD in the common ancestor of all seed plants and a subsequent WGD in the common ancestor of all angiosperms, respectively.
Fig. 1. Duplication and calibration nodes in the phylogenetic gene tree topologies.
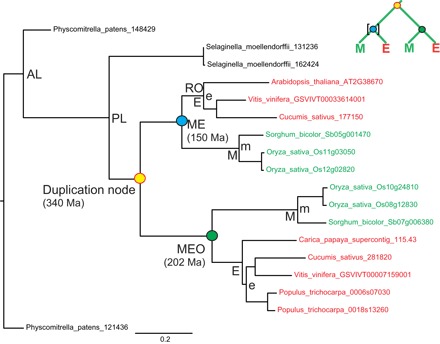
Example of a gene tree with (ME)(ME) topology, tree RAxML_1111 from Jiao et al. (5), in which both paralogs were retained in both monocots (M) and eudicots (E) after the duplication event. Age estimates of nodes were extracted from the original r8s output file of Jiao et al. (5) and are given in parentheses for colored nodes. The nodes for the split of bryophytes (AL node), lycophytes (PL node), monocots and eudicots (ME and MEO nodes), and rosids (RO node) were also extracted from the original r8s output file. The green MEO node was the uncalibrated ME node in the r8s analysis of Jiao et al. (5) (indicated by the absence of square brackets in the small schematic tree at the top right). M and E nodes represent the crown nodes of monocots and eudicots, respectively. m and e nodes are additional calibration nodes that were used when testing the potentially too young upper constraint for the ME nodes (see Methods for details). Examples of gene trees with (ME)(M) and (ME)(E) topologies can be found in fig. S1
In the context of a related project, we reanalyzed the data from Jiao et al. (5). Surprisingly, we found that the conspicuous bimodality of the age distribution was likely due to technical issues. Moreover, we were unable to reproduce this result of Jiao et al. (5) using a different molecular dating algorithm.
RESULTS
Using data provided by Jiao et al. (5), we were able to reproduce the bimodal age distribution of gene duplications (Fig. 2A). This distribution was supported by two distinct classes of topologies of the gene (sub)trees composed of a gene duplication node and its two child clades: (i) Both paralogs were retained in both monocots (M) and eudicots (E), referred to as topology (ME)(ME) (Fig. 1) or (ii) a paralog was lost in either all monocots or all eudicots, referred to as topologies (ME)(E) and (ME)(M), respectively (fig. S1). Our first observation was that Jiao et al. (5) calibrated only one of the two child clades, that is, one of the two ME nodes, in the (ME)(ME) trees. Notably, the dating algorithm had estimated most (85%) of these calibrated ME nodes at exactly 150 Ma (Fig. 2B), which is the upper age limit of the calibration range, suggesting that this age for the upper limit of the ME node was too young. The ages of the other uncalibrated ME node (hereafter named MEO node) in the (ME)(ME) trees were instead estimated without age constraints by the molecular clock analysis. This parameterization resulted in much older age estimates of the MEO nodes, which showed a broad age distribution with a peak at ~220 Ma, and was thus estimated on average ~70 million years older than the calibrated ME nodes (Fig. 2B). This was surprising because the ME and MEO nodes should represent the same evolutionary event in a tree, that is, the divergence of monocots and eudicots, and thus should have very similar date estimates.
Fig. 2. The two duplication peaks correspond to two distinct classes of gene tree topologies.
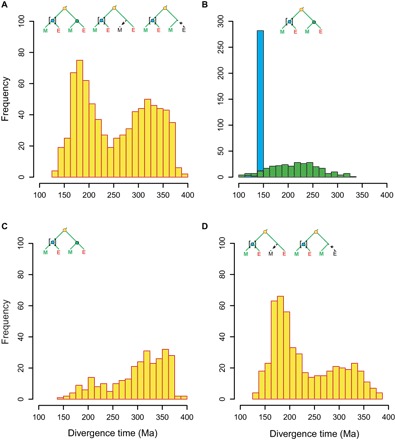
Age estimates of nodes were extracted from the original r8s output file of Jiao et al. (5). (A) Age estimates of gene duplication nodes in all trees (n = 777). (B) Age estimates of ME nodes (blue) and MEO nodes (green) in (ME)(ME) trees (n = 283). (C) Age estimates of gene duplication nodes in (ME)(ME) trees (n = 283). (D) Age estimates of gene duplication nodes in (ME)(E) and (ME)(M) trees (n = 494). In all panels, the small schematic trees illustrate the general topology of the corresponding trees with color of nodes matching color of age estimates showed in the histograms (yellow circle indicates the gene duplication node; blue and green circles indicate ME and MEO nodes, respectively). Square brackets indicate which node/clade had been calibrated.
Jiao et al. (5) deduced that the younger of the two WGD events occurred ~192 Ma, and thus occurred before the ME split. However, many of the MEO nodes, contradictorily, were estimated to be considerably older (~220 Ma; Fig. 2B) than this inferred WGD event. Therefore, we hypothesized that gene duplication age estimates in the (ME)(ME) trees might be skewed toward older ages beyond the age distribution of MEO nodes. We found a strong bias toward older estimated gene duplication ages (~300 to 370 Ma) in the (ME)(ME) trees (Fig. 2C, also compared to the MEO node distribution in Fig. 2B). These older estimates coincided with the inferred dates (~319 Ma) of the more ancient WGD (5). In contrast, we found a skew toward younger gene duplication age estimates in the (ME)(M) and (ME)(E) trees (~160 to 220 Ma; Fig. 2D and fig. S2, A and B), and these younger estimates coincided with the predicted more recent WGD inferred at ~192 Ma (5). These data showed that two different classes of gene tree topologies, that is, (ME)(ME) versus (ME)(M)/(ME)(E), could, to a large extent, explain the bimodality in the age distribution of gene duplication nodes in the study of Jiao et al. (5).
Jiao et al. (5) used the molecular dating program r8s, which uses branch lengths in a phylogenetic tree to estimate absolute dates for the tree nodes (6). We reanalyzed the original data using BEAST, a widely used Bayesian molecular dating algorithm that includes sequence alignments in the analysis (7). Using the same calibration constraints as Jiao et al. (5), our BEAST analysis showed a gene duplication peak at ~300 Ma for the (ME)(ME) trees and at ~210 Ma for the (ME)(M) and (ME)(E) trees (Fig. 3, A and B). Although the peaks shifted somewhat closer together (Fig. 3C), BEAST showed a similar pattern compared to the dating results of Jiao et al. (5). Consistent with r8s, BEAST estimated the ages of the uncalibrated MEO node also at ~220 Ma (fig. S3A), which, similar to the r8s analyses (5), might have skewed the duplication ages in the (ME)(ME) trees to older estimates.
Fig. 3. Distribution of gene duplication estimates using BEAST for phylogenomic dating.
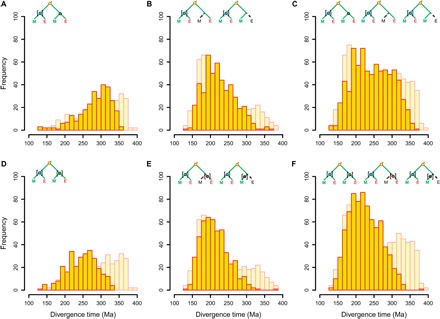
Top row: Age estimates of gene duplication nodes in trees with calibration of only one ME node [the same as in Jiao et al. (5); illustrated by blue node with square brackets in small schematic trees]. (A) Age estimates in (ME)(ME) trees (n = 285). (B) Age estimates in (ME)(E) and (ME)(M) trees (n = 487). (C) Age estimates in all trees (n = 772). Bottom row: Age estimates of gene duplication nodes in trees with calibration of both child nodes of a gene duplication node (illustrated by colored nodes with square brackets in small schematic trees). (D) Age estimates in (ME)(ME) trees; calibration of both ME and MEO nodes (n = 285). (E) Age estimates in (ME)(E) and (ME)(M) trees; calibration of both ME and E or M nodes (if this node exists), respectively (n = 487). (F) Age estimates in all trees; calibration of both ME and MEO, E, or M nodes (n = 772). For comparison, the distribution of the original data of Jiao et al. (5) is given in light yellow in the background. In all panels, the small schematic trees illustrate the general topology of the corresponding trees (yellow circle indicates the gene duplication node). Square brackets indicate which node/clade has been calibrated.
To address the presumed problem of an uncalibrated MEO node, we applied the calibration constraint of the ME node to both the ME and MEO nodes in the (ME)(ME) trees—that is, we calibrated both child clades of a gene duplication node. This new set of BEAST analyses resulted in a substantial shift of the gene duplication age estimates in the (ME)(ME) trees from ~300 to ~250 Ma (Fig. 3D and fig. S4), indicating that the calibration of only one of the two ME nodes caused a skew in duplication ages in the (ME)(ME) trees. Similarly, we also calibrated the second non-(ME) child clade of a gene duplication node in (ME)(M) and (ME)(E) trees by introducing an additional calibration node, that is, an M node in the (M) clade or an E node in the (E) clade, respectively (see Fig. 1 and the Supplementary Materials for details). This also caused a shift of the gene duplication age estimates, albeit only a minor one, from ~210 to ~200 Ma (Fig. 3E and fig. S4). The calibration of both child nodes of a gene duplication node consequently moved the age distributions of gene duplications from the two classes of gene tree topologies much closer together. Thus, the strong bimodal age distribution of gene duplications observed by Jiao et al. (5) (Fig. 2A) was no longer evident when using BEAST with stricter, more coherent calibration constraints (Fig. 3F, tables S1 and S2, and fig. S5).
To examine the effect of the potentially too young age for the upper limit of the calibration constraint on the ME node(s), we conducted an additional analysis using BEAST. We removed the age constraints on all ME node(s) in all trees and instead used new alternative calibrations on younger nodes within all monocot (M) and eudicot (E) child clades of a gene duplication or ME node (see Methods). This resulted in a shift of gene duplication age estimates for all trees to ~300 Ma, again without support for a clear bimodal distribution [fig. S6A; (ME)(ME) trees alone, ~320 Ma, fig. S6B; (ME)(M)/(ME)(E) trees alone, ~280 Ma, fig. S6C]. Age estimates of the ME nodes (now all uncalibrated in the entire set of gene trees) peaked again at ~220 Ma (fig. S6D). These data indicated that the calibration constraints for the ME node(s) only affected the timing and not the distribution of the gene duplication age estimates.
DISCUSSION
The study of Jiao et al. (5) represented a landmark for the investigation of ancient polyploidy events in plants. However, we show here that their main evidence in support of two ancient WGD events in early angiosperm and seed plant evolution—a clear bimodal age distribution of gene duplications—should be interpreted with caution and is likely caused by technical issues in the phylogenomic dating analysis.
In most of our reanalysis of the data of Jiao et al. (5) using BEAST, we deliberately kept age constraints and calibration parameters as close as possible to the ones used by Jiao et al. (5) for r8s to be able to directly compare the results between both phylogenetic software tools and particularly to assess the effects of the uncalibrated MEO node. We did not attempt to provide a better molecular dating of these ancient plant gene duplications, nor do we claim that our analysis provides clear evidence for only one ancestral plant WGD as opposed to two or more. Great care needs to be taken in any phylogenomic dating study, especially if ancient evolutionary events are being investigated. Thus, a better dating analysis should ideally examine the effects of varying age constraints and calibrations (for example, uniform versus nonuniform prior distributions and their parameters), as well as the models and methods of the molecular clock (for example, with regard to handling rate variations among branches, which are likely present here, given the tremendous evolutionary distances involved, and fixed versus estimated gene tree topologies), and then carefully summarize and interpret these results (8–10). As we show for the upper age limit of the constraint on the ME nodes, calibration settings can strongly influence the estimated timing of events in the trees. Similarly, arguments can be made whether the other calibrations used by Jiao et al. (5), and therefore also by us, and their characteristics are the most appropriate. For example, the fixed-point constraint of 400 Ma used by Jiao et al. (5) for the PL node (the split of lycophytes and euphyllophytes) may be too young and strict. Fossil evidence supports a minimum age constraint for this node of at least 416 Ma, and estimated node ages range up to 446 Ma (11–13). Furthermore, we believe that the inclusion of high-quality gymnosperm and early diverging angiosperm genomes will likely be crucial to resolve the number and timing of ancestral plant WGD events.
Note that, since the publication of the study of Jiao et al. (5), there have been some additional claims in support for ancient WGDs predating the origin of flowering plants. For instance, synteny analysis of the genome of the early diverging angiosperm Amborella trichopoda unveiled evidence for one WGD event before the origin of angiosperms (14). A second WGD event could only be identified using the same phylogenomic dating approach as in the study of Jiao et al. (5), which, according to the described methods of the Amborella Genome Project (14), may have suffered from the same technical issues raised here. Based largely on the assumption of two WGDs, the WGD derived from the synteny data was then placed into the common ancestor of angiosperms (14); our analyses potentially question this timing and phylogenetic placement (see the Supplementary Materials for a detailed discussion). In another recent study, analysis of Ks-based paralog age distributions of several gymnosperms combined with a novel approach based on gene tree reconciliation showed putative evidence for an ancestral seed plant WGD (15). However, the study did not include analyses of any (ancestral) angiosperm duplication events, that is, events after the divergence of gymnosperms and angiosperms (15). Thus, this study also did not provide evidence for both the polyploidy events proposed by Jiao et al. (5).
In conclusion, although there is quite some evidence from different sources that ancient WGDs have occurred in the early evolution of seed plants, we feel that it is premature to conclude the exact number, timing, and phylogenetic position of these ancient duplications. A careful and detailed molecular clock analysis and well-assembled genome sequences with high-quality annotations from early diverging angiosperms and different gymnosperms, providing structural evidence on intra- and interspecies collinearity, are probably key to settling this issue.
METHODS
The original r8s output file was provided on request by Jiao et al. (5). For all individual gene trees, the age estimates of nodes of interest and the location of the AL, PL, ME, and RO nodes were manually extracted from this r8s output file. Unmarked duplication and MEO nodes were inferred with some guidance by Y. Jiao, the author who conducted the original analysis.
BEAST analysis
Dating of each gene tree was conducted with BEAST (v1.7.4) (7) using the original alignments and gene trees published by Jiao et al. (5) and the original calibrations on the same nodes as extracted from the r8s output file (unless indicated otherwise, see below) (5). BEAST was configured and run as described in detail by Vanneste et al. (4) using an uncorrelated relaxed clock model (UCLD) (16) and an LG+G (four rate categories) evolutionary model. The number of trees dated with BEAST (n = 722) was slightly lower than the ones dated by Jiao et al. (5) using r8s (n = 779) because several trees did not fulfill the minimal criteria for duplication nodes, as described by Jiao et al. (5). Although Jiao et al. (5) dated more than one gene duplication in a small number of trees, we only dated one gene duplication per tree, because it was unclear which nodes Jiao et al. (5) used for scoring the second duplication in these trees. We used three different sets of prior calibrations: (i) same age constraints as in Jiao et al. (5), that is, a uniform 400- to 450-Ma calibration prior on the AL node, a uniform 399.5- to 400.5-Ma calibration prior on the PL node, a uniform 125- to 150-Ma calibration prior on the ME node, and a uniform 0- to 125-Ma calibration prior on the RO node; (ii) all the calibration priors above, plus an additional uniform 125- to 150-Ma calibration prior on the MEO node in (ME)(ME) trees, an additional uniform 0- to 70-Ma calibration prior on the M node, the non-ME child node of a gene duplication node in (ME)(M) trees [if this node existed because some (M) clades only consisted of a single monocot gene], and an additional uniform 0- to 125-Ma calibration prior on the E node, the non-ME child node of a gene duplication node in (ME)(E) trees [if this node existed because some (E) clades only consisted of a single eudicot gene]; and (iii) no age constraints on the ME and MEO nodes but instead constraints on nodes within all (M) and (E) clades in a tree [including the (M) and (E) child clades of ME and MEO nodes]: a uniform 400- to 450-Ma calibration prior on the AL node, a uniform 399.5- to 400.5-Ma calibration prior on the PL node, uniform 0- to 125-Ma calibration priors on a node in each of the (E) clades (e nodes, similar but not identical to an RO node; see below for a detailed definition of these nodes), and uniform 0- to 70-Ma calibration priors on a node in each of the (M) clades (m nodes; see below for a detailed definition of these nodes). BEAST starting trees with branch lengths satisfying all of the prior constraints were automatically constructed.
We ran one set of BEAST analyses for each of the three prior calibration sets above. For the first two sets, all 772 trees were used, but the third set was run on a smaller subset of 455 trees for the following reasons. This set was defined by no calibration priors on any of the ME and MEO nodes and thus required substitute calibration priors. Because the results of the first two sets highlighted the importance of calibrating both child clades of a gene duplication node, we decided to calibrate one node within each of the existing (M) and (E) clades, that is, four substitute calibration nodes in (ME)(ME) trees and three substitute calibration nodes in (ME)(M) and (ME)(E) trees. To avoid any bias in choosing nodes between these clades, we algorithmically specified m and e nodes: m nodes were required to specify a clade with two to four genes that had at least one gene from each of the two monocot species (Oryza sativa and Sorghum bicolor), and e nodes were required to specify a clade with two to four genes that had at least one gene from at least two different eudicot species each (see fig. S1 for examples). In addition, we required that all (M) clades only contained monocot genes and all (E) clades only contained eudicot genes [surprisingly, this was not always given in the original trees (5)]. Any tree that did not match all of the above criteria was excluded, such as trees that had less than two genes in any of the (M) or (E) clades, resulting in the smaller subset of 455 trees. We note that the subset of age estimates of gene duplications from the original data set of Jiao et al. (5), including only estimates from these 455 trees, retained the bimodal distribution; however, the younger peak was more strongly reduced than the older peak (see light yellow background distribution in fig. S6A).
Contrary to common procedures in BEAST analyses, where molecular datings of trees are accepted only if the minimum effective sample size (ESS) for all statistics is higher than a certain value (commonly ≥200), we accepted and plotted age estimates for all trees to be able to compare the BEAST results against the original r8s results (5). Excluding all trees that had an ESS lower than 200 for any of the statistics gave, however, qualitatively similar results, that is, there seemed to be no marked bias in gene tree topology or gene duplication age estimate among the trees that were excluded [242 (~31%) of the trees in the BEAST data set with ME node calibration only (Fig. 3C and fig. S5B) had an ESS < 200; 230 (~30%) of the trees in the BEAST data set with ME node and MEO, E, or M node calibrations (Fig. 3F and fig. S5C) had an ESS < 200; and 126 (~28%) of the trees in the BEAST data set without ME and MEO node calibrations (figs. 6A and 5D) had an ESS < 200].
Supplementary Material
Acknowledgments
We want to thank V. Storme for the assistance with the statistical analyses of modality. Funding: Y.V.d.P. acknowledges the Multidisciplinary Research Partnership “Bioinformatics: From nucleotides to networks” Project (no. 01MR0310W) of Ghent University and funding from the European Union Seventh Framework Programme (FP7/2007-2013) under European Research Council advanced grant agreement 322739–DOUBLEUP. S.P. was funded by a R@MAP Professorship at University of Melbourne and an Australian Research Council FT grant (FT160100218). Author contributions: C.R. and R.L. designed the study, performed most of the analyses, and drafted the manuscript. K.V., M.M., and Z.N. analyzed data. C.R., R.L., Y.V.d.P., and S.P. wrote the manuscript with help and final approval from all authors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/7/e1603195/DC1
Differences in duplication age estimates between (ME)(ME), (ME)(E), and (ME)(M) trees
Timing and phylogenetic placement of the WGD derived from the Amborella synteny data
table S1. Statistical analyses of modality of duplication age distributions
table S2. Bayesian information criterion values from the EMMIX analysis to estimate the number of significant components in the duplication age distributions
fig. S1. Phylogenetic gene trees with (ME)(E) and (ME)(M) topology.
fig. S2. Distribution of duplication estimates in the (ME)(M) and (ME)(E) trees.
fig. S3. Correlation of the gene tree topology with the duplication estimate.
fig. S4. Correlation of the gene tree topology with the duplication estimate.
fig. S5. Identification of significant components using SiZer.
fig. S6. Replacing all ME node calibrations does not change the general pattern of the distribution of gene duplication ages estimated by BEAST.
REFERENCES AND NOTES
- 1.Vekemans D., Proost S., Vanneste K., Coenen H., Viaene T., Ruelens P., Maere S., Van de Peer Y., Geuten K., Gamma paleohexaploidy in the stem lineage of core eudicots: Significance for MADS-box gene and species diversification. Mol. Biol. Evol. 29, 3793–3806 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Ming R., VanBuren R., Wai C. M., Tang H., Schatz M. C., Bowers J. E., Lyons E., Wang M.-L., Chen J., Biggers E., Zhang J., Huang L., Zhang L., Miao W., Zhang J., Ye Z., Miao C., Lin Z., Wang H., Zhou H., Yim W. C., Priest H. D., Zheng C., Woodhouse M., Edger P. P., Guyot R., Guo H.-B., Guo H., Zheng G., Singh R., Sharma A., Min X., Zheng Y., Lee H., Gurtowski J., Sedlazeck F. J., Harkess A., McKain M. R., Liao Z., Fang J., Liu J., Zhang X., Zhang Q., Hu W., Qin Y., Wang K., Chen L.-Y., Shirley N., Lin Y.-R., Liu L.-Y., Hernandez A. G., Wright C. L., Bulone V., Tuskan G. A., Heath K., Zee F., Moore P. H., Sunkar R., Leebens-Mack J. H., Mockler T., Bennetzen J. L., Freeling M., Sankoff D., Paterson A. H., Zhu X., Yang X., Smith J. A. C., Cushman J. C., Paull R. E., Yu Q., The pineapple genome and the evolution of CAM photosynthesis. Nat. Genet. 47, 1435–1442 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bowers J. E., Chapman B. A., Rong J., Paterson A. H., Unravelling angiosperm genome evolution by phylogenetic analysis of chromosomal duplication events. Nature 422, 433–438 (2003). [DOI] [PubMed] [Google Scholar]
- 4.Vanneste K., Baele G., Maere S., Van de Peer Y., Analysis of 41 plant genomes supports a wave of successful genome duplications in association with the Cretaceous–Paleogene boundary. Genome Res. 24, 1334–1347 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jiao Y., Wickett N. J., Ayyampalayam S., Chanderbali A. S., Landherr L., Ralph P. E., Tomsho L. P., Hu Y., Liang H., Soltis P. S., Soltis D. E., Clifton S. W., Schlarbaum S. E., Schuster S. C., Ma H., Leebens-Mack J., dePamphilis C. W., Ancestral polyploidy in seed plants and angiosperms. Nature 473, 97–100 (2011). [DOI] [PubMed] [Google Scholar]
- 6.Sanderson M. J., r8s: Inferring absolute rates of molecular evolution and divergence times in the absence of a molecular clock. Bioinformatics 19, 301–302 (2003). [DOI] [PubMed] [Google Scholar]
- 7.Drummond A. J., Suchard M. A., Xie D., Rambaut A., Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol. Biol. Evol. 29, 1969–1973 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ho S. Y. W., Duchêne S., Molecular-clock methods for estimating evolutionary rates and timescales. Mol. Ecol. 23, 5947–5965 (2014). [DOI] [PubMed] [Google Scholar]
- 9.Sauquet H., A practical guide to molecular dating. C. R. Palevol 12, 355–367 (2013). [Google Scholar]
- 10.Warnock R. C. M., Parham J. F., Joyce W. G., Lyson T. R., Donoghue P. C. J., Calibration uncertainty in molecular dating analyses: There is no substitute for the prior evaluation of time priors. Proc. R. Soc. B 282, 20141013 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Clarke J. T., Warnock R. C. M., Donoghue P. C. J., Establishing a time-scale for plant evolution. New Phytol. 192, 266–301 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Smith S. A., Beaulieu J. M., Donoghue M. J., An uncorrelated relaxed-clock analysis suggests an earlier origin for flowering plants. Proc. Natl. Acad. Sci. U.S.A. 107, 5897–5902 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Magallón S., Using fossils to break long branches in molecular dating: A comparison of relaxed clocks applied to the origin of angiosperms. Syst. Biol. 59, 384–399 (2010). [DOI] [PubMed] [Google Scholar]
- 14.Amborella Genome Project , The Amborella genome and the evolution of flowering plants. Science 342, 1241089 (2013). [DOI] [PubMed] [Google Scholar]
- 15.Li Z., Baniaga A. E., Sessa E. B., Scascitelli M., Graham S. W., Rieseberg L. H., Barker M. S., Early genome duplications in conifers and other seed plants. Sci. Adv. 1, e1501084 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baele G., Li W. L. S., Drummond A. J., Suchard M. A., Lemey P., Accurate model selection of relaxed molecular clocks in Bayesian phylogenetics. Mol. Biol. Evol. 30, 239–243 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Naik P. A., Shi P., Tsai C. L., Extending the Akaike Information Criterion to mixture regression models. J. Am. Stat. Assoc. 102, 244–254 (2007). [Google Scholar]
- 18.Vanneste K., Van de Peer Y., Maere S., Inference of genome duplications from age distributions revisited. Mol. Biol. Evol. 30, 177–190 (2013). [DOI] [PubMed] [Google Scholar]
- 19.SAS Institute Inc., SAS/STAT User’s Guide (SAS Publishing, ver. 6, ed. 4, 1990). [Google Scholar]
- 20.Hartigan J. A., Hartigan P. M., The dip test of unimodality. Ann. Statist. 13, 70–84 (1985). [Google Scholar]
- 21.Pfister R., Schwarz K. A., Janczyk M., Dale R., Freeman J. B., Good things peak in pairs: A note on the bimodality coefficient. Front. Psychol. 4, 700 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chaudhuri P., Marron J. S., SiZer for exploration of structures in curves. J. Am. Stat. Assoc. 94, 807–823 (1999). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/7/e1603195/DC1
Differences in duplication age estimates between (ME)(ME), (ME)(E), and (ME)(M) trees
Timing and phylogenetic placement of the WGD derived from the Amborella synteny data
table S1. Statistical analyses of modality of duplication age distributions
table S2. Bayesian information criterion values from the EMMIX analysis to estimate the number of significant components in the duplication age distributions
fig. S1. Phylogenetic gene trees with (ME)(E) and (ME)(M) topology.
fig. S2. Distribution of duplication estimates in the (ME)(M) and (ME)(E) trees.
fig. S3. Correlation of the gene tree topology with the duplication estimate.
fig. S4. Correlation of the gene tree topology with the duplication estimate.
fig. S5. Identification of significant components using SiZer.
fig. S6. Replacing all ME node calibrations does not change the general pattern of the distribution of gene duplication ages estimated by BEAST.


