A multiplexed, heterogeneous, and adaptive code for navigation in medial entorhinal cortex

Summary

Medial entorhinal grid cells display strikingly symmetric spatial firing patterns. The clarity of these patterns motivated the use of specific activity pattern shapes to classify entorhinal cell- types. While this approach successfully revealed cells that encode boundaries, head direction, and running speed, it left a majority of cells unclassified, and its pre-defined nature may have missed unconventional, yet important coding properties. Here, we apply an unbiased statistical approach to search for cells that encode navigationally-relevant variables. This approach successfully classifies the majority of entorhinal cells and reveals unsuspected entorhinal coding principles. First, we find a high degree of mixed selectivity and heterogeneity in superficial entorhinal neurons. Second, we discover a dynamic and remarkably adaptive code for space that enables entorhinal cells to rapidly encode navigational information accurately at high running speeds. Combined, these observations advance our current understanding of the mechanistic origins and functional implications of the entorhinal code for navigation.

Introduction

Historically, progress in neuroscience has often been marked by the discovery of single cells with firing rates that are modulated in a simple manner by an intuitively understandable stimulus. Canonical examples include the discovery of V1 cells that fire maximally to local visual edges at particular orientations (Hubel and Wiesel, 1959) and auditory A1 neurons that respond strongest to pure tones at specific frequencies (Merzenich et al., 1975). The response properties of these neurons are often described by tuning curves, which reflect their firing rate in response to families of simple sensory stimuli. Such families could include, for example, all orientations of a sinusoidal grating (Hubel and Wiesel, 1959). Recently, the application of tuning curves to characterize neurons in medial entorhinal cortex (MEC) has revealed striking single cell codes for navigational variables. For example, MEC grid cells fire at remarkably symmetric and periodic spatial locations, yielding single cell spatial tuning curves that depict hexagonal arrays of neural activity over physical space (Hafting et al., 2005). Other MEC cell types with simple, quantifiable tuning curves include border cells that fire maximally near environmental boundaries, head direction cells that fire only when an animal faces a particular direction, and speed cells that increase their firing rate with running speed (Kropff et al., 2015; Sargolini et al., 2006; Solstad et al., 2008).

The distinct features of MEC tuning curves, coupled with the preservation of tuning curve structure across spatial contexts, led to the development of methods for classifying MEC cells based on the shape of their tuning curve in two-dimensional environments (Hafting et al., 2005; Kropff et al., 2015; Krupic et al., 2012; Langston et al., 2010; Sargolini et al., 2006; Savelli et al., 2008; Solstad et al., 2008; Wills et al., 2010). These methods classify cells as a particular cell type if quantifications of specific tuning curve features score statistically higher than that observed in null distributions. Consequently, this tuning curve score (TCS) approach requires classified cells to have tuning curves that follow a pre-defined shape. Often, this pre-defined shape biases the search for cells to those with tuning curves that obey certain pre-conceived notions of regularity, such as the symmetry and periodicity of a spatial tuning curve, border localization, monotonicity in speed, or unimodality of tuning in head direction.

Thus, while using tuning curves to explore MEC coding supported the discovery of new functionally-defined cell types, the heavily supervised nature of the resulting TCS approach has led to several critical limitations. First, a large population of MEC neurons remain unclassified in many studies of MEC (Kropff et al., 2015; Sun et al., 2015) yielding a form of entorhinal “dark matter” that may include cells with unconventional, mixed selective, or heterogeneous tuning to navigational variables (Hinman et al., 2016; Kraus et al., 2015; Krupic et al., 2012). Heterogeneity in the shape of position and head direction tuning curves across the MEC population would have critical implications for grid and head direction cell computational models that rely on translation-invariant networks, which constrain the ability of simulated neurons to code for variables in mixed or heterogeneous ways (Bonnevie et al., 2013; Burak and Fiete, 2009; Couey et al., 2013; Guanella et al., 2007; Pastoll et al., 2013; Redish et al., 1996; Skaggs et al., 1995; Zhang, 1996). Second, proposals of MEC function have utilized the discrete classification of MEC spatial neurons to hypothesize how specialized spatial tuning properties support specific behaviors like navigation based on path-integration (Moser et al., 2014). However, requiring particular features in the shape of a tuning curve to pass a statistical threshold may artificially discretize a population of cells with more continuous representations (Krupic et al., 2012), which could have implications for how the MEC, as a population, controls behavior. Third, many MEC analyses have assumed static tuning curves that do not dynamically change with respect to other variables, such as behavioral state. The highly adaptable nature of sensory codes upstream of MEC however (Dragoi et al., 2002; Felsen et al., 2002; Hosoya et al., 2005; Sharpee et al., 2006), suggests that the MEC code itself could exhibit dynamic coding that is also adaptive.

Here we employed a statistical approach that quantitatively characterized MEC coding without imposing pre-defined assumptions about regularity in the shapes of neural tuning curves, allowing us to revisit MEC cell-type classification and coding principles in an unbiased manner. This approach enabled us to search for cells with firing rates that are informative about any arbitrary subset of navigational variables, such as position, speed, and head direction, or intrinsic modulators of firing, like theta oscillations. We applied this method to a large data set of single-unit MEC recordings from rodents performing a classic foraging task in a familiar environment, the primary task used to classify functionally-distinct MEC neurons (Hafting et al., 2005; Kropff et al., 2015; Krupic et al., 2012; Sargolini et al., 2006; Solstad et al., 2008). Even in this simplified foraging task, the unbiased model-based approach captured navigationally- relevant coding in the vast majority of superficial MEC neurons. Moreover, this method revealed high levels of mixed selectivity, in which representations of multiple navigational variables were multiplexed at the level of single neuron firing rates, and a high degree of heterogeneity in the tuning curves of identified cells. This degree of multiplexing and heterogeneity in superficial MEC was much higher than previously reported (Kropff et al., 2015; Krupic et al., 2012; Sargolini et al., 2006; Solstad et al., 2008). In addition, we found that the neural code for position and head direction is both dynamic and adaptive, enabling downstream circuits to accurately decode position and orientation during rapid movement.

Results

Capturing navigational coding within a model-based framework

We developed a general statistical approach to identify the coding properties of 794 layer II/III MEC neurons in mice (n = 14) foraging for randomly scattered food in open arenas (see Method Details in STAR Methods: “Details on LN model”). We focused our analyses on the navigational variables position (P), head direction (H), and running speed (S), as well as the phase of the theta rhythm (T), as MEC neurons show strong tuning to these variables during open field foraging tasks (Hafting et al., 2005; Kropff et al., 2015; Sargolini et al., 2006; Solstad et al., 2008; Tang et al., 2014) (Figure 1). To identify which variables each neuron encodes, we fit multiple, nested linear-nonlinear-Poisson (LN) models to the spike train of each cell (Figure 2, Figures S1, S2; Method Details in STAR Methods: ‘Details on LN model’). The dependence of neural spiking on a variable was visualized by constructing model-derived response profiles, which are qualitatively similar to tuning curves and plotted with identical units (Figure 2B). To identify the simplest model that best described neural spiking, we used a forward-search procedure that determined whether adding variables significantly improved model performance (Atkinson et al., 2010; Guyon and Elisseeff, 2003) (Figure 2C). Model performance was quantified by the log-likelihood increase from a fixed mean firing rate model, and assessed on data held out from the model-fitting procedure (Figure S3). Intuitively, this model performance measure enabled us to quantify how well any subset of navigational variables and internal theta oscillations predict single cell spiking activity.

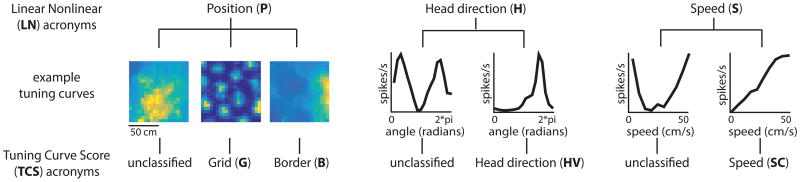
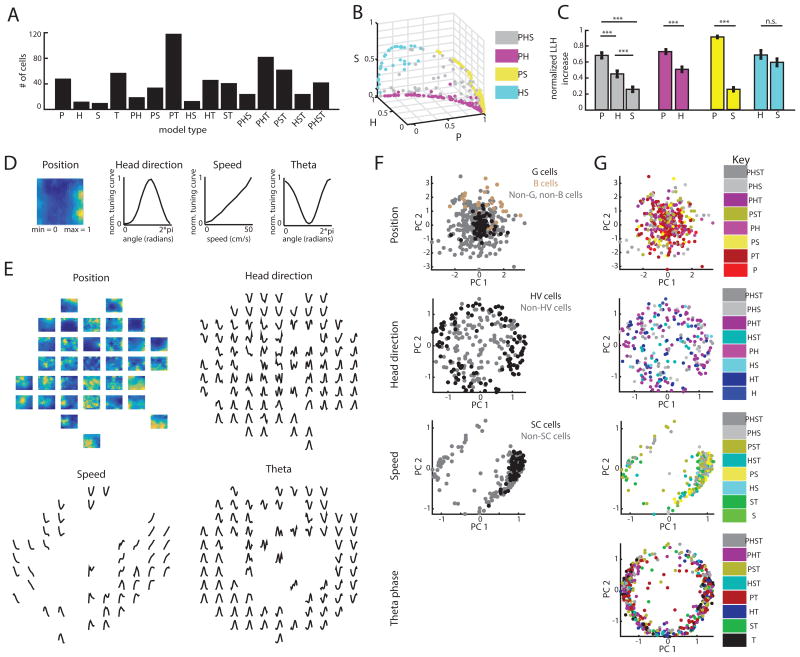
Figure 1.

The LN model approach and the TCS approach represent two distinct ways of characterizing MEC responses. LN method: P = position-encoding cells, H = head direction-encoding cells, S = speed-encoding cells. TCS method: G = grid cells, B = border cells, HV = head direction cells, SC = speed cells. Lines within the chart signify which response profiles are captured by each approach. (See also Figure S1)

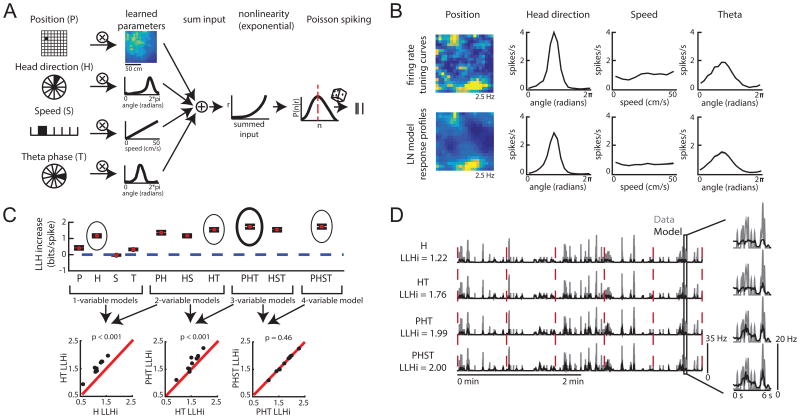
Figure 2.

The LN model provides an unbiased method for quantifying neural coding. A. Schematic of LN model framework. P, H, S and T are binned into 400, 18, 10, and 18 bins, respectively. The filled bin denotes the current value, which is projected (encircled x) onto a vector of learned parameters. This is then put through an exponential nonlinearity that returns the mean rate of a Poisson process from which spikes are drawn. B. Example firing rate tuning curves (top) and model-derived response profiles (bottom, computed from the PHST model; means from 30 bootstrapped iterations shown in black and the standard deviation in gray). C. Top: Example of model performance across all models for a single neuron (mean ± SEM log- likelihood increase in bits, normalized by the number of spikes [LLHi]). Selected models are circled, with the final selected model in bold. Bottom: comparison of selected models. Each point represents the model performance for a given fold of the cross-validation procedure. The forward-search procedure identifies the simplest model whose performance on held-out data was significantly better than any simpler model (p < 0.05). D. Comparison of the cell's firing rate (gray) with the model predicted firing rate (black) over 4 minutes of test data. Model type and model performance (LLHi) listed on the left. Red lines delineate the 5 segments of test data. Firing rates were smoothed with a Gaussian filter (o = 60 ms). (See also Figures S1 and S2)

Using the LN model, we detected 617/794 (77%) MEC cells with firing rates that were significantly influenced by some combination of P, H, S, or T variables. Of these, 561 cells (71%) encoded at least one navigational variable (P, H, or S). Many of these cells exhibited preference for current values of P, H, or S as opposed to time-shifted P, H, or S values (Figure S3), consistent with the framework classically used in the tuning curve score (TCS) approach.

To compare this classification to that derived from the TCS approach, we classified the same 794 MEC cells as grid (G), border (B), head direction (HV, for Head direction Vector length), or speed (SC, for Speed Correlation) cells if their tuning curve score was higher than the 99^th percentile of a distribution of scores obtained from randomizing a cell's spike train (Shuffled P99 G = 0.57, n = 101; B = 0.57, n = 42; HV = 0.24, n = 154; SC score = 0.07, SC stability = 0.51, n = 89; Figure 1, Figure S3). The TCS approach classified 332/794 (42%) cells, significantly fewer cells than detected as encoding a navigational variable (P, H or S) with the LN model (comparison of proportions z = 11.58, p < 0.001; Figure 3A). The results remained qualitatively unchanged even when we reduced the criteria for significance from the 99^th to the 95^th percentile (Figure S4). This points to the LN model approach as a method capable of capturing the coding of the majority of MEC neurons.

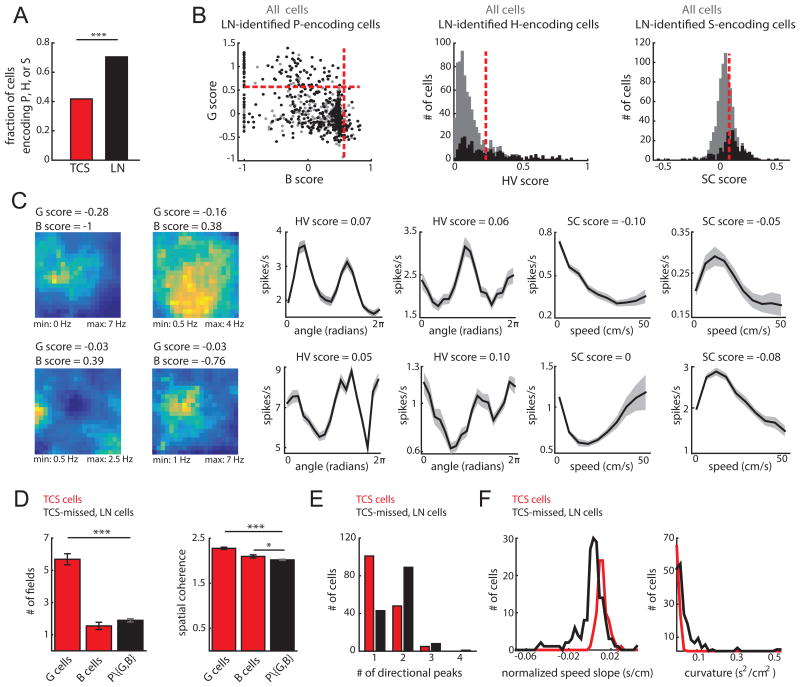
Figure 3.

The LN model captured coding for the majority of superficial MEC neurons. A. Fraction of cells that encode position, head direction, or running speed based on the TCS (red) or LN (black) approach (*** indicates p < 0.001). B. The tuning-curve scores of cells detected by the LN model (black) as encoding P (left), H (center) and S (right). Score values for all cells are shown in gray. Red lines indicate the TCS 99^th percentile threshold. In total, 307/421 P cells, 141/254 H cells, and 176/242 S cells were not classified as G or B (left), HV (middle) or SC (right) cells, respectively. C. Example model-derived response profiles. P response profiles colored coded for minimum (blue) and maximum (yellow) values (left two columns). H (middle two columns) and S coding (right two columns) are denoted by the mean ± SD of a response profile across 30 bootstrapped iterations of the model-fitting procedure. Models used to compute response profiles: top row: PHS, PS, HS, HST, PHS, ST; bottom row: PST, PST, HST, HS, PST, PST. D. P cells captured only by the LN model (P\{G,B}) had significantly fewer firing fields (left) than G cells (mean field number ± SEM: G = 5.69 ± 0.35, B = 1.55 ± 0.23, P\{G,B} = 1.90 ± 0.10; G and P\{G,B} t-test t(406) = -14.3, p = 5.1e-38; B and P\{G,B} t-test t(347) = 1.2, p = 0.22) and lower spatial coherence (right) than G and B cells (mean coherence ± SEM: G = 2.28 ± 0.03, B = 2.10 ± 0.04, P\{G,B} = 2.02 ± 0.01; G and P\{G,B} t(406) = -9.6, p = 5.7e-20; B and P\{G,B} t-test t(347) = -2.1, p = 0.04). (***p < 0.001; *p < 0.05). E. H cells captured only by the LN model had significantly more peaks in their tuning curves than HV cells (mean peaks ± SEM; HV = 1.37 ± 0.05, H = 1.77 ± 0.05, t-test t(293) = -5.96; p = 7.3e-9). F. S cells captured only by the LN model exhibited negative modulation of firing rate by running speed (left) and significantly higher curvature in their tuning curves than SC cells (mean curvature ± SEM; SC = 0.007 ± 5e-4, S = 0.04 ± 0.005, t-test t(263) = 4.72, p = 3.9e-6). For D-F, *** p<0.001. (See also Figure S3)

Why did the LN model capture coding in a larger proportion of MEC neurons compared to the TCS approach? The LN model successfully classified the majority of cells classified by the TCS method (283/332 cells; Figure S3-4), with cells missed by the LN model exhibiting less stable tuning curves across the recording session (Figure S3). Overall, TCS cells and LN-only cells (LN cells with scores below threshold) exhibited similar tuning stability across recording sessions (Figure S4). At the same time, the unbiased nature of the LN model did not require that a neuron's tuning curve match a pre-defined shape. Consequently, the LN model captured unconventional, yet meaningful, neural coding. This was indicated by the low tuning curve scores of many neurons detected by the LN model as significantly encoding navigational variables (334/617 LN-detected neurons did not pass any TCS threshold; Figure 3B). Model- detected cells with low tuning curve scores included, for example, spatially irregular P-encoding cells with few firing fields and low spatial coherence, H-encoding cells with more than one peak, and S-encoding cells negatively modulated by running speed or exhibiting non-monotonic speed-firing rate relationships (Figure 3C-F). Taken together, these observations reveal that while the majority of MEC neurons encode navigational variables during open field foraging, they do so in a highly variable manner.

Mixed selectivity in superficial medial entorhinal neurons

We next used the LN model framework to examine the encoding of multiple navigationally-relevant variables by a single MEC neuron, referred to as mixed selectivity. While prior studies have observed neurons that encode multiple navigational variables in deep MEC layers, superficial MEC layers are reported to contain a higher percentage of cells that encode a single navigational variable (Kropff et al., 2015; Sargolini et al., 2006; Solstad et al., 2008). However, given that the TCS approach has often failed to detect coding in a large fraction of MEC neurons, mixed selectivity in superficial MEC may have been underestimated. Consistent with this idea, we found that the LN model approach defined 37% (292/794) of superficial MEC neurons as mixed selective (MS) for combinations of P, H or S variables; this number is significantly more than the 7% (54/794) of mixed selective cells found by the TCS approach in our data (comparison of proportions z = 14.47, p < 0.001) (Figure 4A-C).

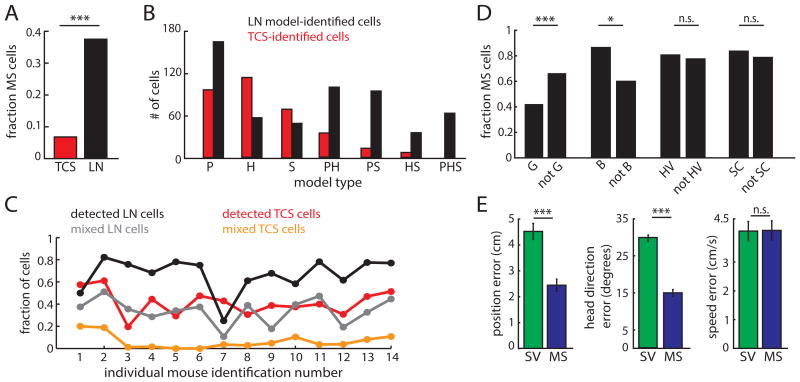
Figure 4.

Mixed selectivity is a ubiquitous coding scheme utilized by superficial MEC neurons. A. The LN approach (black) reveals significantly more mixed selectivity (MS) for P, H, and S compared to the TCS approach (red). (*** indicates p<0.001.) B. Comparison of model types classified by the LN (black) and TCS (red) methods for navigational variables. C. Proportion of TCS-detected, LN-detected, mixed TCS (cells that cross 2 or more score thresholds), and mixed LN (cells that significantly encode multiple variables) cells for each mouse. D. Comparison of the fraction of model-defined MS cells that either pass, or do not pass, the G, B, HV, or SC thresholds. Number of MS cells/total: G = 36/86, non-G = 221/335; B = 24/28, non-B = 233/393; HV = 90/113, non-HV = 108/141; SC = 55/66, non-SC = 138/176. * indicates p<0.05, *** indicates p<0.001, n.s. = not significant. E. Error in decoding position (left), head direction (middle), and running speed (right) when using either MS or SV cells (n = 332 for both groups; P. *** p < 0.001, n.s. p > 0.5. (See also Figures S3 and S4)

We found that the LN model identified mixed selectivity in cells from multiple TCS- defined cell classes. While 42% of superficial grid cells coded for more than one navigational variable, they were less likely to show mixed selectivity than the non-grid, position-encoding MEC population. This result supports the notion that the grid cell population preferentially, but not universally, encodes a single variable (SV) in open-field foraging tasks (P-encoding MS cells: z = 4.08, p = 4.3e-5; Figure 4D). On the other hand, the vast majority of superficial border (86%), head direction (80%), and speed (83%) cells encoded multiple navigational variables and were more or equally likely to show mixed selectivity compared to the rest of the MEC population (P-encoding B cells: z =2.77, p = 0.006; H-encoding HV cells: z = 0.58, p = 0.56; Sencoding SC cells: z = 0.84, p = 0.40; Figure 4B-C).

Unlike the increase in the spatial distance between grid firing fields along the dorsalventral MEC axis (Hafting et al., 2005), the degree of mixed selectivity did not change from dorsal to ventral MEC (see Quantification and Statistical Analyses in STAR Methods; ‘Custom statistical analyses’; Figure S4). Mixed selectivity also did not reflect differences in firing rates, spike sorting cluster quality, or tuning stability (Figure S4). Taken together, these data demonstrate that mixed selectivity is a common coding strategy employed by superficial MEC neurons. This has significant implications for models of coding in MEC as well as in brain regions that receive MEC input, as mixed selectivity offers significant advantages when decoders must infer large numbers of discrete states from population-level activity (Barak et al., 2013; Fusi et al., 2016; Rigotti et al., 2013). Consistent with this idea, we found that decoding position and head direction from populations of MS cells out-performed a decoder based solely on the activity of SV cells (n = 269 cells, P error: MS = 2.44 ± 0.05 cm, SV = 4.51 ± 0.07 cm, p = 2e-4; H error: MS = 15 ± 0.02 degrees, SV = 29.8 ± 0.18 degrees, p = 9e-5; S error: MS = 4.1 ± 0.07 cm/s, SV = 4.1 ± 0.07 cm/s, p = 0.7; Figure 4E; Method Details in STAR Methods; ‘Decoding from MS and SV populations’).

Diversity and heterogeneity in MEC coding

As the LN model approach identified navigationally-relevant coding in a large population of MEC neurons with diverse response profile shapes, we next sought to fully characterize MEC tuning variability. Such a characterization is essential for the continued development of MEC computational models, as many current models capable of generating position or direction codes utilize neurons with response profiles well described by simple tuning curves with similar shapes. We focused on two forms of tuning variability across our data set: (1) diversity in the strength with each navigational variable was encoded, and (2) heterogeneity in the response profile shape of LN model-defined cell types (Figure 5).

Figure 5.

MEC neurons show highly heterogeneous response profile shapes. A. Histogram of the selected models for the 617 cells identified by the LN model approach. B. 3D scatter plot of the normalized contribution of P, H, and S to the model performance of MS cells. Cells are color-coded by model. Variable contributions were measured as the average change in model performance due to addition or deletion of that variable from the selected model (e.g. the contribution of P to a PH neuron is the log-likelihood difference between the H and PH models). C. Mean (± SEM) contribution of P, H, and S for cell-types shown in (B). *** p < 0.001, n.s. = not significant. D. Example of normalized model-derived response profiles. E. For each variable, we constructed a 2-dimensional ‘response-profile’ space, where location in each space is determined by a cell's normalized response profile for that variable. Here, we show the normalized response profiles of a randomly chosen set of cells that were plotted in this space, demonstrating that diverse response profiles vary smoothly across location. Panels F-H use these same four axes to indicate where the response profiles of all the cells lie. F. Projected data, colored according to TCS identification (gray indicates cells not identified by the TCS approach). Each point is a single cell (P: 421 cells, H: 254 cells, S: 242 cells, T: 464 cells). The location of each point is determined by the shape of that cell's response profile. G, HV, and SC cells were significantly clustered for at least one value of k, while B cells trended towards significance for k = 1. G. Same as (F), but colored according the each cell's selected LN model. (See also Figure S5)

First, to investigate the diversity in the extent to which navigational variables drive neural spiking, we computed the relative contribution of position, head direction, and speed in predicting the spikes of LN model-defined mixed selectivity cells (Method Details in STAR Methods; ‘Heterogeneity of entorhinal coding’). In essence, this analysis allowed us to determine how strongly a mixed selective neuron encoded any given navigational variable. For all mixed selective cell types, we observed a high degree of diversity within the variable contributions that did not clearly cluster into distinct cell types (Figure 5B). However, the relative contribution of P, H, and S to mixed selectivity cells was not uniformly random, as P tended to be significantly more predictive of neural spiking than H or S (PHS n = 64, ANOVA F(2,189) = 36.1, p = 5e-14, with P>H t(126) = 4.38, p = 2.4e-5, P>S t(126) = 9.0, p = 2.6e-15; PH n = 99, P>H t(196) = 5.3, p = 3.6e-7; PS n = 94, P>S t(186) = 23.7, p = 4.9e-58; Figure 5C). This indicated that while mixed selective cells encode multiple navigational variables in diverse ways, position tends to be the most salient feature driving MEC spiking activity.

Next, we investigated the heterogeneity in how neurons encode P, H, S or T by looking for structure in the shapes of LN response profiles. For all LN identified neurons, we grouped the response profiles according to the variable they encode. Then, we used principal component analysis to project each group of response profiles onto a low-dimensional space (Figure 5D-G). In essence, if two cells appear close to each other in this low-dimensional space, the shapes of their response profiles for a given variable are similar. The similarity between response profile shapes was quantified by computing, for each cell, the average distance to the k-nearest cells of the same type, and comparing these values to a null distribution of distances (k = 1-10; see Method Details in STAR Methods; ‘Heterogeneity of entorhinal coding’, and Quantification and Statistical Analysis in STAR Methods: ‘Custom statistical analyses’).

We first verified that this analysis could identify clustering by considering cells classified by the TCS approach, as the TCS approach requires that the tuning curves of classified cells conform to a pre-defined shape. As expected, we found that G, HV, and SC cells significantly clustered (Bonferroni-corrected; G p < 0.0001, B p = 0.01, HV p < 0.005, SC p < 0.001; Figure 5F). We then considered LN model-defined cell types. We found that LN model-defined cell types coded for navigational variables in a highly heterogeneous manner, as only 4/32 response profile sets significantly clustered (H of HST cells, S of PS cells, T cells and P cells; Figure 5G, Figure S5). This result holds when data from single animals were analyzed individually, indicating that the heterogeneity we observed did not reflect differences in cells recorded across animals (Figure S5). These results are consistent with our previous observation that the LN model captured a high degree of variability in MEC navigational coding and provide a ‘snapshot’ into the heterogeneity of this coding when considering the majority (> 75%) of the MEC neural population. This high degree of heterogeneity within entorhinal coding points to the need for computational models of MEC to incorporate a continuum of cell diversity and a vast array response profile shapes.

Speed-dependent changes in spatial coding

The application of LN models to sensory systems has revealed that many sensory neurons adaptively change their neural code based on the statistics of the sensory input (Dragoi et al., 2002; Felsen et al., 2002; Hosoya et al., 2005; Sharpee et al., 2006). However, many methods utilized to classify entorhinal cells assume a fixed relationship between a stimulus (e.g. position) and neural spiking, which may obscure dynamic coding properties. A dramatic change in the statistics of sensory inputs during open field foraging occurs as an animal varies its running speed. Therefore, to test whether MEC neurons dynamically encode navigational variables, we examined P and H-encoding properties of single cells as the animal's running speed varied.

We split each recording session into fast running speed epochs (10 – 50 cm/s) and slow running speed epochs (2 – 10 cm/s). Epochs were then down-sampled until spike number, directional sampling, positional sampling, and the number of time bins matched between the two epochs (average epoch length = 594 seconds; Figure 6, Figure S7). We then re-fit the P, H, and PH models to the fast and slow epochs separately, and used the forward-search model selection procedure to determine the coding properties of a neuron during fast versus slow speeds (Figure 6A, Figure S6). We repeated this process 50 times due to the stochastic nature of down-sampling and subsequently focused our analyses on neurons with consistent model selection across iterations (n = 234 cells) (see Method Details in STAR Methods: ‘Investigating dynamic coding properties’).

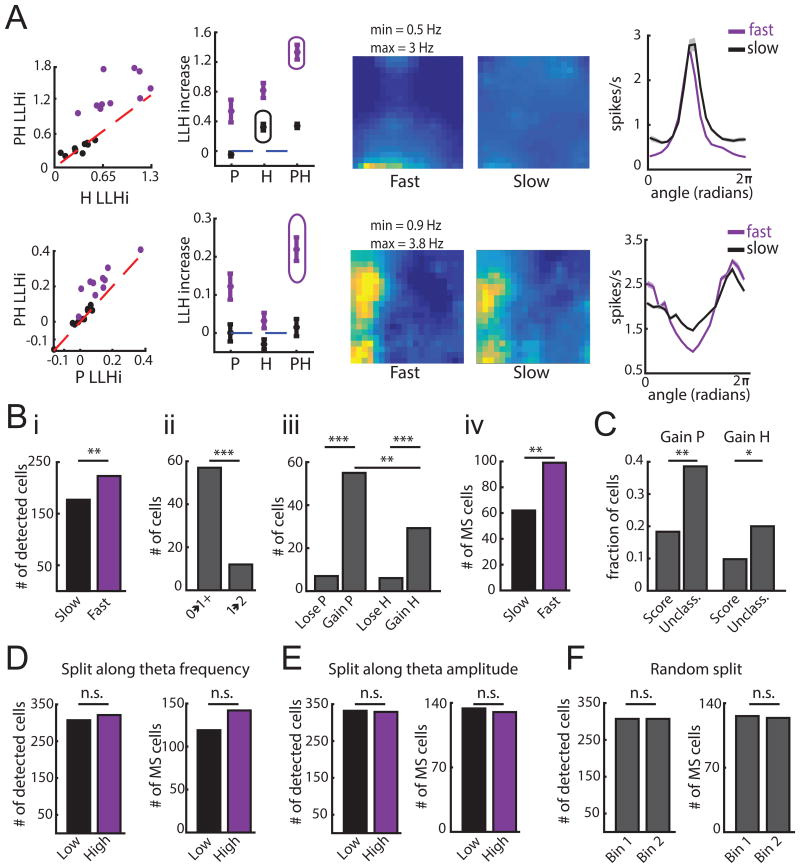
Figure 6.

Dynamic spatial coding in MEC. A. Example model selection procedures for each epoch. Top row: example cell that encodes H at slow speeds and PH at fast speeds. Bottom row: example cell that gains PH at fast speeds. Both rows; Left: Comparison of model performance for both epochs. Performance (mean ± SEM) of P, H, and PH models during fast and slow epochs with the selected model circled (shown for a single iteration). Middle: Response profiles for P of PH model during fast and slow speeds, color-coded for minimum (blue) and maximum (yellow) values across both epochs. Right: Response profiles (mean ± SD) for H of PH model during fast and slow speeds. B. i. Number of cells encoding P, H, or PH increases at fast speeds. ii. Cells gain coding for P or H at high speeds in two ways. Cells that do not encode P or H at slow speeds encode P, H or PH at fast speeds (0→1+) and cells that encode P or H at slow speeds encode PH at fast speeds (1→2). Significantly more cells fall into the former group (comparison of proportions z = 5.5, p = 3e-8). iii. More cells gain rather than lose P or H at fast speeds; more cells gain P than H. iv. More cells exhibit mixed selectivity at fast speeds. *** p < 0.001, ** p < 0.01, n.s. = not significant. C. Cells unclassified by the TCS method were more likely to gain P or H at fast speeds. ** p < 0.01, * p < 0.05. D.-F. Same as (Bi, ii and iv), but for data split along theta frequency (D), theta amplitude (E) or randomly (F). In the first two cases, speed coverage was matched between epochs. n.s. = not significant. (See also Figures S6 and S7)

We found that within individual sessions, the total number of cells encoding position, head direction or both significantly increased during fast speeds (Number of cells encoding P, H or PH: fast speeds = 223 cells, slow speeds = 177 cells, z = 2.65, p = 0.008; Figure 6B). We noted that cells gained coding for navigational variables at fast speeds in two ways. First, a subset of cells that did not significantly encode P or H at slow speeds gained coding for P, H or PH (n = 57). Second, some cells encoding only P or H at slow speeds began encoding PH at fast speeds (n = 12). These two effects led to a greater number of mixed selective (PH) cells at fast speeds (MS fast speeds = 99 cells, MS slow speeds = 62 cells, different proportions z = 3.08, p = 0.002). These results strongly support the notion that the degree of mixed selectivity increases with running speed (Figure 6B). Interestingly, this dynamic code was most frequently observed in neurons with unconventional tuning curves. Cells unclassified by the TCS approach were more likely to gain coding for P or H at high speeds compared to cells classified as grid, border, head direction or speed cells (comparison of proportions: P gained z = 3.26, p = 0.001; H gained z = 2.10, p = 0.036; Figure 6C, Figure S7). Thus, the presence of dynamic coding in MEC could contribute to the difficulty in classifying MEC neurons when using methods that assume a static tuning curve structure across behavioral states.

In addition, we found that across the MEC population, the gain of variables encoded by a neuron reflected an increase in position compared to head direction coding, raising the possibility that running speed modulates the position code more than directional code (z = 2.92, p = 0.004; Figure 6B). This dynamic code, present in a wide range of MEC cell classes (Figure S7), appeared specific to running speed and did not reflect changes in theta oscillatory activity, which might be expected given that theta frequency is known to correlate with running speed (Jeewajee et al., 2008). Splitting the data based on theta frequency or theta amplitude did not yield significant differences in the number of variables encoded, the number of variables gained, or the degree of mixed selectivity (Figure 6D-F). Taken together, these data point to a large population of MEC neurons that dynamically vary their coding properties in response to changes in the animal's running speed.

Response profiles become more informative at faster running speeds

We then investigated whether the shape of model-derived response profiles change with running speed. We restricted our analyses to cells that either gained or retained coded variables with running speed (P: n = 189 cells, H: n = 114 cells), as only a very small number of cells lost coded variables (P: n = 7 cells, H: n = 6 cells). First, for cells that gained coding for a variable, we observed that model-derived response profiles for P and H were more informative during fast speeds, as measured by the mutual information between position or head direction and neural spiking (sign-rank test; P: z = 4.24, p = 2e-5, n = 55; H: z = 3.04, p = 0.002, n = 29; Figure 7A-C; see Method Detail in STAR Methods: ‘Investigating dynamic coding properties’). This was also true for cells that encoded the same navigational variable during both slow and fast speeds, (sign-rank test; P: z = 2.63, p = 0.009, n = 134; H: z = 2.07, p = 0.039, n = 85; Figure 7C). This suggests that cells can exhibit speed-dependent adaptive coding not only by encoding an additional variable, but also by increasing the informational content of its response to the same variable.

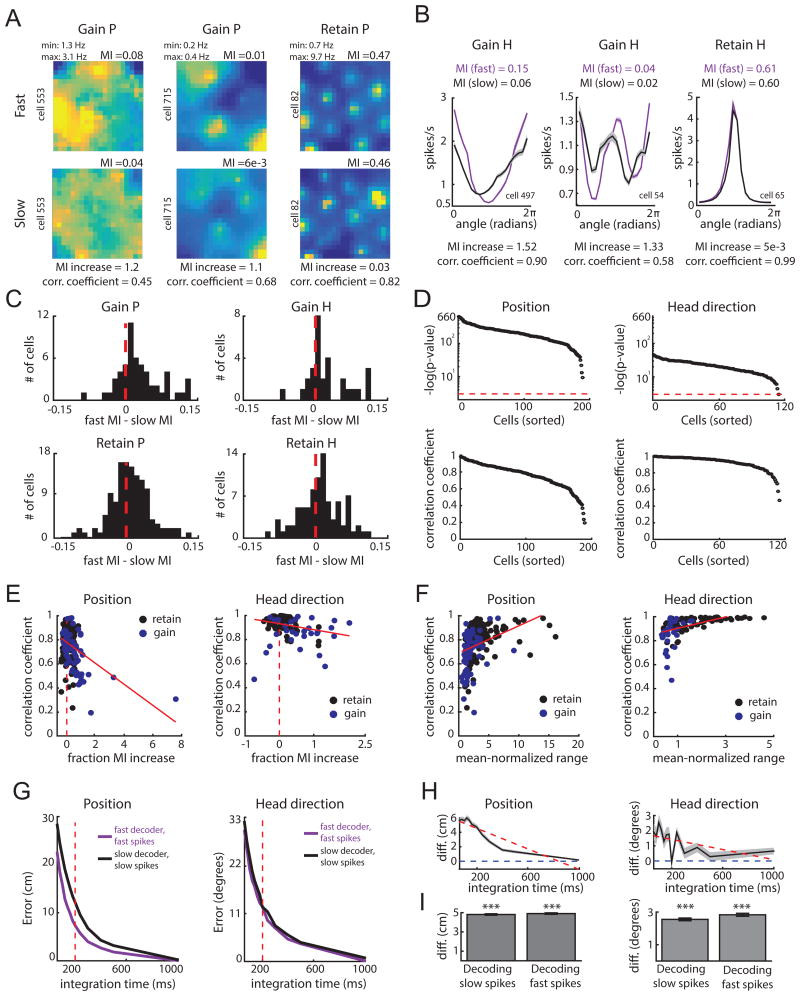
Figure 7.

Tuning is more informative at fast speeds and is adaptive. A-B. Example response profiles for cells that gain or maintain P or H coding (follows plot conventions of Figure 6). Response profiles, and all comparisons in this figure unless stated otherwise, are derived from the more complex selected model across epochs. For each pair, the mutual information (MI), fractional increase in MI [(MI_fast - MI_slow)/MI_slow], and Pearson correlation coefficients, are computed. C. Difference in MI for position (left) and head direction (right) for cells that gain P (top left) or gain H (top right) at fast speeds, and cells that retain P (bottom left) or retain H (bottom right) across speeds. D. Negative log of p-values (top) and coefficients (bottom) for correlations between the slow and fast-epoch response profiles for cells that gain or retained P or H coding. The red line indicates p = 0.05, with cells above this line attaining significance. E. Scatter plot of MI fractional increase and correlation coefficient between response profiles for cells that gained (blue) or retained (black) P (left) or H (right) coding features with fast speeds. Dashed red line indicates an MI increase of 0, while the solid red line indicates the best-fit line to the data. F. Scatter plot of the mean-normalized range of the slow-derived response profile and correlation coefficients from (E) for cells that gained or retained coding P (left) or H (right) with fast running speeds. G. Top: P and H decoding error of a decoder trained and tested on data derived from parameters of the selected model during fast epochs (purple) versus parameters of the selected model during slow epochs (black). H. Difference in error in decoding position (left) and head direction (right) between the slow and fast decoders in (G). I. Decoding error difference for position (left) or head direction (right) between the slow and fast decoder when decoding data from slow epochs (‘slow spikes’; left of each plot) or when decoding data from fast epochs (‘fast spikes’; right of each plot). Mean difference is computed by averaging across all decoding iterations and tested integration times. Error bars correspond to standard error of the mean across the decoding iterations. *** p < 0.001. (See also Figure S7)

Does the increase in information content reflect a change in the gain of a cell's response profile or the shape of the response profile? To examine this, we computed the Pearson correlation between fast and slow speed response profiles. The correlation coefficient will approach 1 if the gain of a cell's response profile increases at fast speeds, without any change in the underlying response profile shape. Consistent with this idea, all pairs of P and H response profiles were significantly and positively correlated (Figure 7D). We also noted however, that cells with the largest increases in information at fast speeds tended to exhibit lower correlation coefficients (correlation between information gained and correlation coefficient, P: -0.395, p = 1.9e-08, [excluding MI increases > 2, correlation coefficient = -0.355, p = 6e-7]; H: -0.266, p = 0.004; Figure 7E). This could result from cells with nearly flat response profiles during slow speeds gaining strong tuning during fast speeds, an effect that would lead to a low correlation between the two response profiles. Consistent with this idea, we found that the range of a neuron's slow-epoch response profile, which will be small for nearly flat response profiles, significantly predicted correlation coefficients for both position and head direction (mean- normalized range vs correlation coefficient; P: r² = 0.14, p = 7e-9; H: r²= 0.25, p = 2e-8, using a linear model; Figure 7F). Together, these results suggest that changes in coding at different running speeds reflect an increase in the gain of position and head direction coding.

A dynamic speed-dependent code that is adaptive

How might speed-dependent changes in coding impact computation in regions attempting to decode the animal's position and head direction from MEC? In order to avoid error during fast running speeds, the brain must obtain high fidelity position and direction estimates over short periods of time. Thus, one possible function of the speed-dependent code is to serve as an adaptive code by facilitating accurate position and direction estimates at fast running speeds. To investigate this idea, we first simulated the activity of two neural populations: one representing the population activity during fast running speeds (‘fast population’), and one representing the population activity during slow running speeds (‘slow population’). For each cell within a given population, we generated spike trains using the model parameters learned for that cell at slow or fast speeds (see Method Detail in STAR Methods: ‘Investigating dynamic coding properties’). Using a maximum-likelihood decoder trained on each population separately, we found that decoding position and head direction from the fast population is more accurate than from the slow population during short (60-200 ms) integration times (averaged over 1000 iterations at 8 integration times; P: (slow error – fast error) = 5.4 ± 0.02 cm, slow error > fast error with p = 5e-122; H: (slow error – fast error) = 1.61 ± 0.21 degrees, slow error > fast error with p = 1.6e-12; sign-rank test; Figure 7G). The difference in decoding accuracy between the two populations decreased with integration time, suggesting that at slow running speeds the slow population can be used to decode position and head direction as accurately as the fast population (slope in error difference over integration time; P = -7.02 cm/s, significantly negative slope p < 0.001; H = -1.68 degrees/s, significantly negative slope p < 0.001, Figure 7G-H). These results indicate that dynamic coding in MEC is adaptive in that it supports high decoding accuracy at fast running speeds.

Finally, we considered the idea that adaptive speed-dependent codes may require downstream regions to know the running speed of the animal in order to accurately decode the animal's position and head direction. Consistent with this notion, we found that the decoder learned from the slow population (‘slow decoder’) performed poorly when decoding spikes from the fast population, and the decoders learned from the fast population (‘fast decoder’) performed poorly when decoding spikes from the slow population (Figure S7). However, this may result from the fact that each pair of cells can exhibit different selected models (e.g. for an example cell, the H model may be selected at slow speeds, but the PH model is selected at fast speeds). This means that the spike trains in each population are generated from a fundamentally different set of parameters. To address this effect, we matched the selected models across the slow and fast epochs for each cell by choosing the more complex model (e.g. if the H model was selected at slow speeds but the PH model was selected at fast speeds, we used the PH model for both slow and fast speeds). Again, we found that the slow decoder performed poorly when decoding fast spikes, and vice versa (P: error difference for slow spikes: 4.81 cm ± 0.10, > 0 with p = 3e- 165, error difference for fast spikes: 4.91 cm ± 0.08, > 0 with p = 9e-164; H: error difference for slow spikes: 2.55 ± 0.08 degrees, > 0 with p = 4e-116, error difference for fast spikes: 2.83 ± 0.09 degrees, > 0 with p = 2e-120; Figure 7I, Figure S7). This indicates that our model selection procedure itself does not lead to significantly different downstream decoders and that downstream circuits dedicated to estimating the animal's position and head direction from MEC neural activity cannot do so without simultaneously estimating speed.

Discussion

Many current perspectives on MEC coding are driven by the quantification of tuning curve features and subsequent categorization of MEC neurons into discrete cell classes. While this approach supported the discovery of multiple MEC cell classes that encode specific navigational variables, it has often left the majority of MEC cells uncharacterized. We developed unbiased statistical procedures that enable us to effectively explore the information encoded by uncharacterized cells and to search for cells that are informative about navigational variables without making pre-defined assumptions about their tuning. By applying this unbiased approach, we successfully identified coding in the vast majority of MEC neurons, revealing extensive mixed selectivity and heterogeneity in superficial MEC, as well as adaptive speed-dependent changes in MEC spatial coding. While we find a large population of MEC cells display heterogeneous and mixed response profiles, these cells co-exist with a smaller population of single variable cells characterized by more stereotypical and simple tuning curves (Hafting et al., 2005; Kropff et al., 2015; Sargolini et al., 2006; Solstad et al., 2008). Taken together, the mixed selective, heterogeneous and adaptive coding principles revealed by the LN model approach have important implications for our understanding of both mechanism and function in MEC.

In particular, the ubiquitous nature of mixed selectivity and heterogeneity in MEC uncovered by our LN approach has important implications for computational models that generate spatial and directional coding. Many models of grid and head direction cell formation rely on translation-invariant attractor networks. In these models, an animal's movement drives the translation of an activity pattern across a neural population, with accurate pattern translation achieved only when all neurons in the network are characterized by the same simple tuning curve shape (Burak and Fiete, 2009; Couey et al., 2013; Fuhs and Touretzky, 2006; McNaughton et al., 2006; Pastoll et al., 2013; Skaggs et al., 1995). While attractor network models have been successful in describing multiple features of MEC coding (Bonnevie et al., 2013; Couey et al., 2013; Pastoll et al., 2013; Stensola et al., 2012; Yoon et al., 2013), most such models do not exhibit the large degrees of mixed selectivity and heterogeneous tuning observed in our data. In particular, these models cannot account for the continuous nature of mixed selectivity that we observe (Figure 5B), and only a few attractor states survive in the presence of even small amounts of heterogeneity (Renart et al., 2003; Stringer et al., 2002; Tsodyks and Sejnowski, 1997; Zhang, 1996). It does remain possible that sub-populations of single variable position or direction-encoding cells with similar tuning curve shapes could form progenitor attractor networks. These networks could then endow separate mixed selective and heterogeneous neurons with spatial or directional tuning. However, this scenario requires unidirectional MEC connectivity from the single variable and homogeneous cell populations to the mixed and heterogeneous cell populations, a potentially biologically unrealistic assumption given the non-negligible levels of recurrent connectivity known to exist in superficial MEC (Couey et al., 2013; Fuchs et al., 2016; Pastoll et al., 2013). A definitive answer to this question awaits a detailed understanding of how navigationally-relevant neurons are functionally connected in the MEC – a study that requires large numbers of simultaneously recorded cells. Alternatively, future models could incorporate new mechanisms that allow single variable nonheterogeneous networks to couple to networks with mixed selectivity and heterogeneous coding in such a way that each network does not destroy the other's unique coding properties. Such an advance may require the development of theories for how coherent pattern formation (Cross and Greenside, 2009) can arise from disordered systems (Zinman, 1979). Some recent models have at least taken promising steps to address mixed selectivity coding for velocity and position (Si et al., 2014; Widloski and Fiete, 2014). However, such models still lack extensive heterogeneity in tuning curve shapes. The integration of such mixed selective and heterogeneous coding features into attractors is an important issue for future work, as it could lead to conceptual revisions in our understanding of the mechanistic origin of MEC codes for navigational variables.

Our findings of non-linear mixed selectivity and adaptive coding in superficial MEC, as demonstrated by the LN model-based approach, also reveal important functional principles of decoding that apply to any downstream region reading out MEC spatial information. In multiple high-order cortical regions, such as parietal and frontal cortex, mixed selective neurons nonlinearly encode multiple task parameters (Mante et al., 2013; Park et al., 2014; Raposo et al., 2014; Rigotti et al., 2013). This gives rise to high-dimensional neural representations, which allow linear classifiers to identify large numbers of contexts or behavioral states (Fusi et al., 2016; Rigotti et al., 2013). The same theory could apply in the MEC, with non-linear mixed selective response profiles increasing the number of linearly independent neural patterns and thus allowing downstream decoders to identify a large number of unique spatial or navigational states. This could prove particularly beneficial to the dentate gyrus, a downstream hippocampal region proposed to transform MEC signals into distinct memory representations (Gilbert et al., 2001; Jung and McNaughton, 1993; Krueppel et al., 2011; Leutgeb et al., 2007; McNaughton and Morris, 1987; O’Reilly and McClelland, 1994; Treves and Rolls, 1992). At the same time, our finding that the MEC code for position and direction adaptively changes with running speed introduces the requirement that any region decoding this information must know the animal's running speed, or risk significant error in estimating the animal's location and heading. This fundamental requirement arises more generally in any adaptive code (Fairhall et al., 2001). This requirement could point to the importance of representing speed signals across multiple brain regions. Indeed, in addition to its encoding by MEC neurons, speed information is encoded by the firing rates of cortical projecting mesencephalic locomotor neurons and the frequency of parahippocampal theta oscillations (Jeewajee et al., 2008; Lee et al., 2014; Roseberry et al., 2016). These, as well as yet undiscovered, speed signals could thus support highly accurate decoding of position and heading from dynamic MEC codes across multiple cortical and parahippocampal regions.

The theoretical principles that mixed selective and heterogeneous coding offer significant computational benefits, together with our decoding simulations, raise the question of why some MEC neurons, such as grid cells, do not show even higher degrees of mixed selectivity. However, it is possible that more complex behavioral tasks will reveal that MEC neurons encode a much larger set of variables (McKenzie et al., 2016). In addition, our finding of adaptive coding highlights that many MEC neurons may flexibly change from encoding single variables to combinations of variables based on multiple behavioral demands, a phenomenon that could be more easily detectable in richer tasks (Gao and Ganguli, 2015). In support of these ideas, recent rodent work using complex tasks has demonstrated that the variables encoded by grid cells extend beyond navigation to include elapsed time and non-spatial task components (Keene et al., 2016; Kraus et al., 2015; McKenzie et al., 2016). Taken together, our statistical approach of nested LN model selection provides a general, unbiased procedure that can be applied to confront heterogeneous coding and mixed selectivity in the brain across multiple behavioral and internal variables. When combined with rich behavioral tasks, we hope this approach will provide new insights into the mechanisms, principles and function of neural coding, in the MEC and beyond.

Star Methods

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Lisa Giocomo (giocomo@stanford.edu).

Experimental Model and Subject Details

Mice

Data included both unpublished neural recordings (405 MEC cells from 5 male and 2 female C57BL/6 mice) and previously published neural recordings (389 MEC cells from 7 male 50:50% hybrid C57BL/6J:129SVEV mice Eggink et al., 2014) from adult wildtype mice. At the time of surgery, mice ranged were between 2 and 12 months in age. Mice and their littermates were housed together until surgical implantation of the microdrive. After implantation, mice were individually housed in transparent cages on either a reverse light cycle, with testing occurring during the dark phase (Eggink et al., 2014), or a normal light cycle, with testing occurring during the light phase (unpublished data). For unpublished data, all techniques were approved by the Institutional Animal Care and Use Committee at Stanford University School of Medicine. For data from Eggink et al., 2014, all experiments were performed in accordance with the Norwegian Animal Welfare Act and the European Convention for the Protection of Vertebrate Animals used for Experimental and Other Scientific Purposes and approved by the National Animal Research Authority of Norway.

Method Details

Data collection

Surgical implantation of chronic recording devices

Prior to surgery, two polyimide-coated platinum iridium 90-10% tetrodes (17 μm) were attached to a microdrive, cut flat, and had their impedance reduced to ∼200 kΩ at 1 kHz. For surgical implantation, mice were deeply anesthetized with isoflurane (induction chamber 3.0% with air flow at 1200 ml/min, reduced to 1-2% after the animal was appropriately placed in stereotaxic apparatus) and given a subcutaneous injection of buprenorphrine (0.3 mg/ml). The tetrode bundle was implanted in one hemisphere, 3.1 – 3.4 mm from the midline, angled 0 - 8 degrees in the posterior direction in the sagittal plane, 0.3 – 0.7 mm in front (AP) of the transverse sinus, and 0.8 – 1.1 mm below the dura. The microdrive was secured to the skull using dental cement and five jeweler's screws. A wire wrapped around a single screw fixed to the skull served as the ground electrode.

In vivo recording in mice during random foraging in open fields

For the collection of both datasets, ∼3 days after surgery, mice were placed in the recording environment and were allowed to explore untethered. In both data sets, the recording environment was a large open environment with black walls, with 228/275 sessions in 100 × 100 cm boxes, 29/275 sessions in 91.4 × 91.4 cm boxes, and 18/275 sessions in 70 × 70 cm boxes. Each environment contained a white polarizing cue on a single wall and was surrounded by a black curtain.

Approximately one week after surgery, data collection commenced and mice were connected to the recording equipment via AC coupled unity-gain operation amplifiers. During each recording session, mice foraged for chocolate flavored cereal randomly sprinkled across the environment. Each mouse experienced the environment not more than twice per day, with sessions separated by > 3 hours. Sessions where mice covered < 75% of the environment were not included in our analyses. The majority of recording sessions lasted 30 – 50 minutes (227/275 sessions) with the remaining sessions ranging between 12 and 122 minutes in length. During each session, position, head direction, and running speed were recorded every 20 ms by tracking the location of two LEDs placed on either side of the mouse's head. Spikes from single units were recorded at a 10 kHz sampling rate, and the local field potential was recorded with a 250 Hz sampling rate. After each session, tetrodes were moved by 25 μm until new well- separated cells were encountered. To ensure that each cell was only included in the analyses once, clusters and waveforms in TINT were compared between sessions. In cases were the same cell was repeatedly sampled, the session in which the cell had the largest number of spikes was chosen as the representative data point. Between recording sessions of different mice, the floor of the environment was washed with either soapy water or wiped with 70% ethanol. Mice rested in their home cage between recording sessions.

Spike sorting and the local field potential

After data collection, spikes were sorted manually with offline graphical cluster-cutting software (TINT software, Axona Ltd.). Isolation quality was computed for each unit recorded across all four channels (Schmitzer-Tobert et al., 2005). The local field potential (LFP) was filtered for theta frequency (4-12 Hz) using a Butterworth filter. The phase of the theta oscillation was computed using a Hilbert transform; this was then down-sampled to match the sampling frequency of position, head direction, and speed.

Histology

After the final recording session, mice were killed with an overdose of pentobarbital and transcardially perfused with 0.9% saline (wt/vol) followed by 4% formaldehyde (wt/vol). The brains were extracted and stored in 4% formaldehyde at ∼4 degrees Celsius. At least 24 hours later, the brains were frozen, cut in sagittal sections (30 μm), mounted onto transparent microscope slides and stained with cresyl violet. The location of the recording electrode tips were determined from digital pictures of the brain sections made using AxioVision (LE Rel. 2.4).

Details on LN model

LN model framework

To quantify the dependence of spiking on a variable, or combination of variables (position, head direction, speed, or theta power), LN models estimate the spiking rate (r_t) of a neuron during time bin t as an exponential function of the sum of the relevant value of each variable (e.g. the animal's position at time bin t, indicated through an ‘animal-state’ vector) projected onto a corresponding set of parameters. Models of this nature have been used to describe navigational coding in hippocampus, as well as the coding of running speed and time elapsed in the MEC (Acharya et al., 2016; Burgess et al., 2005; Hinman et al., 2016; Kraus et al., 2015). Mathematically, this is expressed as:

$$r=exp\left(\sum _i{X}_i^T{w}_i\right)/dt$$

where r denotes a vector of firing rates for one neuron over T time points, i indexes the variable (i ∈ [P,H,S, T]), X_i is a matrix where each column is an animal-state vector x_i for variable i at an instant of time, w_i is a column vector of learned parameters that converts animal state vectors into a firing rate contribution, and dt is the time bin (20 ms). For example, the PH model is: $r=exp({\sum }_P{X}_P^T{w}_P+{\sum }_H{X}_H^T{w}_H)/dt$. The exponential function here operates element-wise and gives rise to multiplication between exponentiated features (as e^a+^b = e^ae^b), which is consistent with known MEC coding principles (Burgess et al., 2005) and analyses of our owndata (Figure S2). Each animal-state vector denotes a binned variable value, all of whose elements are 0, except for one element, which is 1, corresponding to the bin the current animal state occupies. For example, animal position at time t is denoted by the t^th column of X_p, which contains 400 elements due to the 20 × 20 binning of position. Each element in the t^th column of X_p is 0, except for the element representing the bin containing the animal's position at time t.

Model optimization

To learn the variable parameters w_t for each cell, which convert the binned animal state for variable i into a firing rate contribution, we maximize the Poisson log-likelihood of the observed spike train (n) given the model spike number (r * dt) and under the prior knowledge that the parameters should be smooth. That is, we find $\widehat{w}=arg{max}_w{\sum }_{t}logP\left(n_t|exp({\sum }_i{X}_{i,t}^T{w}_i)\right)-{\sum }_i{\beta }_i\left({\sum }_j\frac{1}{2}{(w_{i,j}-w_{i,j+1})}^2\right)$,.where J indexes over parameter elements for a single variable and β_i represents the smoothing hyper-parameter for variable i (higher β_i values enforce smoother parameters). Position parameters are smoothed across both dimensions (rows and columns) separately. Values for β_i were constant across all cells and were chosen via cross-validation based on several randomly selected cells. The parameters were optimized using MATLAB's fminunc function. Model performance for each cell is quantified by computing the log-likelihood of held out data under the model. This cross-validation procedure was repeated 10 times (10-fold validation) and penalized models that over-fit the data, thus allowing valid performance comparisons between models of varying complexity.

Model selection

Models considered included 4 single variable models (P, H, S, T), 6 double variable models (PH, PS, PT, HS, HT, ST), 3 triple variable models (PHS, PHT, PST, HST) and one full model (PHST). To select the simplest model that best described the neural data, we first determined which single variable model had the highest performance. We then compared this model to all double variable models that included this single variable. If the highest performing double-variable model, on held out data, was significantly better than the single variable model, we then compared this model to the best triple variable model, and so forth. In all cases, if the more complex model was not significantly more predictive of neural spikes, the simpler model was preferred. Cells for which the selected model did not perform significantly better than a fixed mean firing rate model were marked unclassified. In all cases, significance is quantified through a one-sided signed rank test, with a significance value of p = 0.05.

Model-derived response profiles

We defined model-derived response profiles for a given variable j to be analogous to a tuning curve for that variable. These were computed as y = exp(w_j) * α/dt, where α = Π_i=[all other variables ≠j]^mean(exp(w_i)) is a scaling factor that marginalizes out the effect of the other variables. The scaling factor dt transforms the units from bins to seconds. Thus in essence, for each navigational variable, the exponential of the parameter vector that converts animal state vectors into firing rate contributions is proportional to a model-derived response profile; it is a function across all bins for that variable, and is analogous to a tuning curve. The mean and standard deviation of each parameter value was computed through 30 bootstrapped iterations in which data points were randomly sampled with replacement prior to the model fit.

Multiplicative versus additive codes

Related to Figure S2. Based on previously described features of conjunctive position × head direction tuning (Sargolini et al., 2006), our model assumes that cells exhibit ‘multiplicative’ tuning, defined as r(x,y) = r(x)*r(y). Alternatively however, cells could exhibit additive tuning, defined as r(x,y) = r(x) + r(y). Differentiating between these two models has important implications for medial entorhinal cortex (MEC) function, as multiplicative coding may point to a fundamental transformation of information in MEC, while additive coding suggests signals simply linearly combine in MEC.

To quantify the nature of conjunctive MEC coding and verify our assumption that tuning curves ‘multiply’, we examined cells that significantly encoded both position (P) and head direction (H) based on the single-variable model performance (e.g. both the P and H models had to perform significantly better than a mean firing rate model). To distinguish tuning curve multiplication from addition, we exploited differences in how the tuning curve for r(x*,y), or the tuning curve across y for a fixed value x*, will change as a function of r(x*). For example, in the multiplicative model, an increase or decrease in r(x*) will stretch or compress r(x*,y), whereas in the additive model it will simply shift r(x*,y). To quantify these differences, we took × to be position and y to be head direction, and first binned position into 400 bins. We then computed the firing rate for each position bin (i.e. computed r(x*) for every x*), sorted the position bins according to their firing rate values, and divided the sorted bins into four segments. Each segment thus corresponded to a (potentially fragmented) region of the environment with approximately the same firing rate. We then generated a series of head direction tuning curves based on the spikes and head directions visited during each segment.

Two analyses were then applied to dissociate multiplicative and additive coding. First, we examined the range (max firing rate [FR] – min FR) of each HD tuning curve (hereafter referred to as r_i(HD)) as a function of the mean FR for position segment i. Under the multiplicative model, the range should increase with mean position segment FR, while under the additive model, the range should be constant. We observed that the relationship between the range of the HD tuning curve and mean position segment FR exhibited a positive, rather than flat, slope in the majority of neurons (85/89; median slope > 0 with p = 5e-16). Thus, because the range of the head direction tuning curve scales with the average firing rate of position, these data point towards a multiplicative model. Next, to confirm our results, we examined if the family of head direction tuning curves across different position segments within a given cell were better related through shifting or scaling (see Figure S2 for an example). We computed, for each pair of head direction tuning curves r_i(HD) and r_j(HD), the optimal β that satisfies r_i(HD) = β + r_j(HD) (the additive model) and the optimal γ that satisfies r_i(HD) = γ *r_j(HD) (the multiplicative model). We then determined how well the prediction of r_i(HD) (predicted using β +r_i(HD), or γ * γ_j(HD)) matched the true r_i(HD)by computing the fraction of variance explained for each model. The fraction of variance explained was computed as 1 minus the ratio of the mean-squared error of the model and the total sum of squares. Finally, we computed how often the multiplicative model out-performed the additive model across every pair of tuning curves for each cell. Pairs were only considered if ry contained non-zero elements (i.e. the tuning curve was not perfectly flat at 0 spikes/s). Consistent with our previous method, we found that for a majority of cells with at least two pairs that were considered, the multiplicative model estimate of r_i(HD) more closely matched the real r_i(HD) (58/75, median > 0.5 with p = 1.0e-10).

Investigating time-shifted models

Related to Figure S3. For each cell (N = 794), 33 time-shifted position, head direction, and speed (11 models for each variable) models were fit. For each variable, values were shifted {-1500, -1000, -740, -500, - 240, 240, 500, 740,1000, 1500} milliseconds in time compared to the spike train. The log-likelihood of each model was then computed, and compared with a model in which P, H, or S values were not shifted. Models in which a shifted model performs significantly higher than the non-shifted model (in addition to performing significantly better than a mean-firing rate model) were recorded according to their preferred shift. If a shifted model does not out-perform the non-shifted model, the cell is recorded as non-shifting if the non-shifting model performance is significantly higher than a mean firing rate model.

Details on tuning curve-score method

Computing tuning curve scores

Grid and border scores were generated by first computing a position tuning curve, or spatial map, in which animal location was binned into 2 cm × 2 cm bins and the mean number of spikes/s was computed for each bin (Langston et al., 2010; Wills et al., 2010). Only data in which the animal traveled between 2 and 100 cm/s were included. For grid scores, a circular sample of the 2-d autocorrelation of this spatial map was computed and correlated with the same sample, rotated 30°, 60° 90°, 120° and 150°. The minimum difference between the (60° 120°) rotations, and the (30° 90°, 150°) rotations was then defined as the grid score (Langston et al., 2010). Border scores were generated from an adaptively-smoothed version of the spatial map (Solstad et al., 2008). Border scores were computed by $\frac{CM-DM}{CM+DM}$, where CM is the proportion of high firing-rate bins location along one wall and DM is the normalized mean product of firing rate and distance to the nearest wall of a high firing rate bin.

Head direction scores were computed by first binning head direction into 3° bins and computing the mean number of spikes/s for each bin (only data in which the animal traveled between 2 and 100 cm/s were included). The resulting tuning curve was then smoothed using a boxcar filter (span = 14.5°), and the mean Rayleigh vector length of the tuning curve was recorded as the head direction score.

Speed scores were computed from the correlation between firing rate (binned into 20 ms bins, smoothed with a Gaussian filter following Kropff et al., 2015) and running speeds between 2 and 100 cm/s (Kropff et al., 2015). Speed stability was computed as the mean correlation between speed tuning curves (mean spikes/s in every 5 cm/s bin) generated from quarters of the session. Only speed cells that passed both the speed score and speed stability thresholds were included in the analysis.

Computing tuning curve score thresholds

Thresholds for each score value (grid, border, head direction, and speed), in addition to speed stability, were computed by taking the 99^th percentile of a null (shuffled) distribution of scores. Null distributions of score values were computed by time-shifting the spike trains of individual cells by a random amount between 20 seconds, and the length of the trial minus 20 seconds, and re-computing the relevant score value.

Calculation of stability metrics

Spatial stability was computed as the mean correlation between the spatial maps generated from the first and second halves of a recording session. Angular stability was computed as the mean correlation between head direction tuning curves generated from the first and second half of the data.

Comparing LN and TCS methods

Field number and spatial coherence

Fields were detected in the spatial maps as connected regions containing at least 5 bins with a firing rate above 1 Hz and at least 20% of the peak firing rate (Figure 3D). Spatial coherence calculates the extent to which the firing rate in a given position bin (a pixel in the spatial map) predicts the mean firing rate of neighboring bins (or neighboring pixels). This is computed as the arc-tangent, or the Fisher z-transformation, of the correlation between a given pixel and the average value of the neighboring 3-8 pixels, for all pixels in the spatial map (Brun et al., 2008) (Figure 3D).

Peak number in head direction tuning

Peaks in the directional tuning curve were detected using the findpeaks MATLAB function on a smoothed version of the head-direction tuning curve. Each tuning curve is smoothed using a Gaussian filter with σ = 30 degrees, computed over the 20 nearest neighbors of each point. Each tuning curve is padded with 10 extra points of the tuning curve, wrapped around, on each side to avoid edge-effects of the convolution. In order to account for situations in which the peak is split across 0 and 360 degrees (in which case findpeaks would return 0), the tuning curve was circularly shifted and the maximum number of peaks detected across all shifts was recorded (Figure 3E).

Analysis of speed slope and curvature

The normalized speed slope was computed by dividing the slope of the best-fit line in the least-squares sense of the speed tuning curve by the mean value of the speed tuning curve (Figure 3F). The speed curvature quantifies the degree to which the speed response profile exhibits curves; a straight line would receive a minimum curvature score, while a high-frequency sine wave would exhibit a large curvature score. To account for the difference in range across tuning curves, we first normalized each speed tuning curve to have unit range. In addition, each tuning curve was smoothed using a Gaussian filter with σ = 2 bins, computed over the 6 nearest neighbors of each point. We then directly computed the curvature as the summed squared second-derivative of range-normalized, smoothed tuning curves (Figure 3F).

Decoding from MS and SV populations

Cells were first split into two groups based on whether they exhibited mixed selectivity (PHST, PHS, PHT, PST, HST, PH, PS, or HS cell types) or single variable (PT, HT, ST, P, H, S) coding properties. As there are more MS than SV cell types, cell numbers were matched in each group (n = 269 in both) by randomly rejecting MS cells. Decoding accuracy was assessed by first simulating spike trains, which were based on Poisson statistics and a time-varying rate parameter. In each group, spikes (n_c) for neuron c were generated by drawing from a Poisson process with rate r_c where $r_c=exp({\sum }_i{X}_i^T{w}_{i,c})/dt,w_{i,c}$ are the learned parameters from the selected model for neuron c, X_i is the behavioral state vector, and i denotes the variable (P, H, S). If the model selection procedure determined that a cell did not significantly encode variable i, then w_i,c = 0. The behavioral state vector is derived from the position, head direction, and speed information from a randomly chosen recording session.

Next, the simulated spikes – in conjunction with the known parameters – were used to estimate the most likely position, head direction, and running speed. To decode position, head direction, and running speed at each time point t under each decoder, we found the animal state that maximized the summed log-likelihood of the observed simulated spikes from t – L to t:

$$\widehat{X(t)}=arg{max}_{X^t}\sum _{l=0}^L\sum _{c=1}^{C=N}logP\left(n_c|exp\left(\sum _i{X}_i^{{(t-l)}^T}{w}_{i,c}\right)\right)$$

where C is the number of cells in that population. Decoding was performed on 100 randomly selected time points of the session, and using 400 ms (L = 20 time bins) of spiking history. The average position, head direction, and speed decoding error were recorded. This procedure was performed 20 times, over which the mean and standard error of the mean were computed and statistics were performed.

Heterogeneity of entorhinal coding

Relative contributions of P, H, and S

To investigate the diversity in the contribution of P, H, and S to spike train prediction, we first identified all cells that encoded PH, PHT, PS, PST, HS, HST, PHS or PHST by the LN model selection procedure. We then identified the contribution of a given variable by finding the difference in model performance (spike-normalized log-likelihood increase from baseline) between the selected model and the model that contains all variables in the selected model, minus the given variable. For example, if a cell's selected model is PH, we find the P contribution by computing LLH(P) = LLH(PH) - LLH(H), where LLH(model) indicates spike- normalized log-likelihood increase of that model (Figure 5B-C).

To plot the contribution of P, H and S in three dimensional space (Figure 5B), we calculated the contributions of variables as described above but additionally calculated the contribution of variables even when they were not contained within the selected model of a cell, for example S is not contained in the PH model. We find the contribution by taking the difference between the log-likelihood of the model containing the variables in the selected model plus the variable of interest and the selected model. For example, the contribution of S to a cell with a selected PH model is computed as LLH(S) = LLH(PHS) - LLH(PH). Frequently, contributions of variables that were not significantly encoded by a cell were very small, consistent with the model selection procedure indicating that the LLH increase for these variables was not significant. In the case that the more complex model performed worse that the simpler model, negative values were reset to 0. This is reflected in the plot in Figure 5B, where very few values for the PH, PS and HS cells fall in the center of the graph. After computing the contribution of P, H, and S variables to the spike prediction for each cell, we then normalized the contribution by enforcing LLH(P)²+ LLH(H)² + LLH(S)² = 1 (the unit norm).

Using PCA to identify neural clusters

To compare all parameters of a given variable across cells (Figure 5D-G), we built a n × m matrix X for each set of parameters, where n = number of cells in the analysis and m = number of parameters. For example, since there are 421 cells that encode position, the X matrix will be 421 × 400. While we cannot visualize this, we could imagine plotting the 421 data points in a 400 dimensional space, where each of the 400 axes correspond to the (model-derived) firing rate for a given position bin. In order to visualize these data, we used principal component analysis (PCA) to project these data points onto a 2 or 3-dimensional subspace. To do this, each row is first mean-subtracted and re-scaled to have unit range. This pre-processing step first centers the data around the origin (through mean-subtraction), and then re-scales all response profiles so that cells with similar shapes in the response profiles are close to each other in the reduced subspace. We then projected the data onto the first 2-3 principal components of X (3 for position parameters, 2 for all other parameters), which allowed us to visualize the structure of response profiles. Three principal components were chosen for position as there were three large eigenvalues; two principal components were chosen for head direction, speed, and theta as there were only two large eigenvalues. Interestingly, the projected data for each set of parameters appeared to have some interpretable organization: position response profiles were organized such that high frequency, grid-like patterns were in the center of the plot, while low-frequency, border-like patterns were on the edge of the plot; head direction and theta phase response profiles were organized by mean vector length and preferred direction, such that uni-modal responses were on the outside and multi-modal responses were on the inside; speed response profiles were organized by the overall slope and curvature.

Investigating dynamic coding properties

Down-sampling procedure for speed analysis

Each session was split into epochs of fast (10-50 cm/s) and slow (2-10 cm/s) running speeds. To match the position and head direction coverage for each epoch, we first binned position and head direction into 100 bins and 18 bins, respectively, and computed the occupancy time for each bin. We then matched the position and head direction coverage across the two epochs by down-sampling data points from either epoch so that occupancy time was matched for each position bin, with points removed based on the difference in head direction occupancy. Finally, we matched total spike numbers for each epoch through random rejection of spikes in the epoch with more spikes. We repeated this entire procedure 50 times, as several steps in this procedure were stochastic and thus could affect model selection (described in next section).

Model selection across epochs

To identify the population of cells that robustly gain, lose, or maintain coding features for fast compared to slow running speeds, we analyzed the selected models across the 50 downsampling iterations for each cell. This procedure allowed us to identify the population of cells for which the gained, lost, or retained coding features were not a strict function of which specific time points or spikes were rejected. We identified the cells that gained, lost, or maintained position or direction coding as those that gained, lost, or maintained coding for a variable for ≥75% of the iterations. The cell had to gain, lose or maintain coding for the same variable – for example, gain coding for position at fast speeds - over 38+ iterations to be counted. In addition, mixed selective cells (cells that robustly encode PH) during each epoch were identified as those that encode PH for at least 75% of the iterations. To ensure that our selection of 75% as the threshold did not influence the results, we repeated a subset of the analyses relevant to Figure 5 under different thresholds (50%, 60%, and 80%) and observed all the same effects (Figure S6C).

In Figure 6Biii, cells that gained P or H were split into two groups: those that encoded neither P nor H at slow speeds and encoded at least one variable during fast speeds (0→1+), and those that encoded either P or H at slow speeds and encoded PH at fast speeds (1→2). As cells can exhibit slightly different selected models across each iteration, we split these cells according to the method of variable gaining (0→1+ or 1→2) that happened most frequently across 50 iterations.

Computing mutual information

First, we computed the model-derived response profiles for each cell. This procedure is identical to that described for the full-session analyses, with one exception: we do not assume uniform coverage and thus compute $\alpha ={\prod }_{i=[P,H,S,T]}exp(P_i^T{w}_i)$, where $P_i^T$ is the probability distribution of animal occupancy across bins for variable i.

Mutual information between the neural spikes (n) and binned position or head direction (q) is given by:

$$MI(n,q)=\sum _{q}P(q)\left[\sum _{n\in \{0,\mathit{\text{max}}\}}P(n|q)log\frac{P(n|q)}{{\sum }_{q=1}^{Q}P(n|q)P(q)}\right]$$

where Q is the total number of bins (400 for P, 18 for H), and P(q) is the probability that the animal occupies bin q. Following our Poisson model framework, we can compute $P(n|q)=\frac{{(y_q)}^n{e}^{-y_q}}{n!}$, Where y_q is spike count in bin q.

Decoding variables during fast/slow epochs

Spike trains for cells within the ‘fast’ or ‘slow’ populations were first simulated using the set of learned parameters from each epoch. Spikes (n_c) for neuron c were generated by drawing from a Poisson process with rate r_c where $r_C=exp({\sum }_i{X}_i^T{w}_{i,c})/dt,w_{i,c}$ are the learned parameters for that epoch, X_i is the behavioral state vector, and i denotes the variable (P or H). If the model selection procedure determined that a cell did not significantly encode variable i, then w_i,c = 0.

To decode the animal's state (the position and head direction) at each time point t under each decoder, we found the animal state that maximized the summed log-likelihood of the observed simulated spikes from t - L to t:

$$\widehat{X^{(t)}}=arg{max}_{X^t}\sum _{l=0}^L\sum _{c=1}^{C=N}logP\left(n_c|exp\left(\sum _i{X}_i^{{(t-1)}^T}{w}_{i,c}\right)\right)$$

where C is the number of cells in that population. The decoder type (slow or fast) was determined by whether the w_i,c parameter values were derived from slow speed or fast speed epochs, while the spikes decoded (slow spikes or fast spikes) were determined by whether the n_c values were computing using the parameters learned during slow speed or fast speed epochs. For a single decoder, decoding error for each variable was then computed as the mean absolute difference between the estimated and actual position or head direction. L was varied from 3 to 50 time bins (60 ms to 1000 ms) in 13 steps. We repeated this process (simulating spike trains and then decoding a randomly chosen, fixed animal state over 13 integration times) 1000 times.

Quantification and Statistical Analysis

Custom-written MATLAB scripts were used to analyze all data. Unless stated otherwise, all error bars and data quantifications are expressed as mean ± standard error of the mean (SEM). Statistical tests are listed following the relevant result given in the results, figure legend, or Method Details. Unless otherwise stated, p < 0.05 was taken as the criterion for significance. Multiple comparisons were corrected using a Bonferroni correction.

Custom statistical analyses

Comparison of proportions

This metric was determined by first computing the proportion for the first population $(p_1=\frac{n_1}{{\mathit{\text{total}}}_1})$, the proportion for the second population $(p_2=\frac{n_2}{{\mathit{\text{total}}}_2})$, and the average proportion across both populations: $(p=\frac{n_1+n_2}{{\mathit{\text{total}}}_1+{\mathit{\text{total}}}_2})$. We then compute a z-statistic through $z=\frac{|p_1-p_2|}{\sqrt{p}(1-p)(1/{\mathit{\text{total}}}_1+1/{\mathit{\text{total}}}_2)}$, and a p-value using p = 2 * (1 - normcdf(z, 0,1), where normcdf is a MATLAB function.

Frequency of MS neurons along DV axis

We first generated a bar graph for the proportion of MS cells across different dorsalventral depths (depth binned into 4 bins; bin size = 385 μm), with depth measured from the dorsal border of the MEC. Due to the angle at which the tetrodes are implanted, more cells are sampled in dorsal compared to ventral MEC. We then computed the slope of this graph by fitting a line to bar values (slope = 5e-5 MS proportion/pm); this slope indicates the proportion of observed MS cells slightly increases along the dorsal-ventral axis. To next determine if the experimentally-observed slope was significantly larger than what would be expected by chance, given the uneven sampling across the dorsal-ventral axis, we generated a series of null data sets. For each null data set, we randomly selected N cells as ‘mixed selective’ (N = 292 cells, the number of MS cells in the original data set, drawn from the entire dataset of 794 cells), recomputed the bar graph of proportion of ‘mixed selective’ cells observed across 4 depth bins, and then re-computed the slope. This process was then repeated 10,000 times to generate a distribution of slopes to which the experimentally-observed slope can be compared. P-values were computed by analyzing the fraction of slopes that were smaller (or larger) than what was observed in the data.

Identification of neural clusters in a reduced space

To determine whether neurons of a given type were clustered in the space defined by the first 2-3 principle components, the average distance (μ) to each neuron's k-nearest neighbors (where each neighbor is of the same type as the reference neuron) was computed. The value of k was varied from 1-10. We chose 10 as the maximum as some sub-populations had small numbers of cells (e.g. S cell n = 9; in this case k=9 and k=10 are equivalent). We computed the likelihood of observing μ by comparing it to a null distribution. This distribution was generated by scrambling cell labels and re-computing mean nearest-neighbor distances. P- values were computed by analyzing the fraction of mean nearest-neighbor distances that were smaller than what was observed in the data. The resulted p-value is Bonferroni corrected, with significance being achieved by p = 0.05/10.

Comparison of decoding accuracy over integration time

We applied two analyses to compare the performance of two decoders (termed ‘slow decoder’ and ‘fast decoder’) as a function of their integration time. In the first, we determined whether the difference in error between the slow and fast decoder was positive, meaning that the fast decoder outperformed the slow decoder, for short (60-200 ms) integration times. To do this, we determined whether the average pairwise decoding error between 1000 iterations of the slow and fast decoders, averaged over all integration times, was significantly greater than zero using a signed-rank test. In the second, we determined whether the difference in error between the two decoders decreased with integration time. We computed the slope of the best-fit line to the average error difference (computed pair-wise across iterations) across integration times. We then compared this to a null distribution of slopes, which was generated by computing the slopes of error differences of 10,000 null data sets. Each null data set was generated by first pooling the errors for each population across integration times (i.e. creating a set of 2,000 13- element vectors; 13 arises from the number of tested integration times), randomly assigning each vector to either the slow or fast population, and then computing slope of the difference in decoding error between the two populations across integration time. Vectors, rather than individual data points, were shuffled due to the fact that individual data points within the vector are statistically related (since they are all associated with decoding a particular animal state). P- values were computed by analyzing the fraction of shuffled-data slopes that were smaller than what was observed in the data, and multiplying by 2 (for a two-tailed test).

Data and Software Availability

Custom MATLAB code generated to fit the series of LN models and identify the highest- performing models can be found at: https://github.com/GiocomoLab/ln-model-of-mec-neurons. All other code and data will be made available upon request (fulfilled by Lead Contact, giocomo@stanford.edu).

Highlights.

• -An unbiased statistical approach reveals novel entorhinal codes for navigation
• -Superficial entorhinal has multiplexed representations of navigational variables
• -Entorhinal cells exhibit highly heterogeneous but informative firing patterns
• -Entorhinal codes adapt with running speed to better code position and direction