AN APPROACH TO RECONCILING COMPETING ETHICAL PRINCIPLES IN AGGREGATING HETEROGENEOUS HEALTH PREFERENCES

Abstract

Background

Health-related quality of life (HRQL) scores are used extensively to quantify the effectiveness of medical interventions. Societal preference-based HRQL scores aim to produce societal valuations of health by aggregating valuations from individuals in the general population, where each aggregation procedure embodies different ethical principles, as explained in social choice theory.

Methods

Using the Health Utilities Index as an exemplar, we evaluate societal preference-based HRQL measures in the social choice theory framework.

Results

We find that current preference aggregation procedures are typically justified in terms of social choice theory. However, by convention, they use only one of many possible aggregation procedures (the mean). Central to the choice of aggregation procedure is how to treat preference heterogeneity, which can affect analyses that rely on HRQL scores, such as cost-effectiveness analyses. We propose an analytical-deliberative framework for choosing one (or a set of) aggregation procedure(s) in a socially credible way, which we believe to be analytically sound and empirically tractable, but leave open the institutional mechanism needed to implement it.

Conclusions

Socially acceptable decisions about aggregating heterogeneous preferences require eliciting stakeholders’ preferences among the set of analytically sound procedures, representing different ethical principles. We describe a framework for eliciting such preferences for the creation of HRQL scores, informed by social choice theory and behavioral decision research.

Introduction

Generic health-related quality of life (HRQL) measures place individuals’ health status on a common scale, allowing researchers to compare the effects of clinical trials across individuals and summarize the results of population health studies [1]. Utility-based measures are a subset of HRQL measures, and attach scores to states of health. These scores can be used for outcomes, e.g., quality-adjusted life years, providing the estimates needed by regulatory analysts [2, 3].

To produce societal preference-based HRQL scores, the common practice is to aggregate the preferences of a sample of individuals designated as representing the target population. That might mean eliciting the preferences of patients with a disease, experts in a disease, or individuals held to represent society as a whole. For example, a sample of individuals with naturally varying vision might be asked to assess, in numeric terms, the relative quality of life with blindness and 20/20 vision.

Although analysts need such aggregation procedures so that they can incorporate HRQL estimates into their models, aggregating individuals’ estimates into societal ones poses a fundamental problem in social choice theory [4, 5, 6, 7, 8]. It has long been known that, under certain general assumptions, there is no unique solution to this aggregation problem, given any heterogeneity in individuals’ preferences. Rather, many solutions are possible. Selecting a method to collapse a distribution of preferences into a single number implies an ethical judgment about what distributional information matters.

Foundational work in utility-based HRQL measurement (e.g., [9]) recognized the preference aggregation problem. Concurrent research in social choice theory revealed the implications of alternative aggregation procedures (e.g., [10]). Here, we integrate the two fields, taking advantage of advances in both during the ensuing years. We use the Health Utilities Index (HUI) as an exemplar [11, 12, 13], examining it in terms of key concepts in social choice theory [5, 8, 10], thereby providing a concrete example that could be followed with other societal preference-based scores.¹

We first identify the conditions under which HUI is normatively justified, and then show the range of acceptable aggregation procedures, each of which expresses an ethical stance. Finally, we offer an approach for choosing among these options. Related concerns can be found in assessments of other forms of analysis [14, 15, 16, 17]. Our approach is generalizable to any societal preference-based HRQL measurement system.

Methods

Below, we describe relevant results from social choice theory, applicable to specifying any societal preference-based HRQL measurement system. Additional background material on societal preference-based HRQL scores and the HUI system is available in the online supplemental information (https://osf.io/2xz2a).

Social choice theory

Social choice theory characterizes preference aggregation procedures that define societal preferences. It begins with a set of axioms that a preference aggregation procedure must satisfy, in order to be deemed rational. One commonly used set has these three axioms:²

1. Unrestricted Domain: Any set of individual preferences is allowed.

2. Independence of Irrelevant Alternatives: If two groups of utility functions agree on a subset of health states, then the societal preferences of the two groups agree on that same subset.

3. Weak Pareto Criterion: If all individuals prefer health state x to health state y, then the societal preference should as well.

A fundamental result from social choice theory is Arrow’s Impossibility Theorem [5], which states that the only guaranteed way to aggregate individual preferences that satisfies these axioms is dictatorship: impose the preferences of one individual on the entire group. It is called an impossibility theorem because “non-dictatorship” is an axiom in Arrow’s framework, making it impossible to satisfy the full set of axioms.

Arrow’s result has been interpreted as precluding any non-dictatorial aggregation procedure from being normatively justified. However, as Sen [8] initially showed, and Roberts [10] elaborated, Arrow’s theorem is a special case of a more general result about preference aggregation. Sen and Roberts identified two aspects of individuals’ preferences that determine the type of aggregation that is possible: informational content and interpersonal comparability. Together, they constitute the informational basis of the preferences.

The informational content of an individual utility function reflects its measurement scale; for example, ordinal or interval. Ordinal preferences provide only enough information to rank options. For example, assigning 15 to option A, 5 to option B, and 0 to option C means that A is preferred to B, B to C, and A to C, but nothing more. With cardinal preferences, utility is on an interval scale, so that units of utility have consistent meaning across the scale. Thus, in the example, A is preferred to B by twice as much as B is preferred to C, meaning that there is intrapersonal comparability of utility differences. Ordinal and cardinal preferences, on ordinal and interval scales, respectively, define what can be said about an individual’s preferences, but say nothing about interpersonal comparisons among individuals’ preferences.

Following Sen and Roberts, we distinguish two types of interpersonal comparability: level comparability and unit comparability. Level comparability allows saying whether one person’s HRQL is better, or worse, than another’s. Unit comparability allows saying whether a change in one person’s HRQL is greater or less than a change in another’s (e.g., one person improves more with a treatment) [18].

If preferences have cardinal informational content, level comparability, and unit comparability, then they satisfy cardinal full comparability. Sen and Roberts showed that Arrow’s result applies to the special case of preferences that are ordinal and completely non-comparable – and that non-dictatorial aggregation procedures are possible when preferences are cardinal or allow interpersonal comparability.

We apply the Sen-Roberts framework to determine when aggregation procedures in HRQL measurement can be normatively justified. We use HUI as an example, and then consider general conditions. We begin by examining the assumptions that HUI makes about the informational content and comparability of individual preferences. We then describe the preference aggregation procedures that these assumptions allow. Finally, we describe an empirical framework for choosing among these procedures, which can be applied to current aggregation procedures and might suggest new ones.

Results

Utility elicitation

The normative justification of any aggregation procedure, including those used in HUI,³ depends on its ability to meet social choice theory’s demands regarding the informational basis of the preferences and the appropriateness of its axioms. In the case of HUI, that means establishing the informational content (ordinal or cardinal) and interpersonal comparability (level and unit) of preferences elicited on a scale from 0 to 1, where 0 represents the utility of some lower anchor state (e.g., dead, the most-disabled state) and 1 represents the utility of the full health state (i.e., the most-able state). Participants then assign numbers between 0 and 1 to a set of intermediate health states using methods that rely on the standard gamble technique, producing cardinal preferences [19]. Furthermore, HUI assumes full comparability: both utility values and changes in utility values are treated as comparable across people.⁴ Thus, HUI assumes cardinal full comparability.

Determining the applicability of the social choice axioms requires evaluating utility elicitation and aggregation procedures in their light. The first axiom, Unrestricted Domain, deals with both utility elicitation and aggregation, while the other axioms deal primarily with aggregation. We consider each axiom in turn.

The axiom of Unrestricted Domain requires that the preference aggregation procedure can be followed with any set of individuals. A classic violation of this axiom is majority rule in Arrow’s context, where preferences are ordinal and non-comparable. Majority rule is a permissible aggregation procedure only if one is allowed to remove some number of individuals. Thus, majority rule does not conform to this axiom, because it necessarily excludes individuals in order to produce societal preferences. In contrast, HUI adheres to the axiom of Unrestricted Domain because it can accept any individual’s preferences as inputs – although in practice HUI disallows incoherent responses, such as valuing a health state higher than one that dominates it (i.e., a health state that is as good or better on all attributes [11]).

Independence of Irrelevant Alternatives requires the societal ranking of any subset of states to be solely a function of individuals’ utilities for each of those states. Therefore, preferences for other health states should be irrelevant, as should an individual’s current health state. HUI combines preferences according to this principle, defining the societal preference of a given state as a function of individuals’ preferences for that state alone.

The Weak Pareto Criterion ensures that unanimous preferences, should they exist, prevail, precluding any other concerns.⁵ HUI methods adhere to this axiom, meaning that unanimity about a ranking would result in the societal preference preserving that ranking.

Therefore, by examining how HUI elicits individuals’ preferences and combines them to produce its aggregate score, we find that HUI assumes cardinal full comparability, and satisfies the three axioms of Unrestricted Domain, Independence of Irrelevant Alternatives, and the Weak Pareto Criterion. The informational basis and the axioms then determine the aggregation procedures that are normatively permissible. An analogous examination of the elicitation and aggregation procedures of any other societal preference-based score should be sufficient to determine its informational basis, and thus its normatively justifiable aggregation procedures. In the next section, we define those procedures for the HUI system.

Normatively justifiable aggregation procedures

The aggregation procedure used in HUI is based on the mean. It can be written as:

$$U=U_{\mathit{avg}}=\frac{1}{n}{\displaystyle \sum _i{u}_i}.$$ (1)

Thus, the societal utility function (U) is the average of the individual utility functions (u_i). Applying the Sen-Roberts test means asking whether this function U_avg respects the cardinality and interpersonal comparability conditions of the individual utility functions (i.e., cardinal full comparability).

Roberts [10] describes the set of such normatively justifiable societal utility functions, under many different informational bases. With cardinal full comparability, averaging individuals’ utilities is one such function. Thus, the HUI averaging strategy (equation (1)) is consistent with social choice theory. However, there are, as Roberts notes, an infinite number of other normatively justified aggregation procedures under cardinal full comparability, each of which adjusts the average (equation (1)) by another function.⁶ For example, one could define the societal utility of health state x (i.e., U(x)) as a weighted average of U_avg(x) and the minimum utility among the individual utility functions evaluated at that health state.⁷ In contrast to U_avg, this alternative U penalizes health states that leave one person with a low utility, even if everyone else is well-off. We explore the implications of such differences in the next section. Table 1 lists other normatively justifiable alternative forms for U.

Table 1. Normatively Justifiable Aggregation Procedures under Cardinal Full Comparability.

A variety of aggregation procedures (and their associated societal utility functions) when cardinal full comparability applies, i.e., when preferences are cardinal and when utility levels and differences in utility are comparable across people. The general form of any societal utility function in this context is $U\left(x\right)=U_{\mathit{avg}}\left(x\right)+g(u\left(x,·\right)-U_{\mathit{avg}}\left(x\right)),$ where U_avg(x) is the average utility at health state x, g is a homogeneous function of degree 1, and u(x, ·) denotes the function that maps an individual to their utility for health state x. See Roberts [10, p. 431] for more detail on the first four of these functions, as well as for other examples.

Aggregation Procedure	Societal Utility Function	Description	Features
Mean	U(x) = Uavg(x)	Societal utility is average utility.	Insensitive to preference heterogeneity.
Minimum-adjusted	U(x) = αUavg(x) + (1−α) mini u(x, i), α ε [0, 1]	Adjust average utility to account for the minimum utility. The parameter α weights the contribution of the average and the minimum in defining the societal utility.	Health states with lower minimum utilities relative to their means – leaving some people much worse off than average – have lower societal utility. When α = 0, it is concerned only with the worst off.
Maximum-adjusted	U(x) = αUavg(x) + (1−α) maxi u(x, i), α ε [0, 1]	Adjust average utility to account for the minimum utility. The parameter α weights the contribution of the average and the maximum in defining the societal utility.	Health states with higher maximum utilities relative to their means – leaving some people much better off than average – have higher societal utility. When α = 0, it is concerned only with the best off (for whom a treatment could be most cost-effective).
Variance-adjusted	U(x) = Uavg(x) + kσ, k ε ℝ, α ε [0, 1]	Adjust average utility by the standard deviation of the distribution. The parameter k allows control over how much the standard deviation affects the utility function.	When k < 0, treats health states with inequitable distributions of utility – where a given mean utility is attained by balancing those who are well off with many who do very poorly – as having lower societal utility. This is one way to operationalize equity.
Skew-adjusted	$U\left(x\right)=U_{\mathit{avg}}\left(x\right)+k\sqrt[3]{\mathrm{skew}},k\mathrm{\epsilon }ℝ$	Adjust average utility by the skew of the distribution. The parameter k allows control over how much the skew affects the utility function.	Can distinguish between health states based on their skew. For example, could penalize negatively-skewed distributions, whose health states leave many poorly off. Similarly, can favor health states that leave many well off.
nth moment	$U\left(x\right)=U_{\mathit{avg}}\left(x\right)+k\sqrt[n]{m^n},k\mathrm{\epsilon }ℝ$	Adjust average utility by the nth root of the nth moment of the distribution (mn). The parameter k allows control over how much the nth moment affects the utility function.	(Subject to the definition of mn.)

HUI’s cardinal fully comparability and adherence to the set of social choice axioms, demonstrated in the previous section, determines its normatively acceptable aggregation procedures. The procedure that the HUI system chose – averaging, U_avg – is normatively permissible. However, so are an infinite number of alternatives. That raises the question of how to choose among these possibilities. We frame the answers in terms of what is lost by relying on each.

Criteria for choosing among normatively acceptable aggregation procedures

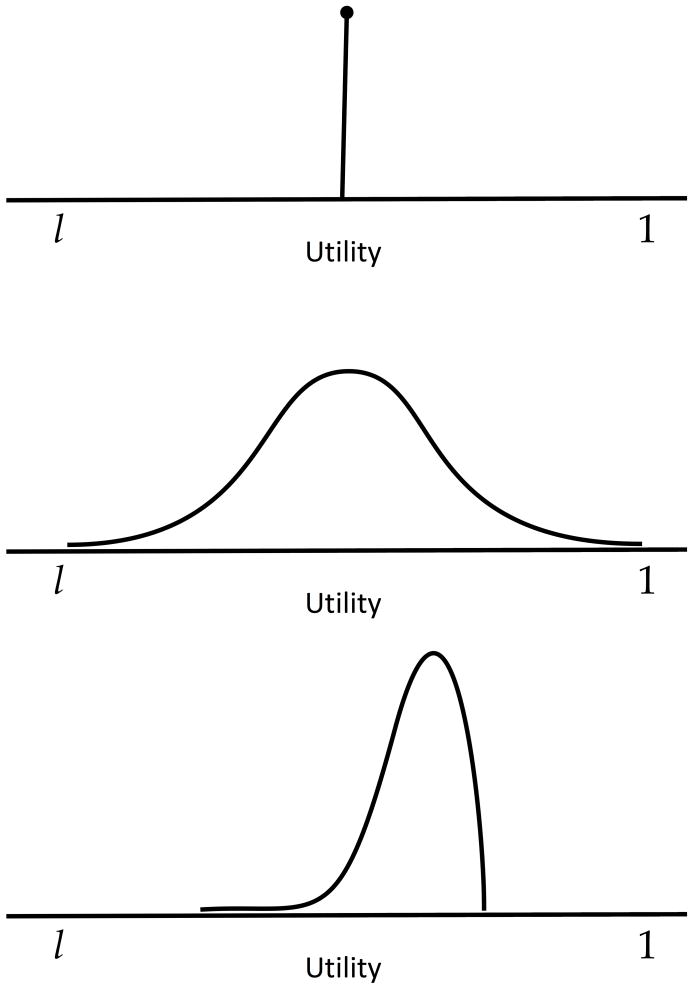
As a way of illustrating the impact of alternative preference aggregation procedures, Figure 1 shows three hypothetical distributions of individuals’ utilities for a health state. All three have the same mean value. The top distribution represents a health state with unanimity: everyone agrees on its utility. The middle distribution is bell-shaped. Utilities assigned to walking with a cane might have this shape, if they were elicited from individuals whose lifestyles range from sedentary to highly active. The bottom distribution is left-skewed. It might capture the utility assigned to imperfect but correctable vision, which is moderately high for most people, for whom glasses are only a minor inconvenience, but could be devastating for pilots who need perfect vision.

Figure 1.

Three distributions of utility corresponding to three hypothetical states of health. The maximum utility is 1, usually defined as the utility of full health, and the minimum utility is l, usually defined as the utility of some lower anchor state (e.g., dead). All three distributions have the same mean value of $\frac{1-l}{2}$. Thus, U_Avg would not be able to distinguish between them.

Because these three distributions have the same mean value, U_avg (equation (1)) treats them identically, thereby holding that the existence and nature of heterogeneity does not matter. Thus, the special needs of pilots might be washed out, when deciding what resources to allocate to vision research and treatment, just as the proportion of sedentary people in a population will affect the resources allocated to prime physical fitness. In these examples, the issue is not that members of these groups experience different health states (though they might), but that they value the health states differently, reflecting heterogeneity in preferences that U_avg ignores.

As an example of a normatively acceptable aggregation function that addresses heterogeneity, consider

$$U\left(x\right)=U_{\mathit{avg}}\left(x\right)-k\sigma ,k>0.$$

It defines the utility of a health state as the mean of the distribution minus the standard deviation. As a result, it assigns a lower societal utility to health states with less societal consensus on their value (given a fixed mean). Rather than treating the three distributions in Figure 1 and their underlying health states equally, it would rank them top > bottom > middle. Table 1 and Roberts [10] provide other aggregation options.

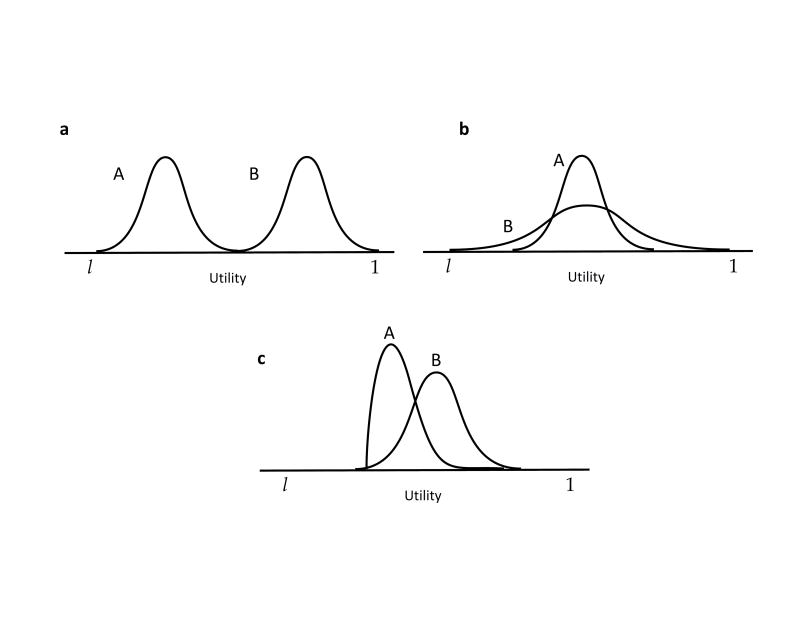
Figure 2 extends this logic to show how the treatment of heterogeneous preferences can affect the allocation of resources across health states. It shows three sets of distributions of utilities for two health states, A and B. In the first (a) the distributions have the same shape, but differ in their mean values. U_avg would assign a higher utility to B than to A. In the second (b), A and B have the same mean value, but B has a higher standard deviation, with some people valuing that state highly, whereas others are averse to it. A decision maker who valued equity, in the sense of being opposed to having some people with high utility, whereas others have low utility (for that same state), would choose A over B; one who cared only about the average (U_avg) would be indifferent. A decision maker who wanted to ensure that no one is too badly off would also prefer A to B, but for a somewhat different reason. In contrast, a decision maker focused on maximum values would choose B over A – as might happen when seeking medical treatments that make a big difference in some individuals’ lives. The same social values might lead to preferring A to B given the distributions in c, which have similar means and variances, but differ in their skew. The fraction of people with outstanding health utility with A could outweigh the majority who fare somewhat worse than average.

Figure 2.

Distributions of utility underlying hypothetical states of health. In a, B is simply a mean-shift of A. In b, A and B have the same mean, but different variances. In c, A and B have similar means and variances, but different skews. (Adapted from Fischhoff [44, Figure 2].)

Relying on U_avg ignores such ethical concerns, treating each distribution of utilities as though it were the top distribution in Figure 1. Table 1 describes other potential aggregation procedures, along with the social values that each expresses. Choosing the aggregation procedure to use in analyses requires a preference – a meta-preference – over the set of normatively acceptable procedures [21]. In the next section, we outline a method for deriving meta-preferences applicable to any societal preference-based measurement system.

A method for applying the criteria

In the absence of a dictator [5], a socially acceptable approach is needed for selecting an aggregation procedure. We propose one that uses behavioral decision research methods [22, 23] to implement an analytical-deliberative process, as advocated in Understanding Risk [24]. A consensus report of the National Research Council, Understanding Risk proposes that defining the terms of analyses requires an iterative process, whereby analysts interact with decision makers to clarify the implications of alternative definitions (e.g., of societal utility functions and their associated aggregation procedures). We propose such a procedure for identifying socially acceptable societal utility functions. It has the following steps:

1. Select individuals with standing for making the choice.

2. Interview those individuals regarding the ethical principles that they wish to see in an aggregation procedure.

3. Select potential procedures from the (infinite) set of normatively acceptable procedures.

4. Develop materials for explaining the principles embodied in the procedures and their application to illustrative cases.

5. Elicit preferences (i.e., meta-preferences) among these procedures from individuals with standing.

6. Assess the construct validity of the elicited (meta-)preferences.

7. Repeat the process, as necessary.

1. Select individuals with standing for making the choice

By convention, societal preference-based HRQL scores reflect the preferences of the individuals who form society, depend on the healthcare system shaped by these scores, and pay its costs. That perspective could mean selecting a representative sample of the general public. However, one might also argue for disproportionate representation of individuals from groups such as insurers, regulators and providers, rather than members of the public. For example, one might justify that choice by claiming that such professionals are better informed about the “lifecycle” of medical conditions, and can put the public’s interests above their own. Determining who has standing is outside social choice theory or any other mathematical formalism. Those individuals who have been chosen to have standing must be ensured the opportunity to articulate and express informed preferences [25, 26].

2. Interview those individuals regarding the ethical principles that they wish to see in an aggregation procedure

Potential principles may come from philosophical analyses, legislation, or interviews, asking people to discuss allocation vignettes. The set of options should include the principles embodied in current approaches, in order to assess the social acceptability of the analytical conventions guiding them [27]. In addition to including widely discussed principles, such as differentially weighting end-of-life care or disease severity, the search should be broad enough to elicit principles that analysts might have neglected. Dolan, Shaw, Tsuchiya, & Williams [15] review surveys that ask respondents to evaluate the relevance of such principles for various policy and personal decisions.

3. Select potential procedures from the (infinite) set of normatively acceptable procedures

Researchers should identify aggregation procedures that address the ethical concerns emerging from the previous step, screened to satisfy the axioms of social choice theory and categorized by what they assume about individual preferences (ordinal or cardinal) and the types of interpersonal comparability that they allow. Due to the possibly large number of potential aggregation procedures (as we saw with the HUI system), researchers may choose heuristics such as “absence of evidence is evidence of absence” in order to reduce the set of possible functions. For example, if no one mentions skew-related concerns, then researchers might reasonably ignore skew-sensitive aggregation procedures. Thus, there may be normatively acceptable procedures that express socially irrelevant (or unacceptable) principles, just as there may be principles that individuals endorse that violate the normative axioms or cannot be operationalized in a utility function. Principles of the last type could still play a role in the decision-making process – just not in the creation of the societal utility scores.

4. Develop materials for explaining the principles embodied in the procedures and their application to illustrative cases

In order to render informed preferences, participants need clear explanations of the procedures and their implications. For example, Wittenberg, Goldie, Fischhoff, & Graham [28] used vignettes to explicate the principle of treating voluntarily and involuntarily incurred health effects differently. These vignettes presented scenarios about distributing finite medical resources among heterogeneous patient populations, illustrated with two examples (asthma, liver disease). There is an extensive empirical literature on methods for eliciting preferences for distributional justice [29, 30, 31], some of which are used in studies eliciting utility scores for the Patient-Reported Outcomes Measurement Information System (PROMIS^®) [32]. As with any social research, careful development and pre-testing is needed to ensure that questions are interpreted as intended [33].

5. Elicit preferences (i.e., meta-preferences) among these procedures from individuals with standing

Using the materials developed in the previous section, elicit preferences for defining societal preferences for health. Given the complexity of the task, an iterative process may be needed to ensure that participants understand the issues and the implications of their expressed (meta-)preferences. Following decision-analytic procedures, the protocol would have a skilled facilitator or use interactive internet-based methods to help participants articulate the implications of their basic values for these specific questions [4]. Instructions must ensure that participants understand the roles that gave them standing in the process (e.g., answering on behalf of their present selves, their future selves, their families, the general public). That may mean acting as though they were behind a “veil of ignorance,” not knowing how the procedures will affect them [7], or applying some other principle from distributive justice that can guide them and the interpretation of their responses [30].

6. Assess the construct validity of the elicited meta-preferences

Construct validity assesses responses’ internal and external consistency [34]. Internal consistency can be evaluated with tests such as scope sensitivity, namely, whether individuals prefer more of a valued outcome to less (when the comparison is not transparent). External consistency can be evaluated by tests such as whether individuals who self-identify as egalitarian also favor egalitarian aggregation procedures.

7. Repeat the process, as necessary

All empirical measures are imperfect. As a result, policy makers need to decide whether a set of expressed (meta-)preferences is good enough to guide social policy. One natural contrast may be whether the judgments of lay respondents are superior to those of the experts who would otherwise define social preferences. Experts are likely to have a better understanding of the technical issues, while lacking insight regarding lay concerns – unless they wish to claim that they know the public better than it knows itself.

Conclusion

Any societal utility function summarizes a distribution of individual utilities with a single number, necessarily making a value judgment about which features of the distribution matter. The procedure used in HUI is a normatively justified aggregation procedure, in social choice theory terms. However, there are infinitely many other aggregation procedures that are normatively justifiable as well. Eliciting preferences for aggregation procedures, or meta-preferences, provides an empirical basis for choosing among those possibilities. This framework could be implemented during the construction of new societal preference-based measures of HRQL or adapted for pre-existing measures. Its logic applies to the design of discrete choice experiments in public policy domains, where similar preference aggregation is required.

Our framework makes explicit the ethical content of aggregating individual utilities into societal HRQL estimates, avoiding the potential for unintended ethical consequences created by policy choices made without normative analyses [35, 36]. Our approach complements other approaches that adjust HRQL estimates defined by conventional aggregation methods (e.g., the mean) by other factors [14, 15, 17], such as the severity of individuals’ health states [17]. It is also consistent with the ethos of societal preference-based HRQL measurement, which holds that societal utilities should be defined by social values [2], rather than determined a priori by some authority – although experts could suggest principles for societal representatives to consider.

Thus, we propose an analytical-deliberative process for addressing the well-documented heterogeneity in health-state utilities [11, 37, 38, 39, 40, 41, 42]. It enlists individuals with standing in evaluating normatively acceptable aggregation procedures, including the conventional averaging method. Who has standing for choosing aggregation procedures is a political-ethical question. The sample might be drawn from the general public, individuals with a condition, experts, patient advocates, etc. Unless the analytical-deliberative process produces a consensus, the distribution of (meta-)preferences that it elicits could be a source of inputs to sensitivity analyses. Fundamentally different ethical principles might still lead to the same choices, as has been found in risk perception studies (e.g., whether risks are incurred involuntarily and have delayed effects) [16, 23, 43]. Of course, sensitivity analyses that reflect variation in the statistic used to summarize preferences are asking a very different question than sensitivity analyses that reflect disagreement about what summary statistic to use in the first place. Unlike the former source of uncertainty, the latter would remain even with error-free measurement of the preferences of every individual in the population.

We hope that our proposal will advance research into the choice of aggregation procedure and clarification of the ethical issues that it inevitably entails [27, 39], by connecting the formal analyses of social choice theory and the empirical procedures of behavioral decision research. The ultimate goal is to ensure that analytical methods reflect the values of the individuals whose welfare they affect [16].