Collective foraging in spatially complex nutritional environments

Abstract

Nutrition impinges on virtually all aspects of an animal's life, including social interactions. Recent advances in nutritional ecology show how social animals often trade-off individual nutrition and group cohesion when foraging in simplified experimental environments. Here, we explore how the spatial structure of the nutritional landscape influences these complex collective foraging dynamics in ecologically realistic environments. We introduce an individual-based model integrating key concepts of nutritional geometry, collective animal behaviour and spatial ecology to study the nutritional behaviour of animal groups in large heterogeneous environments containing foods with different abundance, patchiness and nutritional composition. Simulations show that the spatial distribution of foods constrains the ability of individuals to balance their nutrient intake, the lowest performance being attained in environments with small isolated patches of nutritionally complementary foods. Social interactions improve individual regulatory performances when food is scarce and clumpy, but not when it is abundant and scattered, suggesting that collective foraging is favoured in some environments only. These social effects are further amplified if foragers adopt flexible search strategies based on their individual nutritional state. Our model provides a conceptual and predictive framework for developing new empirically testable hypotheses in the emerging field of social nutrition.

This article is part of the themed issue ‘Physiological determinants of social behaviour in animals’.

1. Introduction

Animals, from insects to primates, have evolved strategies for balancing their intake of multiple nutrients simultaneously to reach physiological states maximizing growth, development, metabolic health, lifespan, immune functions, cognition and reproduction [1,2]. State–space models based on Euclidean geometry, known as ‘nutritional geometry’ [3], have been increasingly used to study these complex feeding decisions and their fitness consequences across a wide range of species, feeding guilds and ecological contexts [4–6]. In nutritional geometry models, individual animals and foods are represented in a multi-dimensional nutrient space defined by key food components (typically the macronutrients proteins, carbohydrates and fats). The challenge facing animals is to consume the available foods in amounts and balances to reach the area of the nutrient space that provides maximal fitness (the intake target). When this is not possible, individuals must compromise between under-eating some food components and over-eating others [3].

Recently, these concepts have been extended to study feeding decisions in animal groups and societies [7]. Social interactions complicate nutrient regulation, often leading animals to trade-off between choosing foods that best address their individual nutritional needs versus the collective needs of the group [8,9]. A striking example is the cooperative nutrient regulation of social insects, such as ants and bees, where individuals in charge of food collection (the foragers) must integrate the divergent nutritional requirements of all colony members, including the other workers, the breeders (queens and males) and the larvae, to maintain a balanced nutritional state at the colony level [10–12]. To account for this social dimension in nutritional geometry, animal groups can be viewed as a collection of individuals, each defined by their own nutritional state and attempting to reach a nutrient intake target while interacting in a common nutritional space [8,9]. In this approach, individual-based models of nutritional geometry have been developed to investigate the nutritional decisions of socially interacting animals and their consequences at the collective level, such as the emergence of social structures (leadership [9], dominance hierarchies [13], social networks [14]) and collective behaviours (collective foraging decisions [15], collective nutrient regulation [8]).

So far, however, studies of social nutrition have considered animals foraging in relatively simplified experimental environments defined by the presence of discrete food resources of fixed composition (e.g. binary choice tests [10], cafeteria assays [16]) and models implementing two-dimensional nutrient spaces [15], without taking into account the potential effects of variation in the spatio-temporal distribution of foods on selective feeding [17]. At best, models have assumed spatial constraints in the form of time-costs for travelling between foods with different nutrient contents [8,15] or of increased competition for accessing foods [13,14]. In nature, however, animals often face highly unpredictable environments where the fine-scale distribution of nutrients, be they in plants or prey, varies spatially and temporarily [17], and this heterogeneity probably affects the way foragers find food patches and move between them [18–22].

Several studies suggest that social interactions provide important benefits to animals exploiting spatially complex foraging environments [23–26]. In a social group, individuals can be seen as information processing units whose interactions may provide collective benefits [27,28], and if each forager is error prone in its detection of a good food patch, grouping can facilitate the spontaneous averaging of individual measurements and lead to improved foraging choices [29]. Accordingly, foragers are expected to rely more on social information to increase their probability of locating foods in uncertain environments (e.g. where food is hard to locate), whereas personal sampling should be more advantageous to avoid competition in highly predictable environments (e.g. where resources are evenly distributed across a landscape) [30]. In social pollinators, for instance, it is hypothesized that food recruitment has evolved to increase the efficiency of foragers exploiting large isolated flower patches found in tropical habitats, whereas solitary foraging is better adapted to the more homogeneously distributed resources of temperate habitats [30,31]. In order to determine whether these collective benefits apply more generally for nutritionally complex environments (i.e. where individuals must balance their intake of multiple nutrients), it is necessary to compare the foraging success of animals exhibiting various levels of social interactions across environments with known food types, abundances and spatial distributions. Developing foraging models that take into account the spatial distribution of nutrients is therefore a critical step to improve prediction accuracy and inform the data collection required to tackle this fundamental problem [7–9].

Here we introduce a spatially explicit individual-based model of nutritional geometry for studying the nutritional behaviour of socially interacting animals in large and unpredictable environments. In the model, individual animals forage for foods containing different mixes of two focal nutrients (protein and carbohydrate) that are distributed across a two-dimensional landscape, and decide whether and how much of these foods they eat in order to maintain a balanced nutritional state. We ran simulation experiments to examine the nutrient regulatory performances of foragers adopting different social strategies and search behaviours in environments containing foods with defined nutrient contents, abundances and degrees of patchiness.

2. Material and methods

(a). Model

Our stochastic model (written in C++) simulates the behaviour of animals foraging in environments containing foods with set abundance, spatial distribution and nutritional content. The animals must eat foods in amounts and at a balance that will enable them to get as close as possible to their intake target. On each time step, individuals that are not on a food move. Movement direction is based on previous orientation, social interactions and noise [32–34]. Individuals that are on a food: eat of that food (the amount is a function of their nutritional state) or leave (if they do not need to ingest more of this food). Once the actions are determined for all individuals, they are applied in a randomized order. The spatial coordinates and nutritional state of individuals, and the environment content, are then updated. Below we describe the main components of the model. All parameters and variables are defined in table 1.

Table 1.

Model parameters and variables, their notation, level of operation and values.

variable/parameter	notation	level	description	value
nutritional state	NS	individual	an individual's nutritional state, as tracked by its (p, c) position in the nutrient space, and denoting total intake of the two nutrients	variable (p, c)
intake target	IT	global	an individual's IT is the (p, c) coordinate in the nutrient space that maximizes F	variable (p, c)
distance to the IT	D	individual	the Euclidean distance between an individual's NS and the IT	variable
food rail	V	global	the nutritional composition of a food in terms of the amount of carbohydrate (c) in a given food relative to single equivalent unit of protein (p)	1, 3, 0.333, 16 and 0.667 (figure 1)
appetite	A	individual	the amount of a given food that an individual would consume to minimize D	variable
ideal food rail	αideal	individual	the angle of a hypothetical ideal food rail connecting an individual's NS with their IT	variable
meal size	φ	global	the maximum amount of food that an individual is able to consume at a given time	0.0368
social influence	σ	individual	the weight of the social interactions relative to the individual orientation when moving	0, 0.005, 0.01, 0.025, 0.2
noise weight	η	individual	the weight of a random unit vector relative to vectors corresponding to social and individual influences during movement	fixed at 0.0025, 0.0275 or 0.0525; or variable (see §2a(iii) Movement rules)
higher noise limit	U	individual	upper bound value when calculating the variable noise as a function of D	0.0525
lower noise limit	L	individual	lower bound value when calculating the variable noise as a function of D	0.0025
noise decrease constant	K	individual	slope constant when calculating the variable noise as a function of D	0.0075
repulsion range	Rr	individual	range at which neighbours exert a repulsion force on an individual	1
alignment range	Ra	individual	range at which an individual aligns with its neighbours	6
attraction range	Rp	individual	range at which an individual is attracted to its neighbours	56
proportion of individuals within alignment range psoc	psoc	global	the proportion of moving individuals who have at least one neighbour with alignment range Ra or closer	variable
spatial coordinates of an individual	Λ	individual	the {x, y} spatial coordinates of an individual	variable

(i). Nutritional environment

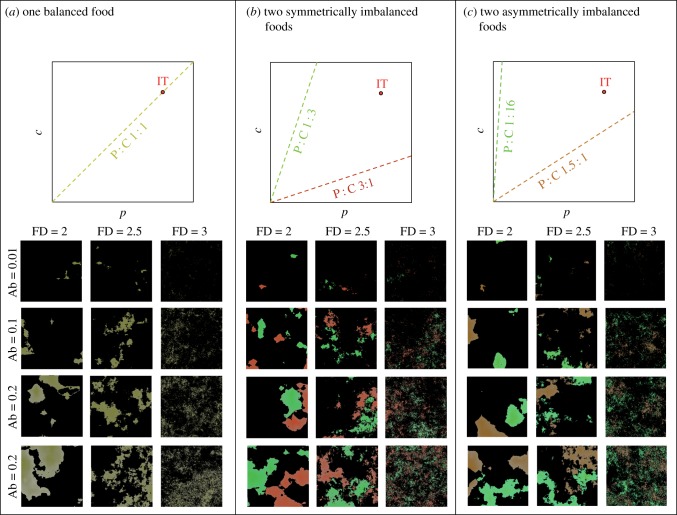
The environment consists of a two-dimensional grid (384 × 384 cells) in which foods are layered. Each food has its own protein and carbohydrate content (P : C), overall abundance (proportion of all cells with some of that food) and patchiness (fractal dimension of all cells containing that food). The food is placed using the Diamond-Square algorithm, a recursive method of creating three-dimensional landscapes [35], and is distributed fractally through the environment with an associated fractal dimension (FD). A low FD is characteristic of isolated large patches, whereas a high FD is indicative of evenly distributed small patches (e.g. figure 1). Once the three-dimensional landscape is created for each food, a cut-off level is determined using a binary search to find the height (i.e. the third dimension) at which the proportion of cells whose height is above that threshold is as close as possible to the desired total food abundance (Ab). In practice, this has a very small error (±0.01%). The amount of food supplied to each cell is then normalized to the landscape height (i.e. [0,1] interval). In order to keep the environment generation process identical regardless of food composition, we always distributed two foods, which had either the same P : C (i.e. equivalent to a one food environment) or two different P : Cs (i.e. two foods environments). Any grid cell that ended up filled with food twice was set to be empty. We removed these overlaps to avoid generating cells containing two complementary foods in experiments in which individuals were challenged to actively balance their diet from two individually imbalanced but collectively complementary foods (figure 1b,c). We used environments with a maximum combined Ab of 0.4 (Ab = 0.2 for each food in two food environments), for which spatial overlaps of foods are limited (9.3% observed on average, see the electronic supplementary material, text S1), to avoid situations where an individual could obtain two different foods from the same cell. Once all of the food contained in a cell is consumed it is not replenished. None of our simulations resulted in all food being consumed.

Figure 1.

Each environment contains one or two foods defined by their protein to carbohydrates ratio (P : C), abundance (Ab) and fractal dimension (FD). Upper panels show schematic of nutritional geometry, in which foods are represented as nutritional rails (dashed lines) in a two-dimensional nutritional space (p,c) defined by protein and carbohydrates. The challenge for an individual is to eat foods in amounts and proportions that enable it to reach its intake target (IT; a position in the nutritional space that maximizes fitness). Lower panels show examples of two-dimensional landscapes for each environment type, and for all combinations of ABs and FDs tested. Colours reflect the nutrient content of foods (scaled from red = high P to green = high C). The total amount of coloured pixels reflects the Ab of the food. (a) Environment containing a single balanced food whose nutritional rail intersects the IT. Individuals can reach their IT by eating from this food. (b) Environment containing two individually imbalanced but collectively complementary foods whose nutritional rails fall symmetrically on opposite sides of the IT. Individuals can reach their IT by eating an equal amount of both foods. (c) Environment containing two imbalanced but complementary foods whose nutritional rails fall asymmetrically on opposite sides of the IT (same angular difference as in b). Individuals can reach their IT by eating three times more of P : C 1.5 : 1 than P : C 1 : 16.

(ii). Nutritional rules

Our aim was to develop a simple, generic, model, that is neither nutrient- nor species-specific. Each individual has a nutritional state (NS) defined by two coordinates in a Cartesian space (p, c) representing the individual's total intake of protein (p) and carbohydrate (c) at a given time. Although we refer to protein and carbohydrate, our approach is generalizable to any food components that affect fitness [8,9]. The optimal NS is the intake target (IT). For the sake of simplicity, this local optimum is modelled as a single coordinate [8,9,13–15] rather than a surface in the nutrient space whose shape can greatly vary depending on species [3]. Here an individual's performance is estimated by the p/c ratio of its NS and the Euclidean distance (D) between its NS and the IT. All individuals begin with an initial NS and IT of (0.00217, 0.00217). To simulate the individuals' continual need for nutrients (i.e. metabolic cost of living) the IT increases at a rate of 0.00217 in each dimension (p, c) on each time step. Both nutrients were thus assumed to be metabolized at the same rate.

Foods are modelled as rails (V), which denote the nutritional composition in terms of c content for an equivalent unit of p. When an individual finds a food (i.e. its spatial coordinates fall within a grid cell containing food) the amount consumed is governed by its appetite (A). Individuals follow a ‘closest distance’ rule of compromise, meaning that foods are consumed to minimize D. This simple rule of compromise, which allows individuals to over eat one nutrient while under eating the other up to a certain point, has been experimentally observed in many animals [3] and has the advantage of making the same assumption for both nutrients. A is calculated as follows:

where φ is the maximum amount of food an individual can eat on one time step, α_ideal is the angle of a hypothetical ‘ideal’ food rail connecting an individual's NS to its IT, and V is the food rail of the food being consumed. After consuming food, an individual will leave the food on the next step if the food is depleted, or if it would not get closer to its IT by consuming any food that is left (φ ≥ A).

(iii). Movement rules

We modelled individuals as moving at a constant speed and with a direction that was partly random and partly determined by individual (previous orientation) and social (repulsion, alignment or attraction towards nearby individual) influences [32–34]. The weight of the random component was either kept fixed (resulting in a correlated random walk in the absence of social influences) or was variable according to the NS of the individuals, resulting in a new type of random walk that we named a ‘nutritionally driven random walk’. At the outset, all individuals are uniformly distributed at random in the environment. Their positions and movements are implemented in a continuous two-dimensional coordinate system (where each cell in the environment grid has a side of length 1). At each time step, each individual moves at a constant speed v₀ and updates its position λ_i by following the direction of a unit movement vector θ. That is, θ is updated and then . The new value of θ is calculated as a weighted sum of vectors corresponding to the previous individual orientation, social interactions with neighbours and noise, as follows:

where θ is a unit vector representing the direction of movement of the individual at the previous time step t, S is a unit vector representing the influence of neighbours on the individual's direction, and ξ is a random unit vector representing noise. Each of these individual, social and noise components of movement are weighted by the parameters σ and η. The environment is set up to have reflective boundaries where individuals reaching the limits of the landscape have their orientation set to −θ_t and λ_i adjusted accordingly. We denote the vector from individual i to individual j as e_ij = λ_j − λ_i, and the distance between them as d_ij = |e_ij|.

The weight of the noise component η (hereafter referred to as ‘noise’) is either a constant or varies as a function of D. When it is variable, η follows a linear relationship in the form of with a minimum value of L. A variable η thus produces a nutritionally driven random walk in which the trajectory of an individual is more tortuous when its NS is close to the IT and straighter when it is further away. If σ > 0, movement is influenced by the presence of neighbour individuals based on repulsion, alignment and attraction rules [33] as follows:

• (1) When neighbours are within the repulsion range R_r of the focal individual i, we calculate a repulsion force that results from normalizing the sum 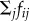over all individuals j ≠ i of pairwise repulsion forces between individuals i and j. The repulsive force that individual j exerts on individual i is 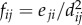, where e_ji is the vector from individual j to individual i.

• (2) For those neighbours within the alignment range R_a and outside the repulsion range, the social force corresponds to the sum of all neighbours' orientation vectors, each again divided by the distance to individual i, that is, θ_j/r_ij. The resulting sum is normalized.

• (3) For those neighbours within the attraction range R_p and outside the shorter ranges, the attractive force is calculated as the negative of the repulsion formula .

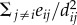(b). Simulation experiments

We simulated groups of 50 individuals for 10 000 time steps. For a given group, all individuals responded to the same nutritional and movement rules. We explored three environment types providing increasingly challenging nutritional conditions: (1) a single balanced food (P : C 1 : 1) whose nutritional rail intersects the IT (i.e. individuals can reach their IT by eating only from that food; figure 1a), (2) two symmetrically imbalanced but complementary foods (P : C 1 : 3, P : C 3 : 1) whose nutritional rails fall symmetrically on opposite sides of the IT (i.e. individuals can reach their IT by eating 50% of each food; figure 1b) and (3) two asymmetrically imbalanced but complementary foods (P : C 1 : 16, P : C 1.5 : 1) whose nutritional rails fall asymmetrically on opposite sides of the IT with the same angular difference as in 2 (i.e. individuals can reach their IT by eating 20% of P : C 1 : 16 and 80% of P : C 1.5 : 1; figure 1c). In each environment type, foods were characterized by one of four combined Abs (Ab = 0.01, 0.1, 0.2, 0.4) and one of three combined FDs (FD = 2, 2.5, 3; figure 1b). Individuals could have one of five social influence weights (σ = 0, 0.005, 0.01, 0.025, 0.2) and one of four noise modes (η = 0.0525, 0.0275, 0.0025, variable). We ran 100 simulations for each condition (i.e. 72000 simulations in total).

For each simulation, we generated outputs on the spatial coordinates of foods and individuals, the amount and type of food ingested by each individual, and their NS at each time step. We computed p/c and D as proxies of individual nutrient regulation efficiency. D_t+1 − D_t (the increase rate of D at time step t + 1) was used to examine the dynamics of nutrient regulation through time. A low increase rate is indicative of an individual that closely tracks its IT, and is performing well. We also calculated p_soc, the proportion of individuals having at least one neighbour in their alignment range, as a measure of group cohesion. Average final values (±95CI) of D, p/c and p_soc are shown in the electronic supplementary material, tables S1–S4. Examples of simulations are shown in the electronic supplementary material, movies S1–S12.

3. Results

(a). Food spatial distribution affects nutrient detection and balancing

We examined the influence of food spatial distribution on the ability of individuals to track their IT by varying the number of available foods (1 or 2), their nutrient content (P : C), total Ab and FD. We focused on the simplest scenario where foragers do not interact socially (σ = 0) and have a fixed movement noise (η = 0.0025).

In environments with a single nutritionally balanced food (figure 1a), individuals were consistently more efficient at tracking their IT as both food Ab and FD increased, reaching a minimum final D in high-Ab, high-FD environments (figure 2a; electronic supplementary material, table S1). The probability that an individual finds food increased with Ab and FD, as illustrated by the reduced D_t+1 − D_t in high-Ab, high-FD environments compared with in low-Ab, low-FD environments (figure 2b). Individuals were less efficient at finding food for very low food Ab (0.01; e.g. electronic supplementary material, movie S1) irrespective of the FD, resulting in relatively high and stable D_t+1 − D_t. The rate of change in D decreased dramatically for moderate food Ab (0.1, 0.2), approaching zero for high food Ab (e.g. electronic supplementary material, movie S2).

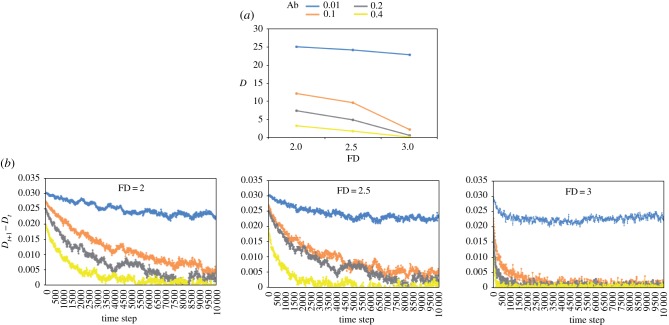
Figure 2.

(a) Average (95CI range: 0.001–0.055) final distance (D) between the nutritional state of individuals and their intake target in environments containing one balanced food in 12 combinations of abundance (Ab) and fractal dimension (FD) (figure 1a). Social influence (σ) = 0, movement noise weight (η) = 0.0025. (b) Average (95CI range: 0.00006–0.0001) rate of change in D (D_t+1 – D_t) for the same simulations showed in (a). All model parameters and variables are described in table 1.

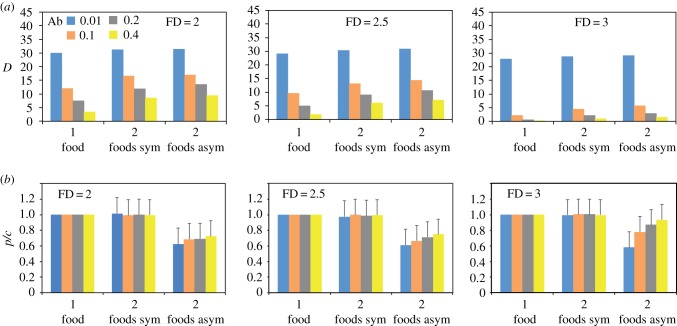
The same overall tendency was observed in nutritionally more complex environments containing two complementary foods (figure 3; electronic supplementary material, table S1), be they symmetrically imbalanced (figure 1b) or asymmetrically imbalanced (figure 1c). Nonetheless, moving from an environment with two imbalanced foods imposed a more complex nutritional challenge to individuals, resulting in a general increase (range: 4–752%) in final average D (figure 3a; see also the electronic supplementary material, figure S1a–c). This effect was more pronounced for high-Ab, low-FD environments, presumably because of the increased probability of encountering large patches of imbalanced foods and not finding the complementary food within the allotted time (e.g. electronic supplementary material, movie S3), whereas individuals may be able to quickly alternate between visiting nearby complementary foods in high-Ab, high-FD environments (e.g. electronic supplementary material, movie S4). Individuals also had higher final average D when foraging on asymmetrically imbalanced foods than when foraging on symmetrically imbalanced foods, because of the additional challenge of eating different amounts of each food to reach the IT. This increased complexity was evident when comparing the final average p/c of individuals across environment types (figure 3b; electronic supplementary material, table S2). While foragers successfully maintained a balanced NS (p/c = 1) with one balanced food (when each food intake yields exactly p/c = 1) or two symmetrically imbalanced foods (when a random food intake would result p/c = 1), their NS drifted away with asymmetrically imbalanced foods. The average final p/c was lower (range: 6–42%) in environments with two asymmetrically imbalanced foods than in environments with two symmetrically imbalanced foods (electronic supplementary material, figure S1d,e) but remained higher than an average random intake in most environments (an expected random food intake would result in an average p/c between 0.306 and 0.576; see the electronic supplementary material, Text S2). The higher the food Ab and FD, the closer p/c was to 1 (figure 3b). These simulations thus confirm that the behavioural mechanisms implemented in our model enable nutrient intake regulation by randomly moving and non-socially interacting individuals, even when confronted with spatially and nutritionally challenging environments. In the following analyses, we focused on environments with asymmetrically imbalanced foods, which are the most challenging environments.

Figure 3.

(a) Average (95CI range: 0.001–0.055) final distance (D) between the nutritional state of individuals and their intake target for environments with one balanced food, two symmetrically imbalanced foods, and two asymmetrically imbalanced foods for 12 combinations of abundance (Ab) and fractal dimension (FD) (figure 1) under four movement noise weight modes (η). Social influence (σ) = 0. (b) Average (+95CI) final nutritional state (p/c) for the same simulations showed in (a). All model parameters and variables are described in table 1.

(b). Social interactions improve nutrient detection

We explored the influence of social interactions (σ) on the ability of foragers to track their IT. When foraging on two asymmetrically imbalanced foods (figure 1c), strong-σ individuals (σ = 0.2) always had a higher D, and thus a poorer nutrient regulatory performance, than individuals with weaker σ (0, 0.005, 0.01, 0.025), regardless of food Ab and FD (figure 4; electronic supplementary material, movies S5 and S6). In these conditions, the social influence might be too strong to allow individuals to escape the group and make efficient foraging decisions relative to their own individual IT, as has been observed in previous studies [8,9]. Interestingly, weak-σ individuals (σ = 0.005) outperformed zero-σ individuals (σ = 0) in low-FD environments and for most food Abs (Ab = 0.01, 0.1, 0.2; figure 4). By contrast, zero-σ individuals outperformed individuals with any level of σ in high-FD environments and for all Abs. This effect was most pronounced for a low food Ab (Ab = 0.01; figure 4). Presumably, when foods are extremely scarce and clumpy (and therefore hard to find), socially facilitated movements improve search efficiency in comparison to individual sampling (e.g. electronic supplementary material, movies S3 and S7). However, when foods are abundant and scattered (and therefore easy to find; e.g. electronic supplementary material, movies S4 and S8), the social benefits for locating foods may be much reduced while competition may considerably increase on small patches. The fact that weak-σ individuals (σ = 0.005) always outperformed zero-σ individuals under extremely low η (0.0001, 00005) indicates that the social benefit is not just a consequence of interacting individuals using straighter trajectories (equivalent to a decrease in η) due to the stronger alignment force (electronic supplementary material, table S4). The nutrient balance (i.e. p/c ratio of final NS) did not improve in any level of σ compared to simulations with zero-σ individuals (electronic supplementary material, table S2). Consequently, in the following analyses we focused on σ = 0.005, which was the most efficient social strategy overall.

Figure 4.

Average (95CI range: 0.01–0.08) final distance (D) between the nutritional state of individuals and their intake target for various social influences (σ) in environments containing two asymmetrically imbalanced foods for 12 combinations of abundance (Ab) and fractal dimension (FD) (figure 1c). Movement noise weight (η) = 0.0025. All model parameters and variables are described in table 1.

(c). Social influences are magnified by nutritionally based movements

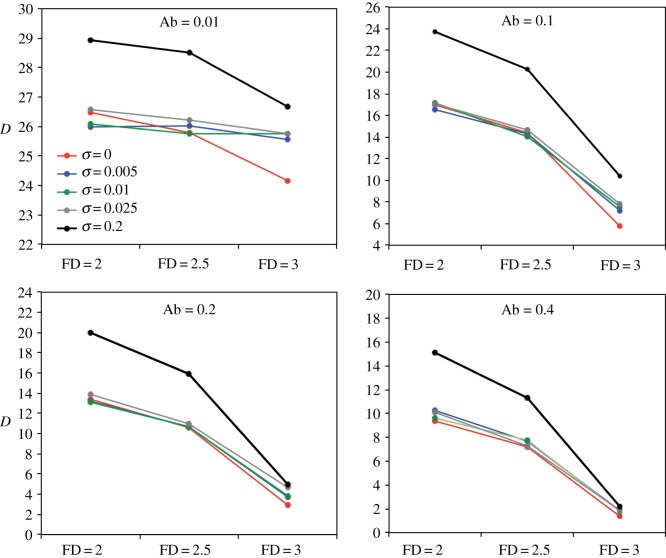
To explore the effect of noise (η) on the ability of foragers to move through the landscape and track their IT, we compared fixed η (0.0025, 0.0275, 0.0525) to variable η based on NS (equivalent to a nutritionally driven random walk). Overall, variable-η individuals outperformed fixed-η individuals for most combinations of food Ab and FD and across all environment types (figure 5a; electronic supplementary material, table S1). For instance, in environments with two asymmetrically imbalanced foods (figure 1c), at moderate food Ab (Ab = 0.2) and high-FD (2), both high-η (0.0525) and variable-η individuals behaved similarly with D increasing faster than for low-η (0.0025) individuals during the early stage of the simulations (see example in the electronic supplementary material, figure S2). As initial D was low, η was similar in variable-η and high-η individuals. With time, however, D increased and variable-η individuals started to behave like low-η individuals, moving away from their initial positions in trajectories that became increasingly straight (e.g. electronic supplementary material, movie S12). Towards the end of the simulations, D_t+1 − D_t remained high in the high-η individuals, while approaching zero for both variable-η and low-η individuals. Ultimately, variable-η individuals outperformed low-η individuals, presumably because the modulation of η allowed them to remain longer on desirable food patches. The only exception was observed in high-Ab, high-FD environments, where low-η individuals outperformed variable-η individuals (electronic supplementary material, table S1). In these extreme nutritional environments, when very small amounts of foods are homogeneously distributed, local search resulting from variable-η or high-η reduces the probability of finding foods in comparison to the more diffusive trajectories of low-η individuals (e.g. electronic supplementary material, movies S8, S9 and S10). Importantly, variable-η individuals were also able to maintain a NS with p/c closer to 1 than fixed-η individuals for all combinations of food Abs and FDs, and with asymmetrically imbalanced foods (figure 5b; electronic supplementary material, table S2). This held true for nutritionally simpler environments and at most social parameters (electronic supplementary material, tables S1 and S2). Thus, in heterogeneous environments, a flexible search strategy based on NS is generally more efficient at finding and regulating intake of nutrients than any fixed random walk.

Figure 5.

(a) Average (95CI range: 0.02–0.07) final distance (D) between the nutritional state of individuals and their intake target in environments containing two asymmetrically imbalanced foods for various movement noise weight modes (η) for 12 combinations of abundance (Ab) and fractal dimension (FD) (figure 1c). Social influence (σ) = 0.005. (b) Average (+95CI) final nutritional state (p/c) for the same simulations showed in (a). All model parameters and variables are described in table 1.

Importantly, the advantage of weak social interactions (σ = 0.005) over no social interactions (σ = 0) in low-Ab, low-FD environments described above (figure 4) was magnified under variable η. Overall, D was 4.7% lower and p/c 1.5% higher (up to 5.8% and 10.7% at FD = 2 and Ab = 0.05 and Ab = 0.1, respectively) in weak-σ simulations than in zero-σ simulations (electronic supplementary material, figure S3, e.g. electronic supplementary material, movies S11 and S12). Therefore, under variable η, weak σ not only provides higher probabilities of locating foods but also increases chances of achieving nutrient balancing, particularly in clumpy environments.

(d). Nutrient distribution and movement noise modulate group cohesion

Both the nutritional environment and η influenced the spatial distribution of individuals and group cohesion, as measured by the proportion of individuals having at least one neighbour in their alignment range (p_soc). In the presence of social interactions (σ > 0), p_soc decreased with increasing food Ab and FD (figure 6a). Overall, low-η simulations resulted in the highest p_soc regardless of food Ab and FD when compared with variable-η and high-η simulations. Accordingly, high-η simulations showed the lowest p_soc in most environments. Presumably, the spatial distribution of nutrients affects the level of synchronization at which individuals alternate between feeding and moving between foods. When a group encounters a large food patch (low-FD environments), all individuals start eating the same food simultaneously, thereby synchronizing their nutritional states and future foraging activities (e.g. electronic supplementary material, movie S12). By contrast, when a group encounters several homogenously distributed food patches (high-FD environments), some individuals start eating while others do not, resulting in a population of uncoordinated foragers (e.g. electronic supplementary material, movie S9). The decrease in p_soc with increasing food Ab and FD was most evident under variable η, where a loss of synchrony between feeding individuals combined with a generally lower D (therefore higher η), disrupted group cohesion further than in fixed-η simulations (figure 6b). As expected in the absence of social interactions (σ = 0), p_soc remained low and relatively stable across all environment types except for low-FD environments containing a single balanced food (figure 1a) where individuals tended to form larger temporary groups (electronic supplementary material, table S3), a clustering effect of food distribution previously described in swarming animals [36].

Figure 6.

(a) Average (95CI range: 0.001–0.016) proportion (p_soc) of individuals having at least one neighbour in the alignment range in environments containing two asymmetrically imbalanced foods for 12 combinations of abundance (Ab) and fractal dimension (FD) (figure 1c). Social influence (σ) = 0.005, movement noise weight (η) = variable. (b) Average p_soc (95CI range: 0.001 – 0.019) for FD = 2 under different Ab and η. σ = 0.005. (c) Average p_soc (95CI range: 0.001–0.016) for FD = 3 under different Ab and η. σ = 0.005. All model parameters and variables are described in table 1.

4. Discussion

We developed an individual-based model that uses key concepts of nutritional geometry to explore the ability of animals to regulate their intake of nutrients across a range of spatially and nutritionally complex environments. We found that social interactions can improve an individual's nutrient balancing performance in the most heterogeneous environments where foods are complementary, rare and clumpy, a social advantage magnified by nutritionally driven random walks, when the individual's search strategy is based on its nutritional state. However, independent foraging remains the most efficient strategy when foods are abundant and evenly distributed. We discuss the implications of our results for future research on social nutrition.

Many animals use social information to locate and select food resources in their environment [37,38]. In gregarious species, this often results in collective foraging decisions whereby all, or the majority, of the group makes a choice to feed on one of several possible foods [28], an emerging group property allowing individuals to make faster and more accurate choices than if they were alone [26]. Our model shows that this collective advantage applies to complex nutritional decisions, enabling grouped animals to balance their diet more efficiently than solitary conspecifics in adverse nutritional environments. The nutritional benefits are dependent on the type of foods available and their spatial distribution, suggesting that collective foraging is adaptive in certain types of environments only. Social interactions (here in the form of socially facilitated movements) are most beneficial for finding foods and maintaining a balanced diet in challenging nutritional environments where foods are scarce and clumpy, an observation in line with current hypotheses for the evolution of social learning and food signalling [30,31]. By coordinating the feeding activities of individuals, social interactions may also synchronize their nutritional states, future movement behaviour and nutritional decisions, which favours efficient diet balancing through collective movements between large isolated patches of complementary foods. By contrast, in environments where food is locally limited, the same phenomena may impair diet regulation efficiency by increasing competition, for instance, in environments containing a constellation of small patches homogeneously distributed across the landscape.

Interestingly, the random search strategies employed by foragers can have a strong impact on individual nutrient regulation performance and collective foraging dynamics. While nearly straight trajectories (i.e. low movement noise) are generally better than very tortuous trajectories (i.e. high movement noise) across most environments, a strategy based on nutritional state allowing for alternating between both types of trajectories (i.e. variable movement noise) significantly improves nutrient balancing performances. This nutritionally driven random walk produces movement patterns composed of local sampling and long jumps that are reminiscent of search patterns known to be efficient across foraging environments and spatial scales (e.g. near-far search [39], Lévy flight [19]). Movements influenced by nutritional state have been observed in many animals, for instance, following periods of dietary restriction (i.e. reduced intake of one or more food components) [40,41]. In migratory insects, such as crickets and locusts, a single nutrient deficit can increase or reduce the locomotor activity of individuals, ultimately impacting movement at the collective level [16,21]. The advantage of such behavioural plasticity [42] (variable movement noise component in our model) attuned to nutritional state in comparison to classical random search implementations is that individuals or groups only perform straight stretches of movement when they have a strong deficit of one or more nutrients, while they tend to remain in a local area when they are performing well. This behaviour may outperform other search strategies in complex environments by allowing individuals that find themselves on a high-value patch to remain there. Nutritionally driven random walks may be especially beneficial in highly dynamic heterogeneous environments, for instance, in the case of predators, where individuals must regularly move between complementary food patches whose spatial distributions can rapidly change from sparse and clumpy to abundant and scattered [20].

Our modelling approach is based on generic nutrient regulatory mechanisms described in a taxonomically diverse range of herbivores, omnivores and carnivores across ecological contexts [43–46], and thus provides considerable promise for future empirical comparative research in nutritional ecology. Accordingly, the model is readily adjustable to account for variations in life-history traits and social behaviour, in order to generate species-specific predictions. For instance, one fundamental aspect of nutrient regulation in socially interacting animals is the diversity in nutrient needs (nutritional states, intake targets) and regulatory behaviours among group members, as can be observed in groups composed of males and females [47,48] or adults and juveniles [10]. Other sources of nutritional variance within groups may include pathogen infection, exposure to toxins, predators and past nutrient deficiencies [47–51]. Even if individuals have the same nutritional needs there will always be consistent behavioural and physiological differences among individuals that can have strong effects on both group members' and collective nutritional behaviour [50,52,53]. Individual foraging history and knowledge about available foods are also of potential importance since personal assessment of resource spatial distribution often changes foragers' tendency to rely on personal versus social information [37]. For instance, many animals exploit stable home ranges, or foraging sites, from a central place and develop near-optimal foraging routes linking familiar places based on learning and memory [54]. Other important insights may arise from comparing animal groups exhibiting various levels of social complexity, in which individuals interact asymmetrically with each on another, for instance, by testing groups with set social structures (e.g. social networks [14], cooperative rules [8] or assortative interactions [15]). Cross-species comparisons may also allow us to identify the importance of specific nutritional traits, such as dietary breadth (e.g. generalists versus specialists), appetite (e.g. rules of compromise [3]) or tolerance to suboptimal diets (e.g. shape of IT surfaces and fitness landscapes [5]), on these social nutritional phenomena. An empirical exploration of such predictions is now becoming possible thanks to the fast development of automated technologies (e.g. computer vision [55], GPS [56]) to experimentally measure the behaviour of individuals across large spatial and temporal scales, and track their nutritional states as they exploit food resources and exchange nutrients, both in the laboratory (e.g. using measures of food intake in chemically defined diets [57]) and in the field (e.g. using chemical analyses of food samples [58]).

Individual-based models of nutritional geometry, as proposed here, provide a new mechanistic basis for understanding how nutritional interactions scale up from the individual to the collective level, and how higher-order phenomena in turn feed back into local interactions and individual behaviour [8]. In principle, the same approach could be used to test specific ecological hypothesizes involving nutritional interactions beyond the levels of groups and populations, between species within communities and ecosystems, and across spatio-temporal scales [7]. For example, one could envisage studying the role of nutrition in mediating vital ecosystem services by examining how the nutritional performances of pollinators exploiting patchily and nutritionally variable floral resources effect plant reproduction and community structures [12,59]. Spatial nutritional modelling could also yield new insights into the role of nutrition in permitting the successful settlement of invasive species across large landscapes [60], or in favouring the resilience of declining populations [6]. Scenarios of climate change could also be simulated to examine how the degradation of nutritional environments alters the foraging patterns and nutritional performances of animals. Ultimately, these fundamental processes should be considered within an evolutionary context to precisely assess the consequences of nutrition on individual fitness on population growth, trophic interactions, community changes and ecosystem dynamics.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Authors' contributions

M.L. and J.B. designed the study. M.L., M.A.C., A.M.S. and J.B. developed the model. J.B. collected the data. M.L. and J.B. analysed the data and wrote the first draft of the manuscript. M.A.C., A.M.S., F.J.C., D.R. and S.J.S. contributed to writing the final version of the manuscript.

Competing interests

We have no competing interests.

Funding

M.L. is supported by the CNRS, the ANR (ANR 16CE0200201), the Fondation Fyssen, and research grants from the IDEX of the federal University of Toulouse. A.M.S. is supported by a J&D Coffey Fellowship from the University of Sydney. D.R. is an affiliate of the New Zealand Institute for Advanced Study. S.J.S. is supported by an ARC Laureate Fellowship. J.B. is supported by ARC Future Fellowship (ARC FT110100082) and ARC Discovery Projects (ARC DP1030101670) programmes.