Comparison of optomotor and optokinetic reflexes in mice

We provide the first quantitation of head gain during optomotor response in mice and show that optomotor and optokinetic responses have similar psychometric curves. Head gains are far smaller than eye gains. Unrestrained mice combine head and eye movements to respond to visual stimuli, and both monocular and binocular fields are used during optokinetic responses. Mouse OMR and OKR movements are heterogeneous under optimal and suboptimal stimulation and are affected in mice lacking ON direction-selective retinal ganglion cells.

Abstract

During animal locomotion or position adjustments, the visual system uses image stabilization reflexes to compensate for global shifts in the visual scene. These reflexes elicit compensatory head movements (optomotor response, OMR) in unrestrained animals or compensatory eye movements (optokinetic response, OKR) in head-fixed or unrestrained animals exposed to globally rotating striped patterns. In mice, OMR are relatively easy to observe and find broad use in the rapid evaluation of visual function. OKR determinations are more involved experimentally but yield more stereotypical, easily quantifiable results. The relative contributions of head and eye movements to image stabilization in mice have not been investigated. We are using newly developed software and apparatus to accurately quantitate mouse head movements during OMR, quantitate eye movements during OKR, and determine eye movements in freely behaving mice. We provide the first direct comparison of OMR and OKR gains (head or eye velocity/stimulus velocity) and find that the two reflexes have comparable dependencies on stimulus luminance, contrast, spatial frequency, and velocity. OMR and OKR are similarly affected in genetically modified mice with defects in retinal ganglion cells (RGC) compared with wild-type, suggesting they are driven by the same sensory input (RGC type). OKR eye movements have much higher gains than the OMR head movements, but neither can fully compensate global visual shifts. However, combined eye and head movements can be detected in unrestrained mice performing OMR, suggesting they can cooperate to achieve image stabilization, as previously described for other species.

NEW & NOTEWORTHY We provide the first quantitation of head gain during optomotor response in mice and show that optomotor and optokinetic responses have similar psychometric curves. Head gains are far smaller than eye gains. Unrestrained mice combine head and eye movements to respond to visual stimuli, and both monocular and binocular fields are used during optokinetic responses. Mouse OMR and OKR movements are heterogeneous under optimal and suboptimal stimulation and are affected in mice lacking ON direction-selective retinal ganglion cells.

vertebrates use involuntary compensatory mechanisms for image stabilization during self-motion. The vestibulo-ocular reflex (VOR) integrates information from the semicircular canals to evoke eye movements in the opposite direction of occurring head movements. Compensatory eye (optokinetic response, OKR) and/or head (optomotor response, OMR) reflexes integrate information from the global shift of the visual image over the retina. Stereotypical OKR movements (hereafter “events”) consist of a slow (hereafter “tracking”) phase during which the eye moves in the stimulus direction, followed by a fast saccade-like (hereafter “reset”) phase that occurs in the opposite direction (Collewijn 1969; Stahl 2004b). Optokinetic events are also known as optokinetic nystagmus (Spering and Carrasco 2015; Ter Braak 1936). The OKR is well described in species with frontal eyes endowed with a fovea or area centralis [e.g., cats, humans (Dubois and Collewijn 1979; Honrubia et al. 1967)] and afoveated, laterally positioned eyes [e.g., rabbits, mice (Collewijn 1969; Sinex et al. 1979; Stahl et al. 2000)]. Because OKR is evoked easily and reliably, it can be used to measure visual function in human subjects (Fahle et al. 2011; Naber et al. 2011).

The term “optomotor response” typically refers to compensatory head and/or body movements in stimulus direction that can be followed by a quick reset phase (Benkner et al. 2013; Gresty 1975; Kopp and Manteuffel 1984). The quick reset phase can be observed more commonly in fish (Anstis et al. 1998), salamander (Kopp and Manteuffel 1984), and frogs (Dieringer et al. 1982) but also is present in mammals (Collewijn 1977; Fuller 1985, 1987; Gresty 1975). Based on the prominent movement of the neck in rat, rabbit and pigeon compensatory head movements are also referred to as the optocollic reflex (OCR) in these species (Fuller 1985, 1987; Gioanni 1988a, 1988b). Given the distinct ecological niches and head mobility relative to neck and body, the contribution of head and eye movements to image stabilization can vary significantly between species (Gioanni 1988a, 1988b).

OKR and OMR are driven by ON direction-selective retinal ganglion cells (ON-DS RGCs) (Oyster et al. 1972, 1980; Yonehara et al. 2008, 2009), sending their axons into the accessory optic system (AOS) (Simpson 1984). In mammals, axons of ON-DS RGCs follow the main optic tract or the accessory optic tract (AOT), and innervate the nucleus of the optic tract (NOT) and the dorsal, lateral, and medial terminal nuclei (DTN, LTN, and MTN, respectively), mostly on the contralateral side (Dhande et al. 2013; Distler and Hoffmann 2003; Oyster et al. 1972, 1980; Yonehara et al. 2008). Electrophysiological evidence suggests that NOT and DTN are predominantly perceiving motion in the temporonasal direction, whereas LTN and MTN are preferentially tuned to vertical motion components (e.g., Simpson et al. 1988; Soodak and Simpson 1988). We had previously reported that mice missing the transcription factor Brn3b/Pou4f2 (Brn3b^KO/KO mice) have specific defects in RGC numbers, with complete loss of MTN, DTN, and LTN projections; partial loss of RGC projections to the pretectal area (NOT and olivary pretectal nucleus, OPN), lateral geniculate nucleus (LGN), and superior colliculus (SC); and preserved RGC innervation to the suprachiasmatic nucleus (SCN) (Badea et al. 2009). In mice with genetic ablation of MTN and/or LTN projecting RGCs (Badea et al. 2009; Sun et al. 2015), there is a complete loss of vertical OKR. Loss or reduction of RGC numbers projecting to the pretectal area, including the NOT and the DTN, results in partial loss of horizontal OKR (Badea et al. 2009; Osterhout et al. 2015). OMR has never been tested in Brn3b^KO/KO mice, and it is yet unclear how their residual horizontal OKR compares to the full wild-type response.

The relative contributions of OKR and OMR to image stabilization have not been studied in mice, due to technical limitations. Specifically, whereas an extensive body of data is available for mouse OKR, there are few quantitative assessments of mouse head movements during OMR (Benkner et al. 2013; Kretschmer et al. 2013). For mouse OKR and VOR, eye motion is detected using videographic detection of pupil and corneal reflection in head-fixed mice, providing precise information on the number and gain of saccadic eye movements and the regions of the retina involved (Stahl et al. 2000). Previous work has shown that OKR gain decreases with increasing stimulus velocities (Collewijn 1969; Stahl et al. 2006; Tabata et al. 2010; van Alphen et al. 2001), consistent with the tuning of ON-DS ganglion cells to slow speeds (1–2°/s) (Oyster et al. 1972; Sun et al. 2006). OKR spatial acuity thresholds range between 0.5 and 0.6 cycle/° (Cahill and Nathans 2008; Sinex et al. 1979; van Alphen et al. 2001, 2009, 2010).

The most common method for characterizing OMR in mice relies on a trained human observer, which directly records number of mouse head movements under different conditions to determine visual thresholds (Prusky et al. 2004). More recently, a forced-choice test involving the human observer has been implemented to increase the objectivity of the test (Umino et al. 2008). In essence, these approaches rely on counting the number of head tracking movements detected by the human observer under various stimulus conditions and report an optimal stimulus velocity of 12°/s and an absolute visual acuity threshold of 0.39 cycle/° (Prusky et al. 2004; Umino et al. 2008, 2012). However, no information on head angular velocity or amplitude and duration of mouse OMR events is available.

Previous studies described combined head and eye movements in unrestrained animals of several species, either under free-behaving circumstances or upon optokinetic visual stimulation (Collewijn 1977; Fuller 1985, 1987; Gresty 1975). These studies suggest that the combined gains of the two systems can match stimulus speed only for optokinetic stimuli of low velocities. In rats and rabbits, eye movements may be optimized to preserve the binocular visual field of the animal during head rotations around the pitch and roll axes (Hughes 1971; Maruta et al. 2001; Wallace et al. 2013). Controlled head tilts in head-fixed mice reveal compensatory eye movements (tilt maculo-ocular reflex) that predict a vertical eye angle of ~22° during ambulation (Oommen and Stahl 2008). Therefore, eye position in the freely behaving animal may seek to optimize binocularity. However, there is essentially no information on optokinetic eye movements in unrestrained mice and to what extent OKR responses in restrained and unrestrained conditions are related.

We have recently developed apparatus and software allowing for the recording of head movements during OMR, eye movements during OKR, or combined head and eye movements in unrestrained mice (Kretschmer et al. 2013, 2015). We introduce a quantitative video-tracking approach to the determination of mouse head movements during OMR. We report the properties (angular velocity, duration, angular amplitude) of OMR head movements in mice and compare them with properties of eye movements during OKR under identical stimulation conditions. We then show that unrestrained mice, like other species, can respond to moving gratings with concomitant head and eye tracking movements. We apply our methodologies to analyze OMR and OKR responses in Brn3b^KO/KO mice, which have a complete ablation of RGCs projecting into the AOS while preserving some innervation to the LGN and SC.

MATERIALS AND METHODS

Mice.

Mice were Brn3b^KO/KO and Brn3b^WT/WT littermate controls, all on a C57Bl6 background. Male and female mice 2-6 mo old were used in all experiments. Numbers of tested animals for each experiment are specified in figure legends and results. Controls for behaviors in blind mice were derived from 6-mo-old rd1/rd1 mutants, which are devoid of rods and cones (Chang et al. 2002). All mouse handling procedures used in this study were approved by the National Eye Institute Animal Care and Use Committee under protocol NEI 640. All National Institutes of Health rodent surgery guidelines were followed. For OKR experiments, head posts were implanted as previously described (Cahill and Nathans 2008; Kretschmer et al. 2015).

Apparatus and visual stimulus design.

Our custom-built setup includes hardware and software for stimulus presentation, calibration procedures, and video tracking of head and eye movements and is described in great detail in Kretschmer et al. (2015). The software used to present the stimuli is available on request from the authors and is provided as free software under GNU GPLv3 license (OKR arena; http://openetho.com). Visual stimuli are projected on a virtual sphere displayed onto four screens. Patterns are mapped onto the inside wall of this sphere, and portions of the visual field can be masked. To reduce the light levels inside the setup to scotopic conditions, we used neutral density filters. For calibration, we measured the light intensity at the center of the platform while presenting a 0.2 cycle/° grating (at maximal contrast, see below) on the four screens. This resulted in a combined light intensity of 9 × 10¹³ photons·s⁻¹·cm⁻² (~41 cd/m²) for photopic light conditions or 9 × 10¹⁰ photons·s⁻¹·cm⁻² (~0.041 cd/m²) for scotopic light conditions (neutral density filters in front of the screens). The grating contrasts are calculated using the Michelson contrast formula C_M = (L_max − L_min)/(L_max + L_min), where the maximum (L_max) and minimum (L_min) luminance values are set at the extreme values allowed by the hardware (screen lookup table RGB values are [255 255 255] and [0 0 0], respectively, corresponding to about a 700-fold range in luminance). Thus the maximal contrast achievable was 0.997. For simplicity, we refer to this condition as “contrast = 1” for the rest of the article.

In this study we used rotating sinusoidal gratings to evoke OKR and OMR and a set of masks to cover the binocular and/or monocular field of the animal. Depending on the experiment, we have varied grating contrast, spatial frequency, velocity, direction, and duration of unidirectional rotation epochs. Each combination of conditions constituted one trial, and the number of trials per animal and experimental condition are indicated in figure legends. For experiments represented in Figs. 2–5, 7A, 7B, and 8, each trial lasted for 1 min, during which the stimulus rotated at constant speed around the animal (12°/s) but reversed direction every 5 s (for a total of 12 unidirectional stimulation epochs per minute); i.e., the stimulus follows a triangular position profile (square-wave velocity profile) at a replication rate of 0.1 Hz. Stimulus position profiles are represented at the bottom of exemplary head or eye traces (Figs. 3 and 8). For experiments in Fig. 2, the light levels (scotopic vs. photopic), contrast level (range = 0.05 to 1), and spatial frequency (range = 0.025 to 0.45) of the gratings were changed between trials. Three trials for each combination of parameters and animal were collected. For experiments in Figs. 3–5, grating velocity (12°/s), contrast (1), and illumination level (photopic) were kept constant, but spatial frequencies were changed on every trial. Experiments in Fig. 6 explored OKR/OMR dependency on visual stimulus velocity, so individual trial conditions were slightly different: unidirectional stimulus epochs lasted for 30 s, under constant illumination level (photopic), contrast (1), and spatial frequency (2 cycles/°), but grating velocities varied between 2 and 24°/s. For experiments in Fig. 7, A and B, masks were superimposed on the stimuli as described in results and figure legends. For experiments in Fig. 7E, the unidirectional stimulus epoch duration was set by the angular displacement of the stimulus (between 20° and 120°), and illumination (photopic), contrast (1), grating spatial frequency (0.2 cycle/°), and stimulus velocity (12°/s) were kept constant. Stimuli were generated by the “patternGen” component of our OMR stimulation and recording software suite as described previously (Kretschmer et al. 2015), and protocols were created containing all stimuli for each set of conditions. Protocols consisted of presentation of one trial for each condition, in randomized succession, to avoid learning and/or adaptation. Individual trials were separated by 30-s recovery pauses during which a gray screen was presented.

Fig. 2.

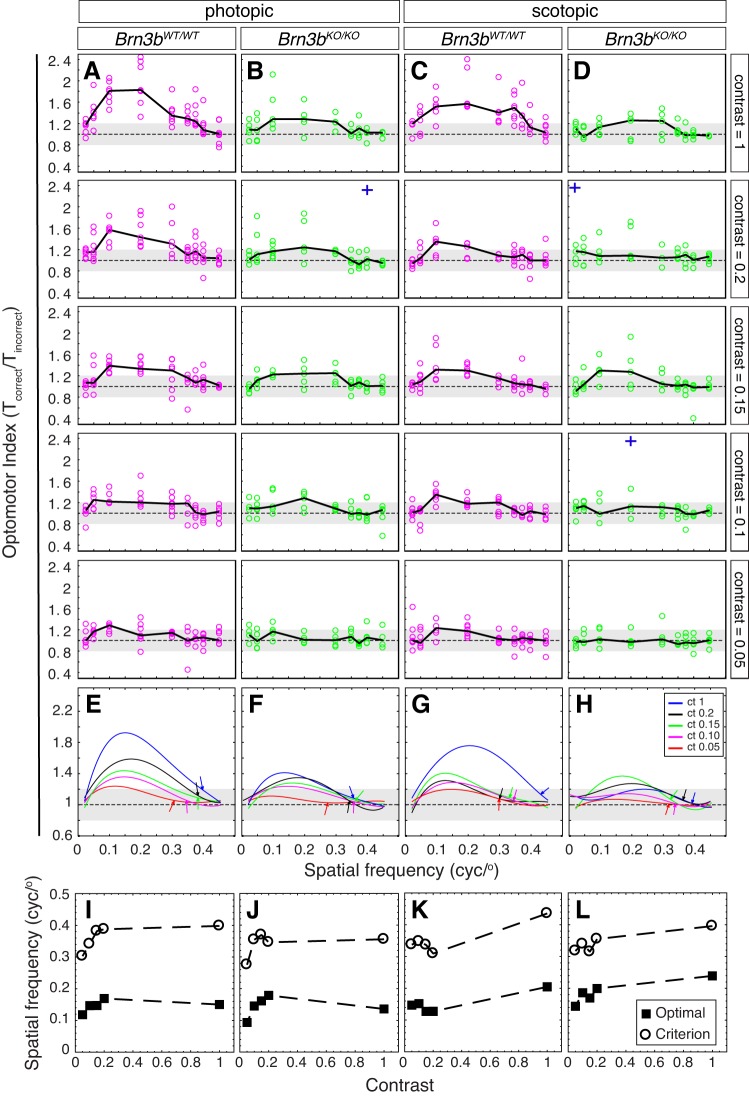
OMR dependency on visual stimulus contrast, spatial frequency, and photopic/scotopic conditions in Brn3b^KO/KO and Brn3b^WT/WT mice. A–D: OMR index (see Fig. 1Aiv) collected from Brn3b^WT/WT (A and C, n = 7) and Brn3b^KO/KO mice (B and D, n = 5) under photopic (A and B) and scotopic conditions (C and D) at 5 contrast levels (top to bottom: contrast = 1, 0.2, 0.15, 0.1, and 0.05) and 9 spatial frequencies (x-axis: 0.025, 0.05, 0.1, 0.2, 0.3, 0.35, 0.375, 0.4, 0.45). Black solid lines represent medians for all mice of the same genotype, and data points (circles) represent medians for individual animals. Each animal was measured 3 times at each condition. Note that some poor recordings were discarded from the analysis (e.g., mouse jumping off the platform), resulting in lower numbers of observations at some combinations of spatial frequency and contrast. Three outlier observations are represented as blue crosses, placed at the spatial frequencies at which they occurred. The OMR_ind values for the outliers were as follows: B, second plot = 3.53; D, second plot = 2.72 and fourth plot = 3.16. E–H: fourth-order polynomial fits [f_(x) = a·x⁴ + b·x³ + c·x² + d·x + e] for data in A–D. Coefficients a–e, R² values, maximal OMR_ind, and optimal spatial frequencies are provided in Supplementary Table S1. Curve fits for contrasts (ct) = 1 (blue), 0.2 (black), 0.15 (green), 0.1 (magenta), and 0.05 (red) for each genotype and light condition have been superimposed. Throughout, the dashed horizontal line and gray area represent the median and upper and lower quartiles of the OMR index previously collected in the same setup from a set of 3 blind control animals (retinal degeneration rd1, 6 mo old). We include it to illustrate the degree of variation of the OMR index resulting from random movements in a blind mouse (i.e., independent of vision). Arrows point at the spatial frequency at which the fit has reached the 25% threshold. I–L: contrast dependency of optimal and threshold (criterion) spatial frequencies for Brn3b^WT/WT (I and K) and Brn3b^KO/KO mice (J and L) under photopic (I and J) and scotopic conditions (K and L), as computed from the fits in E–H (cyc/°, cycle/°). See also Supplementary Table S1.

Fig. 5.

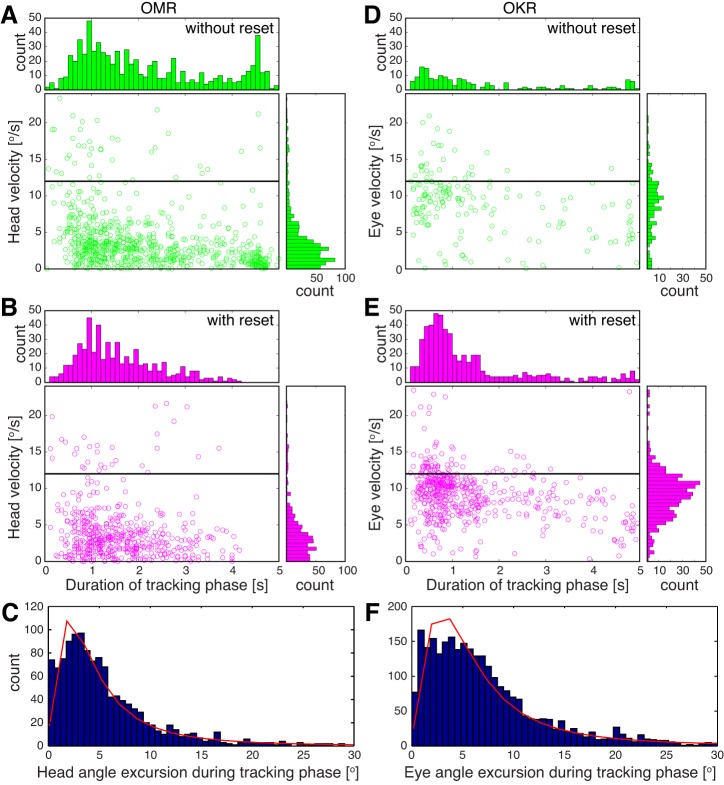
Velocity, duration, and amplitude of OMR and OKR slow phases. OMR (A–C) and OKR (D–F) were recorded from 3 Brn3b^WT/WT mice at the reported optimum for OMR (contrast = 1, spatial frequency = 0.2 cycle/°, velocity = 12°/s). A and D: scatter plots and histograms for tracking phases that were not followed by reset phases. B and E: scatter plots and histograms for tracking phases that were succeeded by reset phases. Horizontal black line indicates stimulus velocity (12°/s). C and F: histograms for head (C) and eye (F) slow-phase amplitudes overlaid with the log-logistic fit (red). For C and F, slow phases were pooled regardless of the presence or absence of a fast phase.

Fig. 7.

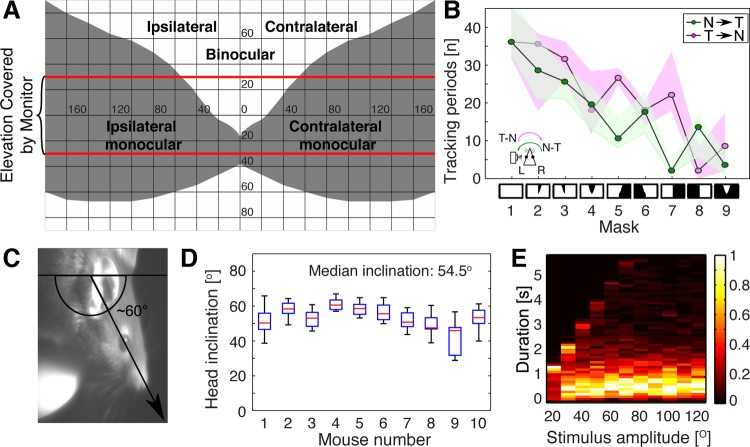
OKR dependency on visual field topography and on stimulus direction and duration. For all experiments, stimulation was done at contrast = 1, spatial frequency = 0.2 cycle/°, and speed = 12/°s. A and B: OKR masking experiments. A: planar projection of the virtual sphere displayed in our apparatus, showing the subdivisions of the mouse visual field (based on coordinates provided in Dräger 1978). Binocular and monocular regions and angular eccentricities in horizontal and vertical plane are indicated for a mouse facing the schematic and pointing its snout at the intersection of zero horizontal and vertical axes. The red lines at ±30° indicate the limits of the virtual sphere as visible on the 4 screens. Ipsilateral and contralateral fields are identified relative to the recorded (left) eye. B: number of slow tracking phases during presentation of sinusoidal vertical grating stimuli moving in either temporonasal (T→N; magenta) or nasotemporal direction (N→T; green) relative to the recorded (left) eye. Nine different masks were applied to the visual field, indicated at bottom, ordered from left to right as follows: 1, full field visible; 2, contralateral binocular field occluded; 3, ipsilateral binocular field occluded; 4, bilateral binocular field occluded; 5, contralateral monocular field occluded; 6, ipsilateral monocular field occluded; 7, full contralateral field occluded; 8, full ipsilateral field occluded; and 9, bilateral monocular fields occluded. White areas in the diagrams are visible; black areas are occluded. Bottom left, schematic of the mouse head seen from the top with camera imaging left eye, and convention for stimulus directions relative to the imaged eye. Note that the magenta stimulus direction is T→N for the imaged left eye but N→T for the right eye. Recordings are from 2 animals, with 3 trials for each condition. Results are presented as medians (black lines) and observation ranges of all measurements (magenta and green areas). C and D: inclination of the head during OMR experiments. C: head inclination is defined as the angle between a horizontal axis through the mouse trunk and a head axis through the snout tip and orbit. D: angles were computed for 10 trials for each of 10 animals and are presented as box-whisker plots. Red lines are medians, boxes define the interquartile intervals, and whiskers indicate the range of observations. The median inclination over all animals is 54.5°. E: dependency of OKR tracking phase duration (y-axis) on the angular amplitude of the unidirectional stimulation epoch (angle after which the stimulus changes direction; x-axis). Angular amplitudes were varied between 20° and 120° in increments of 10°. The number of slow movements are presented normalized to the maximal value within each angular amplitude (scale ranging from 0 to 1; heat map at right). The maximum length of a tracking phase cannot be longer than the duration of one unidirectional stimulus epoch (e.g., 2.5 s at amplitude = 30°; 5 s at amplitude = 60°). Results were derived from 4 animals, with 3 trials each.

Fig. 8.

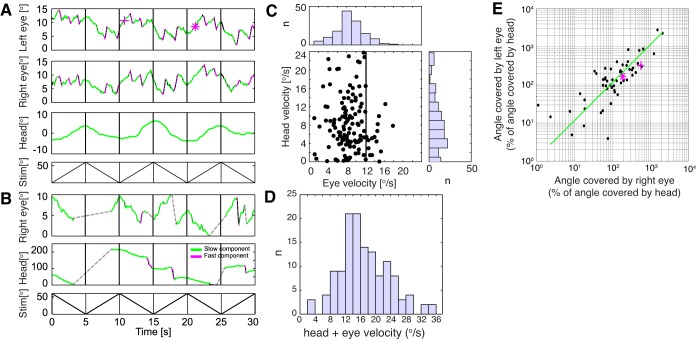
Simultaneous recording of head and eye movements. Recording conditions were as described in Fig. 1C. Visual stimuli are sinusoidal vertical bars of contrast = 1, spatial frequency = 0.2 cycle/° moving at speed = 12°/s, reversing direction every 5 s (A and B, bottom panels). Two C57Bl6 Brn3b^WT/WT mice were used for these recordings. Eye angles were calculated from the images acquired by the side camera, using a conversion based on a spherical eye model and ignoring perspective distortion. Head angles were calculated as for all previous OMR experiments, using the data provided by the top camera. A: simultaneous recording of both eyes and head. Top 3 panels represent angular velocities for left eye, right eye, and head. Tracking phases (green) and reset phases (magenta) were semiautomatically annotated. Eye velocities for the two marked tracking phases (magenta cross and asterisk) are indicated in the scattergram in E. B: example of recording in which large head movements prevented collection of meaningful images for the left eye (middle panel) and only intermittent focused eye images for the right eye (top panel). Periods during which the right eye was out of focus are marked as gray dotted lines. Note different y-scales for the different plots. Bottom panels of A and B show stimulus positions plots. C: velocity of head and eye movements (tracking phases where collected from 7 recordings, 1 min each). The histograms depict the distribution of head and eye velocities. All recordings where at least one eye was in focus were analyzed. D: histogram of combined (head + eye) velocities for the observations shown in C. E: the relative angle covered during individual tracking phases by left (y-axis) and right (x-axis) eyes, expressed as a percentage of head movement. Tracking phases were collected from 5 recordings, 1 min each, in cases where both eyes and the head were in focus. A linear regression line is shown (green; R² = 0.76).

Fig. 3.

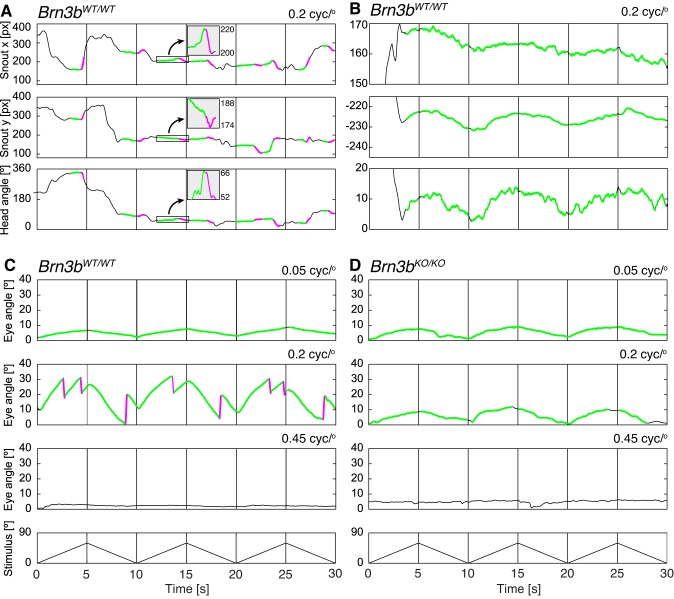
Exemplary annotated head and eye movements. A and B: examples of head movement traces collected with the top camera (Fig. 1A) from a Brn3b^WT/WT mouse exposed to moving vertical sine gratings (contrast = 1, spatial frequency = 0.2 cycle/°, and stimulus velocity = 12°/s, changing direction every 5 as indicated in C and D, bottom). The coordinates along the orthogonal directions (x, top; y, middle) and head angle (bottom) are presented (px, pixels). In A, tracking phases (green) are followed by reset phases (magenta) of opposing direction, and the animal follows only infrequently (most of the trace is black). The boxed regions along the trace have been magnified along the y-axis and are shown in the insets. In B, the mouse followed continuously and only once repositioned its body/head (black trace at ~3 s). C and D: example traces of recorded eye movements (OKR; Fig. 1B) from Brn3b^WT/WT (C) and Brn3b^KO/KO mice (D) at 3 different spatial frequencies (0.05, 0.2, and 0.45 cycle/°). The Brn3b^WT/WT mouse (C) exhibits high-gain tracking phases frequently followed by reset phases at optimal spatial frequency (0.2 cycle/°) and low-gain tracking phases not followed by reset phases at suboptimal spatial frequency (0.05 cycle/°). The Brn3b^KO/KO mouse (D) tracks with low-gain slow phases not followed by fast phases at both 0.05 and 0.2 cycle/°. Neither genotype exhibits observable eye movements at high spatial frequency (0.45 cycle/°).

Fig. 6.

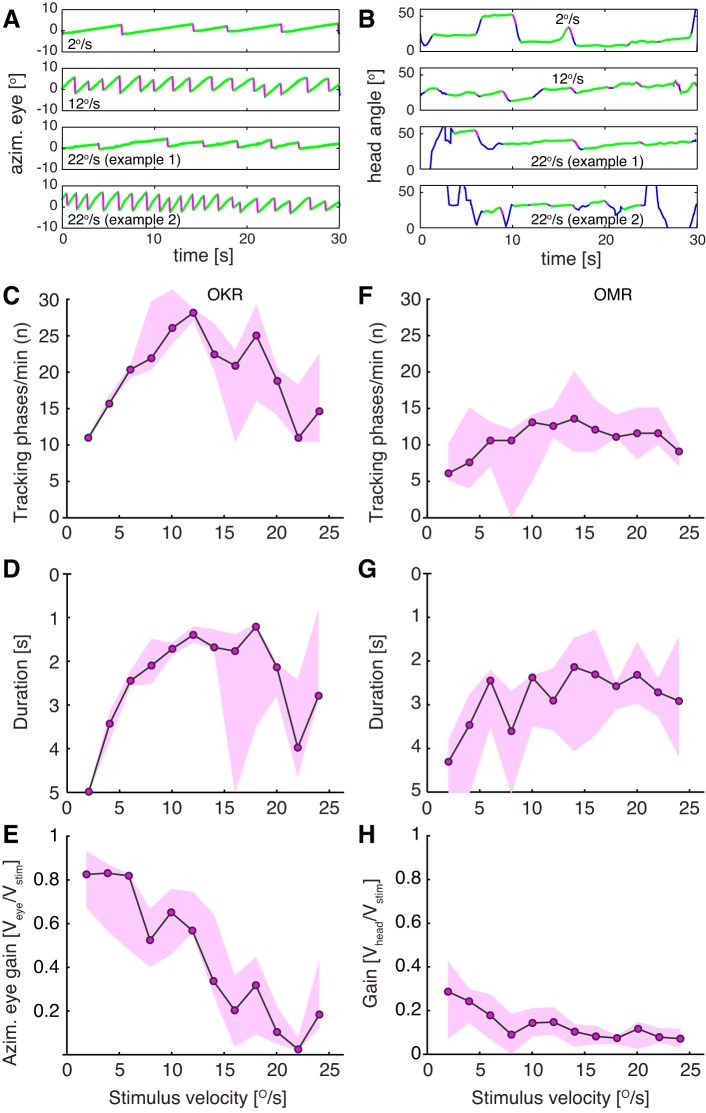
Comparison of OKR and OMR dependency on stimulus velocity. OMR and OKR were recorded from 5 animals (measured 3 times each) at contrast = 1 and spatial frequency = 0.2 cycle/°. Individual unidirectional stimulus epochs lasted for 30 s. A: example traces of eye movements at 3 different stimulus velocities (2, 12, and 22°/s). At 22°/s the animals were not able to keep up with stimulus velocity most of the time (example 1) and performed fewer tracking phases. On rare occasions, eye velocity was significantly higher and more tracking phases were performed (example 2). B: example traces of head movements at 3 different stimulus velocities (2,12 and 22°/s; examples 1 and 2). Green traces represent slow movements in stimulus direction, and magenta traces represent fast reset movements. C–H: number (C and F), duration (D and G), and gain (E and H) of OKR (C–E) and OMR (F–H) tracking phases exhibit distinct dependencies on stimulus velocity. Note that y-axes (duration) for D and G are inverted. Data are presented as medians across all animals (median of medians; black line) and range of medians for each animal (magenta areas).

Infrared illumination is provided by LED strips fixed to the corners of the setup (Fig. 1Aii), and the recording camera placed at the top of the arena is fitted with a high-pass infrared filter to minimize animal coat color and stimulus reflection effects during image processing. The setup can be easily converted between the OKR and OMR configurations. In OMR configuration, mirrors are placed on the ceiling and floor of the arena, and the camera is looking down at the animal from the center of the ceiling (Fig. 1A). In OKR configuration, the animal is held by an implanted head mount, and a video camera is imaging the pupil through a transparent infrared total reflection mirror (Fig. 1B). In this configuration, top and bottom mirrors are removed. To measure both reflexes simultaneously (Fig. 1C), the apparatus was configured for OMR, and a second camera was placed on one of the side panels, elevated from the platform by 12 cm. Traditionally, the gain (eye or head velocity/stimulus velocity) is used as a measure to determine the tuning of the visual system to the spatial and temporal aspects of the stimulus. In this study we also analyzed the total number and duration of tracking (slow) phases for each individual trace based on the found onsets and offsets of the slow and fast phases. Statistical significance was determined using a two-sample t-test (after testing for normal distribution using a Kolmogorov-Smirnov test), or alternatively, by applying the Kolmogorov-Smirnov test for unknown distributions. Optimal curve fits were determined by minimizing the residual mean square error and maximizing the correlation (R²) using the MATLAB curve fitting toolbox (cftool).

Fig. 1.

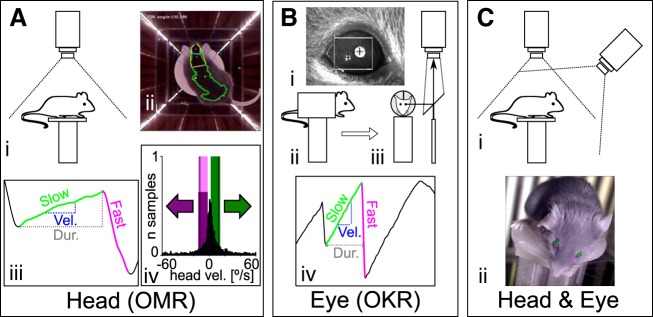
Recording configurations for OMR and OKR measurements. Three different apparatus configurations were used to evaluate OMR (A), OKR (B), and eye movements in freely behaving animals (C). Experiments in A and B were carried out using the same conditions as presented in Kretschmer et al. (2015). A: measurement of head movements (OMR). i, Schematic of recording configuration. The animal moves unrestrained on a platform and is monitored from above with a camera fitted with an infrared (IR) high-pass filter. ii, Example of a frame recorded by the top camera, with annotations of the automated online tracking algorithm. Four screens are presenting a stimulus consisting of vertical sinusoidal bars, and the arena is illuminated with IR LED strips placed at the corners between the screens. The green dot represents the center of mass for the automatically detected mouse contour (green outline), and the two red dots define the head orientation of the animal (for examples, see Supplementary Movies S1 and S2). iii, Example and naming convention for the manual trace annotation. Tracking movements were identified from the automatically derived head tracking trace. x-Axis is time, y-axis is head angle. The onset and offset of the slow (“tracking”; green) and fast (“reset”; magenta) phases were derived, and then the duration (Dur.; gray dashed line) and the velocity (Vel.; blue dashed line) of the slow phase were computed. iv, Calculation of the OMR index. For the automated analysis of head movements, the pairwise head angle differentials between all successive frames of the recording were determined (histogram, normalized to total number of observations). We then defined windows of (+2 to −10°/s) around the stimulus speed (±12°/s, black vertical lines) for the correct (green) and incorrect (magenta) directions and counted the total correct (T_c) and incorrect (T_i) movements contained within the two windows. The OMR index was computed as T_c/T_i. B: measurements of eye movements (OKR). i, example of pupil tracking using the ISCAN video camera. Pupil position is calculated relative to an IR corneal reflection landmark, and the pixel displacement is converted to angular coordinates using the calibration technique adapted from Stahl et al. (2000). ii and iii, Schematics of the recording setup, showing side view (ii) and front view (iii) of the mouse in the holder. The animal is restrained using an implanted head mount, and the eye image is projected to the camera through a 45° IR reflective mirror (placed in a plane parallel to the axis of the mouse). iv, Eye movements were analyzed semiautomatically. Several parameters were derived from the ISCAN recorded traces: the onset and offset, the duration (gray dashed line), the velocity (blue dashed line) of the slow (tracking) phase (green), and the onset of the fast (reset) phase (magenta). The automatically detected phases were checked manually in a second step. C: for simultaneous head and eye detection, we recorded the head movements of the unrestrained mouse as in A while imaging the eyes with an additional camera fixed onto the arena wall at 12-cm elevation above the mouse platform (i). ii, Pupil locations (green circles) and the nasal edges of the eyes (magenta cross) are determined by a pattern-matching algorithm, whereas head position was collected using the same protocol as in A.

Measurement of the optomotor response.

For OMR, the mice were placed on a platform in the center of the setup and virtual sphere (Fig. 1, Ai and Aii). Experiments were started after a short period of habituation once the animal calmed down. We recorded each animal for at most 30 min and interrupted recordings for at least 5 min, allowing us to clean the mirrors and platform. Monitors where turned off during this time period to cool down. The same animal was not measured again until it had rested at least 2 h. Recordings were acquired at 25 frames/s. For recording analysis, a thresholding algorithm was used to define the mouse shape, compute the contour, and define head angle [Fig. 1Aii; Supplementary Movies S1 and S2 (Supplemental material for this article is available online at the Journal of Neurophysiology website) (Kretschmer et al. 2015)]. Angular head speed, V_head, was calculated as the differential between head angle for each pair of successive frames. For the automated OMR analysis (Fig. 1Aiv), the ratio of time the animal moved in the correct direction (T_c) and incorrect direction (T_i) is defined as the OMR index: OMR_ind = T_c/T_i. In this study, we only calculated the OMR index for experiments using stimulus speeds of 12°/s. T_c represents the number of frames for which the mouse head moved in stimulus direction with speed V_head ranging from

$$\left(V_{\text{stim}}-10\right)\le V_{\text{head}}\le \left(V_{\text{stim}}+2\right),$$

where V_stim is the stimulus angular velocity (Fig. 1Aiv, trials falling within the green window). T_i represents the number of frames in which the head moved in a direction opposed to the stimulus with speed

$$\left(V_{\text{stim}}-10\right)\le \left(-V_{\text{head}}\right)\le \left(V_{\text{stim}}+2\right)\mathrm{.}$$

Note that for T_i, the head moves with the same absolute speed window as for T_c (Fig. 1Aiv, trials falling within the magenta window). The (V_stim −10°/s) to (V_stim +2°/s) interval has been previously shown to be optimal for angular head movements detection when OMR stimuli are moving at 12°/s (Kretschmer et al. 2015). To calculate spatial frequency dependency of OMR_ind and individual OKR and OMR event parameters, we derived the optimal fits for our data (e.g., Fig. 2, A–D; Fig. 4, A–H) using the cftool function in MATLAB. By optimizing the residual mean square error and R² values, we determined the fourth-order polynomial fit [f_(x) = a·x⁴ + b·x³ + c·x² + d·x + e] as ideal for our data. Optimal spatial frequencies and maximal OMR_ind (maxOMR_ind) values were derived from the fitted curves, and then a threshold criteria was calculated as [(maxOMR_ind – 1)/4 + 1]. Because a complete lack of visual response results in an OMR_ind of 1 (i.e., the animal preforms a similar number of random moves in the correct and incorrect directions, T_c/T_i = 1), this formula returns the 0.25 of maximal OMR_ind amplitude. During manual analysis (Fig. 1Aiii) the video file and head tracking locations were loaded into a MATLAB program used to navigate through the video and the recorded traces and identify the onsets and offsets of slow (tracking) and fast (reset) phases. To select OMR events, the user navigated through the video file together with the x and y coordinates of the two markers defining the head angle (red dots in Fig. 1Aii, see examples in Fig. 3A) frame by frame. The tracking and reset phases have strong translational components along the axes and hence are more easily detectable when the x and y projections are plotted separately (see insets in Fig. 3A; detailed description in Kretschmer et al. 2015). Note that whereas the head angle tracking and reset phases in Fig. 3A have significant angular jitters, the projection along the x-axis has a more smooth trajectory, which can be easily separated in tracking and reset phases.

Fig. 4.

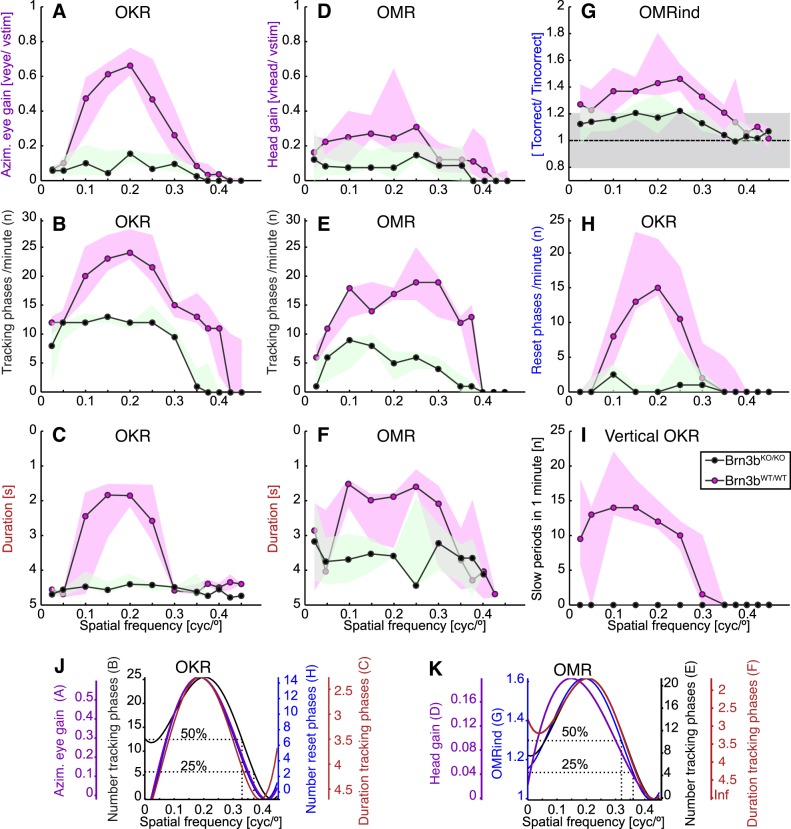
Comparison of OKR and OMR dependency on spatial frequency in Brn3b^KO/KO and Brn3b^WT/WT mice. A–F: spatial frequency dependency of gain (A and D), number (B and E), and duration (C and F) of tracking phases for OKR (A–C) and OMR recordings (D–F) of Brn3b^KO/KO (green; n = 3) and Brn3b^WT/WT mice (magenta; n = 3). Data are presented as medians (black lines) and observation ranges (shaded areas; observations represent medians of individual mice). For recording conditions and example traces, see Fig. 3. Note that the y-scale for C and F is inverted. G: automated OMR index for the same experiments as in D–F. Horizontal dashed line at 1 and shaded gray area (0.8–1.2) represent the OMR index median and interquartile interval for a blind mouse. H: number of reset phases for OKR experiments in A–C. I: vertical OKR recordings for Brn3b^KO/KO (green; n = 2) and Brn3b^WT/WT mice (magenta; n = 3). J and K: data for Brn3b^WT/WT mice shown in A–H were fitted following the fourth-order polynomial function (using the MATLAB curve fitting toolbox and the nonlinear least absolute residual method: f_(x) = a·x⁴ + b·x³ + c·x² + d·x + e. We used a degrees of freedom-adjusted R² value to determine the goodness of fit. For OKR measurements: number of slow OKR phases (black; data from B), R² = 0.84; number of reset phases (blue; data from H), R² = 0.68; gain (purple; data from A), R² = 0.80; duration of tracking phases (red; data from C), R² = 0.50. For OMR curves: number of tracking phases (black; data from E), R² = 0.80; OMR_ind (blue; data from G), R² = 0.72; gain of OMR (purple; data from G), R² = 0.46; duration of OMR phases (red; data from F), R² = 0.79. The curves were scaled for better comparison of the qualitative trends and are color-coded together with their respective axes.

OMR was collected using the following sets of varying conditions: 1) variation of the spatial frequency under scotopic and photopic light conditions at various contrasts (automated analysis), 2) variation of the spatial frequency (manual analysis) under photopic light condition, and 3) variation of stimulus velocity under photopic light conditions.

Measurement of the optokinetic reflex.

For a detailed description of all procedures used to record and analyze OKR, see Kretschmer et al. (2015). The mouse was restrained in an acrylic holder through an implanted head post. The holder was then positioned in the center of the setup and the virtual sphere (Fig. 1, Bii and Biii). The eye was illuminated with an infrared light source, and the eye image was reflected through an infrared mirror to an ETL-200 video camera (ISCAN, Burlington, MA) positioned at the top of the arena (Fig. 1, Bi–Biii). Before recording began, each mouse eye was calibrated using a variant of the procedure previously described by Stahl et al. (Kretschmer et al. 2015; Stahl et al. 2000; Zoccolan et al. 2010). The corneal reflection and pupil position were detected via the DQW software (ISCAN) and converted into angular coordinates using a MATLAB procedure and the acquired calibration data. We recorded each animal for at most 30 min and interrupted recordings for at least 5 min, allowing us to clean the mirrors and platform. Monitors where turned off during this time period to cool down. The same animal was not measured again until it had rested at least 2 h. Recordings were then analyzed semiautomatically. In a first step, a MATLAB program was used to detect onsets and offsets of tracking (slow) and reset (fast) phases in the recordings. In a second step, the onsets and offsets were checked manually by the user. On the basis of the annotated onsets and offsets, we then calculated the number of occurring tracking phases and their duration, velocity, and gain (Fig. 1Biv). Eye velocity was approximated by a linear regression over each detected time window (Kretschmer et al. 2015). For operational purposes, if the stimulus reversed direction during a tracking phase, it was split into two tracking phases at the point of direction reversal (e.g., for each stimulus of Fig. 3C at 0.05 cycle/°, 6 eye tracking phases not followed by reset phases were annotated, one for each unidirectional stimulus epoch). The following experiments for OKR measurements were performed under photopic light conditions: 1) variation of the spatial frequency, 2) variation of the stimulus velocity, 3) variation of stimulus amplitude (total angle covered while stimulus moves in one direction), and 4) masking of the visual field subdivisions.

Simultaneous measurement of optokinetic and optomotor responses.

Simultaneous eye and head measurements were recorded from unrestrained animals placed on the platform in the OMR configuration, with an additional lateral camera (Pro 9000; Logitech, Lausanne, Switzerland) placed on one of the arena walls elevated ~12 cm above the mouse platform (Fig. 1Ci). Recordings from the lateral camera were synchronized to the recordings of the camera monitoring the animal from the top. Because the mouse was not restrained, the eye was not continuously in the focus of the lateral camera. Hence, we recorded around 500 trials (1 min each) during several sessions, of which only around 100 were used for analysis. The recordings (resolution of 1,280 × 720 pixels and 25 frames/s) were analyzed semiautomatically using a custom MATLAB program. The pupil position of the left and right eye and the two reference locations at the nasal edge of the eyes (Fig. 1Cii) were detected using a template-matching algorithm based on a normalized cross-correlation (see expanded/corrected version of Lewis 2007; http://scribblethink.org/Work/nvisionInterface/nip.pdf), which was applied to a manually defined region of interest. The four templates were manually selected for each recording. The coordinates with the highest correlations were then calculated for the pupil positions and reference locations. The reference locations were subtracted from the pupil locations. All recordings with the lateral camera were done using sine grating stimuli of 0.2 cycle/° spatial frequency rotating at 12°/s and changing its direction every 5 s.

RESULTS

Automated quantitation of OMR at scotopic and photopic light conditions and various contrasts.

Mice generate OMR only infrequently during any individual recording period, even under optimal stimulation conditions. It is perhaps for this reason that previous approaches were focused on counting the number of OMR events per unit time. We have recently proposed an unbiased approach in which angular head velocities are recorded for all frames of the recording, and then a “overall direction bias,” which we call OMR index (OMR, see material and methods and Fig. 1Aiv), is calculated (Kretschmer et al. 2013, 2015).

Figure 2 shows OMR_ind dependency on visual stimulus contrast, spatial frequency, and scotopic/photopic regime. Experiments were performed at a stimulus angular speed of 12°/s (Fig. 2, A–D, and Supplementary Table S1). Data were fitted with a fourth-order polynomial function, and a criterion for the visual threshold was defined as the spatial frequency at which the fit curve of the measured response reaches 0.25 of its maximum (see material and methods; Fig. 2, E–H). Under photopic conditions, the OMR_ind dependency on spatial frequency in Brn3b^WT/WT mice is similar to previously published observations (Prusky et al. 2004; Umino et al. 2008, 2012; Fig. 2, A, E, and I, and Supplementary Table S1) with maximum OMR at 0.15–0.17 cycle/°, decreasing toward both lower and higher spatial frequencies, and reaching baseline at 0.4 cycle/°. Both optimal and threshold OMR_ind amplitudes gradually diminished for contrast levels ranging from 1 to 0.05, and OMR_ind threshold spatial frequencies decreased from 0.39 to 0.3029 cycle/° (Fig. 2, E and I, and Supplementary Table S1). At contrast level 0.05, the maximal OMR_ind amplitude was still marginally higher than the levels of random variation seen in blind animals (Fig. 2, A and E), but the polynomial fit was poor (R² = 0.1955), and most of the curve fit was essentially aligned to the baseline. Brn3b^WT/WT mice exhibited qualitatively similar OMR_ind values under scotopic and photopic light conditions (compare Fig. 2, A, C, E, and G). The scotopic maximal OMR_ind amplitudes are somewhat (not statistically significant) lower than the photopic amplitudes (e.g., at spatial frequency = 0.2, P values at contrast levels 1, 0.2, 0.15, and 0.1 are 0.2330, 0.0518, 0.4232, and 0.6208, respectively). Under scotopic conditions, the threshold values range between 0.43 and 0.31 cycle/° for contrast levels 1–0.05 (Fig. 2, G and K, and Supplementary Table S1), comparable to those observed under photopic conditions.

Maximal photopic OMR_ind amplitudes of Brn3b^KO/KO mice were significantly reduced compared with those of Brn3b^WT/WT mice at full contrast levels (Fig. 2, A, B, E, and F; Kolmogorov-Smirnov test, at spatial frequency = 0.2 and contrast = 1, P = 0.0204); however, the differences at lower contrast levels were not statistically significant (e.g., at spatial frequency = 0.2, for contrast = 0.2, P = 0.9719, and for contrast = 0.15, P = 0.4428), and the optimal and threshold spatial frequencies were in similar ranges compared with the Brn3b^WT/WT littermates (Fig. 2, A, B, E, F, I, and J, and Supplementary Table S1) for all contrast levels. Under scotopic conditions, the maximal amplitude of the OMR_ind in Brn3b^KO/KO mice was drastically affected at full contrast (Fig. 2, C, D, G, and H; Kolmogorov-Smirnov test, at spatial frequency = 0.2 and contrast = 1, P = 0.0023). Whereas the maximal amplitudes for all other contrast levels were diminished, differences from those observed in Brn3b^WT/WT littermates were not significant. Interestingly, just as for photopic conditions, the optimal and threshold spatial frequencies were only minimally affected in Brn3b^KO/KO mice compared with Brn3b^WT/WT littermate controls (Fig. 2, G, H, K, and L). However, it should be noted that most curve fits for OMR_ind in Brn3b^KO/KO mice under scotopic conditions were relatively poor (R² ≤ 0.2; Supplementary Table S1 and Fig. 2H), and OMR_ind amplitudes were comparable to the range of variation in blind mice (Fig. 2D, gray area representing the interquartile intervals for OMR_ind in 6-mo-old rd1/rd1 rodless and coneless mice).

Analysis of individual OMR and OKR events.

Whereas the OMR_ind quantitation reveals global biases in head angle movements relative to stimulus direction, this approach cannot directly describe the characteristics of individual OMR events. We therefore manually defined individual optomotor and optokinetic responses on the automatically produced traces (Fig. 3). We defined individual events tracking (slow) phases and reset (fast) phases that follow/interrupt the slow phase for both OMR and OKR (Fig. 3, green and magenta lines, respectively). Under optimal OMR stimulus conditions (photopic light levels, contrast = 1, stimulus angular speed = 12°/s, spatial frequency = 0.2 cycle/°), OMR in wild-type (Brn3b^WT/WT) mice can alternate between continuous tracking phases in stimulus direction (Fig. 3B) and brief tracking (slow) movements in stimulus direction followed by reset (fast) movements in reverse direction (Fig. 3A). This second type of movement was essentially absent from Brn3b^KO/KO mice. We note that, in our recordings, head OMR events have strong translational components, and hence are more easily recognized by projections onto the orthogonal axes (Fig. 9 in Kretschmer et al. 2015 and in this work, Fig. 3A, top two traces).

We also systematically recorded OKR responses at various spatial frequencies under the same stimulus conditions as for OMR in Brn3b^WT/WT and Brn3b^KO/KO animals. Tracking and reset phases of OKR events were identified automatically (examples in Fig. 3, C and D; quantitation in Fig. 4). In Brn3b^WT/WT OKR, slow tracking phases of very low gain (0.1 in median) occurred continuously at low spatial frequencies up to 0.05 cycle/° (Fig. 3C, top, and Fig. 4A). These movements lasted for almost the entire 5 s of the unidirectional stimulus epoch, uninterrupted by reset phases (Fig. 3C, top, and Fig. 4C), similar to the head movement example in Fig. 3B. At optimal spatial frequencies (0.2 cycle/°), tracking phases were more numerous, much faster (gain 0.7 in median), shorter (2 s), and typically followed by a fast phase (Fig. 3C, middle). As spatial frequencies increased beyond the optimum, the slow phase gain decreased, resulting in OKR movements similar to those seen at 0.05 cycle/°. Finally, at spatial frequencies above 0.4 cycle/°, animals completely stopped performing OKR (Fig. 3C, bottom). During these trials, the pupil of the animal rested in the default axis position and only very rarely were spontaneous saccade-like eye movements recorded, more frequently associated with the animal repositioning its body in the holder. To summarize, visual stimuli of optimal spatial frequency (0.2) result in frequent events (25 per min in median), with high gain (0.7 in median) and short duration (2 s). Outside the optimum, the number of movements declined, and they became longer and slower, and were rarely followed by fast phases (Fig. 4, A–C, magenta traces for Brn3b^WT/WT animals). The spatial frequency dependency of OMR events paralleled the results seen for OKR, in terms of both curve shapes and absolute values, with the exception of gain, which was significantly lower (maximum = 0.3 OMR vs. 0.7 OKR; Fig. 3, A and B, and Fig. 4, D–F).

In Brn3b^KO/KO mice, both OKR and OMR were dominated by low-gain slow phases tracking the stimulus continuously, essentially uninterrupted by reset phases. For the OKR, the eye constantly moved in stimulus direction (Fig. 3D), at very low gain (around 0.1; Fig. 4A), with individual tracking phases essentially covering the entire unidirectional stimulus epoch (Figs. 3D and 4B; 12 tracking phases per minute, and hence 1 tracking phase for each of the 12 5-s trial segments). Fast reset phases were very rare (Fig. 4H), and hence individual tracking phases lasted for the whole 5 s of the stimulation epoch (Figs. 3D and 4C). For the OMR, head gain was around 0.1 (Fig. 4D), and the head tracking movements were less frequent than for OKR (Fig. 4E, around 6 per minute, or only 1 every other 5-s unidirectional stimulus epoch) and lasted only ~4 s (Fig. 4F).

We had previously reported complete loss of vertical OKR in Brn3b^KO/KO mice (Badea et al. 2009). We therefore measured vertical eye movements in response to a stimulus presented on a virtual sphere rotated around the roll axis (Fig. 4I). For Brn3b^WT/WT mice, the optimal spatial frequency lied at 0.1–0.15 cycle/° in median, whereas the threshold was reached at 0.35 cycle/°. As previously reported, Brn3b^KO/KO mice did not respond to stimuli rotating around the roll axis, and thus the number of tracking phases was consistently zero.

The automatically determined OMR_ind was consistent with the individual OMR movement analysis for both Brn3b^WT/WT and Brn3b^KO/KO mice in this data set (Fig. 4G). The peak was less well pronounced but in the range of 0.15 to 0.25 cycle/°. The responses decreased toward both higher and lower spatial frequencies, and at 0.4 cycle/°, both Brn3b^WT/WT and Brn3b^KO/KO mice moved the same amount of time in the correct and in the incorrect directions (ratio = 1).

We used fourth-order polynomial functions as optimal fits for the Brn3b^WT/WT data shown in Fig. 4, A–H, to directly compare the qualitative trends in the different parameters of the responses. Figure 4J shows the fit curves for OKR gain, number and duration of tracking phases, and number of reset phases, corresponding to data in Fig. 4, A–C and H. All four parameters show similar trends, with the threshold spatial frequency lying between 0.33 (duration of the tracking phases) and 0.37 cycle/° (number of tracking phases). Given the pendular movement of our stimulus, which reverses direction every 5 s, the maximum duration of a tracking phase is 5 s. The plateau of the duration from 0.3 to 0.425 cycle/° (Fig. 4B) is likely a consequence of this quantification. For OMR, the automated OMR_ind (Fig. 4G), the manually annotated number of tracking phases (Fig. 4E), and the duration of these phases (Fig. 4F) also show very similar spatial frequency fit curves (Fig. 4K). All three parameters show a maximum at 0.2 cycle/°, whereas the 0.25 quartile threshold ranges from 0.36 to 0.375 cycle/°. The only parameter that does not show this trend is the OMR head gain (Fig. 2, D and K). The head gain remains relatively constant (0.25) in the spatial frequency range of 0.1 to 0.3 cycle/° and only drops to 0.15 at the edges of the spatial frequency range with the goodness of fit being much worse than for the other parameters.

Data presented in Fig. 3 suggested that both OKR and OMR could be heterogeneous in angular velocity and duration. To get a better understanding of the range of their variation, we recorded head and eye movements at the reported optimum for OMR (contrast = 1, spatial frequency = 0.2 cycle/°, stimulus velocity = 12°/s; for OMR: 10 mice were measured 10 times for 1 min; for OKR: 7 mice were measured 3 times for 1 min). After manually annotating the traces, we calculated the duration and velocity of all occurring tracking phases. We distinguished two types of OMR and OKR episodes, based on the presence or absence of the fast reset phase in stimulus-opposed direction following a slow movement phase in stimulus direction (Fig. 5). Overall, OMR duration shows a much higher degree of variation compared with eye movements (compare Fig. 5, A and B, with Fig. 5, D and E). Most OMR have durations of around 1 s and a velocity of 2°/s, and only about half are followed by a reset movement (Fig. 5, A and B). Slow and long movements (>4 s) are never followed by such a retraction. In contrast, OKR velocity is only slightly below stimulus velocity. Most OKR movements are performed at 10°/s, last 800 ms (median), and are followed by a fast reset movement (Fig. 5, D and E). To relate the head/eye excursions of the animal to the maximal unidirectional stimulus excursion (60°), we calculated the angle the head and eye cover during an individual tracking phase. Most eye and head tracking phases cover 1° to 10° angular amplitude (Fig. 5, C and F). The log-logistic fit suggests a very similar maximum of 3° for both OMR and OKR, and very few events extend to 30°, thus far from the maximum unidirectional stimulus angular amplitude of 60°. In conclusion, OMR head movements are more heterogeneous, much slower, and less likely to be followed by fast reset phases than OKR eye movements; however, they typically cover similar angular amplitudes.

Optomotor and optokinetic responses at various stimulus velocities.

Our experiments, performed at a stimulus speed of 12°/s, reported to be optimal for OMR (Prusky et al. 2004; Umino et al. 2008), revealed much smaller gains for OMR compared with OKR. We therefore reevaluated the stimulus speed dependency of OMR and OKR gain under maximal contrast and optimal spatial frequency (0.2 cycle/°) conditions. The stimulus rotated around the animal in either clockwise or counterclockwise direction for 30 s at a time (unidirectional stimulation epoch = 30 s). Epochs of different directions and speeds were presented in random order to prevent adaptation, and results for the two directions were pooled. Figure 6, A and B, depict exemplary traces showing dissimilar number/durations of the slow phases at different stimulus velocities (2 and 12°/s, top panels) but also within the same stimulus velocity (22°/s, example 1 and example 2 traces). The stimulus velocity dependency curves for number and duration of tracking phases for both OKR and OMR had a bell shape, with the maximum number of movements being evoked at around 10–15°/s (Fig. 6, C, D, F, and G). However, the gain for both OMR and OKR decreased with increasing stimulus velocity, with maximal gains of 0.7–0.8 for OKR (Fig. 6E) and 0.3 for OMR (Fig. 6H). Therefore, eye and head velocities (gain × stimulus velocity) were highest in the interval 10–15°/s stimulus velocity, and thus the number of OKR or OMR movements per unit time was highest and their duration shortest (1–2 s) within this interval. At high stimulus velocities, the spread of response duration increased (Fig. 6, D and G, at velocities ≥15°/s) as the result of a mixture of frequent, low-velocity eye or head drifts (Fig. 6, A and B, example 1) and less common trials during which eye or head were able to better keep up with stimulus velocity (Fig. 6, A and B, example 2).

Relative contribution of visual field to OMR and OKR.

We find that OMR and OKR have equivalent sensitivity curves with respect to spatial frequency and speed of moving stimuli but strongly differ in gain. If both reflexes are driven by the same detectors, what could be the conditions that result in the gain difference? An obvious difference between OMR and OKR recording is the head fixation, which results in differential input from the vestibular and proprioceptive systems and different effector muscle groups involved, but also in constraints on the areas of the field of view of the animal that are stimulated (e.g., monocular vs. binocular, eye excursions within the orbit vs. head and body excursions). During OMR the mouse might observe the visual stimulus under a variety of angles, and with distinct relative contributions of the monocular and binocular fields of view, depending on the head angle under the yaw, pitch, and roll axes. To determine whether different retinal regions have distinct efficiency in eliciting OKR, we designed virtual masks to cover the left (ipsi; measured) or right (contra) binocular or monocular hemifields, either individually or in combination (Fig. 7, A and B). Figure 7A depicts the unfolded virtual sphere as projected onto our four screens in the recording setup and highlights the boundaries between presumed monocular and binocular fields of view (Bleckert et al. 2014; Dräger 1978; Sterratt et al. 2013). The ipsilateral and contralateral fields are labeled relative to the recorded (left) eye. The set of masks (1–9) are represented as symbols at the bottom of Fig. 7B, with black areas signifying the subdivisions of the visual field that were occluded. This set of masks were overlaid on top of the sinusoidal vertical gratings moving under optimal stimulation conditions (0.2 cycle/°, 12°/s, contrast = 1) in either nasal-to-temporal (N-T) or temporal-to-nasal (T-N) direction relative to the recorded (left) eye. In the subsequent description, the T-N and N-T directions, as well as the ipsi-contra distinctions, always refer to the recorded (left) eye. Although the OKR is conjugate, it has previously been reported that monocular stimulation in the temporal nasal (T-N) direction relative to the stimulated eye is more effective (Cahill and Nathans 2008; Stahl et al. 2006). Under full field stimulation (mask 1), 36 tracking phases per minute (median) are detected for either stimulus direction. We indeed find that the effects of masking either the monocular or binocular hemifields are highly dependent on the direction of the stimulus relative to the stimulated eye (for statistical comparisons, see Supplementary Table S1). Thus right (contra) binocular hemifield occlusion impaired OKR only during N-T stimulation (median = 29 phases, mask 2, green; P = 0.0183 vs. mask 1), whereas left (ipsi) binocular hemifield occlusion affected OKR under N-T (median = 25 phases, mask 3, green; P = 0.0023 vs. mask 1) and not significantly for T-N conditions (median = 32 phases, mask 3, magenta; P = 0.367). Occlusion of the entire binocular field resulted in an even stronger reduction in OKR regardless of stimulus direction (median = 20, mask 4; P = 0.0023 for either T-N or N-T vs. mask 1). The effects of the left or right monocular hemifield occlusions were even more pronounced, reducing the number of OKR phases to almost half compared with the unmasked condition, under either T-N or N-T stimulation. Occlusion of the left (ipsi) eye reduced OKR response in both directions of stimulation (median =  17 phases, mask 6; P = 0.0023 for either T-N or N-T vs. mask 1). However, occlusion of the contra eye was more deleterious to the OKR response during stimulus presentation in the N-T direction (mask 5, N-T, green, median = 10 vs. T-N, magenta, median = 26; P = 0.0013). Finally, occlusions of the complete left or right hemifields impaired OKR more than just occluding the monocular hemifields (masks 7 and 8), and the least potent OKR stimulation was elicited by stimulating the full binocular field alone (mask 9, N-T = 4, T-N = 8 in median; P = 0.0023 for either T-N or N-T vs. mask 1). Covering the entire right (contra) field had dramatically different consequences depending on stimulus direction (mask 7). Stimulation of the ipsi eye in its preferred direction (mask 7, T-N, magenta) resulted in around 22 OKR events (median), whereas N-T stimulation (mask 7, green) yielded only 2 (median; P = 0.0013). The effect was reversed when the left (ipsi) field of view was covered, only stimulating the right eye (mask 8, N-T, green, median = 13 vs. T-N, magenta, median = 2; P = 0.0122).

In our hands, stimulation of the recorded eye results in a moderate but consistent increase in OKR tracking compared with stimulation of the contralateral eye, even when the stimulus direction is optimal for the respective stimulated eye (e.g., masks 5 and 7 in T-N vs. masks 6 and 8 in N-T; P = 0.0013).

Thus both binocular and monocular fields can elicit OKR. In our experiments, the binocular field (see Fig. 7A), represented by the area centered around vertical meridian 0 and delimited by the horizontal meridian at 30° and the two gray monocular regions, is relatively small. However, it has an unexpectedly large contribution to the OKR compared with its size relative to the monocular fields. Thus, for mask 4, almost half of OKR movements are gone when the full binocular region is covered.

Significantly, during OKR recordings, the mouse head is positioned in the setup on a horizontal axis. In unrestrained mice, distinct areas of the visual field can actively be directed toward stimuli by adjusting the body posture, most importantly, head inclination. We therefore determined the inclination of the head during 100 OMR recordings (10 mice, 10 trials each) with the mouse freely moving on the platform (Fig. 7, C and D). All animals incline their head by 40°–60° in median during OMR experiments, most likely resulting in a larger portion of the binocular field of view facing the stimulus.

Influence of visual stimulus angular amplitude.

As described in Fig. 5, the slow phases of head and especially eye movements clustered around an angular amplitude of ~3.5° but reached as much as 30°. During those experiments, the visual stimulus moved at 12°/s, changing direction every 5 s and therefore covering an angular amplitude of 60°. At suboptimal spatial frequency conditions, or in Brn3b^KO/KO mice, head or eye movements exhibit mostly a low gain and can continuously follow the stimulus over multiple unidirectional stimulation epochs of 5 s, without being interrupted by fast reset movements, and reversing direction together with the stimulus; however, such events can also be observed in Brn3b^WT/WT mice under optimal stimulation conditions (Fig. 3B and Fig. 3, C and D, top traces). We therefore wanted to explore the influence of stimulus angular amplitude on the length of slow phases of eye movements. We designed a set of stimuli that change direction after a defined angular amplitude. We varied the amplitude from 20° to 120° in steps of 10° while stimulating under optimal conditions, (stimulus velocity = 12°/s, spatial frequency = 0.2 cycle/°, contrast = 1). We then analyzed the effect the amplitude has on the length of the slow phase of OKR movements (Fig. 7E). At an amplitude of 20°, the animal manages to follow the stimulus for the entire duration of one epoch (20° divided by 12°/s = 1,666 ms) on most trials. At higher amplitudes the animal is still able to track for the entire stimulus amplitude up to 60° but mostly performs movements that last up to 1s. Thus mice can perform OKR movements of up to 5.5 s (~55° amplitude, considering a gain of 0.8 and stimulus velocity of 12°/s); however, the most stereotypical OKR eye movements last for 0.5 s (~5°, representing the customary range) or less, regardless of unidirectional stimulation epoch amplitude.

Simultaneous recordings of head and eye movements in response to moving gratings.

We find in this study that mouse head gains during OMR are significantly lower than eye gains during OKR. One potential explanation is that image stabilization is achieved through combined head and eye movements in freely behaving mice, as has been seen in other species (Collewijn 1977; Fuller 1987; Gresty 1975). We therefore recorded eye and head movements simultaneously under OMR stimulation and recording conditions (Figs. 1C and 8, and Supplementary Movies S3 and S4). Supplementary Movies S3 and S4 show examples of the lateral camera recording of a mouse performing head and eye tracking simultaneously. Note that whereas eyes are almost continuously engaged in OKR events, clear head OMR episodes are noticeable between seconds 2–5 and 11–13 of the movie. Figure 8, A and B, shows exemplary traces of head and eye movements recorded simultaneously under optimal stimulation conditions. Figure 8A illustrates eye movements that look similar to those observed during head-restrained OKR experiments. The two eyes perform synchronized tracking phases, followed by fast reset phases, whereas the head moves in stimulus direction at a very low gain. No head retractions/resets could be observed. However, in the recording shown in Fig. 8B, head movements had larger gain, shorter tracking phases at constant velocity in stimulus direction, followed by fast reset phases. Because of the expansive head movements, only the right eye was in focus during the recording, and fewer saccadic movements were observed. Figure 8C shows the distribution of eye and head velocities during head-eye coincident tracking movements. Because no calibration for the spherical eye shape is possible under head-free conditions, we used a theoretical spherical model of the eye to transform pixel distances in the image plane into eye angular coordinates. Relative velocities should hence be seen as estimates. The eye velocity histogram has a maximum in the 8–10°/s interval, slightly lower than the value derived for eye velocities in the head-restrained animal (Fig. 5, D and E), whereas the head velocity histogram exhibits the same distribution as in previous experiments (Fig. 5, A and B). There seems to be no strong correlation between eye and head velocity (Fig. 8C), whereas the correlation between angles covered by the two eyes during coincident OKR movements is reasonably high (Fig. 8E; R² for the linear regression line = 0.76). Interestingly, the distribution of summated head and eye velocities peaks between 12 and 16°/s, slightly higher than the stimulus speed (12°/s). Given the various measurement constraints, this falls very close to unitary gain.

DISCUSSION

We have used our automated head tracking algorithm to report the first determinations of head angular velocities during mouse OMR and perform a direct, quantitative comparison between OMR and OKR responses. We have found that mouse OMR and OKR tuning for stimulus speed and spatial frequency are in good agreement for most parameters investigated, but that OMR gain is significantly lower than OKR gain under all stimulation conditions. We also provide the first evidence that mice, like other mammalian species, perform combined head and eye movements during unrestrained horizontal optokinetic response. We have then shown that Brn3b^KO/KO mice, previously known to be devoid of ON-DS RGCs, the input neurons to the accessory optic system, have profound defects in both OMR and OKR.

Previous work had reported that optimal stimulus conditions for eliciting mouse OMR range around velocities of 12°/s and spatial frequencies of 0.15–0.2 cycle/°, and found that the OMR spatial visual acuity threshold is around 0.4 cycle/° (Prusky et al. 2004; Umino et al. 2008). In these experiments, an observer was asked to identify mouse head movements in the stimulus direction, a decision that might be related to the number, amplitude, and speed of the movements made by the tested animals and the subjective perception of the observer. Our own quantitations, based on an automatic overall directional bias index of the head movement (OMR_ind) or the direct computation of gain, number, and duration of individual OMR slow (tracking) phases, yield similar ranges for spatial frequency optimum (0.15–0.2 cycle/°) and visual acuity threshold (0.375–0.4 cycle/°) (Figs. 2 and 4). These values are also in good agreement with OKR tuning for spatial frequency, when parameters such as the gain, number, and duration of slow (tracking) and fast (reset) phases are computed (Fig. 4 and Sinex et al. 1979; Tabata et al. 2010; van Alphen et al. 2009). The absolute value of head or eye velocity, as well as the customary ranges for head and eye excursions during OMR and OKR, are probably more related to the kinematic properties of the systems subserving them (head and neck muscles, oculomotor muscles, interactions with vestibular and proprioceptive systems, etc.). However, the similar tuning of OKR and OMR parameters to spatial frequency suggests that they derive their input from similarly tuned visual inputs (possibly ON-DS RGCs). This notion is further supported by the fact that both OKR and OMR gain are maximal at low stimulus velocities (<5°/s; Fig. 6 and Stahl 2004a, 2006; Tabata et al. 2010; van Alphen et al. 2009), consistent with reported optima for the ON-DS RGCs in rabbits and mice (Collewijn 1969; Oyster et al. 1972; Sun et al. 2006; Yonehara et al. 2009). At higher stimulus velocities (beyond 16°/s), the variability of both OMR and OKR increases, and mice seem to alternate between high- and low-gain tracking, in both head and eye movements (see examples 1 and 2 in Fig. 6, A and B). It is possible that these stimulus speeds occasionally engage alternative visual mechanisms driven by other detectors, for instance, ON-OFF-DS RGCs, which respond optimally to stimulus speeds of 25°/s in rabbits and mice (Collewijn 1969; Elstrott et al. 2008; Oyster et al. 1972; Weng et al. 2005).

In our experiments, the eye continuously participates in OKR events during (optimal) stimulus presentation under head-fixed conditions, with most slow (tracking) phases exhibiting rather stereotypical velocities, durations, and eye angle excursions, followed by fast (reset) phases (Fig. 5; see also Cahill and Nathans 2008). Hence, the duration, number and velocity of slow tracking (eye) phases are linked; e.g., a higher velocity results in a quicker reach of preferred angular excursion of the eye (customary range), hence shorter movements, more consistently followed by fast (reset) phases and overall more OKR events per unit time. In contrast, participation during OMR (under the same stimulus conditions) is far less consistent; i.e., the amount of time the mouse spends engaging in OMR events is reduced and highly variable (see Figs. 3–5). As a result, mouse OMR quantitations are more dependent on the number of events per unit time, and their duration, to relay a sense of how salient the stimulus is. We now show that mouse head gain decreases with increasing stimulus velocity, and the maximal velocities for both eye and head are reached at a stimulus speed of ~12°/s (see also Stahl 2004a, 2006; Tabata et al. 2010; van Alphen et al. 2009) for OKR stimulus speed dependency). Hence, mice perform most head and eye tracking phases at velocities of 10–14°/s, and determining the number of individual tracking phases results in a bell-shaped curve around this “optimum.” Similar gain dependencies on stimulus velocities for head and eye movements have been previously reported for rabbits, guinea pigs, and rats (Collewijn 1969, 1977; Fuller 1985, 1987; Gresty 1975).

An interesting observation to us is that slow (tracking) phases for head movements during OMR and to a lesser degree for eye movements during head-fixed OKR can exhibit heterogeneity with regard to velocity, duration, and presence or absence of the reset (fast) phase (examples in Fig. 3, quantitated in Fig. 5). Mice alternate between type I responses, consisting of low-gain, continuous head tracking phases in stimulus direction, amounting to small angular excursions and uninterrupted by reset phases, and type II responses, consisting of shorter, faster head tracking phases that are followed by reset phases, essentially resembling classic OKR eye movements (equivalent to a head nystagmus). Type I head OMR events can be seen quite often even under optimal conditions for stimulus spatial frequency and velocity, but are predominant at suboptimal stimulus spatial frequencies or speeds. This phenomenon was previously described for tracking (slow) phases in the cited mouse OKR literature, as well as for head and eye movements in the rat, gerbil, and rabbit (e.g., Collewijn 1969, 1977; Fuller 1985, 1987). Given the presence of OKR eye movements in unrestrained mice, one trivial explanation could be that the mouse alternates between movement of eyes, head, or a summation of both to achieve image stabilization (e.g., Collewijn 1969, 1977; Fuller 1985, 1987; Gioanni 1988a, 1988b). We note that type I tracking (slow) phases can also be seen for head-fixed OKR, predominantly under suboptimal stimulus conditions. Heterogeneity in excursion angular amplitude of eye slow (tracking) phases during OKR can also be influenced by the angular amplitude of the unidirectional stimulation epoch (Fig. 7E). It appears that for small stimulus angular amplitudes (20°), mice prefer to follow the stimulus with uninterrupted slow (tracking) phases, akin to our type I movements. Tracking movements covering the entire unidirectional stimulation epoch become less and less frequent as the stimulus angular amplitude increases from 20° to 120°, and gradually get replaced by the more stereotypical short tracking phases covering the “customary range” of 3.5°–5°.

Head and eye velocity ranges we recorded in unrestrained mice are consistent with the isolated head OMR and head-restrained eye OKR recordings (compare Fig. 8C and Fig. 5), despite the discussed limitations to angular eye velocity calibration. A somewhat unexpected finding to us is that pairs of head and eye velocities under unrestrained conditions do not show a strong anticorrelation, as would be expected if the head and eye velocities were to add up to result in a constant gaze velocity, close to or matching the stimulus speed (Fig. 8C). However, our estimate suggests that head and eye gain could almost fully compensate for stimulus motion (histogram peak head 4°/s + histogram peak eye 8°/s = 12°/s = stimulus velocity), and the histogram of combined (head + eye) velocities has a peak between 12 and 16°/s, resulting in a combined gain of 1–1.33. Studies in other afoveated species come to similar conclusions, i.e., that full image stabilization as a result of combined head and eye movements is not consistently achieved unless stimulus speeds are in the range of a few degrees per second. Interspersed periods of stabilization have been observed (Fuller 1985; 1987; Gresty 1975), resulting in minimized retinal slippage through combined eye and head motion. It should be noted that, as described above, slow and fast phases of horizontal head OMR are not necessarily taking the trajectory of rotations around the yaw axis, but in many cases have strong translational components (see detailed examples in Kretschmer et al. 2015). For illustration, in Supplementary Movie S4, between 5 and 11 s there are several iterations of head tracking movements with strong rotational components, whereas between 22 and 25 s the head slow (tracking) phase exhibits a strong downward trajectory, with the snout nearly reaching the lower edge of the image. Be that as it may, the angular excursions for the two eyes relative to the head are comparatively well synchronized (Fig. 8D). The variation of head and eye movement participation and gain could be explained by alternation between different viewing modes (Dawkins 2002) and could be affected by the level of attention and the behavioral context (see Maurice and Gioanni 2004 for examples in pigeons). Similarly, in fish, OKR is mainly driven by rotational motion, whereas OMR is mainly driven by translational movement and rapid head displacements might occur during voluntary search (Kubo et al. 2014).

The correct estimation of combined head and eye gaze orientation, and hence the relative contributions of head and eye angular velocities to image stabilization during optokinetic stimulation, depends on the angle of the head around the pitch axis and the axes of the eyes relative to the head. In our head-fixed OKR recordings aimed at determining the contribution of monocular and binocular fields to OKR, the head was fixed in the OKR apparatus such that the snout would point at the 0° meridian, with an inclination of the snout-orbit axis of ~15–20° forward around the pitch axis. In contrast, the head inclination during OMR recordings, as defined by a line connecting the snout to the center of the orbit, is ~55° forward around the pitch axis, which seems consistent with the ambulatory position described by Oommen and Stahl (2008) and hence placing the eye inclination at ~22° on the vertical axis. This difference in head inclination around the pitch axis could result in an enlarged binocular field of view contribution to the OMR compared with the OKR, and reorientation of the eyes relative to the head as a result of the maculo-ocular tilt reflex (Maruta et al. 2001; Oommen and Stahl 2008; Wallace et al. 2013). Our head-fixed OKR data seem to suggest a significant participation of the binocular field of view to OKR, so given the differences in head pitch, it is entirely possible that its contribution is much higher during OMR. Monocular and binocular subdivisions of the retina could provide distinct contributions to OKR/OMR by exhibiting relative differences in either cell-type density/distribution and/or receptive field sizes. In humans, peripheral and central velocity detectors might operate in different velocity ranges, and OKR stimuli can elicit different gains when presented at different retinal eccentricities (Dubois and Collewijn 1979; Van Die and Collewijn 1986). In mice, RGC types do exhibit topographic differences in dendritic arbor (and receptive field) size across the retina (Badea and Nathans 2011; Bleckert et al. 2014). However, we are unaware of such topographic distinctions for ON and ON-OFF DS RGCs, the likely substrates of OKR/OMR.

Mice lacking the Brn3b transcription factor (Brn3b^KO/KO) have significant losses in multiple RGC cell types and exhibit major defects in pupil constriction and OKR responses, accompanied by inconsistent defects in circadian photoentrainment (Badea et al. 2009). We now report a more complete picture of the OKR deficit and, in addition, identify OMR defects. The overall directional index OMR_ind, as well as OMR slow (tracking) phase gain, duration, and number, is reduced in Brn3b^KO/KO mice compared with Brn3b^WT/WT controls, but the tuning to spatial frequency is not significantly affected, with both optimal and threshold spatial frequencies in ranges similar to those in the control animals. The gain of horizontal OKR tracking (slow) phases is dramatically affected, and Brn3b^KO/KO OKR events consist of essentially continuous, low-gain tracking uninterrupted by reset (fast) phases (as shown in examples in Fig. 3 and quantitated in Fig. 4), whereas the vertical OKR is completely abolished. Both OMR and horizontal OKR events are highly reminiscent of Brn3b^WT/WT type I OKR and OMR events (low-gain, continuous tracking phases in stimulus direction, uninterrupted by fast reset phases). One could interpret the residual optokinetic behavior in Brn3b^KO/KO mice in several ways: 1) a few remaining ON-DS RGCs projecting into the NOT/DTN provide a low level of visual input that converts into low-gain tracking phases that do not reach the effector customary range; 2) other types of RGCs, which project to the SC and LGN, engage an alternative circuit, which is characterized by the type I movements; or 3) the RGCs surviving in the Brn3b^KO/KO mice, regardless of the targeted nucleus, have altered stimulus input functions and hence drive the low gain. An argument for alternative RGCs being involved is that the type I movements are also present in wild-type mice, at suboptimal but also optimal stimulation conditions. However, our mutants preserve spatial frequency tuning for both OKR and OMR. This fact is more consistent with the loss of detectors that can signal motion individually (ON-DS RGCs) than with the loss of single units from a mosaic that conveys motion information in a cooperative fashion (e.g., alpha or parasol RGCs). Intuitively, losing individual ON-DS RGCs will result in reduced response strength (number of movements and gain) but should only affect spatial frequency tuning after extensive RGC loss, because each individual ON-DS cell can detect the movement, and the whole retina would have to lose a large number of ON-DS RGCs before the edges of the pattern would fall on tissue devoid of detectors. However, motion detection dependency on stimulus spatial frequency would be much more rapidly affected by the fallout of RGCs from the parasol/alpha system, because it depends on the pattern moving across neighboring RGC receptive fields. In addition, if RGCs projecting to LGN or SC could drive a hypothetical alternative circuit, they should be able to do so for the vertical OKR component, which is not what we observed (Fig. 4I).

In conclusion, we have shown that OMR and OKR are similarly tuned for stimulus speed and spatial frequency and are similarly affected by loss of AOS-projecting RGCs, arguing for common visual afferent inputs. The previously reported differences in spatiotemporal tuning for OMR and OKR are a function of the applied metrics (human observer detecting mouse motion for OMR vs. gain for OKR). Our “overall directional bias” OMR index offers an objective assessment of OMR dependency on stimulus properties but will not provide more in-depth information regarding gain and other individual head OMR event properties. Although OKR signal-to-noise ratios are much better, we show that OMR can yield similar results without the need for invasive procedure, fixation of the animal, or calibration procedures. However, unrestrained mice perform OKR-type eye movements, and head gains are very small compared with eye gains, and therefore OMR experiments may miss subtle differences under suboptimal conditions (see Brn3b^WT/WT vs. Brn3b^KO/KO OMR_ind comparison at lower contrast values). We therefore advocate for a graded approach where automated OMR_ind determinations can be used to screen for effects of manipulations suspected to affect optokinetic responses, followed by in-depth investigations of the OMR head traces, and eventually OKR responses if needed. OMR gain dependency on stimulus parameters is probably the most appropriate measure, as is customary for OKR in mice (Stahl 2004a, 2006) or other species. Ideally, combined head and eye recordings are necessary and to a certain degree feasible by expansions of the approach we employed.

GRANTS

This research was supported by National Eye Institute Division of Intramural Research.

DISCLOSURES

A commercial system based on our design is commercialized by PhenoSys, GmbH, however, the authors have no financial ties to the company. No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

F.K. and T.C.B. conceived and designed research; F.K., M.T., and B.W. performed experiments; F.K., M.T., W.C., and T.C.B. analyzed data; F.K., M.T., and T.C.B. interpreted results of experiments; F.K., M.T., and T.C.B. prepared figures; F.K. drafted manuscript; F.K., M.T., and T.C.B. edited and revised manuscript; F.K., M.T., W.C., B.W., and T.C.B. approved final version of manuscript.