Moving Beyond Managing Realized Genomic Relationship in Long-Term Genomic Selection

Abstract

Long-term genomic selection (GS) requires strategies that balance genetic gain with population diversity, to sustain progress for traits under selection, and to keep diversity for future breeding. In a simulation model for a recurrent selection scheme, we provide the first head-to-head comparison of two such existing strategies: genomic optimal contributions selection (GOCS), which limits realized genomic relationship among selection candidates, and weighted genomic selection (WGS), which upscales rare allele effects in GS. Compared to GS, both methods provide the same higher long-term genetic gain and a similar lower inbreeding rate, despite some inherent limitations. GOCS does not control the inbreeding rate component linked to trait selection, and, therefore, does not strike the optimal balance between genetic gain and inbreeding. This makes it less effective throughout the breeding scheme, and particularly so at the beginning, where genetic gain and diversity may not be competing. For WGS, truncation selection proved suboptimal to manage rare allele frequencies among the selection candidates. To overcome these limitations, we introduce two new set selection methods that maximize a weighted index balancing genetic gain with controlling expected heterozygosity (IND-HE) or maintaining rare alleles (IND-RA), and show that these outperform GOCS and WGS in a nearly identical way. While requiring further testing, we believe that the inherent benefits of the IND-HE and IND-RA methods will transfer from our simulation framework to many practical breeding settings, and are therefore a major step forward toward efficient long-term genomic selection.

GENOMIC selection (GS), initially proposed by Meuwissen et al. (2001), uses existing phenotypes and marker information to obtain breeding values for untested selection candidates. With cheap high density genotyping becoming available, GS has been introduced in many animal and plant breeding programs over the last decade. The added value of GS is generally attributed to accelerated breeding by shortened generation intervals, and to higher selection accuracy, especially for traits that are difficult to observe (Hayes et al. 2009; VanRaden et al. 2009; Wiggans et al. 2011; Daetwyler et al. 2013). Unfortunately, GS also accelerates loss of genetic diversity due to the quick fixation of large effect loci, and likely also due to the higher selection accuracy of individuals with close relationship to the training set (Wientjes et al. 2013; Badke et al. 2014). Because this loss of diversity limits long-term gain for the trait under selection (Jannink 2010), and also jeopardizes future breeding for other traits, we need GS strategies that balance genetic gain with diversity.

Animal breeders have widely adopted optimal contributions selection (OCS; Meuwissen 1997) to manage population diversity during long-term selection. OCS maximizes genetic gain under a predefined pedigree-based inbreeding rate by calculating the optimal contribution of all selection candidates to the next generation by means of Lagrangian multipliers. Since its introduction, OCS has been considerably refined to accommodate operational breeding constraints, such as restricting the number of individuals contributing to the next generation, and imposing upper or lower limits on how much an individual contributes. Meuwissen (2002) manages these additional constraints with an iterative heuristic wrapped around the original solution that removes individuals with a too low contribution, and truncates contributions exceeding the maximum, while repeatedly reoptimizing the remaining contributions (Woolliams et al. 2015). Alternatively, the operational constraints can be modeled directly using semidefinite programming, which may provide slightly higher gains at the cost of a more complex problem formulation (Pong-Wong and Woolliams 2007; Ahlinder et al. 2014). A different strategy is to leave the strict constrained optimization framework and maximize a weighted index that balances genetic gain and inbreeding (Carvalheiro et al. 2010; Clark et al. 2013). Optimizing this simple index with general purpose metaheuristics, such as a differential evolution algorithm (Storn and Price 1997), allows us to easily accommodate alternative or additional objectives, trading optimality of solutions for flexibility. For example, this allowed Kinghorn (2011) to move from assigning individual contributions to identifying optimal mating pairs. OCS can also handle typical plant breeding applications that often have a fixed number (n) of selected individuals contributing equally to the next cycle. Using the Meuwissen (2002) heuristic, with minimum and maximum contributions set to $1/n$, works well here; a more exact solution with a branch-and-bound algorithm (Mullin and Belotti 2016) provided only marginally better results that do not justify the additional complexity and computation time. As such, OCS has become a well-established method that can be used in many, if not all, practical animal and plant breeding applications.

In the genomics era, the availability of marker data for the selection candidates has allowed a further extension of OCS: genomic OCS or GOCS (Sonesson et al. 2012). In GOCS, the realized genomic relationship matrix $G,$ computed from marker data, replaces the expected additive relationship matrix $A,$ inferred from the pedigree, in the OCS formulas (Woolliams et al. 2015). Intuitively, this makes a lot of sense, as, due to selection pressure, we expect the realized relationships to differ from the pedigree-based average, as well as being unequally distributed across the genome. For these reasons, GOCS is the current method of choice for controlling inbreeding in a GS context.

Avoiding the loss of favorable rare alleles has also received attention in view of increasing long-term selection gain. For GS, Jannink (2010) proposed a weighted strategy (WGS), in which the effect of rare favorable alleles is amplified following theory by Goddard (2009). Extensions of WGS were proposed, with additional parameters to balance short- and long-term gain (Sun and VanRaden 2014), or to dynamically reduce the focus on rare favorable alleles over a fixed time horizon (Liu et al. 2015). Many other weighting schemes could be explored, including one derived from the theory of Liu and Woolliams (2010) that determines the optimal QTL allele trajectory from its initial frequency to fixation, although, in our own comparison based on simulated data, these weights provided very similar results as standard WGS (H. De Beukelaer, G. De Meyer, personal communication). Instead of amplifying allele effects in the selection index calculated for every individual, it might be more effective to directly control rare allele frequencies in the set of selected individuals, following the approach of Li et al. (2008) to stack known QTL. These authors maximized a weighted index including the summed QTL allele effects and one of several diversity measures for the selected set. They found that avoiding loss of rare favorable alleles most effectively maximized long-term gain. As this approach has not yet been evaluated in a GS setting, the merit of maintaining rare favorable alleles for long-term genomic selection cannot be fully appreciated. To our knowledge, strategies based on maintaining rare favorable alleles, or rare alleles in general, have not yet been directly compared to GOCS.

In this paper, we provide a detailed comparison of several diversity management strategies for increasing long-term GS gain and maintaining overall genetic diversity. We focus on a typical recurrent selection plant breeding scheme, with a fixed number of individuals selected in each cycle that equally contribute to the next generation. Through simulations, we first compare existing implementations of WGS and GOCS, and assess their relative improvement over standard GS. Next, we use a unified optimization framework based on a weighted index containing breeding value and a population diversity measure, to contrast WGS and GOCS to new alternative methods that address some of their inherent limitations. Based on the results, we discuss the pros and cons of the different selection strategies from both a practical and theoretical perspective.

Materials and Methods

Haplotypes, base populations and genetic trait architecture

To serve as the backbone for the simulations, we derived haplotypes from genotypes of 192 founder inbred lines from the Oregon State University winter barley breeding program (Blake et al. 2012) using the consensus map (Close et al. 2009) for marker positions, spanning a total of 1091 cM. The raw genotype dataset contained 2591 SNPs and was preprocessed to retain 2031 polymorphic SNPs at unique positions, with >99% homozygous values (Supplemental Material, Section 1 in File S1). Haplotypes were inferred using Beagle (Browning and Browning 2007, 2009) through synbreed (Wimmer et al. 2012). Following Sonesson et al. (2012), we positioned additional artificial identity-by-descent (IBD) markers with unique founders alleles at an equal distance of 10 cM on all chromosomes. These IBD markers were not used for selection or prediction, but only to evaluate inbreeding based on genomic IBD. We simulated 200 base populations by randomly mating the 192 founders, followed by doubled haploid (DH) creation. In each base population, 1000 out of 2031 SNPs were randomly selected to be additive QTL for a complex trait and removed from the marker dataset. The remaining 1031 SNPs were used as genetic markers. QTL effects were sampled from a standard normal distribution. The residual trait variance was derived from the assumed heritability and the observed genetic variance in the base population, and was kept fixed for the entire simulation.

Genomic prediction

We used Bayesian ridge regression to estimate marker effects based on the linear model

$$y=\mu +X\mathit{\beta }+e$$

where $y$ is a vector of phenotypes, μ is the population mean, $X$ is a design matrix containing the 0/1-coded DH marker data (individuals × markers), $\mathit{\beta }$ is a vector of marker effects, and $e$ is a vector of random residuals. The model was fit using the R package BGLR (de los Campos and Pérez 2015), with default prior distributions and initial values. The estimated genomic breeding value (GEBV) of prediction individuals with genotypes $X$ was calculated as

$$\text{GEBV}=X\cdot \widehat{\mathit{\beta }}$$

where $\widehat{\mathit{\beta }}$ is the vector of estimated marker effects.

Breeding program simulations

For all four combinations of low ($h^2=0.2$) and high ($h^2=0.5$) heritability as well as a small (TP = 200) and large (TP = 1000) initial training population (TP), we performed 200 simulations of the breeding program defined in Jannink (2010) for the duration of 30 cycles. Each simulation run starts from a different base population that serves as the initial selection population, and as the TP to fit an initial genomic prediction (GP) model. In case of a large TP, the base population was complemented with 800 additional phenotyped individuals that were obtained from the founder dataset using the same procedure, but these were not considered candidates for selection. Input for the prediction model are the marker genotypes and phenotypes, inferred from the summed QTL effects and a random error sampled from a normal distribution with variance equal to the residual trait variance. Using standard GS or alternative selection strategies (see below), 20 individuals are selected for random intermating followed by doubled haploid creation to generate 200 new selection candidates. In cycle 2, the same selection procedure is applied using the original GP model, while, in parallel, the 200 selection candidates are phenotyped to augment the model for use in cycle 3. The process then iterates until the final selection is obtained in cycle 30.

For each simulation scenario, several variables were extracted and averaged over the 200 replicates. The first tracked variable is (cumulative) genetic gain, expressed as the increase in average true genetic value as compared to the base population. Prior to calculating gain, genetic values were normalized to $\left[-1,1\right]$ based on the minimum and maximum attainable value over all possible genotypes. In addition, we also tracked the inbreeding rate (Falconer et al. 1996)

$$\Delta F=\frac{F_t-F_{t-1}}{1-F_{t-1}}$$

where $F_t$ is operationalized as the average expected homozygosity of either the IBD markers ($\Delta F_{\mathrm{IBD}}$) or the actual SNP marker panel ($\Delta F_{\mathrm{IBS}}$):

$$F_t=\frac{1}{m}{\displaystyle \sum _i{\displaystyle \sum _j{p}_{ij}^2}}$$

where $p_{ij}$ is the frequency of the jth allele of the ith marker (IBD or SNP), and m is the number of markers. In this way, inbreeding is expressed as the relative decrease in expected heterozygosity based on either IBD ($\Delta F_{\mathrm{IBD}}$) or identity-by-state ($\Delta F_{\mathrm{IBS}}$). At selection population level, we also tracked the number of favorable QTL alleles lost, and their total effect, the mean QTL favorable allele frequency, and the number of SNP alleles lost in general.

Standard and weighted genomic selection

Both standard (GS) and weighted (WGS) genomic selection rank individuals according to their (w)GEBV, and select the n candidates with the highest value. With WGS, marker effects are scaled to obtain weighted breeding values

$$\text{wGEBV}=X\cdot \left[\begin{array}{c}{w}_1{\widehat{\beta }}_1\\ ⋮\\ w_n{\widehat{\beta }}_n\end{array}\right]$$

where ${\widehat{\beta }}_i$ is the estimated effect of the ith marker, and $w_i$ is the weight assigned to that marker. We used the weights

$$w_i=f_i^{-0.5}$$

as defined by Jannink (2010), where $f_i$ is the favorable allele frequency of the ith marker in the selection population.

Optimal contributions selection

For GOCS (Sonesson et al. 2012; Woolliams et al. 2015) optimal contributions $c_t$ are assigned to the selection candidates by maximizing the expected genetic level $g_{t+1}$ in the next generation under a constraint that aims to realize a predefined target inbreeding rate $C_{t+1}=\Delta F_{\text{target}}:$

$$\max g_{t+\mathbf{1}}=c_t^{\mathrm{⊺}}\text{GEB}{V}_t$$

$$\text{with}\hspace{1em}{C}_{t+1}=\frac{c_t^{\mathrm{⊺}}{G}_t{c}_t}{2}.$$

Here, $\text{GEB}{V}_t$ is a vector with breeding values in generation t, and the realized genomic relationship matrix $G_t$ is used to constrain the expected inbreeding in the next generation. We followed VanRaden (2008) to calculate $G_t=Z_t{Z}_t^{\mathrm{⊺}}/\left[2{\displaystyle \sum p_j\left(1-p_j\right)}\right],$ where $Z_t$ contains reference allele counts relative to the population mean (Woolliams et al. 2015). As opposed to OCS, where $C_{t+1}$ is increased over generations to account for accumulated absolute inbreeding using the formula $C_{t+1}=1-{\left(1-\Delta F_{\text{target}}\right)}^t$ (Grundy et al. 1998), a fixed value $C_{t+1}=\Delta F_{\text{target}}$ is set over all generations in GOCS, as, unlike the expected pedigree-based relationship matrix $A,$ the realized genomic relationship matrix $G$ is naturally scaled relative to the population mean. More details are provided in Subsection 2.1 in File S1.

To match the simulated breeding scheme that crosses n parents with equal contribution, we imposed a minimum and maximum contribution of $c_{\min }=c_{\max }=1/n,$ using the iterative heuristic of Meuwissen (2002). This algorithm discards individuals with a too low contribution, and truncates those exceeding the maximum, while repeatedly reoptimizing the remaining contributions. Due to the operational constraint, it is not always possible to achieve precisely the desired value for $C_{t+1}.$ Therefore, at a certain iteration, the heuristic may switch to minimizing realized genomic relationship to assign the remaining contributions, as explained in detail in Subsection 2.2 in File S1.

Unified set selection framework

To compare different selection strategies, we implemented these in the same optimization framework that uses general purpose metaheuristics to identify optimal subsets. We select a set of individuals by maximizing a weighted index

$$F\left(S\right)=\left(1-\alpha \right)\cdot V\left(S\right)+\alpha \cdot D\left(S\right)$$

where S is a subset of the selection candidates, and $\alpha \in \left[0,1\right]$ is a weight used to balance genetic merit $V\left(S\right),$ defined as the average GEBV of the selection, and diversity $D\left(S\right).$ Both components are dynamically normalized to $\left[0,1\right]$ using the procedure described in Section 3 in File S1. We experimented with three different diversity measures, including minimization of the realized genomic relationship as used in GOCS (IND-OC):

$$D_{\mathrm{OC}}\left(S\right)=-\frac{c_t^{\mathrm{⊺}}{G}_t{c}_t}{2}$$

where $c_t$ is a vector with $1/n$ for each selected parent in S, and 0 for each remaining individual (Lindgren and Mullin 1997). A second version (IND-HE) balances gain and expected heterozygosity, in an attempt to control the inbreeding rate when defined as the relative decrease in expected heterozygosity computed from the SNP markers ($\Delta F_{\mathrm{IBS}}$):

$$D_{\mathrm{HE}}\left(S\right)=\frac{1}{m}{\displaystyle \sum _{i=1}^{m}2p_i\left(1-p_i\right)}$$

where $p_i$ is the minor allele frequency of the ith marker, in the selected set S, and m is the number of markers. Finally, IND-RA directly manages rare alleles using a criterion inspired by Li et al. (2008):

$$D_{\mathrm{RA}}\left(S\right)=\frac{1}{m}{\displaystyle \sum _{i=1}^m\log \left(p_i\right)}$$

where $p_i$ and m are again the minor allele frequency and the number of markers, respectively. In contrast to Li et al. (2008), we consider all alleles and not only the favorable ones. The logarithm was truncated at

$$\log \left(0\right):=-\left(\log \left(n\right)+1\right)$$ (1)

to avoid that all selections in which at least one allele becomes fixed would be incomparably evaluated at minus infinity (n being the selection size). As optimization engine, we used the parallel tempering local search heuristic (Earl and Deem 2005; Thachuk et al. 2009) with ten cooperating replicas, a temperature range of $\left[{10}^{-8},{10}^{-3}\right],$ and a neighborhood function that randomly swaps a single selected and unselected item in an attempt to improve the value of the selection. The algorithm terminated when no improvement was found during 5 sec.

Parameter values

For GOCS, IND-OC, IND-HE, and IND-RA, we considered two values for the parameters $C_{t+1}$ and α, respectively. First, we searched for the lowest value of $C_{t+1}$ (highest α, respectively) that still yields at least the same short-term gain as WGS. Second, we determined parameter values that resulted in roughly the same observed inbreeding rate $\Delta F_{\mathrm{IBS}}$ for these four methods. The optimal values for both scenarios (Table 1) were determined empirically, through a grid search with $\alpha \in \left[0,1\right]$, and a step size of 0.05 for IND-OC, IND-HE, and IND-RA, and $C_{t+1}\in \left[0.01,0.1\right]$ with a step size of 0.01 for GOCS.

Table 1. Considered parameter values when using the OCS method, and when maximizing a weighted index containing average breeding value and a specific diversity measure (IND-OC, IND-HE, IND-RA).

	GOCS ($C_{t+1}$)	IND
		OC (α)	HE (α)	RA (α)
Scenario 1	0.05	0.35	0.35	0.35
Scenario 2	0.02	0.65	0.35	0.35

Data and source code availability

Raw data can be retrieved from http://www.hordeumtoolbox.org. Preprocessed data, the 200 pregenerated base populations used in the simulations, and all R and Java code are available at https://github.com/hdbeukel/gs-simulation. Stochastic simulations and analysis were performed in R 3.2.1 (R Core Team 2015). Table S1 in File S1 provides a complete list of R packages used, and their versions. We maximized the weighted indices of IND-OC, IND-HE, and IND-RA in Java 8 using the JAMES framework for discrete optimization with local search metaheuristics (De Beukelaer et al. 2016). Java code was executed within R using the rJava package (Urbanek 2016).

Results

Simulation framework

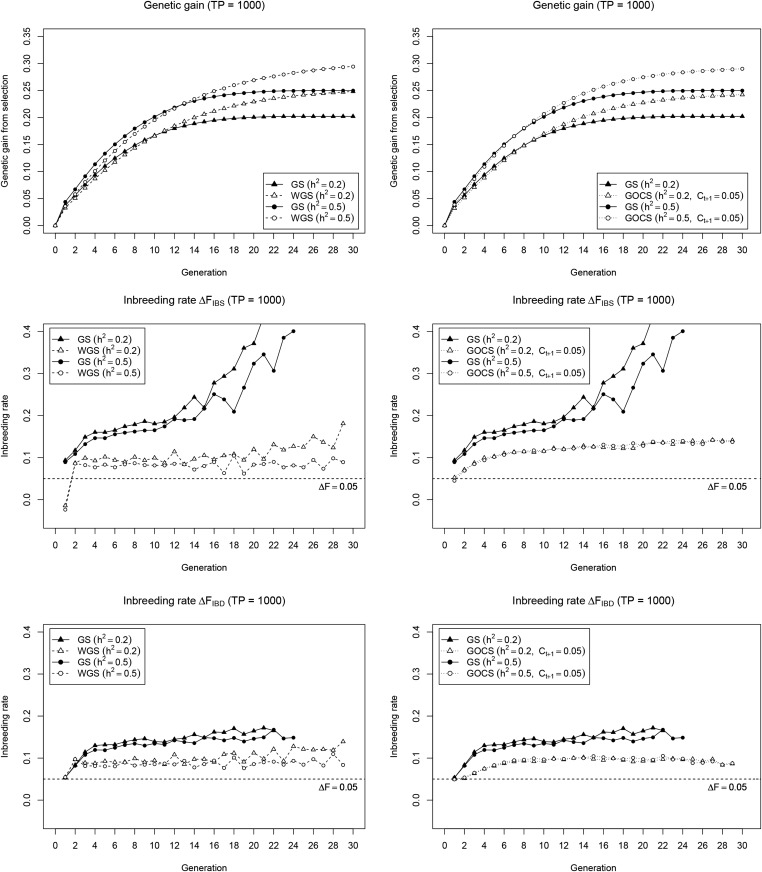
We compare several long-term selection strategies in the GS-based recurrent selection plant breeding scheme from Jannink (2010). Simulations were performed on a genome with 2031 SNPs (∼1 SNP/cM) allowing the positioning of a 1000 QTL quantitative trait while leaving the remaining 1031 SNPs to be used for selection and diversity management. Because, for some selection strategies, genetic gain was still observed beyond the 20 cycles considered by Jannink (2010), we extended the scheme to 30 cycles to fully appreciate the long-term dynamics. In our simulation framework, trait heritability ($h^2=0.2$ vs. $h^2=0.5$) had a major effect on genetic gain (Figure 1), with, as expected, a higher genetic gain plateau for the high heritability. We also observe significant inbreeding under GS, which is more pronounced for $\Delta F_{\mathrm{IBS}}$ as compared to $\Delta F_{\mathrm{IBD}}.$ Varying the size of the TP (TP = 200 vs. TP = 1000) to build the initial genomic prediction model had less effect on genetic gain and on the relative performance of the selection strategies. Therefore, we provide the TP = 200 results as Supplemental Material (see File S1).

Figure 1.

Cumulative genetic gain (top) and inbreeding rate (IBS: middle; IBD: bottom) for WGS (left) and GOCS (right) as compared to standard GS. Results are reported for a low ($h^2=0.2$) and high ($h^2=0.5$) heritability, with a large initial TP (= 1000), and are averages of 200 simulation runs. The inbreeding rates are reported until at least half of the simulation runs have lost all variability for the SNP marker panel used.

Weighted GS and genomic OCS

Irrespective of trait heritability, WGS slightly reduces short-term genetic gain compared to GS—by at most one cycle—to achieve a significantly higher long-term gain (Figure 1 and Figure S1 in File S1; left panel). This goes hand in hand with a general control of the inbreeding rate, with minor differences between $\Delta F_{\mathrm{IBS}}$ and $\Delta F_{\mathrm{IBD}}$, but with a clear dependency on TP size and heritability with higher inbreeding rates for low heritability and/or small TP. At the first cycle, the inbreeding rate is exceptionally lower and even negative for $\Delta F_{\mathrm{IBS}}.$ GOCS, with its constraint set at 0.05 to mimic the WGS short-term gain, performed very similar to WGS in terms of long-term gain (Figure 1 and Figure S1 in File S1; right panel). GOCS also reduced inbreeding compared to GS, and more consistently so than WGS. In particular, GOCS provides more stable inbreeding rates across cycles, that are independent of the TP size and heritability. Yet, as opposed to WGS, the GOCS inbreeding rate $\Delta F_{\mathrm{IBS}}$ is higher than $\Delta F_{\mathrm{IBD}}.$ Also, the response during the first cycles is different, with GOCS gradually building up to a stable value while WGS only had a low spike at the first cycle. Most notably, over generations, the GOCS inbreeding rate consistently deviates from the constraint value of $C_{t+1}=0.05,$ which should match the inbreeding rate $\Delta F,$ despite the fact that this constraint was always closely reached in the optimization routine (results not shown). To explore possible underlying mechanisms for this observation, we also ran our simulations without genomic selection—i.e. with a random selection of 20 individuals in each cycle—and with a selection size of 50 instead of 20 (Figure S2 in File S1). In the absence of selection, both $\Delta F_{\mathrm{IBS}}$ and $\Delta F_{\mathrm{IBD}}$ remained constant at 0.05, which is the expected drift ($1/20$) when randomly mating 20 doubled haploids. Exactly the same average value of 0.05 was observed when evaluating the GOCS criterion $c_t^{\mathrm{⊺}}{G}_t{c}_t/2$ in this setting. When selecting 50 individuals, GOCS moves toward the $\Delta F=0.05$ plateau for $\Delta F_{\mathrm{IBD}},$ but not for $\Delta F_{\mathrm{IBS}}$, which still exceeds the target level. We conclude that WGS and GOCS achieve similar long-term genetic gain but have different behavior at the level of the inbreeding rate, where, in particular, GOCS does not control inbreeding at the target level.

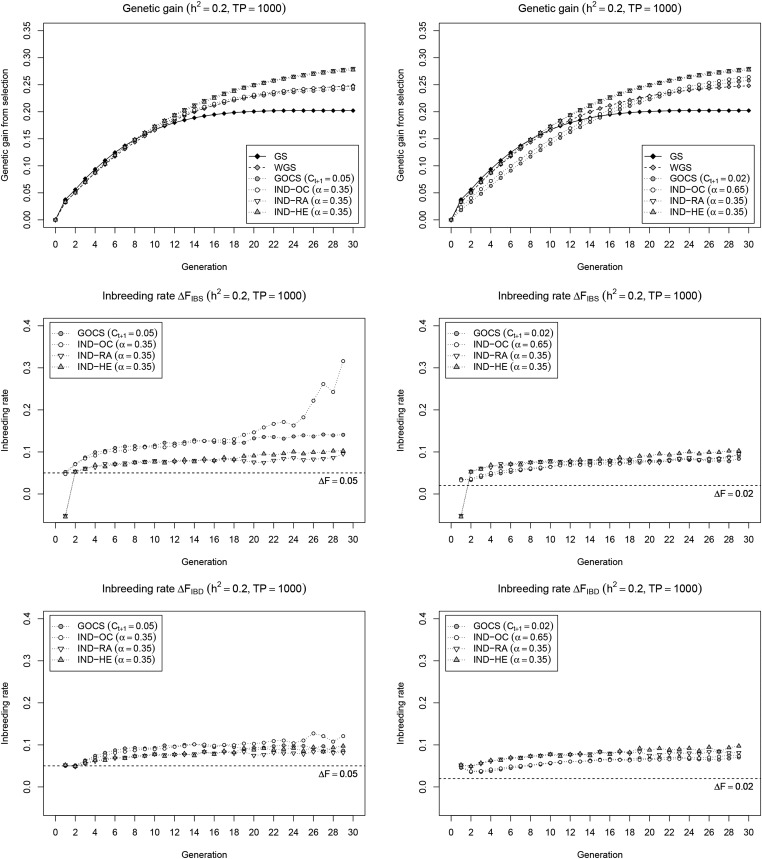
Unified set selection framework

To more directly compare selection strategies, we used a unified optimization framework that maximizes a weighted index of average breeding value and a diversity measure chosen to either minimize realized genomic relationship (IND-OC), maximize expected heterozygosity (IND-HE), or retain rare alleles (IND-RA). In a first scenario with GOCS and the index-based methods parametrized for a short-term genetic gain comparable to WGS (Figure 2; left panel), IND-OC provides a genetic gain profile similar to GOCS and WGS, while IND-RA and IND-HE give clearly higher long-term gains. IND-OC roughly parallels GOCS in terms of inbreeding rate (except for $\Delta F_{\mathrm{IBS}}$ in the last few cycles), again with clearly higher values for $\Delta F_{\mathrm{IBS}}$ as compared to $\Delta F_{\mathrm{IBD}}.$ IND-RA and IND-HE give similar inbreeding rates below those of IND-OC and GOCS, with almost no difference between $\Delta F_{\mathrm{IBS}}$ and $\Delta F_{\mathrm{IBD}}.$ In contrast to IND-OC and GOCS, IND-RA and IND-HE show a strongly negative inbreeding rate $\Delta F_{\mathrm{IBS}}$ in the first generation, which resembles that of WGS (Figure 1). In a second scenario with GOCS and IND-OC parametrized so that the realized inbreeding rate $\Delta F_{\mathrm{IBS}}$ does not exceed that of IND-RA and IND-HE during the entire simulation (Figure 2; right panel), the higher long-term gain obtained by both GOCS and IND-OC comes with a major penalty on short-term gain, and is still outperformed by IND-RA and IND-HE. In this setting, with a less pronounced selection for the simulated trait, inbreeding rates $\Delta F_{\mathrm{IBS}}$ and $\Delta F_{\mathrm{IBD}}$ of GOCS and IND-OC are more similar, and, although also more stable over time, still clearly deviate from the expected value of 0.02. Very similar results are observed for the small TP (Figure S3 in File S1) and $h^2=0.5$ settings (Figures S4 and S5 in File S1). Overall, we conclude that IND-RA and IND-HE are roughly equivalent selection strategies that outperform WGS and GOCS in our simulation framework.

Figure 2.

Current and new selection strategies in a unified optimization framework. Cumulative genetic gain (top) and inbreeding rate (IBS: middle; IBD: bottom) of selection strategies that maximize a weighted index containing breeding value and a diversity measure chosen to control inbreeding (IND-OC, IND-HE), or to avoid loss of rare alleles (IND-RA). Results for GS, WGS, and GOCS are provided as a reference. For clarity, inbreeding rates of GS and WGS are omitted. Two scenarios were considered to set the parameters $C_{t+1}$ and α: maintain the same short-term gain as WGS (left), or achieve a similar inbreeding rate $\Delta F_{\mathrm{IBS}}$ (right). Results are reported for a low heritability ($h^2=0.2$), with a large initial TP (= 1000), and are averages of 200 simulation runs.

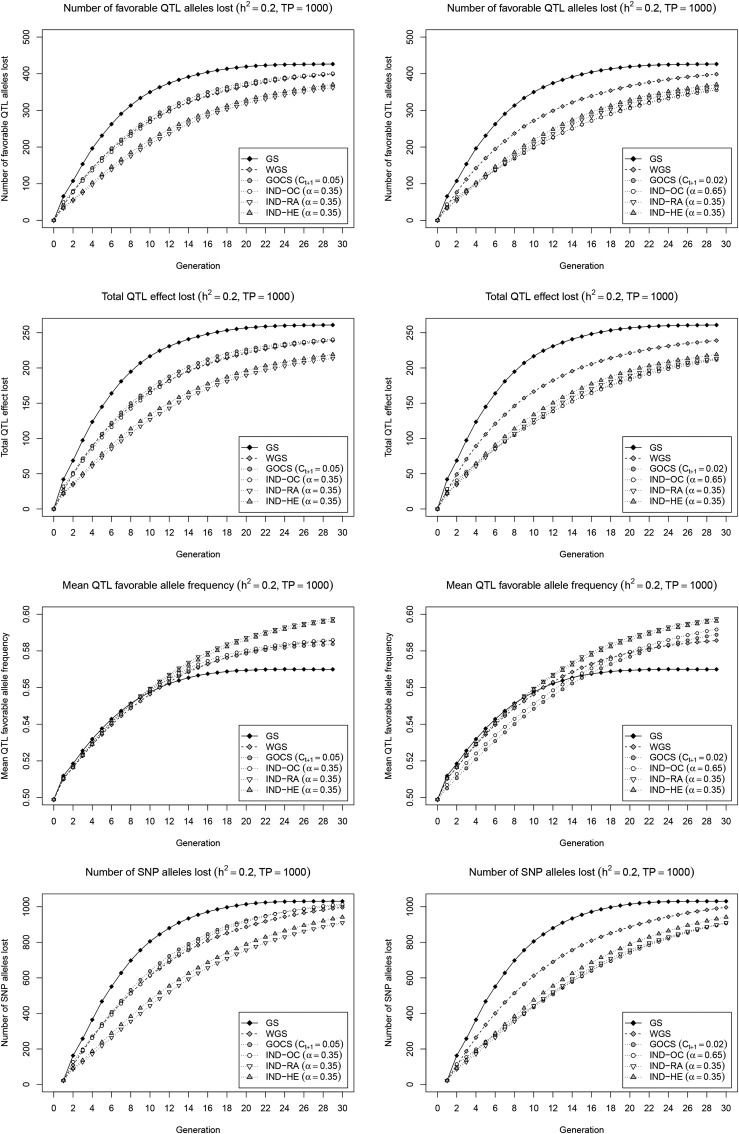
Drift and selection at locus level

To better understand the underlying mechanisms operating in Figure 2, we quantified the loss of favorable QTL alleles, the corresponding QTL effect, the increase of favorable QTL allele frequencies, and the number of SNP alleles lost in general (Figure 3). In the strong short-term gain scenario on the left panel, IND-RA and IND-HE retained clearly more favorable QTL alleles than WGS, GOCS, and IND-OC, which, in turn, retained considerably more favorable alleles than standard GS. This allowed IND-RA and IND-HE, and, to a lesser extent, WGS, GOCS, and IND-OC, to increase the frequency of these favorable alleles to higher levels beyond cycle 10 as compared to GS, in a pattern that closely resembles genetic gain. For maintaining SNP alleles in general, which reflects a combination of what happens near QTL and at neutral loci, all methods show a very similar trend as for the favorable QTL alleles. As compared to IND-HE, IND-RA managed to retain slightly more alleles for SNPs in general, as well as for favorable QTL. When a stronger restriction on inbreeding is imposed for GOCS and IND-OC (Figure 3; right panel), these methods retain slightly more favorable QTL alleles, accounting for a similar total effect, and, presumably, thus with similar effect distribution, as compared to IND-HE and IND-RA. A parallel increase is observed for the number of maintained SNP alleles in general. Unfortunately, these improvements are combined with a lower performance for increasing the favorable QTL allele frequencies, suggesting that IND-RA and IND-HE achieve a better balance between selection and avoiding drift as compared to the OC-based methods.

Figure 3.

Favorable QTL and general SNP allele trajectories. Number of favorable QTL alleles lost (first row), total QTL effect lost (second row), mean QTL favorable allele frequency (third row), and number of SNP alleles lost (fourth row) with the simulated selection strategies. Two scenarios were considered to set the parameters $C_{t+1}$ and α: maintain the same short-term gain as WGS (left), or achieve a similar inbreeding rate $\Delta F_{\mathrm{IBS}}$ (right). Results are reported for a low heritability ($h^2=0.2$) with a large initial TP (= 1000), and are averages of 200 simulation runs.

Discussion

GOCS increases gain without full inbreeding control

We used a simulation framework based on a recurrent selection plant breeding scheme to compare long-term GS strategies. In this breeding scheme, GOCS outperforms GS for long-term genetic gain, and also results in a lower inbreeding rate, in line with earlier observations (Woolliams et al. 2015). Nearly identical results were obtained with the standard iterative algorithm (Figure 1; right panel), and an index-based implementation of the same criterion (IND-OC; Figure 2). This confirms the finding by Carvalheiro et al. (2010) and Clark et al. (2013) that maximizing genetic gain while controlling inbreeding can also be achieved by optimizing a weighted index. It also shows that, as observed by Mullin and Belotti (2016), the Meuwissen (2002) heuristic works fine for a fixed number of selected individuals and equal contributions.

Surprisingly, however, despite the fact that all simulations closely approach the imposed GOCS constraint $C_{t+1}=\Delta F_{\mathrm{target}},$ both $\Delta F_{\mathrm{IBS}}$ and $\Delta F_{\mathrm{IBD}}$ significantly deviate from this target level over generations. This observation, which was also reported by Gómez-Romano et al. (2016), differs from previous results by Sonesson et al. (2012), who did find that GOCS controls $\Delta F_{\mathrm{IBD}}$ at the imposed constraint value. The fact that the GOCS criterion $C_{t+1}=c_t^{\mathrm{⊺}}{G}_t{c}_t/2$ does equal the inbreeding rate when no GS is performed (Figure S2 in File S1; left panel) suggests that this discrepancy is linked to selection. This hypothesis is confirmed by the theoretical expression of $\Delta F_{\mathrm{IBS}}$ in terms of allele frequencies and their changes (Section 2 in File S1), showing that the inbreeding rate is the sum of $c_t^{\mathrm{⊺}}{G}_t{c}_t/2$, and a second term involving cross products ${\Delta }_j\left(2p_j-1\right)$ of frequencies and frequency changes. The latter term is expected to be close to zero when allele frequencies and their changes are independent, such as in a scenario without selection. Under GS, however, it becomes positive, and increases over generations as selection pushes favorable alleles toward fixation. Once the frequency of a favorable allele exceeds 0.5, a beneficial ${\Delta }_j$ has the same sign as $2p_j-1,$ making their product positive. As such, the inbreeding rate can be seen as the sum of a first component relating to the frequency changes at all loci in general, which is constrained by GOCS, and a second component that captures additional inbreeding due to specific selection pressure, which is not controlled by GOCS. The latter explains why the observed inbreeding rates exceed the target when constraining $C_{t+1}=c_t^{\mathrm{⊺}}{G}_t{c}_t/2$ to $\Delta F_{\mathrm{target}}.$

That GOCS does not fully control inbreeding under GS leaves the question of why this was not observed by Sonesson et al. (2012). Here, the details of the simulation framework become important. We followed Sonesson et al. (2012) to calculate genomic IBD, by working with a large collection of unique founder alleles positioned at equal distances across the genome. These founder alleles are specified irrespective of the QTL, meaning that the same QTL allele can be linked to different founder alleles. As a result, inbreeding at loci with favorable QTL can go undetected because the linked founder alleles are different, particularly when many founder alleles are still around in the population. This is likely the case in the simulations of Sonesson et al. (2012), where 200 individuals are selected in every generation, and not in our setting, with only 20 individuals selected, and therefore at most 20 founder alleles per population, except for the base population. In our simulations, the effect of the large number of different founder alleles at the IBD markers is visible in the one-generation lag of $\Delta F_{\mathrm{IBD}}$ as compared to $\Delta F_{\mathrm{IBS}}$ (Figure 1), and a less pronounced deviation of $\Delta F_{\mathrm{IBD}}$ from the target inbreeding rate. Moreover, when selecting 50 instead of 20 individuals in every generation (Figure S2 in File S1), $\Delta F_{\mathrm{IBD}}$ starts below the target of 0.05—due to the large selection intensity it is impossible to achieve this fairly high inbreeding rate in early cycles—and then converges to the target level, while $\Delta F_{\mathrm{IBS}}$ is still not controlled at the target. Along these lines, we also conclude that $\Delta F_{\mathrm{IBS}}$ measured with the actual marker panel will best represent loci under selection, while the multi-allelic IBD markers may better represent loci that are not under selection. Taken together, GOCS effectively increases long-term genetic gain of GS, with the restriction of only fully controlling inbreeding at loci not subjected to selection.

Weighted GS

WGS, which amplifies rare favorable allele effects when calculating GEBVs, also outperforms GS for genetic gain (Figure 1; left panel) to a similar extent as in previous simulations by Jannink (2010). This confirms earlier results and validates our simulation framework. Compared to GS, WGS clearly controls the inbreeding rate. It also yields very similar $\Delta F_{\mathrm{IBS}}$ and $\Delta F_{\mathrm{IBD}}$ (Figure 1) suggesting that it operates equally on neutral loci, and loci under selection, which is further supported by the parallel pattern for loss of favorable QTL alleles and SNPs (Figure 3). This general effect on inbreeding is somewhat surprising because WGS operates on rare favorable alleles. Considering that the effect estimates for rare alleles in the genomic prediction model are likely very imprecise, and might often even be of the wrong sign, WGS might in fact operate on rare alleles in general, at least in our setting with a 1000 QTL trait. It remains unclear, however, whether WGS would operate in a more trait-specific way when used for less complex traits. Variability in the individual allele effect estimates might also be a reason for the somewhat unstable inbreeding control (Figure 1), making WGS highly dependent on external factors such as trait heritability and TP size. Comparing WGS and GOCS, we find that they provide the same short- and long-term genetic gain (Figure 1), although it should be noted that both methods can be further tweaked through parameter settings. Overall, WGS appears a valid strategy to combine genetic gain with inbreeding control, and performs similarly to GOCS, albeit with some hints of intrinsic instability.

New index-based selection strategies

We explored possible improvements on GOCS and WGS in a unified optimization framework that weighs genetic gain vs. a specific diversity metric. The optimal subset of selection candidates is then approximated using a powerful local search metaheuristic that maximizes the weighted index. A first strategy, IND-HE, aims to control inbreeding more generally than GOCS by also addressing the component related to loci under selection. IND-HE does so by balancing genetic gain with high expected heterozygosity in the selected set, which is equivalent to minimizing $\Delta F_{\mathrm{IBS}}.$ In our simulation framework, IND-HE clearly outperforms GOCS and IND-OC under various settings. In the scenario with similar short-term gain (Figure 2; left panel), IND-HE realizes the same genetic gain during the first 10 cycles but with a lower inbreeding rate. This is likely because the IND-HE objective specifically quantifies inbreeding under selection, and, as such, captures the unavoidable penalty of fixing favorable alleles intrinsically linked to genetic gain. Therefore, to maintain gain, IND-HE leads toward selections where this inevitable additional inbreeding near QTL is compensated with lower inbreeding at neutral loci, and at loci not yet under selection. As such, IND-HE is able to achieve the same genetic gain with less total inbreeding as compared to GOCS and IND-OC. This makes that IND-HE retains more favorable QTL alleles (Figure 3), which enables higher long-term gain when these conserved favorable alleles move toward fixation.

When keeping the realized inbreeding rates of GOCS and IND-OC below the level of IND-HE (Figure 2; right panel), both methods retain a similar amount of favorable QTL alleles as IND-HE (Figure 3). Yet, in this scenario, GOCS and IND-OC show a considerably lower short-term gain than IND-HE, without leading to a significant increase in long-term gain. We see two main reasons for this observation. First, to keep the realized inbreeding rate below that obtained with IND-HE, over all generations, we needed to correct manually for the additional inbreeding due to selection that is ignored by GOCS. As such, the target value for GOCS was reduced from 0.05 to 0.02, resulting in a lower inbreeding rate than IND-HE up to cycle 10 (except from the first cycle), which impedes gain. In addition, GOCS limits squared allele frequency changes regardless of their direction, assuming that deviations from the current frequency always decrease diversity due to inbreeding. The latter holds when pushing favorable allele frequencies already above 0.5 toward fixation. However, especially in early cycles, both gain and diversity could be simultaneously improved at certain loci, i.e., by amplifying favorable alleles with a frequency currently below 0.5. For such loci, the inbreeding term ${\Delta }_j\left(2p_j-1\right)$ is negative, and may compensate for positive crossproducts at other loci. Yet, this term is ignored by GOCS, due to which allele frequency changes may be overly constrained, again impeding gain. In both scenarios, we conclude that IND-HE controls inbreeding more effectively as compared to GOCS, in particular also at loci under selection, and, as such, provides a better balance between genetic gain and diversity.

The fact that the criterion used by GOCS and IND-OC ignores the direction of allele frequency changes is immediately visible in the first generation of our simulations, where IND-HE simultaneously realizes a strongly negative inbreeding rate and a high genetic gain (Figure 2), which is similar to observations for WGS (Figure 1). We believe this is possible due to the presence of several large effect favorable alleles at very low frequencies in the population, in which case a strong selection for the trait can go hand in hand with increasing population-level heterozygosity. WGS and IND-HE are able to adapt to this situation and exploit this benefit, while constraint-based methods like GOCS do not have the flexibility to go below the target inbreeding rate. This is a particular advantage for populations new to GS, as they are more likely to encounter positive large effect rare alleles as compared to populations already exposed to long-term GS. Even when relaxing the constraint to $c_t^{\mathrm{⊺}}{G}_t{c}_t/2\le C_{t+1}$ instead of $c_t^{\mathrm{⊺}}{G}_t{c}_t/2=C_{t+1}$ (Pong-Wong and Woolliams 2007), GOCS would go below the target level only if this yields higher immediate gain, which is unlikely, and still fails to recognize that amplifying rare favorable alleles is beneficial for both gain and diversity. Therefore, at the start of a GS program, there may be a particularly pronounced difference between the OC-based methods and IND-HE.

In an attempt to improve WGS, we accommodated the specific focus on rare alleles in the diversity component of the set selection framework (IND-RA) using a metric inspired by Li et al. (2008). This metric is the mean of the log-transformed minor allele frequencies calculated in the set of selected individuals, with the log-transformation giving additional weight to rare alleles, as compared to IND-HE. For genetic gain, as well as for controlling the inbreeding rate, IND-RA clearly outperforms WGS (Figure 2). We see two reasons for this observation. First, and likely most importantly, IND-RA resolves an intrinsic shortcoming of WGS, i.e., that truncation selection based on scores assigned to selection candidates cannot guarantee that the optimal set is selected. For example, it is possible that multiple individuals carrying the same beneficial rare allele are selected, while it might be better to choose complementary individuals that carry different rare alleles. The latter is favored by IND-RA because the rare allele frequencies are evaluated for the selected set. A second advantage is that IND-RA makes the management of rare alleles independent of the estimation of their effects in the genomic prediction model, that come with a high error, and are dependent on external factors, such as trait heritability and TP size. This is likely the reason why IND-RA gives a more stable inbreeding rate than WGS (Figure 1 and Figure 2), and brings the additional benefit that rare alleles are managed in general and are not specific for the trait under GS and its genetic architecture. We do note that, if desired, it is possible to modify IND-RA to penalize loss of favorable alleles only, resulting in a more trait-specific approach, like WGS. However, such alternatives gave similar or slightly worse gains (H. De Beukelaer, G. De Meyer; personal communication), suggesting that the simulated trait has too many underlying QTL to benefit from focusing on favorable alleles due to inaccurate effect estimates. We conclude that IND-RA is superior to WGS for a selection strategy that actively retains rare alleles.

Contrasting the IND-HE and IND-RA methods that best represent their respective selection strategies, we find that both perform almost identically across a wide range of conditions (Figure 2 and Figure 3). This is not too surprising, as avoiding loss of alleles is a specific aspect of controlling inbreeding. Both methods push toward high expected heterozygosity at population level, and the main difference is their exponentially (IND-RA) vs. quadratically (IND-HE) increasing focus on rare alleles. IND-RA indeed retains slightly more alleles than IND-HE (Figure 3), but this is likely not important enough to affect long-term genetic gain within 30 cycles. Experiments with a different founder dataset (H. De Beukelaer, G. De Meyer; personal communication) having fewer QTL (100) and SNP markers (∼800) revealed that, in such cases, there was a slight benefit of IND-RA over IND-HE when looking at long-term gain, likely because then 30 cycles were sufficient to realize some of the additional potential gained by retaining more favorable QTL alleles. Overall, we conclude that, as compared to WGS and GOCS, IND-RA and IND-HE better balance genetic gain with avoiding loss of rare alleles, and controlling inbreeding in general.

Practical considerations for IND-RA and IND-HE

Although the index-based optimization objectives for IND-RA and IND-HE are straightforward to compute for a given set of selection candidates, these methods need to identify the best subset from a huge number of possibilities. Achieving this within reasonable time requires intelligent combinatorial optimization algorithms, which is a major complication as compared to WGS, where only wGEBVs have to be calculated, and as compared to GOCS, where specific software is available. To allow for high flexibility in terms of diversity metrics, without having to adjust the optimization engine, we used a general purpose metaheuristic to approximate the optimal selection. The parallel tempering algorithm is ideally suited for discrete optimization, as in the adopted breeding scheme, where a fixed number of individuals are selected with equal contribution. For breeding schemes involving unequal contributions, continuous optimization algorithms can be used instead, such as differential evolution (Carvalheiro et al. 2010; Clark et al. 2013) or Lagrangian multipliers (Woolliams et al. 2015)—also for the newly proposed diversity metrics (see below). We note that the time needed for the heuristic search is not limiting. In our simulation framework it only takes a few seconds, and that would increase to at most a few minutes when e.g., multiple 10,000 of markers would be available, as computation times increase linearly with the number of markers for the diversity measures used.

Furthermore, it should be mentioned that the log-criterion used by IND-RA could be further refined, for example by modifying the penalty assigned to losing an allele due to selection in Equation (1). It is also possible to adjust the IND-RA and IND-HE methods for breeding schemes that allow unequal contributions by calculating the respective diversity metrics for the expected frequencies in the offspring, instead of the frequencies in the selection, and using a continuous optimization engine to find the contributions that best balance gain and diversity. Finally, we note that, in practice, it may not be easy to find the best weight α, and that an index-based selection strategy does not allow a predefined inbreeding rate to be imposed. On the other hand, Woolliams et al. (2015) argue that it is also not straightforward to set the target inbreeding rate for (G)OCS, and we believe that simulating the breeding scheme at hand from its actual base population may be the most effective way to find appropriate parameter values, resulting in the desired balance between gain and diversity, when using any selection strategy.

Conclusions

We investigated the performance of several long-term GS strategies to balance genetic gain and population diversity, in a simulation framework for a recurrent selection plant breeding scheme. GOCS, which extends pedigree-based OCS, and constrains the realized genomic relationship among selected individuals, unexpectedly did not control the inbreeding rate at the target level. This happens because the GOCS criterion does not incorporate the specific increase in inbreeding due to selection pressure at loci linked to QTL. This issue can be resolved with an index-based method (IND-HE) that balances genetic gain with expected heterozygosity in the selected set. IND-HE provides better results under a variety of settings, and is particularly more effective during the first cycles of a GS breeding program, where gain and diversity may not yet be competing. We also showed that weighted genomic selection (WGS), which amplifies rare allele effects when calculating GEBVs, is not fully effective at maintaining these rare alleles, because it was implemented as a truncation selection. An alternative method, IND-RA, that weighs genetic gain with rare allele frequencies in the set of selected individuals, outperforms WGS, with results that are very similar to IND-HE. Both IND-HE and IND-RA clearly provide a better balance between genetic merit and diversity than GOCS or WGS, and proved stable and effective irrespective of trait heritability and initial TP size. While requiring further testing in other breeding schemes, we believe that the inherent benefits of the IND-HE and IND-RA methods will transfer from our simulation framework to many practical breeding settings, and are a major step forward toward efficient long-term GS.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.194449/-/DC1.