Abstract
Mathematical and computational modeling of cardiac excitation–contraction coupling has produced considerable insights into how the heart muscle contracts. With the increase in biophysical and physiological data available, the modeling has become more sophisticated with investigations spanning in scale from molecular components to whole cells. These modeling efforts have provided insight into cardiac excitation–contraction coupling that advanced and complemented experimental studies. One goal is to extend these detailed cellular models to model the whole heart. While this has been done with mechanical and electophysiological models, the complexity and fast time course of calcium dynamics have made inclusion of detailed calcium dynamics in whole heart models impractical. Novel methods such as the probability density approach and moment closure technique which increase computational efficiency might make this tractable.
Keywords: Calcium, Heart, Model, Excitation–contraction coupling, Calcium spark
1. Introduction
Mathematical and computational modeling have long played a role in understanding the physiology of the heart. This started with empirical relations derived to understand the pumping of the heart such as the Frank–Starling law. It was followed by more detailed and mechanistic descriptions as more experimental information became available. The result is that currently models spanning many spatio-temporal scales, going from single ion channels, to individual cardiac myocytes, and finally to the whole heart are being used to gain understanding into function of the heart and the disease processes that affect human health. This review paper will focus on cellular and subcellular modeling of cardiac excitation–contraction (EC) coupling.
Cardiac excitation–contraction coupling refers to the series of events initiated by the electrical excitation of the heart. With each heart beat, ions flowing through ion channels in the plasma membrane generate currents which cause characteristic changes in membrane voltage referred to as the action potential (AP). This AP triggers calcium release from internal stores (i.e., the sarcoplasmic reticulum), via a process known as calcium-induced calcium release (CICR) which results in a transient increase in internal calcium concentration. These calcium ions interact with myofilaments to initiate cell contraction (Fig. 1). Various ion pumps and exchangers then work to restore ion concentrations back to their previous levels before the next beat.
Fig. 1.
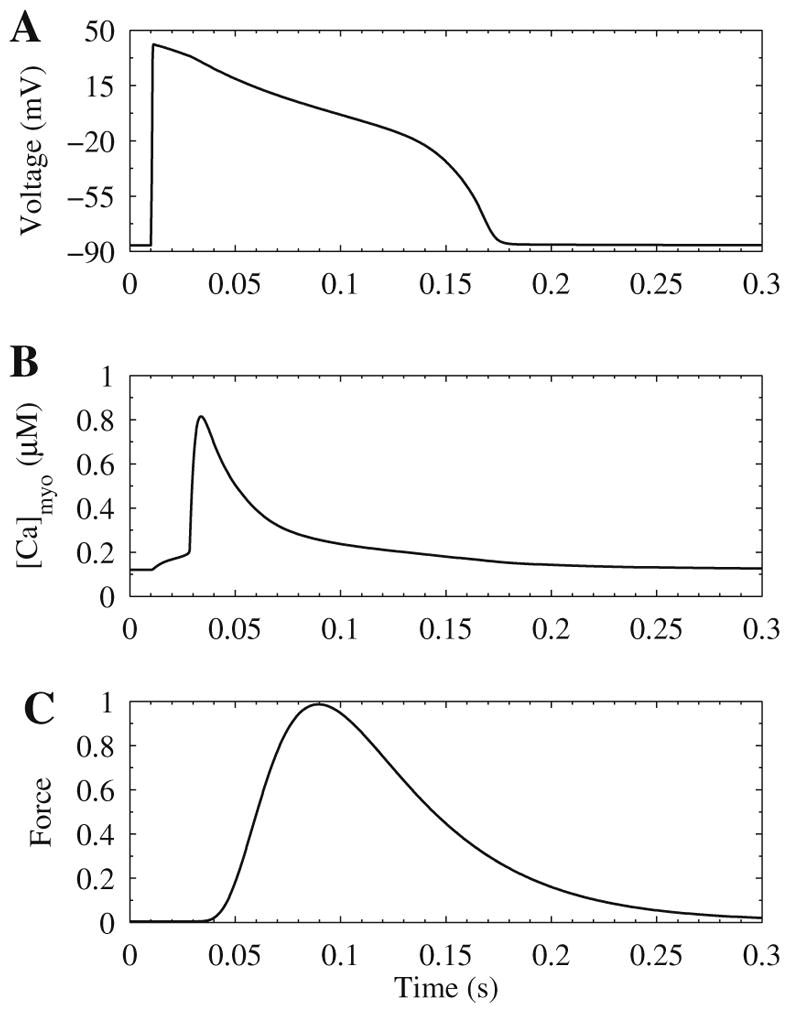
Excitation–contraction (EC) coupling is the processes linking electrical excitation which triggers the action potential shown in (A) membrane potential. This leads to calcium mobilization shown in (B) bulk myoplasmic (intracellular) calcium concentration. The increase calcium binds to myofilaments and causes force generation shown in (C) normalized force. These time courses are simulated using the Jafri–Rice–Winslow model of the guinea pig ventricular myocyte coupled to the Rice–Hunter–Winslow model for isometric force generation.
In order to understand EC coupling, we must understand the basic physiology and the closely related morphology. The basic contractile unit in the cardiac myocyte is the sarcomere, which is a repeated structure giving the myocyte its banded or striated appearance due to the arrangement of the proteins present in its different regions. During normal contraction all the sarcomeres shorten uniformly. The z-lines, located at the two ends of the sarcomere, are the location of the t-tubules. The t-tubules are regions of extra-cellular space created by tubular invaginations of the sarcolemma (i.e., the cell’s outer membrane). EC coupling occurs in the dyadic subspaces, regions of restricted space bounded by the t-tubular and sarcoplasmic reticulum (SR) membrane (Fig. 2).
Fig. 2.
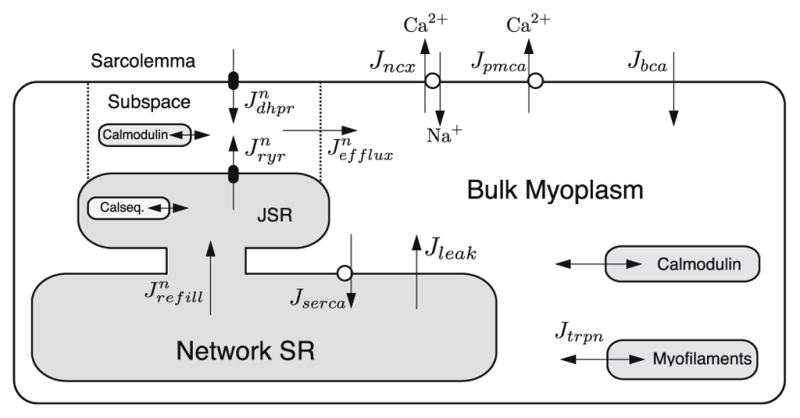
Schematic diagram for cardiac EC coupling.
The action potential is caused by the opening of voltage-gated ion channels, proteins that span the sarcolemma and when open allow the movement of ions down their electro-chemical gradient which is generated by ion motive ATPases and exchangers in the sarcolemma. The initial depolarization phase of the AP is caused by a fast sodium current followed by opening of the voltage-sensitive L-type or dihydropyridine receptors (DHPR) calcium channels (Jdhpr) located primarily at in the t-tubular membrane. The L-type calcium current helps maintain the plateau phase of the action potential. The plateau and repolarization phase that follows is governed primarily by voltage-gated potassium channels.
The opening of the L-type calcium channel allows calcium to flow down its electro-chemical gradient into dyadic subspace. This presence of calcium ions in the subspace serves two roles. First, it is responsible for triggering the opening of the calcium-sensitive intracellular ryanodine receptor calcium channel which releases calcium (Jryr) from intracellular stores via CICR. Second, this elevated dyadic subspace calcium concentration induces calcium-dependent inactivation of the L-type channel by binding to calmodulin, a protein tethered to the L-type calcium channel. Calcium in the dyadic subspace is then free to diffuse (Jefflux) out into the myoplasm and throughout the sarcomere where it binds to the calcium binding protein troponin in the myofilaments and initiates cell contraction. Calcium is resequestered to the network SR by the sarco-endoplasmic reticulum calcium ATPase (SERCA) pump flux (Jserca) and then diffuses into the junctional SR (Jrefill) where it becomes available for release. A passive SR calcium leak (Jleak) helps moderate SR calcium concentration. Throughout this process calcium is buffered by calcium binding proteins such as calmodulin and troponin. Homeostasis of total cellular calcium is maintained predominantly by the sodium–calcium exchanger (Jncx) and the plasma membrane calcium ATPase (Jpmca).
2. Deterministic common-pool, whole myocyte models
2.1. History
The earliest mathematical model of cardiac EC coupling was the Noble model for the Purkinje cell published in 1962 [1]. The model was an enhanced version of the Hodgkin–Huxley model for the action potential in the nerve axon [2] which included a second type of potassium channel, but lacked any calcium currents. Further enhancements followed with the addition of an inward calcium current in [3] and the 1985 DiFrancesco and Noble model [4]. The DiFrancesco–Noble model of the Purkinje fiber, while intended to describe a multicellular preparation, included membrane bound ion channels and transporters (used to generate the action potential) and also a description of intracellular concentration changes. This was the first biophysically detailed model of excitation contraction coupling as it included a more complete description of the ion channels and ionic homeostasis mechanisms. This model increased the understanding of the action potential by integrating knowledge about the ionic mechanisms to show that they could account for the action potential. Hilgemann and Noble [5] developed a model of rabbit atrial cell that included calcium dynamics including SR uptake and release mechanisms as well as transarcolemmal fluxes. Later work by Demir et al. [6] in rabbit sinoatrial cells used a modified form of the this model.
The first model for the ventricular myocyte was developed by Beeler and Reuter in 1977 [7]. It followed the earlier models of McAllister, Noble and Tsien, but added a slow inward current to give an action potential and included changes of intracellular calcium. The first published biophysically detailed model of the ventricular cell was developed by Luo and Rudy in 1991 [8] as it contained experimentally verified descriptions of the many membrane currents found in the guinea pig ventricular myocyte. This was followed by their Phase II model in 1994 [9,10] that included dynamic equations for ion concentrations. Another family of models for the ventricular myocyte was developed by the Noble group based upon their previous work which are reviewed in [11].
The Luo–Rudy phase II model produces robust action potential wave trains under a number of experimental protocols. The model and its improvements [12–14] allow the study of many phenomena involved in EC coupling and suggested that the action potential in guinea pig ventricular myocytes show decreased action potential duration with decreased interbeat intervals (i.e., increased pacing frequency) due to the incomplete deactivation of the potassium currents between beats. These more recent modeling efforts, while describing ionic currents and exchangers constrained by biophysical data, included empirical descriptions of calcium dynamics.
Many early models are termed common-pool models [15] as calcium release by the SR is controlled by a single compartment into which release occurs. In some cases this is the myoplasmic calcium concentration that is described by one continuously stirred pool. The release of calcium from the sarcoplasmic reticulum was formulated to give the desired calcium transient behavior, but lacked physiologically realistic descriptions of the ryanodine receptor. This was due in part to the difficulties introduced by the strong positive feedback caused by the regenerative nature of CICR, a fundamental property of the ryanodine receptor.
2.2. Models with detailed calcium dynamics
The Jafri–Rice–Winslow guinea pig ventricular myocyte model (1998), was the first ventricular myocyte model to provide a detailed description of calcium dynamics during excitation–contraction coupling [16]. This model built upon the Luo–Rudy Phase II model, but reformulated the calcium dynamics. While previous models included phenomenological descriptions of calcium release, this model co-localized the voltage-gate L-type calcium channels and the ryanodine receptors in a restricted subspace to approximate the dyadic space. This formulation prepared the foundation of many of models that followed including those developed for mouse, rat, dog, and rabbit [17–20].
The notable benefits of the Jafri–Rice–Winslow model over previous models are the enhanced description of calcium dynamics and the resulting improvements in model behavior. This model added a second compartment, referred to as the subspace, to represent the total of all the dyadic spaces in the myocyte. The L-type calcium channels and ryanodine receptors both deposited calcium into this subspace. Furthermore, this was the first model to depart from the Hodgkin–Huxley approach by developing Markov state models of the L-type calcium channel (Fig. 3) and the ryanodine receptors [21] to reflect recent experimental findings about their properties. Many models that followed incorporated Markov state representations of ion channels. For example, Irvine et al. developed a Markov state model of the sodium channel [22]. The best example of the use of Markov state models of ion channels to study the molecular basis of arrhythmias and possible pharmacological intervention comes from the work of Rudy and co-workers [23–25]. For example, they have used the model to predict how mutations to the sodium channel (ΔPQ) can result in the arrhythmia known as long QT syndrome. They also suggest, based upon model findings, that the drug mexiletine would be more effective in preventing the arrhythmia generated by the ΔPQ sodium channel mutation that would the drug lidocaine [24].
Fig. 3.
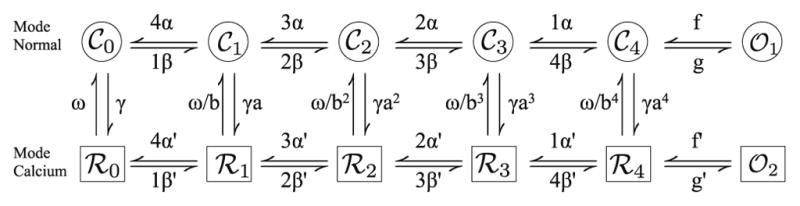
Markov state model of the L-type calcium channel.
The L-type calcium current displays voltage-dependent activation, voltage-dependent inactivation, and calcium-dependent inactivation. The L-type calcium current was traditionally modeled with the open probability depending upon the product of these three independent processes (i.e., gates),
| (1) |
where d is the fraction of activated channels, f is the fraction of voltage inactivated channels, and fCa is the fraction of calcium inactivated channels. The reversal potential (ECa) is described by the Nernst potential and the maximal whole cell L-type calcium current conductance is ḡCa. Alternatively, the current could be described using Goldman–Hodgkin–Katz equation scaled by the open probability given by dffCa.
At the time Imredy and Yue [26] observed that the calcium-dependent inactivation was more significant than previously thought and proposed that there were two modes of gating for the channel a normal mode and a high calcium mode. In mode calcium, the channel does not open and hence is inactivated. The new formulation the L-type channel takes this into account. It is described by a number of states reflecting the biophysics of the channel (Fig. 3). The top and bottom rows reflect normal and high calcium concentration mode gating, respectively. The channel consists of four subunits and each subunit can be in the closed or in the permissive state. In the top row (i.e., mode normal), the subscript i in 𝒞i denotes the number of subunits in the permissive state. Voltage-dependent transitions for each subunit are indicated by α and time-dependent reverse transitions are indicated by β. Once all four subunits are in the permissive state (𝒞4) there is a voltage-independent transition (f) into the channel’s open state. The channel transitions into mode calcium via calcium-dependent transitions (γ). The high calcium mode has voltage-dependent transitions similar to those described above, however, the transition to the open state (f′) is very slow, thus allowing calcium-dependent inactivation of the channel. The channel displays Hodgkin–Huxley style voltage-dependent inactivation.
The ryanodine receptor model consisted of a Markov state model developed by Keizer and Levine [21] that included adaptation of the ryanodine receptor observed by Gyorke and Fill [27]. In the process of adaptation, the open probability decreases or inactivates with a half-time of about 150 ms in response to a step change in calcium concentration. If the concentration is increased further, the open probability will also increase indicating that this inactivation state is not long-lived. The Keizer–Levine model matched single channel data of open and closed probabilities and dwell times of bilayer data. The Jafri–Rice–Winslow model successfully simulates action potential trains and the underlying calcium dynamics at different pacing frequencies. In Fig. 1, simulated action potential and calcium transients for the model are shown. The force transient comes from the Rice–Hunter–Winslow model for isometric force generation [28]. The model was also used to explore certain scientific questions described below.
2.3. Termination of release in common-pool models
Activation of the ryanodine receptor occurs with strong positive feedback through the process of calcium-induced calcium release (CICR). The mechanism that ends calcium release, thus allowing the system to return to resting values is a topic of active study. Two potential mechanisms for termination in deterministic common-pool simulations are inactivation of the ryanodine receptor or emptying of the sarcoplasmic reticulum. In either case, the calcium flux would diminish the release would terminate. The Jafri–Rice–Winslow model was use to explore these two possible mechanisms (Fig. 4). If the rate of adaptation/inactivation is increased 10-fold, there is only a slight influence on the morphology of the simulated calcium transient. On the other hand, if the store content is fixed at its full value, release does not terminate. However, if the SR calcium is fixed in a depleted state above the minimum during a transient (600 μM), release is not initiated indicating that depletion of the SR limits the flux out of the ryanodine receptor to such an extent that CICR is no longer possible (not shown). Lack of releasable calcium therefore is not a prerequisite for termination of release. This is consistent with experiments where additional calcium release can be triggered after a release induced by depolarization.
Fig. 4.
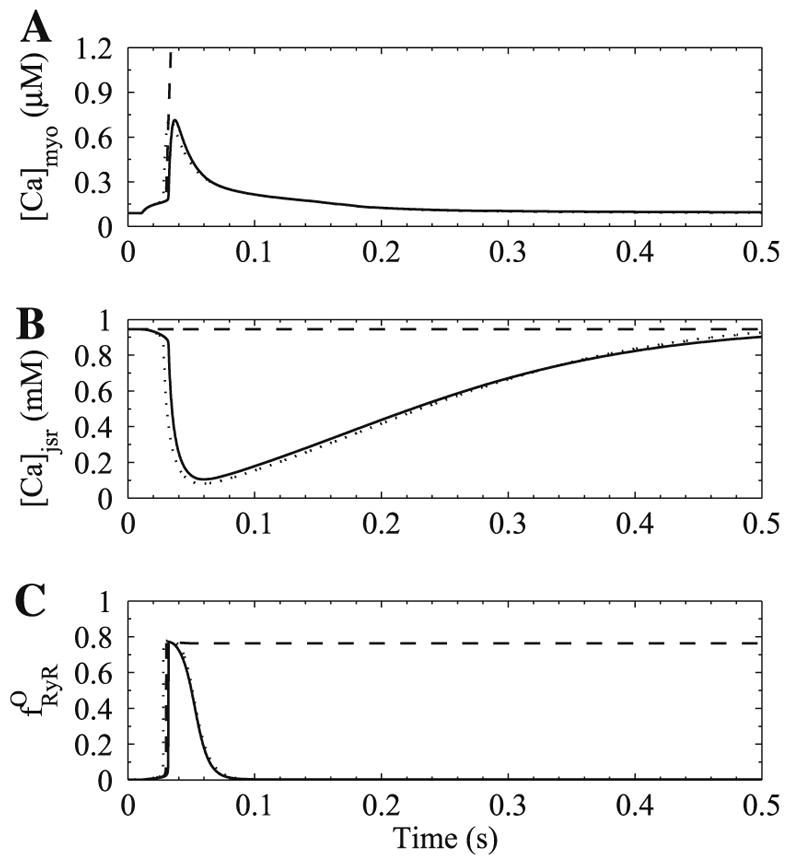
Termination of release was tested by simulation. Shown in the figure are (A) bulk myoplasmic calcium concentration, (B) junctional SR calcium concentration, and (C) fraction of open ryanodine receptor channels. A control calcium transient (solid line) terminates reliably. However, holding the SR calcium concentration at its full value (dashed line) results in no termination of calcium release. If the rate of ryanodine receptor adaptation is increased 10-fold, there is little change in calcium release (dotted line).
The observation of Bassani et al. [29] also support this model prediction. They found that as the amount of calcium in the SR (SR load) increases, the fractional amount of calcium available for release increases. In the model, release terminates when the SR calcium concentration falls to a low value so that CICR cannot be sustained. This amount is roughly the same regardless of the starting value (as long as the starting value can induce sustained CICR). Hence if the SR starts with a larger amount it would have a higher release fraction than if the SR starts at a lower value. Therefore, as the SR load increases, the fraction released increases consistent with experiment.
2.4. Interval force relations
In the heart and in individual cardiac myocytes, if the pacing frequency is changed, the force generated and the calcium transient also change. These observations are termed interval–force relations. For example, when the pacing frequency increases, the action potential duration shortens. Previous modeling studies [14] suggested that the shortening of the action potential duration during increases in pacing frequency is due mainly to increased potassium currents. However, in the Jafri–Rice–Winslow model, the shortening of action potential durations resulted from both the failure of the potassium current to deactivate completely and the failure of the L-type calcium current to recover from voltage-dependent inactivation. This is shown in Fig. 5 where stable action potentials at 1 Hz (solid bold) and 4 Hz (solid normal) are simulated. Using the initial conditions for the 1 Hz action potential various gating variables were modified using their initial conditions from the 4 Hz action potential in order to show their relative contributions to action potential shortening. The model suggested that the L-type current contributed significantly to the change in action potential shape during pacing. The contribution of the L-type current to changes in action potential duration and morphology was shown later in experiments [30]. The net result is clear in Fig. 5D where the sum of the potassium current (Fig. 5B) and L-type calcium current (Fig. 5C) are shown to follow the action potential shortening seen in Fig. 5A.
Fig. 5.
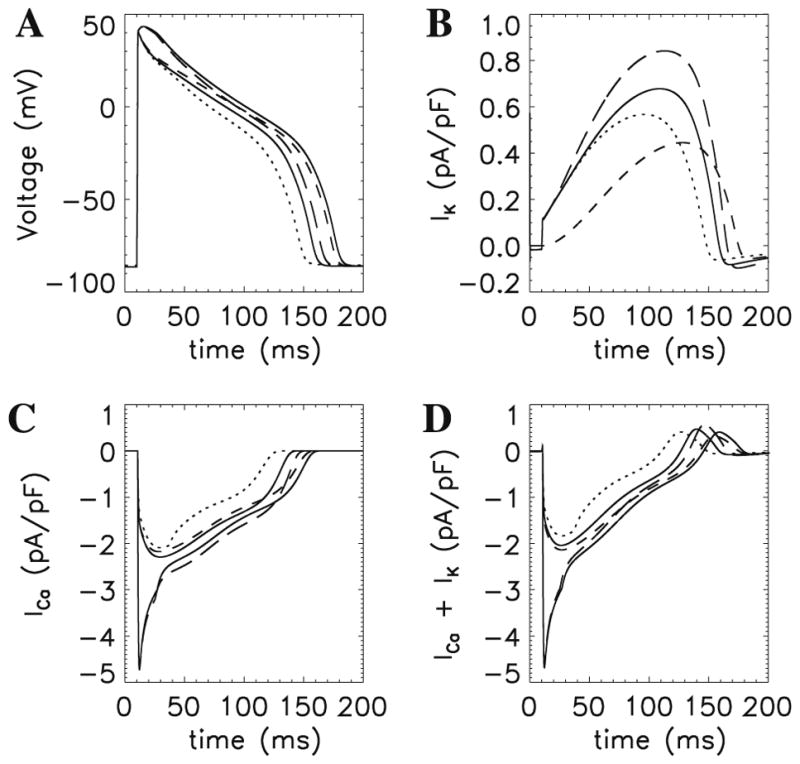
Mechanism of action potential shortening during pacing of guinea pig ventricular myocytes. Shown in the figure are (A) action potentials, (b) potassium current, (C) L-type calcium current, and (D) sum of (B) and (C). For each panel the traces are as follows: 1 Hz (dotted) and 4 Hz (solid thin) with the other traces using the 1 Hz simulation initial conditions with the individual ion channel gating variables set using the initial condition from the 4 Hz simulation as follows: activation gate (x) of the IK1 potassium channel (dot-dashed), voltage-dependent inactivation gate (y) of the L-type calcium channel (long dashed) and both (short dashed line).
In the guinea pig heart, the amount of steady-state peak force generated as the pacing frequency first rises then falls yielding a dome-shaped relation. The model myocyte was stimulated at different pacing frequencies until a steady train of force transients was obtained. The peak bulk myoplasmic calcium concentration, peak junctional sarcoplasmic reticulum calcium concentration, and peak fraction of open ryanodine receptor channels are shown in Fig. 6. The model produces this behavior and suggests a mechanism. As the pacing frequency increases the sarcoplasmic reticulum loads with calcium as shown in experiments [31]. However, at the same time, the fraction of ryanodine receptors accumulated in the adapted/inactivated state increases, resulting in reduced peak fraction of open ryanodine receptor channels. The release flux is given by
Fig. 6.
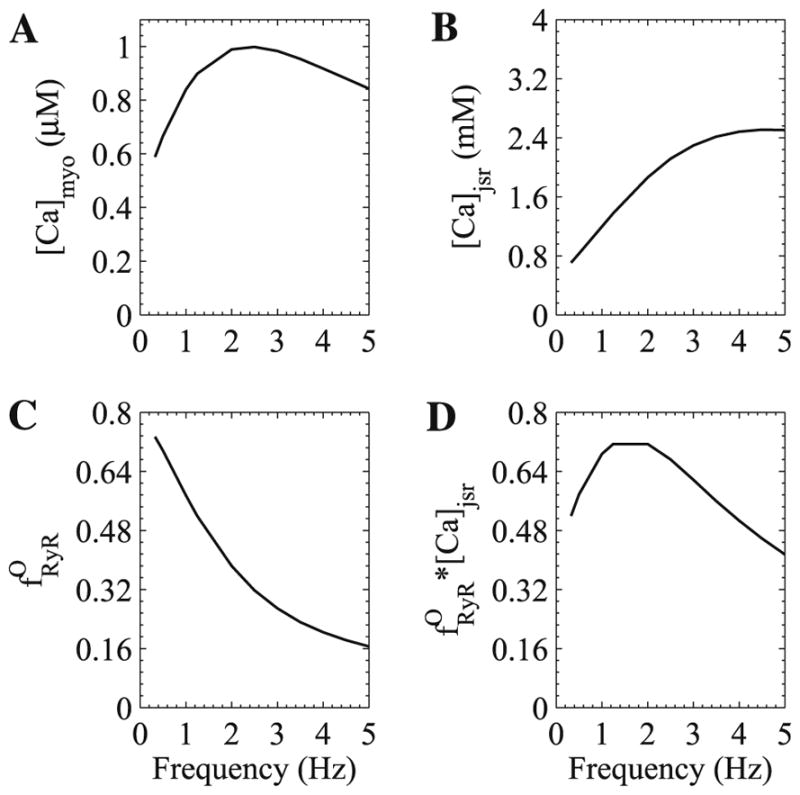
Simulated steady-state peak force-frequency relation for guinea pig ventricular myocytes. (A) Peak bulk myoplasmic calcium concentration, (B) peak junctional SR calcium concentration, (C) peak fraction of open ryanodine receptor channels, and (D) product of (B) and (C).
| (2) |
where νryr is the peak ryanodine receptor conductance, is the fraction of open channels, and the terms in parenthesis describe the calcium concentration gradient between the JSR and subspace. Given this relation and that the JSR concentration is much larger than the subspace concentration at rest, the dome-shaped curve results from the product (Fig. 6D).
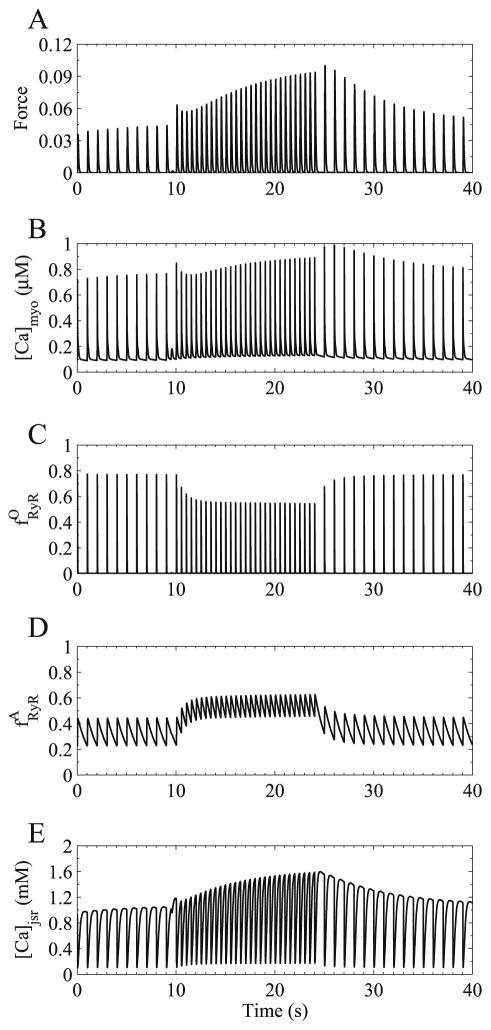
The Jafri–Rice–Winslow model is the first model to simulate the experimentally observed changes in calcium transient amplitudes (force) with changes in the pacing frequency and provides a mechanistic explanation. For example, the model was used to simulate a change in the pacing frequency changes from 1.0 Hz to 2.0 Hz at 9.0 s and back to 1.0 Hz at 24.0 s (Fig. 7). Initially upon the frequency change, there is a skipped calcium release event as the L-type calcium chancel has not recovered from voltage-dependent inactivation and hence does not activate to trigger calcium release from the SR. This is followed by an potentiated calcium transient as the SR has experienced additional refilling (Fig. 7E). The increased SR calcium concentration enables the calcium-induced calcium release mechanism to overcome the reduced trigger current. At the higher frequency the peak ryanodine receptor fraction of open channels drops (Fig. 7C) as the ryanodine receptor has less time to recover from the adapted state, i.e., it accumulated in the adapted state (Fig. 7D). This results in transient decline in force and peak bulk myoplasmic calcium concentration (Fig. 7A and B) followed by an gradual increase in force and myoplasmic calcium as the SR calcium rises (Fig. 7E). When the frequency is restored to 1.0 Hz, there is a transient elevation in force due to the increased SR calcium level and recovered ryanodine receptor fraction of open channels, followed by a gradual decline back to normal values. The model reproduces these changes as seen in the calcium transient amplitudes (Fig. 6).
Fig. 7.
Mechanisms of interval–force relations shown by changing pacing frequency from 1.0 Hz to 2.0 Hz (from 9 to 24 s) and back to 1.0 Hz. (A) Normalized force, (B) bulk myoplasmic calcium concentration, (C) fraction of open ryanodine receptor channels, (D) fraction of ryanodine receptor channels in adapted state, and (E) junctional SR calcium concentration.
An improved version of the guinea pig ventricular myocyte model was developed by Rice, Jafri, and Winslow in 2000 [32] to further explore interval–force relations. It was used to study the mechanisms behind mechanical restitution and postextrasystolic potentiation. Mechanical restitution is the property that when pacing at a fixed frequency, if the next beat (termed extrasystolic) is triggered at various intervals, the force generated is small for shorter intervals and increases with increasing interval until it returns to the control value. Postextrasystolic potential is the property that a second paired beat (a postextrasystolic beat) triggered a fixed interval after a smaller extrasystolic initial beat (due to restitution), will result in a potentiated (postextrasystolic) beat. The Rice–Jafri–Winslow model simulates restitution and postextrasystolic potentiation and provides an alternate explanation.
In previous modeling studies the restitution and potentiation was attributed to slow refilling between the JSR and NSR (a time constant of hundreds of ms) [33,10]. However, experiments by Bers estimated that the transfer between the two stores to be much faster (time constant of a several ms) [31]. The Rice–Jafri–Winslow model used an intermediate value of 34 ms for the time constant. In fact, recent experiments measured a time constant of 93 ms [34], and other experimental studies have indicated that there is heterogeneity in the connectivity of individual junctional SR to the network SR [35].
The Rice–Jafri–Winslow model suggested mechanisms similar to those described above for other interval force relations explained by this model. Mechanical restitution resulted from the ability of the ryanodine receptor to recover from the adapted state. When the interval was short, the ryanodine receptor remained in the adapted state and shows a lower fraction of open channels when activated. As the stimulus interval lengthened the ryanodine receptor recovered and could produce larger calcium release. Similarly the potentiated beat has the property that the higher the degree of attenuation of the extrasystolic beat the larger the potentiated beat. This resulted because with little release from the SR, there was a low degree of calcium-dependent inactivation of the L-type channel. This allowed more calcium entry into the cell which increased SR load, augmenting the calcium it retained from the attenuated release. The next beat with a overloaded SR resulted in a large potentiated beat.
2.5. Heart failure model
The dog is a commonly used model to study heart failure. In the canine heart failure model, an electrode is placed on the heart to induce rapid pacing. After a number of weeks under rapid pacing, heart failure develops. Winslow–Rice–Jafri developed a model of the canine ventricle by modifying the Jafri–Rice–Winslow guinea pig ventricular cell model [19,16]. By simulating excitation–contraction coupling in the canine ventricle, this model was used to study heart failure (Fig. 8). In heart failure, the duration of the action potential increases and the calcium transient amplitude decreases while its duration increases. In experiments, it was also observed that expression of certain potassium currents decrease, expression of sodium–calcium exchange increases, and SERCA expression decreases. At the time it was thought that the decrease in potassium currents was the main cause of the prolongation of action potential seen in heart failure. The model was used to see if these changes could explain the changes to action potential and calcium transient morphology. A simulated healthy canine action potential and calcium transient at a pacing rate of 1.0 Hz are shown in Fig. 8 (solid line). A 50% reduction in the potassium current (IK1), a 100% increase in the sodium–calcium exchanger (NCX) and a 50% reduction in SERCA activity are all needed to simulate the experimentally observed changes in action potential duration and calcium handling. The heart failure model was also more prone to produce early after depolarizations which are considered to be a underlying mechanism for cardiac arrhythmias. When the canine model was put into a network model for the whole left and right ventricle, the normal physiology produced well coordinated beating when paced, however, the heart failure model quickly produced cardiac arrhythmia [36].
Fig. 8.
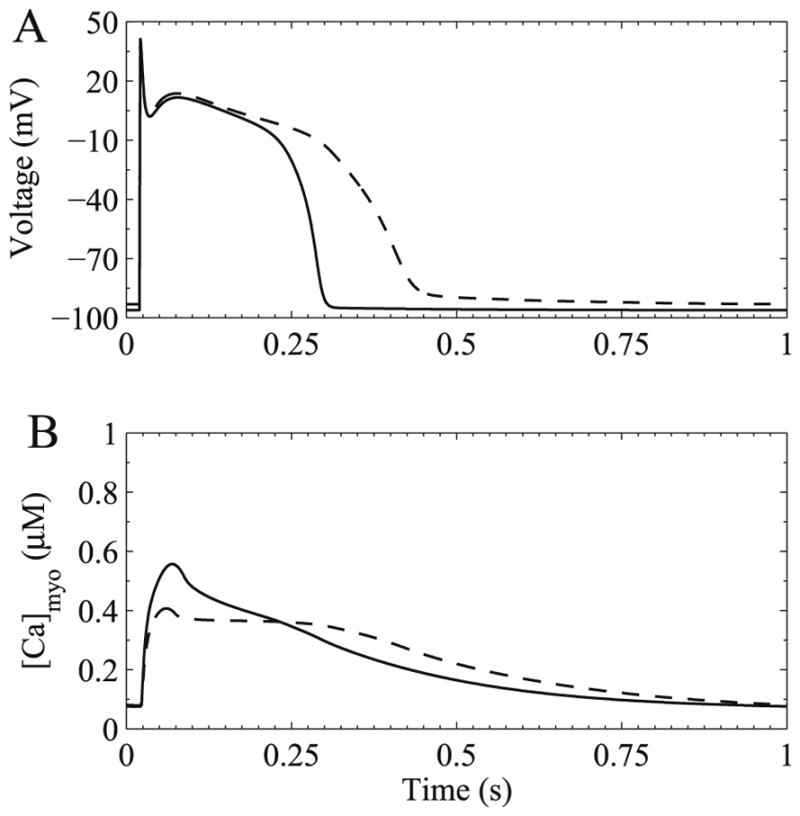
Simulated heart failure in a canine ventricular myocyte. (A) Membrane potential and (B) bulk myoplasmic calcium. The healthy action potential and calcium transient are show with the solid trace. The heart failure simulation is shown by the dashed trace.
2.6. Cardiac alternans
Alternans are a beat-to-beat variation in the amplitude and duration of the action potential, calcium transient and force generated. These are termed action potential alternans, calcium alternans, and mechanical alternans, respectively. Alternans are considered to be a mechanism for arrhythmia in the heart. Moreover, action potential alternans have been linked to life threatening arrhythmia. Calcium alternans are thought to underlie the action potential alternans and mechanical alternans. They occur on the whole heart, tissue, and cellular levels. Considerable modeling efforts have been conducted to understand this complex phenomenon.
Shiferaw et al. [37] developed a model of calcium cycling in ventricular myocytes that included the effect of sarcoplasmic reticulum calcium content on ryanodine receptor gating. This model produced calcium transient alternans at high pacing rates. The underlying mechanism in the model is the steep non-linear dependence of sarcoplasmic reticulum calcium release on sarcoplasmic reticulum calcium content and the effect of diastolic calcium level in the cytosol on L-type calcium current (through inactivation). Restrepo et al. [38] advanced this work by developing a model of calcium cycling in the ventricular myocyte that included spatially distributed release sites. The gating of the ryanodine receptors in the release sites was mediated by calcium in the sarcoplasmic reticulum lumen via calsequestrin. This model demonstrated that increased calsequestrin content of the sarcoplasmic reticulum increased the likelihood of calcium transient alternans as well as increasing the refractory period for calcium sparks, i.e. calcium release. Adding to the understanding of alternans, Xie and co-workers concluded from their computational models that sarcoplasmic reticulum leak, uptake and release all had independent direct effects on calcium alternans. In more recent work, Restrepo and Karma [39] have developed a model of the ventricular myocyte with spatially distributed calcium release sites and a full set of ionic membrane currents. The results demonstrate that the stochastic gating of ion channels at the level of a release site can influence whole cell alternans. Other studies by the same group, Sato et al. [40] have shown how two coupled ventricular myocytes lead to spatially discordant alternans using computational models. In spatially discordant alternans, the action potential duration and calcium transient alternate with opposite phase in different regions of tissue. The model showed how phase reversal of alternans of both action potential and calcium transients were possible.
Livshitz and Rudy [12] used their model to study alternans as well. They concluded that calcium transient alternans resulted from refractoriness of sarcoplasmic reticulum calcium release, that the L-type calcium channels had negligible effect, that action potential alternans involved the sodium–calcium exchanger, and that increase calcium/calmodulin dependent protein kinase II activity extends the range of alternans to slower frequencies.
Tao et al. [41] developed a model of calcium cycling in a one dimension string of calcium release sites under voltage clamp conditions to study the mechanism of alternans. The model produces calcium transient alternans generated by waves of calcium release. In this model, it is the spatial heterogeneity of calcium release leading to alternans without any required refractoriness of the ryanodine receptor or L-type calcium channel.
Huertas et al. [42] used the probability density and moment closure methods (see Sections 4.3 and 4.4) to develop a model of calcium cycling in the ventricular myocyte under voltage clamp conditions. This model allowed for heterogenous release sites with heterogenous junctional sarcoplasmic reticulum. These studies suggest that the steepness of the load-release function does not completely explain the conditions needed for alternans. They suggest that defective calcium cycling (the uptake and release processes) are important for understanding alternans.
3. Local control of calcium-induced calcium release
3.1. Calcium sparks
Calcium sparks are considered to be the elementary event in cardiac excitation–contraction coupling. They are thought to be observable calcium release at a single release site. Calcium sparks were first reported in 1993 by Cheng et al. [43]. A single release site typically consists of a cluster of ryanodine receptors and the associated L-type channels in the dyad. The dyad is delineated by the t-tubule and the junctional sarcoplasmic reticulum. A typical calcium spark lasts 20–30 ms with a peak calcium release current of 3–4 pA. Therefore, due to its short duration and small amplitude, the measurement of the calcium spark is difficult. Measurements are performed using confocal fluorescent microscopy and calcium indicator dyes in a line-scan image which allows resolution of the time course and spatial spread of the calcium spark. In this experimental procedure, a cell is loaded with fluorescent calcium indicator dye. The dye will fluoresce at a particular wavelength when excited by a laser. In the confocal microscope, the cell is excited by a laser and the resulting fluorescence is recorded. In a normal run the whole cell is scanned line by line. In line-scan mode, the cell is scanned along a single line resulting in higher temporal resolution because it takes time to scan the whole cell. Pictured in Fig. 9 is a simulated line-scan (without the introduction of any noise). In this figure, we can resolve the temporal and spatial profiles of the calcium spark. Ideally, these profiles are taken at the spark center where the profiles yield a maximum value. Often to characterize the spatial spread of a spark, the full width at the half amplitude of the maximal (FWHM) profiles is reported. Two fundamental questions concerning spark dynamics that are as yet unresolved are as follows: (1) What is the mechanism of termination of the calcium spark? (2) What are the mechanisms that give a spark it characteristic spatial spread throughout the cell? The first question is important because given the strong positive feedback of CICR, it is not clear what ends release. This has implications for pathological conditions where there is an excess of calcium release that results in cardiac arrhythmias. The second question is also important as the spatial characteristics of the spark enable sparks to distribute calcium across the sarcomere. During an action potential sparks sum up to cause global calcium release which activates contraction throughout the cell. Aberrant calcium release can cause activation of adjacent spark sites that can lead to intracellular calcium waves which can result in cardiac arrhythmias.
Fig. 9.
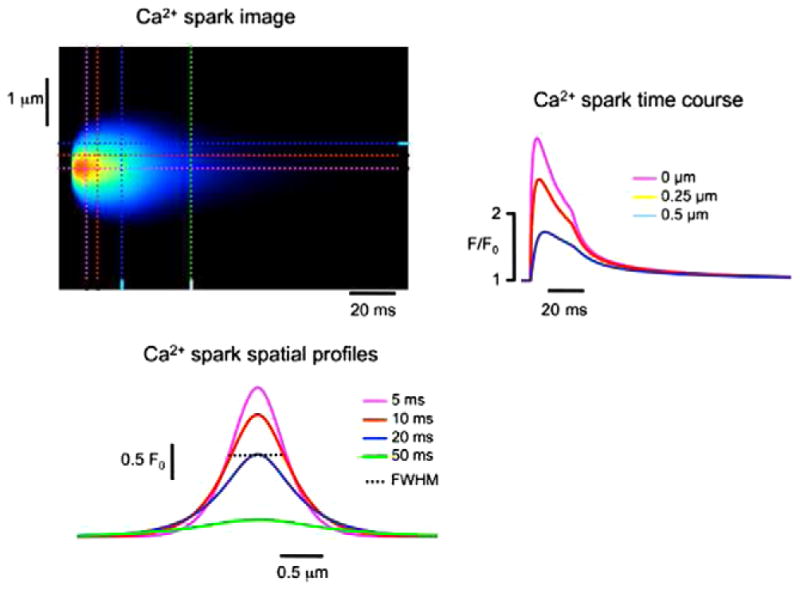
Simulated line-scan image of a calcium spark (top left) with the time course (top right) and spatial profile (bottom left).
The positive feedback in CICR has been considered to be the primary mechanism for initiation of the calcium spark. However, the mechanism of termination is less clear. Previous studies had suggested potential mechanisms for spark termination; however, each has its shortcomings (for review see [44]):
Stochastic attrition: Sparks might terminate due to stochastic attrition [15], a mechanism where all open channels (RyRs) simultaneously close stochastically in the absence of any other mechanism (e.g., calcium-dependent inactivation or allosteric coupling). Under the assumption that RyRs gate independently, mathematical analysis suggests that stochastic attrition is possible for a small number of channels, but unlikely for clusters of more than 10 RyRs [44]. However, when the physiological coupling of RyRs mediated by released Ca2+ is taken into account, stochastic attrition is not so easily eliminated as a potential spark termination mechanism [45]. Both of these analyses assume that the cytosolic Ca2+ domain rapidly collapses upon RyR closure, an assumption that works in favor of stochastic attrition [46,47]. Electron micrograph studies have suggested that there are 30–300 RyRs in each release site [48], and unless a significant fraction of these RyRs are not participating in spark generation and termination, it would seem that stochastic attrition alone cannot be responsible for spark termination.
Lumenal depletion: It is possible that calcium release terminates when the SR is empty because there is no calcium left to release, or because the decreased driving force for Ca2+ release decreases the size of the cytosolic domain resulting in deactivation of RyRs (see Fig. 10). Modeling studies focusing on the dynamics of lumenal depletion and the stochastic gating of coupled RyRs suggest that the rate of cytosolic domain collapse and lumenal domain refilling control whether Lumenal depletion is a viable termination mechanism in release sites that include Ca2+ activation but no Ca2+ inactivation [47]. However, after a contraction, additional calcium can be released by caffeine, an agonist of the RyR. Furthermore, under certain experimental manipulations such as the addition of ryanodine, sparks of duration of over a second are possible. If a typical spark terminates after 20–30 ms from SR emptying, these long sparks should not be possible.
RyR inactivation: It has been suggested that inactivation of RyRs can lead to termination of calcium sparks. Theoretical studies clearly indicate that the presence of Ca2+-dependent or -independent inactivation in an RyR model can lead to sparks whose termination is facilitated by the recruitment of inactivated channels throughout the duration of the release event. However, the only well-documented inactivation-like process found for the RyR is adaptation [27]. Adaptation has a half-time of 150 ms which is far too slow for recruitment of inactivated RyRs to account for termination of sparks with average duration of 20–30 ms. On the other hand, computational studies have shown that Ca2+ inactivation may be an important negative feedback mechanism even when its time constant is much greater than the duration of sparks [49].
Lumenal regulation: It has been hypothesized that the decrease in RyR open probability with SR lumenal depletion might play a role in the termination of calcium release. Experiments with isolated ryanodine receptors in planar lipid bilayer display a decreased open probability [50]. However, these investigators also observed that at low lumenal calcium levels the mean closed time was decreased while the mean open time remained relatively unchanged making the possible role of lumenal regulation in termination less clear.
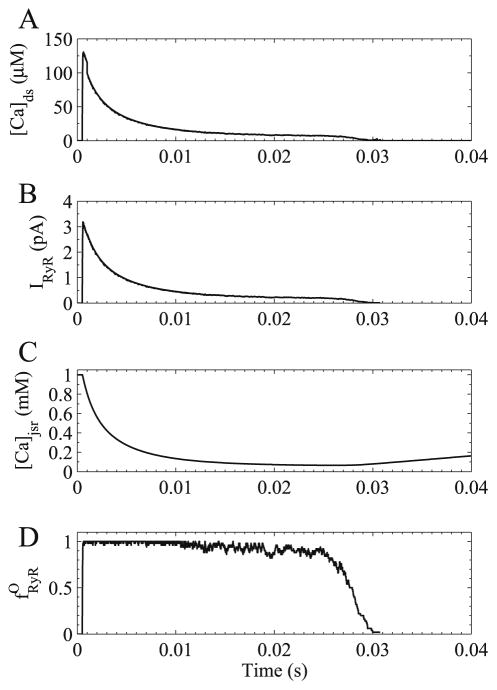
Fig. 10.
Simulated time courses of calcium spark. (A) Dyadic subspace calcium concentration, (B) ryanodine receptor calcium release flux, (C) junctional SR calcium concentration, and (D) fraction of open ryanodine receptor channels.
Mathematical and computational models have been used to interpret calcium spark data and understand the fundamental mechanisms that give rise to their behaviors. Early spark models sought to understand the calcium fluxes and calcium buffering processes that gave rise to calcium sparks [51]. This work used a simple step function to describe calcium release and observed how buffering and SR calcium pump distribution gave rise to spark profiles. This yielded the insight that the mobility, kinetics and concentration of the calcium indicator dye were essential determinants of spark shape and that stationary calcium buffers (binding proteins) played a lesser role. Furthermore, it suggested that anisotropic diffusion of calcium ions and indicator dye provided a better explanation of spark shape that heterogeneity of the sarcomere geometry such as SR calcium pump location. In spite of these advances, the spatial spread of sparks in this model was smaller than that seen in experiments.
3.2. Monte Carlo spark models
The first published work to explore the stochastic mechanisms of calcium sparks was developed by Stern et al. [52]. In this model, they proposed that calcium sparks terminate by inactivation of the ryanodine receptor. The model suggests that in order for inactivation be a viable mechanism for spark termination, inactivation would have to be 15 times faster than the rates used in previously published models of the ryanodine receptor based upon experiment data.
Sobie et al. [53] was the next effort to try to explain the mechanism of termination of calcium sparks. This work developed a dynamic model of calcium release in the dyadic junction to understand mechanisms of spark formation and termination. This model will be described in some detail as it is used the basis of much of the work discussed herein.
This model combines the large number of ryanodine receptors, with two other experimental findings. First, the ryanodine receptor open probability has been shown to increase due to an decrease in mean closed time as the lumenal calcium concentration increases [50]. Second, ryanodine receptors extracted from cells have shown to open and closed in synchrony. This coupled gating can be reversible disrupted by pharmacological agents such as FK506 and rapamycin. This suggests that the protein FKBP (FK506 binding protein) which is associated with the ryanodine receptor is likely involved. The model consists of a stochastically gating ryanodine receptors with an open and closed state with the opening and closing transition rates
and
where and are the maximal opening and closing rates, Km is the lumenal dependence of open probability (Km = 17.14 − 0.00686cjsr), and χ𝒪 and χ𝒞 represent cooperativity factors,
which depend on the number of open ryanodine receptors and number of closed ryanodine receptors , and the cooperativity factor (kcoop). It is important to note that these representations of cooperativity were created to make χ𝒪 an increasing function of the number of open channels and to make χ𝒞 an increasing function of the number of closed channels.
The stochastic gating of the channels is solved by Monte Carlo simulation. Notice that lumenal depletion decreases the opening rate of the ryanodine receptor channel. The calcium flux through a cluster of ryanodine receptors is given as
| (3) |
where νryr is the single ryanodine receptor permeability. Release from the ryanodine receptors is triggered by the opening of the L-type calcium channel (Jdhpr). Calcium efflux from the subspace is given by
| (4) |
where (cmyo) is the bulk myoplasmic calcium concentration (0.1 μM) and τefflux is the time constant of efflux. Calcium in the subspace is buffered by the binding protein calmodulin (calm) and the negative charges associated with the SR membrane (srm) and t-tubular membrane (ttm), which combine to form, The calcium bound buffer concentration ([CaB]) is described by
| (5) |
where i indexes into the buffers (calm, srm, and ttm), and are the on and off rates for calcium binding, and is the total concentration of the ith buffer.
The dynamic equation for the subspace calcium is
| (6) |
where the buffering flux Jbuffer is
| (7) |
The dynamics equation for the junctional SR calcium is
| (8) |
with
| (9) |
where cnsr is the network SR calcium concentration (1.0 mM), Vds and Vjsr are the dyadic subspace and junctional SR volumes, and τrefill is the time constant of refilling and βjsr described buffering in the JSR by the rapid buffering approximation [54]
| (10) |
where is the concentration of the calcium binding protein calsequestrin in the junctional SR and Kcsq is the calcium binding constant.
The efflux from the subspace is used as the source flux in a model for diffusion and buffering by endogenous buffers and fluorescent dyes in the myoplasm to create spark images. These images are subject to a point spread function to simulate the optical blurring imposed by the confocal microscope and simulated experimental noise for comparison to experimental recordings.
The Sobie et al. calcium spark model reproduces realistic sparks that display many of the correct properties. For example, the sparks show realistic, spark duration, spontaneous spark frequency and the frequency dependence upon both myoplasmic and SR calcium levels. The model correctly simulates the increase in spark duration seen during addition of agents such as rapamycin and FK506 which reduce coupling between ryanodine receptors. The model also suggests a critical role for the lumenal dependence in spark termination as simulations with lumenal dependence removed results in extremely long sparks.
The model also suggested that the mechanism for spark initiation was the positive feedback of CICR and that coupling played a minor role in activation of the spark. It also suggested a novel mechanism for spark termination. In Fig. 10 the spark cluster fraction of open channels quickly becomes close to 1 (Fig. 10D). With spark opening, the subspace calcium rises and quickly declines (Fig. 10A) as the JSR calcium depletes (Fig. 10C). With this depletion, the opening rate or opening transition probability of the ryanodine receptors decrease so that as they stochastically close, they do not reopen as can be seen by the increasing fluctuation in Fig. 10D. Once a critical mass does not reopen, cooperativity encourages others to close leading to spark termination. This mechanism, hence in essence, contains components of stochastic attrition, lumenal depletion, and inactivation (inability to open due to JSR depletion). However, in this model, the NSR still remains quite full allowing additional release or long sparks under certain manipulations (such as if the lumenal dependence or coupling were removed/reduced).
The Sobie et al. calcium spark model has been quite successful as many experimental studies that followed confirmed aspects and predictions of the model. For example, local depletion of the junctional SR has been shown experimentally [55,56]. The role of SR lumenal depletion on spark termination has been shown in three types of experiments. First, the addition of SR calcium buffers slowed the rate of depletion resulting in an increased spark duration [57,58]. Second, inhibition of the ryanodine receptors using tetracaine slowed the rate of depletion and lengthened calcium sparks [35,59]. Third, the rate of refilling of the SR controls the ability of a second SR calcium release event after termination [57,60,61]
3.3. Allosteric coupling of ryanodine receptors
The Sobie et al. spark model presented a representation of coupling in the cluster by scaling the transition rate constant by a cooperativity factor that depended on the number of channels in each state in the cluster. Alternate approaches for modeling allosteric coupling between ryanodine receptors have been proposed. Sobie et al. [62] proposed a coupling scheme based upon the strategy used by Bray and co-workers to describe bacterial chemotaxis [63,64]. In this model, if a ryanodine receptor’s neighbors are in the same state it is energetically stabilized by a coupling energy that is included in the transition rate expression for the channel. If the neighbors are in a different sate, the energy barrier for transition to the state of the neighbors is reduced making a transition more likely.
Another approach was presented in recent work by Groff and Smith [65] who expanded upon the methodology introduced by Stern et al. [66] for incorporating allosteric coupling in clusters of RyRs. Similar to the Sobie et al. model [53] this method allows channels to be coupled via both calcium and allosteric interactions and uses the mean-field approach to aggregate states based on the number of channels open at the release site. However, this approach defines dimensionless free energies of interaction that specify the change in free energy for a channel in physical contact with another channel. This allows for interactions that stabilize (or destabilize) closed channel pairs, open channel pairs, or both. In this way, the allosteric interactions can have a synchronizing (or desynchronizing) influence on channel gating. Groff and Smith performed full and reduced model calculations that demonstrating that the mean-field approach to modeling RyR clusters (i.e., ignoring the spatial arrangement of RyRs as in [53]) often performs well. The functional form for cooperativity factors representing the coupled gating of RyRs that best approximates the full model simulations is
| (11) |
| (12) |
where ε𝒞𝒞 is a dimensionless free energy of interaction (units of kBT) that specifies the change in free energy experienced by a channel in state 𝒞 when allosterically coupled to a channel in state 𝒞, and similarly for ε𝒪𝒪 (without loss of generality ε𝒞𝒪 = ε𝒞𝒪 = 0).
3.4. Models of the spatial spread of sparks
A considerable amount of modeling has applied to understand the spatial spark of calcium spark. Spark spread is measured by the full width of the spark at the half of the maximal amplitude (FWHM). Typically spark FWHM is 1.8–2.0 μM. However, spark models have not yet produced this amount of spatial spread. A related question is how does calcium spread between release sites to give rise to spontaneous calcium waves. Spontaneous calcium waves are observed in heart failure and in experimentally created conditions of calcium overload. Calcium overload is characterized by increased SR calcium load and elevated resting myoplasmic calcium. During heart failure, calcium overload is observed as well as increased sensitivity of the ryanodine receptor through phosphorylation of the channel.
Early work includes the modeling by Smith et al. [51] and Sobie et al. [53] both mentioned previously. As these previous models of cardiac sparks did not produce sufficient FWHM Izu et al. [67] presented a potential solution in their model. Previous experimental evidence estimated the spark flux at approximately 3–4 pA. In their model, they demonstrated that if the spark current was increase to greater than 11 pA they were able to get sparks with FWHM of 2.0 μm. That raises the suggestion that spark fluxes should be 10–20 pA, however, this has not been confirmed experimentally. In other work, Izu et al. [68] studies the properties of calcium sparks that give rise to intracellular calcium waves. In this work, they suggested that multiple release sites need to activate simultaneously in order to give rise to a calcium wave. They also observed that in a stochastic model a moderately increased calcium sensitivity of the ryanodine receptor resulted in spontaneous calcium waves. However, in a deterministic model the calcium sensitivity of the ryanodine receptor had to be augmented even further to cause calcium waves.
Ramay et al. [69] have incorporated the Sobie et al. spark model [53] into a three dimensional model of the sarcomere. In their model, they were able to get FWHM of close to 2.0 μm by increasing the spatial domain of activation for spark generation. Electron microscopy has indicated that two diads are typically found on both sides of the t-tubule. Often these two dyads are actually connected forming a ring or other connect structure. In the Ramay et al. model, when calcium release is activated nearly simultaneously on both sides of the t-tubule sparks with appropriate spatial spread is achieved. In related work, Ramay et al. also looked at the spread of calcium from one site to another to produce calcium waves in a model with multiple release sites in a sarcomere [70]. They concluded that in order for calcium activation to occur in an adjacent release site at a realistic separation, there would have to be increased calcium release, increased myoplasmic calcium levels, and increased calcium sensitivity of the ryanodine receptors.
Another approach by Tan et al. suggests that Fickian diffusion is not adequate to explain the spread of calcium sparks. Instead these authors proposed a novel model of anomalous space subdiffusion due to the electrical field of the calcium ions, the viscoelasticity of the cytoplasm, and structure in the cell [71]. In their model, anomalous subdiffusion simulations result in wider sparks than did their simulations with Fickian diffusion.
3.5. Local control and graded release
Calcium sparks are the elementary events in EC coupling. During a whole cell calcium transient, the summation of sparks yields the global calcium transient. There are approximately 20000 calcium release sites in the ventricular cardiac myocyte. Hence, the global calcium transient, modeled deterministically, is the result of a large number of stochastic events. The deterministic models, however, fail to capture mechanistically a fundamental property of EC coupling called graded release.
Graded release, first observed by Fabiato [72] is the property that the amount of force or tension generated increases with increasing trigger calcium. This was later shown in cardiac myocytes that the about of calcium released increases with increasing trigger calcium (i.e. entry from the L-type calcium channels) [73–75]. If the amount of calcium released is divided by the amount of trigger calcium this produces the EC coupling gain function (Fig. 11). This is considered to be a measure of EC coupling efficiency. In diseases such as heart failure, the EC coupling gain is decreased.
Fig. 11.
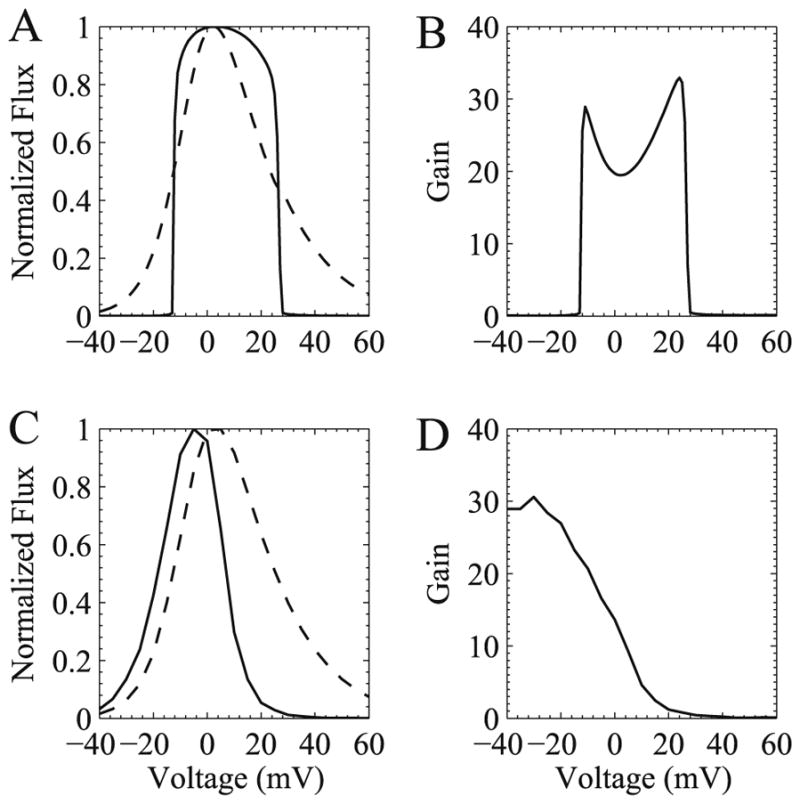
Realistic graded release (A) and EC coupling gain (B) cannot be produced in a common-pool model but can be produced in a local control model (C and D, respectively). Normalized calcium flux (ryanodine receptor – solid trace and L-type calcium current – dashed trace) is shown in (A) and (C) to demonstrate graded release. Panels (B) and (D) show EC coupling gain.
The deterministic common-pool models fail to capture graded release in a mechanistic fashion. For example, the 1994 Luo–Rudy model ties calcium release from the SR to the upstroke of the action potential, the Livshitz–Rudy [12] ties RyR opening rate to L-type calcium channel current, cand the Jafri–Rice–Winslow model produces an all-or-none release in response to different levels of trigger calcium (Fig. 11). A solution to this was proposed by Stern [15] in the theory of local control. In local control, opening of different numbers of L-type calcium channels recruit different number of calcium release units (dyads) yielding a graded response. Stern demonstrated this with a simple model.
The idea of local control in a biophysically more realistic model was shown by Rice–Jafri–Winslow [76] in which they divided the release seen in the Jafri–Rice–Winslow model for the guinea pig ventricular myocyte into 5500 independent stochastic release units each consisting of one L-type channel and eight ryanodine receptors in a dyadic subspace with fixed NSR and bulk myoplasmic calcium concentration. This work was followed by work by Greenstein and Winslow [77] who integrated a model of local control into the Winslow et al. model [19] of the canine ventricular myocyte. This model included 12500 release sites each containing four L-type channels and 20 ryanodine receptors. This model simulated realistic action potentials, membrane currents, calcium transients in addition to producing realistic graded release and EC coupling gain. It was very computationally expensive and would take overnight to run 1 second of simulation time on a 12 processor computer available at that time. The model indicated that using local control, the modeling of the L-type current could more closely match experimentally measured voltage- and calcium-dependent inactivation that common-pool models (which would become unstable using these representations).
As calcium transients consist of calcium sparks, the next logical progression is to create a model of all 20000 release units and observe is this better explains cardiac EC coupling. Previous stochastic whole cell models did not create release units that produced realistic calcium sparks. This was first done by Chikando et al. [78] who integrated the Sobie et al. [53] spark model into a model of the rat ventricular myocyte. The model included dynamic variables for each subspace, each JSR, and one bulk myoplasm and one bulk NSR. The calcium handling sarcolemmal mechanism such as non-junction L-type calcium channels, sodium–calcium exchange, and the sarcolemmal calcium ATPase were also included. The model also included calcium binding proteins in the JSR, subspace and bulk myoplasm. The model accurately produced graded release, EC coupling gain and realistic calcium transients in response to both voltage clamp and action potential clamp simulations. The model also included the allosteric coupling formulation developed by Sobie et al. [53] of ryanodine receptor coupling in a cluster. This model was, however, very computationally expensive taking 1 month on a single processor to run 1 second of simulation time. This makes it impractical to use these detailed approaches in models of the whole ventricle. This motivates the development of faster methods for solving such a system which are discussed in the topics that follow.
4. Methods to improve computational efficiency
4.1. Model reduction methods
Quasi-static approximation based on a separation of time scales is a well-established approach to reducing ordinary differential equation (ODE) models of the dynamics of whole cell Ca2+ responses. For example, the four-state Keizer–Levine RyR model can be reduced to a two-state model that can be represented by a single Hodgkin–Huxley style gating variable in whole cell models of Ca2+ oscillations, because the process of Ca2+ activation is much faster than the process of Ca2+-independent inactivation (i.e., adaptation) in this model [21]. In the spark model of Sobie et al. [53], this approach was used to derive a simple two-state RyR model from the more complex RyR gating scheme presented in Rice–Jafri–Winslow [76].
Such fast/slow reduction was performed by Hinch et al. in order to overcome the computational complexity encountered in stochastic local control models [79,80]. They started with the 12 state L-type calcium channel used by Greenstein and Winslow [77] and the five-state RyR model of Stern et al. [66] in which inactivation of the RyR was necessary for termination of release. Using quasi-static approximation they reduced the 12-state L-type calcium channel to a three-state channel and the five-state RyR to a three-state RyR. The model also assumed a simplified dyad geometry with a single L-type calcium channel and a single RyR, and equilibrium between network and junctional SR (so the latter could be omitted). They further assumed that the dyadic subspace calcium concentration was in rapid equilibrium so it could be represented as an algebraic function of bulk myoplasmic calcium, SR calcium and the states of the RyRs and L-type calcium channels. It is important to note that in this model RyR inactivation terminated release so depletion of the junctional SR was not necessary. This approach was later incorporated into a model of the canine ventricular myocyte that produced realistic EC coupling gain and gradedness as well as interval–force behavior [81]. These models successfully produced physiological behavior with computationally efficiency that resulted in solution times that made them practical for use in long pacing protocols.
4.2. Simplified Monte Carlo EC coupling model
Williams et al. presented a simplified model of EC coupling and developed computational strategies for its efficient solution [82]. The all-or-none nature of calcium release from each dyad allows a complex ryanodine receptor cluster model containing potentially hundreds of states to be reduced to a single mega-channel representation containing only a few states. Utilizing this simplified release site structure one can create a realistic but minimal representation of a whole cell model of CICR incorporating local control. Such a Monte Carlo model would consist of 2N + 2 ODEs representing the time-evolution of calcium concentration in the bulk myoplasm (cmyo), network SR (cnsr), and N junctional SRs and N dyadic subspace compartments. Consistent with Fig. 2, the concentration balance equations are
| (13) |
| (14) |
| (15) |
| (16) |
where 1 ≤ n ≤ N, λnsr, λjsr, and λds are volume fractions (e.g., λnsr = Vnsr/Vmyo), and βmyo, βnsr, βjsr, and βds are constant fraction buffering constants. is the flux of calcium from the nth dyadic subspace to the bulk myoplasm and is the flux of calcium from bulk NSR to the nth JSR. Jserca is the sarco-endoplasmic reticulum ATPase which pumps calcium from the myoplasm back to the NSR, Jncx is the sodium–calcium exchanger which allows the entry of 3 Na+ ions in exchange for the extrusion of a single calcium ion, Jbca is the calcium leak across the sarcolemma, and Jleak is the calcium leak across the SR membrane. and are the L-type and ryanodine receptor channel fluxes. The total refill and efflux terms are given by and , respectively.
4.3. Probability density approach
The probability density approach to modeling local calcium signaling and calcium release unit activity during cardiac EC coupling is an alternative to Monte Carlo simulation that is valid when the number of calcium release units is large. This technique allows local calcium concentrations (dyadic subspace (c̃ds) and junctional SR (c̃jsr)) to be represented by probability density functions (ρi (cds, cjsr, t)) jointly distributed with the state of the release site [46,82–84], that is,
| (17) |
where the index i runs over the various release unit states and the tildes on c̃ds, c̃jsr, and S̃ (t) indicate random quantities. To better understand Eq. (17), it may be helpful to imagine performing a Monte Carlo simulation with a very large number of calcium release units each containing a local dyadic subspace and junctional SR calcium concentration and a Markov chain representing the stochastic gating of the L-type and ryanodine receptor channels. At any point in time (t) one could randomly sample a single calcium release unit from this population to produce an instance of the random variables c̃ds, c̃jsr, and S̃ (t), corresponding to the current state of the calcium release unit and the local calcium concentrations associated with that release site. The quantity ρi (cds, cjsr, t) defined in Eq. (17) indicates the probability with which you would find this sampled calcium release unit in state i with dyadic subspace calcium concentration in the range [cds, cds + dcds] and junctional SR calcium concentration in the range [cjsr, cjsr + dcjsr] provided the total number of calcium release units is very large.
For the multivariate probability densities defined by Eq. (17) to be consistent with the dynamics of the Monte Carlo model of cardiac EC coupling described in the previous section, they must satisfy the following system of advection-reaction equations [46,47,82,85],
| (18) |
where the advection rates and capture the deterministic dynamics of dyadic subspace and junctional SR calcium concentration (consistent with Eqs. (15) and (16)) while the reaction terms ([ρQ]i) capture the stochastic gating of the channels contained in the release site. Q is the infinitesimal generator matrix for the Markov chain used to represent the release site,
| (19) |
where the elements of Kϕ(V) are the calcium-independent transitions (including voltage-dependent ones), and the elements of Kds and Kjsr are the association rate constants for the transitions mediated by dyadic subspace and junctional SR calcium concentration, respectively.
Recent work has shown that Monte Carlo model parameters often lead to rapid equilibrium of the dyadic subspace calcium concentration with the junctional SR and bulk myoplasm calcium concentration [82,88], allowing dyadic subspace calcium concentration (cds) to be expressed in terms of junctional SR calcium concentration (cjsr), myoplasmic calcium concentration (cmyo), and release site state (S̃).
In this situation, model dynamics can be captured by a univariate probability density approach, that is,
| (20) |
which solves a corresponding advection-reaction equation,
| (21) |
This modeling approach was presented in detail in [82] and was shown to be roughly 100 times faster than the corresponding Monte Carlo simulation. Note that the probability density approach can be applied to any release site configuration which can be put in the form of Eq. (19) and is not limited to mega-channel representations like the one presented here.
4.4. Moment closure technique
The computational advantages of the probability density approach can be extended by representing the local calcium concentration in the junctional SR compartments as the moments of the univariate probability density functions. These moments are dynamic variables which capture the evolution of the local junctional SR calcium concentration and calcium release unit state changes, defined as,
| (22) |
where the non-negative integer q indicates the moment degree in and is an exponent in (cjsr)q. Recall that ρi (cjsr, t) is the distribution of calcium concentration in a large number of junctional SR compartments jointly distributed with release site state. Differentiating Eq. (22) with respect to time and using the equations of the univariate probability density approach yields an open system of ODEs that describe the time-evolution of these moments where higher moments are dependent on lower moments, that is,
| (23) |
where we write as a shorthand for .
However, since the time-evolution of the qth moments (Eq. (23)) requires knowledge of the (q + 1) th moments, this open system of ODEs must be truncated. One method for doing this is to express the third moment as an algebraic function (ϕ) of the moments , and , that is,
This modeling approach was presented in detail in [88] and was shown to be up to 10000 times faster than the corresponding Monte Carlo simulation.
4.5. Heterogenous local calcium concentrations
To better understand how each technique represents local calcium concentration, consider a hypothetical model containing a large number of two-state calcium-activated intracellular calcium channels each affiliated with a ‘fast’ cytosolic compartment (cds) and ‘slow’ luminal compartment (cjsr). Fig. 12 shows the distribution of junctional SR calcium concentration conditioned upon the state of the channel at a particular moment in time. As one would expect a closed channel is likely to experience elevated cjsr values while an open channel experiences depleted values of cjsr, indicating the release of calcium from the junctional SR to the diadic subspace. The histograms show the distribution of calcium for a Monte Carlo simulation containing N = 10000 two-state release sites. The solid line shows the corresponding probability density function and the filled diamonds show a beta distribution with the same mean and variance from the moment closure technique. While each technique represents the junctional SR calcium concentration differently they qualitatively agree quite well. Note that integrating either the closed or open distributions yields the probability of the channel being either closed (π𝒞) or open (π𝒪).
Fig. 12.
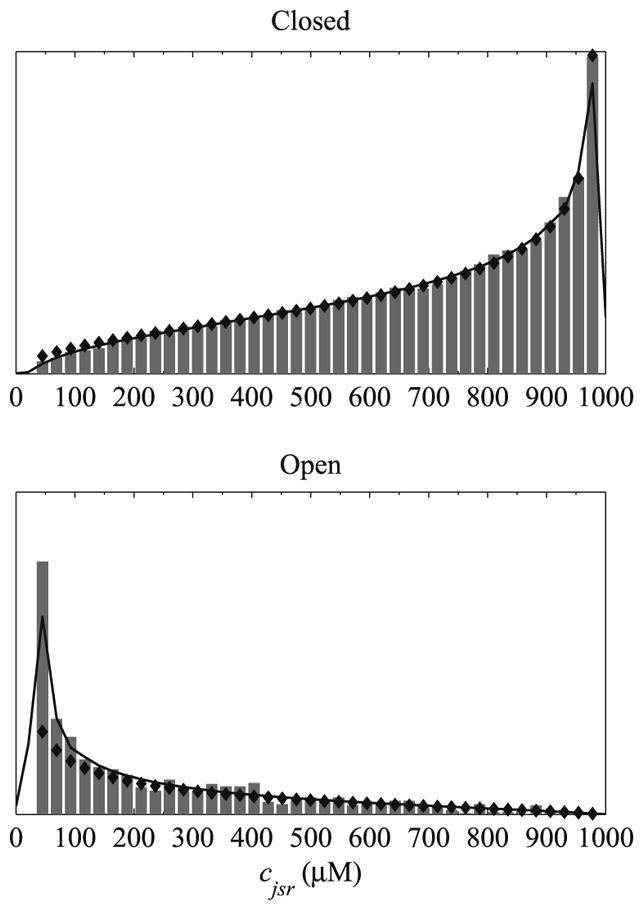
Distribution of junctional SR calcium concentration conditioned upon the state of a hypothetical two-state Ca-activated intracellular calcium channel. Histrograms show the distribution of calcium for a Monte Carlo simulation where N = 10000. The solid lines show the corresponding probability density functions and the filled diamonds show beta distributions with the same mean and variance.
4.6. Benefits and limitations of probability density methods
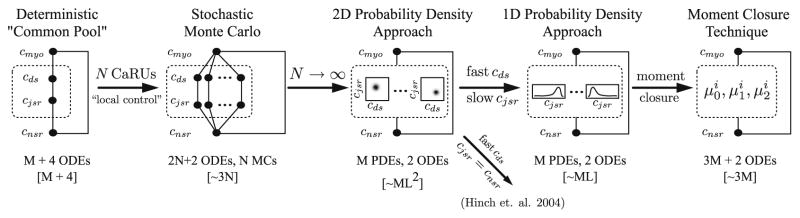
Fig. 13 shows a schematic representation of the common methods used for modeling CICR in cardiac myocytes. Filled circles and solid lines represent compartments and fluxes, respectively. Values contained within the square brackets indicate the relative computational complexity of each method. For example, a typical deterministic common-pool model might include an ODE for each of the bulk compartments (myoplasmand network SR), an ODE for each shared domain concentration, and ODEs representing the fraction of channels in each of the state (or alternatively, several ODEs for Hodgkin–Huxley style gating variables). A stochastic local control Monte Carlo model of whole cell EC coupling would include a large number (N) calcium release units and its computational demand would scale roughly like 3 × N. Therefore, a typical Monte Carlo simulation where N = 10000 would require roughly 30000 computational operations for each time step. In the limit of a large number of calcium release units, an alternative probability density approach [82] can be used in which domain concentrations are represented by multivariate probability density functions (one for each of the M states in the Markov chain used to represent the calcium release unit). In this case, the computational demand of the probability density method will scale roughly like M × L2 where L is the length of the mesh required to represent the densities. A hypothetical probability density method where M = 10 and L = 50 would require approximately 25000 computational operations per time step, which is not a dramatic improvement over the Monte Carlo efficiency, it is not a dramatic one. However, since common parameters often lead to a separation of time scales between the diadic subspace and junctional SR calcium concentration, the probability density approach can be reduced to a univariate function of cjsr. In this case, the probability density method will scale roughly like M × L or 500 computational operations per time step. This is a significant improvement over the Monte Carlo technique, however, the computational advantages of the probability density approach can be extended even further by representing the domain calcium concentrations by the moments of univariate probability density functions [88]. This moment closure technique scales roughly like 3 × M since three moment ODEs are required each of the M states. Using the same value of M as above results in a computational demand of 30, a 1000-fold improvement over the traditional Monte Carlo value of 30000. The probability density and moment closure techniques can achieve another 10-fold improvement since they allow for a larger time step while maintaining numerical stability (see [82,88]).
Fig. 13.
Schematic representation of the common methods used for modeling CICR in cardiac myocytes. Filled circles and solid lines represent compartments and fluxes, respectively. The ellipsis in the Monte Carlo diagram indicates a large number (N) calcium release units. The ellipsis in the 2D and 1D probability density diagram indicate the number of states (M) in the Markov chain (MC) used to represent the two calcium channels in the release site. Similarly, the index i in the moment closure diagram indexes into the M states of the release site. Values contained with square brackets indicate the relative computational complexity of the various techniques where N is the number of releases sites, M is the number of states in the Markov chain, and L is the length of the mesh required to represent the densities.
It is important to distinguish the fast subspace reduction utilized here from that of Hinch et al. [79] which assumed fast cds and lacked a junctional SR compartment, therefore providing a single cds value for each state of the release site. In this case, however, since cds is in rapid equilibrium with cjsr and there is a distribution of cjsr values for each state of the release site, there is a corresponding distribution of cds values as well.
While the probability density and moment closure techniques are capable of incorporating clusters or ryanodine receptors rather than a ‘mega-channel’ approximation these techniques are susceptible to the state space explosion that occurs when considering a large cluster of multi-state channels. For example, a spatially explicit release site model of N M-state channels would contain MN distinguishable states. Fortunately, this state space explosion can be alleviated somewhat by utilizing the mean-field approximation which results in state space of size (N +M − 1)!/(N!(M − 1)!). The number of states in a calcium release unit containing Ndhpr identical L-type calcium channels coupled to Nryr identical ryanodine receptor calcium channels is given by
| (24) |
where each single channel ryanodine receptor and L-type calcium channel model contains Mdhpr and Mryr states, respectively. It is important to consider the number of states a release site will contain before attempting to implement approaches that scale with M such as the probability density and moment closure techniques. In fact, if the number of states in the release site M approaches the number of release sites N the computational advantage of these approaches over Monte Carlo becomes marginalized. For this reason, automated largeness tolerance and largeness avoidance methods applicable to Ca2+ release site models that are compositionally defined in terms of a large number of single channel models is an area of active research [89,90].
5. Discussion
Computational modeling has proven to be a powerful tool for studying cardiac physiology and its implications for disease. Deterministic common-pool models have been used successfully to study the mechanism of cardiac EC coupling as well as how ion channel mutations and drugs can affect it. There have been many model predictions that were later verified by experiments. However, in spite of these successes, the deterministic common-pool models have some short comings such as the inability to produce graded release with a physiological mechanism. Incorporation of a physiological mechanism for graded release is possible with local control models; however, these approaches can be very computationally expensive. Recent advances in computational methods applicable to local control models such as the probability density approach, the associated moment closure technique, and automated model reduction techniques have made the computations more efficient. However, each of these has their caveats. The probability density approach and moment closure technique suffer from a state space explosion as the Markov models used for the release site description get more complex. Model reduction methods often make assumptions about the reactions to simplify the complex models that not be valid under certain experimental or pathological conditions. Hence judicious choices of what aspects of the physiology to include and which simplifying assumptions to make are essential. Furthermore, these reductions methods reduce the stochastic system to a deterministic one perhaps eliminating stochastic events that might be involved in arrhythmogenesis.
As there are situations where model reduction and approximation methods are inadequate, Monte Carlo simulation might be needed. In this case, fast efficient algorithms need to be developed for solution of these types of models. In addition to algorithms, new computer hardware also will make these problems more tractable. For example, parallel architectures such as multi-CPU and multicore computers are increasing in computational speed and number of computational cores. Also, the advent of graphics processor unit (GPU) based calculations and the maturing of code development for them promise to boost computing power available for computationally intensive calculations.
When developing complex models, the question often arises concerning the proper way to assure the correct choice of parameter values. This issue especially applies to Markov chain models of ion channels containing a large number of parameters. To address this issue it is important that the ion channel model used be able to reproduce multiple experimental data sets. Additionally, if the model is judiciously constructed, such as the L-type channel model of Jafri–Rice–Winslow [16] shown in Fig. 3, the number of free parameters is limited. This model has 12 states, but only 10 free parameters as the channel consists of four identical subunits. This is far fewer than if each transition had its own rate constant. Once the ion channel models are developed, they will be additionally constrained once they are incorporated in whole cell models to additional sets of more macroscopic data. Optimization methods are often used to fit model parameters to experimental data. However, there is often no guarantee that the optimal parameters are chosen. To some this presents a limitation, however, it should not be an impediment. As additional data sets are used to constrain a model, it will be clear if the parameter choice is adequate. An important thing to note is that for a given ion channel, the same characterization might be performed in different papers, with significantly different results indicating the variability of experimental preparation and the physiology itself.
In the realm of calcium sparks, while several possible mechanisms of spark termination have been suggested, they have not been verified experimentally. Furthermore, the mechanism for how sparks spread to neighboring release sites is still an open question. Possible solutions include an increased release site area, increased release current, or alternate models for diffusion of calcium in the cell. These need to be verified experimentally and studied further with computational models. Also, how calcium sparks can lead to calcium waves in the myocyte is still unclear. Another related question is how calcium sparks contribute to calcium leak from the sarcoplasmic reticulum. Understanding SR calcium leak is important due to its role in the homeostasis of cell calcium. A large part of the leak is thought to come from spontaneous calcium sparks. However, it has been suggested that there is still some component not explained by sparks. For these and other questions, more realistic models of the release unit might be needed. For example, the role of FKBP12 and FKBP12.6 remains unclear with differing results in the experimental literature. Modeling will most likely play a role in answering these questions.
This review only addresses some of the potential questions where modeling has helped improve understanding of cardiac excitation–contraction coupling. Computational modeling will also almost certainly play a role in understanding how signaling pathways are involved in modulating calcium signaling. There have been significant modeling efforts in understanding β-adrenergic regulation and phosphorylation dependent regulation of excitation contraction coupling [91–94]. Other efforts have endeavored to include the role of energy metabolism and mitochondrial signaling on excitation contraction coupling [95,96]. These papers provide a good start but additional investigations are required to better our understanding in these areas. Finally, the use of detailed ventricular myocyte models can be used to build more realistic tissue and whole ventricle models that can help in the understanding in cardiac function, dysfunction, and arrhythmias.
Investigating these and other areas related to cardiac excitation–contraction coupling will require and create opportunities for collaboration between those knowledgeable about the biology and those knowledgeable about the mathematical methodologies needed to answer these open questions.
Acknowledgments
This material is based upon work supported by the National Science Foundation under Grant Nos. 0133132 and 0443843.
References
- 1.Noble D. A modification of the Hodgkin–Huxley equations applicable to Purkinje fibre action and pace-maker potentials. J Physiol. 1962;160:317. doi: 10.1113/jphysiol.1962.sp006849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hodgkin A, Huxley A. The components of membrane conductance in the giant axon of loligo. J Physiol. 1952;116(4):473. doi: 10.1113/jphysiol.1952.sp004718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.McAllister R, Noble D, Tsien R. Reconstruction of the electrical activity of cardiac Purkinje fibres. J Physiol. 1975;251(1):1. doi: 10.1113/jphysiol.1975.sp011080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.DiFrancesco D, Noble D. A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philos Trans Roy Soc Lond B: Biol Sci. 1985;307(1133):353. doi: 10.1098/rstb.1985.0001. [DOI] [PubMed] [Google Scholar]
- 5.Hilgemann D, Noble D. Excitation–contraction coupling and extracellular calcium transients in rabbit atrium: reconstruction of basic cellular mechanisms. Philos Trans Roy Soc Lond B: Biol Sci. 1987;230(1259):163. doi: 10.1098/rspb.1987.0015. [DOI] [PubMed] [Google Scholar]
- 6.Demir S, Clark J, Murphey CR, Giles WR. A mathematical model of a rabbit sinoatrial cell. Am J Physiol. 1994;266(3 Pt 1):C832. doi: 10.1152/ajpcell.1994.266.3.C832. [DOI] [PubMed] [Google Scholar]
- 7.Beeler G, Reuter H. Reconstruction of the action potential of ventricular myocardial fibres. J Physiol. 1977;268(1):177. doi: 10.1113/jphysiol.1977.sp011853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Luo C, Rudy Y. A model of the ventricular cardiac action potential: depolarization, repolarization, and their interaction. Circ Res. 1991;68(6):1501. doi: 10.1161/01.res.68.6.1501. [DOI] [PubMed] [Google Scholar]
- 9.Luo C, Rudy Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ Res. 1994;74(6):1071. doi: 10.1161/01.res.74.6.1071. [DOI] [PubMed] [Google Scholar]
- 10.Luo C, Rudy Y. A dynamic model of the cardiac ventricular action potential. II. After depolarizations, triggered activity, and potentiation. Circ Res. 1994;74(6):1097. doi: 10.1161/01.res.74.6.1097. [DOI] [PubMed] [Google Scholar]
- 11.Noble D. Computational models of the heart and their use in assessing the actions of drugs. J Pharmacol Sci. 2008;107(2):107. doi: 10.1254/jphs.cr0070042. [DOI] [PubMed] [Google Scholar]
- 12.Livshitz L, Rudy Y. Regulation of Ca2+ and electrical alternans in cardiac myocytes: role of CamKII and repolarizing currents. Am J Physiol Heart Circ Physiol. 2007;292(6):H2854. doi: 10.1152/ajpheart.01347.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Decker K, Heijman J, Silva J, Hund T, Rudy Y. Properties and ionic mechanisms of action potential adaptation, restitution, and accommodation in canine epicardium. Am J Physiol Heart Circ Physiol. 2009;296(4):H1017. doi: 10.1152/ajpheart.01216.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zeng J, Rudy Y. Early after depolarizations in cardiac myocytes: mechanism and rate dependence. Biophys J. 1995;68(3):949. doi: 10.1016/S0006-3495(95)80271-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stern M. Theory of excitation–contraction coupling in cardiac muscle. Biophys J. 1992;63(2):497. doi: 10.1016/S0006-3495(92)81615-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jafri M, Rice J, Winslow R. Cardiac Ca2+ dynamics: the roles of ryanodine receptor adaptation and sarcoplasmic reticulum load. Biophys J. 1998;74(3):1149. doi: 10.1016/S0006-3495(98)77832-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bondarenko V, Bett G, Rasmusson R. A model of graded calcium release and L-type Ca2+ channel inactivation in cardiac muscle. Am J Physiol Heart Circ Physiol. 2004;286(3):H1154. doi: 10.1152/ajpheart.00168.2003. [DOI] [PubMed] [Google Scholar]
- 18.Pandit S, Clark R, Giles WR, Demir S. A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys J. 2001;81(6):3029. doi: 10.1016/S0006-3495(01)75943-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Winslow R, Rice J, Jafri S, Marbán E, O’Rourke B. Mechanisms of altered excitation–contraction coupling in canine tachycardia-induced heart failure, II: model studies. Circ Res. 1999;84(5):571. doi: 10.1161/01.res.84.5.571. [DOI] [PubMed] [Google Scholar]
- 20.Shannon T, Wang F, Puglisi J, Weber C, Bers D. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys J. 2004;87(5):3351. doi: 10.1529/biophysj.104.047449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Keizer J, Levine L. Ryanodine receptor adaptation and Ca2+-induced Ca2+ release-dependent Ca2+ oscillations. Biophys J. 1996;71(6):3477. doi: 10.1016/S0006-3495(96)79543-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Irvine L, Jafri M, Winslow R. Cardiac sodium channel markov model with temperature dependence and recovery from inactivation. Biophys J. 1999;76(4):1868. doi: 10.1016/s0006-3495(99)77346-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rudy Y. From genome to physiome: integrative models of cardiac excitation. Ann Biomed Eng. 2000;28(8):945. doi: 10.1114/1.1308484. [DOI] [PubMed] [Google Scholar]
- 24.Clancy C, Zhu Z, Rudy Y. Pharmacogenetics and anti-arrhythmic drug therapy: a theoretical investigation. Am J Physiol Heart Circ Physiol. 2007;292(3):H1641. doi: 10.1152/ajpheart.00312.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Clancy C, Rudy Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature. 1999;400(6744):566. doi: 10.1038/23034. [DOI] [PubMed] [Google Scholar]
- 26.Imredy J, Yue D. Mechanism of Ca2+-sensitive inactivation of L-type Ca2+ channels. Neuron. 1994;12(6):1301. doi: 10.1016/0896-6273(94)90446-4. [DOI] [PubMed] [Google Scholar]
- 27.Györke S, Fill M. Ryanodine receptor adaptation: control mechanism of Ca2+-induced Ca2+ release in heart. Science (New York, NY) 1993;260(5109):807. doi: 10.1126/science.8387229. [DOI] [PubMed] [Google Scholar]
- 28.Rice J, Winslow R, Hunter W. Comparison of putative cooperative mechanisms in cardiac muscle: length dependence and dynamic responses. Am J Physiol. 1999;276(5 Pt 2):H1734. doi: 10.1152/ajpheart.1999.276.5.H1734. [DOI] [PubMed] [Google Scholar]
- 29.Bassani J, Yuan W, Bers D. Fractional sr ca release is regulated by trigger ca and sr ca content in cardiac myocytes. Am J Physiol. 1995;268(5 Pt 1):C1313. doi: 10.1152/ajpcell.1995.268.5.C1313. [DOI] [PubMed] [Google Scholar]
- 30.Linz K, Meyer R. Control of L-type calcium current during the action potential of guinea-pig ventricular myocytes. J Physiol. 1998;513(Pt. 2):425. doi: 10.1111/j.1469-7793.1998.425bb.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bers D. Excitation–Contraction Coupling and Cardiac Contractile Force. 2. Kluwer Academic Publishers; Dordrecht: 1992. [Google Scholar]
- 32.Rice J, Jafri M, Winslow R. Modeling short-term interval–force relations in cardiac muscle. Am J Physiol Heart Circ Physiol. 2000;278(3):H913. doi: 10.1152/ajpheart.2000.278.3.H913. [DOI] [PubMed] [Google Scholar]
- 33.Wier W, Yue D. Intracellular calcium transients underlying the short-term force–interval relationship in ferret ventricular myocardium. J Physiol. 1986;376:507. doi: 10.1113/jphysiol.1986.sp016167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Swietach P, Spitzer K, Vaughan-Jones R. Ca2+-mobility in the sarcoplasmic reticulum of ventricular myocytes is low. Biophys J. 2008;95(3):1412. doi: 10.1529/biophysj.108.130385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zima A, Picht E, Bers D, Blatter L. Partial inhibition of sarcoplasmic reticulum ca release evokes long-lasting ca release events in ventricular myocytes: role of luminal ca in termination of ca release. Biophys J. 2008;94(5):1867. doi: 10.1529/biophysj.107.114694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Winslow R, Scollan D, Holmes A, Yung C, Zhang J, Jafri M. Electrophysiological modeling of cardiac ventricular function: from cell to organ. Ann Rev Biomed Eng. 2000;2:119. doi: 10.1146/annurev.bioeng.2.1.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shiferaw Y, Watanabe M, Garfinkel A, Weiss J, Karma A. Model of intracellular calcium cycling in ventricular myocytes. Biophys J. 2003;85(6):3666. doi: 10.1016/S0006-3495(03)74784-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Restrepo J, Weiss J, Karma A. Calsequestrin-mediated mechanism for cellular calcium transient alternans. Biophys J. 2008;95(8):3767. doi: 10.1529/biophysj.108.130419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Restrepo J, Karma A. Spatiotemporal intracellular calcium dynamics during cardiac alternans. Chaos (Woodbury, NY) 2009;19(3):037115. doi: 10.1063/1.3207835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sato D, Shiferaw Y, Garfinkel A, Weiss J, Qu Z, Karma A. Spatially discordant alternans in cardiac tissue: role of calcium cycling. Circ Res. 2006;99(5):520. doi: 10.1161/01.RES.0000240542.03986.e7. [DOI] [PubMed] [Google Scholar]
- 41.Tao T, O’Neill S, Diaz M, Li Y, Eisner D, Zhang H. Alternans of cardiac calcium cycling in a cluster of ryanodine receptors: a simulation study. Am J Physiol Heart Circ Physiol. 2008;295(2):H598. doi: 10.1152/ajpheart.01086.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Huertas M, Smith G, Györke S. Analysis of calcium alternans in a cardiac myocyte model that uses moment equations to represent heterogeneous junction sr calcium. Biophys J. 2009;96(Suppl 1):277a. doi: 10.1016/j.bpj.2010.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cheng H, Lederer W, Cannell M. Calcium sparks: elementary events underlying excitation–contraction coupling in heart muscle. Science. 1993;262(5134):740. doi: 10.1126/science.8235594. [DOI] [PubMed] [Google Scholar]
- 44.Stern M, Cheng H. Putting out the fire: what terminates calcium-induced calcium release in cardiac muscle? Cell Calcium. 2004;35(6):591. doi: 10.1016/j.ceca.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 45.DeRemigio H, Smith G. The dynamics of stochastic attrition viewed as an absorption time on a terminating Markov chain. Cell Calcium. 2005;38(2):73. doi: 10.1016/j.ceca.2005.06.007. [DOI] [PubMed] [Google Scholar]
- 46.Mazzag B, Tignanelli C, Smith G. The effect of residual Ca2+ on the stochastic gating of Ca2+-regulated Ca2+ channels. J Theor Biol. 2005;235(1):121. doi: 10.1016/j.jtbi.2004.12.024. [DOI] [PubMed] [Google Scholar]
- 47.Huertas M, Smith G. The dynamics of luminal depletion and the stochastic gating of Ca2+-activated Ca2+ channels and release sites. J Theor Biol. 2007;246(2):332. doi: 10.1016/j.jtbi.2007.01.003. [DOI] [PubMed] [Google Scholar]
- 48.Franzini-Armstrong C, Protasi F, Ramesh V. Shape, size, and distribution of Ca2+ release units and couplons in skeletal and cardiac muscles. Biophys J. 1999;77(3):1528. doi: 10.1016/S0006-3495(99)77000-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Groff J, Smith G. Calcium-dependent inactivation and the dynamics of calcium puffs and sparks. J Theor Biol. 2008;253(3):483. doi: 10.1016/j.jtbi.2008.03.026. [DOI] [PubMed] [Google Scholar]
- 50.Györke I, Györke S. Regulation of the cardiac ryanodine receptor channel by luminal Ca2+ involves luminal Ca2+ sensing sites. Biophys J. 1998;75(6):2801. doi: 10.1016/S0006-3495(98)77723-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Smith G, Keizer J, Stern M, Lederer W, Cheng H. A simple numerical model of calcium spark formation and detection in cardiac myocytes. Biophys J. 1998;75(1):15. doi: 10.1016/S0006-3495(98)77491-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Stern M, Pizarro G, Ríos E. Local control model of excitation–contraction coupling in skeletal muscle. J Gen Physiol. 1997;110(4):415. doi: 10.1085/jgp.110.4.415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sobie E, Dilly K, dos Santos Cruz J, Lederer W, Jafri M. Termination of cardiac Ca2+ sparks: an investigative mathematical model of calcium-induced calcium release. Biophys J. 2002;83(1):59. doi: 10.1016/s0006-3495(02)75149-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wagner J, Keizer J. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys J. 1994;67(1):447. doi: 10.1016/S0006-3495(94)80500-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Brochet D, Yang D, Maio AD, Lederer W, Franzini-Armstrong C, Cheng H. Ca2+ blinks: rapid nanoscopic store calcium signaling. Proc Natl Acad Sci USA. 2005;102(8):3099. doi: 10.1073/pnas.0500059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Shannon R, Guo T, Bers D. Ca2+ scraps: local depletions of free [Ca2+] in cardiac sarcoplasmic reticulum during contractions leave substantial Ca2+ reserve. Circ Res. 2003;93(1):40. doi: 10.1161/01.RES.0000079967.11815.19. [DOI] [PubMed] [Google Scholar]
- 57.Terentyev D, Viatchenko-Karpinski S, Valdivia H, Escobar A, Györke S. Luminal Ca2+ controls termination and refractory behavior of Ca2+-induced Ca2+ release in cardiac myocytes. Circ Res. 2002;91(5):414. doi: 10.1161/01.res.0000032490.04207.bd. [DOI] [PubMed] [Google Scholar]
- 58.Terentyev D, Viatchenko-Karpinski S, Györke I, Volpe P, Williams S, Györke S. Calsequestrin determines the functional size and stability of cardiac intracellular calcium stores: mechanism for hereditary arrhythmia. Proc Natl Acad Sci USA. 2003;100(20):11759. doi: 10.1073/pnas.1932318100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zima A, Picht E, Bers D, Blatter L. Termination of cardiac Ca2+ sparks: role of intra-SR [Ca2+], release flux, and intra-SR Ca2+ diffusion. Circ Res. 2008;103(8):e105. doi: 10.1161/CIRCRESAHA.107.183236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Szentesi P, Pignier C, Egger M, Kranias E, Niggli E. Sarcoplasmic reticulum Ca2+ refilling controls recovery from Ca2+-induced Ca2+ release refractoriness in heart muscle. Circ Res. 2004;95(8):807. doi: 10.1161/01.RES.0000146029.80463.7d. [DOI] [PubMed] [Google Scholar]
- 61.Sobie EA, Song LS, Lederer WJ. Local recovery of Ca2+ release in rat ventricular myocytes. J Physiol. 2005;565(Pt 2):441. doi: 10.1113/jphysiol.2005.086496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sobie E, Guatimosim S, Gómez-Viquez L, Song L, Hartmann H, Saleet Jafri M, Lederer W. The Ca2+ leak paradox and rogue ryanodine receptors: Sr Ca2+ efflux theory and practice. Prog Biophys Mol Biol. 2005;90(1–3):172. doi: 10.1016/j.pbiomolbio.2005.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Duke T, Bray D. Heightened sensitivity of a lattice of membrane receptors. Proc Natl Acad Sci USA. 1999;96(18):10104. doi: 10.1073/pnas.96.18.10104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Duke T, Le Novère N, Bray D. Conformational spread in a ring of proteins: a stochastic approach to allostery. J Mol Biol. 2001;308(3):541. doi: 10.1006/jmbi.2001.4610. [DOI] [PubMed] [Google Scholar]
- 65.Groff J, Smith G. Ryanodine receptor allosteric coupling and the dynamics of calcium sparks. Biophys J. 2008;95(1):135. doi: 10.1529/biophysj.107.119982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Stern MD, Song LS, Cheng H, Sham JS, Yang HT, Boheler KR, Ríos E. Local control models of cardiac excitation–contraction coupling. A possible role for allosteric interactions between ryanodine receptors. J Gen Physiol. 1999;113(3):469. doi: 10.1085/jgp.113.3.469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Izu L, Mauban J, Balke C, Wier W. Large currents generate cardiac Ca2+ sparks. Biophys J. 2001;80(1):88. doi: 10.1016/S0006-3495(01)75997-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Izu L, Wier W, Balke C. Evolution of cardiac calcium waves from stochastic calcium sparks. Biophys J. 2001;80(1):103. doi: 10.1016/S0006-3495(01)75998-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Ramay H, Sobie E, Lederer W, Jafri M. A model of calcium dynamics in the rat ventricular sarcomere. Biophys J. 2004;86(1 Pt. 2 Suppl S):112A. [Google Scholar]
- 70.Ramay HR, Sobie EA, Lederer WJ, Jafri MS. A Monte Carlo simulation study of spontaneous calcium waves in the heart. Biophys J (Suppl S) 2007:257A. [Google Scholar]
- 71.Tan W, Fu C, Fu C, Xie W, Cheng H. An anomalous subdiffusion model for calcium spark in cardiac myocytes. Appl Phys Lett. 2007;91(18):183901. [Google Scholar]
- 72.Fabiato A. Time and calcium dependence of activation and inactivation of calcium-induced release of calcium from the sarcoplasmic reticulum of a skinned canine cardiac purkinje cell. J Gen Physiol. 1985;85(2):247. doi: 10.1085/jgp.85.2.247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Cannell M, Berlin J, Lederer W. Effect of membrane potential changes on the calcium transient in single rat cardiac muscle cells. Science. 1987;238(4832):1419. doi: 10.1126/science.2446391. [DOI] [PubMed] [Google Scholar]
- 74.duBell W, Houser S. Voltage and beat dependence of Ca2+ transient in feline ventricular myocytes. Am J Physiol. 1989;257(3 Pt 2):H746. doi: 10.1152/ajpheart.1989.257.3.H746. [DOI] [PubMed] [Google Scholar]
- 75.Wier W. Voltage dependence of intracellular [Ca2+]i transients in guinea pig ventricular myocytes. Circ Res. 1987;61(1):148. doi: 10.1161/01.res.61.1.148. [DOI] [PubMed] [Google Scholar]
- 76.Rice J, Jafri M, Winslow R. Modeling gain and gradedness of Ca2+ release in the functional unit of the cardiac diadic space. Biophys J. 1999;77(4):1871. doi: 10.1016/s0006-3495(99)77030-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Greenstein J, Winslow R. An integrative model of the cardiac ventricular myocyte incorporating local control of Ca2+ release. Biophys J. 2002;83(6):2918. doi: 10.1016/S0006-3495(02)75301-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Chikando AC, Ramay HR, Sobie EA, Jafri MS. A detailed computational study of calcium dynamics incorporating rogue ryanodine receptors contribution. Biophys J (Suppl S) 2007:137A. [Google Scholar]
- 79.Hinch R, Greenstein J, Tanskanen A, Xu L, Winslow R. A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes. Biophys J. 2004;87(6):3723. doi: 10.1529/biophysj.104.049973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Greenstein J, Hinch R, Winslow R. Mechanisms of excitation–contraction coupling in an integrative model of the cardiac ventricular myocyte. Biophys J. 2006;90(1):77. doi: 10.1529/biophysj.105.065169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hinch R, Greenstein J, Winslow R. Multi-scale models of local control of calcium-induced calcium release. Prog Biophys Mol Biol. 2006;90(1–3):136. doi: 10.1016/j.pbiomolbio.2005.05.014. [DOI] [PubMed] [Google Scholar]
- 82.Williams GSB, Huertas MA, Sobie EA, Jafri MS, Smith GD. A probability density approach to modeling local control of calcium-induced calcium release in cardiac myocytes. Biophys J. 2007;92(7):2311. doi: 10.1529/biophysj.106.099861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Bertram R, Sherman A. Population dynamics of synaptic release sites. SIAM J Appl Math. 1998;58(1):142. [Google Scholar]
- 84.Nykamp D, Tranchina D. A population density approach that facilitates large-scale modeling of neural networks: analysis and an application to orientation tuning. J Comput Neurosci. 2000;8(1):19. doi: 10.1023/a:1008912914816. [DOI] [PubMed] [Google Scholar]
- 85.Huertas M, Smith G. A multivariate population density model of the dLGN/PGN relay. J Comput Neurosci. 2006;21(2):171. doi: 10.1007/s10827-006-7753-2. [DOI] [PubMed] [Google Scholar]
- 88.Williams G, Huertas M, Sobie E, Jafri M, Smith G. Moment closure for local control models of calcium-induced calcium release in cardiac myocytes. Biophys J. 2008;95(4):1689. doi: 10.1529/biophysj.107.125948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.DeRemigio H, Kemper P, LaMar M, Smith G. Markov chain models of coupled intracellular calcium channels: Kronecker structured representations and benchmark stationary distribution calculations. Phys Biol. 2008;5(3):36003. [PubMed] [Google Scholar]
- 90.Hao Y, Kemper P, Smith G. Reduction of calcium release site models via fast/slow analysis and iterative aggregation/disaggregation. Chaos Focus issue: intracellular calcium dynamics – a change of modeling paradigm? 2009;5(3):36003. [Google Scholar]
- 91.Greenstein J, Tanskanen A, WRL Modeling the actions of beta-adrenergic signaling on excitation–contraction coupling processes. Ann N Y Acad Sci. 2004;1015:16. doi: 10.1196/annals.1302.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Saucerman J, McCulloch A. Cardiac beta-adrenergic signaling: from subcellular microdomains to heart failure. Ann N Y Acad Sci. 2006;1080:348. doi: 10.1196/annals.1380.026. [DOI] [PubMed] [Google Scholar]
- 93.Saucerman J, Bers D. Calmodulin mediates differential sensitivity of CamKII and calcineurin to local Ca2+ in cardiac myocytes. Biophys J. 2008;95(10):4597. doi: 10.1529/biophysj.108.128728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Hashambhoy Y, Winslow R, Greenstein J. Camkii-induced shift in model gating explains L-type Ca2+ current facilitation: a modeling study. Biophys J. 2009;96(5):1770. doi: 10.1016/j.bpj.2008.11.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Cortassa S, O’Rourke B, Winslow R, Aon M. Control and regulation of mitochondrial energetics in an integrated model of cardiomyocyte function. Biophys J. 2009;96(6):2466. doi: 10.1016/j.bpj.2008.12.3893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Michailova A, McCulloch A. Model study of atp and adp buffering, transport of Ca2+ and Mg2+, and regulation of ion pumps in ventricular myocyte. Biophys J. 2001;81(2):614. doi: 10.1016/S0006-3495(01)75727-X. [DOI] [PMC free article] [PubMed] [Google Scholar]