SPA-LN: a scoring function of ligand–nucleic acid interactions via optimizing both specificity and affinity

Abstract

Nucleic acids have been widely recognized as potential targets in drug discovery and aptamer selection. Quantifying the interactions between small molecules and nucleic acids is critical to discover lead compounds and design novel aptamers. Scoring function is normally employed to quantify the interactions in structure-based virtual screening. However, the predictive power of nucleic acid–ligand scoring functions is still a challenge compared to other types of biomolecular recognition. With the rapid growth of experimentally determined nucleic acid–ligand complex structures, in this work, we develop a knowledge-based scoring function of nucleic acid–ligand interactions, namely SPA-LN. SPA-LN is optimized by maximizing both the affinity and specificity of native complex structures. The development strategy is different from those of previous nucleic acid–ligand scoring functions which focus on the affinity only in the optimization. The native conformation is stabilized while non-native conformations are destabilized by our optimization, making the funnel-like binding energy landscape more biased toward the native state. The performance of SPA-LN validates the development strategy and provides a relatively more accurate way to score the nucleic acid–ligand interactions.

INTRODUCTION

Nucleic acids (DNA and RNA) have been recognized not only to store and transfer genetic information, but also play important roles in many other biological processes in the cell (1,2). Functional nucleic acids, such as riboswitches, ribozymes and non-coding RNAs, are increasingly identified as potential drug targets (3–5). It has been realized that targeting nucleic acids with small molecules is an promising area in both therapeutics and biotechnology (6–8). In addition, nucleic acid aptamers have attracted growing interests in the applications of biosensing, diagnostics and therapeutics due to their advantages in molecular recognition and chemical synthesis (9,10). The past decade witnessed an rapid increase of determined nucleic acid structures (11,12). This provides an opportunity to apply structure-based virtual screening approaches for the discovery of nucleic acid binders as well as novel aptamers, as an alternative to the expensive and time-consuming high-throughput screening in vitro.

The scoring function is the heart of structure-based virtual database screening (13,14). Computationally, both nucleic acids-based drug discovery and aptamer selection demand a scoring function to quantify the nucleic acid–ligand interactions. Compared to progresses in predicting protein-ligand interactions, however, much less effort has been devoted in developing scoring functions of the nucleic acid–ligand interactions. The predictive power of nucleic acid–ligand scoring functions and its general applicability are urgently needed to be improved (15–17). This is partially due to the limited structural information of native nucleic acids–ligand complexes to learn the energetic rules. On the other hand, the development and improvement of algorithms for optimizing nucleic acid–ligand scoring functions are also urgently needed compared to the progress of protein–ligand scoring functions.

The binding of a ligand onto the nucleic acid is similar as other types of biomolecular recognition which requires both stability and specificity to accomplish the selective recognition and specific function (9,18,19). The stability is directly determined by the binding affinity while the specificity is determined by the discrimination of preferred binding partners against competitive ones. The specificity is critical for designing new ligands selectively binding onto their own targets rather than other competitive receptors (20–24). Thus, an accurate scoring function should aim not only to quantify the binding affinity but also discriminate the specific binding partners against non-specific ones. This requires that the optimization strategy of scoring function is designed to maximize the preference of forming specific complexes while minimize the preference of forming competitive complexes which are probably formed by competitive biomolecules. Previous scoring functions of nucleic acid–ligand interactions were developed by optimizing only the binding affinity rather than both specificity and affinity (15,16,25,26). This limitation was resulted from the difficulty in quantifying the specificity for the optimization since the specificity is not known experimentally and challenge to compute with limited structural information.

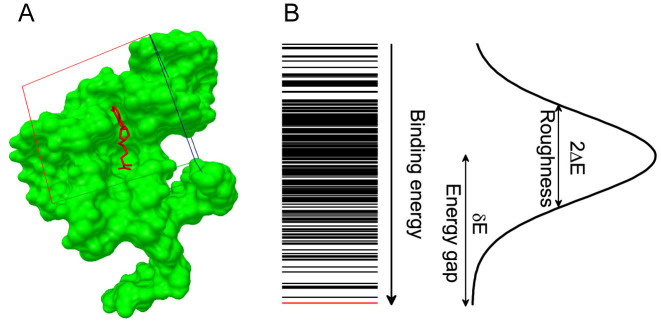
In light of the concept of intrinsic specificity, the binding specificity refers to the discrimination of native binding mode against other non-native binding modes of the same complex. The binding process is physically visualized as a funnel-shaped energy landscape toward the native binding mode with many other non-native binding modes along the downhill binding paths (18,21,23,27). The intrinsic specificity ratio (ISR) was defined to quantify the magnitude of intrinsic specificity based on the topography of the binding energy landscape (Figure 1). ISR provides an quantitative indication in discrimination of the native binding mode against the non-native binding ones. It is in equivalence of discriminating specific complex against competitive ones provided that the receptor is large enough for ligand binding (21,23,24) so that all types of interactions are encountered. In this way, exploring recognition through different sequences (competitive targets) and different conformations of the complex is approximately equivalent. With the quantification of specificity, it is important to design a development strategy which couples the affinity and specificity for optimizing the scoring function of nucleic acid–ligand interactions (23,28–30).

Figure 1.

Quantification of binding specificity. (A) Representative nucleic acid–ligand binding complex (PDB ID: 3NPN) with the RNA structure shown in molecular surface and the ligand shown in sticks, the native pose of the ligand is colored in red and the conformation ensemble is distributed within the docking box covering the binding pocket as well as its surrounding surface. (B) Binding energy spectrum for the conformation ensemble, the line for native conformation is colored in red. The binding energy of the conformation ensemble follow a statistical Gaussian-like distribution, from which the binding specificity is quantified with the dimensionless intrinsic specificity ratio (ISR) by 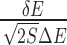(18,21,23,27). The energy gap (δE) is computed with <E > −E_N and the energy fluctuation or roughness (ΔE) is computed with , E_N is the binding energy of the native conformation and S is the conformational entropy of the ligand.

In this work, we developed a knowledge-based scoring function named as SPA-LN by optimizing both specificity and affinity of ligand–nucleic acid interactions. The scoring function was iteratively optimized based on the requirement that the stability and specificity of the native binding conformation are sufficiently favored among the binding conformation ensemble. SPA-LN was tested on the benchmark dataset and compared with some other nucleic acid–ligand scoring functions. The performance of SPA-LN validates the development strategy, this allows it to be implemented into the docking software and used in the virtual screening for discovering lead compounds of nucleic acid targets.

MATERIALS AND METHODS

Construction of training dataset

The reliability of structural information is crucial for the derivation of the knowledge-based scoring function. To obtain a relatively high-quality dataset of nucleic acid–ligand complexes for training, the training dataset of nucleic acid–ligand complexes were selected and compiled according to a series of criteria. First, only complex structures with nucleic acids (including DNA, RNA or hybrid) and ligands were selected from the PDB (Protein Data Bank) (31). Second, the structures with X-ray resolutions larger than 3.0Å were removed. Third, the structures having metal atoms in the ligands or receptors were removed due to that the occurrence of metal atoms are infrequent to derive knowledge-based atomic pair potentials. Fourth, the structures overlapped with our testing dataset were removed. Finally, 437 nucleic acid–ligand complexes were remained as the training dataset (Supplementary Table S1).

Generation of docking decoys

As discussed, the aim of the optimization is not only to stabilize the native conformation but also discriminate the native conformation against non-native conformations. This requires sufficient sampling of the conformational space to explore underlying binding energy landscape. Except for the native conformation obtained from experimentally determined PDB structure, conformational decoys were generated by molecular docking with AutoDock4.2(32). The conformational decoys were sampled aiming to represent all possible conformations other than the native conformation of the crystal structure. Given different sizes of the ligands, the edges of the grid box for ligand docking were set to be five times as the radius of gyration of the native conformations of the ligands. The geometric center of the ligand coordinates from the native conformation was taken as the center of the grid box with a grid spacing of 0.375Å. Lamarckian genetic algorithm was employed to search the conformational space. The ligand was set to be flexible with its rotatable bonds. For each nucleic–ligand complex, 1000 docking runs were conducted, this led to a conformation ensemble with 1000 decoys for each nucleic acid–ligand complex.

Derivation of knowledge-based statistical potentials

Knowledge-based statistical potentials in essence are a set of discrete distance-dependent atom-pair potentials (33). In general, the initial statistical potentials are extracted from the available structures with widely used reverse Bolzmann relation. That is

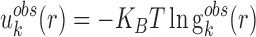(1)

where K_B and T are the Boltzmann constant and absolute temperature respectively. K_BT is the same (room temperature) for all types of knowledge-based pair potentials, thus, it is set to be unit for simplifying the computation. 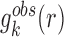is the observed distance distribution function of atomic pair k from the experimentally determined nucleic acid–ligand complex structures in the training dataset, it is derived through

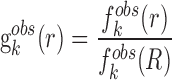(2)

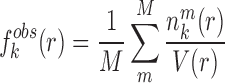(3)

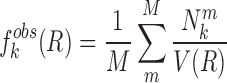(4)

where 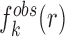represents the observed number density of atomic pair k within a spherical shell ranging from radius r to r+Δr. It is extracted from the structural coordinates of M nucleic acid–ligand complexes. 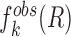is the number density within the reference sphere where no interactions are assumed to occur between atoms. The reference state is based on the approximation that the atom-pair k is uniformly distributed in the sphere of the reference state (34,35). 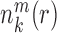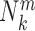and are the occurred numbers of atomic pair k within the spherical shell and the reference sphere for nucleic acid–ligand complex m, and 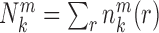. 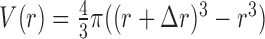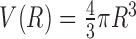and are the volumes of the spherical shell and the reference sphere, where Δr is the thickness of each spherical shell and R is the radius of the sphere.

Based on the equations above, the atomic pair potentials were directly computed from M (=437) nucleic acid–ligand complexes of training dataset (Supplementary Table S1). In terms of the classification of atom types by SYBYL (36), 16 atom types were employed to represent the heavy atoms involved in nucleic acid–ligand interactions (Supplementary Table S2). OpenBabel (37) was used to generate these atom types from PDB files. In the computation, Δr and R were set as 0.3Å and 7.0 Å, respectively, resulting in 16 spherical shells from the shortest radius 2.2Å. In order to remove the statistically insufficient occurrences of atomic pairs, a threshold (=100) of total occurrences for atomic pair k (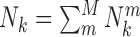) was employed. 75 effective types of atomic pairs were remained for the nucleic acid–ligand interactions (Supplementary Table S3). For the effective types of atomic pairs, if there is no occurrence in a particular spherical shell, the corresponding pair potential was replaced by the van der Waals interaction within this shell, which often happens in the first shell where repulsion is dominant.

Computation of binding affinity and specificity

With the atomic pair potentials, the binding affinity and specificity (quantified by ISR) can be readily computed for each conformation (Figure 1). The binding affinity was represented with the energy score by summing up the inter-molecular atomic pair potentials among the interface of nucleic acid–ligand conformation. That is

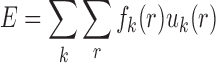(5)

where f_k(r) is the occurrence frequencies of the atomic pair k between distance r and r + Δr. The ISR (Figure 1) was computed by

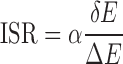(6)

where δE is the difference between the energy of the chosen conformation and the average energy of the conformation ensemble including the native conformation and the decoys, ΔE is the energy fluctuation or the width of the energy distribution of conformation ensemble. α is a scaling factor for the effect of the entropy on the specificity. Normally, the conformational entropy is evaluated by the number of degrees of the freedom which includes translation, orientation, rotation of the whole ligand and the flexibility inside the ligand. The first three degrees of freedoms are the same for each ligand when moving. The flexibility is determined by the number of rotatable bonds of the ligand. The flexibility directly depends on the chemical feature of the ligand itself. Each ligand has a fixed number of rotatable bonds which can not be manually adjusted. Thus, the conformational entropy is computed here with the number of rotatable bonds of the ligand (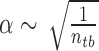). The magnitude of ISR gives a quantitative measure of the native binding mode against other competitive binding modes or decoys.

Optimization of statistical potentials

Knowledge-based statistical potentials are based on the assumption of the reference state where atoms are randomly disconnected and atomic pair interactions are independent (34,38). This ideal assumption doesn’t always reflect the reality of the excluded volume, sequences and connectivity for the nucleic acid–ligand interactions. Different methods have been developed to circumvent the reference state problem by optimizing observed knowledge-based statistical potentials (16,35,39–42). Our recent studies proposed a way to improve the statistical potentials by taking both affinity and specificity into account. The strategy is to obtain the expected potentials which not only stabilize the native conformation but also discriminate against non-native conformations, mimicking the energetic rules that enable stable and specific complexes in nature.

The expected statistical potentials are computed with similar form as the observed statistical potentials while the expected atomic pair distribution function is extracted from the conformation ensemble including the native and non-native conformations. That is

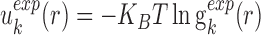(7)

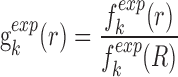(8)

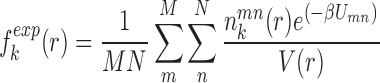(9)

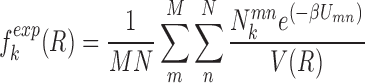(10)

where M is the number of native complexes in the training dataset, N is the number of total conformations including the native conformation and non-native decoys for each complex. m and n are the complex index and conformation index, respectively. β is a constant analogous to the inverse of temperature. The potentials are expected to favor the native conformation over the decoy conformations. This results in the population of the native conformation dominating in the conformation ensemble according to the Boltzman distribution. Thus, the expected number density of atomic pair k was computed with Boltzmann-averaged weighting (28,35,42). The weighting factor U_mn couples the affinity and specificity in our optimization, which is given by

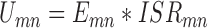(11)

To improve the expected atomic pair potentials, the iterative method (35) was utilized to perform the optimization. It is realized by

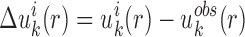(12)

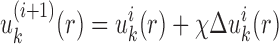(13)

Equations (5 6) and Equations (7 11) were iteratively updated with the differenc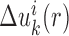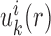e . (i.e. 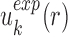) starts from i=0 and χ controls the speed of the convergence and was set as 0.1.The iterative procedure was repeated until the success rate of identifying the native or near-native conformation converges. The optimized scoring function of nucleic acid–ligand interactions is from the final set of the expected pair potentials, i.e. SPA-LN.

Validation of SPA-LN

Normally, the performance of a novel scoring function should be tested on the benchmarks. For the testing of the SPA-LN, the well-complied benchmark dataset of nucleic acid–ligand complexes from version 2014 of PDBBind database (43) were taken as the testing dataset 1 (Supplementary Table S4). It is a collection of nucleic acid–ligand complexes which contain both experimentally determined structures and affinities. The benchmark can be readily employed for evaluating the performance of SPA-LN in 2-fold: the ability to predict the binding affinity and the ability to identify the native pose. The ability of predicting binding affinity is quantified by the Pearson correlation between the computed and experimental affinities. That is

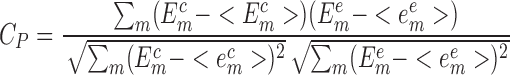(14)

where m represents the index of nucleic acid–ligand complexes in the testing dataset, 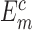and 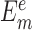are computed and experimental binding affinities. The ability to predict the native pose is defined by the success rate of identifying the top-scored conformations within a RMSD threshold as native or near-native poses out of the decoy ensemble. It is given by

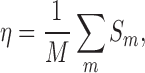(15)

S_m equals 1 for the complex m once at least one of the top-scored conformations has RMSD lower than the threshold value, otherwise it is 0. The binding decoys for each complex of the testing dataset 1 were generated as done for the training dataset.

In addition, the performance was validated by comparing to other nucleic acid–ligand scoring functions listed in an evaluation literature (15). The literature performed comparative assessment of 11 different scoring functions implemented in 5 docking software. As done in this literature, the criteria to evaluate the ability of identifying the native pose is represented by C(X,Y), i.e. at least one of top X ranked poses is under the threshold RMSD value Y.

RESULTS AND DISCUSSION

Convergence of the optimization

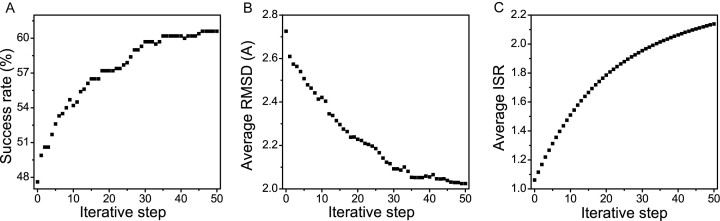
The optimization of the scoring function was carried out on the training dataset and the strategy of optimization is to improve the performance on correctly predicting interactions and poses of native conformations of the training dataset. The success rate of identifying the best-scored conformation as the native or near-native conformation (RMSD ≤ 1.5Å) is taken to validate the effectiveness of the optimization. As shown in Figure 2A, the success rate increases and converges well within 50 iterative steps, indicating that the performance of the scoring function was improved by the iteration. In other words, the stability of native or near-native conformations is enhanced after optimization. This is validated by the average RMSD of best-scored conformations in Figure 2B. The best-scored conformations become more native or near-native as the average RMSD decreases via optimization.

Figure 2.

Optimization of the scoring function via iterative method. (A) Success rate of identifying the the best-scored pose as the native or near-native conformation. (B) Average RMSD of the top-scored poses. (C) Average ISR of the native conformations.

Different from previous methods (16,17,25,26) which only focused on the improvement of accuracy in computing the binding affinity of nucleic acid–ligand interactions, binding specificity quantified by the ISR was incorporated in the optimization. It can be seen that the average ISR value of the training dataset was increased by the optimization (Figure 2C). This suggests that the native conformations become more discriminated against the decoy ensembles and binding energy landscape becomes more funneled toward the native binding mode. The increase of ISR value also indicates that the competitive binding modes are suppressed, smoothing the energy funnel (18,27,44). Thus, the optimization satisfies the requirement that the stability of the native conformation is enhanced while the stabilities of the non-native conformations are weakened.

As described, the native conformations of the training dataset are directly obtained from the X-ray crystal structure while the non-native conformations were generated by the docking tool AutoDock4.2 (32). The reason to choose AutoDock 4.2 as the docking tool in our work is based on several aspects. First of all, except AutoDock and rDock (17), most of the docking tools were originally designed to docking small molecules to proteins rather than nucleic acids. Second, AutoDock is the most popular one among a large number of docking tools. It is well known and widely recognized in the research community. Third, AutoDock is an open-source tool and has well-maintained tutorial documents and forum on the website (http://autodock.scripps.edu/). Whereas, the docking tool is just the conformation generator aiming to sample all possible conformations. Different docking tools can give similar answers if enough conformations are sampled to explore the underlying binding energy landscape. In this sense, the optimization of scoring function should be less sensitive to the docking tools. To validate this point, the alternative docking tool rDock (17) was used to generate another set of 1000 decoys for each nucleic acid–ligand complex of the training dataset. The procedure of docking with rDock was conducted in three steps as introduced in the website (http://rdock.sourceforge.net/docking-in-3-steps/). The scoring functions optimized based on the decoys generated by AutoDock4.2 were applied on the decoys generated by rDock. It can be seen that the optimization has similar effect as Figure 2 on the decoy conformations generated by rDock (Supplementary Figure S1). This validates the robustness of the optimization on the decoys generated by different docking tools, i.e. the convergence of the optimization is intrinsically dependent on the underlying binding energy landscape which is unique for each nucleic acid–ligand complex.

Test of SPA-LN

The scoring function is often used in structure-based drug discovery for seeking the lead compounds from the large database of the small molecules and identifying specific targets. This requires that the scoring function needs to not only accurately predict the binding affinity but also correctly discriminate the native pose (or ligand) against non-native ones. Thus, the performance of SPA-LN was tested by the ability in predicting the binding affinity and bind pose.

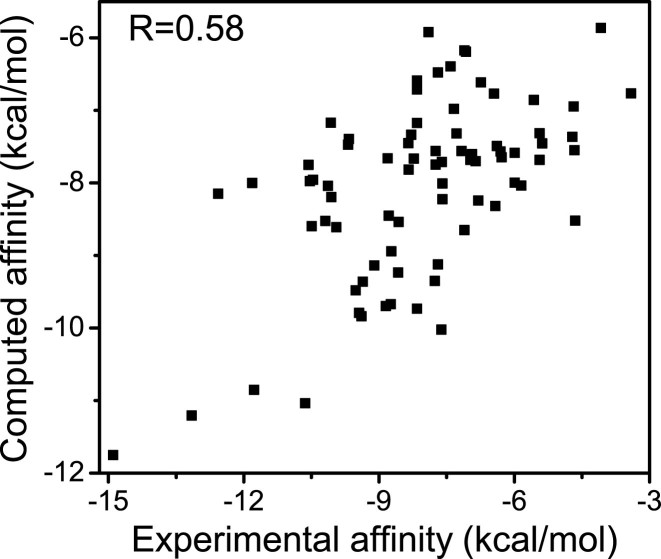
The performance of predicting the binding affinity is reflected by reproducing experimental determined affinities. Pearson correlation between the computed affinities predicted by SPA-LN and experimental affinities of the benchmark is shown in Figure 3. The correlation coefficient (R = 0.58) is high compared to those predicted by other scoring functions (see Table 1) (15). This suggests that SPA-LN is relatively accurate in predicting the binding affinities. It is noting that the performance of SPA-LN is still modest compared to the predictions of some protein–ligand scoring functions (30,45). The limited number of available high-quality nucleic acid–ligand complex structures could be one of the main obstacles for improving the knowledge-based scoring functions.

Figure 3.

Pearson correlation between computed affinities and experimental affinities for 77 nucleic acid–ligand complexes of the testing dataset. The correlation is 0.58 with statistical significance P < 0.001.

Table 1. Performance of nucleic acid–ligand scoring functions in predicting binding affinities and identifying the native pose.

Scoring function	Affinity prediction	Pose identification(%)
	Correlation (R2)	C(5, 3.0)	C(3,1.5)
SPA-LN	0.33	76.62	50.64
Gold Fitness@GOLD5.0.1	0.25	73.21	42.86
ChemScore@GOLD5.0.1	0.03	53.57	23.21
ASP@GOLD5.0.1	0.29	66.07	42.86
AutoDock4.1 Score@AutoDock4.1	0.22	30.36	17.86
Surflex-Dock Score@Surflex 2.415	0.05	44.64	26.79
GlideScore (SP)@Glide 5.6	0.10	53.57	28.57
Emodel (SP)@Glide 5.6	0.14	55.36	28.57
GlideScore (XP)@Glide 5.6	NA	35.71	23.21
Emodel (XP)@Glide 5.6	NA	33.93	23.21
rDock@rDock 2006.2	0.15	60.71	33.93
rDock_solv@rDock 2006.2	0.18	73.21	41.07

The performance of predicting the binding pose is reflected by the success rate of identifying near-native poses mimicking known experimental structure. The success rate predicted by SPA-LN is compared to other scoring functions (Table 1). SPA-LN achieves 76.62 and 50.64% successes for the loose criterion C(5, 3.0Å) and the stringent criterion C(3, 1.5Å ) (C(X,Y) means that at least one of the top X ranked poses has RMSD under the threshold RMSD value Y). As expected, SPA-LN ranks best among the compared scoring functions whenever the loose criterion or the stringent criterion was imposed. This suggests that SPA-LN also has relatively high capability in characterizing the binding specificity by discriminating native or near-native poses against non-native ones. The collective advantages of SPA-LN in both predictions of binding affinity and pose (Table 1) validates the effectiveness of our development framework coupling the specificity and affinity together. It also provides a promising direction in improving available nucleic acid–ligand scoring functions.

In addition, another two sets of benchmarks with smaller number of nucleic acid–ligand complexes were employed to evaluate the performance of SPA-LN, here named as testing dataset 2 (Supplementary Table S5) (15) and testing dataset 3 (Supplementary Table S6) (17). As done in the previous literatures, testing dataset 2 was used to validate the ability of affinity prediction and testing dataset 3 was used to validate the ability of native pose identification. SPA-LN achieved correlation coefficient of R = 0.60 between the computed and experimental affinities for the testing dataset 2 (Supplementary Figure S2) and success rate of 54% in identifying the native pose for the testing dataset 3 (Supplementary Table S7). The evaluation results for testing dataset 2 and 3 are consistent with those for the testing dataset 1 and further validate the performance of SPA-LN.

Performance illustration with examples

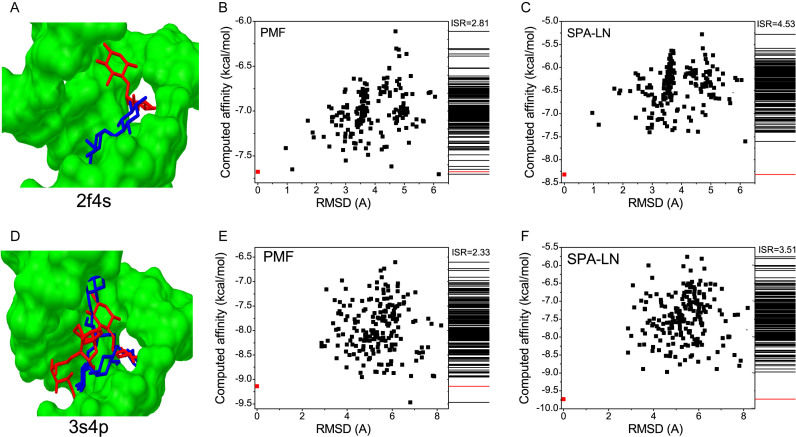
SPA-LN is optimized based on PMF (potential of mean force) directly extracted from available structures by the widely used inverse Boltzmann relation as Equation 1. In order to show how the performance of SPA-LN was improved by the optimization, the performance of predicting the native pose was compared between SPA-LN and PMF for the testing dataset (Supplementary Table S8). As shown in Figure 1A, the best-scored conformation is considered to be native or near-native pose if its RMSD value is smaller than the RMSD threshold value (=1.5Å). Under this criterion, SPA-LN achieves 51 successful cases among the testing dataset 1 while PMF achieves 46 successful cases. There are 45 overlaps between them except the case 2ku0 successfully predicted by PMF. There are 6 cases for which SPA-LN succeeds but PMF fails to identify the best-scored pose as the native one (Supplementary Table S8). Among all the seven cases, the two cases (3s4p and 2f4s) were chosen to illustrate the improvement of SPA-LN over PMF since their RMSD deviations of the best-scored conformations predicted by PMF are large (>6.0Å). The best-scored conformation with large RMSD to the native or near-native conformation means that there could be a highly competitive state (or binding pocket). The competitive conformations can be predicted falsely as best-scored conformations by scoring functions.

In Figure 4, the conformation-energy relations are shown for these two cases. For both cases, the binding sites consist of competitive pockets which are occupied by the native pose and competitive pose as shown in Figure 4A and D. Competitive conformations as local minima are dominant in energetics when the conformations are scored by PMF (Figure 4B and E). Whereas, the competitive conformations are suppressed in energetics by the scoring of SPA-LN. It indicates that SPA-LN stabilizes the native conformation and makes the competitive conformations less favorable in energetics (Figure 4C and F). Moreover, the ISR values of two cases are increased when scored by SPA-LN, suggesting that the optimization smoothes funnel-like binding energy landscape toward the native conformation. The performance of SPA-LN over PMF validates the optimization strategy of SPA-LN which not only stabilizes the native pose but also minimizes the stabilities of non-native conformations. The coupling of the affinity and specificity in the optimization improves the performance of SPA-LN by stabilizing the native state as well as discriminating the native state against competitive states.

Figure 4.

Performance improvement of SPA-LN over PMF. (A and D) The structure of the ligand binding onto the pocket of nucleic acid, the nucleic acid in green is shown in molecular surface, the pose of the ligand is shown in sticks. The pose (native pose) in red is predicted by SPA-LN and the the pose in blue is predicted by PMF. (B and E) Energy-conformation relation and the spectrum of binding affinities for the conformation ensemble computed by PMF, the native pose is colored in red. (C and F) Energy-conformation relation and the spectrum of binding affinities for the conformation ensemble computed by SPA-LN, the native pose is colored in red.

CONCLUSION

In summary, we developed a knowledge-based scoring function SPA-LN. Different from previous scoring functions for quantifying nucleic acid–ligand interactions, the optimization strategy of SPA-LN couples the improvement of both binding affinity and specificity which are two essential ingredients of biomolecular recognition. The funnel-like binding energy landscape becomes more smoothed and biased toward the native state via optimization, making the native conformation dominant in distribution. By testing on the benchmark dataset, SPA-LN achieves relatively high accuracy in predicting binding affinities and in identifying the native poses compared to other scoring functions. The good performance of SPA-LN is resulted from the improvement over PMF in stabilizing the native conformation as well as destabilizing the non-native conformations. Our development strategy of SPA-LN also provides a feasible approach in seeking and designing nucleic acid inhibitors and aptamers by considering both the specificity and affinity.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Ministry of Science and Technology of China [2016YFA0203200 to J.W., 2013YQ170585 to J.W.]; National Natural Science Foundation of China [91430217 to J.W., 21403208 to Z.Q.Y.]; National Science Foundation [NSF-PHY-76066 to J.W.]. Funding for open access charge: National Natural Science Foundation of China [21403208].

Conflict of interest statement. None declared.