Statistical analysis of genetic interactions in Tn-Seq data

Abstract

Tn-Seq is an experimental method for probing the functions of genes through construction of complex random transposon insertion libraries and quantification of each mutant's abundance using next-generation sequencing. An important emerging application of Tn-Seq is for identifying genetic interactions, which involves comparing Tn mutant libraries generated in different genetic backgrounds (e.g. wild-type strain versus knockout strain). Several analytical methods have been proposed for analyzing Tn-Seq data to identify genetic interactions, including estimating relative fitness ratios and fitting a generalized linear model. However, these have limitations which necessitate an improved approach. We present a hierarchical Bayesian method for identifying genetic interactions through quantifying the statistical significance of changes in enrichment. The analysis involves a four-way comparison of insertion counts across datasets to identify transposon mutants that differentially affect bacterial fitness depending on genetic background. Our approach was applied to Tn-Seq libraries made in isogenic strains of Mycobacterium tuberculosis lacking three different genes of unknown function previously shown to be necessary for optimal fitness during infection. By analyzing the libraries subjected to selection in mice, we were able to distinguish several distinct classes of genetic interactions for each target gene that shed light on their functions and roles during infection.

INTRODUCTION

Tn-Seq is an experimental method for probing the functions of genes through construction of complex random transposon insertion libraries and quantification of each mutant's abundance using next-generation sequencing (1). High-density mutagenesis of a bacterial chromosome by transposons such as the Mariner Himar1 element (2) produces a pool of mutants, each with an insertion at a different locus. Insertion of this >1353 bp element into an open reading frame (ORF) creates non-functional alleles that are marked by the insertion sequence. Amplification and deep-sequencing of the transposon–chromosome junctions present in a complex mutant pool allows the relative abundance of each mutant to be accurately quantified (1,3). The most common application of Tn-Seq involves exposing a single mutant library to different selective conditions to identify mutants with altered fitness. These simple studies rely on pairwise comparisons between differentially-selected mutant pools, and methods for these analyzes are well developed (4–7).

In addition to identifying conditionally essential genes, Tn-Seq has also been used to discover genetic interactions, which can reveal networks of functionally related genes that participate in related pathways or complexes (8). A genetic interaction experiment is conducted by creating a transposon insertion library in a null mutant (knockout (KO) strain) for a gene of interest, and then identifying transposon mutants whose abundance changes compared to a wild-type (WT) strain. There are several different types of genetic interactions that each imply a different type of functional interaction (8,9). Transposon insertions that specifically decrease fitness in the mutant background are termed ‘aggravating’ (or synergistic) and could imply redundant functionality between the two mutated genes (e.g. duplicate pathways). Two mutations that both decrease fitness but have a less than additive effect are termed ‘alleviating’ (or antagonistic) and could imply functional coupling between the mutated genes (e.g. a shared pathway). Finally, ‘suppressive’ (or masking) mutations reverse the fitness defect caused by the initial mutation, which could indicate a variety of relationships, including regulation and detoxification. While genetic interaction networks have been discovered by pairwise comparison of transposon pools generated in distinct genetic backgrounds (10), existing analytical strategies (such as identification of genes with significantly different insertion counts by a permutation test; (7)) have several limitations. Firstly, differences in transposon mutant representation between libraries can occur stochastically during library generation, and pairwise comparisons in a single condition of interest are unable to discriminate between these differences in background and those that were due to subsequent selection. Secondly, alleviating and suppressive interactions need to be distinguished, as genes exhibiting either type of interaction will tend to have Tn insertions that are more abundant in the mutant library compared to the WT library.

Genetic interaction studies require a four-way experiment designed to specifically assess the relative change in Tn mutant abundance between libraries during a defined period of selection. The genes of interest are those that exhibit a statistically significant change in enrichment that can be ascribed to the difference in genetic backgrounds. There are several existing analytical methods that could be applied for this purpose. The approach described by van Opijnen et al. (8) is to calculate individual fitness scores, W_i, at each insertion site in a gene, and then to test the difference in fitness between the KO strain to WT using a t-test. However this approach could be overly sensitive due in part to how it calculates these ratios. Due to the stochastic nature of insertions, datasets often do not have insertions in the same location (particularly between different libraries). These could lead fitness ratios to appear different when insertions do not happen to coincide across datasets. In addition, the frequentist nature of the t-test depends too heavily on the observed counts without incorporating other (prior) information about the variability of read-counts. One could also imagine applying methods originally developed to identify differentially expressed genes in RNA-Seq experiments. For example, limma (11) is a widely-used tool (R package) that uses generalized linear models (GLM) for analyzing DNA microarray data (and similarly, edgeR (12) for RNA-Seq). The assumption is that the strain and conditions are two orthogonal factors that can be used to explain gene expression levels, and the relative contribution of each can be determined by fitting coefficients (like slopes) in a linear regression, which can be tested for significance using a t-statistic. However, it is not straight-forward to apply these RNA-Seq analysis methods to Tn-Seq data. One important difference between RNA-Seq and Tn-Seq data is that Tn-Seq generally contains observations at multiple insertion sites within a gene, and it is not clear how best to treat these in methods intended for RNA-Seq. Several recent Tn-Seq methods that rely on edgeR for statistical calculations (4,13) simply sum the counts across all the TA dinucleotide sites in a gene, but this approach loses information about site-specific variations in abundance levels and reduces the number of observations. In doing so, it cannot distinguish between a gene with 1 or 20 TA sites, and must rely on the variability among replicates to evaluate significance of differences in enrichment.

In this work, we develop a Bayesian method for analyzing data from genetic interaction experiments and validate it by defining genetic interactions in Mycobacterium tuberculosis (Mtb) that are involved in this pathogen's adaptation to the host environment. Previous genome-wide transposon mutant screens in Mtb have defined sets of genes that are essential for optimal growth under different conditions (14,15). Similar to other bacteria, 10–15% of ORFs in the genome of Mtb are necessary for survival in axenic laboratory media (16), and therefore Tn insertions in these genes are not present in random libraries. An additional subset of ∼200 genes in Mtb is specifically required for survival during growth in mouse tissues (17). While the genes necessary for in vitro growth are common to other bacteria, and are comparatively well annotated, a large fraction of the genes specifically necessary for infection are specific to mycobacteria and have not been assigned to functional pathways. Using our novel analytical approach, we show that several of these ‘virulence genes’ can be confidently associated with genes of known function through genetic interaction mapping, providing insight to their function and a strategy to ultimately delineate the functional pathways necessary for infection.

MATERIALS AND METHODS

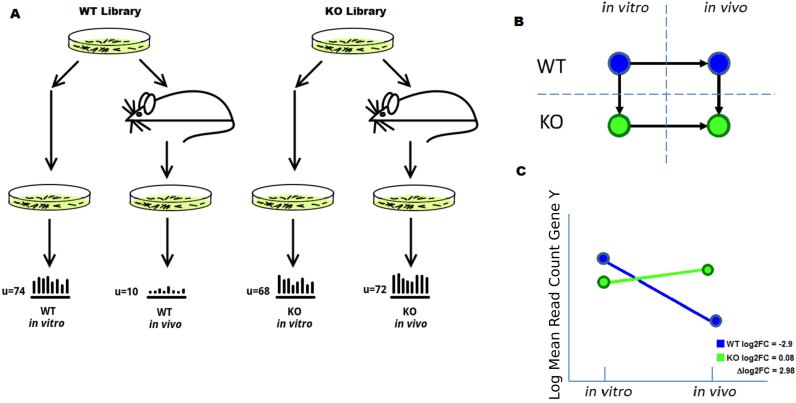
In order to apply Tn-Seq to the discovery of genetic interactions for target genes, an analysis that accurately defines genetic interactions must satisfy two criteria. First, it must specifically identify mutants with altered fitness during a period of selection, so pre-existing differences in library composition are discounted. Second, the change in relative abundance of each mutant during the selection must be assessed, in order to discriminate between alleviating and suppressing interactions. To achieve this, we designed an experimental strategy in which two libraries are compared in two conditions (e.g. a condition of interest, like a stress condition or passaging in vivo, and a reference condition, like growth on rich medium) and assessing the significance in the change in enrichment (Figure 1A). The enrichment of a single library between two conditions is typically calculated as log-fold-change (log FC = log₂(c_B/c_A), where c_B are the insertion counts for the condition of interest, and c_A are the counts observed in the reference condition). The genes that form genetic interactions with the knocked-out gene of interest are defined as those that exhibit a significant change in enrichment, defined as Δlog FC = log FC^KO − log FC^WT. Thus the experiment requires collecting four datasets in total—the WT and KO libraries each evaluated before and after selection—and then performing a four-way comparison by calculating Δlog FC to rank genes and identify potential genetic interactions (Figure 1B). Our approach can be conceptualized as comparing the ‘slopes’ defined by the relative abundance of each mutant before and after the period of selection, as illustrated in Figure 1C.

Figure 1.

Diagram of experimental setup. (A) Tn mutant libraries are constructed for two strains, wild-type (WT) and a knockout strain (KO) for a gene of interest. Each library is grown in two conditions (e.g. in vitro and in vivo) and sequenced, and the read-counts are determined for each. (B) Illustration of the multiple ways the resulting read-counts can be compared (arrows). Pairwise analyzes are limited to comparing only one pair of datasets at a time. (C) Analysis of the log2FC (which can be thought of as comparing the slopes between the counts) provides a way to compare insertions counts of gene Y in a KO of gene X across both condition and strain at the same time.

A significant challenge in the analysis of Tn-Seq data is the assessment of statistical significance of observed changes. There is typically a great deal of intrinsic variability in read-counts in Tn-Seq experiments, which can be attributed to various sources of noise/stochasticity, making it inappropriate to use observed log-fold-changes directly. Instead, it is necessary to treat log-fold-changes based on observed counts as only samples and use them to estimate true effects (in a Bayesian sense). In the case of genetic interaction experiments, a statistical test is needed to determine which Δlog FCs resulting from a four-way comparison are significant.

Assumptions of the model

As in most Tn-Seq analyzes, our model rests on the following assumptions. Insertions occur randomly at candidate insertions sites throughout the genome (e.g. restricted to random TA dinucleotides for Himar1 (2)). We assume abundance of mutants in the library reflects relative fitness (i.e. insertions that result in growth defects will lead to decreased abundance of the mutant in the population due to slower growth rates) (3). Read-counts proportionally reflect abundance of mutants in the library (having sufficient sequencing depth helps to ensure sampling of low-abundance clones) (8). To the extent that the library is unsaturated, the representation of neutral (non-essential) insertion sites is stochastic (Bernoulli, in the sense that whether each neutral site is represented in the library is equally probable). We also assume differences in sequencing depth or number of generations of expansion of the mutant populations have already been accounted for through normalization (5,7,18). Position-specific effects, such as those caused by chromosomal distortion are assumed to have been normalized (e.g. through normalization techniques such as Locally Estimated Scatterplot Smoothing or LOESS (19)) if not relevant to the desired comparison. Other effects like regions that are difficult to sequence, presence of essential and non-essential protein domains, or tolerance of insertions at ORF termini (15), are assumed to affect conditions equally.

Test for statistical significance of changes in enrichment

To determine which genes exhibit a significant change in enrichment (Δlog FC ) at two time points (before and after selection) between two libraries generated in different genetic backgrounds (e.g. WT and KO), we take a Bayesian approach by estimating the posterior distribution over this unknown quantity for each gene, and then evaluating if it is significantly different than zero (implying no change due to the knocked-out gene). Correct estimation of the variance of Δlog FC is critical to properly determining statistical significance. The variance of Δlog FC depends on the variance of the log FC values for each strain (KO and WT), requiring estimation of the distribution of individual log FCs. The variability of this value is ultimately derived from the observed variability of the insertion counts in a given gene and condition.

Let 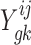represent the read-count for the k-th TA site in gene g, in a dataset of strain i under condition j. The log-fold-change in the mean read-count for gene g in strain i is represented by the random variable 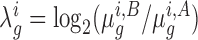, where A and B are the two conditions of interest (such as in vitro and in vivo). Importantly, note the log-fold-change is a function of the means (or expected counts) in each condition, 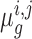. These are unknown parameters that must be estimated from the counts observed in the experiment.

Consistent with a Bayesian view, rather than choosing particular values for the means (such as the maximum likelihood estimates), we instead model the distributions over these parameters by combining the data with priors and obtaining a distribution for each 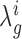by integrating out these unknowns (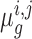). Assuming dependence on some hyperparameters θ (to be defined later), the posterior distribution over the log-fold-change, 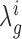, can be expressed as a double-integral, marginalizing over the unobservable parameters:

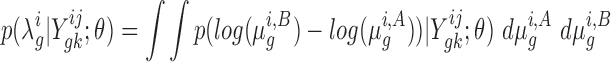(1)

The distribution of log-fold-changes depends on the posterior distributions of the mean read-counts. To calculate the posterior distribution over the mean count for a given gene, strain and condition, we combine the likelihood function with prior distributions for the mean and variance. Typically read-counts in a gene are assumed to follow a negative binomial distribution (i.e. Y_i ∼ NB(p, r)), which is commonly used to model count data because it has an extra degree of freedom (size parameter r) to capture over-dispersion (4,20). However, since the negative binomial distribution does not have simple conjugate priors (21), we approximate the Negative Binomial (NB) likelihood through the use of a normal distribution which allows us to choose convenient priors which are conjugate. Specifically, the prior on the mean is chosen to be normal with hyperparameters μ₀ and κ₀, and the prior on the variance is chosen to be Inverse-Gamma with hyperparameters ν₀ and 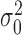. Taken together, the joint distribution of the data and unknown parameters is:

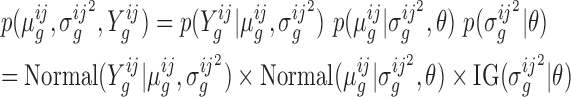where θ represents the hyperparameters (i.e. 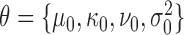), and 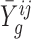and s² represent the sample mean and sample variance respectively. From this, the posterior distributions for mean and variance, which are used for sampling, can be derived and are given in Supplementary Section S1.

As the posterior distribution of the mean of a negative binomial approaches a normal distribution asymptotically (22,23), this choice of likelihood should approximate the true likelihood while greatly simplifying the derivation of conditional distributions. That is, the distribution over the mean of a negative binomial can be approximated by sampling from a normal distribution with the same sufficient statistics.

The hyperparameters of the prior distributions were set individually for each condition based on the data in a manner similar to empirical Bayes (24): the prior mean, μ₀, was taken to be the average mean read-count observed among the genes in a given condition. Similarly, the location parameter for the variance, 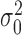, was set as the average variance observed among the genes in a given condition. In doing so, the prior probabilities help incorporate shrinkage in to the estimate of the mean, thus making them less sensitive to the raw observations. The hyperparameters κ₀ and ν₀, which can be thought of as representing the sample size of these prior distributions, were set to one (uninformative).

Monte Carlo sampling procedure

Ultimately we are interested in the distribution of the difference in log-fold-change, λ. Because the integral in Equation (1) does not have an analytic solution, we employ a Monte Carlo (MC) sampling procedure to integrate out the unknown means and obtain samples of 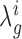. An outline of the MC procedure is contained in Algorithm 1. First we draw samples for the posterior variance, and then the posterior mean for each of the strains and conditions (e.g. WT and KO libraries in a reference condition A, and a condition of interest B). The sampled means will vary around the empirical (observed) means, with a dispersion based on the observed variability of counts at TA sites in the gene. Samples of the log-fold-changes for the strains are obtained by taking ratios of the sampled means, e.g.:

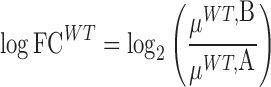Finally, the difference of the log FCs is taken to generate a distribution of the Δlog FC (Figure 2A).

Figure 2.

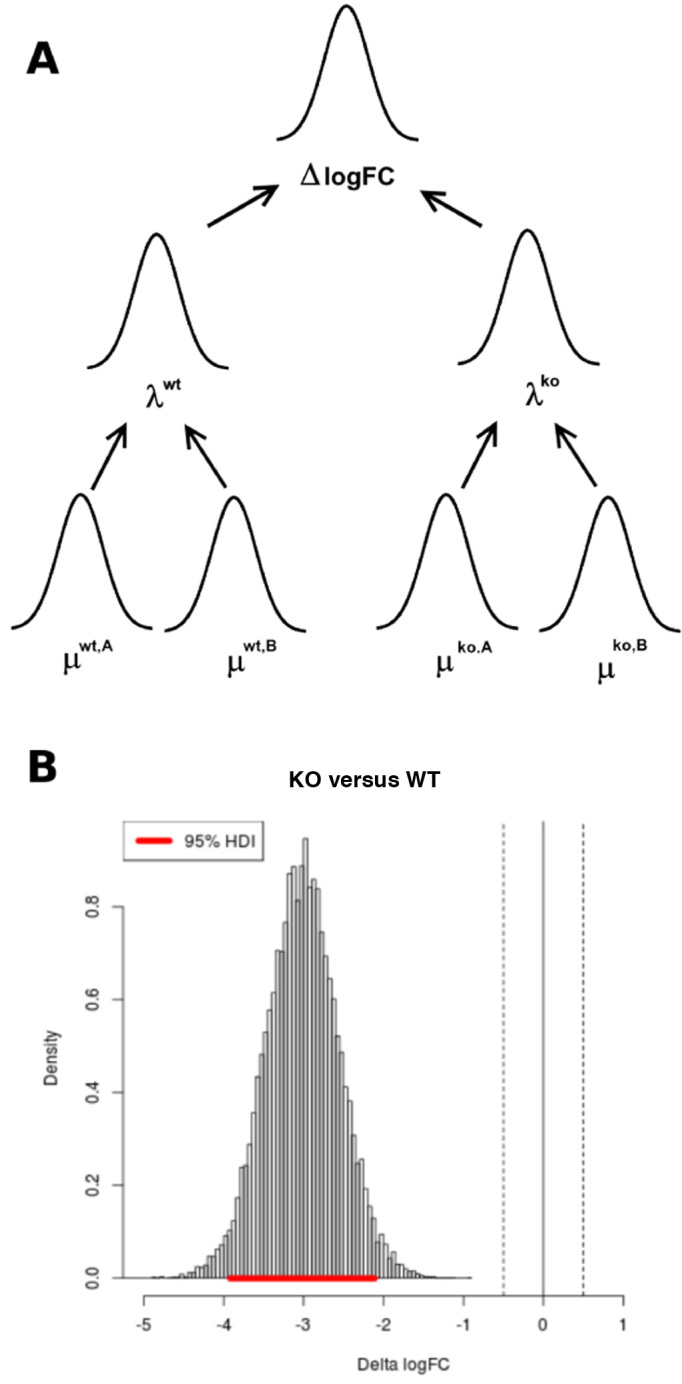
(A) Graphical illustration of Monte Carlo (MC) sampling procedure. Samples from the posterior means (μ) are generated for each strain and condition. A sample of the log-fold-change in means (λ) is then obtained from the sample of means. Finally, the difference in the log-fold-change in means is obtained. (B) Example distribution of Δlog FC. The highest density interval gives the 95% credible region for the Δlog FC, shown in red.

Algorithm 1: Algorithm for obtaining MC samples of the difference in log fold-change in mean read-counts for two strains (i.e. WT and KO) under two conditions (i.e. A and B).

To identify genes with significant changes in enrichment, the overlap of the distribution of Δlog FC with a [−0.5, 0.5] region around 0 (See Figure 2B) is calculated. This region is called a ‘Region of Practical Equivalence’ or ROPE (25,26), and represents values of Δlog FC that are practically equivalent to 0.0 (i.e. the null hypothesis of no difference in log-fold-changes between strains). A ROPE of ±0.5 was chosen because log-fold-changes of one-half or less are conventionally considered to be insignificant in gene-expression studies. As the ROPE represents values of Δlog FC which show no significant difference, the overlap of the Δlog FC distribution and the ROPE can be considered to be the posterior probability of the null hypothesis of no genetic-interaction (H₀):

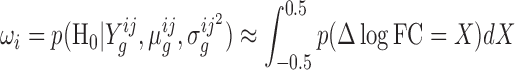As typically there are many genes being analyzed, corrections for multiple tests must be considered. However since our approach is Bayesian, traditional frequentist methods for controlling the false discovery rate (FDR) like the Benjamini–Hochberg procedure are not appropriate. In order to determine a threshold for significance that controls for the FDR in this context, we utilize the Bayesian FDR (BFDR) method (27). Briefly, the BFDR method estimates the FDR by averaging the posterior probability of the null hypothesis over the total number of cases rejected so far. This can thought of as an estimate of the posterior proportion of false positives in the list of identified genes (28). A conservative threshold of BFDR < 0.01 is chosen to identify significant genetic interactions.

RESULTS

To evaluate the method for identifying genetic interactions, we constructed Himar1 transposon insertion libraries in three mutant strains of M. tuberculosis, in which we deleted a single gene of unknown function that was previously shown to be required for optimal fitness a mouse model of infection (10): Rv1432, Rv2680 and Rv1565c (Table 1). KOs of these genes were made by allelic exchange, which replaced the entire ORF with a hygromycin-resistance cassette (see Supplementary Data for detailed description of experimental methods).

Table 1. Genes selected for this study that are non-essential in vitro but for which transposon insertion causes attenuation in vivo.

Gene	In vitro	In vivo	Fold-change	log FC	P-val
Rv2680	881.3	116.8	0.132	−2.92	0
Rv1432	774.4	6	0.008	−7.02	0
Rv1565c	2115.6	244.4	0.116	−3.11	0

The data shown are normalized insertion counts from a Tn-Seq experiment with an H37Rv transposon library, averaged over two replicates for each condition. ‘log FC’ is the enrichment, calculated as log2(in vivo/in vitro). The P-value is based on comparison to a simulation of the null distribution by permuting the counts between conditions in each gene (7).

Each of the four transposon libraries (one in WT and three in mutant backgrounds) was inoculated into five C57BL/6 mice by tail-vein injection, with an approximate inoculum of 10⁶ bacilli. After 24 h (‘d0’), two mice in each group were sacrificed, and bacteria were recovered from the spleen by plating. This was chosen to represent the ‘pre-selection’ library to account for possible biases introduced during inoculation. Bacteria were harvested from the remaining three mice in each group after 32 days of infection (‘d32’), representing the ‘post-selection’ condition. This period of infection encompasses the full spectrum of immune responses, including adaptive immunity which is initiated ∼10 days post-infection in this model.

Transposon–chromosome junctions from replicate samples of all four libraries at the two time points (d0 and d32) were amplified and sequenced on an Illumina HiSeq 2500 using established methods (29). On average, 4.1 million paired-end reads were collected for each sample. The reads were processed and mapped to the H37Rv genome using Transit (7). The resulting saturation (percent of 74 603 TA sites represented) for each sample ranged between 27 and 42%, and the mean template count at non-zero sites was in the range of 40–219 templates per site. Sequencing statistics on the individual samples are shown in Supplementary Table S1. The statistical analysis of genetic interactions described above was applied to the KO libraries of Rv1432, Rv2680 and Rv1565c compared to WT (H37Rv).

Analysis of the Rv1432, Rv2680 and Rv1565 KOs identified 46, 84 and 90 genes, respectively, with a Δlog FC that was significantly different from zero, representing likely genetic interactions with the knocked-out genes (Supplementary Table S2). Our analytical framework was sufficient to resolve different classes of genetic interactions. Aggravating interactions were defined as those significant hits with a negative Δlog FC, indicating that there was significantly less enrichment in the mutant strain. To distinguish between alleviating interactions and suppressive interactions, we considered the magnitude of the enrichment (log FC) in each strain:

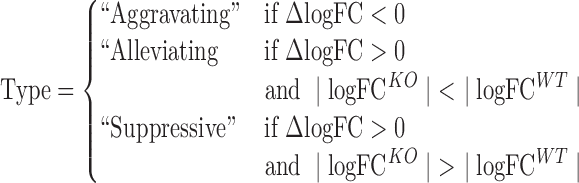Those genes which had greater enrichment in the KO (i.e. |log FC^KO| ≥ |log FC^WT|) were considered to represent suppressive interactions. Genes which had greater enrichment in the WT strain (i.e. |log FC^KO| ≤ |log FC^WT|), yet still had positive Δlog FC, were considered to be alleviating interactions.

The resulting gene-specific interaction networks consisted of biochemically related pathways and known protein complexes, supporting their functional relevance, as described below. Several genes appeared to interact with multiple knocked-out genes. For example, Rv0806c/cpsY (UDP-glucose-4-epimerase) exhibits a significant interaction in all three mutant backgrounds. Sixteen genes showed this behavior and 35 additional genes appeared to interact with two of the three genes of interest (see Figure 3; repeated genes listed in Supplementary Table S3). While it is possible that these apparently promiscuous interactions represent some unknown functional overlap among the three genes of interest, a more probable explanation is that they reflect unintended genetic differences between mutant and WT, such as due to the expression of the hygromycin resistance gene in the engineered strains. Consistent with this interpretation, all the genes show Δlog FC in the same direction (i.e. all increasing or all decreasing) among the three KO in comparison to counts in the WT sample. In the subsequent analysis, we focus on the unique hits for each deleted gene.

Figure 3.

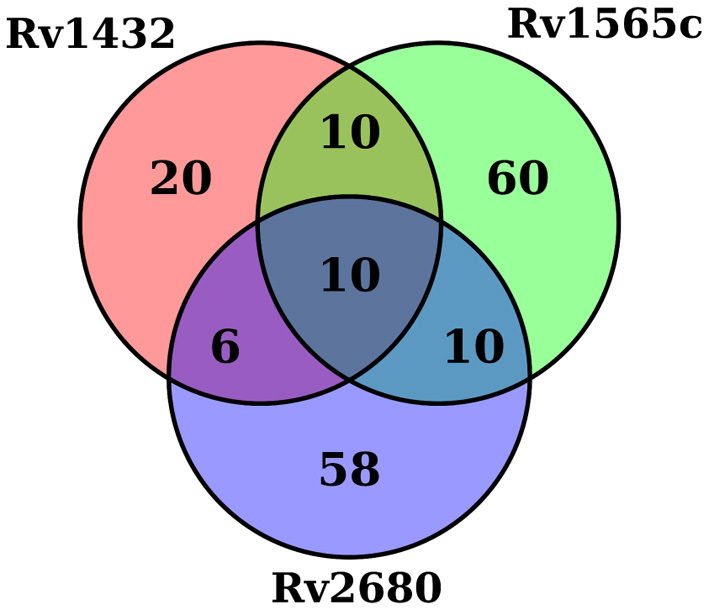
Venn diagram of genes that interact with three KO studied.

Different classes of genetic interaction are easily discriminated.

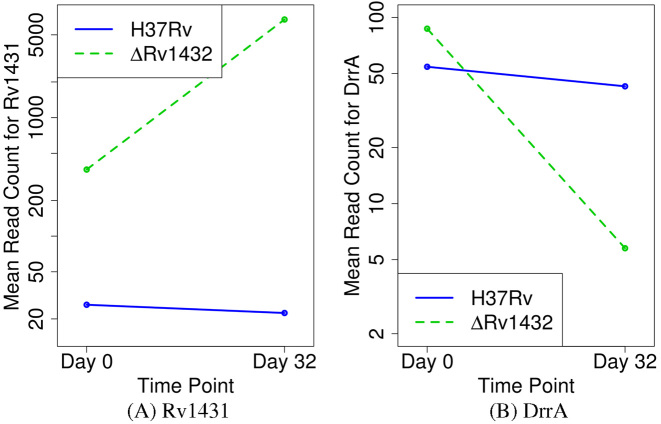
The genetic interaction network for Rv1432 consisted of only 20 unique genes. Among these were all three classes of interaction (aggravating, alleviating and suppressive). A strong suppressive interaction was found between rv1432 and the adjacent gene, rv1431 (Figure 4A), which is in the same operon. This interaction was manifest as a massive increase in the number of template counts at TA sites in rv1431 at d32 in the KO strain (18-fold more insertions between d0 and d32 in KO). In addition, five significant alleviating interactions were found. And finally, mutants with insertions in DrrA and DrrC decreased specifically in the Δrv1432 library (Figure 4B), defining an aggravating interaction, and DrrB, the other member of this ABC transporter, shows a similar pattern (although it was not unique to this KO). Together, both the identity of each interacting gene, and the class of interaction suggests plausible biochemical hypotheses to explain these interactions. For example, Rv1431 and Rv1432 could be members of a biochemical pathway: Rv1431 → intermediate → Rv1432 → product. In this scenario, deletion of rv1432 would result in an increase in a possibly toxic intermediate, and this effect would be abrogated when rv1431 is deleted. As evidence supporting that Rv1431 and Rv1432 might participate in the same enzymatic pathway, Rv1431 was found to bind to Rv1432 in an affinity pull-down experiment (see Supplementary Data). Proteins that physically interact (i.e. form complexes) are often functionally related, and a similar association holds for genes located in the same operon. The increased requirement for DrrABC in the rv1432 KO could suggest that the toxic intermediate is exported by this pump. The different relationships of Rv1431 and DrrABC–Rv1432 (i.e. aggravating versus suppressive) demonstrate why it is necessary to accurately distinguish genetic interactions to generate testable hypotheses.

Figure 4.

Plot of the mean read-counts (log-scale) for Rv1431 (A) and DrrA (B) between H37Rv (WT) and the KO of Rv1432 (KO). Rv1431 illustrates a suppressive interaction with Rv1432, while DrrA shows an aggravating interaction.

Genetic interaction mapping identifies entire functional pathways.

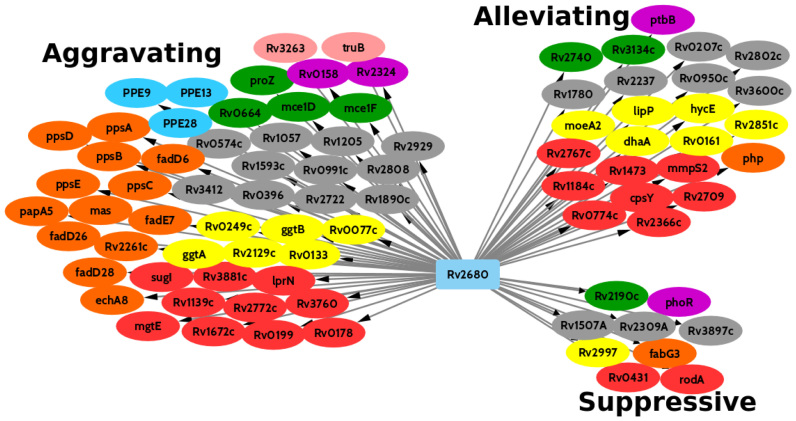
Our analysis identified 58 genes that exhibit a significant change in enrichment between WT libraries and those specifically in the KO of rv2680. Notably, nine of these genes are in the biosynthetic cluster for phthiocerol dimycocerosate (PDIM), a lipid that constitutes a significant fraction of the outer cell envelope of Mtb (30) (Table 2) (see network diagram in Figure 6). Template counts for each of these genes, rv2930–rv2941 increase slightly (log FC of ∼0.5) in the WT library over the course of infection, but decrease significantly in the KO library (∼10-fold at d32). These effects result in Δlog FC scores of around −3.5 (Figure 5). This effect was not observed in the other KO (Δrv1432, Δrv1565c) and hence is specific to Δrv2680. This implies that the requirement for the PDIM locus is more stringent in the absence of rv2680 (aggravating interaction). In addition, a large number of genes involved in the synthesis/modification/transport of fatty acids or the very long-chain mycolic acid components of the cell envelope show differential enrichment, including fadE7 and fabG3 (see network diagram in Figure 6).

Table 2. Select genes found to interact with Rv2680. The list of genes was enriched for genes involved in PDIM biosynthesis.

Orf	Name	Mean WT0	Mean WT32	Mean KO0	Mean KO32	log FC WT	log FC KO	Δlog FC
Rv2930	fadD26	70.32	72.69	16.41	1.55	0.05	−3.52	−3.57
Rv2931	ppsA	33.89	39.57	10.65	1.13	0.14	−3.27	−3.41
Rv2932	ppsB	25.58	52.09	7.11	0.91	1.01	−3.04	−4.05
Rv2933	ppsC	29.53	45.06	8.52	1.30	0.56	−2.76	−3.33
Rv2934	ppsD	27.12	49.26	10.47	1.47	0.84	−2.86	−3.69
Rv2935	ppsE	34.91	55.8	9.16	1.53	0.66	−2.62	−3.28
Rv2939	papA5	47.09	90.11	12.44	2.07	0.88	−2.65	−3.53
Rv2940c	mas	56.87	97.06	25.5	3.34	0.76	−2.94	−3.70
Rv2941	fadD28	31.62	57.84	16.49	2.82	0.85	−2.55	−3.40

Figure 6.

Genetic interactions with Rv2680. Genes on the left showed positive interactions, while genes on the right showed negative interactions. The genes are colored by functional category: Yellow: intermediary metabolism and respiration; Orange: lipid metabolism; Red: cell wall and cell processes; Blue: PE/PPE; Purple: regulatory proteins; Green: virulence, detoxification, adaptation; Light Gray: conserved hypotheticals; Pink: information pathways.

Figure 5.

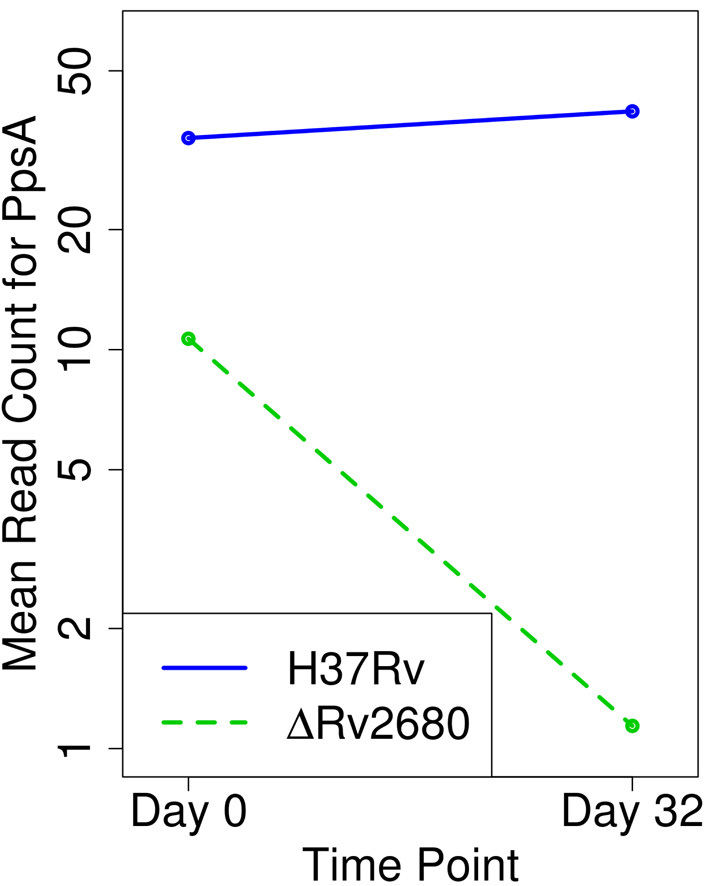
Mean read-counts (log-scale) for PpsA in WT versus the KO of Rv2680. Read-counts in the WT strain exhibit a slight increase after passage through mice for 32 days. On the other hand, a 10-fold decline is observed for the KO strain after 32 days, suggesting PpsA is essential for virulence in the absence of Rv1432. Other PDIM biosynthesis genes exhibited similar declines in the KO strain.

The anabolism of long-chain lipids, such as PDIM, plays an important but complex role in Mtb. Not only do these lipids serve important roles individually (e.g. modulating immune response (31)), but their synthesis is also linked to each other and to the overall metabolic state of the cell (32). Thus, decreasing the synthesis of one abundant lipid has been found to increase the synthesis of others, and to alter the balance of acyl-CoA metabolites that are central to carbon metabolism (33). As a result, it is not surprising that PDIM synthesis is a member of a genetic interaction network that contains a number of other genes involved in lipid metabolism, and our studies add rv2680 to this core metabolic network. These data strongly suggest that our analytical framework is sensitive enough to identify most members of an interacting biochemical pathway.

Genetic interaction networks encompass complex cellular processes and provide strong functional information

The genetic interaction network for rv1565c included 60 unique genes. The most quantitatively robust interaction was the suppressive effect of mutations in ponA2 (Figure 7. This gene exhibits a 30-fold increase in insertions at d32 in the Δrv1565c mutant, reflecting a robust growth advantage in this background. PonA2 is one of multiple high molecular weight penicillin-binding proteins in the Mtb genome, and is involved in the trans-peptidation and trans-glycosylation reactions necessary for peptidoglycan synthesis (34). Conversely, some genes exhibit alleviating interactions with Rv1565c. For example, ceoB (Rv2691), potassium uptake protein, exhibits an alleviating interaction with Rv1565c. It is required in WT H37Rv at d32 (consistent with its previous observations that it is required for growth in macrophages (35)), but is no longer required at d32 in the context of the KO of Rv1565c.

Figure 7.

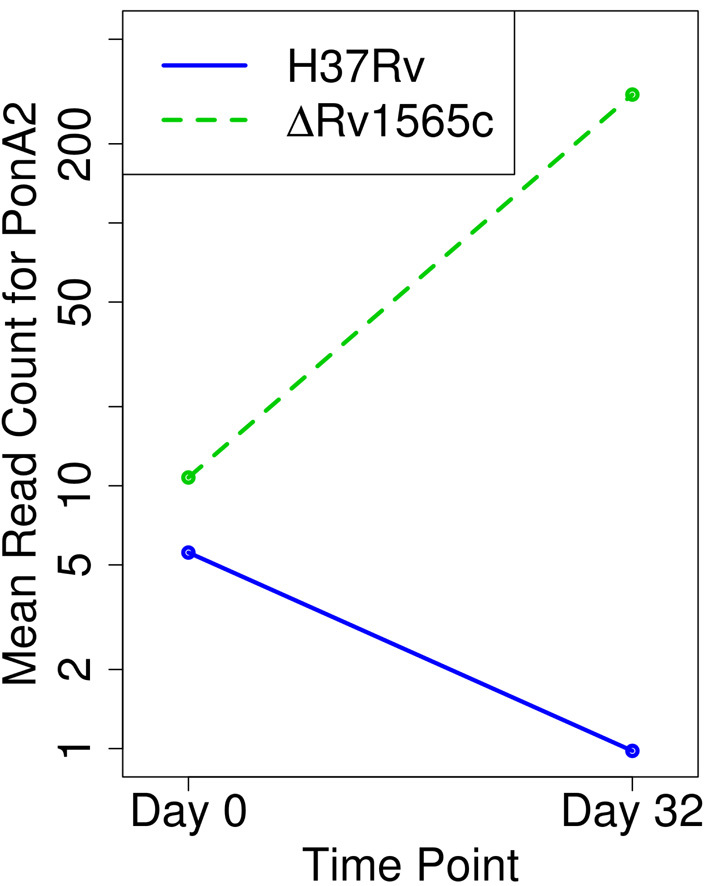
Plot with the mean read-counts (log-scale) showing a suppressive interaction for PonA2.

Rv1565c is annotated only as a ‘transmembrane acyltransferase’. It has weak homology to OafA in Gram-negative organisms like Salmonella (∼30% amino acid identity over the N-terminal half). OafA is an O-acetyltansferase of lipopolysaccharide (LPS) (36). However, mycobacteria lack LPS. The cell wall alterations observed upon mutation of the rv1565c ortholog of Mycobacterium marinium (37) previously led to speculation that this protein might be involved in the synthesis of mycobacterial glycolipids. While these observations suggested a possible role in biogenesis of the cell envelope, it remained unclear which cell wall-related process was affected by Rv1565c. The strong genetic interaction we find with ponA2 suggested a specific role for this putative O-acetyltransferase in peptidoglycan synthesis. This hypothesis is supported by previous genetic interactions studies of peptidoglycan synthetic enzymes (38). Rv0007, another membrane protein, demonstrated a similar suppressive genetic interaction as ponA2. This gene, along with rv1565c, was also found to become essential for in vitro growth specifically in a strain lacking the ponA2 paralog, ponA1 (38). Similarly, previous studies found that rv1565c-deficient strains have been shown to be hypersensitive to the transpeptidase-inhibitor, imipenem (39). Thus, a variety of genetic evidence implicates rv1565c in peptidoglycan synthesis. More generally, these data demonstrate that even complex cellular functions such as cell wall synthesis can be dissected using genetic interaction analysis, and this approach can provide strong clues to the function of uncharacterized genes.

DISCUSSION

TnSeq is a rapidly growing experimental technique for determining essential genes/regions in bacterial chromosomes that has found many applications, ranging from pathway association and functional annotation, to identification of new drug targets (40). Computational methods are evolving for analysis of Tn-Seq data, including software packages like ESSENTIALS (4), Tn-Seq Explorer (6), ARTIST (5), TRANSIT (7), etc. Statistical analysis of Tn-Seq data is challenging because of the high level of noise in these experiments, including variability due to sampling (differences between replicates), differences between libraries (e.g. saturation, abundance) etc. Thus, like RNA-Seq, Tn-Seq experiments require a rigorous statistical evaluation (coupled with appropriate normalization, etc) to determine which differences/effects (if any) are significant.

An important emerging application of Tn-Seq is to identify genetic interactions (8). Genetic interaction studies are complex experiments involving comparison of multiple libraries across multiple conditions (and possibly including multiple replicates). Of interest are those genes that show a significant change in enrichment between the strains (i.e. the degree of change is dependent on the strain, not just condition). The approach utilized by van Opijnen et al. is to calculate a fitness score W_i at each TA site in a gene, and then compare the scores for the KO to WT using a t-test. This requires matched pairs of datasets from multiple independent transposon libraries (for each strain) assessed in parallel in each condition. The fitness values estimated by van Opijnen et al. (8) are an estimate of relative growth rate of a strain between two conditions after a transposon insertion. Based on the ‘multiplicative model’ of genetic interactions, interacting genes are identified as those for which simultaneous disruption causes a greater (or lesser) growth impairment, as inferred from the data, compared to the product of impairments expected from disrupting each gene alone.

A limitation of the approach used by van Opijnen et al. (8) is that it relies on directly comparing the read-counts observed at each TA site between two datasets (by calculating a fitness score, W_i). Comparison of datasets that do not have insertions at the same sites (as is common in datasets coming from different libraries) will lead to artificially inflated fitness scores (e.g. at sites with positive counts in one dataset but zeros in the other). Additionally, this method is susceptible to outlier fitness ratios estimated from sites with low counts, which is handled in an ad-hoc way (assigning lower weights to such sites in the t-test). This could result in their method being overly-sensitive, potentially leading to false positives. The method may also detect spurious differences which are not biologically meaningful, because it only tests genes against a null hypothesis of no difference, a common criticism of classical hypothesis tests typical of frequentist methods (41).

One benefit of the approach used by van Opijnen et al. is that it calculates and expansion factors (d) which normalizes the actual fitness effects (i.e. absolute growth rate multipliers) between libraries and can be used to estimate their corresponding growth rates. In practice, however, the experimental setup may make it difficult to estimate expansion factors, d, necessary to estimate true growth-rates and fitness scores. The experimental setup used in our study involved passaging libraries through mice for up to 32 days; the estimation of the expansion factors in this case is not as simple as estimating the number of doublings in vitro (due to birth/death dynamics in vivo (42)). Instead of estimating absolute fitness values, our method only relies on relative changes in fitness, from which we can still make inferences about changes in essentiality.

Our model is fundamentally a Bayesian one. We interpret the insertion counts observed at TA sites as independent samples from a stochastic process that ultimately reflects underlying biological effects for each gene (i.e. changes in abundance of mutants in population due to treatment or conditions). These observations are combined with prior information to yield conditional distributions of the mean for each gene. From these distributions, we can estimate a distribution over the Δlog FC, representing the change in enrichment, and use this to identify potential genetic interactions. Since we are ultimately comparing the distribution of the mean insertion counts in the gene between conditions, genes are not required to have insertions at the same sites, unlike the fitness model of van Opijnen et al.

An important feature of our model is that the variance around the estimate of Δlog FC is ultimately derived from the variance of counts among TA sites in a gene. The insertion counts can vary a great deal between individual TA sites in a gene, which reflects an important component of noise in these experiments, and capturing this variance is necessary to determine whether the difference in means (or log-fold-change) is significant. This is because even a large observed difference for a gene in two conditions might not be significant if the means were calculated from widely varying counts among individual TA sites in the gene. Conversely, if a small increase is observed systematically from one condition to another over many TA sites in a gene, the difference in means could be considered more reliable. The variability of individual insertion counts determines the breadth of the posterior distribution of Δlog FC, and thus the degree of certainty that it is different from 0. While the posterior distribution Δlog FC does not have an analytic solution, our algorithm uses a simple MC sampling procedure to simulate it, allowing for computationally efficient inference.

One advantage of the Bayesian approach is that the priors can help to compensate for sparse data. Mean and variance estimates derived from the observations are combined with other information (like the expected magnitude of counts or expected amount of variability), to produce a weighted combination of this information. Those genes with few insertion sites are more heavily influenced by the prior (i.e. shrinkage); whereas, for larger genes, the data comes to dominate the estimates of mean and variance. This approach naturally filters out many small genes that numerically might have larger Δlog FCs (based on raw counts), but are not justifiably significant because they are based on too few observations. In this way, lack of data is handled in a more robust way than the ad-hoc filtering or addition of pseudocounts typical of frequentist methods.

Another method that has been proposed for analyzing Tn-Seq data is to apply statistical methods for analyzing RNA-Seq data, such as limma (11) or edgeR (12). These methods are based on GLM. In these approaches, count data (in matrix form, typically normalized and log-transformed) is decomposed to a linear combination over different treatment effects 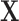by fitting a vector of coefficients 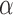: 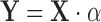. Differences attributable to a strain or condition show up as coefficients α_i in the model. Ultimately, the significance of these coefficients is tested by computing a t-statistic on an α_i, though this depends crucially on careful estimation of variance (derived by fitting to observations, e.g. variability between replicates, but also shared across genes using empirical Bayes (24)). Evaluating changes in enrichment can be accomplished by including an interaction term to the model (e.g. strain × condition), the fitted coefficient of which is effectively equivalent to the Δlog FC in our approach. Hence, interacting genes could in theory be detected as those for which the changes in counts cannot be systematically explained in a linear model by strain or condition alone, but where the amount of enrichment between conditions changes depending on the strain.

One problem with applying a linear modeling approach like limma to Tn-Seq data is how to handle the multiple TA sites in each gene. In a traditional RNA-Seq experiment, read-counts are summed over all the reads mapping to a gene. This is how Tn-Seq data has been treated in several software packages that utilize methods initially developed for expression data (like limma or edgeR) to perform statistical calculations of essentiality, including ESSENTIALS (4) and TraDIS Toolkit (13). That is, they sum the insertion counts over all TA sites in a gene and then fit a linear model and test for effects via significance of coefficients. The collapsing of read-counts into a single measurement (representing the sum) loses vital information. For example, it discards the number of TA sites on which the total count is based, which ideally should influence the significance of genes as a function of whether they are large or small. Furthermore, summing insertion counts obscures a key source of variance—the variability of counts between TA sites. This limits the number of observations for estimating the variance to the number of replicates (which might be few). Our approach is designed to capture this variability among insertion sites by estimating posterior distributions over means, which ultimately can be used to determine a credible interval around the Δlog FC.

The Tn-Seq libraries utilized in this study were created using the Himar1 transposon. While, in principle, nothing prevents our model from being applicable to analysis of libraries generated with other transposons (provided there are enough candidate insertion sites), their characteristics could make analysis difficult. For instance, the Tn5 transposon has a weak sequence preference bias (43), which makes it difficult to determine which genomic locations are the candidate insertions sites. If we assume that every site in the genome is a potential insertion site, then genes will have a large proportion of empty sites, which would artificially reduce the estimate of the variance, making read-counts appear less variable and increasing the risk of false positives.

Some essential genes can tolerate insertions at the N- or C- termini, or in linkers between domains (15). Furthermore, some genes have a mixture of essential and non-essential domains (44). This can cause problems for some essentiality analysis methods, especially those which restrict analysis to regions with predefined boundaries, such as ORFs. However, this should not be problematic for analysis of genetic interactions. The comparative nature of our analysis means such insertions should affect both strains (or conditions) equally, and thus should not bias the calculation of Δlog FC.

As is typical in most Tn-Seq analysis methods, the utility of the method is limited by the amount of data available, including saturation of the libraries. The datasets do not have to be fully saturated. However, saturation has to be high enough so that each gene has a least a few occupied insertion sites. Our results show that the method is effective in identifying genetic interactions even with datasets in the 27–42% range of saturation. Furthermore, this limitation can be mitigated by collecting multiple replicates, which increases the amount of observations proportional to the number of replicates (i.e. N TA sites by K replicates), improving the estimates of the distributional parameters.

A potential limitation is that our method utilizes a normal distribution to approximate a negative binomial likelihood, which may not be as accurate for small genes (e.g. with 1-2 TA sites). This choice was made to facilitate the derivation of posterior distributions of the mean, which should approximate a normal distribution asymptotically, regardless of the true distribution of the data. Although the normal approximation of the mean will be less accurate for genes with few insertion sites, the parameter estimates for these genes will also have higher variance and will be more strongly influenced by the priors, thus reducing the probability that such small genes will be predicted to be genetic interactions. This was supported by our results, which identified no interacting genes with fewer than three TA sites (effectively equivalent to nine data points, given three replicates).

We applied our method to define genetic interaction networks that are functionally associated with three different genes of unknown function, Rv1432, Rv2680, Rv1565c. These three genes were selected because their disruption decreased bacterial fitness during infection, but are not essential for in vitro growth. While the functions of this class of ‘virulence’ genes are of great interest, they have proven particularly difficult to characterize, since they are only required in this experimentally inaccessible environment (in vivo). Genetic interaction mapping is a particularly attractive approach to characterize the functions of these genes, as Tn mutant libraries can be subjected to selection (i.e. passaged through mice), and thus the resulting functional networks reflect the bacterium's cellular state during infection. Using this approach, we found evidence suggesting that Rv1431 and Rv1432 participate in the same pathway. Our analytical method is also sensitive enough to identify complete biochemical pathways (e.g. functional relationship of Rv2680 to PDIM synthesis). Finally, we identified PonA2 and Rv0007 to be in strongly suppressive interactions with Rv1565c, implicating it in peptidoglycan biosynthesis.

AVAILABILITY

A Python implementation of the sampling method described in this paper is publicly available and can be downloaded from http://saclab.tamu.edu/essentiality/GI/.

ACCESSION NUMBERS

The sequencing datasets for the Tn-Seq experiments in this paper can be obtained from NCBI SRA (Short Read Archive) under accession number SRP081827.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health (www.nih.gov/) [U19 AI107774 to T.R.I., C.M.S.; AI064282 to C.M.S.]. Funding for open access charge: NIH [U19 AI107774].

Conflict of interest statement. None declared.