A new model for ancient DNA decay based on paleogenomic meta-analysis

Abstract

The persistence of DNA over archaeological and paleontological timescales in diverse environments has led to a revolutionary body of paleogenomic research, yet the dynamics of DNA degradation are still poorly understood. We analyzed 185 paleogenomic datasets and compared DNA survival with environmental variables and sample ages. We find cytosine deamination follows a conventional thermal age model, but we find no correlation between DNA fragmentation and sample age over the timespans analyzed, even when controlling for environmental variables. We propose a model for ancient DNA decay wherein fragmentation rapidly reaches a threshold, then subsequently slows. The observed loss of DNA over time may be due to a bulk diffusion process in many cases, highlighting the importance of tissues and environments creating effectively closed systems for DNA preservation. This model of DNA degradation is largely based on mammal bone samples due to published genomic dataset availability. Continued refinement to the model to reflect diverse biological systems and tissue types will further improve our understanding of ancient DNA breakdown dynamics.

INTRODUCTION

The genomic era of massively parallel DNA sequencing has driven a revolutionary body of research using ancient DNA-based genomics (1,2). Paleogenomics has led to the re-writing of recent hominin evolutionary history (3), nuanced understandings of historical human movements and interactions around the globe (4,5), breakthroughs in Quaternary paleontology (6–8), evolutionary ecology, the biology of extinct species (9), impacts of humans on ancient ecosystems and biodiversity (10) and the evolution and movements of domestic plants and animals (11–14). The successful probing of ancient epigenomes, microbiomes and metagenomes further illustrates the flexibility and information value of ancient DNA-based research in the genomic age (15–17). In sum, time-series genomic datasets have proven extremely valuable in diverse research avenues.

In addition to the scale and sensitivity of analysis afforded by genomic methods in ancient DNA research, genomic datasets allow for a revised understanding of the patterns and expectations of DNA survival over millennia. This is beneficial in two key ways: (i) Criteria of ancient DNA authenticity warrant updating for the genomic era and formalized expectations of DNA degradation are necessary for this process; and (ii) Better predictive models of DNA degradation may help researchers target specimens likely to yield high information value where destructive analysis is unavoidable. Generally, ancient DNA is expected to be highly fragmented (18–20) and to carry an abundance of characteristic misincorporations—deaminated cytosine residues appearing as C-to-T transitions in single-stranded fragment overhangs (21). Further, DNA fragmentation is biased by biomolecular context. For example, a short-range (∼10 bp) periodicity observed in the distribution of fragment lengths is attributed to the period of a complete turn of the DNA double-helix around a histone (22), which is thought to offer some protection against breakage at histone-adjacent sites. Finally, base compositional biases have been observed in DNA preservation, especially enrichment of GC-content in ancient DNA (23).

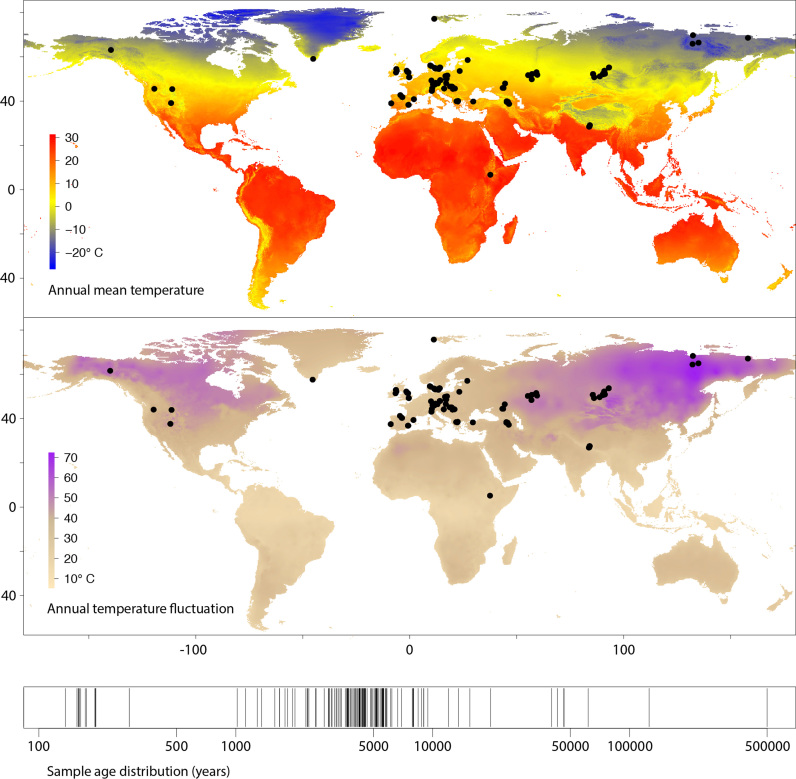
The relationships between these characteristic patterns of DNA degradation and the preservational environment and age of tissues are poorly understood. We carried out a meta-analysis of 185 ancient genomic datasets—dating from the Middle Pleistocene to the nineteenth century from 21 published studies (Figure 1)—to test for relationships between sample age, environmental variables and DNA diagenesis. We used mapDamage 2.0 (24) to quantify deamination and we developed tests for assessing fragmentation, histone periodicity and energetic base-compositional biases in ancient genomic data. We analyzed these damage statistics in relation to sample age, annual mean temperature, temperature fluctuation and precipitation—treated as a proxy for humidity—using simple multivariate linear models. Ultimately, we aimed to establish the key determinants of DNA survival and the specific patterns of DNA breakdown expected under variable conditions.

Figure 1.

Locations of 185 samples (n = 94 unique sites) used in paleogenomic meta-analysis, global variation in mean temperature and temperature fluctuation, and timeline of sample ages. Note the absence of sites with annual mean temperature >20°C, reflecting known preservation bias toward cooler climates (25).

MATERIALS AND METHODS

Dataset compilation and initial processing

We obtained unmapped (fastq) or mapped (bam) sequence reads from each of 185 publicly available ancient DNA datasets generated by shotgun sequencing without uracil removal, comprising anatomically modern humans (n = 156 (26–38)), herbarium plant samples (n = 15, aligned to the host plant rather than the pathogen examined in ref (39), with environment data estimated at the herbaria of long-term storage rather than the site of collection), Colombian and woolly mammoths (n = 4 (7,40)), neandertals (n = 3 (41)), horses (n = 5 (13,42–43)) and polar bear (n = 1 (44)). We avoided data generated through target capture experiments to avoid possible hybridization biases introduced by misincorporated residues or read length variation. For unmapped samples, we used Flexbar (45) to trim adapter sequences in single-end read data, and PEAR (46) to perform adapter trimming and read merging in paired-end datasets. We used the bwa-backtrack algorithm within the Burrows–Wheeler Aligner (47) to map read data to the corresponding reference genome and collapsed duplicates using the ‘rmdup’ function in SAMtools (48). We filtered all bam files for a minimum mapping quality of 20 using the SAMtools ‘view’ function and filtered for minimum read length of 20 using Unix tools. We separated nuclear and organellar reads (mtDNA in mammals, plastid DNA in plants) into separate bam files. For the mammoth samples mapped to the African elephant genome (n = 4), we removed mitochondrial reads from the bam file and re-mapped the complete raw datasets to a woolly mammoth mitochondrial sequence (NC_007596.2). Sample latitude and longitude were used to estimate annual mean, minimum and maximum temperature estimates, plus annual precipitation for each of the samples. These were taken from the WorldClim (49) current condition database using the R ‘raster’ package (50) at a resolution of 2.5 arc-min. In cases where specific site location was not available at the longitude/latitude level, Google Earth was used to estimate longitude and latitude from details or site maps provided in the relevant publications. Location details and temperature estimates are given in Supplemental Dataset S1. Climate estimates reflect modern climate conditions rather than a complete climate legacy over the time span of each sample. We then estimated DNA preservation and breakdown parameters as described below.

Deamination

We used mapDamage 2.0 (24) to estimate cytosine deamination in single-stranded overhangs, δ_s, invoking default settings with the following exceptions: we subsampled large bam files to correspond with 1 Gigabyte input file (∼10–20 million reads with typical dataset complexity and a human genome) using the mapDamage ‘-n’ option. We analyzed the mapDamage Markov chain Monte Carlo (MCMC) output from each sample using the ‘coda’ R package (51) to estimate an effective sample size (ESS) for each of the six variables estimated by the mapDamage simulation. ESS values are reported in Supplemental Dataset S1. We enforced a minimum ESS of 200 in all variables to ensure MCMC simulation convergence, excluding nine datasets for deamination analysis. For libraries with highly asymmetrical 3΄ and 5΄ C-to-T mismatch observed visually in misincorporation plots, indicating the likely use of a non-proofreading DNA polymerase for library amplification—incapable of recovering uracils in template DNA—we re-ran mapDamage with the ‘–reverse’ option to estimate damage from the 3΄ end only. We noted extremely high deamination and overhang termination values in the output from Mammoth M4 (7), which suggested a much higher rate of deamination than even much older permafrost samples. However, that library is dominated by very short fragments (ref (7); summarized in the fragment length plot on Dryad), which we hypothesized could influence the mapDamage MCMC to over-estimate both parameters. We re-analyzed that sample considering only reads ≥40nt, yielding the damage parameter values reported in Dataset S1. Data from the Saqqaq Palaeo-Eskimo genome (32) were mostly generated using a non-proofreading enzyme, but a small proportion of read files were reported to have been generated using a proofreading Platinum High Fidelity Taq polymerase (22). We mapped all Saqqaq read files from the Sequence Read Archive (n = 218) to a human mitochondrial genome (EU256375.1), used PMDtools (52) to rapidly generate misincorporation plots and visually inspected each for elevated 5΄ C-to-T mismatch. This approach yielded two libraries apparently produced using a proofreading enzyme, one of which (SRR030983) was carried through for analysis. All mapDamage output files (run logs, plots, MCMC trace files and summary statistics) from the 185 final runs are available in the Dryad Digital Repository (see Availability below). Finally, we summarized a deamination rate for each sample according to the equation:

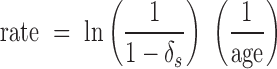Fragment length distribution

Fragment lengths are expected to form an exponential distribution under random breakdown. The distribution of DNA fragment sizes can therefore be summarized as λ (53), the single parameter of the exponential distribution. To estimate λ, we first summarized a frequency distribution table of fragment lengths. If a frequency spike was observed at the maximum fragment length—indicating fragments greater than the read length and an artifactual peak among reads with no adapter trimming—we re-estimated the maximum reliable fragment length as follows: beginning with the longest fragment, we pruned the table back to the point at which the next shorter fragment was observed more frequently, eliminating up to 6 length values (mean = 3). We iterated over all ranges of at least 20 consecutive length values in the table, attempting to fit an exponential formula using the R function: nls(y ∼ N*exp(−k*x)), with starting values of k = 0.05, N = 0.1 and λ represented by the inferred value of k. We retained the top 5% of best fits on the basis of P-values obtained by summarizing the formula output in R and estimated the value of λ from the table segment producing the best overall fit. We visualized the results in the top 5% of best fits to confirm a reasonable λ estimate by eye (e.g. Supplementary Figure S1). We observed fragment length heterogeneity in some cases, likely created by mapping biases and occasional anomalous spikes in length frequencies that disrupted automated estimation of λ. Therefore, during visual inspection, we sometimes opted to override the inferred λ value by (i) manually defining a range of fragment lengths over which to re-calculate λ and/or (ii) clipping artifactual frequency spikes by imposing a single frequency threshold value (e.g. Supplementary Figure S1). All summary statistics and plots for λ estimation are available on Dryad, including run logs detailing manual override decisions. Perl and R code for λ estimation are available on Dryad.

Histone periodicity estimation

To estimate the intensity of a preserved histone signal (22), we analyze periodic deviations from a medium-range smoothing algorithm imposed on the fragment length frequency tables (Supplementary Figure S2). Using a fragment length frequency table, we again eliminated the artifactual peak at the maximum length as above for λ and trimmed the distribution to the innermost length values each representing at least 0.002 of the total fragments. Additionally, for artifactual spikes within the frequency table, we adjusted any single frequency greater than 1.5× the midpoint of its flanking neighbors down to the midpoint. This approach affected only artifacts and not the underlying distribution. We then fit a locally weighted scatterplot smoothing (lowess) curve with the R ‘lowess’ function, using a smoothing span of 20 to normalize over histone periods expected to be ∼10nt (22). We then removed four additional length values from each end of the distribution to eliminate increased terminal deviations from the lowess curve.

We observed that in samples with a histone signal, the deviation of the observed values from the lowess curve is best approximated by a series of local exponential functions with the midpoint of a complete histone period set to x = 0 (Supplementary Figure S2). That is, frequency values across a single histone period form a parabolic curve when normalized for overall fragmentation described by λ. Therefore, we tested for this pattern in all subranges of 8–12 consecutive length values in the table, setting the midpoint of each subrange to x = 0 and using the observed value divided by the lowess values for the y-axis. We used the R function nls(y ∼ k+|N|*x∧2)), with starting values of k = 1 and N = 0.1, so that k should deviate minimally from 1 to absorb noise, and positive values of N provide a metric of signal intensity. That is, N increases linearly with the degree of observed frequency deviation from the lowess curve at local maxima. We retained the starting position, range lengths and N values of all significant fits on the basis of P-value. We then used an optimized one-dimensional k means clustering algorithm in the R ‘Ckmeans.1d.dp’ package (54) to localize strongly significant starting locations of histone periods. For all adjacent (i, j) pairs of cluster positions representing the putative best locations for histone peaks, a periodicity coefficient was calculated: If j − i ≥ 8 and j − i ≤ 12, the coefficient increases by 1/(n clusters −1). Otherwise, if some value v in 2 through (range of values)/10 satisfies (j − i)/v ≥ 8 ∪ (j − i)/v ≤ 12, coefficient increases by (1/v)/(n clusters −1). Thus, given a minimum of three clusters and a minimum periodicity coefficient of 0.3, cluster position values satisfying the requirement could include 10,20,40 (coefficient = 0.75); 10,20,50 (0.67), 10,30,50 (0.5) or 10,40,70 (0.33), but not 10,50,80 (0.29).

To optimize histone signal estimation, we used the organellar datasets (which lack histones in vivo) to calibrate model parameters against false positive results (Supplementary Figure S3). We permuted the minimum number of significant clusters detected (2,3,4), a minimum observed proportion of all plausible histone periods given the range of values analyzed (0, 0.1, 0.2 and 0.4), the minimum periodicity coefficient (0.2, 0.3, 0.4 and 0.5) and a minimum P-value threshold for significant exponential fit (0.05, 0.01 and 0.001). We summarized the number of nuclear and organellar datasets satisfying the requirements of 144 separate model permutations (n = 53 280 total iterations). P-value, minimum cluster count and minimum periodicity coefficient proved the best predictors of false positive rates, accounting for 79% of the variance in false positive rate under a simple linear model (Supplementary Figure S3), while proportional number of clusters did not add predictive power. Under a range of parameter values, we were able to estimate nuclear histone signal intensity with no organellar false positives in up to 112 of the 185 samples for a given model. Given a 5% allowable false positive rate in the single model with the highest ratio of nuclear to organellar estimates, we were able to recover 138 nuclear estimates. We recorded the median value of the N intensity parameter for all samples under strict conditions with no organellar false positives (n = 112) for analysis (Dataset S1 ‘Histone_Intensity’ for estimates; see the Dryad repository for pdf and run files). Notably, the Thistle Creek horse genome (43) displays a clear short-range periodicity on visual inspection, but at about half the normal length (∼5 bp). The reason for this behavior is unclear, but this distribution violates the model assumption of ∼10 bp period and therefore this sample only ever presented as a likely false positive during model calibration.

Base composition

To assess biases in base composition related to preservation, we first summarized 8-mer frequencies in each reference genome, excluding soft- and hard-masked repeat regions. We then summarized 8-mer frequencies in the bam files from sequence reads in mapped orientation to match the reference. For each 8-mer, a simple enrichment factor was calculated as (frequency in mapped reads)/(genomic frequency). The enrichment and depletion of ancient DNA motifs is affected by a complex range of conditions, as suggested by clear multimodality in the distribution of 8-mer enrichment factors (Supplementary Figure S4). Additionally, in vitro variables further bias the datasets through penalizing GC-extreme reads, for example (55), and chromatin modeling and nucleosome occupancy is expected to have differential effects on the protection and survival of coding versus non-coding DNA. To isolate these effects, we calculated a simple GC proportion for each 8-mer and based on known systematic sequence complexity biases among genomic element types (56), we calculated 8-mer Shannon entropy (H) using the following formula after ref (57):

Finally, we calculated a simple kmer enthalpy as the sum of all dimer base-stacking energy values (kcal/mol/dimer) reported in table IX of ref (58), using the values from the ‘corrected optimized potential’ method. We first visualized kmer enrichment in relation to all three sequence variables—GC content, entropy and enthalpy—and noted extensive variation among samples as expected (e.g. Supplementary Figure S4, kmer summary files for all datasets, code for 3D scatterplots and code for enthalpy-biased kmer frequency estimation are available on Dryad). For example, GC content and entropy are parabolically related by definition—equal base frequencies are required for maximum entropy. As such, disentangling enrichment of high-entropy kmers from in vitro penalization of GC-extreme kmers is intractable, and kmer enrichment patterns varied extensively in terms of entropy and GC-content. However, we noted a strong relationship between enrichment and enthalpy in several samples (Supplementary Figure S4), and therefore we opted to isolate enthalpy from GC content and entropy for analysis as follows:

In total, there are 52 unique GC-content—Shannon entropy combinations for DNA 8-mers. Each of the 52 configurations of invariant GC and entropy values represents between 2 and 6720 kmers (n = 65 536 total kmers) representing a distribution of enthalpy values and enrichment factors. From within each of the 52 GC–entropy configuration bins, we reiteratively selected random pairs of kmers up to the total number of kmers in the bin (i.e. given a bin containing 32 kmers, 32 random pairs were selected and a total of 65 536 pairs are drawn from the dataset). We then compared enrichment factors and enthalpy values between the two kmers. Given a ‘success’ if the higher-enthalpy kmer was also the more enriched kmer, as hypothesized, we incremented a counter and decremented the counter for failures. Following iterations, we recorded the value of the counter divided by the number of trials and used this value as the test statistic to compare with environmental variables, where positive values indicate overall enrichment of higher-enthalpy motifs (Dataset S1, ‘Enthalpy_bias’).

Linear models

We carried out multiple linear regression analyzes to test for relationships between preservation parameters (above) and environmental variables. Specifically, we tested in turn for significant predictors of each damage parameter using a linear model analysis with four independent variables: annual mean temperature, annual temperature fluctuation, annual mean precipitation and the natural log of sample age using the R ‘lm’ function (59). Results presented are from analysis of the nuclear datasets after excluding the organellar data.

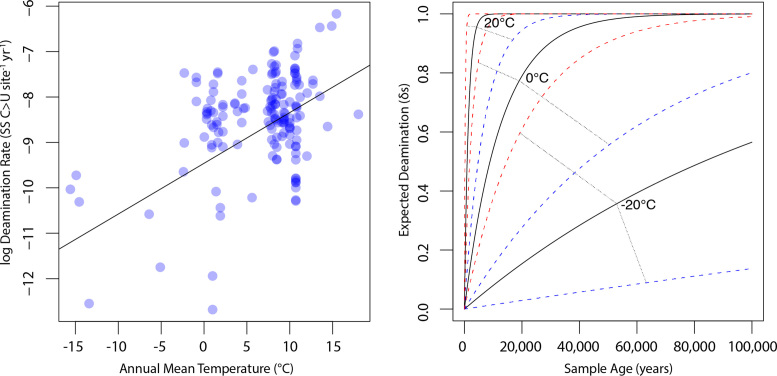
Deamination prediction from temperature

We calculated a density distribution of deamination rates using default parameters and bandwidth in the R ‘density’ function and creating a weighting vector where each point's weight value was calculated as 1-(local density/maximum density). We then fit a weighted linear regression between temperature and deamination rate using the R ‘lm’ function with the ‘weight’ option invoked using the above weighting vector. We used the R ‘predict’ function to predict a rate and 95% confidence intervals at temperature values of −20°C, 0°C and 20°C. The R code to replicate the analysis and re-create Figure 3 from Dataset S1 is available on Dryad in the ‘expedient code’ file.

Figure 3.

Expectations of deamination over time for variable temperatures. Left: density-weighted linear regression of temperature and log deamination rate calculated using the formula rate = ln (1/(1−δ_s)) * (1/age). Right: using rate estimates from the weighted regression, we calculated the expected δ_s values over a 100 000 year time span using the formula δ_s = 1−(1/e^rate*age) re-arranged from the above, as well as δ_s values for rates estimated from 95% confidence intervals of the regression. We visualized the expected deamination levels for samples from −20, 0 and 20°C contexts (solid lines), along with upper (red) and lower (blue) confidence bounds. This predictive model is necessarily based primarily on mammalian bone tissue, and we expect refinements to these expectations based on sample type, for example, as more datasets become available.

Simulating DNA fragmentation and deamination

We hypothesize below (Results and Discussion) that a time-dependent fragmentation process may be incongruent with the observation of total cytosine deamination in single-stranded overhangs (δ_s = 1). We therefore carried out a set of simulations to test the effects of varying the fragmentation rate on the accumulation of deaminated residues. Simulations were executed using a custom perl script. Beginning with a λ value of fragmentation (e.g. 0.013–0.157 range from our meta-analysis), we infer the number of random fragmentation events necessary to yield the lambda value as λ x (total length of all fragments). We then randomly select a simulated number of imposed total fragmentation events from a Poisson distribution, using the exact number of fragmentation events as the Poisson lambda parameter. We pre-allocate the selected number of breakage events—without replacement, as breakage is impossible twice at the same location—to locations in a population of starting molecules. Breakage occurs at zero-width sites between simulated residues in our simulation, such that molecules can be reduced to 1 nt but not lost completely. We then allocate fragmentation events to timing bins by sampling from the probability density function of a beta distribution with the α parameter held at 1 and the β parameter varying ≥1 to introduce a changing rate profile: β = 1 describes a constant rate of fragmentation and higher values of β describe increasingly skewed scenarios where fragmentation occurs in the early cycles of the simulation. For example, when α = 1 and β = 10, roughly 90% of fragmentation has occurred when 20% of time has passed. Alternatively, α = 1 and β = 1 describes a uniform distribution of fragmentation where the rate parameter k = λ/time, as per ref (18). To complete setup, we impose a δ_s value and calculate a deamination rate as described above in terms of probability of deamination per site per year, and impose a value to describe fragment overhangs per mapDamage 2.0 (0.3 in our simulation).

We then carry out a forward simulation through cycles of drawing from the randomized predetermined breakage sites according to the timing bin allocations and introduce new single-stranded overhangs at newly broken sites by sampling randomly from a Poisson distribution described by the overhang λ value. Following each breakage cycle, each overhang is subjected to a round of deamination according to the rate calculated from δ_s, where each site is given the opportunity to undergo deamination if a pseudo-random number falls below the rate value. Finally, at the end of each deamination cycle, we summarize the current fragmentation λ value as 1/(mean current fragment length) and the current δ_s value as the (number of deamination sites)/(all overhang sites). When α = 1 and β = 1, λ increases linearly to approach the imposed λ value, while with higher β values, alternative patterns occur (Supplementary Figure S5).

RESULTS AND DISCUSSION

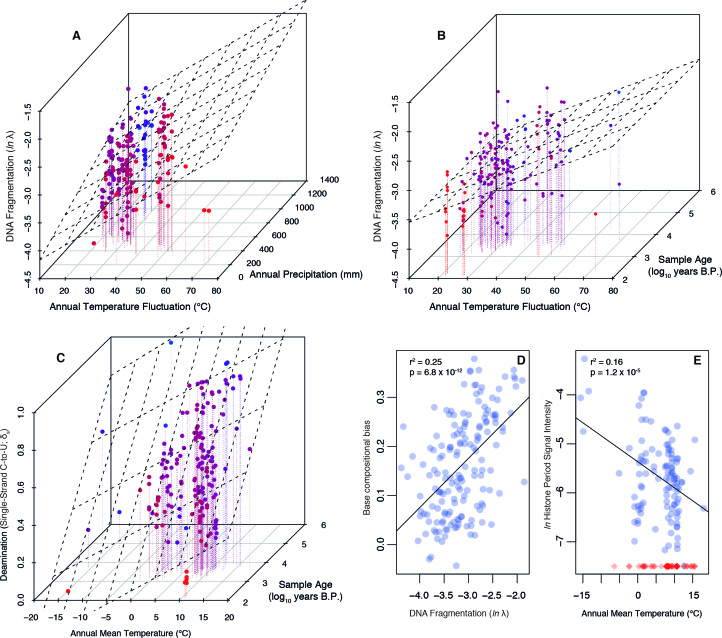
We found that cytosine deamination is strongly influenced by both sample age and site mean temperature (multiple r² = 0.264; age P = 1.9 × 10⁻⁹; temperature P = 1.52 × 10⁻⁵, model P = 2.54 × 10⁻¹⁰; Figure 2). Previous studies have identified age as the key critical predictor of deamination (60), but our finding is in line with predictions of a time-dependent hydrolytic process where activation energy is achieved more often at higher ambient temperatures. A rate of deamination can be calculated for any sample with a known age and partial conversion of exposed cytosines (Figure 3). The resulting rates vary widely and show a strong correlation with temperature (r² = 0.279; P = 1.23 × 10⁻¹²). In sum, deamination is a time-dependent process heavily modulated by temperature. When analyzing DNA fragmentation, however, we found that precipitation and thermal fluctuation were strongly significant predictors (multiple r² = 0.202; precipitation P = 0.0025; temperature fluctuation P = 6.18 × 10⁻⁸) but that age was not significantly correlated with the degree of fragmentation (P = 0.77), even when controlling for environmental conditions. We also find that in addition to the humidity and thermal fluctuation pattern, the degree of DNA fragmentation correlates strongly with base compositional biases. Specifically, datasets dominated by short fragments are significantly depleted of weakly-bonded nucleotide motifs (P = 6.79 × 10⁻¹², r² = 0.253; Figure 2), indicating that DNA breakdown follows predictable patterns with regard to microenvironment and nucleic acid biochemistry. Relatedly, we detected a histone-associated fragmentation bias (22) in the majority of our samples (n = 112), and we find that annual mean temperature is strongly associated with the intensity of this pattern (P = 1.2 × 10⁻⁵, r² = 0.16; Figure 2). Specifically, DNA breakdown in colder environments appears to more faithfully reflect cellular architecture and the in vivo genome context, whereas breakdown in warmer conditions is much less discriminant.

Figure 2.

Relationships between DNA degradation parameters and environmental variables. (A) DNA fragmentation is correlated with thermal fluctuation and precipitation. (B) DNA fragmentation is correlated with thermal fluctuation but is not influenced by sample age. (C) Deamination is a thermal age parameter, strongly associated with both age and temperature. Coloring in (A–C) is used to enhance the z-axis variation: red points are the nearest and blue are the most distant. (D) DNA fragmentation is highly predictive of base compositional biases, with fragmented datasets depleted of motifs with low base-stacking energy. (E) Histone periodicity in fragment length distribution is most pronounced in samples from cold environments. Blue circles represent samples where a histone periodicity estimate was possible (n = 112; see ‘Materials and Methods’ section for calibration against false positive results), red diamonds are samples where no periodicity was observed, visualized at −7.5 on the y-axis to reflect the observation of no detectable bias.

At present, the ancient DNA literature lacks clear consensus on the fundamental predictors of DNA fragmentation: one recent study identified a strong age dependency in DNA recovery through quantitative polymerase chain reaction (qPCR) analysis of a regionally controlled time series of bone samples (18). The authors proposed, on the basis of this result, that DNA degradation in ancient bone is mainly driven by thermal age-dependent hydrolytic depurination driving rate-constant fragmentation over time. Under this model, fragmentation is gradual and continues under a rate described by a decay constant until the bonds between all DNA fragments are destroyed and DNA is completely lost. Alternatively, a separate analysis (60) found no significant link between sample age and the degree of fragmentation. Consistent with this finding, early ancient DNA research pointed to very rapid initial DNA decay followed by subsequent stabilization (61), rather than fragmentation as an exponential random decay process. Additionally, controlled experiments using qPCR with recently deceased tissues demonstrate a precipitous immediate decline of endogenous DNA content and/or quality, followed by stabilization hypothesized to be linked to the mineral environment of bone (62). This model likewise contradicts the idea that DNA decay can be thought of strictly in terms of exponential breakdown under a decay constant. In total, evidence has been presented for both a rate-constant decay model and a more age-independent scenario. Here, our meta-analysis points to the statistical decoupling of age and fragmentation. We aimed to further test this finding with three strategies:

First, we recognize that there are numerous sources of variance that cannot be controlled in our meta-analysis across several studies—including sample excavation and storage, wet lab and computational methods, and species and tissue types—and that these sources of variance have the potential to obscure subtle relationships. If major sources of inter-study confounding variance in DNA fragmentation were present, the result would be the dampening of any statistical relationship between natural variables and fragmentation as the in situ signal for fragmentation is lost. If age was a significant predictor of DNA decay along with thermal fluctuation and humidity, it is difficult to imagine that only the age relationship would be lost due to post-excavation handling and inter-study variation. Therefore, we suggest that confounding variance is not a parsimonious explanation for the lack of a clear age-fragmentation relationship in the presence of a robust environmental association. However, to test this possibility more directly, we restricted our analysis from 185 datasets across 21 studies to 97 Bronze Age human genomes generated from a single study (26). We thereby control for species, tissue type, and biases in sample preparation and we consider a narrower timeframe and more constrained set of preservational conditions, eliminating several potential sources of confounding variance. Additionally, we recognize that by using modern climate estimates, we might obscure some subtle variation driven by climate fluctuations over long time periods. Restricting our analysis to just this Bronze Age dataset substantially constrains the temporal and geographic ranges, so that the sample set is expected to have been exposed to a less variable range of climate fluctuations compared with, for example, much older samples exposed to Pleistocene shifts. Under the same linear model as above (see ‘Materials and Methods’ section), we find that exactly as in the broader dataset, thermal fluctuation and precipitation were significant predictors of fragmentation (respectively, P = 0.014 and P = 4.2 × 10⁻⁴; multiple r² = 0.25), but age was still not a significant predictor of overall fragmentation (P = 0.420).

Second, we tested the fundamental assumption that from a single site, DNA from older samples is expected to be more fragmented than from younger ones. While we initially analyzed data from 94 different sites, the meta-dataset includes 114 pairs of samples from the same site separated by at least 100 years. Thus for these 114 pairs where we can eliminate inter-site variation, the older sample is predicted to be the more fragmented sample a significant majority of the time under the fundamental assumption that fragmentation increases with age in a single environment. Given 114 pairs of samples, only 55 (0.48) satisfy this assumption (‘successes’). The null hypothesis of 47–67 successes (P = 0.05 calculated using the β-distribution) cannot be rejected and indeed fewer than half of cases satisfy the basic assumption. By increasing the minimum age difference to 1000 years, we retain 55 valid pairwise comparisons and still observe no relationship between age and fragmentation, with only 27 (0.49) satisfying the basic assumption (null hypothesis at P = 0.05: 23–32 successes). We validated this approach by replicating the procedure with deamination, a known age-linked variable (26 and above). With deamination, we reject the null hypothesis and find a significant age effect (131 comparisons possible, 80 successes (0.61); null hypothesis at P = 0.05: 55–76 successes).

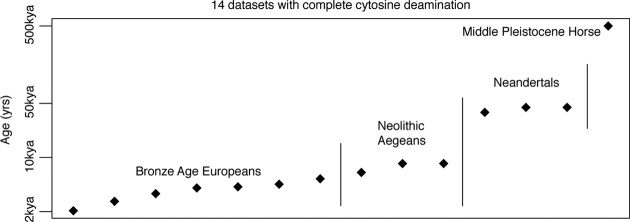
Finally, we routinely observe complete deamination of all exposed cytosine residues. This saturation of measurable deamination has been described in several samples previously (24) and is observed in 14 out of the 185 (7.6%) datasets analyzed here, spanning 2–500 kya (Figure 4). However, complete deamination in single-stranded overhangs is incongruent with a rate-constant fragmentation model: if fragmentation followed a simple rate-constant process that would yield a robust association between thermal age and fragmentation, new overhangs would continually be exposed with the expectation of intact cytosine, suppressing the proportion of deaminated residues and pre-empting complete deamination. Even by simulating deamination rates 10 fold faster than the most extreme of those estimated in our meta-analysis, deamination fails to converge to saturation under a rate-constant fragmentation model (see ‘Materials and Methods’ section; Supplementary Figure S5). In total, observing complete deamination under a rate-constant fragmentation model would require that the deamination rate outpaces the fragmentation rate so that new overhangs are rapidly saturated with deamination—all exposed cytosine residues are rapidly converted to uracil. Under such extreme deamination rates, however, it is implausible that deamination would show such a robust correlation with age across samples as observed here and elsewhere (60).

Figure 4.

Fourteen samples included in the meta-analysis with saturated cytosine-to-uracil deamination in single-stranded overhangs.

We find strong validation that age does not predict DNA fragmentation in our meta-dataset. However, we recognize that DNA breakdown by hydrolytic depurination is a well-validated and immutable chemical mechanism by which DNA decays exponentially according to first-order kinetics, producing a measurable half-life signal of molecular depletion (63). The mismatch between this predicted behavior and our findings indicates that the preservation state of ancient DNA is determined by multiple processes and cannot be attributed to a simple fragmentation rate as suggested in a rate-constant fragmentation model. Instead, we propose a multi-stage DNA fragmentation model: first, physical and biotic stressors cause rapid breakdown of nucleic acids shortly after organism death. While microbes and cellular processes (e.g. autolysis and nuclease activity) rapidly degrade a large fraction of endogenous DNA—depending on tissue type and depositional environment—fragmentation appears to reach an initial threshold and then stabilize somewhat in contexts where DNA has the potential for long-term preservation.

The strong association of humidity and thermal fluctuation with DNA fragmentation suggests that processes like the loss of bioapatite surface area caused by diagenetic recrystallization and physical shearing effects of hydraulic fluctuations in bone, for example, play a role in the initial breakdown process. Further, DNA may reach a size in bony contexts—the majority of our re-analyzed datasets—where it can penetrate the protective internal porosity of bone and gain some additional protection. The counterintuitive result that DNA is sometimes better preserved in cooked than uncooked medieval bone may offer support for this scenario ((64), although see (65) for for further analysis of cremated bone). In our analysis, 15 plant samples from herbaria (39) fit with the overall fragmentation model—comparing linear model residuals reveals no significant difference between plant samples and non-plant samples (Welch's t-test, P = 0.44). However, they make up a very small fraction of the variation here and because of the possible role of the mineral makeup of bone in DNA preservation across samples (62), we suggest that re-analysis of plant data across a much greater age range will be important in understanding any possible differences in preservation between plant and animal tissues. Over a short time span, age-dependency in fragmentation has been suggested in plant tissues (66), but a paucity of paleogenomic plant data currently precludes a comprehensive analysis spanning thousands of years. In total, our meta-analysis and model are necessarily focused on mammalian hard tissue (n = 169 out of 185 datasets) given dataset availability. As more datasets are generated from diverse systems and tissue types, we expect further refinement of these general findings to reflect a more nuanced understanding behind the specific drivers of DNA diagenesis and factors underlying preservation. For example, DNA is integrated into hair during programmed cell death and keratinization leading to some amount of immediate shearing which might affect downstream processes (67). Thus ancient DNA in hair might warrant a modified set of expectations for preservation relative to bony tissue given a certain background environment. Recent experimentation comparing tooth cementum and petrous bone DNA characteristics reinforces the necessity of integrating sample type information in assessing DNA degradation in the future (65). Finally, the relationships between biomolecule preservation and the microenvironment of sample deposition (e.g. soil pH, mineral content, sample depth and aerobic activity) bear significant further investigation as more datasets become available.

Previous research identified a strong age dependency in DNA recovery—assayed by qPCR—in a controlled time-series of bone samples from a regional set of depositional sequences and interpreted the result as evidence for an exponential decay process due to time-dependent DNA fragmentation (18). However, bulk diffusion of DNA—rather than rate-constant fragmentation—provides an equally parsimonious scenario for the observed signal. Specifically, the previous study estimated a 521-year half-life for a target fragment of 242 bp under the conditions of the site (18). In the example from that study (18), researchers inferred a nucleotide fragmentation rate (k) of 5.5 × 10⁻⁶ damage events per nucleotide per year on the basis of a strong relationship between age and 242 bp target molarity across a large set of mass-standardized bone samples. Under a rate-constant fragmentation model where k = 5.5 × 10⁻⁶, the probability of retaining any fragment of length L per year is the probability that no random breakage event occurs at any of its sites, or (1−k)^L and the probability of fragment loss (k_L) is 1−(1−k)^L. For a 242 bp target, therefore, k₂₄₂ = 1.33 × 10⁻³—each year 0.0013 of remaining 242 bp templates are severed on average. However, this model assumes no time-dependent loss in DNA by mechanisms other than fragmentation; if fragmentation stabilizes and bulk depletion of endogenous DNA continues, a similar pattern would result. Specifically, if each fragment has a 0.0013 probability of being lost to bulk DNA movement rather than fragmentation, the same qPCR signal of decreasing target molarity over time would result.

Our results do not conflict with the previous experiment identifying a time-dependent decay behavior in relative copy number of a given fragment size, but decay behavior in the molarity of a target DNA fragment over time in a qPCR assay could be attributed to either rate-constant fragmentation (18) or bulk loss of endogenous DNA. We propose that bulk DNA loss is congruent with both the previous qPCR signal (18) and our meta-analysis, whereas exponential decay by fragmentation is not supported as the primary mechanism of DNA loss in our study. Therefore, we propose that much of the time-dependent nature of ancient DNA recovery may be due to bulk loss of DNA from tissue. Recent research focusing on the dense, non-vascularized petrous part of the temporal bone as a source of high endogenous DNA content (27,65) demonstrates that targeting ‘semi-closed’ systems with little opportunity for chemical exchange may be the best strategy to continue pushing the boundaries of DNA preservation by combating this diffusion process. This idea has also been illustrated in studies dealing with DNA preserved in hair, which is thought to confer a protective microenvironment that impedes biological degradation, leaching and possibly hydrolytic damage, and therefore often constitutes a good source of relatively high-quality endogenous DNA (32,67).

We suggest that rate-constant fragmentation through hydrolytic depurination is seldom the limiting factor to long-term DNA preservation, but we offer some caveats: fragmentation through depurination is a well-characterized process (63) and we do not propose that it is irrelevant for long-term DNA degradation. We suggest, rather, that the rate of this process is significantly slower than previously estimated in many ancient tissues (18) and the signal over the time span re-analyzed here is overprinted by other factors in a multi-faceted breakdown process. Thus when estimating the value of ‘lambda’ for a dataset—the parameter describing fragment length distribution—we are analyzing the outcome of multiple processes rather than inferring a simple decay rate. Further, importantly, any paleogenomic meta-analysis is fundamentally limited to those scenarios in which DNA actually survives over Quaternary timescales and so hydrolytic fragmentation as previously described might be a central mechanism for the total postmortem depletion of DNA in many tissues and conditions. That is to say, we can only analyze DNA that has survived, which may represent an abnormal mode of diagenesis. Our model for ancient DNA decay therefore necessarily speaks only to the special case in which conditions exist for long-term DNA survival. The immutable depurination process likely still imposes practical limits on DNA recovery in deep time and recovering Mesozoic DNA, for example, remains extremely unlikely. However, semi-closed chemical exchange systems like the petrous bone, though rare, offer excellent potential for the long-term retention of DNA in tissues and extraordinary preservational microenvironments created by chemical interactions have proven valuable for deep-time protein preservation (68). Breaching the current Middle Pleistocene age boundary of genomics seems entirely plausible.

AVAILABILITY

Analyzes were based on publicly available datasets. Summary data are available for reanalysis as Supplemental Dataset S1. Additionally, all metadata and results from analyzes, custom scripts and run logs from analyzes have been uploaded to the Dryad Digital Repository (doi:10.5061/dryad.5r10j).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.

FUNDING

Natural Environment Research Council Independent Research Fellowship [NE/L012030/1 to L.K.]. Funding for open access charge: Natural Environment Research Council.

Conflict of interest statement. None declared.