Abstract
Synthetic DNA is a highly programmable nanoscale material that can be designed to self-assemble into 3D structures that are fully determined by underlying Watson–Crick base pairing. The double crossover (DX) design motif has demonstrated versatility in synthesizing arbitrary DNA nanoparticles on the 5–100 nm scale for diverse applications in biotechnology. Prior computational investigations of these assemblies include all-atom and coarse-grained modeling, but modeling their conformational dynamics remains challenging due to their long relaxation times and associated computational cost. We apply all-atom molecular dynamics and coarse-grained finite element modeling to DX-based nanoparticles to elucidate their fine-scale and global conformational structure and dynamics. We use our coarse-grained model with a set of secondary structural motifs to predict the equilibrium solution structures of 45 DX-based DNA origami nanoparticles including a tetrahedron, octahedron, icosahedron, cuboctahedron and reinforced cube. Coarse-grained models are compared with 3D cryo-electron microscopy density maps for these five DNA nanoparticles and with all-atom molecular dynamics simulations for the tetrahedron and octahedron. Our results elucidate non-intuitive atomic-level structural details of DX-based DNA nanoparticles, and offer a general framework for efficient computational prediction of global and local structural and mechanical properties of DX-based assemblies that are inaccessible to all-atom based models alone.
INTRODUCTION
Synthetic DNA nanotechnology leverages the secondary structure of DNA to reliably program 3D geometries for diverse applications in biotechnology and nanoscale materials science (1–3). Scaffolded DNA origami (4,5) employs a single-stranded DNA (ssDNA) scaffold strand that forms a template for shorter DNA substrands called staples, offering near-quantitative yield over the final, self-assembled product for DX-based wireframe scaffolded DNA origami structures. Watson–Crick base pairing between the scaffold strand and staple strands enables folding ssDNA into structured DNA assemblies with diverse geometries, including wireframe structures (6–11), 2D surfaces (4,12–15), and 3D solids (16–20). Alternatively, structured DNA assemblies of these three types of geometries can be programmed without scaffold strands (21–26).
Integral to the effective design and synthesis of structured DNA assemblies is computer-aided design (CAD). Manual software tools including caDNAno (27) and Tiamat (28) have been developed to aid in this process. More recently, the top-down, geometry-based algorithms vHelix (10) and DAEDALUS (11) have been developed to automate the design of nucleic acid sequences in near-fully and fully automated manners, respectively, for wireframe geometries. The finite element (FE) modeling approach CanDo is also routinely used to predict the 3D equilibrium conformation of programmed DNA assemblies based on a coarse-grained representation of B-form DNA (5,29,30). Because numerous applications of structured DNA assemblies exploit control over the angstrom-level positioning of individual bases (20,31–33), computational investigation of atomic-level structure together with automated tools that predict non-intuitive equilibrium shapes are of great utility to the field of structural DNA nanotechnology.
While numerous computational tools are capable of predicting equilibrium solution structures of nucleic acid assemblies, all-atom molecular dynamics (MD) simulations (34) in principle represent the gold standard for 3D structure prediction (35,36). All-atom models are capable of capturing the detailed structural, mechanical, and physicochemical properties of DNA assemblies, albeit at significant computational cost that limits their application using conventional computing resources to short time-scale simulations and low molecular weight assemblies. Larger-scale assemblies can be simulated on limited time-scales of tens to hundreds of nanoseconds using high performance computing resources that are not broadly available (34). In contrast, coarse-grained models use united atom representations to model clusters of atoms and their interactions, thereby reducing the total number of degrees of freedom (DOF) and associated computational cost (37–49) at the expense of all-atom resolution.
In order to maximize structural prediction accuracy while reducing computational cost, numerous coarse-grained models for DNA have been developed (50–53). Nucleotide-level models represented in oxDNA2 (54), an enhanced version of oxDNA (55), treat each nucleotide as a rigid body that interacts with other nucleotides via an empirical potential. This coarse-grained model has been applied to simulate hybridization kinetics (56), overstretching (57), equilibrium structures (58), and self-assembly (59) of DNA. An alternative category of models, the 3-site-per-nucleotide (3SPN) model (60,61), uses three interaction sites to simulate the base, sugar, and phosphate group of a nucleotide, and has been used to predict DNA melting curves and persistence lengths (62). In addition, chemical group-level models such as the MARTINI coarse-grained force field (63–65) have been extended to model DNA by treating each nucleotide as six or seven beads (66). These coarse-grained models of DNA have been discussed in more detail in recent review articles (67–69). While useful for predicting conformational dynamics of DNA assemblies, particularly involving duplex dissociation, large-scale equilibrium structural and mechanical properties of highly structured DNA assemblies programmed using the principle of scaffolded DNA origami remain challenging to predict using these models.
As an alternative, here we apply our FE modeling framework CanDo to solve for the ground-state equilibrium structure and mechanical properties of structured DNA nanoparticles. Compared with the aforementioned computational tools, our FE model treats DNA duplexes as worm-like chains from polymer physics (70) or elastic beams from mechanical engineering (71) accounting for the full axial, torsional, and bending properties of duplex B-form DNA. Double and single-crossovers are treated explicitly by constraining the relative motions of joined duplexes, and bulges and open nicks are similarly modeled empirically using spring-like elements. A nonlinear FE solver is then used to compute the ground-state equilibrium structure (5,29,30) and mechanical properties of stable DNA assemblies, the latter comprising thermal fluctuations (29,30,72) and force-deformation responses (20), with significantly reduced computational cost compared with all-atom and nucleotide-level models. Previously, we introduced the FE framework CanDo (5,29) to compute equilibrium structures of a class of DNA assemblies in which DNA duplexes are placed on a honeycomb (16) or square (18) lattice. This lattice requirement is relaxed in the lattice-free version of CanDo (30), which places DNA duplexes in arbitrary positions and orientations in 3D space. Because each of these models neglected the presence of bulges and open nicks that are commonplace in DX-based assemblies (9,11,23), here we incorporate these motifs by parameterization using all-atom models. Specifically, we derive the ground-state configurations of the FE models of bulges and open nicks from their respective all-atom models and perform all-atom MD simulations of the bulge to determine its rotational stiffness coefficients. Further, we apply all-atom MD to model the equilibrium geometry and mechanical properties of a limited set of DX-based nanoparticles to compare predictions of our coarse-grained model with both experimental cryo-electron microscopy (cryo-EM) data and all-atom modeling.
MATERIALS AND METHODS
Lattice-free finite element model of structured DNA assemblies
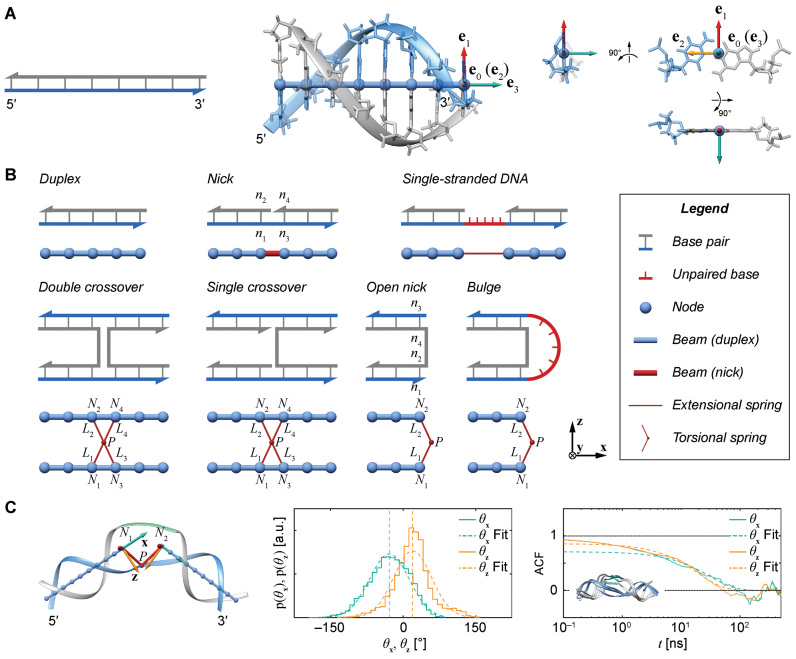
The FE method was originally used to model four distinct topological motifs defined by the secondary structure of programmed DNA assemblies, which included duplexes, nicks, ssDNA, and double crossovers (5,29), where duplexes were assumed to reside on a square or honeycomb lattice. Subsequently, the requirement that duplexes reside on such lattices was removed and single crossovers were also incorporated into the model to account for their higher conformational flexibility with respect to double-crossovers (30). Here, we additionally introduce a bulge model to facilitate simulation of DX-based objects, and also differentiate between open and closed nicks due to their distinct mechanical properties associated with stacked versus non-stacked base pairs (Figure 1). Closed nicks are identified using the four nucleotides denoted n1, n2, n3 and n4, in the CAD design, where base pair n1–n2 stacks with base pair n3–n4 (Figure 1B). Otherwise, the two base pairs are modeled as an open nick (Figure 1B).
Figure 1.
Mechanical models of secondary structural motifs of programmed DNA assemblies considered in this work. (A) Each base pair in the secondary structure of a programmed DNA assembly (left) is modeled as a FE node represented as a blue sphere located at 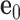 with three reference axes
with three reference axes 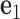 ,
, 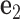 and
and 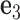 (center). There is a one-to-one correspondence between the reference frame
(center). There is a one-to-one correspondence between the reference frame 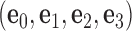 and the all-atom model of the same base pair (center). Thus, the FE model can be represented by an all-atom model (right). The arbitrarily chosen strand, to which axis
and the all-atom model of the same base pair (center). Thus, the FE model can be represented by an all-atom model (right). The arbitrarily chosen strand, to which axis 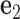 points to, is colored in blue, and the other strand is in gray. (B) A set of secondary structural motifs (top) and the corresponding FE models (bottom) in programmed DNA assemblies. Nucleotides and the FE model in a given motif are colored in red, while those in the flanking base pairs are colored in gray. A global reference coordinate system
points to, is colored in blue, and the other strand is in gray. (B) A set of secondary structural motifs (top) and the corresponding FE models (bottom) in programmed DNA assemblies. Nucleotides and the FE model in a given motif are colored in red, while those in the flanking base pairs are colored in gray. A global reference coordinate system 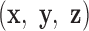 is defined for the FE models of double crossovers, single crossovers, open nicks, and bulges. The mechanical model for a double crossover and that for a single crossover each contain two torsional springs: one connects nodes
is defined for the FE models of double crossovers, single crossovers, open nicks, and bulges. The mechanical model for a double crossover and that for a single crossover each contain two torsional springs: one connects nodes  and
and 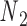 , and the other one connects nodes
, and the other one connects nodes 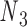 and
and 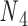 . Base pair n1–n2 stacks with base pair n3–n4 in a nick but not in an open nick. (C) (Left) FE and the corresponding all-atom model, rendered in ribbons, of a bulge between nodes
. Base pair n1–n2 stacks with base pair n3–n4 in a nick but not in an open nick. (C) (Left) FE and the corresponding all-atom model, rendered in ribbons, of a bulge between nodes 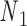 and
and 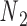 . The 5΄-end and the 3΄-end of the blue strand are marked. In addition, the reference axes x, y and z are defined as the reference axes
. The 5΄-end and the 3΄-end of the blue strand are marked. In addition, the reference axes x, y and z are defined as the reference axes 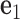 ,
, 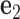 , and
, and 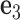 of node
of node 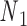 . (Center) Two probability distributions of the two rotation angles
. (Center) Two probability distributions of the two rotation angles  and
and 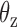 about axes x and z, respectively, computed from all-atom MD simulations. A Gaussian is fitted to each distribution. Means of the fitted Gaussians are plotted as vertical dashed lines. (Right) The autocorrelation functions (ACFs) of
about axes x and z, respectively, computed from all-atom MD simulations. A Gaussian is fitted to each distribution. Means of the fitted Gaussians are plotted as vertical dashed lines. (Right) The autocorrelation functions (ACFs) of 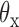 and
and 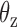 from all-atom MD simulations. A single exponential is fitted to each ACF. The inset shows four snapshots sampled at 200, 400, 600, and 800 ns in the MD trajectory of the bulge. These snapshots are aligned with each other.
from all-atom MD simulations. A single exponential is fitted to each ACF. The inset shows four snapshots sampled at 200, 400, 600, and 800 ns in the MD trajectory of the bulge. These snapshots are aligned with each other.
Each base pair in a DNA assembly is modeled as a FE node with three translational DOF and three rotational DOF in a global 3D Cartesian coordinate system (Figure 1A). Such a node is rigidly connected to a right-handed orthonormal reference frame 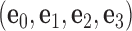 with the center
with the center 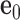 located at the position of the node. The all-atom model of a DNA assembly determines the reference frames of all nodes, and vice versa. From the all-atom base pair model, the convention used by the software 3DNA (73) defines the origin of the reference frame and its three orthogonal directions: the minor-major groove direction, the base-base direction, and the direction normal to the base pair plane. The center
located at the position of the node. The all-atom model of a DNA assembly determines the reference frames of all nodes, and vice versa. From the all-atom base pair model, the convention used by the software 3DNA (73) defines the origin of the reference frame and its three orthogonal directions: the minor-major groove direction, the base-base direction, and the direction normal to the base pair plane. The center 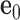 is defined as the reference point, and axes
is defined as the reference point, and axes 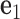 ,
, 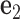 and
and 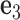 coincide with the three reference directions. In this study,
coincide with the three reference directions. In this study, 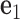 points to the major groove,
points to the major groove,  points to the base in an arbitrarily chosen strand, and
points to the base in an arbitrarily chosen strand, and 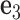 is perpendicular to the base pair plane and points in the 5΄ to 3΄ direction of the chosen strand. From the reference frame of a node, the all-atom model of the same base pair is constructed by placing the standard reference atomic structure such that its reference point and reference axes coincide with the center and axes of the frame, respectively (30,33).
is perpendicular to the base pair plane and points in the 5΄ to 3΄ direction of the chosen strand. From the reference frame of a node, the all-atom model of the same base pair is constructed by placing the standard reference atomic structure such that its reference point and reference axes coincide with the center and axes of the frame, respectively (30,33).
In its ground-state configuration with zero mechanical free energy, an isolated duplex consisting of N base pairs (bp) has the geometry of a straight line-segment with length 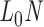 , where
, where 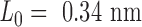 per nucleotide. The duplex has empirical stretch modulus of 1100 pN, bend modulus of 230 pN nm2, and twist modulus of 460 pN nm2, and is therefore modeled as N FE nodes connected by
per nucleotide. The duplex has empirical stretch modulus of 1100 pN, bend modulus of 230 pN nm2, and twist modulus of 460 pN nm2, and is therefore modeled as N FE nodes connected by  two-node Hermitian beam elements with the same stretch, bend, and twist moduli (Figure 1B) (5,29). The connection of two stacking base pairs in a duplex is modeled as a beam element with geometric and mechanical properties from experimental values of B-form DNA duplexes. Specifically, the beam element has a ground-state axial length of 0.34 nm and a right-handed twist-angle of
two-node Hermitian beam elements with the same stretch, bend, and twist moduli (Figure 1B) (5,29). The connection of two stacking base pairs in a duplex is modeled as a beam element with geometric and mechanical properties from experimental values of B-form DNA duplexes. Specifically, the beam element has a ground-state axial length of 0.34 nm and a right-handed twist-angle of 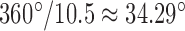 . Duplexes with a nick between two stacked base pairs are assumed to have the same ground-state geometric and mechanical properties as a standard B-form duplex, and are therefore modeled using the same beam element (Figure 1B) (30). Un-stacked, or open nicks are instead modeled using a reduced empirical stiffness factor that corresponds to the 100-fold reduced bending and twisting stiffness of B-form DNA assumed previously based on TEM images of honeycomb or square lattice-based geometries (29). Consistent with our previously published modeling approach, ssDNA is modeled to have nonlinear spring-like mechanical properties of an extensible worm-like chain (29).
. Duplexes with a nick between two stacked base pairs are assumed to have the same ground-state geometric and mechanical properties as a standard B-form duplex, and are therefore modeled using the same beam element (Figure 1B) (30). Un-stacked, or open nicks are instead modeled using a reduced empirical stiffness factor that corresponds to the 100-fold reduced bending and twisting stiffness of B-form DNA assumed previously based on TEM images of honeycomb or square lattice-based geometries (29). Consistent with our previously published modeling approach, ssDNA is modeled to have nonlinear spring-like mechanical properties of an extensible worm-like chain (29).
Double crossovers have a ground-state geometry defined by two antiparallel duplexes with an interhelical distance 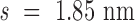 and a right-handed interhelical angle
and a right-handed interhelical angle 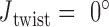 (30). The mechanical properties of a double crossover are represented by a torsional spring with linear stiffness connecting two duplexes and are modeled as two alignment elements implemented in the commercial FE software ADINA (ADINA R&D, Watertown, MA, USA) (Figure 1B) (30). In the first alignment element, line segments
(30). The mechanical properties of a double crossover are represented by a torsional spring with linear stiffness connecting two duplexes and are modeled as two alignment elements implemented in the commercial FE software ADINA (ADINA R&D, Watertown, MA, USA) (Figure 1B) (30). In the first alignment element, line segments  and
and  each have one end rigidly attached to nodes
each have one end rigidly attached to nodes  and
and 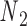 , respectively, and the other end located at a pivot P, which is located at the centroid of the four nodes
, respectively, and the other end located at a pivot P, which is located at the centroid of the four nodes 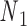 ,
, 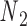 ,
,  , and
, and  . The second alignment uses line segments
. The second alignment uses line segments 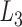 and
and  to connect nodes
to connect nodes 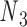 and
and 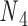 with the same pivot. Note that the conformation of a double crossover may reside in one of multiple ground-states, each of which has a different value of
with the same pivot. Note that the conformation of a double crossover may reside in one of multiple ground-states, each of which has a different value of 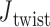 . For example, the ground-state value of
. For example, the ground-state value of 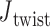 can be 60° for concentric rings and lattices (30) or 180° for paranemic crossovers consisting of two parallel duplexes (74). The two alignment elements allow the duplex with nodes
can be 60° for concentric rings and lattices (30) or 180° for paranemic crossovers consisting of two parallel duplexes (74). The two alignment elements allow the duplex with nodes 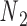 and
and 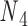 to rotate about the pivot. Determined in previous work (30), the rotational stiffness coefficients of the rotation of the helix with nodes about the reference axes x, y and z (Figure 1B) are
to rotate about the pivot. Determined in previous work (30), the rotational stiffness coefficients of the rotation of the helix with nodes about the reference axes x, y and z (Figure 1B) are 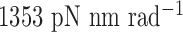 ,
, 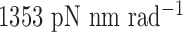 and
and 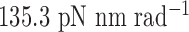 , respectively (Table 1).
, respectively (Table 1).
Table 1. Rotational stiffness coefficients of the double crossover, the single crossover, the open nick and the bulge.
| Rotational stiffness coefficients [pN nm rad–1] (Figure 1B) | Double crossover | Single crossover | Open nick | Bulge |
|---|---|---|---|---|
| About axis x | 1353 | 1353 | 13.53 | 13.53 |
| About axis y | 1353 | 1353 | 0 | 0 |
| About axis z | 135.3 | 13.53 | 13.53 | 13.53 |
Single crossovers are assumed to have a ground-state geometry that is identical to double crossovers. The FE model of a single-stranded crossover is identical to that of a double-stranded crossover except that the rotational stiffness defined by pivoting about the reference axis z is reduced (Figure 1B) (72). In contrast, rotation about the x-axis or the y-axis results in steric overlap between the duplexes in the single crossover (Figure 1B). Thus, the rotational stiffness about the x-axis and that about the y-axis are partially contributed by the interaction between the two duplexes in the single crossover and are not reduced. In the present work, we set the rotational stiffness about the z-axis to be 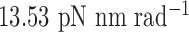 , the same value as in open nicks and bulges shown below, while keeping the other two rotational stiffness coefficients the same as those in a double crossover (Table 1).
, the same value as in open nicks and bulges shown below, while keeping the other two rotational stiffness coefficients the same as those in a double crossover (Table 1).
Open nicks and bulges have the same ground-state geometry as double crossovers with base pairs on one side of the pivot point P removed. In contrast to a double crossover or a single crossover, an open nick or a bulge is modeled as only one alignment element (Figure 1B). The position of the pivot P relative to the nodes  and
and  is determined from the average Cartesian coordinates of atoms P and O3΄, the chemical bond between which connects two neighboring nucleotides on the same strand, in the reference coordinate system of a base pair (Supplementary Figure S1). The alignment element allows the duplex with node
is determined from the average Cartesian coordinates of atoms P and O3΄, the chemical bond between which connects two neighboring nucleotides on the same strand, in the reference coordinate system of a base pair (Supplementary Figure S1). The alignment element allows the duplex with node 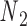 to rotate about the pivot (Supplementary Figure S1). Compared with those of double crossovers, the rotational stiffness coefficients of bulges about the reference axes x and z are reduced by factors of 100 and 10, respectively, which is estimated in the Results and Discussion section from the amplitude of thermal fluctuations in MD trajectories using the equipartition theorem. Therefore, these two rotational stiffness coefficients are both set to 13.53 pN nm rad−1 (Table 1). In a collection of recently published assemblies, bulges can rotate about the reference axis y without causing significant structural deformation (9), and thus the rotational stiffness coefficients of bulges about the reference axis y are reduced to zero. An open nick has the same secondary structure as a bulge except for the absence of an unpaired strand that is mechanically flexible (Figure 1B). Therefore, we assume the three rotational stiffness coefficients of open nicks to be identical to those of bulges.
to rotate about the pivot (Supplementary Figure S1). Compared with those of double crossovers, the rotational stiffness coefficients of bulges about the reference axes x and z are reduced by factors of 100 and 10, respectively, which is estimated in the Results and Discussion section from the amplitude of thermal fluctuations in MD trajectories using the equipartition theorem. Therefore, these two rotational stiffness coefficients are both set to 13.53 pN nm rad−1 (Table 1). In a collection of recently published assemblies, bulges can rotate about the reference axis y without causing significant structural deformation (9), and thus the rotational stiffness coefficients of bulges about the reference axis y are reduced to zero. An open nick has the same secondary structure as a bulge except for the absence of an unpaired strand that is mechanically flexible (Figure 1B). Therefore, we assume the three rotational stiffness coefficients of open nicks to be identical to those of bulges.
Generation and solution of finite element models
The solution procedure for finding the ground-state minimum energy structure is identical to that presented in our previous work (30). Briefly, the nucleotide sequences and secondary structure of a DNA nanostructure are modeled as a graph in which each vertex represents a nucleotide, and each edge models either a phosphodiester bond or a Watson–Crick base pair. An algorithm then traverses the graph and finds all double crossovers and single crossovers, as well as the connectivity between them via duplexes, nicks, ssDNA, open nicks, and bulges, in order to generate the initial configuration of the FE model as interconnected secondary structural motifs at their individual ground states. The mechanical properties of the FE model are assumed to be linear, even though geometric nonlinearities are accounted for in the FE model and solution procedure. FE model solution is performed by ADINA Version 8.9 (ADINA R&D, Watertown, MA, USA) using the full Newton iteration method that relaxes the FE model and finds the equilibrium structure with minimum mechanical free energy. The FE solution procedure performs a dynamic analysis with the Bathe Composite method and Rayleigh damping (71). The solution procedure consists of 1230 solution time steps. At time step zero, the FE model is in its initial configuration, which is chosen to be the ground-state FE model of secondary structural motifs placed in the same positions and orientations as those in the CAD design. Restorative forces and moments are then exerted on each pair of ends of connected motifs such that they coincide in the positions and orientations by time step 1000. The simulation is then run for an additional 230 time steps to ensure relaxation of the entire FE model. Energy and force/moment convergence criteria are used with relative energy tolerance of 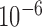 and relative force and moment tolerances of 0.01.
and relative force and moment tolerances of 0.01.
All-atom molecular dynamics simulations
All-atom MD simulations were performed for two DNA origami nanoparticles, a tetrahedron and an octahedron (Figure 3A–E), as well as an unconstrained DNA duplex bulge consisting of five ssDNA bases (Figures 1C and 2C), an unconstrained 3-arm vertex region corresponding to the vertices of the tetrahedron, and an unconstrained 4-arm vertex region corresponding to the vertices of the octahedron (Figure 2B and C). Both the 3-arm and 4-arm vertices have 21 bp per edge, with a vertex bulge region consisting of five ssDNA bases. The 3-arm vertex includes two double-crossovers and one single-crossover on the edges, and the 4-arm vertex includes two double-crossovers and two single-crossovers on the edges. All-atom Protein Data Bank (PDB) files for the tetrahedron (63 bp per edge), the octahedron (52 bp per edge), the bulge, and the 3-arm and 4-arm vertices were generated using the atomic structure generator in the lattice-free implementation of CanDo (30), where the DNA scaffold routing for the tetrahedron and the octahedron were constructed using DAEDALUS (11). All-atom systems were solvated in TIP3P water (75) with explicit Mg2+ and Cl− ions added to neutralize DNA charges and to set the simulation cell Mg2+ ion concentration to 12 mM, consistent with experimental conditions (11).
Figure 3.
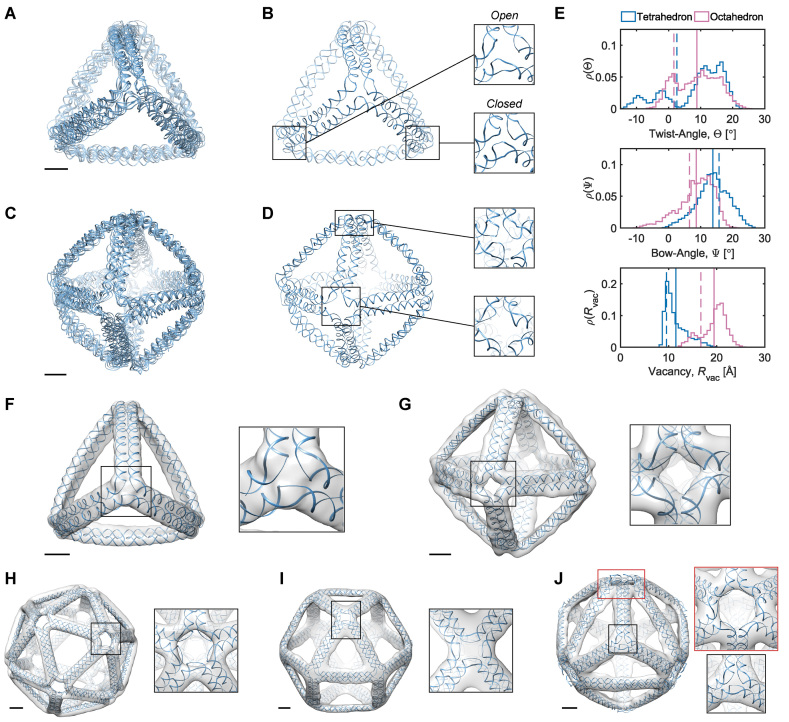
Equilibrium structures of the polyhedral nanoparticles generated by the FE framework and the MD simulations. (A) Four aligned snapshots at 25, 50, 75, and 100 ns of the MD trajectory of the tetrahedron. (B) The snapshot at 25 ns of the tetrahedron with vertices with the absence and presence of interactions between unpaired bases termed as ‘open vertices’ and ‘closed vertices’, respectively. (C) Four snapshots at 25, 50, 75, and 100 ns of the MD trajectory of the octahedron are rendered in the same way as in (a). (D) The snapshot at 25 ns of the octahedron. (E) The distribution of the twist-angle, bow-angle, and radial vacancy during the MD simulations of the tetrahedral and octahedral nanoparticles. Each angle is averaged over the four vertices of the tetrahedron or the six vertices of the octahedron. Solid lines indicate the mean value during the MD trajectory and dashed lines indicate the value obtained from the ground-state FE model. (F–J) FE equilibrium structures, colored in blue, of (F) the tetrahedron, (G) the octahedron, (H) the icosahedron, (I) the cuboctahedron, and (J) the reinforced cube were fit into the reconstructed cryo-EM map using the software UCSF Chimera (91). All scale bars are 5 nm.
Figure 2.
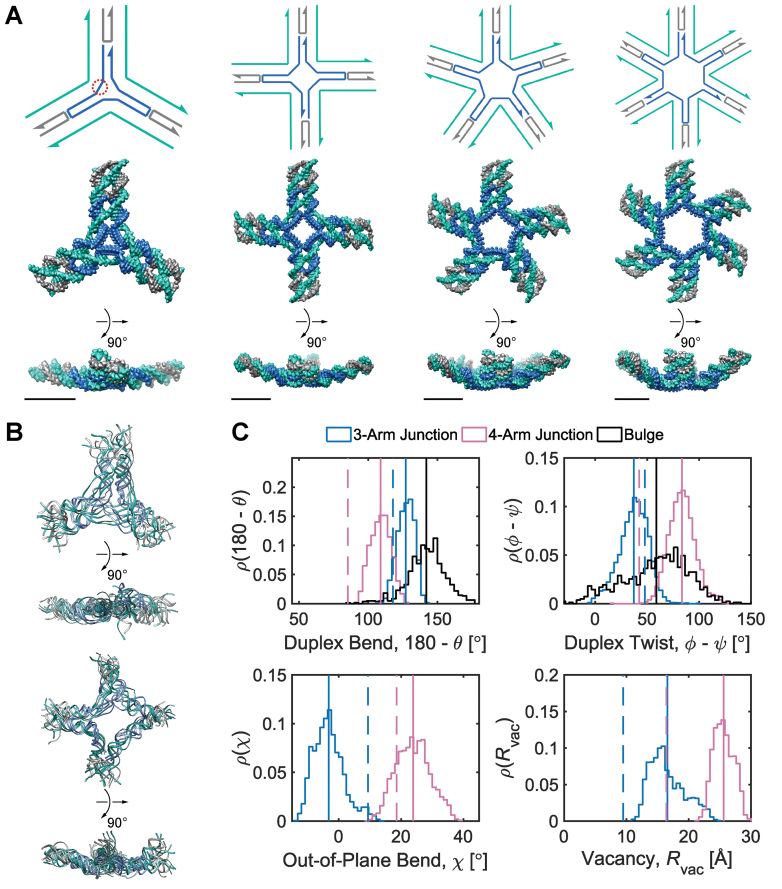
Mechanical models of unconstrained multi-arm vertices. (A) Secondary structures (top) and corresponding FE models at the ground-state mechanical free energy (bottom) of 3-arm, 4-arm, 5-arm, and 6-arm vertices consisting of duplexes, double crossovers, single crossovers, and bulges. An N-arm vertex contains N ssDNA regions, each of which comprises five unpaired thymine bases. As an example, one of the three ssDNA regions in the 3-way vertex is encircled by red dots. The secondary structure and the first orthogonal view of each vertex are oriented such that the minor grooves of DNA at the center of the vertex face the reader. The FE models are represented as all-atom models with DNA stranded colored in the same way as in the secondary structures. All scale bars are 5 nm. (B) (Top) Four aligned snapshot sampled at 100, 200, 300, and 400 ns in the MD trajectory of the 3-arm junction. (Bottom) Four aligned snapshot sampled at 100, 200, 300, and 400 ns in the MD trajectory of the 4-arm junction. (C) Histogram of various geometric values calculated from MD trajectories. Duplex bend-angles in degrees (top left), duplex torsional twist-angles in degrees (top right), out-of-plane bend-angles in degrees (bottom left), and radial vacancies in angstroms (bottom right) during 500-ns (3-arm junction, 4-arm junction) and 1-μs (duplex bulge) MD simulations. Solid lines indicate the mean value during the MD trajectory and dashed lines indicate the value obtained from the ground-state FE model.
MD simulations were performed using the program NAMD2 (76) with the CHARMM36 force field (77–80) and Allnér Mg2+ parameters (81) using an integration time step of 2 fs and periodic boundary conditions applied in an orthogonal simulation cell. Van der Waals energies were calculated using a 12 Å cut-off, a switching function applied from 10 to 12 Å, and a 14 Å pair list distance. The Particle Mesh Ewald (PME) method (82) was used to calculate full electrostatics with a maximum grid point spacing of 1 Å. Full electrostatic forces were computed every two time steps (every 4 fs) and non-bonded forces were calculated at each time step (2 fs). Simulations were performed in the NpT ensemble using the Nosé–Hoover Langevin piston method (83,84) for pressure control with an oscillation period of 200 fs and a damping time of 100 fs. Langevin forces were applied to all heavy atoms for temperature control (300 K) with coupling coefficients of 5 ps−1. All hydrogen atoms were constrained to their equilibrium lengths during the simulation and system configurations were recorded every 1 ps for downstream analysis of coordinate trajectories. Unconstrained all-atom energy minimization was performed in the orthogonal simulation cell prior to dynamics using the conjugate-gradient and line search minimization algorithms implemented in NAMD2 for 10 000 steps. Prior to production MD, solvent and ions were allowed to equilibrate for 1 ns while the nucleic acid atoms were spatially constrained. During this equilibration phase, the integration time step was 1 fs, and Langevin forces were applied to all atoms, including hydrogen atoms. For production MD, all simulated systems were run for a minimum of 150 ns.
Due to the large number of atoms in the all-atom solvated models of the tetrahedron and octahedron, production MD simulations were run only for 150 ns. The unconstrained all-atom solvated models of the 3-arm and 4-arm vertices were run for 500 ns, and the unconstrained all-atom solvated model of the duplex bulge was run for 1 μs. Supplementary Table S1 shows the ramp-up in processor-hours required for the larger systems studied. To determine whether the properties studied in the all-atom models of the tetrahedron, octahedron, unconstrained 3- and 4-arm vertices, and the unconstrained duplex bulge represent equilibrium values, temporal autocorrelation functions (ACFs) are computed for each property (Supplementary Figures S6, S8, S10, and S12).
Edge and vertex analysis of polyhedral MD trajectories
A geometric approach for analyzing each frame in the MD trajectory of a DNA origami nanoparticle (Supplementary Figure S2) was developed. Two M-bp DNA duplexes of each edge are connected with a 1-bp offset along the edge direction, resulting in a protruding base pair at each end of the edge. The protruding base pairs are excluded from downstream analysis, and the remaining base pairs of the edge are indexed as 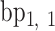 ,
, 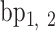 , …,
, …, 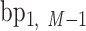 ,
, 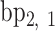 ,
, 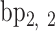 , …,
, …,  . The Python package ProDy (85) then computes the geometric center of atoms in each base pair, denoted
. The Python package ProDy (85) then computes the geometric center of atoms in each base pair, denoted 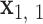 , …,
, …, 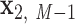 , and the geometric center of atoms in each pair of base pairs
, and the geometric center of atoms in each pair of base pairs 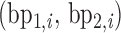 ,
, 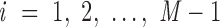 , denoted
, denoted 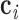 . A right-handed orthonormal basis
. A right-handed orthonormal basis 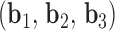 is defined using the three principal axes of the point cloud
is defined using the three principal axes of the point cloud 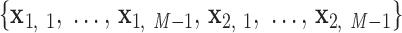 , in which
, in which  is coincident with the first principal axis and points from
is coincident with the first principal axis and points from  to
to 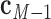 ,
, 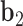 is coincident with the second principal axis and points from
is coincident with the second principal axis and points from 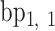 to
to 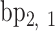 , and
, and 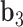 is coincident with the third principal axis and points outwards of the nanoparticle. Next, a L-bp-long region at the starting end of the edge is selected to define a vector
is coincident with the third principal axis and points outwards of the nanoparticle. Next, a L-bp-long region at the starting end of the edge is selected to define a vector 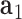 , which is coincident with the first principal axis of the point clouds
, which is coincident with the first principal axis of the point clouds 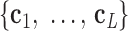 , and points from
, and points from 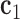 to
to 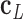 . The bow- and twist-angles associated with the left half-edge are computed by projecting
. The bow- and twist-angles associated with the left half-edge are computed by projecting 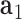 onto the
onto the 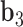 -
-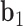 plane and the
plane and the 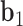 -
-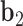 plane as
plane as 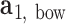 and
and 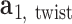 , respectively. The bow-angle is defined as the right-handed rotation angle from
, respectively. The bow-angle is defined as the right-handed rotation angle from 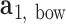 to
to 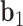 about
about 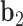 , and the twist-angle as the right-handed rotation angle from
, and the twist-angle as the right-handed rotation angle from  to
to 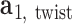 about
about 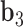 .
.
This geometric approach allows calculation of three properties of an N-arm vertex in each frame: average bow-angle, 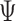 , average twist-angle,
, average twist-angle, 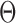 , and radial vacancy,
, and radial vacancy, 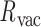 . The average bend- and twist-angles are averaged over the N half-edges that are directly connected to the vertex. The vertex contains N bulges, of which ProDy calculates the geometric centers of atoms of the unpaired nucleotides as
. The average bend- and twist-angles are averaged over the N half-edges that are directly connected to the vertex. The vertex contains N bulges, of which ProDy calculates the geometric centers of atoms of the unpaired nucleotides as 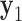 ,
, 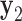 , …
, … 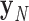 , respectively. In addition, ProDy calculates the geometric centers of atoms of all the unpaired nucleotides in this vertex as y. The radial vacancy of this vertex is defined as the average Euclidean distance between
, respectively. In addition, ProDy calculates the geometric centers of atoms of all the unpaired nucleotides in this vertex as y. The radial vacancy of this vertex is defined as the average Euclidean distance between 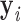 and y,
and y,  .
.
Edge and vertex analysis of unconstrained bulge and vertex MD trajectories
A similar approach for analyzing each frame in the MD trajectory of unconstrained DNA nanoparticles including a duplex bulge, a 3-arm vertex, and a 4-arm vertex was developed, again utilizing the Python package ProDy (85). Duplex bend-angle, 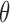 , and duplex torsional twist-angle,
, and duplex torsional twist-angle,  , are defined as previously performed by Schreck et al. (58,86). In the present work, the duplex bend-angle is reported as 180
, are defined as previously performed by Schreck et al. (58,86). In the present work, the duplex bend-angle is reported as 180  , because this quantity is more intuitive to visualize. To determine these duplex properties, a right-handed orthonormal basis
, because this quantity is more intuitive to visualize. To determine these duplex properties, a right-handed orthonormal basis  and
and  is defined for each DNA duplex segment on either side of the bulge. The duplex bend-angle is calculated using
is defined for each DNA duplex segment on either side of the bulge. The duplex bend-angle is calculated using 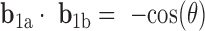 , where a positive
, where a positive 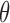 value refers to the duplex arms bending away from the bulge. Next, two vectors
value refers to the duplex arms bending away from the bulge. Next, two vectors 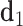 and
and 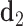 are defined which point from the geometric centers of each base flanking the bulge. The duplex torsional twist-angles
are defined which point from the geometric centers of each base flanking the bulge. The duplex torsional twist-angles 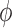 and
and 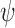 are calculated using
are calculated using 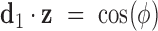 and
and  , where
, where 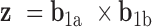 . The relative duplex torsional twist-angle is defined as
. The relative duplex torsional twist-angle is defined as 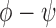 .
.
Next, for the 3-arm and 4-arm vertices the out-of-plane vertex bend-angle, 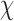 , is calculated. To determine this bend-angle, the geometric center of the last pair of base pairs of the N edges
, is calculated. To determine this bend-angle, the geometric center of the last pair of base pairs of the N edges  is defined. A right-handed orthonormal basis
is defined. A right-handed orthonormal basis 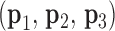 is then calculated using this set of centroids, which is subsequently used to define the planarity of the DNA vertex. The out-of-plane vertex bend-angle is calculated using
is then calculated using this set of centroids, which is subsequently used to define the planarity of the DNA vertex. The out-of-plane vertex bend-angle is calculated using  , where a positive out-of-plane vertex bend-angle refers to the N edges bending away from the N bulges. The radial vacancy of each vertex is defined as in the previous section. Additionally, for the 3-arm and 4-arm vertices
, where a positive out-of-plane vertex bend-angle refers to the N edges bending away from the N bulges. The radial vacancy of each vertex is defined as in the previous section. Additionally, for the 3-arm and 4-arm vertices 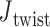 is calculated for each edge, which all contain one single or double crossover. A right-handed orthonormal basis is calculated for the left
is calculated for each edge, which all contain one single or double crossover. A right-handed orthonormal basis is calculated for the left 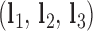 and right
and right 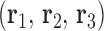 duplex at each crossover using the centroids of each base pair for the left and right duplex, respectively. Left and right duplexes for each edge are defined such that the minor grooves at the bulge regions are facing towards the viewer. The vector pointing from the centroid of the right duplexes at the junction towards the centroid of the left duplexes at the junction is defined as
duplex at each crossover using the centroids of each base pair for the left and right duplex, respectively. Left and right duplexes for each edge are defined such that the minor grooves at the bulge regions are facing towards the viewer. The vector pointing from the centroid of the right duplexes at the junction towards the centroid of the left duplexes at the junction is defined as 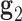 . To compute
. To compute 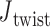 ,
, 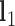 and
and 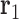 are projected onto the plane orthogonal to
are projected onto the plane orthogonal to 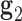 as
as 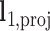 and
and 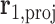 , respectively.
, respectively. 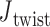 is calculated using
is calculated using 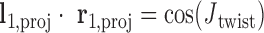 , where positive
, where positive  corresponds to right-handed twist as measured from the left to the right duplex.
corresponds to right-handed twist as measured from the left to the right duplex.
RESULTS AND DISCUSSION
Model parameters determined from molecular dynamics simulations
As previously noted, an all-atom model of an unconstrained duplex bulge was built to generate the ground-state geometry and stiffness coefficients for the FE models. MD simulations of an unconstrained duplex bulge provide insight into the equilibrium structures of building blocks of larger DNA origami nanoparticles. Over a 1-μs MD trajectory, mean values for the duplex bend-angle, 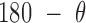 , and the duplex twist-angle,
, and the duplex twist-angle,  , can be identified (Figure 2C and Supplementary Figure S5). The first 200 ns of the MD trajectory were discarded as non-equilibrium relaxation (Supplementary Figure S5E and F, and S6), where both duplex properties equilibrate within this time-frame. The 1 μs MD trajectory of an unconstrained duplex bulge yields mean values of
, can be identified (Figure 2C and Supplementary Figure S5). The first 200 ns of the MD trajectory were discarded as non-equilibrium relaxation (Supplementary Figure S5E and F, and S6), where both duplex properties equilibrate within this time-frame. The 1 μs MD trajectory of an unconstrained duplex bulge yields mean values of 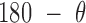 = 142.0 ± 13.6
= 142.0 ± 13.6 duplex bend-angle, and
duplex bend-angle, and  = 58.8 ± 32.8° duplex twist-angle. In Schreck et al., a relaxed duplex represented by oxDNA has a twist-angle of
= 58.8 ± 32.8° duplex twist-angle. In Schreck et al., a relaxed duplex represented by oxDNA has a twist-angle of  = 32°, and a duplex with a bulge contains a second twist-angle distribution ∼70° (86). During the MD simulation, the duplex bulge mainly samples twist-angles ∼70°, and has a tail containing twist-angles ∼32°, both consistent with previous data (86). The MD trajectory for the twist-angle distribution shows the duplex bulge residing in both states, with a clear preference for the twist-angle ∼70° (Supplementary Figure S5).
= 32°, and a duplex with a bulge contains a second twist-angle distribution ∼70° (86). During the MD simulation, the duplex bulge mainly samples twist-angles ∼70°, and has a tail containing twist-angles ∼32°, both consistent with previous data (86). The MD trajectory for the twist-angle distribution shows the duplex bulge residing in both states, with a clear preference for the twist-angle ∼70° (Supplementary Figure S5).
Using the equipartition theorem as done previously (30), we infer the two linear rotational stiffness coefficients about axes x and z, respectively, from the MD trajectories of the unconstrained duplex bulge. The two rotation angles  and
and 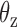 about axes x and z, respectively, are computed from the MD trajectory after 200 ns equilibration. From the probability densities of these two angles (Figure 1C), the equipartition theorem is used to estimate the rotational stiffness about the x-axis as
about axes x and z, respectively, are computed from the MD trajectory after 200 ns equilibration. From the probability densities of these two angles (Figure 1C), the equipartition theorem is used to estimate the rotational stiffness about the x-axis as 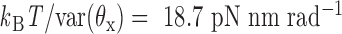 and that about the z-axis as
and that about the z-axis as 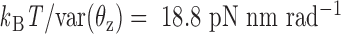 . From these results, we set the rotational stiffness coefficients about the x- and z-axes to 13.53 and 13.53 pN nm rad−1. Note that these values equal the corresponding rotational stiffness coefficients of double crossovers divided by factors of 100 and 10, respectively (Table 1).
. From these results, we set the rotational stiffness coefficients about the x- and z-axes to 13.53 and 13.53 pN nm rad−1. Note that these values equal the corresponding rotational stiffness coefficients of double crossovers divided by factors of 100 and 10, respectively (Table 1).
Equilibrium structures of geometrically distinct DNA origami nanoparticles
We demonstrate the application of the bulge model to DNA origami nanoparticles published in recent work (11). Six of these nanoparticles, a tetrahedron, an octahedron, an icosahedron, a cuboctahedron, a reinforced cube, and a nested cube, have been synthesized and imaged using cryo-EM (11). The architecture of each nanoparticle is a wireframe, of which each edge consists of two parallel DNA duplexes connected by at least two crossovers, and edges are connected to their neighbors at vertices containing bulges. For example, in the design of the 3-arm vertex shown in Figure 2A, two neighboring arms are connected by a single phosphodiester bond in the green strand and five unpaired thymine bases in the blue strand, forming a bulge in the center of the vertex. Geometrically distinct DNA origami nanoparticles have been designed by changing the number of arms in each vertex and the length of each edge (11).
Modeling of DNA origami vertices
As a starting point, we constructed the FE models of unconstrained 3-, 4-, 5-, and 6-arm vertices, respectively, and computed their equilibrium structures (Figure 2A). In the equilibrium structures of all four vertices the arms bend toward the major grooves of DNA at the bulges, which agrees with a previous structural analysis of 4-arm vertices within a self-assembled octahedron imaged using cryo-EM (87). This prediction suggests an enantiomeric preference for the self-assembled nanoparticles with minor grooves facing outwards at the vertices.
Molecular dynamics simulations of the unconstrained 3-arm vertex and the unconstrained 4-arm vertex allow comparison between the duplex bulge building block, and the larger DNA origami nanoparticles, such as the tetrahedron and the octahedron. Over a 500-ns MD trajectory we quantified the average duplex bend-angle, 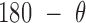 , the average duplex twist-angle,
, the average duplex twist-angle,  , the average out-of-plane bend-angle,
, the average out-of-plane bend-angle, 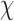 , and the radial vacancy,
, and the radial vacancy, 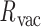 (Figure 2C and Supplementary Figure S5). The first 100 ns of the MD trajectories were discarded as non-equilibrium relaxation (Supplementary Figures S5 and S6). While the duplex properties of the 3- and 4-arm vertex equilibrate within 100 ns, the out-of-plane bend-angle does not, indicating that there may be long time-scale fluctuations that are not accurately captured by the length of this trajectory (Supplementary Figure S6C). The MD trajectory of a 3-arm vertex yields mean values of
(Figure 2C and Supplementary Figure S5). The first 100 ns of the MD trajectories were discarded as non-equilibrium relaxation (Supplementary Figures S5 and S6). While the duplex properties of the 3- and 4-arm vertex equilibrate within 100 ns, the out-of-plane bend-angle does not, indicating that there may be long time-scale fluctuations that are not accurately captured by the length of this trajectory (Supplementary Figure S6C). The MD trajectory of a 3-arm vertex yields mean values of 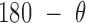 = 127.1 ± 5.9° for duplex bend-angle,
= 127.1 ± 5.9° for duplex bend-angle,  = 37.1 ± 14.0° for duplex twist-angle,
= 37.1 ± 14.0° for duplex twist-angle, 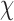 = –3.2 ± 4.8° for out-of-plane bend-angle, and
= –3.2 ± 4.8° for out-of-plane bend-angle, and 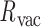 = 16.5 ± 2.8 Å for radial vacancy. The MD trajectory of a 4-arm vertex yields mean values of
= 16.5 ± 2.8 Å for radial vacancy. The MD trajectory of a 4-arm vertex yields mean values of 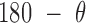 = 108.9 ± 7.0° for duplex bend-angle,
= 108.9 ± 7.0° for duplex bend-angle,  = 83.4 ± 12.6° for duplex twist-angle,
= 83.4 ± 12.6° for duplex twist-angle, 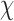 = 23.9 ± 5.5° for out-of-plane bend-angle, and
= 23.9 ± 5.5° for out-of-plane bend-angle, and 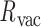 = 25.6 ± 1.6 Å for radial vacancy. Compared with the unconstrained duplex bulge, the 3-arm and 4-arm vertices are unsurprisingly more rigid, with distinct mean values for the duplex bend- and twist-angles. The out-of-plane bend-angle for the 4-arm vertex shows a significant bending towards the major groove of DNA at the bulges, as previously observed by He et al. for DNA tiles, which display preferential inward bending due to chirality (87). This out-of-plane bend-angle is also seen in the majority of the trajectory for the 3-arm vertex, but this trajectory also exhibits an oscillatory behavior towards the opposite out-of-plane bend-angle (away from the major groove of DNA).
= 25.6 ± 1.6 Å for radial vacancy. Compared with the unconstrained duplex bulge, the 3-arm and 4-arm vertices are unsurprisingly more rigid, with distinct mean values for the duplex bend- and twist-angles. The out-of-plane bend-angle for the 4-arm vertex shows a significant bending towards the major groove of DNA at the bulges, as previously observed by He et al. for DNA tiles, which display preferential inward bending due to chirality (87). This out-of-plane bend-angle is also seen in the majority of the trajectory for the 3-arm vertex, but this trajectory also exhibits an oscillatory behavior towards the opposite out-of-plane bend-angle (away from the major groove of DNA).
Additionally, for the unconstrained 3- and 4-arm vertices, 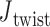 is computed for each crossover from a 500-ns MD trajectory (Supplementary Figure S11) in order to compare to the value of
is computed for each crossover from a 500-ns MD trajectory (Supplementary Figure S11) in order to compare to the value of 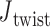 = 0° used as the ground-state value in the FE model. The first 100 ns of the MD trajectories were discarded as non-equilibrium relaxation (Supplementary Figures S11 and S12), and although
= 0° used as the ground-state value in the FE model. The first 100 ns of the MD trajectories were discarded as non-equilibrium relaxation (Supplementary Figures S11 and S12), and although 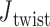 angles are mostly equilibrated after this time, the unconstrained vertices are slower to equilibrate than the bulge and DNA polyhedral nanoparticles. The 3-arm vertex has a mean value of
angles are mostly equilibrated after this time, the unconstrained vertices are slower to equilibrate than the bulge and DNA polyhedral nanoparticles. The 3-arm vertex has a mean value of 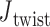 = 6.1 ± 28.8°, and the 4-arm vertex has a mean value of
= 6.1 ± 28.8°, and the 4-arm vertex has a mean value of 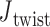 = –6.7 ± 39.6°, comparing favorably with the ground-state value of 0°. Notably, individual crossovers in both the 3- and 4-arm vertices deviate significantly from this mean and form local maxima near –55° (4-arm vertex), –15° (3- and 4-arm vertex), 30° (3-arm vertex), and 55° (3- and 4-arm vertex) (Supplementary Figure S11F).
= –6.7 ± 39.6°, comparing favorably with the ground-state value of 0°. Notably, individual crossovers in both the 3- and 4-arm vertices deviate significantly from this mean and form local maxima near –55° (4-arm vertex), –15° (3- and 4-arm vertex), 30° (3-arm vertex), and 55° (3- and 4-arm vertex) (Supplementary Figure S11F).
Modeling of DNA origami nanoparticles
These N-arm vertices serve as the building blocks of the DNA origami nanoparticles whose equilibrium structures were computed in this work. The tetrahedral nanoparticle comprises four 3-arm vertices connected by six edges, with each edge consisting of two parallel 63-bp DNA duplexes that are connected to one another by crossovers. Both the reconstructed cryo-EM map and the computed equilibrium structure show a slight bowing in each edge (Figure 3F). This bending is due to the rotational stiffness of the three bulges in the center of each 3-arm vertex. Topological constraints force the vertex to deform away from the nearly planar equilibrium structure (Figure 2A) to the constrained 3D structure in a tetrahedron, and most of the deformation in the vertex occurs in the three rotational DOF of each bulge. A parameter scan of the rotational stiffness coefficients of bulges shows that the restorative moment of bulges about the reference axis z, which is defined in Figure 1B, contributes to the bowing of the edges (Supplementary Figure S3). The edge length of DNA origami nanoparticles is also a factor in the degree of edge-bowing, as seen when comparing 52- and 63-bp edge-length tetrahedra, and 52- and 63-bp edge-length octahedra (Supplementary Figure S4). Because the type of nanoparticle appears to affect the degree of edge-bowing, and is likely related to the number of arms per vertex, the optimal edge length for minimizing the degree of edge-bowing should be distinct for each DNA origami nanoparticle.
An MD simulation of the 63-bp edge-length tetrahedral DNA nanoparticle allows the analysis of global features such as the bowing of the edges away from the vertices (Figure 3A, B, and E, Supplementary Figure S7, and Supporting Movie 1). Over a 150-ns MD trajectory, we quantified the average twist-angle around each vertex, 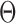 , the average bow-angle of each edge,
, the average bow-angle of each edge, 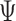 , and the radial vacancy of each vertex,
, and the radial vacancy of each vertex, 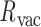 . The first 50 ns of the MD trajectory were discarded as non-equilibrium relaxation (Supplementary Figures S7 and S8). While the vertex geometric properties for the tetrahedral nanoparticle appear to be equilibrated on the time-scale of 50 ns, based on the corresponding ACFs, a longer MD trajectory would offer greater confidence in this assumption. For example, long time-scale dynamics associated with transformation from a right- to left-handed twist-angle may occur, but are not observed during the 150-ns trajectory simulated here. The 150-ns MD trajectory of a tetrahedral nanoparticle yields mean values of
. The first 50 ns of the MD trajectory were discarded as non-equilibrium relaxation (Supplementary Figures S7 and S8). While the vertex geometric properties for the tetrahedral nanoparticle appear to be equilibrated on the time-scale of 50 ns, based on the corresponding ACFs, a longer MD trajectory would offer greater confidence in this assumption. For example, long time-scale dynamics associated with transformation from a right- to left-handed twist-angle may occur, but are not observed during the 150-ns trajectory simulated here. The 150-ns MD trajectory of a tetrahedral nanoparticle yields mean values of 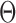 = 8.8 ± 8.8° for twist-angle,
= 8.8 ± 8.8° for twist-angle, 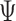 = 13.8 ± 5.0° for bow-angle, and
= 13.8 ± 5.0° for bow-angle, and 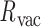 = 11.5 ± 2.3 Å for radial vacancy (Figure 3E and Supplementary Figure S7). The twist-angle shows signs of slight right-handedness, while allowing for some vertices to present left-handed twisting around the vertex.
= 11.5 ± 2.3 Å for radial vacancy (Figure 3E and Supplementary Figure S7). The twist-angle shows signs of slight right-handedness, while allowing for some vertices to present left-handed twisting around the vertex.
The cryo-EM map of the tetrahedral nanoparticle does not present any clear evidence of right- or left-handed twisting (11), so the ability of the tetrahedral nanoparticle in the MD trajectory to assume both forms may have resulted in an averaged cryo-EM structure with no measurable twist-angle (see the trajectory for Vertex D in Supplementary Figure S6). The bow-angle, on the other hand, shows a distinct outward bowing of 14° (Figure 3A), which matches the edge conformation seen in the cryo-EM map (Figure 3F), and no edges present any signs of inward bowing over the MD trajectory (Supplementary Figure S7C). The radial vacancy of the tetrahedral vertices is 12 Å, which allows for interaction between the three bulges at the center of each vertex. These interactions are expected to contribute to stiffening the tetrahedral vertices, and possibly also influence the twist-angles of the vertices and the bow-angles of the edges. Compared with the unconstrained 3-arm junction, the radial vacancy is slightly less, which can be attributed to lower flexibility of each vertex due to the rigidity of the nanoparticle. As seen in Figure 3B, the tetrahedron exhibits some evidence of ‘open vertex’ states, in which little-to-no hydrogen-bonding is present between distinct ssDNA regions within the vertex. In general, the vertices in the tetrahedron adopt ‘closed vertex’ states in which there is some hydrogen-bonding present between distinct ssDNA regions in the vertex, as indicated by the lower average radial vacancy at these vertices. These hydrogen-bonding interactions may affect the global structure of the vertex, resulting in the ability to form both right- and left-handed twisting conformations depending on which ssDNA bases are hydrogen-bonded.
Distinct DNA origami nanoparticles are designed by changing the numbers of arms of each vertex and the numbers of base pairs constituting each edge. Compared with the tetrahedral nanoparticle, an octahedral nanoparticle contains six 4-arm vertices that are connected by twelve edges. In addition, the length of each edge in the octahedral particle decreases from 63 to 52 bp. The shorter length increases the effective, overall bending stiffness of the edges. In fact, the curvature in the edges of the octahedral nanoparticle is seen to be less than that of the tetrahedral nanoparticle as a consequence of the increased bending stiffness (Figure 2B). Interestingly, the reconstructed cryo-EM map of the octahedral nanoparticle indicates a 15° counterclockwise twist from the computed equilibrium structure at each vertex (11) (Figure 2B). This twist may be attributed to the interaction between unpaired bases in the immediate vicinity of vertices, as well as the chirality of the assembled nanoparticle (87).
An MD simulation of the 52-bp edge-length octahedral DNA nanoparticle allows for the comparison of global features with those of the tetrahedron in order to gain insight into the distinct structural dynamics of the equilibrated nanoparticles (Figure 3C–E, Supplementary Figure S9, and Supporting Movie 2). Like the tetrahedral DNA nanoparticle, over a 150-ns MD trajectory, we quantified the average twist-angle around each vertex, 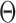 , the average bow-angle of each edge,
, the average bow-angle of each edge, 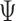 , and the radial vacancy of each vertex,
, and the radial vacancy of each vertex,  . The first 50 ns of the MD trajectory were discarded as non-equilibrium relaxation (Supplementary Figures S9 and S10). While vertex properties for the octahedral nanoparticle appear to be equilibrated on the time-scale of 50 ns, like for the tetrahedral nanoparticle, a longer MD simulation would offer greater confidence on the impact of long time-scale fluctuations on these conformational properties. The 150-ns MD trajectory of the 52-bp edge-length octahedral nanoparticle yields mean values of
. The first 50 ns of the MD trajectory were discarded as non-equilibrium relaxation (Supplementary Figures S9 and S10). While vertex properties for the octahedral nanoparticle appear to be equilibrated on the time-scale of 50 ns, like for the tetrahedral nanoparticle, a longer MD simulation would offer greater confidence on the impact of long time-scale fluctuations on these conformational properties. The 150-ns MD trajectory of the 52-bp edge-length octahedral nanoparticle yields mean values of 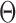 = 8.8 ± 6.6° twist-angle,
= 8.8 ± 6.6° twist-angle, 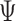 = 8.6 ± 5.5° bow-angle, and
= 8.6 ± 5.5° bow-angle, and 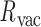 = 19.4 ± 2.6 Å radial vacancy (Figure 3E and Supplementary Figure S9). The twist-angle shows a global right-handedness, with no vertices presenting sustained left-handed twisting around the vertex.
= 19.4 ± 2.6 Å radial vacancy (Figure 3E and Supplementary Figure S9). The twist-angle shows a global right-handedness, with no vertices presenting sustained left-handed twisting around the vertex.
The cryo-EM map of the octahedral nanoparticle shows evidence of an estimated 15° right-handed twist (Figure 3G) (11), which matches the right-handed result from the MD trajectory (Figure 3E). (See the trajectories for all vertices in Supplementary Figure S9.) The bow-angle shows an average slight outward bowing of 8°, which is similar to the edge conformation seen in the cryo-EM map (Figure 3G), and distinct from the noticeable outward bowing of the tetrahedron. Also, several edges present slight signs of inward bowing over the MD trajectory (Supplementary Figure S9C). The radial vacancy of the octahedral vertices is 19 Å, allowing for less interaction between the four bulges at the center of each vertex. These lesser bulge interactions within the octahedral vertices influence the noticeable twist-angles of the vertices, since there is little-to-no stabilization across the bulges. Compared with the unconstrained 4-arm junction, the radial vacancy is slightly less, a relation also seen in the tetrahedral vertices, which is attributed to lower flexibility of each vertex due to the rigidity of the nanoparticle. As observed in Figure 3D, vertices in the octahedron generally reside in the ‘open vertex’ state, in which little-to-no hydrogen-bonding occurs between distinct ssDNA regions within the vertex. This is in contrast to vertices in the tetrahedron, and it may explain the origin of the right-handed twist conformations observed in the former because non-interacting ssDNA regions may not interfere with the preferred chirality at the vertex.
Multi-arm vertices are useful building blocks for constructing larger polyhedral nanoparticles as well as tile-based systems. For example, the icosahedral nanoparticle and the cuboctahedral nanoparticle consist of twelve 5-arm vertices connected by thirty 52-bp-long edges and twelve 4-arm vertices connected by twenty-four 52-bp-long edges, respectively. A nanoparticle may also comprise heterogeneous vertex designs and edge lengths. For example, a reinforced cube is formed by four 3-arm vertices, four 6-arm vertices, twelve 52-bp-long edges as the sides, and six 73-bp-long edges as the diagonals of all faces.
Both the reconstructed cryo-EM map and the computed equilibrium structure for the icosahedral nanoparticle contain at each vertex a pentagonal cavity with the side length about twice the diameter of a DNA duplex (Figure 3H), similar to that existing at an unconstrained 5-arm vertex (Figure 2A). The 5-fold rotational symmetry and the near-planar geometry of the vertex jointly contribute to the formation of the cavity. In contrast, the hexagonal cavity present in an unconstrained 6-arm vertex (Figure 2A) is absent in the 6-arm vertices of the reinforced cube (Figure 3J), which lose the 6-fold rotational symmetry and have the arms bent from the unconstrained structure. The 73-bp diagonal edges are bowed in an outward curvature in both experiment and simulation, similar to that of the tetrahedral nanoparticle. In contrast, the 52-bp edges in the same reinforced cube are nearly straight due to increased bending stiffness (Figure 3J). Despite the cuboctahedral and octahedral nanoparticles both having 4-arm vertices, the cuboctahedral nanoparticle (Figure 3I) does not display the 15° counterclockwise twist seen in the vertices of the octahedral nanoparticle (Figure 3G), indicating the dependence of local base interactions on vertex geometry.
Further application of the finite element bulge model to DNA origami nanoparticles
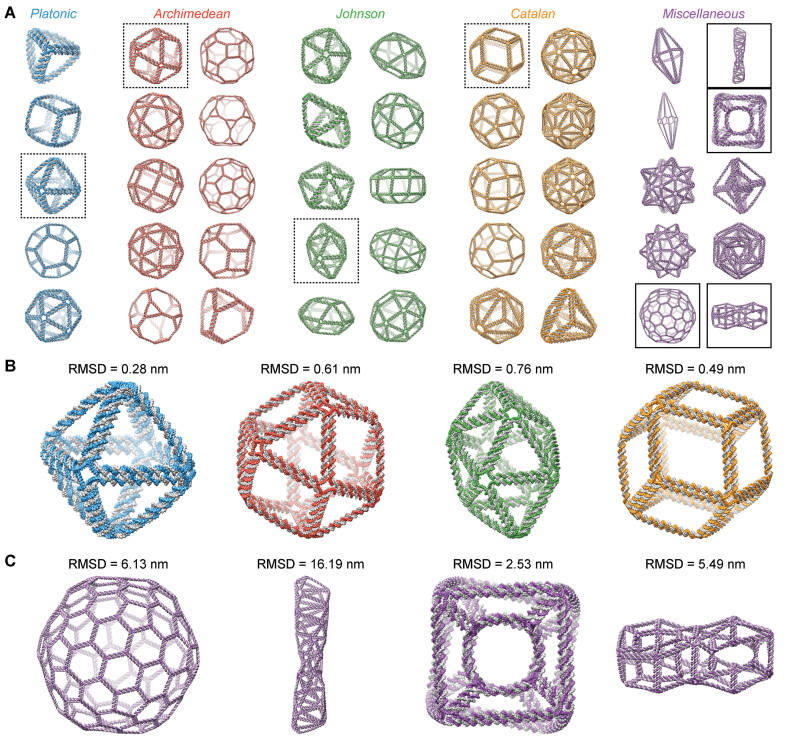
In our final application, we applied our FE modeling framework to compute the equilibrium structures of 45 DNA origami nanoparticles of diverse geometric shapes (Figure 4A) designed in a recent work (11). Our FE modeling framework is also used to compute thermal fluctuations quantified by the root-mean-square fluctuations (RMSF) of base pairs at 298 K for each object (Table 2 and Supplementary Figure S13) (29,30). All structures are qualitatively similar to their corresponding idealized 3D geometric models that are based on target, user-defined CAD designs that assume all DNA duplexes are straight (11). This overall similarity is largely due to the mechanical compliance of bulges that are present in each vertex. Compared with other secondary structural motifs, such as the duplexes, nicks, and crossovers used in these nanoparticles, the stiffness coefficients of bulges are lower by approximately two orders of magnitude. Such mechanical compliance renders bulges capable of connecting arbitrarily placed duplexes and multi-helical bundles in nearly arbitrary directions within large DNA nanoparticles.
Figure 4.
Equilibrium structures generated by the FE framework compared to the geometric model. (A) Equilibrium structures of the 45 polyhedral nanoparticles presented in a recent study (11). The nanoparticles consist of five Platonic solids (blue), 10 Archimedean solids (red), 10 Johnson solids (green), 10 Catalan solids (orange), and 10 polyhedra with miscellaneous shapes (purple). The geometric shapes of these structures are listed in Table 2. (B) Zoom-ins of the octahedron, cuboctahedron, gyroelongated square bipyramid, and rhombic dodecahedron (left to right, boxed in dashed lines in A) highlight similarities between the recent study and the current work, indicated by small RMSD values. (C) Zoom-ins of the Goldberg polyhedron, double helix, nested cube, and double torus (left to right, boxed in solid lines in A) highlight differences between the two works, indicated by large RMSD values.
Table 2. RMSD and average RMSF values of the equilibrium structures of the 45 polyhedral nanoparticles rendered in Figure 4. Each row in this table corresponds to a column in Figure 4.
| Category | RMSD [nm] / 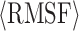 [nm] [nm] |
||||
|---|---|---|---|---|---|
| Platonic | Tetrahedron | Cube | Octahedron | Dodecahedron | Icosahedron |
| 0.61 / 0.93 | 0.38 / 2.07 | 0.28 / 1.03 | 0.45 / 2.82 | 0.64 / 1.18 | |
| Archimedean | Cuboctahedron | Icosidodecahedron | Rhombicuboctahedron | Snub cube | Truncated cube |
| 0.61 / 1.85 | 1.46 / 2.28 | 0.74 / 2.58 | 1.59 / 1.54 | 1.12 / 3.85 | |
| Truncated cuboctahedron | Truncated dodecahedron | Truncated icosahedron | Truncated octahedron | Truncated tetrahedron | |
| 0.99 / 4.72 | 1.08 / 5.15 | 1.38 / 3.68 | 0.66 / 3.40 | 0.92 / 2.55 | |
| Johnson | Gyroelongated pentagonal pyramid | Triangular bipyramid | Pentagonal bipyramid | Gyroelongated square bipyramid | Square gyrobicupola |
| 1.16 / 1.31 | 0.89 / 1.01 | 0.93 / 1.09 | 0.76 / 1.16 | 1.06 / 2.21 | |
| Pentagonal orthocupolarotunda | Pentagonal orthobirotunda | Elongated pentagonal gyrobicupola | Elongated pentagonal gyrobirotunda | Gyroelongated square bicupola | |
| 1.61 / 2.32 | 1.78 / 2.25 | 1.95 / 2.77 | 1.90 / 2.66 | 1.48 / 1.87 | |
| Catalan | Rhombic dodecahedron | Rhombic triacontahedron | Deltoidal icositetrahedron | Pentagonal icositetrahedron | Triakis octahedron |
| 0.49 / 2.48 | 1.25 / 2.77 | 2.20 / 3.24 | 1.31 / 3.62 | 1.10 / 1.48 | |
| Disdyakis dodecahedron | Triakis icosahedron | Pentakis dodecahedron | Tetrakis hexahedron | Triakis tetrahedron | |
| 2.92 / 1.39 | 1.66 / 1.71 | 1.29 / 1.30 | 0.64 / 1.14 | 1.27 / 1.35 | |
| Miscellaneous | Heptagonal bipyramid | Enneagonal trapezohedron | Small stellated dodecahedron | Rhombic hexecontahedron | Goldberg polyhedron G(2,1), dk5dgD |
| 0.74 / 2.16 | 1.62 / 8.83 | 4.62 / 1.73 | 6.66 / 2.83 | 6.13 / 3.13 | |
| Double helix | Nested cube | Nested octahedron | Torus | Double torus | |
| 16.19 / 2.37 | 2.53 / 2.17 | 2.10 / 1.61 | 6.04 / 2.45 | 5.49 / 3.29 | |
For many of the 45 nanoparticles, the idealized geometric model represents an accurate representation of the FE-model-predicted structure, with low root-mean-square deviation (RMSD) (Figure 4A and B). The geometric model has the lowest deviation from the FE model (RMSD < 2.0 nm) for the simplest classes of structures: in increasing order of complexity, the Platonic, Archimedean, and Johnson solids (Table 2). These structures have edges of equal lengths, with their complexity arising from differences in the degree of vertices (N-arms) and face geometries. The Catalan solids have slightly larger deviation as a whole because their edge lengths are not always uniform within the structure. In contrast, the rhombic dodecahedron (Figure 4B) and the rhombic triacontahedron are Catalan solids with uniform edge lengths that also have RMSD values similar to the Platonic solids (Figure 4B).
In general, objects with non-uniform edge lengths, including many of the Catalan solids and miscellaneous geometries, exhibit larger differences between the FE and geometric models. Because of the requirement that each edge length is a multiple of 10.5 bp rounded to the nearest nucleotide, more complex structures require that some edge lengths be adjusted to meet this requirement. However, because energy minimization was not performed to reposition the vertices to account for these edge length changes, the geometric model continues to use the CAD design coordinates (11). For the eight Catalan solids with unequal edge lengths, the amount of adjustment required was small, resulting in an increase of the RMSD only up to 3.0 nm (Table 2).
However, numerous miscellaneous geometries, such as the Goldberg polyhedron, double helix, nested cube, and double torus, display significantly larger RMSD values of up to 16.2 nm, which can largely be attributed to edge-length adjustment, as well as their large size (Figure 4C). In particular, the Goldberg polyhedron has edge lengths close to one another in the CAD design that are then rounded to the same length in the geometric model, which leads to puckering on the surface and a relatively large RMSD value. This level of deviation can be seen in the other, larger spherical structures such as the small stellated dodecahedron and the rhombic hexecontahedron. The model double helix has the largest RMSD value, which is due to the reduced turn of the helix in the FE model as compared with the geometric model. Because the turn of the helix is controlled by the relative lengths of the edges along the structure, deviations from these lengths deform the shape to an under-wound geometry. On a smaller scale, the nested cube resolves its edge-adjustment constraints by undergoing a global twist deformation, though there may not be a propensity for a certain twist direction as Figure 4C might imply. Rather, the computational framework of CanDo only solves for a single equilibrium structure, and the cryo-EM map of the nested cube demonstrates an average non-twisted shape (11), so equal populations of each twist conformation may be present.
Notably, the relatively large RMSD value of the double torus is unlikely to be due to just edge-length adjustment. Since there are two edge lengths present, one twice as long as the other, no edge-length adjustment was required. Rather, the open quadrilateral faces allow the strain at the vertices to be relaxed in a large structural deformation, which could be prevented through the use of reinforcing edges to create triangular faces. Beyond these geometric differences, higher RMSD values across all structures can be attributed to bowing of the edges or twisting at the vertex, as in accordance with the aforementioned comparisons with the cryo-EM maps and MD simulations, as well as highly constrained arms that the current bulge model does not describe well, especially in the concave and non-spherical topologies. Overall, the equilibrium structures of these DNA nanoparticles are adequately predicted using the FE modeling framework, able to take into account structural deviations due to edge-length adjustment that the geometric model does not. While the FE model was improved in this work to predict edge bowing, further accuracy of geometric features, such as twisting at the vertices, can be better approximated using all-atom models.
CONCLUSION
Structured DNA nanoparticles are simulated using all-atom and coarse-grained modeling to reveal their subtle local, as well as global, structural features. Toward this end, we implemented a mechanical model of a bulge, a secondary structure motif widely used in the design of DX-based DNA origami nanoparticles, determining empirical model parameters using all-atom modeling and comparison with reconstructed 3D cryo-EM maps. Understanding the structural and mechanical properties of bulges enables the coarse-grained modeling of high molecular weight DNA origami nanoparticles in a hierarchical way. For example, the nanoparticles studied here consist of a finite number of vertices with N-arm architecture, 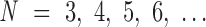 , and an N-arm vertex contains N bulges that connect duplexes together in the center of the vertex. The FE modeling framework is able to capture expected deviations from the geometric model due to edge-length adjustment as well as edge-bowing. The characterization of the latter was particularly improved in the coarse-grained model using refined parameterization based on all-atom models. Further, comparison between all-atom models of the nanoparticles and reconstructed cryo-EM maps demonstrates that the model is able to predict the positions of most atoms in the nanoparticle with an accuracy of within one nanometer. Some geometric features seen in cryo-EM maps, such as the twisting of vertices in the octahedron, are still not yet well predicted using our coarse-grained model, although these features are predicted using all-atom modeling.
, and an N-arm vertex contains N bulges that connect duplexes together in the center of the vertex. The FE modeling framework is able to capture expected deviations from the geometric model due to edge-length adjustment as well as edge-bowing. The characterization of the latter was particularly improved in the coarse-grained model using refined parameterization based on all-atom models. Further, comparison between all-atom models of the nanoparticles and reconstructed cryo-EM maps demonstrates that the model is able to predict the positions of most atoms in the nanoparticle with an accuracy of within one nanometer. Some geometric features seen in cryo-EM maps, such as the twisting of vertices in the octahedron, are still not yet well predicted using our coarse-grained model, although these features are predicted using all-atom modeling.
Besides the aforementioned model of bulges, we also introduced the models of open nicks to assemble a set of secondary structure motifs in programmed DNA assemblies that rely on the canonical Watson–Crick base pairing (Figure 1B). This set of models allows our lattice-free FE framework (30) to compute equilibrium structures of arbitrarily designed DNA assemblies with the exception of those containing non-Watson–Crick base pairs. It is also worth noting that this FE framework requires an immutable secondary structure of the DNA assembly as the input. Assemblies with non-Watson–Crick base pairing, such as those with triple-stranded (88) and quadruple-stranded (89) DNA, and assemblies with mutable secondary structures, such as those containing DNA toeholds (90), are beyond the scope of our FE framework and necessitate nucleotide-level models and all-atom models. In this work, we have improved the ability of the coarse-grained FE modeling framework to predict many of the features of DNA assemblies that use canonical Watson–Crick base pairing, achieving a higher level of accuracy compared with an idealized geometric model. Improvement was achieved not only through the introduction of additional structural motif models, but also through comparison with experiment and all-atom modeling, which predicted structures of highest fidelity.
AVAILABILITY
Our coarse-grained modeling approach is available for use online at the free public server: http://cando-dna-origami.org/ and for license from MIT by e-mailing software-licenses@mit.edu.
Supplementary Material
ACKNOWLEDGEMENTS
Discussions with Rémi Veneziano and the members of the Bathe laboratory are gratefully acknowledged.
Author contributions: K.P., W.P.B. and M.B. conceived of the study. K.P. carried out the FE simulations, and K.P. and S.R. analyzed the FE data. W.P.B. carried out the MD simulations, and W.P.B. and K.P. analyzed the MD data. All authors contributed to discussions regarding the data and its interpretation, and the manuscript was written and edited by all authors.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Office of Naval Research (ONR) [N00014-12-1-0621 to K.P. and M.B.]; Army Research Office (ARO-MURI) [W911NF1210420 to W.P.B. and M.B.]; National Science Foundation (NSF-CCF) [1560425 to S.R. and M.B.]; Office of Naval Research (ONR-DURIP) [N00014-13-1-0664, N00014-15-1-2830]. Funding for open access charge: Office of Naval Research (ONR) [N00014-12-1-0621].
Conflict of interest statement. None declared.
REFERENCES
- 1. Seeman N.C. Nucleic acid junctions and lattices. J. Theor. Biol. 1982; 99:237–247. [DOI] [PubMed] [Google Scholar]
- 2. Seeman N.C. Nanomaterials based on DNA. Annu. Rev. Biochem. 2010; 79:65–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Wang P., Gaitanaros S., Lee S., Bathe M., Shih W.M., Ke W.. Programming self-assembly of DNA origami honeycomb two-dimensional lattices and plasmonic metamaterials. J. Am. Chem. Soc. 2016; 138:7733–7740. [DOI] [PubMed] [Google Scholar]
- 4. Rothemund P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature. 2006; 440:297–302. [DOI] [PubMed] [Google Scholar]
- 5. Castro C.E., Kilchherr F., Kim D.N., Shiao E.L., Wauer T., Wortmann P., Bathe M., Dietz H.. A primer to scaffolded DNA origami. Nat. Methods. 2011; 8:221–229. [DOI] [PubMed] [Google Scholar]
- 6. Shih W.M., Quispe J.D., Joyce G.F.. A 1.7-kilobase single-stranded DNA that folds into a nanoscale octahedron. Nature. 2004; 427:618–621. [DOI] [PubMed] [Google Scholar]
- 7. Han D.R., Pal S., Yang Y., Jiang S.X., Nangreave J., Liu Y., Yan H.. DNA gridiron nanostructures based on four-arm junctions. Science. 2013; 339:1412–1415. [DOI] [PubMed] [Google Scholar]
- 8. Iinuma R., Ke Y.G., Jungmann R., Schlichthaerle T., Woehrstein J.B., Yin P.. Polyhedra self-assembled from DNA tripods and characterized with 3D DNA-PAINT. Science. 2014; 344:65–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Zhang F., Jiang S.X., Wu S.Y., Li Y.L., Mao C.D., Liu Y., Yan H.. Complex wireframe DNA origami nanostructures with multi-arm junction vertices. Nat. Nanotechnol. 2015; 10:779–784. [DOI] [PubMed] [Google Scholar]
- 10. Benson E., Mohammed A., Gardell J., Masich S., Czeizler E., Orponen P., Hogberg B.. DNA rendering of polyhedral meshes at the nanoscale. Nature. 2015; 523:441–444. [DOI] [PubMed] [Google Scholar]
- 11. Veneziano R., Ratanalert S., Zhang K., Zhang F., Yan H., Chiu W., Bathe M.. Designer nanoscale DNA assemblies programmed from the top down. Science. 2016; 352:1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Andersen E.S., Dong M., Nielsen M.M., Jahn K., Subramani R., Mamdouh W., Golas M.M., Sander B., Stark H., Oliveira C.L.P. et al. . Self-assembly of a nanoscale DNA box with a controllable lid. Nature. 2009; 459:73–76. [DOI] [PubMed] [Google Scholar]
- 13. Han D.R., Pal S., Nangreave J., Deng Z.T., Liu Y., Yan H.. DNA origami with complex curvatures in three-dimensional space. Science. 2011; 332:342–346. [DOI] [PubMed] [Google Scholar]
- 14. Dunn K.E., Dannenberg F., Ouldridge T.E., Kwiatkowska M., Turberfield A.J., Bath J.. Guiding the folding pathway of DNA origami. Nature. 2015; 525:82–86. [DOI] [PubMed] [Google Scholar]
- 15. Douglas S.M., Bachelet I., Church G.M.. A logic-gated nanorobot for targeted transport of molecular payloads. Science. 2012; 335:831–834. [DOI] [PubMed] [Google Scholar]
- 16. Douglas S.M., Dietz H., Liedl T., Hogberg B., Graf F., Shih W.M.. Self-assembly of DNA into nanoscale three-dimensional shapes. Nature. 2009; 459:414–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Dietz H., Douglas S.M., Shih W.M.. Folding DNA into twisted and curved nanoscale shapes. Science. 2009; 325:725–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ke Y.G., Douglas S.M., Liu M.H., Sharma J., Cheng A.C., Leung A., Liu Y., Shih W.M., Yan H.. Multilayer DNA origami packed on a square lattice. J. Am. Chem. Soc. 2009; 131:15903–15908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Ke Y.G., Voigt N.V., Gothelf K.V., Shih W.M.. Multilayer DNA origami packed on hexagonal and hybrid lattices. J. Am. Chem. Soc. 2012; 134:1770–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Sun W., Boulais E., Hakobyan Y., Wang W.L., Guan A., Bathe M., Yin P.. Casting inorganic structures with DNA molds. Science. 2014; 346:1258361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Chen J.H., Seeman N.C.. Synthesis from DNA of a molecule with the connectivity of a cube. Nature. 1991; 350:631–633. [DOI] [PubMed] [Google Scholar]
- 22. Goodman R.P., Schaap I.A.T., Tardin C.F., Erben C.M., Berry R.M., Schmidt C.F., Turberfield A.J.. Rapid chiral assembly of rigid DNA building blocks for molecular nanofabrication. Science. 2005; 310:1661–1665. [DOI] [PubMed] [Google Scholar]
- 23. He Y., Ye T., Su M., Zhang C., Ribbe A.E., Jiang W., Mao C.D.. Hierarchical self-assembly of DNA into symmetric supramolecular polyhedra. Nature. 2008; 452:198–201. [DOI] [PubMed] [Google Scholar]
- 24. Winfree E., Liu F.R., Wenzler L.A., Seeman N.C.. Design and self-assembly of two-dimensional DNA crystals. Nature. 1998; 394:539–544. [DOI] [PubMed] [Google Scholar]
- 25. Ding B., Seeman N.C.. Operation of a DNA robot arm inserted into a 2D DNA crystalline substrate. Science. 2006; 314:1583–1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Zheng J.P., Birktoft J.J., Chen Y., Wang T., Sha R.J., Constantinou P.E., Ginell S.L., Mao C.D., Seeman N.C.. From molecular to macroscopic via the rational design of a self-assembled 3D DNA crystal. Nature. 2009; 461:74–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Douglas S.M., Marblestone A.H., Teerapittayanon S., Vazquez A., Church G.M., Shih W.M.. Rapid prototyping of 3D DNA-origami shapes with caDNAno. Nucleic Acids Res. 2009; 37:5001–5006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Williams S., Lund K., Lin C.X., Wonka P., Lindsay S., Yan H.. Goel A, Simmel FC, Sosík P. 14th International Meeting on DNA Computing (DNA14). 2008; 5347:Prague: Springer; 90–101. [Google Scholar]
- 29. Kim D.N., Kilchherr F., Dietz H., Bathe M.. Quantitative prediction of 3D solution shape and flexibility of nucleic acid nanostructures. Nucleic Acids Res. 2012; 40:2862–2868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Pan K., Kim D.N., Zhang F., Adendorff M.R., Yan H., Bathe M.. Lattice-free prediction of three-dimensional structure of programmed DNA assemblies. Nat. Commun. 2014; 5:5578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Li H.Y., Carter J.D., LaBean T.H.. Nanofabrication by DNA self-assembly. Mater. Today. 2009; 12:24–32. [Google Scholar]
- 32. Zhang F., Nangreave J., Liu Y., Yan H.. Structural DNA nanotechnology: state of the art and future perspective. J. Am. Chem. Soc. 2014; 136:11198–11211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Pan K., Boulais E., Yang L., Bathe M.. Structure-based model for light-harvesting properties of nucleic acid nanostructures. Nucleic Acids Res. 2014; 42:2159–2170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Perez A., Luque F.J., Orozco M.. Frontiers in molecular dynamics simulations of DNA. Acc. Chem. Res. 2012; 45:196–205. [DOI] [PubMed] [Google Scholar]
- 35. Yoo J., Aksimentiev A.. In situ structure and dynamics of DNA origami determined through molecular dynamics simulations. Proc. Natl. Acad. Sci. U.S.A. 2013; 110:20099–20104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Maffeo C., Yoo J., Aksimentiev A.. De novo reconstruction of DNA origami structures through atomistic molecular dynamics simulation. Nucleic Acids Res. 2016; 44:3013–3019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Doye J.P.K., Ouldridge T.E., Louis A.A., Romano F., Sulc P., Matek C., Snodin B.E.K., Rovigatti L., Schreck J.S., Harrison R.M. et al. . Coarse-graining DNA for simulations of DNA nanotechnology. Phys. Chem. Chem. Phys. 2013; 15:20395–20414. [DOI] [PubMed] [Google Scholar]
- 38. Becker N.B., Everaers R.. From rigid base pairs to semiflexible polymers: Coarse-graining DNA. Phys. Rev. E. 2007; 76:021923. [DOI] [PubMed] [Google Scholar]
- 39. Khalid S., Bond P.J., Holyoake J., Hawtin R.W., Sansom M.S.P.. DNA and lipid bilayers: self-assembly and insertion. J. R. Soc. Interface. 2008; 5:S241–S250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Morriss-Andrews A., Rottler J., Plotkin S.S.. A systematically coarse-grained model for DNA and its predictions for persistence length, stacking, twist, and chirality. J. Chem. Phys. 2010; 132:035105. [DOI] [PubMed] [Google Scholar]
- 41. Savelyev A., Papoian G.A.. Chemically accurate coarse graining of double-stranded DNA. Proc. Natl. Acad. Sci. U.S.A. 2010; 107:20340–20345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Dans P.D., Zeida A., Machado M.R., Pantano S.. A coarse grained model for atomic-detailed DNA simulations with explicit electrostatics. J. Chem. Theory Comput. 2010; 6:1711–1725. [DOI] [PubMed] [Google Scholar]
- 43. DeMille R.C., Cheatham T.E., Molinero V.. A coarse-grained model of DNA with explicit solvation by water and ions. J. Phys. Chem. B. 2011; 115:132–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Cragnolini T., Derreumaux P., Pasquali S.. Coarse-grained simulations of RNA and DNA duplexes. J. Phys. Chem. B. 2013; 117:8047–8060. [DOI] [PubMed] [Google Scholar]
- 45. Sterpone F., Melchionna S., Tuffery P., Pasquali S., Mousseau N., Cragnolini T., Chebaro Y., St-Pierre J.F., Kalimeri M., Barducci A. et al. . The OPEP protein model: from single molecules, amyloid formation, crowding and hydrodynamics to DNA/RNA systems. Chem. Soc. Rev. 2014; 43:4871–4893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Korolev N., Luo D., Lyubartsev A.P., Nordenskiold L.. A coarse-grained DNA model parameterized from atomistic simulations by inverse Monte Carlo. Polymers. 2014; 6:1655–1675. [Google Scholar]
- 47. Maffeo C., Ngo T.T.M., Ha T., Aksimentiev A.. A coarse-grained model of unstructured single-stranded DNA derived from atomistic simulation and single-molecule experiment. J. Chem. Theory Comput. 2014; 10:2891–2896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Naome A., Laaksonen A., Vercauteren D.P.. A solvent-mediated coarse-grained model of DNA derived with the systematic Newton inversion method. J. Chem. Theory Comput. 2014; 10:3541–3549. [DOI] [PubMed] [Google Scholar]
- 49. Stachiewicz A., Molski A.. A coarse-grained MARTINI-like force field for DNA unzipping in nanopores. J. Comput. Chem. 2015; 36:947–956. [DOI] [PubMed] [Google Scholar]
- 50. Liwo A., He Y., Scheraga H.A.. Coarse-grained force field: general folding theory. Phys. Chem. Chem. Phys. 2011; 13:16890–16901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Saunders M.G., Voth G.A.. Coarse-graining of multiprotein assemblies. Curr. Opin. Struct. Biol. 2012; 22:144–150. [DOI] [PubMed] [Google Scholar]
- 52. Saunders M.G., Voth G.A.. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013; 42:73–93. [DOI] [PubMed] [Google Scholar]
- 53. Noid W.G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013; 139:090901. [DOI] [PubMed] [Google Scholar]
- 54. Snodin B.E.K., Randisi F., Mosayebi M., Sulc P., Romano J., Romano F., Ouldridge T.E., Tsukanov R., Nir E., Louis A.A. et al. . Introducing improved structural properties and salt dependence into a coarse-grained model of DNA. J. Chem. Phys. 2015; 142:234901. [DOI] [PubMed] [Google Scholar]
- 55. Ouldridge T.E., Louis A.A., Doye J.P.K.. DNA nanotweezers studied with a coarse-grained model of DNA. Phys. Rev. Lett. 2010; 104:178101. [DOI] [PubMed] [Google Scholar]
- 56. Ouldridge T.E., Sulc P., Romano F., Doye J.P., Louis A.A.. DNA hybridization kinetics: zippering, internal displacement and sequence dependence. Nucleic Acids Res. 2013; 41:8886–8895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Romano F., Chakraborty D., Doye J.P.K., Ouldridge T.E., Louis A.A.. Coarse-grained simulations of DNA overstretching. J. Chem. Phys. 2013; 138:085101. [DOI] [PubMed] [Google Scholar]
- 58. Schreck J.S., Romano F., Zimmer M.H., Louis A.A., Doye J.P.K.. Characterizing DNA star-tile-based nanostructures using a coarse-grained model. ACS Nano. 2016; 10:4236–4247. [DOI] [PubMed] [Google Scholar]
- 59. Snodin B.E.K., Romano F., Rovigatti L., Ouldridge T.E., Louis A.A., Doye J.P.K.. Direct simulation of the self-assembly of a small DNA origami. ACS Nano. 2016; 10:1724–1737. [DOI] [PubMed] [Google Scholar]
- 60. Knotts T.A., Rathore N., Schwartz D.C., de Pablo J.J.. A coarse grain model for DNA. J. Chem. Phys. 2007; 126:084901. [DOI] [PubMed] [Google Scholar]
- 61. Hinckley D.M., Freeman G.S., Whitmer J.K., de Pablo J.J.. An experimentally-informed coarse-grained 3-Site-Per-Nucleotide model of DNA: structure, thermodynamics, and dynamics of hybridization. J. Chem. Phys. 2013; 139:144903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. de Pablo J.J. Coarse-grained simulations of macromolecules: from DNA to nanocomposites. Annu. Rev. Phys. Chem. 2011; 62:555–574. [DOI] [PubMed] [Google Scholar]
- 63. Marrink S.J., de Vries A.H., Mark A.E.. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B. 2004; 108:750–760. [Google Scholar]
- 64. Marrink S.J., Risselada H.J., Yefimov S., Tieleman D.P., de Vries A.H.. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007; 111:7812–7824. [DOI] [PubMed] [Google Scholar]
- 65. Marrink S.J., Tieleman D.P.. Perspective on the Martini model. Chem. Soc. Rev. 2013; 42:6801–6822. [DOI] [PubMed] [Google Scholar]
- 66. Uusitalo J.J., Ingolfsson H.I., Akhshi P., Tieleman D.P., Marrink S.J.. Martini coarse-grained force field: extension to DNA. J. Chem. Theory Comput. 2015; 11:3932–3945. [DOI] [PubMed] [Google Scholar]
- 67. Sim A.Y.L., Minary P., Levitt M.. Modeling nucleic acids. Curr. Opin. Struct. Biol. 2012; 22:273–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Potoyan D.A., Savelyev A., Papoian G.A.. Recent successes in coarse-grained modeling of DNA. WIREs Comput. Mol. Sci. 2013; 3:69–83. [Google Scholar]
- 69. Dans P.D., Walther J., Gomez H., Orozco M.. Multiscale simulation of DNA. Curr. Opin. Struct. Biol. 2016; 37:29–45. [DOI] [PubMed] [Google Scholar]
- 70. Rubinstein M., Colby R.H.. Polymer Physics. 2003; Oxford: Oxford University Press. [Google Scholar]
- 71. Bathe K.-J. Finite Element Procedures. 2014; 2nd edn, Watertown. [Google Scholar]
- 72. Sedeh R.S., Pan K., Adendorff M.R., Hallatschek O., Bathe K.-J., Bathe M.. Computing nonequilibrium conformational dynamics of structured nucleic acid assemblies. J. Chem. Theory Comput. 2016; 12:261–273. [DOI] [PubMed] [Google Scholar]
- 73. Lu X.J., Olson W.K.. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003; 31:5108–5121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Shen Z.Y., Yan H., Wang T., Seeman N.C.. Paranemic crossover DNA: A generalized Holliday structure with applications in nanotechnology. J. Am. Chem. Soc. 2004; 126:1666–1674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L.. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983; 79:926–935. [Google Scholar]
- 76. Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R.D., Kale L., Schulten K.. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005; 26:1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Foloppe N., MacKerell A.D.. All-atom empirical force field for nucleic acids. I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000; 21:86–104. [Google Scholar]
- 78. MacKerell A.D., Banavali N.K.. All-atom empirical force field for nucleic acids. II. Application to molecular dynamics simulations of DNA and RNA in solution. J. Comput. Chem. 2000; 21:105–120. [Google Scholar]
- 79. Hart K., Foloppe N., Baker C.M., Denning E.J., Nilsson L., MacKerell A.D.. Optimization of the CHARMM additive force field for DNA: improved treatment of the BI/BII conformational equilibrium. J. Chem. Theory Comput. 2012; 8:348–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Denning E.J., Priyakumar U.D., Nilsson L., Mackerell A.D.. Impact of 2΄-hydroxyl sampling on the conformational properties of RNA: update of the CHARMM all-atom additive force field for RNA. J. Comput. Chem. 2011; 32:1929–1943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Allner O., Nilsson L., Villa A.. Magnesium ion-water coordination and exchange in biomolecular simulations. J. Chem. Theory Comput. 2012; 8:1493–1502. [DOI] [PubMed] [Google Scholar]
- 82. Batcho P.F., Case D.A., Schlick T.. Optimized particle-mesh Ewald/multiple-time step integration for molecular dynamics simulations. J. Chem. Phys. 2001; 115:4003–4018. [Google Scholar]
- 83. Martyna G.J., Tobias D.J., Klein M.L.. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994; 101:4177–4189. [Google Scholar]
- 84. Feller S.E., Zhang Y.H., Pastor R.W., Brooks B.R.. Constant pressure molecular dynamics simulation: the Langevin piston method. J. Chem. Phys. 1995; 103:4613–4621. [Google Scholar]
- 85. Bakan A., Meireles L.M., Bahar I.. ProDy: protein dynamics inferred from theory and experiments. Bioinformatics. 2011; 27:1575–1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Schreck J.S., Ouldridge T.E., Romano F., Louis A.A., Doye J.P.K.. Characterizing the bending and flexibility induced by bulges in DNA duplexes. J. Chem. Phys. 2015; 142:165101. [DOI] [PubMed] [Google Scholar]
- 87. He Y., Su M., Fang P.A., Zhang C., Ribbe A.E., Jiang W., Mao C.D.. On the chirality of self-assembled DNA octahedra. Angew. Chem. Int. Ed. 2010; 49:748–751. [DOI] [PubMed] [Google Scholar]
- 88. Rusling D.A., Nandhakumar I.S., Brown T., Fox K.R.. Triplex-directed recognition of a DNA nanostructure assembled by crossover strand exchange. ACS Nano. 2012; 6:3604–3613. [DOI] [PubMed] [Google Scholar]
- 89. Rajendran A., Endo M., Hidaka K., Tran P.L.T., Mergny J.L., Sugiyama H.. Controlling the stoichiometry and strand polarity of a tetramolecular G-quadruplex structure by using a DNA origami frame. Nucleic Acids Res. 2013; 41:8738–8747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Zhang D.Y., Seelig G.. Dynamic DNA nanotechnology using strand-displacement reactions. Nat. Chem. 2011; 3:103–113. [DOI] [PubMed] [Google Scholar]
- 91. Pettersen E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., Ferrin T.E.. UCSF chimera—a visualization system for exploratory research and analysis. J. Comput. Chem. 2004; 25:1605–1612. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.