Abstract
Direct coupling analysis of nucleotide coevolution provides a novel approach to identify which nucleotides in an RNA molecule are likely in direct contact, and this information obtained from sequence only can be used to predict RNA 3D structures with much improved accuracy. Here we present an efficient method that incorporates this information into current RNA 3D structure prediction methods, specifically 3dRNA. Our method makes much more accurate RNA 3D structure prediction than the original 3dRNA as well as other existing prediction methods that used the direct coupling analysis. In particular our method demonstrates a significant improvement in predicting multi-branch junction conformations, a major bottleneck for RNA 3D structure prediction. We also show that our method can be used to optimize the predictions by other methods. These results indicate that optimization of RNA 3D structure prediction using evolutionary restraints of nucleotide–nucleotide interactions from direct coupling analysis offers an efficient way for accurate RNA tertiary structure predictions.
INTRODUCTION
Efficient and accurate methods to build RNA 3D structures from sequences are much needed due to the increasing disparity between the number of known sequences and the number of solved 3D structures (1–15). Over the past 5 years, the accuracy of RNA 3D structure prediction has been greatly improved (1,2,4,16–27). In 2011, for example, Liang and Schlick (28) evaluated the existing methods then and found that most computational predictions differed from the experimental structures with RMSD (Root Mean Square Deviation) values >6 Å. Worse still, for RNAs longer than 50 nucleotides (nt), the mean RMSD value reached 20 Å. Current methods, however, have reduced the mean RMSD to <6 Å for RNAs of <100 nt and simple topology (16,21,23). Yet for RNAs of complex topology and large size of more than 100 nt, the RMSDs of these prediction methods are still high. One of the bottlenecks for achieving better accuracy is the prediction of correct conformations of multi-branch junctions, which reflect the orientations of their branches and thus the tertiary interactions such as the kissing interaction of two hairpin loops. For example, most existing methods of RNA 3D structure prediction, such as fragment-assembling methods (FARNA/FARFAR (6,7), MC-Sym (9), Vfold (16), RNAComposer (22), 3dRNA (21), etc.), use local 3D templates to build the entire 3D structures. If the conformations of local 3D templates are inaccurate, the tertiary interactions, especially multi-branch junctions, will be incorrect. One way to mitigate this problem is to use available information on tertiary interactions as restraints in the RNA 3D structure prediction. A recent method based on Direct Coupling Analysis (DCA) of nucleotide coevolution provides a novel way to do this (29).
DCA was originally used to infer direct interactions (DIs) in proteins as well as between proteins (30,31). Recently it was also applied to RNAs and RNA–protein complexes (29,32). For RNAs, the DCA-based methods first infer physical interactions, both secondary and tertiary, between nucleotides in an RNA molecule by analyzing the co-evolutionary signals of nucleotides across sequences in the RNA family. A global probability model on sequence co-variation is used to disentangle direct from indirect interactions. Then, the inferred DIs are used as restraints in RNA 3D structure predictions. At present, these DI restraints have been used in the sampling process of Rosetta (29) and the folding process of NAST (32) to achieve better accuracies. Here, we show that alternative way of incorporating these restraints in 3D RNA structure prediction methods, however, leads to remarkable improvement in accuracy.
DIs contain only residue-level information on likely interacting pairs of nucleotides in an RNA molecule. Most RNA 3D prediction methods including fragment assembly methods, however, produce models of atom-level precision with detailed contact energies. Instead of using DI as restraints in the sampling or folding processes of RNA 3D structure prediction as was previously done (29,32), we use the DI restraints to optimize the predicted models of the fragment assembly methods, specifically, 3dRNA (Figure 1). This alternative way to incorporate the DI restraints effectively integrates the information at both residue level and atom level. The optimization is performed at residue level by a Monte Carlo algorithm with simulated annealing. In order to preserve the secondary structures during the optimization process, we keep the conformations of all helices and short loops fixed and only change their orientations since the fragment assembly procedure usually assures accuracy of them. For longer loops (hairpin loops of more than 4 nt or internal loops of more than 7 nt), both conformations and orientations are allowed to change. Thus, we no longer need to distinguish the secondary and tertiary interactions in DIs. We find that this way can greatly increase the accuracies of predictions, especially, for those of multi-branch junctions.
Figure 1.
Workflow chart of DCA-enhanced 3D RNA structure prediction.
MATERIALS AND METHODS
3dRNA
3dRNA is a fast and automated method of building 3D RNA structure based on sequence and secondary structure and it builds 3D RNA structure from the smallest secondary elements (SSEs) (21). The SSEs include helix, hairpin loop, internal loop (including bulge loop), pseudoknot loop and junction loop. Recently we have updated 3dRNA in its tree representation, template library, sampling and scoring. 3dRNA works as follows: For a target RNA 3dRNA first represents its secondary structure by a tree in which each node corresponds to an SSE; Second, 3dRNA finds a 3D template for each SSE by matching its sequence and secondary structure type to those of the templates library. Then, 3dRNA traverses the tree and assembles the 3D template of each node with that of its parent node to get a complete tertiary structure. Since each SSE may have multiple templates, 3dRNA can get a set of assembled structures for the target RNA by repeating the process above. If there is no appropriate template for an SSE, 3dRNA uses Distance Geometry (DG) (33) method to construct its 3D templates. Finally, 3dRNA clusters assembled structures and uses 3dRNAscore (34) to rank the cluster centers for user to choose the appropriate structures.
It is noted that the consensus secondary structures from Rfam database (35) are used in building 3D RNA structures in this work. The details of 3dRNA and 3dRNAScore are described in refs. (21) and (34). 3dRNA is provided at the website: http://biophy.hust.edu.cn/3dRNA.
Direct interactions
The detailed description of DCA can be found in refs (29,32). Here we just briefly describe the procedure of calculating the direct-coupling information used in the present paper and it mainly follows ref. (30,31).
-
Multiple sequence alignment (MSA)
DCA infers contact residues in a sequence using co-evolutionary information across all sequences belonging to the same family of the target sequence. In this work Rfam database (35) is used to identify which family each of the target RNA sequences belongs to. The alignment result of the sequences in the same family is extracted from Rfam database and pre-processed before being used to calculate the direct-coupling information:
First, the columns in MSA showing more than 50% gaps are removed except those containing residues of the target sequence.
Second, the sequences in MSA are reweighted to increase their statistical independence. To do this, for each sequence in MSA of M sequences, we count the number (denoted as m) of the sequences that are similar to it. The similarity between two sequences is defined as number of positions with coinciding residues. Two sequences are considered as similar if their similarity is larger than xL, where x is a similarity threshold with 0 < x < 1 and L is the length of sequences in MSA. In this work x is set as 0.9 according to ref. (36), which found that the results were insensitive to the values of x. The weight of a sequence is set to 1/m. Then the single and pair frequencies can be represented as:
where Ai (Aj) is the residue type at position i (j) along the aligned sequences and it may be ‘A, U, G, C, -’;
(1) 
denotes the ith residue in the ath aligned sequence; δ is the Kronecker delta. In this equation a pseudo-count λ is introduced as a standard treatment for finite sample effect and 
. Direct-coupling analysis (DCA)
DCA assumes a global statistical model of residue correlation in a sequence, i.e. the single and pair probabilities depend on the rest of its family, i.e.
 |
(2) |
where 
is the global probability of the sequence 
including residues and gap. Using a maximum-entropy modeling, this leads to a generalized Potts model of sequence variability,
 |
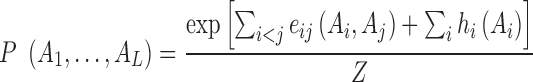(3) |
where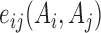 
and 
correspond to residue pair interaction energy (coupling strength) and single energy; Z is the normalization constant.
Under the mean-field approximation, the couplings between residues can be estimated by the inverse of the reduced covariance matrix with gap-gap, gap-residue and hi(gap) being set as 0
 |
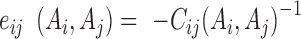(4) |
where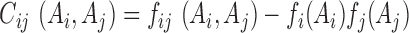 
is the covariance matrix. Since only 4 out of the 5 symbols ‘A’, ‘C’, ‘G’, ‘U’, ‘-’ are effectively independent, we restrict the covariance matrix to the full-rank 4L × 4L submatrix without gap.
The direct-coupling information can be represented as:
 |
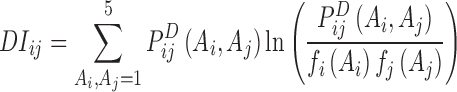(5) |
where,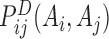 
is determined by a two-site model,
 |
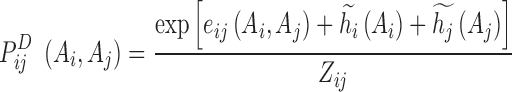(6) |
In this equation 
is determined above, 
, 
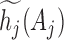and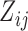 
are determined iteratively by satisfying the condition: 
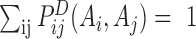and imposing the empirical single-site frequency counts as marginal distributions,
 |
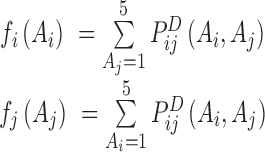(7) |
Optimization with restraints
Original version of 3dRNA contains an atom-level refinement process to eliminate atom clashes and optimize the bond length in the assembled RNA 3D models by using the steepest descent and conjugate gradient methods. To use the restraints from DCA or other experimental measurements, we add a residue-level optimization algorithm to 3dRNA, which uses a Simulated Annealing Monte Carlo (SAMC) algorithm. In order to preserve the secondary structure during the optimization process, we keep the conformations of all helices fixed and only change their orientations. For short loops (hairpin loops of <5 nt or internal loops of <7 nt), their conformations are also fixed but their orientations can be changed. This is because the fragment assembly procedure usually assures the prediction accuracy for short loops. For longer loops, both conformations and orientations are allowed to change.
To speed up the optimization process without losing too much precision, we use a coarse grained model for the optimization. Each residue is represented by 6 atoms: P, C4΄, C1΄, C2, C4, C6 (see Supplementary Figure S1). P is the phosphate atom of the backbone, C4΄ and C2΄ atoms are from the sugar ring, and C2, C4 and C6 atoms from the base. Since the two pseudo-torsions angles η (between atoms C4΄n-1, Pn, C4΄n and Pn+1) and θ (between atoms Pn, C4΄n, Pn+1 and C4΄n+1) are sufficient to describe RNA backbone conformation in most cases (37), P and C4΄ are frequently used to construct coarse-grained model, e.g. Vfold (16), iFoldRNA (8,12) and SimRNA (19,27). C1΄ atom is the joint of the sugar ring and the base. We use this atom for two reasons: first, it is used as the pivot to rotate the base of a randomly selected nucleotide in the moving stage of SAMC; Second, it is used to represent the position of the nucleotide in the grid system which will be illustrated below. The grid system was devised for accelerating the optimization procedure. C2, C4 and C6 atoms are used to help 3dRNAscore to compute the pairing score and stacking score between two bases. They also help to calculate the clash energy to avoid steric clashes when the coarse grained model is converted to all-atom model.
Monte carlo moves
In each step of the simulation, it needs to sample molecular conformation. Since we preserve the conformation of helices and short loops in the sampling process, we move at each step either a randomly selected residue in a randomly selected loop or all residues in a randomly selected helix with or without short hairpin loops and internal loops. This ensures that we will not destroy the structures of helices or the secondary structure of the whole molecule. In addition, this saves the time consumed in forming helices.
To keep the shape of helices, small hairpin loops and small internal loops unchanged in the process of optimization, we use a dedicated moving strategy. In each step, the element to be moved is a fragment, the length of which varies from 1 nt to the length of the whole sequence. All possible fragments should satisfy the condition that any helix or small hairpin loop or internal loop should be included only in one fragment.
To illustrate symbolically, the set of the fragments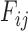 
we would move in each step is:
 |
(8) |
where L is the length of the sequence, and Elk is the kth of all the helices or small hairpin loops or small internal loops.
There are three possible kinds of operations (as shown in Supplementary Figure S2) that are applied to the fragment: the first is simply translating it in space; the second kind of operations is only applied to fragments satisfying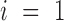 
or j = L. We rotate the fragment around the P atom of the residue j if 
or around the P atom of residue i if 
. The third kind of operations is to rotate the fragment along the axis passing through the atom P of residue i and the atom P of residue j + 1, when i > 1 and j < L.
Using grid system to accelerate optimization
To avoid steric clashes and to check if the distance of two residues satisfies a given distance cutoff, it's needed to calculate the minimum distance of each residue pair. If the molecule has L residues and each residue has n atoms averagely, then the time complexity is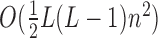 
. As the length of RNA sequence increases, the time is increasing quadratically.
To accelerate optimization, we use a grid system as shown in Supplementary Figure S3. Before the simulation, we construct a cubic lattice in space. Each grid in the lattice records which residues are located in it. If the conformation of the molecule changes, the state of the lattice would update. Thereafter, the time complexity is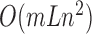 
, where m is the average number of residues in the nearest grids around a certain residue, e.g. those around G-48 within the dashed square in Supplementary Figure S3. The number m is stable that it will not increase with L. Hence, the consuming time will increase linearly rather than quadratically as L.
Energy function for the optimization
We built a residue-level energy function to guide the Monte Carlo simulation. The energy function is composed of six parts:
 |
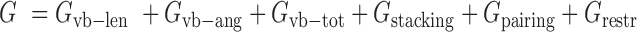(9) |
where,
 |
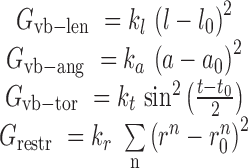(10) |
Here the symbol ‘vb’ means virtual bond representing a dummy link between two adjacent residues. The virtual bond is defined as a fictitious bond between the backbone C4΄ atoms of two adjacent residues.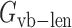
, 
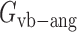, and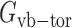 
are the energy functions associated with stretching, bending, and twisting of the standard virtual bond length l0, bond angle a0 and dihedral angle t0 with corresponding weights kl, ka, and kt, respectively. 
and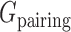 
are energy items used in 3dRNAscore (34) related to base stacking and base pairing. The values of these parameters used in the present study are given in Supplementary Table S1. To incorporate the restraints such as DIs from DCA into the optimization process, we introduce one additional term 
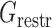as a penalty cost with a weight factor kr for any putative direct contact to deviate from the assigned contact length r0. We set the value of r0 according to the type of the DI restraint. If the DI restraint corresponds to a base pair, we calculate all the distances (
) between atoms of the same type (P-P, C4΄-C4΄, C1΄-C1΄, C2-C2, C4-C4, C6-C6) in the two bases. The values of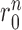 
are given in Supplementary Table S2 and they are derived from statistics of all RNA monomers in PDB databank (38). Then the six energy items between the atoms of the same type in the two bases are calculated according to Equation 10 and added to get the total restraint energy of the base pair. The restraint (i, j) is considered as a base pair if there is a restraint (i+1, j-1) or (i-1, j+1) in addition to the restraint (i, j). If it is not possible to determine whether a DI restraint is a base pair, only the distance between the C1΄ atoms of the two bases is calculated as the value of 
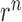and the value of 
is set as 10 Å (as in Supplementary Table S1). Then the restraint energy is also calculated according to Equation 10. As described in the discussion, when the distance between the C1΄ atoms of the two bases is >17 Å, the value of k is set to be small.
Generating and ranking 3D structural models
In this work 3dRNA will generate 1000 candidates (assembled structures) for a target RNA. Then, 3dRNA uses the DBSCAN (39) clustering method to classify all the candidates into clusters. The five largest clusters are selected and scored by 3dRNAscore, and the model with best score in each cluster will be picked out. Thus, we get five final models.
3dRNAscore is an all-atom statistical potential scoring function of atom–atom distances and backbone dihedral angles. We compared 3dRNAscore with several other scoring methods in ref. (34) and 3dRNAscore performed well in distinguishing the near-native (RMSD <7 Å) from non-native structures of RNA molecules.
RNA 2D and 3D structure visualization and plots are generated using Forna (40) and PyMOL (41) (http://www.pymol.org/), respectively. The 2D and 3D structures are generated by Forna. The accuracies of the predicted 3D structures are measured by RMSD (42) against their corresponding experimental structures. The RMSDs are calculated using the method in AMBER molecular dynamics simulation software (43) except when comparing with the results in ref. (32), where the RMSD is calculated by PyMOL in order to be consistent with ref. (32).
RESULTS
Comparison with existing methods
To compare our method with previous approaches (29,32) that combine Rosetta or NAST with the DI restraints, we analyzed two groups of RNAs used by previous approaches. Group I contains the same five RNAs as in ref. (32): 1FIR, 1Y26, 2GDI, 3Q3Z and 4LVV, and Group II the same six RNAs as in ref. (29): 1Y26, 2GDI, 2GIS, 3IRW, 3OWI and 3VRS. Two RNAs (1Y26 and 2GDI) appear in both groups. The detailed information of RNAs of these two groups is given in Supplementary Tables S1 and 2. These nine RNAs constitute Test Set I. We removed 3D templates extracted from these nine RNAs and their homologs from the templates library during the test.
In Group I, the average length of the five RNAs is 78 nt and four of them contain pseudoknots except 2GDI. Figure 2A and Supplementary Table S3 show the prediction results of 3dRNA and NAST using and not using DI restraints. The mean prediction accuracy (RMSD) of NAST without and with DI restraints is about 16.05 Å and 9.75 Å, respectively (32). In comparison, those of 3dRNA are 7.10 Å and 3.97 Å, respectively. In Group II, the average length of the six RNAs is 79 nt and four of them contain pseudoknots except 2GDI and 3OWI (29). Figure 2B and Supplementary Table S4 show the comparison of 3dRNA and Rosetta. The mean prediction accuracies of 3dRNA and Rosetta without DI restraints are 8.99 Å and 13.72 Å, respectively, while those with DI restraints are 6.29 Å and 9.47 Å, respectively. These results show that the prediction accuracies of 3dRNA are much better than those of NAST and Rosetta for the nine RNAs.
Figure 2.
(A) Comparison of predictions of five RNAs in Group I using 3dRNA and NAST without and with restraints. (B) Comparison of predictions of six RNAs in Group II using 3dRNA and Rosetta without and with restraints. (C) Comparison of predictions of multi-branch junctions of nine RNAs in Test Set I using 3dRNA without and with restraints.
The role of DI restraints in improving the prediction accuracy can also be seen intuitively from the changes of optimized structures and their contact maps with and without the restraints (Figures 3 and 4). The promotion of the prediction results using DCA comes from two aspects. First, DCA can capture the existing pseudoknots, and secondly, DCA can predict non-pairing tertiary interactions. A typical example of capturing pseudoknots is RNA 4LVV. Residues 37–41 of 4LVV form a pseudoknot (see Figure 4B) with residues 79–83. The points in the red circle in Figure 4A are the pseudoknot predicted successfully. It can be seen from Figure 4C and D that the use of DIs as restraints can help the formation of helix at the pseudoknot. A typical example of predicting non-pairing tertiary interactions is RNA 3U4M. There are tertiary interactions (see Figure 4F) between the residues 7 and 14 and the residues 39, 40, 43 and 44. The points in the rectangular box in Figure 4E represent residue pairs that have non-pairing tertiary interactions. It can be seen from Figure 4G and H that the use of DIs as restraints can help the formation of non-pairing tertiary interactions. By the way, the contact maps for other RNAs of Test Set I can be downloaded online: http://biophy.hust.edu.cn/resources/3drna_opt_dca.
Figure 3.
Comparison of the optimized structures of the nine RNAs in Test Set I with (dark blue or dark on the right) and without (magenta or dark on the left) DI restraints against their native structure (green or light). The tertiary structures are generated by PyMOL (41).
Figure 4.
Two examples showing the roles of DI-restrains in RNA 3D structure optimization. A–D and E–H are the contact maps, 2D structures, 3D structures optimized without and with DI restraints for RNAs 4LVV and 3U4M, respectively. Cnat, Cnrs and Crs denote the contacts in the native structure and the structures optimized without and with DI restraints, respectively; DI* are the top L DIs but with the isolated points removed; The red circle and rectangular box are the regions of the pseudoknot and tertiary interactions, respectively. The red regions in the 3D structures are residues that would form pseudoknot or tertiary interactions. The 2D and 3D structures are generated by Forna (40) and PyMOL (41), respectively.
Improvement of multi-branch junction prediction
As mentioned above, one of the bottlenecks for accurate predictions of RNA 3D structures is finding correct conformations for multi-branch junctions. Typical examples are 4LVV and 3VRS that have very large RMSD values relative to their native structures before the optimization with DI restraints (Figure 3). The large deviation is due to incorrect conformations of the multi-branch junctions built by 3dRNA. However, the conformations of the multi-branch junctions can be greatly improved through the optimization with the DI restraints since these restraints contain tertiary interactions that restrain the orientation of the helices and in turn the conformations of the multi-branch junctions. To see this we analyzed the conformational changes of the multi-branch junctions due to optimization with and without the DI restraints. The results are presented in Figure 2C, Supplementary Table S5 and Figure 5. They show that the optimization with the DI restraints indeed improve the conformations of most multi-branch junctions greatly, especially for those that are much different from the native ones, such as 4LVV and 3VRS. And the mean RMSDs of the multi-branch junctions change from 6.48 Å to 4.33 Å.
Figure 5.
Comparison of the optimized structures of the multi-branch junctions of the nine RNAs in Test Set I with (dark blue or dark on the right) and without (magenta or dark on the left) DI restraints relative to their native ones (green). The tertiary structures are generated by PyMOL (41).
Improvement of longer RNA prediction
To further see how the co-evolutionary information can be used to improve the prediction accuracy of 3dRNA, we built a Test Set II of 29 RNAs elaborately selected from Rfam database according to the following standard: (i) the longest one from different families; (ii) having complete 3D structures; (iii) having more than 100 homologous sequences; and (iv) longer than 50 nt. In particular, this test set includes 14 long RNAs with their lengths varying from 100 to 388 nt. 3D templates extracted from these RNAs and those of their homology families are removed from the templates library during the test. Figure 6 and Supplementary Table S6 give the results. The mean RMSDs of the predicted structures without and with DI-restrained optimization are 16.90 Å and 14.15 Å, respectively. In particular, for the 14 long RNAs, the mean RMSDs of the predicted structures without and with DI-restrained optimization are 22.64 Å and 18.41 Å, respectively. The RMSDs of most predicted structures are significantly reduced after DI-restrained optimization. It is noted that for the loops in these long RNAs the 3D templates were unavailable in most cases and were generated using the DG method and so the predicted structures usually have larger RMSDs. Furthermore, there are no enough homologous sequences in most cases.
Figure 6.
Comparison of predictions of Test II using 3dRNA without and with restraints.
The prediction accuracy of these long RNAs is similar to the situation of the RNAs with lengths from 50 to 100 nt in 2011 (28). For these long RNAs, it seems that their overall shapes are similar to the native ones if their RMSDs are <20 Å. Figure 7 shows the native and DI-restrained optimization structures of two RNAs 4UE4 (266 nt) and 3IZ4 (377 nt).
Figure 7.
Comparison of the native structures (cyan or light) of (A) 4UE4 (266 nt) and (B) 3IZ4 (377 nt) with the predicted structures (brown or dark) by 3dRNA with DI-restrained optimization. The tertiary structures are generated by PyMOL (41).
In Supplementary Table S6 we also listed the prediction results using RNAComposer web server (22). It is noted that the option of RNAComposer (44) to exclude user-specified structures or templates is not used since we are not sure whether their homologs are used or not. Thus, in the predictions of 9 of the 29 RNAs RNAComposer used the 3D templates from themselves or their homologs. It also gave no result for one of the RNAs. Therefore, only the remaining 19 RNAs are used to test the performance of the optimization procedure. For the remaining 19 RNAs the mean RMSDs of the predictions by RNAComposer and by 3dRNA are 19.37 Å and 18.19 Å, respectively. After DI-restrained optimization, they are reduced to 16.03 Å and 15.36 Å, respectively. Among the remaining 19 RNAs, 10 RNAs have lengths ≥100 nt. For these 10 long RNAs the mean RMSDs of the predictions by RNAComposer and 3dRNA are 22.89 Å and 22.82 Å, respectively. After DI-restrained optimization, they are reduced to 19.39 Å and 18.28 Å, respectively. These results show that the predictions of RNAComposer can be further optimized by using DI restraints.
Improvement of RNA-Puzzles predictions of different laboratories
Challenges 6, 8, 12, 13 of RNA-Puzzles were redone to see if the co-evolutionary information can improve the prediction accuracy of 3dRNA and other methods. The reason of selecting these four RNAs only is that they have enough homologous sequences to support DCA. 3D templates extracted from these four RNAs from the templates library were also removed during the test. These four RNAs constitute Test Set III. The prediction results are given in Table 1. It can be seen that the initial structures of these four challenges assembled by 3dRNA are all around 20 Å, the worst of which is 26.32 Å (challenge 8) and the best is 18.96 Å (challenge 6). If the assembled structures were optimized with DI restraints, the RMSDs of them all decrease to be around 12 Å, the worst of which is 13.98 Å (challenge 12) and the best is 9.82 Å (challenge 13). Table 1 shows that the optimization under the DI restraints can reduce the RMSDs for nearly all the challenges. The performance of the optimization could also be seen from the changes of the ranks of the RMSDs before and after optimization, especially when the RMSD of the initial structure is large.
Table 1. Prediction results of RNA-Puzzles Challenges 6, 8, 12 and 13 (Test Set III).
| Challenge number | Length (nt) | Rfam acc | Number of sequences | Best ranked structure | Initial structure | Optimization with DI restraints | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lab | RMSD (Å) | Laboratory | Rank | RMSD (Å) | Rank | RMSD (Å) | ||||
| Our | 10 | 18.96 | 3 | 13.54 | ||||||
| Das/4 | 1 | 11.70 | 1 | 10.7 | ||||||
| 6 | 168 | RF00174 | 2117 | Das/4 | 11.67 | Das/8 | 9 | 17.96 | 3 | 12.54 |
| Chen/2 | 13 | 22.26 | 6 | 15.25 | ||||||
| Dokholyan/6 | 34 | 37.47 | 12 | 21.98 | ||||||
| Our | 42 | 26.32 | 11 | 11.15 | ||||||
| Das/3 | 1 | 4.80 | 2 | 5.48 | ||||||
| 8 | 96 | RF01725 | 1339 | Das/3 | 4.80 | Bujnicki/9 | 4 | 6.82 | 3 | 6.56 |
| Adamiak/1 | 33 | 13.88 | 5 | 10.29 | ||||||
| Chen/8 | 37 | 15.81 | 11 | 11.21 | ||||||
| Our | 49 | 23.57 | 21 | 13.98 | ||||||
| Ding/12 | 1 | 10.06 | 2 | 10.35 | ||||||
| 12 | 111 | RF00379 | 1686 | Ding/12 | 10.06 | Adamiak/2 | 13 | 13.33 | 5 | 11.42 |
| Chen/4 | 27 | 16.06 | 8 | 12.54 | ||||||
| Chen/1 | 48 | 20.49 | 26 | 14.76 | ||||||
| Our | 47 | 20.23 | 11 | 9.82 | ||||||
| Das/7 | 1 | 5.41 | 3 | 5.79 | ||||||
| 13 | 71 | RF01750 | 669 | Das/7 | 5.41 | Bujnicki/9 | 43 | 17.00 | 11 | 10.32 |
| Ding/8 | 25 | 14.62 | 10 | 9.51 | ||||||
| Xiao/7 | 55 | 27.60 | 12 | 11.52 | ||||||
Four predictions of the four RNA-Puzzles challenges by other laboratories were selected as the initial structures and then refined by the optimization procedure. Table 1 shows the results. The optimization with the DI restraints can further reduce the RMSDs of most of the 14 predictions and only three of them become slightly larger (<1.0 Å) than those of the initial structures. For example, the RMSD of the rank 1 prediction of the Das laboratory in challenge 6 decreases by 1.0 Å. The effect of the optimization with the DI restraints is more significant for the predictions with larger RMSDs. For example, the RMSD of the rank 43 prediction of Bujnicki laboratory in challenge 13 changes from 17.0 Å to 10.32 Å by the optimization with the DI restraint. These results indicate that the nucleotide co-evolution information can be used to further improve the accuracy of 3D RNA structure prediction regardless of the methods.
Structure prediction of RNAs of unknown 3D structures
We also predicted 3D structures of 2377 Rfam families without known 3D structures (35). These RNAs are referred as Test Set IV. The results could be downloaded online: http://biophy.hust.edu.cn/resources/3drna_opt_dca. Figure 8 gives two examples that were predicted in Ref. (29).
Figure 8.
Predicted models of two RNAs of unknown 3D structures. The two RNAs are (A) RF01739 and (B) RF01695 from Rfam. The models are predicted by 3dRNA (left) and Rosetta in ref. 29 (right), respectively. The tertiary structures are generated by PyMOL (41).
Running time
Supplementary Table S6 gives the running times of all the RNAs in Test Set II. Supplementary Figure S5 is the plot of the running time versus sequence length and it shows that the trend of the rise of the time is indeed close to linearity as expected above. For an example, for an RNA of 233 nt (4C4Q), the optimization takes only 49 minutes. The CPU information is: Intel(R) Xeon(R) CPU E5-2620 v2 @ 2.10GHz.
DISCUSSION
The DIs generated by DCA may have false positives. The usual method of reducing the effect of false positives is to select the first L (sequence length) or L/2 largest DIs as the predicted contacts (29,32,36). In the present work the first L largest DIs are taken as the predicted contacts. Furthermore, we did the following treatments to reduce the effects of false positives further: (i) we removed all isolated DI points since the false positive DIs exhibited a significant feature that they were almost isolated points in contact map (see Supplementary Figure S4); (ii) it is also noted that a true positive DI point always appears in the upper left corner or the bottom right corner of another true positive DI point. If two points locate like this, they are likely to be stacked to each other. Hence, the points that don't satisfy this condition are also removed. The bottom right triangle of the contact maps in Supplementary Figure S4 gives the processed DIs, i.e. DI*s, which shows that most false positives are removed. Furthermore, we made the DIs be short-range, i.e. the two residues interact only when their distances are <17 Å because the distance of the C1΄ atoms of two paired residues is always <17 Å, which may avoid the situations that the false positives lead to a false folded state.
Our method still has some limitations. On one hand, for short RNAs whose assembled structures are usually accurate enough, the optimized structures sometimes have higher RMSDs than the former. This is due to the coarse-grained potential we used in SAMC, which may be not so accurate to lead the conformation of the structure to a near-native state. On the other hand, for long RNAs, the assembled structures are usually far from the native ones since in this case appropriate 3D templates of most SSEs are unavailable and are generated by using the DG method. The generated templates may result in serious steric clashes because the generating procedure only considers the conformations of the local SSEs but not the entire structure. This needs more times and more efficient methods to optimize them. Hence we need to improve the method of generating SSEs for large RNA in future work.
AVAILABILITY
Source code, used data and other supported materials are provided through the link http://biophy.hust.edu.cn/resources/3drna_opt_dca. Clicking one of RNAs in Test Sets will fill the input data and switch to 3dNA webpage automatically. The optimization method is integrated in the web server of 3dRNA: http://biophy.hust.edu.cn/3dRNA. Users can switch the task type to ‘Optimization’ to do the optimization with and without restraints separately. A web page that can be used for DCA (http://biophy.hust.edu.cn/DCA) is provided, and users just need to enter an RNA sequence or provide multiple sequence alignment files to get DIs or DI* (DIs after being ranked to pick out the top L DIs and then processed by removing the isolated points to reduce the false positives).
CONCLUSION
In this work we proposed an optimization method to incorporate DI restraints into 3dRNA, a computational suite for RNA 3D structure prediction. Essentially, this optimization process generated additional configurations from those obtained by the original 3dRNA according to a novel energy function that combines force field potential, statistical potential and DI-restraint potential at residual level. All configurations were then subject to selection by the all-atom 3dRNAscore function. This new approach takes advantages of both the atom-level precision of the original 3dRNA and the residue-level tertiary interaction information of DCA. As such, it makes much more accurate RNA 3D structure prediction than the original 3dRNA as well as other existing prediction methods that use DI information. In particular our method demonstrated a significant improvement in predicting multi-branch junction configuration, a major bottleneck for RNA 3D structure prediction. Therefore, using DI information from DCA to optimize traditional RNA 3D structure prediction offers an efficient approach to increase prediction accuracy.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Shengyou Huang for valuable discussions.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
NSFC [11374113, 31570722]. Funding for open access charge: NSFC [11374113, 31570722].
Conflict of interest statement. None declared.
REFERENCES
- 1. Cruz J.A., Blanchet M.F., Boniecki M., Bujnicki J.M., Chen S.J., Cao S., Das R., Ding F., Dokholyan N.V., Flores S.C. et al. RNA-Puzzles: a CASP-like evaluation of RNA three-dimensional structure prediction. RNA. 2012; 18:610–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Miao Z., Adamiak R.W., Blanchet M.-F., Boniecki M., Bujnicki J.M., Chen S.-J., Cheng C., Chojnowski G., Chou F.-C., Cordero P. et al. RNA-Puzzles Round II: assessment of RNA structure prediction programs applied to three large RNA structures. RNA. 2015; 21:1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Dawson W.K., Bujnicki J.M.. Computational modeling of RNA 3D structures and interactions. Curr. Opin. Struct. Biol. 2016; 37:22–28. [DOI] [PubMed] [Google Scholar]
- 4. Sim A.Y., Minary P., Levitt M.. Modeling nucleic acids. Curr. Opin. Struct. Biol. 2012; 22:273–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Massire C., Westhof E.. MANIP: an interactive tool for modelling RNA. J. Mol. Graph. Model. 1998; 16:197–205. [DOI] [PubMed] [Google Scholar]
- 6. Das R., Baker D.. Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl. Acad. Sci. U.S.A. 2007; 104:14664–14669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Das R., Karanicolas J., Baker D.. Atomic accuracy in predicting and designing noncanonical RNA structure. Nat. Methods. 2010; 7:291–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Sharma S., Ding F., Dokholyan N.V.. iFoldRNA: three-dimensional RNA structure prediction and folding. Bioinformatics. 2008; 24:1951–1952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Parisien M., Major F.. The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature. 2008; 452:51–55. [DOI] [PubMed] [Google Scholar]
- 10. Martinez H.M. Jr, Maizel J.V., Shapiro B.A.. RNA2D3D: a program for generating, viewing, and comparing 3-dimensional models of RNA. J. Biomol. Struct. Dyn. 2008; 25:669–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Jonikas M.A., Radmer R.J., Laederach A., Das R., Pearlman S., Herschlag D., Altman R.B.. Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. RNA. 2009; 15:189–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Gherghe C.M., Leonard C.W., Ding F., Dokholyan N.V., Weeks K.M.. Native-like RNA tertiary structures using a sequence-encoded cleavage agent and refinement by discrete molecular dynamics. J. Am. Chem. Soc. 2009; 131:2541–2546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Jossinet F., Ludwig T.E., Westhof E.. Assemble: an interactive graphical tool to analyze and build RNA architectures at the 2D and 3D levels. Bioinformatics. 2010; 26:2057–2059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Schudoma C., May P., Walther D.. Modeling RNA loops using sequence homology and geometric constraints. Bioinformatics. 2010; 26:1671–1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Xu X., Chen S.. Physics-based RNA structure prediction. Biophys. Rep. 2015; 1:2–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Cao S., Chen S.-J.. Physics-based de novo prediction of RNA 3D structures. J. Phys. Chem. B. 2011; 115:4216–4226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Rother M., Rother K., Puton T., Bujnicki J.M.. ModeRNA: a tool for comparative modeling of RNA 3D structure. Nucleic Acids Res. 2011; 39:4007–4022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zhao Y., Gong Z., Xiao Y.. Improvements of the hierarchical approach for predicting RNA tertiary structure. J. Biomol. Struct. Dyn. 2011; 28:815–826. [DOI] [PubMed] [Google Scholar]
- 19. Rother K., Rother M., Boniecki M.L., Puton T., Tomala K., Lukasz P.L., Bujnicki J.M.. Template-based and template-free modeling of RNA 3D structure: Inspirations from protein structure modeling. Nucleic Acids & Molecular Biology. 2012; 27:67–90. [Google Scholar]
- 20. Zhang J., Bian Y., Lin H., Wang W.. RNA fragment modeling with a nucleobase discrete-state model. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 2012; 85:021909. [DOI] [PubMed] [Google Scholar]
- 21. Zhao Y., Huang Y., Gong Z., Wang Y., Man J., Xiao Y.. Automated and fast building of three-dimensional RNA structures. Sci. Rep. 2012; 2:734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Popenda M., Szachniuk M., Antczak M., Purzycka K.J., Lukasiak P., Bartol N., Blazewicz J., Adamiak R.W.. Automated 3D structure composition for large RNAs. Nucleic Acids Res. 2012; 40:e112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Xu X.J., Zhao P.N., Chen S.J.. Vfold: a web server for RNA structure and folding thermodynamics prediction. PLoS One. 2014; 9:e107504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Ulc P., Romano F., Ouldridge T.E., Doye J.P.K., Louis A.A.. A nucleotide-level coarse-grained model of RNA. J. Chem. Phys. 2014; 140:235102. [DOI] [PubMed] [Google Scholar]
- 25. Shi Y.Z., Wang F.H., Wu Y.Y., Tan Z.J.. A coarse-grained model with implicit salt for RNAs: predicting 3D structure, stability and salt effect. J. Chem. Phys. 2014; 141:105102. [DOI] [PubMed] [Google Scholar]
- 26. Kerpedjiev P., Zu Siederdissen C.H., Hofacker I.L.. Predicting RNA 3D structure using a coarse-grain helix-centered model. RNA. 2015; 21:1110–1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Magnus M., Boniecki M.J., Dawson W., Bujnicki J.M.. SimRNAweb: a web server for RNA 3D structure modeling with optional restraints. Nucleic Acids Res. 2016; 44:W315–W319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Laing C., Schlick T.. Computational approaches to RNA structure prediction, analysis, and design. Curr. Opin. Struct. Biol. 2011; 21:306–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. De Leonardis E., Lutz B., Ratz S., Cocco S., Monasson R., Schug A., Weigt M.. Direct-coupling analysis of nucleotide coevolution facilitates RNA secondary and tertiary structure prediction. Nucleic Acids Res. 2015; 43:10444–10455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Morcos F., Pagnani A., Lunt B., Bertolino A., Marks D.S., Sander C., Zecchina R., Onuchic J.N., Hwa T., Weigt M.. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. U.S.A. 2011; 108:E1293–E1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Morcos F., Hwa T., Onuchic J.N., Weigt M.. Direct coupling analysis for protein contact prediction. Methods Mol. Biol. 2014; 1137:55–70. [DOI] [PubMed] [Google Scholar]
- 32. Weinreb C., Riesselman AJ., Ingraham J.B., Gross T., Sander C., Marks D.S.. 3D RNA and functional interactions from evolutionary couplings. Cell. 2016; 165:963–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Havel T.F. Distance geometry: theory, algorithms, and chemical applications. Encyclopedia of Computational Chemistry. 1998; 120:John Wiley & Sons; 723–742. [Google Scholar]
- 34. Wang J., Zhao Y., Zhu C., Xiao Y.. 3dRNAscore: a distance and torsion angle dependent evaluation function of 3D RNA structures. Nucleic Acids Res. 2015; 43:e63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Nawrocki E.P., Burge S.W., Bateman A., Daub J., Eberhardt R.Y., Eddy S.R., Floden E.W., Gardner P.P., Jones T.A., Tate J. et al. Rfam 12.0: updates to the RNA families database. Nucleic Acids Res. 2015; 43:D130–D137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Morcos F., Pagnani A., Lunt B., Bertolino A., Marks D.S., Sander C., Zecchina R., Onuchic J.N., Hwa T., Weigt M.. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. U.S.A. 2011; 108:E1293–E1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Wadley L.M., Keating K.S., Duarte C.M., Pyle A.M.. Evaluating and learning from RNA pseudotorsional space: quantitative validation of a reduced representation for RNA structure. J. Mol. Biol. 2007; 372:942–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Rose P.W., Prlic A., Altunkaya A., Bi C., Bradley A.R., Christie C.H., Costanzo L.D., Duarte J.M., Dutta S., Feng Z. et al. The RCSB protein data bank: integrative view of protein, gene and 3D structural information. Nucleic Acids Res. 2017; 45:D271–D281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Ester M., Kriegel H.P., Sander J., Xu X.. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. 1996; 1:AAAI Press; 226–231. [Google Scholar]
- 40. Kerpedjiev P., Hammer S., Hofacker I.L.. Forna (force-directed RNA): Simple and effective online RNA secondary structure diagrams. Bioinformatics. 2015; 31:3377–3379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. DeLano W.L., Ultsch M.H., Wells J.A.. Convergent solutions to binding at a protein-protein interface. Science. 2000; 287:1279–1283. [DOI] [PubMed] [Google Scholar]
- 42. Kabsch W. A discussion of the solution for the best rotation to relate two sets of vectors. Acta Cryst. 1978; A34:827–828. [Google Scholar]
- 43. Case D., Babin V., Berryman J., Betz R., Cai Q., Cerutti D., Cheatham T. III, Darden T., Duke R., Gohlke H.. Amber 14. 2014; San Francisco: University of California. [Google Scholar]
- 44. Antczak M., Popenda M., Zok T., Sarzynska J., Ratajczak T., Tomczyk K., Adamiak R.W., Szachniuk M.. Newfunctionality of RNAComposer: an application to shape the axis ofmiR160 precursor structure. Acta Biochim. Polonica. 2016; 4:737–744. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.