Mechanism of the Association Pathways for a Pair of Fast and Slow Binding Ligands of HIV‑1 Protease

Abstract

Equilibrium constants, together with kinetic rate constants of binding, are key factors in the efficacy and safety of drug compounds, informing drug design. However, the association pathways of protein–ligand binding, which contribute to their kinetic behaviors, are little understood. In this work, we used unbiased all-atom molecular dynamics (MD) simulations with an explicit solvent model to study the association processes of protein–ligand binding. Using the HIV protease (HIVp)–xk263 and HIVp–ritonavir protein–ligand systems as cases, we observed that ligand association is a multistep process involving diffusion, localization, and conformational rearrangements of the protein, ligand, and water molecules. Moreover, these two ligands preferred different routes of binding, which reflect two well-known binding mechanisms: induced-fit and conformation selection models. Our study shows that xk263 has a stronger capacity for desolvating surrounding water molecules, thereby inducing a semiopen conformation of the HIVp flaps (induced-fit model). In contrast, the slow dehydration characteristic of ritonavir allows for gradual association with the binding pocket of HIVp when the protein’s flap conformation is fully open (conformation selection model). By studying the mechanism of ligand association and understanding the role of solvent molecules during the binding event, we can obtain a different perspective on the mechanism of macromolecule recognition, providing insights into drug discovery.

Graphical Abstract

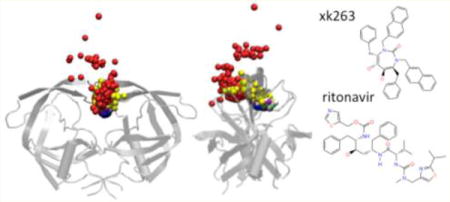
Many diseases can be treated clinically by delivering drugs to specific protein targets. The thermodynamic properties of protein–ligand recognition are important predictors of ligand efficacy,^1–4 but the importance of binding kinetics in biological processes has not been recognized until recently.^5–7 Binding kinetics may be associated with different binding mechanisms. For decades, scientists have discussed various theories to explain protein–ligand binding such as lock and key, conformation selection, and induced fit. Understanding the underlying mechanism of binding kinetics enhances our ability to design ligands.

For some ligands and pharmaceutical targets, binding kinetics could play a significant role in in vivo efficacy.^5,6,8–11 To illustrate this, for the systems without intermediates, the equilibrium constant (K_eq) is the balance between the two rate constants (K_eq = k_on/k).^12–14 off To enhance binding affinity, a good drug candidate is expected to have a fast k_on and a slow k_off, corresponding to a longer residence time.¹⁵ However, in some cases, K_eq is not correlated with in vivo efficacy; rather, k_off is better correlated.¹⁶ Therefore, understanding the details of binding kinetics is critical to drug discovery, for optimizing the drug efficacy and reducing medical attrition.^17–19 However, the physical basis behind fast or slow binding ligands is still unclear.

Revealing the details of the entire binding pathway of a drug via traditional methods is extremely difficult, if not impossible. The available structures for free and bound states of protein systems from X-ray crystallography and nuclear magnetic resonance (NMR) studies provide limited information about binding pathways. Fortunately, molecular modeling provides an alternative for gaining insight into the details of ligand association. However, one of the major challenges with modeling is the time scale of binding events. Typically, to investigate a ligand diffusing toward and binding to a protein, numerous simulations with time scales greater than 1 μs are required. To overcome computational costs, previous studies performed in our lab and in other laboratories used coarse-grained models to study binding kinetics. These studies resulted in valuable information about the diffusion steps of proteins binding with ligands, including xk263 and ritonavir.^20–22 Recently, modeling a nonspecific association of xk263 via Brownian dynamics (BD) with the GeomBD2 program further added to prior work by showing the probability of where the ligand will most likely be found on the surface of HIV-1 protease (HIVp) during diffusion.²³

Because of current advances in technology, today, researchers are able to perform unbiased, all-atom molecular dynamics (MD) to gain better insights that may affect the binding kinetics of drug–protein systems on a microsecond time scale. For instance, a recent study of G-protein-coupled receptors and Src kinase examined the role of water molecules upon association of the drug. The same study revealed multiple metastable intermediates throughout the entire binding process.^24,25 A different study analyzed the water density in the binding interfacial gap. The dewetting process was found to guide the ligand into the binding pocket and accelerate the approach to the final bound state, especially when binding on a hydrophobic surface.²⁶ Thus, hydrophobic dehydration can be considered as an essential driving force for assembly of a ligand to a nonpolar surface.^27,28 Another study involving Barnase protein showed that a hydrogen bond network on the binding interface stabilizes the transition complex with the surrounding water molecules, thereby facilitating protein–protein binding.²⁹ Setny et al. showed that fluctuations in hydration and stochastic motions of a ligand were intimately coupled, thus increasing the entrance friction, which decelerated the association kinetics.³⁰ Finally, free energy calculations of a protein–ligand complex suggested that water molecules moving from the binding site to the solvent act as a rate-determining step in ligand association.^31,32 In technique and in choice of protein systems, these studies greatly differ. However, their results and conclusions highlight common themes during the binding process: overall, transitions of hydrogen bonds (H-bonds) and the movement of water molecules during the binding process are important factors governing the rate of ligand association.^24,33,34 Although the studies mentioned above provided some insights into the mechanism of ligand binding, most of the work did not discuss changes in protein conformations during ligand entry, which affect the binding kinetics of drugs. For example, pioneering work done by Shan and co-workers showed that the binding kinetics of the drug imatinib may provide a probe of the DFG loop transition in the Abl kinase system.³⁵ Also, the mechanisms of fast or slow binding kinetics are still unclear.

To demonstrate the events leading to the association pathway of protein and ligand, we selected HIVp and two ligands, xk263 and ritonavir, as our study systems. HIVp plays an integral role in the HIV life cycle and is one of the major targets in anti-AIDS treatments.³⁶

The HIVp structure features a C₂ axis of symmetry with two flexible glycine-rich flaps that behave as a gate to control ligand access.³⁷ Three conformations of the flaps were detected in the native state: open, semiopen, and closed (Figure 1). Experimental and computational studies revealed that the semiopen conformation is the dominant form in the ligand-free state;^38,39 however, with ligand binding, the flaps favor the closed conformation.^40–42 Two types of handedness orientation, semiopen and closed, are associated with the ligand-free and -bound states, respectively (Figure 1).^42,43 Because the transition from one flap conformation to another of HIVp was observed from early studies, we should expect the flaps to undergo large conformational changes when the protein switches from the free to bound state.

Figure 1.

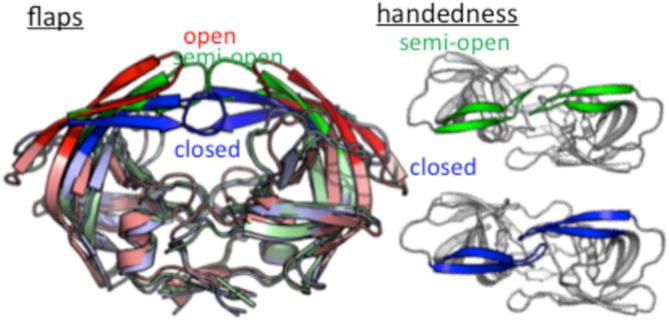
Schematic representation of the HIVp structure. Flaps with open, semiopen, and closed conformations are colored red, green, and blue, respectively. The orientation of the flaps, called handedness, has two forms: semiopen (green) and closed (blue).

Most experimental and computational studies focused on the mechanism of flap opening and closing.^{38,40,44–47} Two proposed binding models have attempted to explain the association process. The induced-fit model hypothesizes that a binding event occurs when a ligand induces conformational changes and interrupts the native movement of a protein;⁴⁸ a ligand could approach HIVp in its semiopen-flap conformation, disrupt the flap–flap interactions to induce flap opening, and enter the binding pocket to form a complex. The other model, conformation selection, proposes an opposite assumption: a ligand directly binds to a preorganized protein conformation, such as HIVp with an open-flap conformation. After the ligand binds and stays in the binding site, the flaps close. A previous study suggested that both of these models can explain HIVp–ligand association⁴⁵ but was unable to elucidate the reason for the fast or slow kinetics of a ligand.

We used two HIVp ligands, as an example, to demonstrate the cases of fast and slow binding: the cyclic urea compound xk263, a fast binder, with a k_on of ~10⁹ M⁻¹ s⁻¹; and the peptide mimic compound ritonavir, a slower binder, with a k_on of ∼10⁶ M⁻¹ s⁻¹ (Figure 1). Despite a difference of 3 orders of magnitude in association rate constants between the two ligands, they bind to HIVp tightly, with a K_d of ∼10⁻⁹ M (approximately −11 kcal/mol).^12,49

With knowledge gained from prior work, we aimed to use unbiased MD simulations to focus on the events leading up to binding and understand the changes in dynamics that result from a ligand binding. We believe that these events can further explain the fast and slow kinetics of binding reported by experimental studies. Overall, we studied different poses of protein–ligand complexes as well as the dynamics of water molecules by using conventional MD simulations for HIVp–ligand systems. We illustrate potential binding mechanisms for ligands with different association kinetics and explain how water molecules affect the rate of binding.

MATERIALS AND METHODS

Molecular Systems

We selected the structure of the ligand-free HIVp from Protein Data Bank (PDB) entry 1HHP (2.70 Å resolution) to study the motions of the free protein.³⁷ The conformations of HIVp binding to xk263 and ritonavir were taken from the PDB entries 1HVR (1.80 Å resolution) and 1HXW (1.80 Å resolution), respectively.^50,51 Of note, xk263 has significantly more ligand hydrophobicity than ritonavir does. The LogP values were computed by using different software packages. Details are given in Text S3.

MD Simulations

We used the Amber 12 package with an efficient GPU implementation for MD simulations of the free HIVp and ligand binding pathways.^52,53 Amber 99SB and General Amber Force Field (GAFF) were applied to HIVp and the two ligands, respectively.^54–56 By checking the unperturbed charge of the system, we placed the counterion Cl⁻ to maintain a neutral system. Minimization of the hydrogen atoms, the side chains, and the entire protein complex was applied for 500, 5000, and 5000 steps, respectively. After the system had been solvated with a rectangular TIP3P water box, the edge of the box is at least 12 Å from the solutes.⁵⁷ The system went through a 1000-step water and 5000-step system minimization to correct any inconsistencies. Next, we relaxed the system by slowly heating it during an equilibrium course of 10 ps at 50, 100, 150, 200, 250, and 300 K. The long-range electrostatic interactions were computed by the particle mesh Ewald method beyond an 8 Å distance.⁵⁸ The time step of the simulations was 0.002 ps with a nonbonded cutoff of 12 Å. We collected the resulting trajectories every 1 ps, with a time step of 2 fs, in an isothermic–isobaric (NPT) ensemble. The Langevin thermostat, with a damping constant of 2 ps⁻¹, was used to maintain a temperature of 300 K. Finally, the SHAKE algorithm was used to constrain hydrogen atoms during the MD simulations.⁵⁹

Because free HIVp has multiple flap conformations, we performed a 250 ns simulation on the free protein to obtain a variety of different protein conformations; four snapshots of the simulation showing different orientations and handedness of the flaps (Figure 2) were selected for molecular docking. MD simulations were based on 58 initial protein–ligand conformations obtained from molecular docking (see the next section for details). We first performed 200 ns MD simulations on each initial conformation by using CPU parallel processing and local gpu machines. Then, conformations with ligands close to the binding site (a result of 17) were selected for further study by using local gpu machines (time scale of 300–1000 ns). To further investigate the association pathway, we chose two promising representative models for xk263 and three for ritonavir and performed 3–14 μs MD simulations with a special-purpose computer, Anton.^60,61 Finally, the trajectories were collected and analyzed at intervals of 1 ps, 100 ps, or 1 ns, depending on the length of the simulation.

Figure 2.

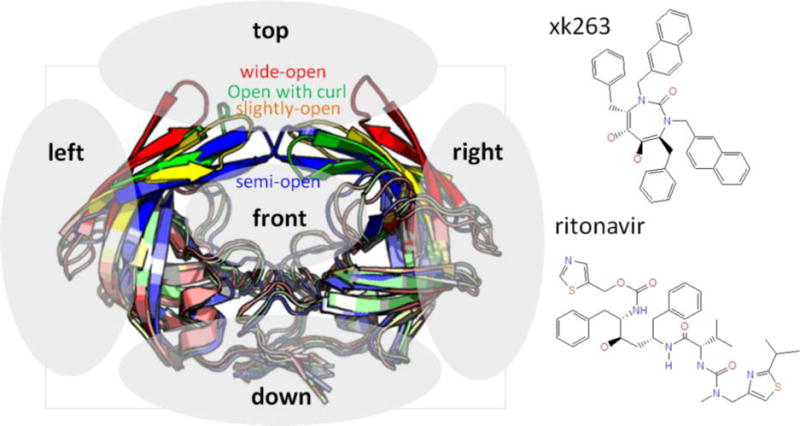
Two ligands, xk263 and ritonavir, are docked to a box placed 20–30 Å away from HIVp. The four initial HIVp conformations with different flap orientations [wide open (red), open with a curl flap (green), slightly open (yellow), and semiopen (blue)] were used in the docking procedure. The ligands were docked on the top, bottom, right, left, and front regions (gray area) as starting conformations in MD simulations.

Docking Protocol

Autodock with the Lamarckian genetic algorithm was used to dock ligands on designated regions of HIVp.⁶² We placed the docking box 20–30 Å from the center of the HIVp binding site; naturally, ligands could approach HIVp from any direction, so the docking box was placed at the top, bottom, left, right, and front regions of the protein (Figure 2). We did not consider the back region because of the symmetry of the protein. The placement of the docking box reflected areas of high probability toward which the ligand would most likely diffuse, as determined from previous work by our group and others.^23,34 In a ligand-free HIVp, the dominant conformation is the semiopen form.^37,38,45 To reflect this form and other open-like forms, we used four different conformations (semiopen, slightly open, open with one flap curled, and wide open) for ligand docking (Figure 2). Combining different protein conformations with different placements of the ligands to areas it would most likely diffuse should sufficiently reflect the events leading to ligand binding. Vcharge was used to assign partial charges for the ligand atoms.⁶³ The Autogrid 4.0 algorithm was used to create a 22.5 Å dimension cubic box with a grid spacing of 0.375 Å, and the ligand was placed 20–30 Å from HIVp. We performed 10 trials for each ligand docking simulation, with 1 million energy evaluations for each trial. We considered only the conformation that had the lowest free energy from each set of trials. Notably, one can randomly place a ligand in the cubic box to set up initial structures for MD simulations. We used molecular docking in this study solely to establish a more systematic procedure for creating initial conformations. Overall, 58 conformations with different flap orientations and ligand positions were generated for sampling ligand association pathways.

Gaussian Accelerated Molecular Dynamics (gaMD) Protocol

Because it takes an excessively long time for a ligand to locate a final bound state shown in a crystal structure, we used gaMD in AMBER 14 for a more efficient conformational search of pathways that could lead the ligands to the final bound form.⁶⁴ Snapshots of ligands that were 5–7 Å from the crystal-bound state were extracted to continue simulations with gaMD for thorough conformational samplings. After multiple runs of gaMD, we took snapshots of ligands that reached a root-mean-square deviation (RMSD) of 3–4 Å of their crystal structure position. These poses were reseeded by using conventional MD (cMD). Overall, we ran 20 gaMD (from 50 to 100 ns) and 44 cMD simulations (100 ns each) for ritonavir and ten gaMD simulations (100 ns) and 35 cMD simulations (from 100 to 350 ns) for xk263.

Post-MD Analysis

RMSD and MM Energy

Root-mean-square deviations (RMSD), distances among atoms, and molecular mechanics (MM) energies from electrostatic and van der Waals contributions were calculated by using VMD.⁶⁵ Reference coordinates for RMSD calculations were from the crystal structures (i.e., PDB entries 1HVR and 1HXW for HIVp with xk263 and ritonavir, respectively).^50,51

Criteria for a “Bound” Ligand

To compare the ligand-bound structures from our MD simulations with the crystal structures, we first aligned the protein backbone. Next, the center of mass (COM) of selected ligand atoms was calculated (see Text S1). Then, the distances between the COM from the MD snapshots and crystal structures were measured. In this study, we considered that a binding event occurred if the COM distance between the ligand-bound structure and the ligand in the crystal structure was <7 Å for >5 ns. From previous Brownian dynamics (BD) studies, this cutoff reflects a high probability of successful binding.²¹

Removal of the Free Energy of Water Molecules

The free energy needed to remove a bound water molecule from a protein in solution can be considered the energy needed to move the water molecule into bulk solution, leaving an empty cavity with the same shape as that of the removed water. Thus, the desired water removal free energy was computed as

$$\mathrm{\Delta }{G}_{\mathrm{\text{wr-liquid}}}^{\circ }={\mu }_{\mathrm{\text{PL}}}^{\circ }+({\mu }_{\mathrm{W}-\mathrm{\text{gas}}}^{\circ }+\mathrm{\Delta }{G}_{\mathrm{\text{gl}}})-{\mu }_{\mathrm{\text{PLW}}}^{\circ }$$

where ${\mu }_{\mathrm{\text{PLW}}}^{\circ }$ is the standard (C° = 1 M) chemical potential of a protein–ligand–water complex, ${\mu }_{\mathrm{\text{PL}}}^{\circ }$ is the standard chemical potential of the protein–ligand complex without the water (but with the water-shaped cavity), and ${\mu }_{\mathrm{\text{W-gas}}}^{\circ }$ is the standard chemical potential of the water in the gas phase (no GB or PB solvation). ΔG_gl is the gas-to-liquid transfer of free energy of the water.⁶⁶ The details for the calculations of ${\mu }_{\mathrm{\text{PLW}}}^{\circ },{\mu }_{\mathrm{\text{PL}}}^{\circ },\mathrm{\Delta }{G}_{\mathrm{\text{gl}}}$ and ${\mu }_{\mathrm{\text{W-gas}}}^{\circ }$ are provided in the Supporting Information.

The removal free energies of water molecules were calculated for each of 21 frames saved every 5 ps for 100 ps, which corresponds to the average life span of the bridge waters in both ritonavir and xk263 complexes. The bridge waters of interest in the 21 frames were chosen by using in-house software for the water removal analysis.

RESULTS AND DISCUSSION

Overview of Ligand Binding Processes

Using all-atom MD simulation, many computational studies have attempted to elucidate and understand the underlying factors that govern kinetic behaviors of various ligands. Our goal was to understand the factors involved in fast and slow binding by analyzing the events leading up to binding and understand the changes in dynamics that result from a bound ligand by using unbiased MD simulations. The diffusion steps for ligands far from HIVp was previously reported,^21,67,68 so we focused on a ligand’s association with HIVp when it is 20–30 Å from the center of the HIVp active site. Because we know that the ligands can diffuse from all directions surrounding the protein, ligands were docked at the top, left, right, front, and bottom regions around the HIVp as starting conformations in MD simulations (see Figure 2). We then performed continuous MD simulations from the 58 different starting conformations (29 for each ligand), ranging from 200 ns to 14.0 μs (55.1 μs in total), in an explicit solvent model. Among all simulations performed, xk263 successfully entered the binding site in six of the MD simulations, and half from the semiopen conformation (see Table S1). Similarly, ritonavir successfully entered the binding site in eight of the MD simulations, and half from the widely open conformation (see Table S1). We used these 14 simulations to observe and analyze the association pathways for both ligands. The figures reported in this paper reflect a representative pathway that was found in common with others. Another 21 of the simulations showed that a ligand (xk263 or ritonavir) interacted with residues near the HIVp active site similar to positions found in previous BD studies. However, we did not consider these simulations to be capable of reaching the bound form in a timely manner, given our limited computational power. In addition, both ligands stayed in other regions, such as the flap elbow and bottom of HIVp, which was also observed by BD simulations with a coarse-grained model (Figure S1).^39,69 Details about all 58 simulations are provided in Table S1.

Our unbiased MD simulations suggest that the initial location of the ligand may affect the probability of successful binding. Nearly 28% of the simulations starting from the top region and 25% from the front region (Figure 2) resulted in binding to HIVp. In contrast, <10% of the simulations starting from regions peripheral to the protein resulted in a bound state. These results agree with a prior study of the diffusion of both ligands to HIV-1 protease.²¹ Because the flaps of the protein are located at the midfront and top region, previous BD simulations with a coarse-grained model showed that the chance of a binding event occurring from regions below or peripheral to the enzyme was low.²¹ In some simulations, when a ligand stayed at the elbow or bottom regions of the HIVp, given enough time, it may diffuse away from the protein and rebind at a different region or remain bound in its general vicinity. Although we can model the probability of successful binding from diffusion via the protein surface, a significantly longer simulation time is needed (perhaps on the scale of hundreds of microseconds to milliseconds for each run), which is not possible with the current computer power. Thus, we did not pursue simulations in which the ligand stayed bound at the bottom or the elbow regions.

Figure 3 shows an example of successful ligand binding. All successful simulations suggested that xk263 and ritonavir first contacted one of the flaps or one of the loops containing Pro79/Pro178 (Figure 3ii). Furthermore, the ligands could be clamped between the two loops via nonpolar interactions (Figure 3iiiB,D). Even after xk263 or ritonavir entered the binding pocket, the flaps kept switching between the open and closed forms. This switching allowed for adjustment of the orientation of the ligand and the handedness of the flaps until they were in the closed conformation. During this rearrangement period, our simulations showed multiple protein–complex intermediates that were not reported in other studies.

Figure 3.

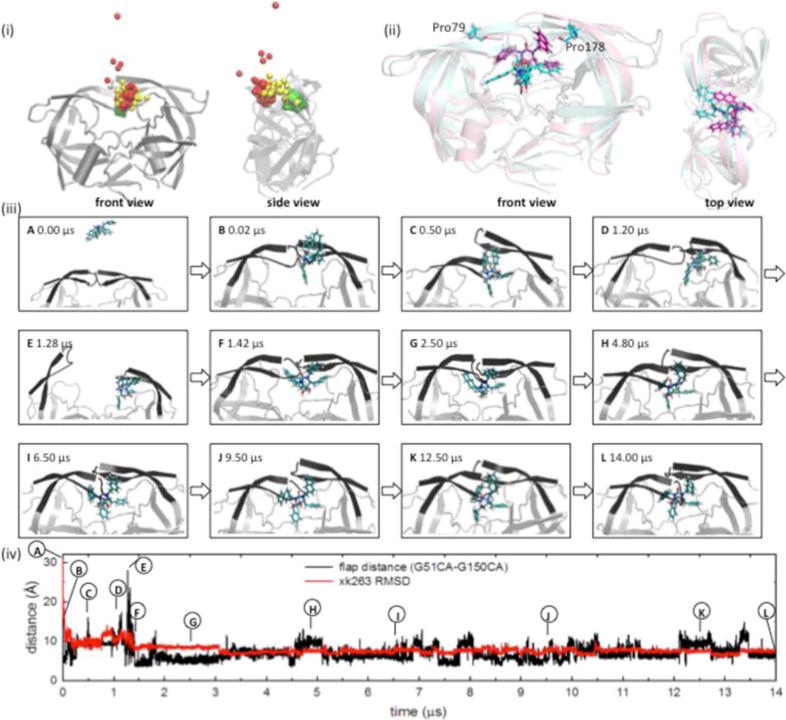
Pathway of binding of xk263 to semiopen HIVp. (i) Trace of the xk263 binding route. One bead indicates a position that the center of mass (COM) for xk263 stays at a specific simulation time. Red, yellow, and green represent the MD simulation time zones of approximately 0–0.5, 0.5–1.5, and 1.5–14.0 μs, respectively. (ii) Alignment of a crystal structure and the predicted conformation from our MD simulation. The crystal structure that is colored cyan was taken from PDB entry 1HVR. The conformation from the MD simulation at 14 μs is colored pink. (iii) MD snapshots of the transient complex conformations during the binding process. (iv) Flap distance and ligand RMSD by MD simulation time. Notably, the pathway reported is from our longest MD simulation for this molecular system. This pathway is representative of common ones found when comparing several other pathways of xk263 associating with HIVp.

Previous studies of apo HIVp with all-atom MD and coarse-grained BD simulations suggested that HIVp flaps stayed in a closed or semiopen conformation for ∼400 ns, on average, and then opened for ∼40–50 ns.^38,45 Therefore, in this study, if the conformation of the complex persisted for >500 ns, we considered this a local intermediate state (Figure 3iii).^34,70 If the flaps opened from a semiopen or closed conformation within 200 ns while a ligand approached, we considered the motion an induced flap motion caused by the presence of the ligand.

Sampling the Crystal-Bound Conformation

By using the distance between the COM of ligand positions obtained from our MD simulations and experimental crystal structures, our longest MD trajectory of 14 μs (xk263) and 8 μs (ritonavir) was <2.5 Å from the bound crystal structure. However, our MD simulations did not sample ligand conformations that exactly reproduce the crystal structures. Ritonavir was in a curled conformation, whereas the naphthanyl rings of xk263 did not rotate to its crystal conformation. Notably, when experiments are performed to determine a bound state for kinetic measurement, a ligand must have a bound form identical to a crystal structure. Additionally, a molecular system takes a long period of time for conformational rearrangements to occur upon generation of a crystal structure. Thus, a significant amount of time is expected for the ligands to reorient themselves to sample the crystal structure conformation. The specialized Anton machine allowed us to sample up to 14 μs, which, however, is not long enough for the molecular system to rearrange solute and solvent conformations to sample the form shown in the crystal structure. Therefore, we combined accelerated gaMD and cMD to widen the range of sampling to find conformations close to the final bound state of the crystal structure (Figure 4). The combined gaMD and cMD simulations showed that the average distance for xk263 was ∼0.45 Å from the bound state of xk263 as compared with the crystal structure (PDB entry 1HVR) (Figure 4A) and for ritonavir was ∼2.70 Å from the bound state as compared with the crystal structure (PDB entry 1HXW) (Figure 4B). Ritonavir has a greater distance than xk263 because the crystal bridge water located between ritonavir and HIVp flaps has not been successfully sampled yet. In addition, ritonavir has more rotatable bonds and polar groups than xk263 does, so it may need a longer simulation time for thorough sampling. With fewer hydrogen bonds to overcome and no need to recruit bridge waters in the complex, xk263 may more easily sample the space seen in the crystal structure. Even though the distance for bound ritonavir is not extremely close to the crystal structure, the orientation and conformation is in good agreement with the crystal structure (Figure 4B). Overall, this study suggests that use of only unbiased conventional MD to model an entire association pathway may not lead to a conformation that can reproduce the crystal structure; enhanced simulations or sampling techniques are required.

Figure 4.

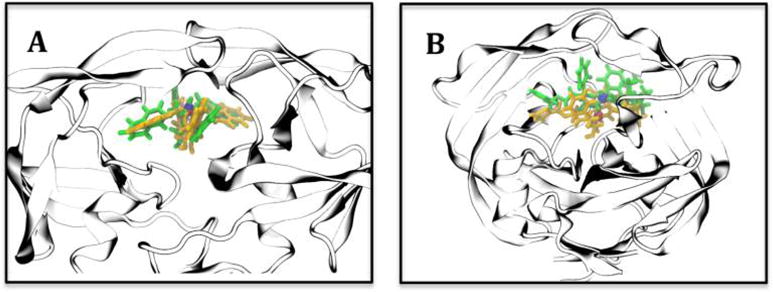
Representative ligand binding modes close to crystal structures. MD snapshot of the shortest center of mass (COM) distance between our simulation (green) and the final bound state (yellow) shown in crystal structures. The COMs from MD and crystal structures are represented by blue and red beads, respectively. (A) The COM distance for xk263 between a MD snapshot and PDB entry 1HVR was 0.45 Å. (B) The COM distance for ritonavir between a modeled position and PDB entry 1HXW was 2.70 Å. Residues 76–82 were omitted for viewing purpose.

Different Binding Mechanisms for Fast and Slow Binding Ligands

Unlike some proteins whose ligands can reach the binding site via a well-defined channel,^24,71 HIVp has an open binding site and flexible gating. Thus, the mechanism for binding is complicated. Early fluorescence and NMR studies of HIVp proposed that ligands binding to it experience both an induced-fit and conformation selection binding mechanisms.^72,73 In addition, from our simulation results, the fast (xk263) and slow (ritonavir) ligands have striking preferences for binding to different initial protein conformations; thus, the two ligands present different association mechanisms. Among 26 sampled paths with the ligands diffused to HIVp in a semiopen-flap conformation, successful binding occurred in 18.8% and 10.0% of the simulations for xk263 and ritonavir, respectively. Conversely, among 22 sampled paths with the ligands diffused to HIVp in an open-flap conformation (including open with a curl flap and wide open), successful binding occurred in 38.5% of the simulations for ritonavir as compared with 11.1% for xk263. If we further consider the simulations of the HIVp conformation with wide open flaps, the successful ligand binding rate was 57.1% for ritonavir but 0% for xk263. Therefore, xk263 and ritonavir feature more efficient binding to HIVp with semiopen and wide open conformations, respectively. Thus, we infer that the fast (xk263) and slow (ritonavir) binding ligands for HIVp use the induced-fit and conformation selection mechanisms, respectively. These results prompted us to investigate why the fast and slow binding ligands prefer different pathways and mechanisms and what factors contribute to these preferences. The difference in the binding paths of the two ligands is also discussed in the following sections.

Induced-Fit Mechanism: Ligands Binding to the Semiopen-Flap HIVp

We examined the binding processes and protein dynamics as both ligands bind to the most common conformation of HIVp in its free state; the major conformation of free HIVp is semiopen flaps with semiopen handedness. The MD simulations for free HIVp show that this dominant flap conformation could change to wide open flaps with semiopen or closed handedness after 100–200 ns (Figures S2 and S3). Although both xk263 and ritonavir can enhance the conformational flexibility of the flaps, as observed by RMSD calculations (Figure S4), the tendency for the two ligands to alter the flap conformation and handed orientation differs. Overall, 90% of the simulations involving xk263 showed induced conformational changes in the flap region, where the flaps switched a conformation from the dominant form to closed flaps with closed handedness within 150 ns (Figures S2 and S3). In some simulations, xk263 induced the flap motions to wide open but did not completely bind inside the pocket. Conversely, only 50% of MD runs with ritonavir showed similar observable flap motions. Ritonavir formed significantly more transient H-bonds with HIVp than xk263 did to stabilize intermediate states, which is consistent with our previous MD simulations with an implicit solvent model.^24,33,34 During the binding process, the flaps need to open up to some extent for ligand access. Once the ligands are bound, HIVp needs to switch from the semiopen to closed handedness to be one step closer to reach the conformation reproduced in the crystal structure. Therefore, ligands such as xk263, which can interact with HIVp in a semiopen conformation, can easily induce the flaps to change their conformations within 200 ns, allowing xk263 to bind to the protein quickly (Figure 5).

Figure 5.

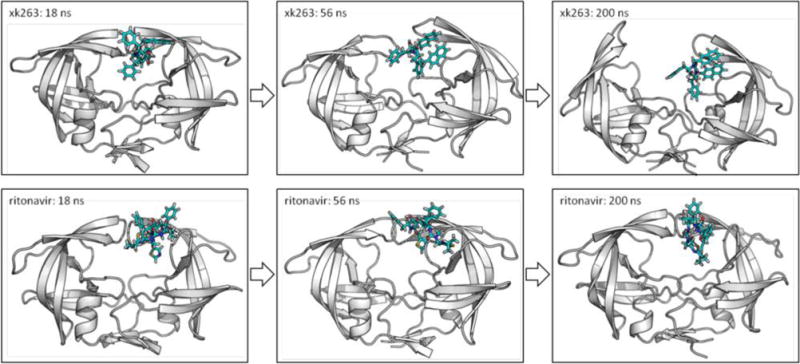
Comparison of binding of xk263 and ritonavir to native semiopen HIVp. MD snapshots during the first 200 ns. The conformation of HIVp is initially semiopen flaps and semiopen handedness. Both xk263 and ritonavir interact with the protein at a similar region around 18 ns. Xk263 desolvated water molecules and therefore induced conformational changes of the flaps in 56 ns; the flaps then open with the association of xk263. However, because ritonavir has more tightly bound transient bridge waters (not shown explicitly in this figure), it did not induce significant conformational changes in the simulation. The simulations reported here are representative of common features seen in other simulations.

Role of Removing Transient Bridge Waters in the Induced-Fit Mechanism

Our simulations revealed that transient bridge waters between HIVp and a ligand stabilize an intermediate state and prevent direct protein–ligand contact. Transient bridge waters act as a buffer zone that weakens interactions between the ligand and HIVp. Our simulations suggest that the flaps show considerable motion only when a ligand contacts HIVp directly without any bridge waters between them. As illustrated in Figure 6, any bridge waters associated with xk263 were quickly stripped out, and xk263, now in direct contact with the flaps, explored several intermediate states. In contrast, water molecules were frequently found between ritonavir and HIVp, which resulted in an intermediate state that lasted >500 ns.

Figure 6.

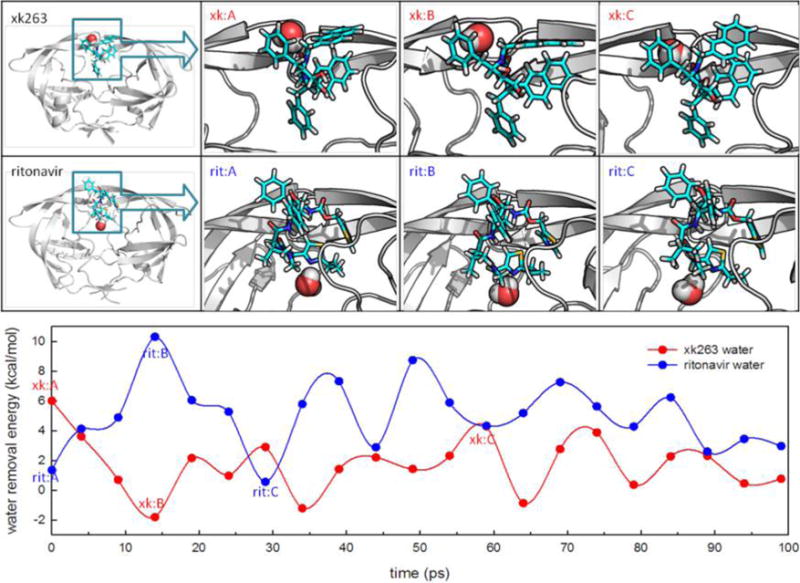
Free energy needed to remove a specific water molecule during ligand association. Red and blue lines in the plot show the free energies needed to remove a bridge water molecule with xk263 and ritonavir binding to HIVp, respectively. Panels xk:A, xk:B, and xk:C show snapshots at 0, 14, and 59 ps, respectively. Panels rit:A, rit:B, and rit:C show snapshots at 0, 14, and 29 ps, respectively. The snapshots represent the beginning snapshot and snapshots with the highest and lowest removal free energies, respectively.

To quantitatively examine the stability of transient bridge waters in the intermediate states of the HIVp–xk263 complex compared to that of the HIVp–ritonavir complex, we calculated the free energy (FE) cost to move these water molecules from the interaction sites to the bulk solvent. From our MD simulations, we focused on the transient bridge waters that stayed between the protein and ligand for >100 ps (Figure 6). Unlike the HIVp–ritonavir complex, with transient bridge waters staying >100 ps, for the xk263 complex, most transient bridge waters stayed for a considerably shorter period of time (i.e., 15 ± 5 ps), which implies that bridge waters with xk263 were less stable (Figure S5). The computed FE for water removal was saved every 5 ps during the 100 ps run. For xk263, the water molecules we studied had removal energies ranging from 1.5 to 2.0 kcal/mol, which demonstrates their loose binding ability in the HIVp–xk263 system. A close inspection of the conformations revealed that water molecules needed to form a hydrogen bond network to bridge the ligand and protein, a network that seems to be vulnerable in the HIVp– xk263 system. For ritonavir, transient bridge waters had a removal energy of >5.0 kcal/mol in a 100 ps MD run (Figure 6 and Figure S6). This water molecule directly bridged the thiazole moiety of ritonavir and several residues of HIVp. Compared to xk263, ritonavir has more polar functional groups that may contribute to the larger FE and longer dwell time of the transient bridge waters in the HIVp–ritonavir intermediate states. These polar functional groups provide more opportunities to form a network of hydrogen bonds with the surrounding water molecules. Because of those stable bridge waters, compared with those of xk263, ritonavir has weaker interactions with HIVp and is thus less likely to induce flap motions. Additionally, the time-consuming dehydration process slows the rate of binding for ritonavir.

Conformation Selection Mechanism: Ligands Binding to the Open-Flap HIVp

Upon investigating the association process with ligands binding to HIVp in its open state, we found that ritonavir prefers binding to the protease in an open-flap conformation. Unlike the semiopen conformation, this pathway does not involve ligand-induced protein conformational change because the flaps are already open. Binding to the open-flap conformation forces the ligand to pass through a funnel-like region containing a large number of water molecules to reach the binding cavity (“channel” in Figure 7A). If the flaps open, ritonavir needs to go through the channel to reach the binding site. Thus, gradual dehydration is necessary for entering the protein (Figure 7). When the ligand is located in the bulk solvent (Figure 7A), ∼200 water molecules surround ritonavir within the second hydration shell (6.0 Å from ritonavir). The number of water molecules continues to decrease as ritonavir approaches the binding site (Figure 7B–F). When the ligand binds to the active site and the flaps of HIVp are nearly closed, ∼100 water molecules are retained within the second hydration shell (Figure 7G). Similar results from another MD simulation are shown in Figure S7. The HIVp–ritonavir complex may sample multiple intermediate states after ritonavir enters the binding site. During this time, the complex adjusts its conformations, and the flaps are slightly reopened. When this occurs, nearby water molecules quickly resolvate the binding cavity (Figure 7H), but the system is dehydrated again, which allows the flaps to close. Also, a rearrangement of the handedness of the flaps occurs before the closed conformation is reached. Our MD simulations indicate that >20 ns is required to close the flaps from an open conformation. Whether the solvent facilitates the closing of the flaps or the attractions between ritonavir and HIVp repel water molecules is still unclear.

Figure 7.

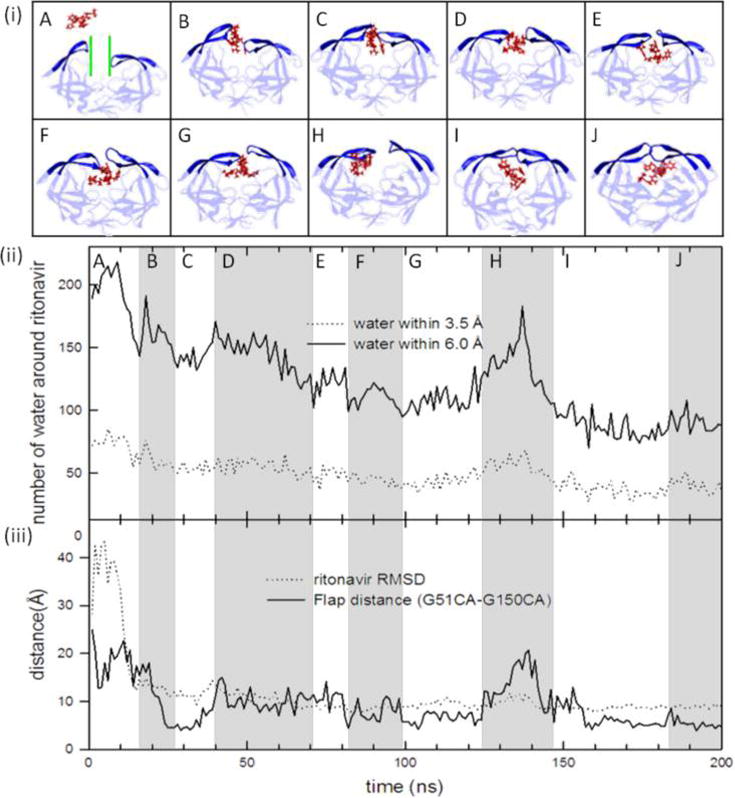
Ritonavir experiences multiple transitions during the association. (i) MD snapshots show ritonavir binding to HIVp with open flaps. Each snapshot represents a major conformation in the simulation time zone from A to J. The channel through which the ligand needs to pass is colored green. (ii) Number of water molecules around ritonavir within its first (3.5 Å) and second (6.0 Å) hydration shells. Gray and white highlight the change in the number of water molecules in different simulation time zones. (iii) Ritonavir RMSD and flap distance during the MD simulation.

We observed that xk263 diffused faster toward the gate of the protein (∼1 ns) than did ritonavir (∼10 ns) before directly contacting HIVp. Because of the highly nonpolar character of xk263, it can quickly dehydrate surrounding waters and interact with nonpolar residues of the protease. The flap regions of HIVp contain nonpolar residues, giving it a hydrophobic characteristic (Figure S8). Overall, the hydrophobic effect plays a role here in that xk263 quickly formed nonpolar interactions with the residues on the surface of the flaps instead of moving onto the binding pocket. As a result, xk263 was found near the entrance of the binding site or was trapped between two flaps (Figure 8 and Figure S9). The strong nonpolar attractions between the flaps and xk263 also led to flaps closing before xk263 could enter and settle into the active site. In addition, xk263 can diffuse along the nonpolar surface of one flap, thereby moving away from the active site of the enzyme (Figure 8). The reopening of the flaps may provide another chance for the ligand to enter the site, but this would extend the time scale of the ligand binding process. Overall, our simulations suggest that fast dehydration of the solvent by xk263 does not help the ligand enter the protease with an open-flap conformation.

Figure 8.

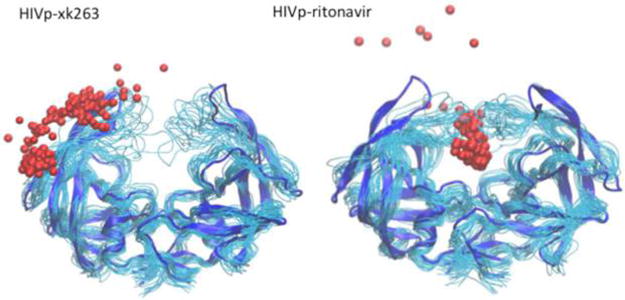
Comparison of the binding pathway used by xk263 and ritonavir to approach HIVp with an open-flap conformation. Trace of xk263 and ritonavir binding to the open-flap HIVp. Each bead represents the COM of the ligand at 1 ns, and the total simulation time is 200 ns. The blue ribbon indicates the initial conformation of HIVp, and the cyan tubes indicate the HIVp conformations during a 200 ns MD simulation.

We calculated protein–ligand and water–ligand MM energies to study the energy contributions, especially electrostatic and van der Waals energies, which drive ligand binding. Nonpolar interactions are typically considered the principal driving force in molecular recognition. However, our calculations show that ritonavir binds to HIVp via strong electrostatic attractions, which is contrary to the binding of xk263 (dominated by nonpolar interactions) (Figure 9A,C). Columbic and van der Waals energy made the same contribution to the total energy during a 200 ns simulation (Figure 9C). Therefore, both polar and nonpolar atoms in ritonavir play a role in the formation of a protein–ligand complex.

Figure 9.

Computed interaction energies between the ligand and water molecules. Coulombic, van der Waals, and total energies are shown as black, blue, and red lines, respectively.

A simple continuum solvent model cannot account for the explicit transient waters located between HIVp and its ligands. Thus, we calculated interaction energies between the ligands and explicit waters from MD snapshots. Although the total interaction energy between the ligand and waters fluctuated, ritonavir generally formed strong electrostatic interactions with water molecules (Figure 9B,D), which suggests that before establishing a stable HIVp–ritonavir complex, ritonavir could interact with many water molecules for an extended period of time.

Implications

In this work, we report the continuous processes (mechanisms) of a fast and slow binding ligand entering the binding site of HIVp. Our work contrasts with early studies of HIVp, which used docking tools or Markov state models to search for potential binding poses or energies of the steady states in the ligand binding pathways.^71,74 We focus on the pathways and mechanism regarding how ligands approach the protein active site and the corresponding protein conformation changes during ligand binding. By studying 14 successful binding paths of xk263 and ritonavir, we show that both ligands can locate the binding pocket and after approaching the binding site, sample multiple local intermediate conformations, thereby extending the time for a ligand to reach one of the global energy minima shown in a crystal structure. For example, in our 14 μs simulation of xk263, the ligand reached the binding site within 1.5 μs. The remainder of the time was spent rearranging its conformation during the simulation (Figure 3i,iii,iv). This result contrasts with early reports by D. E. Shaw Research Co. staff for different protein systems. In their unbiased MD simulations, they studied ligands binding to Src kinases and G-protein-coupled receptors (GPCRs) and found that the ligands moved around the protein surface for an extended period of time. However, once the ligands reached the entrance of the binding site, the steady state conformations or the final bound state could be approached in a few microseconds.^24,25 One difference with our study could be due to the structure of the ligands we studied, which had more atoms and rotatable bonds. For example, the inhibitors in the studies done by Shan et al. and Dror et al. had approximately 20 heavy atoms and 4–8 rotatable bonds,^24,25 compared to xk263, with 46 heavy atoms and 8 rotatable bounds, and ritonavir, with 50 heavy atoms and 19 rotatable bonds. Another difference is the nature of the binding site between HIVp and Src kinase and/or GPCRs. The asymmetrical motions of the HIVp flaps in addition to the wide range of points from where its ligands can associate and enter the active site significantly contrast with those for Src kinase and GPCRs; GPCRs have a well-defined binding pocket limiting the direction from which their substrate can enter. Like the differences mentioned above, the HIVp ligands present different binding paths and mechanisms compared to the existing systems studied. In addition, our results also show the challenge of modeling ligand association of HIVp, which has two unique and flexible flaps. We note that ligand binding mechanisms may highly depend on different protein systems; more studies in ligand binding kinetics should reveal the differences among various classes of proteins in the future.

CONCLUSIONS

The goal of our study was to gain insights that would better explain the fast and slow kinetics of binding by studying the entry and association processes of two different ligands. By using unbiased MD simulations with an explicit solvent model, we provide atomistic insights into protein–ligand association pathways. We studied the binding of ligands xk263 and ritonavir to HIVp. Our simulations showed that binding events were more successful when the ligands initially diffused from the top and front regions of HIVp. In addition, the two ligands studied use different binding mechanisms. The induced-fit model of binding hypothesizes that a binding event occurs when a ligand induces conformation changes and interrupts the native motions of a protein.⁴⁸ The other mechanism of binding, conformation selection, proposes that a ligand directly binds to a preorganized protein conformation.^75,76 The fast binder, xk263, with a predominantly nonpolar property, preferentially binds to HIVp with a semiopen-flap conformation, which reflects the induced-fit mechanism. This binding is accomplished by dehydration of surrounding water molecules, thereby allowing xk263 to directly interact with the protein and induce flap motion to allow xk263 access to the active site. The slower binder, ritonavir, successfully binds to HIVp with an open-flap conformation, which reflects the conformation selection mechanism. Because of the more polar features of ritonavir, the hydration shell surrounding it weakens ritonavir’s ability to directly interact with the protease and induce flap motion; thus, ritonavir must wait for HIVp to sample an open conformation for favorable binding. In addition, ritonavir forms more stable transient hydrogen bonds and retains more bridge water molecules than xk263 does when binding to the protein. Although these bridge waters weaken the protein–ligand interactions so that the induced-fit mechanism is less likely to occur, the waters help ritonavir smoothly reach the active site of HIVp in an open-flap conformation. Computed free energies for the removal of transient waters between the ligands and HIVp show that the bridge water molecules in HIVp–xk263 intermediates are less stable and thus have dwell times shorter than those of the bridge water molecules in HIVp–ritonavir intermediates. Because of this dewetting nature of xk263, the induced-fit mechanism is the preferable route for binding. Overall, our study suggests potential binding mechanisms for ligands with different association kinetics and explains how water molecules affect binding rates.