Abstract
The degree to which genomic architecture varies across space and time is central to the evolution of genomes in response to natural selection. Bulked-segregant mapping combined with pooled sequencing provides an efficient means to estimate the effect of genetic variants on quantitative traits. We develop a novel likelihood framework to identify segregating variation within multiple populations and generations while accommodating estimation error on a sample- and SNP-specific basis. We use this method to map loci for flowering time within natural populations of Mimulus guttatus, collecting the early- and late-flowering plants from each of three neighboring populations and two consecutive generations. Structural variants, such as inversions, and genes from multiple flowering-time pathways exhibit the strongest associations with flowering time. We find appreciable variation in genetic effects on flowering time across both time and space; the greatest differences evident between populations, where numerous factors (environmental variation, genomic background, and private polymorphisms) likely contribute to heterogeneity. However, the changes across years within populations clearly identify genotype-by-environment interactions as an important influence on flowering time variation.
Keywords: genomic mapping, within-population, Mimulus, natural variation, flowering time
THE standing genetic variation in a population is the raw material for evolution. For quantitative traits, a basic question is whether the architecture of this variation is consistent across populations of a species, or even within a single population through time. Consistency requires not only for the same polymorphisms to be present in each population, but also that the genotype-to-phenotype mapping is stable across space and time. The consistency of genomic architecture is relevant to many outstanding questions: How general are the results from QTL mapping studies, typically done on a single population evaluated in a single environment? How frequently will parallel selection pressures produce parallel genetic changes (Cohan 1984a,b; Colosimo et al. 2005; Cooley et al. 2011)? How influential are factors such as genotype-by-environment (G×E) interactions in generating inconsistent architecture from spatial and temporal environmental variation, and to what extent does this alter the balance of evolutionary forces that maintain the quantitative trait variation in the first place?
To address the question of consistency, we performed bulked-segregant mapping of flowering-time variation across multiple, natural populations of Mimulus guttatus over two generations. Bulked-segregant mapping (Michelmore et al. 1991) identifies divergent loci between the tails of the distribution of a phenotype, in this case the earliest and latest flowering plants in a population. QTL for flowering time should exhibit allele frequency divergence between groups (bulks). Because the selection of bulks is equivalent to a single generation of (bidirectional) truncation selection, the expected magnitude of this difference is directly proportional to the “average effect” of alleles on the trait (Fisher 1941; Latter 1965; Kimura and Crow 1978). The average effect measures the association between alleles and phenotypes (Falconer and Mackay 1996), and the extent to which the average effect changes with context directly assays the importance of that context on variation. Changes in average effect across environments reflects G×E interactions, whereas changes in average effect owing to different genetic backgrounds estimate the effect of epistasis.
The three populations chosen for this study are geographically proximal (within 7 km), have very high nucleotide variation (Puzey et al. 2017), and exhibit extensive shared polymorphism (Monnahan et al. 2015). For shared polymorphisms, the difference in allele frequency between early- and late-flowering individuals within a population (∆pEL) can differ between populations for numerous reasons. If the mapping from genotype to phenotype is constant, ∆pEL will differ if the allele frequency is intermediate in one population but extreme in the other. Barring this, ∆pEL will differ if the distribution of genetic backgrounds differs between the populations, and that influences the phenotypic expression of the focal locus. Environmental differences among populations or across generations can alter the magnitude or even direction of ∆pEL. Finally, G×E can generate heterogeneity in ∆pEL between generations within a population if there are temporal changes in the environment.
Flowering time is responsive to multiple environmental variables, is typically highly polygenic, and is central to numerous ecological and evolutionary processes (Fu and Ritland 1994; Bernier and Périlleux 2005; Wellmer and Riechmann 2010; Blümel et al. 2015). For many plants, it is a major determinant of fitness because access to pollination and resources necessary for reproduction vary over the course of a growing season. This is particularly true for annual M. guttatus, in which plants must flower and set seed before water runs out. Although late-flowering plants tend to produce more seed, they risk desiccation prior to seed set (Mojica and Kelly 2010; Mojica et al. 2012). This trade-off may be relevant to the maintenance of genetic variation in flowering time and will surely affect how these populations evolve in response to a changing climate. Shifts in flowering time due to climate change have already been observed for a number of species (Fitter and Fitter 2002).
Estimating the contribution of individual loci to quantitative trait variation is a challenge, particularly when genetic effects are subtle (McCarthy et al. 2008; King et al. 2012). In bulked-segregant mapping, differences in allele frequency owing to random sampling should usually be small if bulks are large; but occasional, large, random fluctuations are inevitable. In the present study, statistical difficulties are acute given that we wish not only to detect loci affecting a trait, but also to test whether these effects vary across years or populations. To this end, we develop a likelihood-based, hypothesis-testing framework analogous to the factorial ANOVA, in which we can test for marginal effects as well as interactions between factors.
We used pooled population sequencing (Pool-seq) (Schlötterer et al. 2014) to estimate allele frequencies in each bulk throughout the genome. Each bulk makes a single pool of DNA to be sequenced, with the resulting read counts estimating allele frequencies. However, an inherent challenge is accommodating the variance introduced by the sampling events prior to sequencing. These include, but are not limited to, sampling of individuals from populations, sampling DNA into pools, sampling events during library preparation (particularly, PCR), and sampling of fragments for sequencing. Multiple methods have been proposed to estimate the variance in allele-frequency estimates obtained from Pool-seq data (Magwene et al. 2011; Gautier et al. 2013; Kelly et al. 2013; Lynch et al. 2014). Here, we build on a method based on Fisher’s angular transformation of allele frequency (Fisher and Ford 1947) using a robust estimator for the variance of dispersive processes (Kelly et al. 2013).
In addition to genome-wide mapping, we estimate flowering-time effects for five structural variants (chromosomal inversions) segregating in one or more of the populations. These variants were identified in prior mapping studies (Fishman and Saunders 2008; Lowry and Willis 2010; Holeski et al. 2014; Lee et al. 2016), and three of these loci (inv6, inv8, and D) have demonstrated phenotypic effects, including developmental timing. The present study provides further evidence of natural selection on alternative orientations of the inversions. Also, the inclusion of “known loci” provides important ground truths for genome scans in which the overwhelming majority of SNPs are effectively anonymous.
Considering both SNPs and structural variants, this study provides several striking observations regarding genomic variation for flowering time in natural populations of M. guttatus. Depending on the population and year, we find anywhere from 10s–1000s of SNPs that differ in frequency between early- and late-flowering plants, broadly distributed throughout the genome. Although individual SNPs are almost entirely idiosyncratic with regard to significance, there is appreciable overlap in the genomic regions harboring this variation. Furthermore, we find that the extent of variability over time itself varies between populations. The Quarry (Q) population, a recently established annual/perennial hybrid swarm, exhibits many more early-late divergent SNPs compared to the other two, and the allele frequency divergence at these SNPs tends to be much more consistent across years. In the following sections, we describe our likelihood framework in detail and interpret the results in relation to the expected degree and scale of parallel evolution, as well as the generality of genetic mapping studies.
Theory
In this section, we describe a likelihood framework for testing divergence in allele frequency; first between two bulks (Early vs. Late) and then extend to treat multiple contrasts simultaneously. Following Fisher and Ford (1947), we conduct tests on transformed allele frequencies: where is the estimated allele frequency (fraction of reads bearing the specified base) in a bulk. For a single bulk, where x is the true (transformed) allele frequency and Here, m is read depth at a SNP, and v is a bulk-specific variance that aggregates the effects of sampling of individuals into bulks, sampling of DNA into the pooled sample, and PCR sampling during library preparation. v is common to all SNPs in the bulk, while m will vary among SNPs. The null hypothesis that ∆pEL = 0 (allele frequency is the same across bulks) is evaluated as:
| (1A) |
| (1B) |
Given values for and we calculate the likelihood of any observed difference from the normal density function. The read depths in a sample are directly observed while the v terms are estimated from a genome-wide aggregation of data (procedure described below).
A likelihood ratio test statistic (LRT) for a difference between bulks requires a maximum likelihood estimator (MLE) for the common allele frequency:
| (2) |
Here, and are the estimates from each bulk at site i and w terms are the reciprocal of where B designates early or late bulk. The log-likelihood of the data under the null model (after dropping a common term across models) is:
| (3) |
This can be compared to an unconstrained model, where with a separate mean estimated for each bulk. Since there is only one observation (allele frequency) in each sample, the estimate is simply the observation, and the log-likelihood becomes zero. The LRT is then −2 times Equation (3), and a P-value for the test is obtained from a χ2 distribution with 1 d.f.
These calculations can be generalized to consider two contrasts (∆pEL from different populations or generations) simultaneously. Table 1 outlines three models appropriate to test for heterogeneity of such contrasts. These models are nested: M1 is a special case of M2, and M2 is a special case of M3. Comparing two generations within a population, a significant LRT for M1 vs. M2 indicates a marginal effect (average divergence) between bulks across the two generations. A significant test for M2 vs. M3 indicates heterogeneous divergence; ∆pEL differs between generations (i.e., an interaction between generation and bulk divergence). M1 vs. M3 represents an overall test for divergence across both years and is simply a sum of the two LRTs from the former tests. There is 1 d.f. for the former tests, and 2 d.f. for the latter.
Table 1. Models to establish significance of marginal and heterogeneous genetic effects across the two contrasts (between years or between populations) within a context.
| Model | Description | Parameter constraints |
|---|---|---|
| M1 | No difference between early/late | |
| M2 | ∆pEL consistent | |
| M3 | ∆pEL variable |
The likelihoods of M1 and M3 are calculated as the sum of the likelihoods for the relevant samples (Equations 2 and 3). For M2, the MLEs for the three parameters are:
| (4A) |
| (4B) |
| (4C) |
where 1 and 2 simply designate the population (or generation) being considered. The log-likelihood of the data for M2 is:
| (5) |
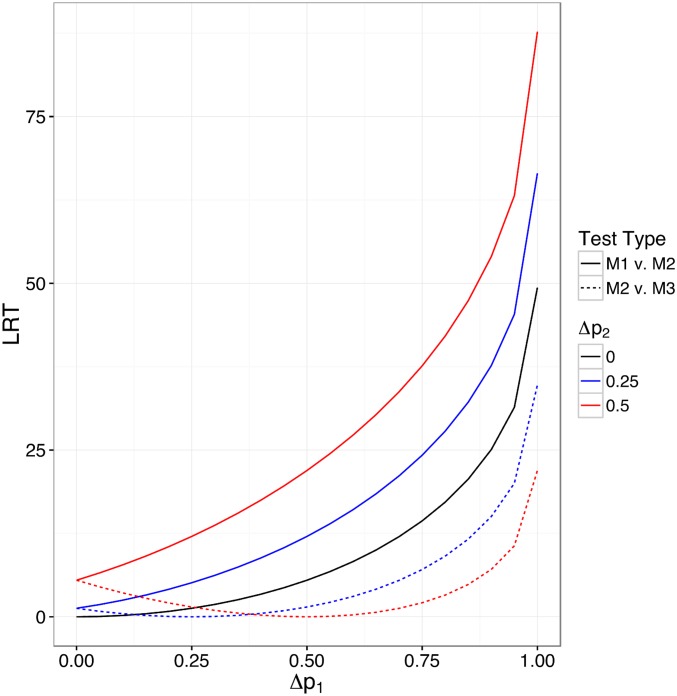
Figure 1 illustrates some key features regarding the marginal and interaction tests with m and v values typical of our data. As expected, if the observed is the same in both populations (or both generations), the LRT for an interaction test (M2 vs. M3) is zero. When the opposite is true (equal magnitude but different sign), the LRT for the marginal-effect test (M1 vs. M2) is zero (note that, when the results for negative are plotted instead of the positive values displayed in Figure 1, the solid line follows the dotted-line trajectory and vice versa). When is nonzero in only one population (or generation), both tests are equally powered (the dashed and solid black line are perfectly overlapping when = 0). As the magnitude of observed average increases, so does the LRT for marginal effects, regardless of whether The interaction LRT increases as and diverge. For a given difference between and the interaction LRT increases as average increases. For example, the interaction LRT is 7.08 when is 0.75 and is 0.25 (i.e., difference between and is 0.5), but is much higher (21.93) when is 1.0 and is 0.5.
Figure 1.
LRT values for the marginal-effect (M1 vs. M2) and interaction (M2 vs. M3) test as a function of allele-frequency difference in the two populations. Note that solid and dashed lines are perfectly overlapping for In all cases, for both populations in the contrast.
We developed a simulation framework to confirm the behavior of our testing procedures under different scenarios, using the real data to calibrate these simulations. We average the observed allele frequencies in the Early and Late bulks to set p for each population/year and incorporate sampling error using observed read counts and v terms. We simulate new values for each site and sample by adding to the population/year allele frequency a deviation due to sampling error as well as a deviation due to an effect (a) of that site. For the sampling error deviation, we add a value drawn from recalling that the sampling variance at a site, is the sample-specific variance (v) plus We first investigated the behavior of our testing procedure under a purely neutral scenario (i.e., a = 0 for all sites). These simulations confirm that our LRTs follow the predicted null distributions (χ2 with 1 d.f. for M1 vs. M2 and M2 vs. M3; χ2 with 2 d.f. for M1 vs. M3) for a SNP with no effect on phenotype.
Next, we consider scenarios where a subset of SNPs exhibit a constant effect on ∆pEL to provide a baseline for comparison of observed heterogeneity in ∆pEL. Given that sampling bulks is a form of truncation selection, the expected allele frequency difference between early- and late-flowering plants can be calculated given values for the effect size (a) and the intensity of selection (i):
| (6A) |
| (6B) |
| (6C) |
where p is the overall frequency in the population (Falconer and Mackay 1996, Chap. 11). The intensity of selection was determined using a truncated normal distribution in which 10% of individuals exceed the truncation point (i = 1.755). This was based on approximations of population size during sampling periods relative to full bloom. We grossly approximate the distribution of standardized allelic effects by assuming that some fraction of sites are neutral with respect to flowering time (1 − f0) and have a = 0, while the remaining sites have a nonzero effect of constant magnitude, c (the sign of c is chosen randomly for each site). For each of the four contexts in which we investigated heterogeneity [Iron Mountain (IM), Q, 2013, and 2014], we performed a heuristic search for values of f0 and c that generate a distribution of LRT for the marginal-effect test (M1 vs. M2) that closely matches the distributions from the real data. Our matching criteria is based on the observed proportion of sites exceeding specified values of LRT (10 and 15, in this case). Here, we aim to match the tails of the LRT distribution as this information pertains most directly to f0 and c (given that f0 is likely small). To accumulate this information into a single measure (Zdiff), we sum the standardized difference between simulated and real data.
Materials and Methods
Populations, plant collection, and phenotyping
The three populations are located in the central Oregon cascades: Q (44.3454243 N, 122.1362023 W), IM (44.402217 N, 122.153317 W), and Browder Ridge (BR) (44.373238 N, 122.130675 W) and are described in detail in Monnahan et al. (2015). Whole-genome sequencing has demonstrated very high levels of nucleotide variation in IM (πsyn = 0.033; Puzey et al. 2017) and results from the present study indicate comparable variation in BR and even greater diversity within Q. In a particular population and year, we sampled early- and late-flowering plants (100 plants per sample) according to the following scheme. First, we established several parallel transects, perpendicular to the slope of the hillside, totaling ∼30 m, and divided each transect into 30-cm intervals. We chose sampling times based on density of flowering plants along a transect. For the early flowering plants, we sampled a transect as soon as two flowering plants could be found within ∼15 cm on either side of the transect within each 30-cm interval. We estimate this cohort to be ∼5–10% of the total population. For the late-flowering plants, we waited until plant density was similar to the early sampling event (5–10% of population remaining relative to full bloom). If a particular interval along a transect had several flowering plants within 15 cm on each side, we randomly selected the two plants nearest the transect line. Whole plants were collected and stored in dry ice until frozen at −20°. Since collection times were dependent on density of flowering plants, sample times varied across populations and across years (see Supplemental Material, Table S1 in File S2 for collection dates). Early bulks were collected earlier in 2014 for all populations. The late bulk for Q was collected earlier in 2014. There was a very hot and dry spell that wiped out the BR population shortly after collecting the Early bulk; therefore, we did not perform contrasts for BR in 2014.
Sequencing and SNP calling
We extracted DNA from each individual and quantified via Qubit (double-stranded DNA BR assay; Invitrogen, Carlsbad, CA). We created 11 pools with equimolar individual contributions corresponding to each of the year-, population-, and bulk-sampling events. We performed whole-genome sequencing with five paired-end 100-bp high-output lanes on an Illumina HiSequation 2500 (three lanes for 2013 samples and two for 2014). Two additional lanes (rapid runs) were performed to equilibrate coverage across samples. We combined data from all lanes to create 11 FASTQ sets corresponding to each of the sampling bulks and ran Scythe (https://github.com/vsbuffalo/scythe) and Sickle (Robinson et al. 2010) to remove adaptors and trim low quality sites, respectively. We mapped reads to the M. guttatus version 2 genome build using Burrows–Wheeler Aligner and removed PCR duplicates using Picard Tools. We called SNPs using the GATK UnifiedGenotyper with the down-sampling feature suppressed (“-dt NONE”). The read counts in the variant call file corresponding to each of the sampling bulks are the input for subsequent likelihood analyses. A SNP was included for testing only if read depth per bulk was 25–100 reads and allele frequency (both bulks combined) was between 0.05 and 0.95. We chose 25 as the lower cutoff, so that sampling variance due to read depth, at its greatest (1/25 = 0.04), would be on the same scale as that due to bulk-specific variance (Table 1). We used the same cutoffs for all samples despite variation in median read depth (Table S1 in File S2) in an attempt to equalize power across samples. Although this differentially removed an appreciable number of sites, the low power to detect differences at these low-read depth sites in conjunction with concerns regarding corrections for multiple testing justified their removal. For these reasons and to exclude sequencing errors, we also chose to filter based on extreme allele frequencies. We imposed the upper bound of 100 reads to exclude paralogous mappings.
Estimation of v terms
In Equations 1–5, the bulk-specific variance terms (v) are treated as known constants. Prior to hypothesis testing, we estimate these variances using a procedure similar to that in Kelly et al. (2013). We first perform a series of pairwise contrasts (difference in transformed allele frequencies at each site) between the four bulks within a population (six pairwise contrasts for IM and Q; three for BR). Under the assumption that divergence among the bulks is random for most of the genome, each of these contrasts will be centered on zero with a variance equal to the sum of the individual sample variances (i.e., the two v terms plus each sample’s variance due to read depth). We estimate using the interquartile range (IQR) (File S1) of the genome-wide distribution of which is robust to the presence of outliers (SNPs that are correlated with flowering time or divergent across generations; see further comments below). We also estimate the read-depth variance as the average of across all SNPs for the contrasted samples. Following Equation 1B, the two v values are equal to the estimated total variance for the contrast minus the read-depth variance. Repeating this entire process for the remaining five pairwise contrasts ultimately produces six equations that are a function of four unknowns. This system is overdetermined (i.e., there are more equations than unknowns), so we use the method of general least squares to obtain an optimal compromise for the v terms (Lynch and Walsh 1998) as well as an estimate of their sampling variance. The only additional information necessary to calculate the v terms are estimates of the (co)variance of the six contrast variances, which we obtain by jackknifing the original data set of read counts, recalculating the contrast variances after deleting a portion (0.1) of the original data. The small SE for the v terms justifies treating these values as constants in our analyses and simulations (File S1).
Linked selection or hitchhiking (Maynard Smith and Haigh 1974; Gompert et al. 2017), particularly on structural variants, could make the null-variance estimation procedure described above excessively conservative. If a substantial proportion of SNPs are affected by selection/linkage, the IQR (third minus first quantile) becomes a less reliable estimate of for neutral SNPs. We recalculated the v terms following removal of all SNPs from within the genomic regions containing the structural variants described below (Table S1 in File S2), and find that v terms are modestly reduced (on average). We chose to use the original values, which are slightly conservative, to include all data simultaneously in our analysis. However, we encourage a careful consideration of linked selection and the null distribution for testing in future applications of these procedures.
Structural variants
Initial genotyping confirmed that five structural variants (inv5, inv6, inv8, inv10, and D) were segregating in one or more of the populations. Two of the variants, inv6 and the meiotic drive locus (D), were previously only known to segregate within IM. The others were mapped in crosses between annual and perennial genotypes of M. guttatus. We cannot identify a single diagnostic SNP for any of these features (recognizing alternative orientations from alternative SNP bases). For inv6 and D, the derived haplotype is associated with a single predominant nucleotide sequence >4 Mb, but the ancestral orientation is internally variable. For the other inversions, both alternative orientations harbor many distinct sequences. For each feature, however, there are differences in SNP allele frequency between the populations of sequences within each orientation. We thus developed a SNP set that is predictive of orientation for each inversion.
We used a collection of 10 fully sequenced inbred lines from the IM population to generate the SNP sets for inv6 and D (Flagel et al. 2014; Lee et al. 2016). PCR-based genotyping of length polymorphic markers indicate that 4 of the 10 lines carry the derived orientation at D, while 2 of 10 have the derived orientation for inv6. We found 11,848 SNPs for the D locus in which at least 5/6 of the nondrive lines harbor the alternative base (the Drive haplotype is always the reference base because the reference genome is based on a line homozygous for Driver). These SNPs are located within three distinct intervals on chromosome 11 (5.7–11.6, 13.9–14.1, and 16.6–21.1 Mb) due to misassembly in the reference genome sequence (Holeski et al. 2014). We identified 26,739 SNPs for inv6 where the two lines homozygous for the derived orientation are fixed for the alternative base and the other eight lines are fixed for reference between 1.34 and 7.61 Mb of chromosome 6 (Lee et al. 2016).
To develop a predictive SNP set for inv5, inv8, and inv10, we assembled and interrogated 10 whole-genome sequences, one plant from each of five annual populations (MAR3, REM8-10, CAC6G, LMC 24, and SLP19) and five perennial populations (TSG3, BOG10, YJS6, SWB, and DUN). All data are available from the Sequence Read Archive (http://www.ncbi.nlm.nih.gov/sra). The relevant genomic regions are 10–18 Mb of chromosome 5 (inv5), 1.5–7.0 Mb of chromosome 8 (inv8), and 2–6 Mb of chromosome 10 (inv10). To include a SNP in the diagnostic set for a feature, we required that the reference base predominate in annuals and vice versa, that at least three lines of each type were called, and at most one contradiction (annual line is alternative or perennial line is reference) was tolerated. With these conventions, the reference base within a structural variant identifies the derived orientation for D, the ancestral orientation for inv6, and the annual orientation for the other three loci. We averaged ∆pEL across SNPs within a feature to estimate the change in orientation frequencies between early- and late-flowering plants. Because the correlation between SNP alleles (reference vs. alternative) and orientation is imperfect, the average SNP ∆pEL should underestimate the magnitude of ∆pEL for inversion orientations.
Data availability
See BioProject under accession number PRJNA336318. Accession numbers for BioSamples: SAMN05508935, SAMN0550981, SAMN0550982, SAMN0550983, SAMN0550984, SAMN0550985, SAMN0550986, SAMN0550987, SAMN0550988, SAMN0550989, and SAMN0550990. Code used for all analyses can be found at https://github.com/pmonnahan/EarlyLate.
Results
Polymorphism
After filtering, we identified ∼7.5 million SNPs, most of which were segregating in more than one population. However, the pattern of shared polymorphism is asymmetric (Figure S1 in File S2). For SNPs in IM or BR with a minor allele frequency of at least 10%, 94% are segregating in the samples from the other two populations. This is a nearly complete overlap given that a population sample with as few as 25 reads is counted (and an allele at ≤10% population frequency will often fail to be sampled). In contrast, Q has a higher frequency of intermediate frequency SNPs that are rare or fixed in IM and BR. SNPs in the 10–90% range in Q are not evident in other populations ∼25% of the time.
Tests for association with flowering time
We first tested for significant within each population/year and then performed the structured hypothesis testing of Table 1. For the former, the number of significant sites was an order of magnitude greater in Q [using the Benjamini–Hochberg procedure to establish genome-wide false discovery rate (FDR) = 0.1] than in IM and BR considering both years of the study together (Table 2). Generally, tends to be larger in magnitude and more variable in Q than in IM (Figure S2 in File S2). Across years, 2013 exhibits many more significant than 2014 (approximately two- to threefold reduction in 2014). These tests depend on the bulk-specific variance for each sample reported in Table 3. If each plant in each bulk contributed equally to the DNA library, then v = 0.005. Several samples are only slightly elevated from this value (e.g., IM, 2014 Early), but the inflation evident in other samples (e.g., BR, 2013 Late) indicates substantial differential representation of sampled genomes in the pool of sequence-suitable DNA.
Table 2. Number of significant sites for the individual tests.
| No. of significant tests | No. of total tests | |||
|---|---|---|---|---|
| 2013 | 2014 | 2013 | 2014 | |
| IM | 590 | 247 | 3,798,948 | 4,488,418 |
| Q | 10,914 | 239 | 4,248,012 | 5,089,848 |
| BR | 13 | – | 3,715,897 | – |
Table 3. The estimates for v, the bulk-specific variance that aggregates the sampling events prior to sequencing, for each sample.
| BR | IM | Q | |
|---|---|---|---|
| 2013 early | 0.0323 | 0.0141 | 0.0152 |
| 2013 late | 0.0355 | 0.0200 | 0.0200 |
| 2014 early | 0.0165 | 0.0066 | 0.0083 |
| 2014 late | — | 0.0110 | 0.0138 |
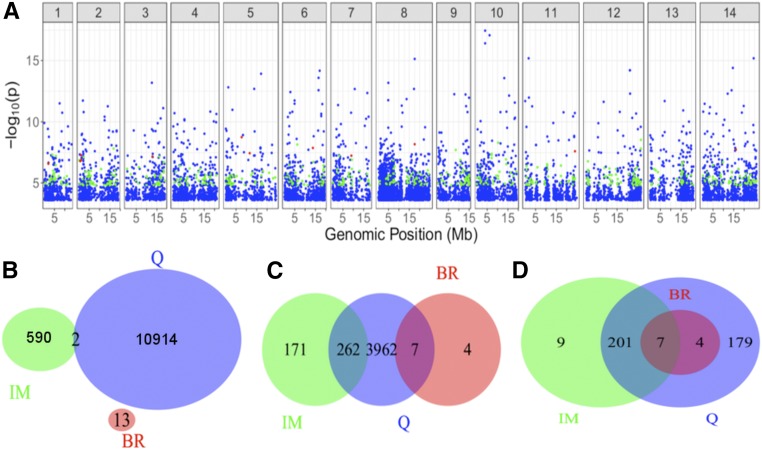
Figure 2 (top) shows the genome-wide distribution of significant sites for each of the three populations from 2013. Here, we observe very little overlap of significant SNPs among the different populations (Figure 2, bottom). However, when we divide the genome into 30-kb or 1-Mb windows, we find that these significant sites are often found in common regions. At both scales, Q shares many more significant regions with IM and BR than the latter share with each other. In 2014, there is more overlap despite fewer significant tests (eight SNPs were shared between IM and Q). Furthermore, we find few sites to be significant across years within populations: nine for Q and two for IM.
Figure 2.
(A) −log10(p) for significant test (FDR = 0.1) for each population in 2013. Blue = Q, green = IM, and red = BR. (B–D.) Overlap in significance across populations in 2013 for (B) individual sites, (C) 30-kb windows, and (D) 1-Mb windows. A window was considered to be in common between two populations if both populations possessed at least one significant site within the window boundaries.
The lack of overlap among populations is partially due to significant SNPs in Q that are not segregating in the other populations. The heterogeneity/interaction test of Table 1 is limited to SNPs passing the filter in multiple samples (in both populations for a given year or in both years for a given population). Results for the three distinct tests (marginal effect, heterogeneity, and overall) across the four different contexts are reported in Table 4. As expected, the two contexts displaying the strongest evidence for significant are Q and 2013. However, the relative proportion of sites that exhibit a marginal effect vs. an interaction effect varies greatly with context. In IM, a nearly equal number of sites are significant for marginal and interaction tests, while in Q the vast majority of significant tests are for marginal effects. Similarly, there are no interactions across the two populations in 2014, whereas 2013 is characterized by an almost equal number of SNPs with variable Importantly, significance for the marginal-effect test (M1 vs. M2) should not be interpreted to mean genuinely fixed effects. Figure 1 indicates that QTL with variable effects can inflate the test statistic for marginal effects (oftentimes more than the heterogeneity test) if has the same direction in each sample.
Table 4. Summary of significance testing.
| Context | Marginal effect M1 vs. M2 | Heterogeneity of effect M2 vs. M3 | Overall effect M1 vs. M3 | No. of tests |
|---|---|---|---|---|
| IM | 155 (327) | 154 (0) | 705 (56) | 3,458,706 |
| Q | 3,565 (3164) | 268 (0) | 5,168 (498) | 3,840,040 |
| 2013 | 1,019 (279) | 790 (0) | 3,490 (16) | 2,416,806 |
| 2014 | 278 (46) | 0 (0) | 368 (1) | 3,193,898 |
A summary of significance testing for the models of Table 1 is reported for each context. The contrasts are across years within IM and Q and across populations in 2013 and 2014, respectively. The number of genome-wide significant tests is reported for both the real data followed (in parentheses) by those obtained from simulation. Simulations were conducted assuming consistent genotypic effects (a) and generated with best-matching values of f0 and c.
Simulations of loci with consistent effects
To evaluate the results of Table 4 and other features of the data, we calibrated a model of consistent QTL effects for each context (see Table S2 in File S2 for a summary of best-matching parameter sets; top two matches were used for simulations). Testing on these simulated data generates a comparable number of significant tests for marginal effects (M1 vs. M2): 5017 for real, 3816 for simulated, across contexts (values in parentheses in Table 4). However, the constant-effect models are otherwise generally inconsistent with the real data. The simulations never produced (genome-wide) significant heterogeneity tests (no false positives), but they were abundant in the real data. Additionally, the number of significant outcomes in the overall test (M1 vs. M3) was invariably far less than for the marginal test in the simulations, but the opposite is true in the real data (recall that the overall test incorporates signal from both marginal and interaction tests). These discrepancies between simulated and real data indicate genuine variability in at shared SNPs, particularly across years within IM and across populations within 2013.
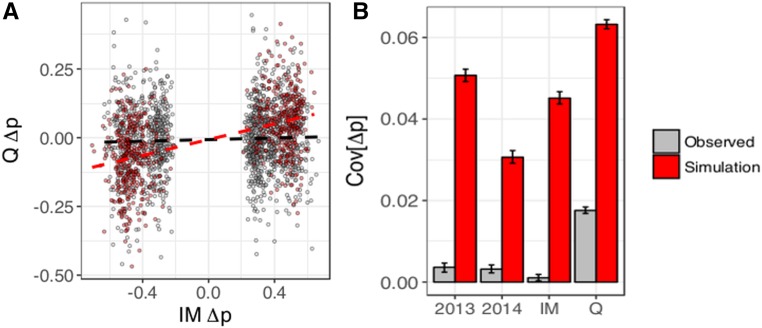
Further evidence comes from the covariance of across samples (Figure 3 and Figure S3–S6 in File S2). If genetic effects are constant, this covariance should be substantially positive. Sampling error in estimates for will reduce the strength of association, but this effect is reiterated in simulations, which are subject to the same degree of sampling variance in In all contexts, simulations using best-matching parameters generated an easily detectable positive correlation between estimates. The real data does not reiterate this pattern. The most striking difference is seen in the 2013 tests (Figure 3, left) followed by IM (Figure S6 in File S2), both of which have near-zero slopes for the real data, but a strong positive slope for the simulated data. For 2014 and Q, the real data exhibits a noticeable positive correlation, which is in agreement with their preponderance of significant marginal-effect tests. In 2014, the slopes for the real and simulated data are near parallel (Figure S4 in File S2), whereas in Q the slope for the simulated data are substantially more positive (Figure S5 in File S2). The covariance in across populations (or years) provides a quantitative measure of QTL (in)consistency (Figure 3, right). There is evidence of both consistent and variable sites, but the relative proportion varies across populations and over time.
Figure 3.
(A) in Q vs. IM in 2013 for simulated (red) and real (gray) data. Only sites in which LRT >15 for the individual in IM are shown. (B) Covariance in for sites (LRT >15 for the test of M1 vs. M3) across time (see bars for IM and Q) and space (2013 and 2014). Confidence intervals are observed 5th and 95th percentiles from bootstrap distribution generated with 100 replicates.
An interesting secondary conclusion from the simulations is that the lack of overlap of significant tests from single estimates (Figure 2, bottom left) is not compelling evidence for heterogeneous effects. Even when effects are constant, as implemented in the simulations, shared significance is rare due to an abundance of false negatives. For example, for a pair of populations where consistent effects are relatively frequent and strong (f0 = 0.1 and a = 0.3), we found only 353 SNPs to be simultaneously significant out of 26,748 that were deemed significant in either population individually.
Structural variation
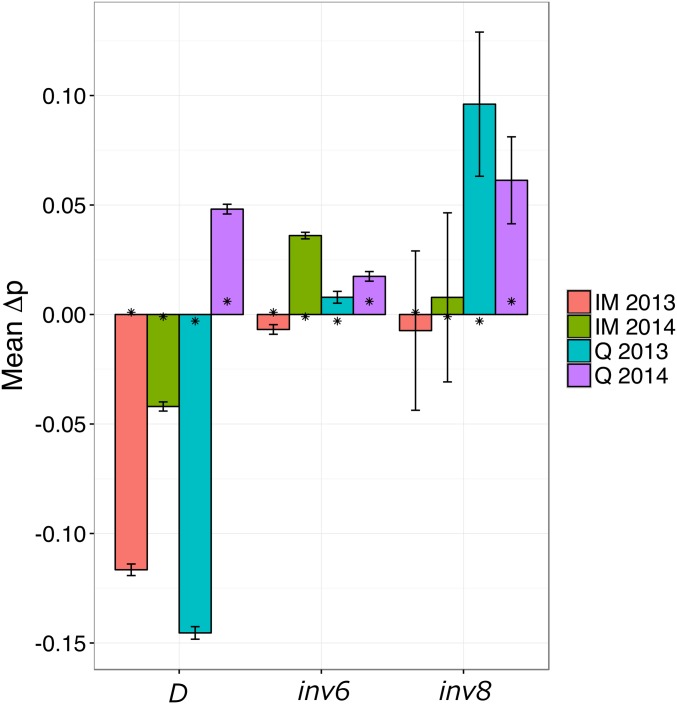
The five structural polymorphisms show strong, but highly variable, effects on flowering time (Figure 4). The first observation is that the D locus, which was previously known to be polymorphic only in IM and one other population (Case et al. 2016), is segregating in Q. The Drive allele, which enjoys a segregation advantage in female gametes (Fishman and Saunders 2008), is elevated in late-flowering samples in IM in both years and in Q in 2013. It is enriched in early-flowering plants in Q in 2014. inv8, which had previously been described mainly as a fixed difference between ecotypes, is also segregating in Q. We find no evidence for an inv8 effect in IM, probably because the perennial orientation is rare due to strong local selection (Puzey et al. 2017). However, the strong effects in Q are consistent with the perennial orientation delaying flowering. Results for inv6, inv5, and inv10 are ambiguous, and it is not clear that the latter two loci are polymorphic in these populations (full results reported in Table S4 in File S2).
Figure 4.
Mean allele frequency divergence between early- and late-flowering plants for three structural variants. Error bars are ±SE taken across the SNPs within each feature/population/year. Asterisks denote genome-wide average calculated in 1 Mb windows.
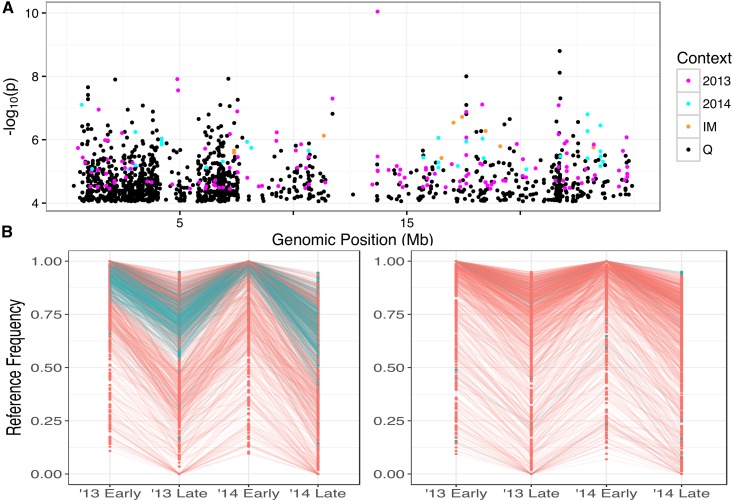
There is also a clear impact of inv8 on our SNP-level analyses. In Figure 2, significant are evenly dispersed with the exception of chromosome 8 (Table S3 in File S2), which has approximately five times more than any other chromosome. This inflation is entirely attributable to inv8 within Q (3749 of the 3801 significant tests on chromosome 8 are due to Q, 2593 of which are within inv8; Table S3 in File S2). Figure 5 (top) shows a very high density of SNPs significant for the marginal-effect test within inv8, and these SNPs are among the highest observed LRTs (see Figure S7 in File S2 for comparison with interaction-effect test). Figure 5 (bottom) plots allele frequency over time for the sites with positive (higher reference frequency in early bulk) and in the 99.95 percentile of the LRT for marginal effect in each population. These SNPs produce remarkably consistent oscillations in both IM and Q, but are almost entirely nonoverlapping (only four of the SNPs in Figure 5 and Figure S8 in File S2 are common across populations). This discrepancy is, again, partly due to the presence of inv8 in Q. In Q, 315/1921 (16.3%) of the SNPs in the 99.95 marginal-effect LRT percentile are from inv8, whereas only 30/1730 (1.7%) are in inv8 for IM. Also, nearly all of these 315 inv8 SNPs in Q exhibit positive (288/315 = 91.4%), indicating that the reference (annual) orientation is at a higher frequency in early-flowering plants. In both populations, there is a tendency toward positive for these consistent SNPs (918 positive vs. 812 negative in IM; 1254 positive vs. 667 negative in Q). This tendency is exaggerated in Q even after accounting for the effect of inv8 (966 positive vs. 640 negative sites are non-inv8). Interestingly, we find that a majority of sites in this 99.95 percentile are at an overall high reference frequency in both populations, with many of these sites fixed for the reference allele in either the early- or late-flowering plants (note the high density of sites in the upper portion of Figure 5 and Figure S8 in File S2).
Figure 5.
(A) −log10(p) for the marginal-effect test plotted along chromosome 8. (B) Reference frequency across the four sampling events for sites in the 99.95 percentile of the marginal-effect test that exhibit a positive Left = Q, right = IM. Color indicates whether site is within inv8 (blue) or not (red).
Discussion
Our question is regarding the extent to which the loci generating intrapopulation variation in quantitative traits are consistent within a species. Across populations, is the same set of loci responsible for within-population variation? Is the average effect of a QTL similar in neighboring populations, or even in the same population from one generation to the next? We develop a likelihood-based testing procedure to distinguish consistent and heterogeneous effects and then apply the procedures to genomic data from 10 population samples. Synthesizing multiple aspects of the results, the experiment strongly supports heterogeneity of QTL effects. This suggests appreciable lability of allelic effects in nature and underscores the importance of a broad sampling of natural variation in genetic mapping studies. Additionally, the results inform the potential for, or perhaps the expected scale at which, parallel or repeated evolution may occur. In the following sections, we discuss explanations for the observed variation within and among populations and their implications for evolution in nature.
Why does ΔpEL vary across time and space?
The expected value for depends on allele frequencies, the selection intensity, the phenotypic variance, and the average effect of alleles (Equation 6C; Falconer and Mackay 1996, p. 200). We controlled selection intensity with our sampling method, but it is clear that each of the other three components varied across space or time in this experiment. Allele-frequency differences are clearly important in explaining the differences among populations. Many intermediate frequency SNPs in Q that exhibited significant are fixed (or nearly so) within IM and BR. We attribute the elevated genomic and phenotypic variation in Q to recent hybridization of annual and perennial genotypes of M. guttatus (Monnahan et al. 2015). IM and BR are annual populations, and although each has high polymorphism, they produce far fewer significant
Q is about twice as divergent from each annual population as the annuals are from each other: genome-wide FST = 0.13 (Q vs. IM), 0.12 (Q vs. BR), and 0.07 (BR vs. IM; supplemental table 3 from Monnahan et al. 2015). This is important not only because is proportional to p(1 − p) at the SNP in question, but also because divergence among populations will affect the distribution of genomic backgrounds in which that SNP is expressed. Changes in average effect with genomic background (epistasis) has been demonstrated in greenhouse studies of M. guttatus for numerous life history traits, including flowering time (Kelly and Mojica 2011; Monnahan and Kelly 2015a,b).
Also, differences in the environment can alter in several ways. Despite the physical proximity of these populations, they differ dramatically in a number of environmental variables that affect flowering time. Q, IM, and BR face south, west, and east, respectively; each experiencing differing sun exposure. Snow clears earliest at Q, lengthening the growing period, and it also has a much shallower grade, particularly in comparison to IM. The primary water source for these plants is from snowmelt, and the shallow grade means that water moves slower and perhaps lasts longer for Q. Lastly, the edaphic substrate differs between populations; dirt and gravel at Q whereas the other two populations grow on a shallow bed of moss atop bedrock. Roots penetrate much deeper at Q, allowing plants access to additional water and perhaps a different nutrient profile.
G×E interactions are routinely observed in QTL experiments and can be appreciable in magnitude relative to the marginal effect across environments (Scheiner 1993). G×E can change the average effect across populations if there is spatial variation in environmental variables. G×E is the most likely cause of temporal heterogeneity in (e.g., IM in Table 4), because other factors such as differences in allele frequency (and thus the distribution of genetic backgrounds) should be relatively limited between successive generations within a population. A major temporal fluctuation between the 2 years of this study was time of snow melt. Snow cleared in May of 2013, but as early as mid-March in 2014. There was also a late bout of rain in mid-July 2014, extending an already elongated growing season. Furthermore, epistasis and G×E may themselves interact. Significant three-way interactions (G×G×E) have been documented in both field and laboratory studies (Caicedo et al. 2004; Zhu et al. 2014; Joseph et al. 2015; Monnahan and Kelly 2015b).
In addition to G×E, environmental variation can alter via at least two other routes. First, the predicted is inversely proportional to the phenotypic SD of the trait (Equation 6). Thus, a shift in environmental conditions that increases the environmental component of variation will reduce all else equal. Consistent with this effect, the phenotypic variance in flowering time was elevated in 2014 relative to 2013 (a greater number of days accrued between early and late collections in both IM and Q) while the number of significant tests was reduced. A second effect of environmental variation on is indirect. Sustained spatial heterogeneity in environmental variables will generate divergent selection and consequent local adaptation. This may be a major cause of allele-frequency differences among populations, which subsequently generates differences in
The context with the greatest consistency of effects was between years in Q (Figure 3 and Table 4), which may be attributable in part to the hybrid nature of this population. This population was established no more than 40 generations ago when a rock quarry fell into disuse and was subsequently colonized by nearby M. guttatus. Extensive linkage disequilibrium (LD) confirms that the population remains highly admixed (Monnahan et al. 2015), which likely reflects both recent formation and continued immigration. Nearly all polymorphic SNPs in IM and BR also segregate in Q, but the reverse is not true. Alternative “alleles” may be fairly substantial haplotypes; descendent from annual or perennial ancestors (or immigrants). Such alleles will be “large effect” if they aggregate the effects of numerous linked polymorphisms. The average in this context should be larger relative to estimation error, increasing the number of significant tests for a marginal effect (Table 4); and positive, given the annual nature of the reference genome and typically delayed flowering in perennials (see final paragraph in Results). The high LD should also inflate the number of noncausal SNPs exhibiting significant hitchhikers in the terminology of Maynard Smith and Haigh (1974). While Q has greater actual genetic variation in flowering time, LD should further inflate the number of significant tests. LD could also exaggerate our observation in the temporal consistency of across years (Figure 5).
The results from Q underscore a number of general points about the analysis. First, while there are 1000s of significant SNPs across populations/years, the number of functionally important variants is likely much smaller. A causal locus for flowering time will “pull” on neighboring SNPs in LD; an effect most pronounced in Q but not negligible in IM or BR. Whole-genome sequencing of lines from IM indicates substantial LD among SNPs at distances of 100s to a few 1000 bp (Puzey et al. 2017). In principle, assortative mating owing to differences in flowering time might generate substructure within populations. If strong enough, such structure might allow LD among unlinked SNPs. In the present study, we do not find strong internal structure. Divergence, measured as FST, is much lower between early- and late-flowering plants within populations (∼1–2%) than it is between populations (12–13% between Q and IM or BR). Still, analysis of divergence in allele frequency can be substantially improved if coupled with information on LD and within-population substructure.
Finally, although polymorphism was largely shared across populations, Q does exhibit a nontrivial amount of “private polymorphism” (Figure S1 in File S2). If a private polymorphism is causal, it might generate a heterogeneous at a linked neutral SNP that is present in multiple populations. We see potential examples of this in our data set, although we do not establish causality. For example, a private polymorphism in Q on chromosome 10 with significant in 2013 is within 2 kb of a shared polymorphism (with IM) exhibiting a significant interaction (M2 vs. M3) test. There are an additional 82 pairs of such sites within 2 kb of each other; however, the average distance between such pairs is >100 kb. Long-range effects of linkage are plausible in Q, particularly with regards to inv8. The perennial orientation of this inversion segregates only in Q, and within this region, we find numerous significant interaction tests across populations in 2013 (Figure S7 in File S2). Thus, our method cannot directly distinguish between a private, causal polymorphism and truly heterogeneous allelic effects as the source of heterogeneous across populations. Rather, it simply determines if genomic architecture varies. This is not an issue for interpreting heterogeneous across years within a population.
Measuring effects for a highly polygenic trait
A recent study of body pigmentation in fruit flies provides a striking contrast to our results. Endler et al. (2016) compared populations of Drosophila melanogaster from Europe and South Africa using a similar bulked-segregant approach. In contrast to the results here, they found relatively consistent architecture across populations. Genome-wide significant tests were contained within two genic regions, both shared between Europe and South Africa. One important difference is that Endler et al. (2016) measured phenotypes from animals reared under common laboratory conditions, thus limiting G×E interactions. A second critical difference is the nature of the traits under study. Coloration phenotypes in both plants and animals are frequently influenced by a few major factors (Epperson and Clegg 1988; Joron et al. 2006; Smith and Rausher 2011; Love et al. 2014). In contrast, flowering time is a highly polygenic trait with extensive environmental influence (Coupland 1995; Simpson and Dean 2002).
The best examples of “major loci” in the present study are the structural polymorphisms segregating in IM and Q (Figure 4). Our estimates at these loci are likely the most precise in the experiment because each is based on an average across many SNPs. Admittedly, we are likely underestimating the magnitude of for the inversions, owing to imperfect association between “diagnostic” SNPs and the actual alternative alleles (inversion orientations). Assuming underestimation to be minor, and noting that the additive variance contributed by a QTL is 2p(1 − p)a2 (Falconer and Mackay 1996), we use observed values to estimate the variance contribution of QTL. An observed of 0.1 (like inv8 in Q 2013) is predicted for a locus that explains almost but not quite 1% of the phenotypic variance. = 0.15 (like the D locus in Q 2013) for a locus that explains 1.5% of the phenotypic variance. While these calculations are coarse, they do emphasize that major flower-time loci are decidedly quantitative in their effects.
Many of our estimates for at significant SNPs are large in magnitude (>0.4; Figure 3, left). However, when considering single SNPs, it is essential to recognize that magnitude is inevitably overestimated in the pool of significant tests (Beavis 1994; Ioannidis 2008). For this reason, the simulation study is fundamental to our conclusion of genuine heterogeneity in the effects of flowering-time loci. Our simulations reiterate the stochastic processes generating exaggerated values for and, also, the ascertainment process by which overestimated values are used for subsequent analyses. These factors are clearly important. For example, the association of between two populations with data generated from constant-effect loci is positive (red line of Figure 3), but the slope is greatly reduced from 1 (the slope of the regression if there were no estimation error). It is the fact that the covariance of between samples within each context is significantly lower than predicted (Figure 3, right), after accounting for error and ascertainment, which indicates heterogeneity.
Our SNP-level hypothesis-testing framework was developed to address two basic issues. The first was to provide statistical evidence regarding the marginal effects of QTL (averaged over populations) as well as the heterogeneity of effects (across populations). The second issue is proper accounting for multiple sources of error inherent to serial sampling in Pool-seq studies. Despite best efforts in DNA quantification, pipetting, etc., variable representation of individuals among the sequenced reads is unavoidable. Contingency tables based directly on read counts (e.g., chi square, Fisher’s exact test) ignore all sampling events prior to the last; essentially treating each read as an independent draw from the ancestral population. Figure S9 in File S2 (see Table S5 for data) illustrates that contingency-table tests can be substantially anticonservative with respect to our method, at least when the bulk-specific sampling variance is nontrivial. P-values can be 1000-fold lower (more extreme) using Fisher’s exact test or chi square. However, the comparisons also indicate that our LRT can occasionally produce lower P-values than the table analyses if the average allele frequency is close to 0 or 1. Such SNPs will not usually be genome-wide significant because there is limited scope for differences in allele frequency between samples if the average is close to 0 or 1. However, for rigorous testing on SNPs where the rare allele is present in only a few copies across populations, generalized linear models that work directly with allele count data, in conjunction with genome-wide variance estimation, might provide a better testing platform. Such software exists for differential expression analyses, for example, EdgeR (Robinson et al. 2010) and DEseq2 (Love et al. 2014), but these methods would need to be generalized (perhaps a fruitful area for future studies) to consider allele frequency differences as opposed to raw total counts.
The elegance of testing arcsin, square root-transformed, allele frequencies is based on two features, each of which can be evaluated by comparison to the full distribution of changes across SNPs. First, the distribution of divergences should be approximately normal, a prediction strongly supported by the observed distributions (Figure S10 in File S2). Normality justifies the likelihood model (Equations 3–5), which also assumes homoscedastic variance. Untransformed allele-frequency differences, generated from a binomial sampling process, are highly heteroscedastic (i.e., the sampling variance of depends on and this heteroscedasticity is greatly reduced for transformed allele frequencies (Table S6). With transformed allele frequencies, average change appears to be slightly greater when the minor allele frequency is <0.1. This is actually an effect of ascertainment and not an “overcorrection” by the transform. If the true frequency of the minor allele at a SNP is <5%, it will only pass filters if sampling substantially moves the allele frequency away from the boundary in either Early or Late. Because we require that the average allele frequency is 0.05–0.95 to include a SNP, we nonrandomly include rare-allele SNPs that exhibit elevated change. This effect does not undermine the conclusions in this article (our significant tests come disproportionately from intermediate frequency SNPs), but the effect of ascertainment on testing should always be considered in genome-wide analyses.
Flowering-time loci
Two qualitatively different kinds of loci are investigated in this experiment. The first are structural polymorphisms, previously mapped in M. guttatus although not necessarily known from these populations. The second are SNPs outside of these regions in (presumably) freely recombining parts of the genome. While the strength of evidence for flowering-time effects of this latter class may be weaker, they potentially provide much finer resolution. For the structural variants, we cannot distinguish the effects of polymorphisms across the 100s of genes within each inversion. For other significant SNPs, we located each in relation to putative flowering time genes (based on M. guttatus version 2 genome annotation). We considered all SNPs significant for the M1 vs. M3 test within a candidate gene or ±2 kb of the flanking DNA. We confirmed, using BLAST, the homology of each candidate to Arabidopsis thaliana flowering time genes, but do not perform formal enrichment analyses given the imperfect, ad-hoc nature of the gene list.
In Q, 46 significant SNPs were located to flowering-time genes. These include genes from the photoperiod pathway and gibberellic acid pathway, as well as multiple interacting genes within each pathway. Gibberellic acid has direct effects on floral development, but also indirectly influences flowering time via its effects on germination and general growth regulation (Mouradov et al. 2002). A total of 7 of the 12 candidates in this pathway are gibberellin (GA) oxygenases, which generally degrade GA and its precursors (Wuddineh et al. 2015). Three of these (Migut.M00902, Migut.M00908, and Migut.M00909) are on a 50-kb stretch of chromosome 13 and all show highly consistent across years and Interestingly, two of these genes (Migut.M00908 and Migut.M00909) were also identified in IM and exhibit a similar pattern across years and In addition, both Q and IM identified GAI (Migut.H01666), a transcription factor that represses GA responses (Peng et al. 1997), as a candidate. In aggregate, these results support the GA pathway as a general source of natural variation in flowering time.
Critical photoperiod requirements are typically much longer for perennial M. guttatus, with most perennials (and even some annuals) requiring vernalization upon previous exposure to short-day conditions (Friedman and Willis 2013). In Q, a SNP ∼1.5-kb downstream of VERNALIZATION1 (VRN1) (Migut.H02193) shows a consistent difference across years and and this SNP is within the major photoperiod and vernalization QTL mapped by Friedman and Willis (2013). VRN1 is also transcription responsive to photoperiod (Dubcovsky et al. 2006) and has distinct effects on flowering time apart from vernalization (Levy et al. 2002). Early Flowering 6 (ELF6) (Migut.F01729) (Clouse 2008), a repressor of the photoperiod pathway, also shows a consistently higher reference base frequency in the early-flowering samples and ; significant for both the M1 vs. M2 and M1 vs. M3 tests). Significant SNPs were also found adjacent to ELF3 and ELF4 (Migut.E01551 and Migut.J00944, respectively), and again, the reference base frequency was higher in early-flowering plants. However, was less consistent across years (ELF3, and ELF4, and The direction of these differences usually positive) may reflect the fact that the reference genome is based on an annual genotype. Thus, the reference base is more likely to be the “annual” allele in an annual/perennial population. Lastly, GIGANTEA (Migut.C00380), a major photoperiod-response regulator that interacts with multiple ELF transcription factors (Mishra and Panigrahi 2015), exhibited a significant interaction across years in Q, with and
Both IM and Q also have significant SNPs in a tandem pair of GDSL-motif lipase genes (Migut.M01081 and Migut.M01082) as well as an RNA-ligase gene (Migut.N02091). The former belong to a class of lipases with broad, ecologically relevant functions including microbial defense (Oh et al. 2005; Kwon et al. 2009), morphogenesis and development (Riemann et al. 2007; Lee et al. 2009), and abiotic stress responses (Hong et al. 2007). While these genes may play a direct role in development, they may function in defense against pests associated with early/late season conditions. RNA ligase is involved in the maturation of transfer RNAs and was recently shown to play a role in auxin-related growth processes (Leitner et al. 2015).
The structural polymorphisms provide clear evidence of flowering-time effects (Figure 4), although without gene-level resolution. However, the estimates for phenotypic and fitness effects for entire karyotypes is valuable when considering the evolutionary dynamics of these polymorphisms. The results for inv8 are fully consistent with expectations based on previous studies of this locus. Alternative orientations distinguish annual and perennial ecotypes of M. guttatus and QTL mapping reveals large effects of inv8 on flowering time, anthocyanin production, and growth-related traits (Lowry and Willis 2010). As in the mapping study, our experiment shows that the perennial orientation delays flowering, and its presence confirms the annual/perennial origin of this population. This study provides the most direct evidence of inv8 segregating within a natural population and contributing to phenotypic variation; although presence in other populations is suggested from marker data (Twyford and Friedman 2015).
The strong effect of the meiotic drive locus on flowering time is more surprising. However, field experiments have demonstrated Drive effects on both male and female fitness components (Fishman and Kelly 2015), which may depend on flowering time. Direct effects of this locus on developmental timing have been documented in a greenhouse experiment (Scoville et al. 2009). It is possible that some delay in flowering is due to the reduction in pollen viability caused by the Drive karyotype. Bee pollinators discriminate against flowers with lower viable pollen (Boluarte-Medina and Veilleux 2002) and lack of visitation prolongs flower life span (Arathi et al. 2002). Finally, the derived orientation of inv6 was associated with earlier flowering in IM in 2014, but not the previous year (Figure 4). Several greenhouse studies have shown inv6 effects on days to flower (Lee 2009; Scoville et al. 2009), although the direction of effect varies with genetic background and perhaps the sequence of the ancestral orientation (which is highly variable and different among experiments).
Conclusion
We have developed and implemented a method to map genomic regions affecting ecologically relevant traits directly within natural populations, while accounting for estimation error in observed allele frequencies. Replicated comparative mapping can inform fundamental biological questions such as how the evolutionary trajectories of local populations will transform an entire species. Uniform selection across a species range generated by climate change might set the stage for parallel evolution, but at what scale will parallelism occur? As sequencing costs continue to decrease, the number of populations and range of distribution that can be surveyed will increase. Though our study focuses on a narrow geographic range, it provides a baseline understanding for how genomic variation in flowering time varies across neighboring populations and from generation to generation.
While most flowering-time loci varied between populations and over time, a subset exhibited fairly consistent effects. These consistent loci, which include large structural variants such as inversions and genes in known flowering-time pathways, are most likely to evolve in parallel if populations were to experience uniform selection on flowering time. The actual degree of parallelism will depend on genetic factors (e.g., the distribution of additive and dominance effects), demographic factors (e.g., population sizes, growth rates, and migration), and selective factors (e.g., strength and consistency of selection on flowering time). However, the existence of consistent loci supports the growing body of evidence that parallel evolution can occur from the recruitment of standing genetic variation (Pigeon et al. 1997; Colosimo et al. 2005; Jones et al. 2012). Statistical considerations aside, this consistency also supports the utility of mapping studies to identify a subset of loci that are general contributors to natural variation within and between populations.
In contrast, the observed variation in genomic architecture testifies, in part, to the influence of divergent environmental conditions and genomic backgrounds on the average effects exhibited by segregating variants. For highly polygenic traits such as flowering time, we would almost certainly expect to find some loci to have evolved in parallel, but this would likely account for a relatively minor portion of the total selection response. Furthermore, a lack of parallelism at the genetic level would not necessarily imply that populations did not have access to the same standing variation and thus evolutionary trajectories. Although private polymorphisms would play a bigger role for more isolated/divergent populations, a lack of parallelism could simply reflect the idiosyncratic interplay between the factors outlined above. Additional studies will help determine whether variation in genomic architecture is a trait- or species-specific phenomenon as well as highlight those genes that are consistently important drivers for natural variation.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.201483/-/DC1.
Acknowledgments
We thank the following individuals for the helpful comments on the manuscript: S. J. MacDonald, M. E. Orive, and L. Hileman. We acknowledge funding from the University of Kansas Botany Endowment, the University of Kansas Graduate Research Fund, and the National Institutes of Health (R01 GM-073990-02).
Footnotes
Communicating editor: T. Juenger
Literature Cited
- Arathi H. S., Rasch A., Cox C., Kelly J. K., 2002. Autogamy and floral longevity in Mimulus guttatus. Int. J. Plant Sci. 163: 567–573. [Google Scholar]
- Beavis W. D., 1994. The power and deceit of QTL experiments: lessons from comparative QTL studies, pp. 250–266 in Proceedings of the Forty-Ninth Annual Corn and Sorghum Industry Research Conference Washington, DC. [Google Scholar]
- Bernier G., Périlleux C., 2005. A physiological overview of the genetics of flowering time control. Plant Biotechnol. J. 3: 3–16. [DOI] [PubMed] [Google Scholar]
- Blümel M., Dally N., Jung C., 2015. Flowering time regulation in crops — what did we learn from Arabidopsis? Curr. Opin. Biotechnol. 32: 121–129. [DOI] [PubMed] [Google Scholar]
- Boluarte-Medina T., Veilleux R. E., 2002. Phenotypic characterization and bulk segregant analysis of anther culture response in two backcross families of diploid potato. Plant Cell Tissue Organ Cult. 68: 277–286. [Google Scholar]
- Caicedo A. L., Stinchcombe J. R., Olsen K. M., Schmitt J., Purugganan M. D., 2004. Epistatic interaction between Arabidopsis FRI and FLC flowering time genes generates a latitudinal cline in a life history trait. Proc. Natl. Acad. Sci. USA 101: 15670–15675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case, A. L., F. R. Finseth, C. M. Barr, and L. Fishman, 2016 Selfish evolution of cytonuclear hybrid incompatibility in Mimulus. Proc. Biol. Sci. 283: 20161493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clouse S. D., 2008. The molecular intersection of brassinosteroid-regulated growth and flowering in Arabidopsis. Proc. Natl. Acad. Sci. USA 105: 7345–7346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohan F. M., 1984a Can uniform selection retard random genetic divergence between isolated conspecific populations? Evolution 38: 495–504. [DOI] [PubMed] [Google Scholar]
- Cohan F. M., 1984b Genetic divergence under uniform selection. I. Similarity among populations of Drosophila melanogaster in their responses to artificial selection for modifiers of ciD. Evolution 38: 55–71. [DOI] [PubMed] [Google Scholar]
- Colosimo P. F., Hosemann K. E., Balabhadra S., Villarreal G., Dickson M., et al. , 2005. Widespread parallel evolution in sticklebacks by repeated fixation of ectodysplasin alleles. Science 307: 1928–1933. [DOI] [PubMed] [Google Scholar]
- Cooley A. M., Modliszewski J. L., Rommel M. L., Willis J. H., 2011. Gene duplication in Mimulus underlies parallel floral evolution via independent trans-regulatory changes. Curr. Biol. 21: 700–704. [DOI] [PubMed] [Google Scholar]
- Coupland G., 1995. Genetic and environmental control of flowering time in Arabidopsis. Trends Genet. 11: 393–397. [DOI] [PubMed] [Google Scholar]
- Dubcovsky J., Loukoianov A., Fu D., Valarik M., Sanchez A., et al. , 2006. Effect of photoperiod on the regulation of wheat vernalization genes VRN1 and VRN2. Plant Mol. Biol. 60: 469–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endler L., Betancourt A. J., Nolte V., Schlötterer C., 2016. Reconciling differences in pool-GWAS between populations: a case study of female abdominal pigmentation in Drosophila melanogaster. Genetics 202: 843–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epperson B. K., Clegg M. T., 1988. Genetics of flower color polymorphism in the common morning glory (Ipomoea purpurea). J. Hered. 79: 64–68. [DOI] [PubMed] [Google Scholar]
- Falconer D. S., Mackay T. F. C., 1996. Introduction to Quantitative Genetics, Ed. 4. Pearson Education, Harlow, United Kingdom. [Google Scholar]
- Fisher R. A., 1941. Average excess and average effect of a gene substitution. Ann. Eugen. 11: 53–63. [Google Scholar]
- Fisher, S. R. A., and E. B. Ford, 1947 The spread of a gene in natural conditions in a colony of the moth Panaxia Dominula L. Heredity 1: 143–174. [Google Scholar]
- Fishman L., Kelly J. K., 2015. Centromere-associated meiotic drive and female fitness variation in Mimulus. Evolution 69: 1208–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman L., Saunders A., 2008. Centromere-associated female meiotic drive entails male fitness costs in monkeyflowers. Science 322: 1559–1562. [DOI] [PubMed] [Google Scholar]
- Fitter A., Fitter R., 2002. Rapid changes in flowering time in British plants. Science 296: 1689–1691. [DOI] [PubMed] [Google Scholar]
- Flagel L. E., Willis J. H., Vision T. J., 2014. The standing pool of genomic structural variation in a natural population of Mimulus guttatus. Genome Biol. Evol. 6: 53–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., Willis J. H., 2013. Major QTLs for critical photoperiod and vernalization underlie extensive variation in flowering in the Mimulus guttatus species complex. New Phytol. 199: 571–583. [DOI] [PubMed] [Google Scholar]
- Fu Y.-B., Ritland K., 1994. Marker-based inferences about the genetic basis of flowering time in Mimulus guttatus. Hereditas 121: 267–272. [Google Scholar]
- Gautier M., Foucaud J., Gharbi K., Cézard T., Galan M., et al. , 2013. Estimation of population allele frequencies from next-generation sequencing data: pool-vs. individual-based genotyping. Mol. Ecol. 22: 3766–3779. [DOI] [PubMed] [Google Scholar]
- Gompert Z., Egan S. P., Barrett R. D. H., Feder J. L., Nosil P., 2017. Multilocus approaches for the measurement of selection on correlated genetic loci. Mol. Ecol. 26: 365–382. [DOI] [PubMed] [Google Scholar]
- Holeski L., Monnahan P., Koseva B., McCool N., Lindroth R. L., et al. , 2014. A high-resolution genetic map of yellow monkeyflower identifies chemical defense QTLs and recombination rate variation. G3 (Bethesda) 4: 813–821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong J. K., Choi H. W., Hwang I. S., Kim D. S., Kim N. H., et al. , 2007. Function of a novel GDSL-type pepper lipase gene, CaGLIP1, in disease susceptibility and abiotic stress tolerance. Planta 227: 539–558. [DOI] [PubMed] [Google Scholar]
- Ioannidis J., 2008. Why most discovered true associations are inflated. Epidemiology 19: 640–648. [DOI] [PubMed] [Google Scholar]
- Jones F. C., Grabherr M. G., Chan Y. F., Russell P., Mauceli E., et al. , 2012. The genomic basis of adaptive evolution in threespine sticklebacks. Nature 484: 55–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joron M., Papa R., Beltrán M., Chamberlain N., Mavárez J., et al. , 2006. A conserved supergene locus controls colour pattern diversity in Heliconius butterflies. PLoS Biol. 4: e303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph B., Lau L., Kliebenstein D. J., 2015. Quantitative variation in responses to root spatial constraint within Arabidopsis thaliana. Plant Cell 27: 2227–2243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly J. K., Mojica J. P., 2011. Interactions among flower-size QTL of Mimulus guttatus are abundant but highly variable in nature. Genetics 189: 1461–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly J. K., Koseva B., Mojica J. P., 2013. The genomic signal of partial sweeps in Mimulus guttatus. Genome Biol. Evol. 5: 1457–1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., Crow J. F., 1978. Effect of overall phenotypic selection on genetic change at individual loci. Proc. Natl. Acad. Sci. USA 75: 6168–6171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King E., Merkes C., McNeil C., Hoofer S., Sen S., et al. , 2012. Genetic dissection of a model complex trait using the Drosophila synthetic population resource. Genome Res. 22: 1558–1566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon S. J., Jin H. C., Lee S., Nam M. H., Chung J. H., et al. , 2009. GDSL lipase‐like 1 regulates systemic resistance associated with ethylene signaling in Arabidopsis. Plant J. 58: 235–245. [DOI] [PubMed] [Google Scholar]
- Latter B. D. H., 1965. The response to artificial selection due to autosomal genes of large effect. I. Changes in gene frequency at an additive locus. Aust. J. Biol. Sci. 18: 585–598. [DOI] [PubMed] [Google Scholar]
- Lee D. S., Kim B. K., Kwon S. J., Jin H. C., Park O. K., 2009. Arabidopsis GDSL lipase 2 plays a role in pathogen defense via negative regulation of auxin signaling. Biochem. Biophys. Res. Commun. 379: 1038–1042. [DOI] [PubMed] [Google Scholar]
- Lee, Y. W., 2009 Genetic Analysis of Standing Variation for Floral Morphology and Fitness Components in a Natural Population of Mimulus guttatus (common monkeyflower). Ph.D. Thesis, Duke University, Durham, NC. [Google Scholar]
- Lee Y. W., Fishman L., Kelly J. K., Willis J. H., 2016. A segregating inversion generates fitness variation in yellow monkeyflower (Mimulus guttatus). Genetics 202: 1473–1484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitner J., Retzer K., Malenica N., Bartkeviciute R., Lucyshyn D., et al. , 2015. Meta-regulation of Arabidopsis auxin responses depends on tRNA maturation. Cell Rep. 11: 516–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy Y. Y., Mesnage S., Mylne J. S., Gendall A. R., Dean C., 2002. Multiple roles of Arabidopsis VRN1 in vernalization and flowering time control. Science 297: 243–246. [DOI] [PubMed] [Google Scholar]
- Love M., Anders S., Huber W., 2014. Differential analysis of count data–the DESeq2 package. Genome Biol. 15: 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowry D. B., Willis J. H., 2010. A widespread chromosomal inversion polymorphism contributes to a major life-history transition, local adaptation, and reproductive isolation. PLoS Biol. 8: 2227 [corrigenda: PLoS Biol. 10: 10.1371 (2012)]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., Walsh B., 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA. [Google Scholar]
- Lynch M., Bost D., Wilson S., Maruki T., Harrison S., 2014. Population-genetic inference from pooled-sequencing data. Genome Biol. Evol. 6: 1210–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magwene P. M., Willis J. H., Kelly J. K., 2011. The statistics of bulk segregant analysis using next generation sequencing. PLoS Comput. Biol. 7: e1002255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith J., Haigh J., 1974. The hitch-hiking effect of a favourable gene. Genet. Res. 23: 23–35. [PubMed] [Google Scholar]
- McCarthy M. I., Abecasis G. R., Cardon L. R., Goldstein D. B., Little J., et al. , 2008. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat. Rev. Genet. 9: 356–369. [DOI] [PubMed] [Google Scholar]
- Michelmore R. W., Paran I., Kesseli R. V., 1991. Identification of markers linked to disease-resistance genes by bulked segregant analysis: a rapid method to detect markers in specific genomic regions by using segregating populations. Proc. Natl. Acad. Sci. USA 88: 9828–9832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra P., Panigrahi K. C., 2015. GIGANTEA – an emerging story. Front. Plant Sci. 6: 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mojica J. P., Kelly J. K., 2010. Viability selection prior to trait expression is an essential component of natural selection. Proc. Biol. Sci. 277: 2945–2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mojica J. P., Lee Y. W., Willis J. H., Kelly J. K., 2012. Spatially and temporally varying selection on intrapopulation quantitative trait loci for a life history trade-off in Mimulus guttatus. Mol. Ecol. 21: 3718–3728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monnahan P. J., Kelly J. K., 2015a Epistasis is a major determinant of the additive genetic variance in Mimulus guttatus. PLoS Genet. 11: e1005201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monnahan P. J., Kelly J. K., 2015b Naturally segregating loci exhibit epistasis for fitness. Biol. Lett. 11: 20150498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monnahan P. J., Colicchio J., Kelly J. K., 2015. A genomic selection component analysis characterizes migration‐selection balance. Evolution 69: 1713–1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouradov A., Cremer F., Coupland G., 2002. Control of flowering time interacting pathways as a basis for diversity. Plant Cell 14: S111–S130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh I. S., Park A. R., Bae M. S., Kwon S. J., Kim Y. S., et al. , 2005. Secretome analysis reveals an Arabidopsis lipase involved in defense against Alternaria brassicicola. Plant Cell 17: 2832–2847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J., Carol P., Richards D. E., King K. E., Cowling R. J., et al. , 1997. The Arabidopsis GAI gene defines a signaling pathway that negatively regulates gibberellin responses. Genes Dev. 11: 3194–3205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pigeon D., Chouinard A., Bernatchez L., 1997. Multiple modes of speciation involved in the parallel evolution of sympatric morphotypes of lake whitefish (Coregonus clupeaformis, Salmonidae). Evolution 51: 196–205. [DOI] [PubMed] [Google Scholar]
- Puzey J. R., Willis J. H., Kelly J. K., 2017. Population structure and local selection yield high genomic variation in Mimulus guttatus. Mol. Ecol. 26: 519–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riemann M., Gutjahr C., Korte A., Riemann M., Danger B., et al. , 2007. GER1, a GDSL motif-encoding gene from rice is a novel early light- and Jasmonate-induced gene. Plant Biol. 9: 32–40. [DOI] [PubMed] [Google Scholar]
- Robinson M. D., McCarthy D. J., Smyth G. K., 2010. edgeR: a bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26: 139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheiner S. M., 1993. Genetics and evolution of phenotypic plasticity. Annu. Rev. Ecol. Syst. 24: 35–68. [Google Scholar]
- Schlötterer C., Tobler R., Kofler R., Nolte V., 2014. Sequencing pools of individuals - mining genome-wide polymorphism data without big funding. Nat. Rev. Genet. 15: 749–763. [DOI] [PubMed] [Google Scholar]
- Scoville A., Lee Y. W., Willis J. H., Kelly J. K., 2009. Contribution of chromosomal polymorphisms to the G-matrix of Mimulus guttatus. New Phytol. 183: 803–815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson G. G., Dean C., 2002. Arabidopsis, the Rosetta stone of flowering time? Science 296: 285–289. [DOI] [PubMed] [Google Scholar]
- Smith S. D., Rausher M. D., 2011. Gene loss and parallel evolution contribute to species difference in flower color. Mol. Biol. Evol. 28: 2799–2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Twyford A. D., Friedman J., 2015. Adaptive divergence in the monkey flower Mimulus guttatus is maintained by a chromosomal inversion. Evolution 69: 1476–1486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wellmer F., Riechmann J. L., 2010. Gene networks controlling the initiation of flower development. Trends Genet. 26: 519–527. [DOI] [PubMed] [Google Scholar]
- Wuddineh W. A., Mazarei M., Zhang J., Poovaiah C. R., Mann D. G., et al. , 2015. Identification and overexpression of gibberellin 2‐oxidase (GA2ox) in switchgrass (Panicum virgatum L.) for improved plant architecture and reduced biomass recalcitrance. Plant Biotechnol. J. 13: 636–647. [DOI] [PubMed] [Google Scholar]
- Zhu C.-T., Ingelmo P., Rand D. M., 2014. G×G×E for lifespan in Drosophila: mitochondrial, nuclear, and dietary interactions that modify longevity. PLoS Genet. 10: e1004354. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
See BioProject under accession number PRJNA336318. Accession numbers for BioSamples: SAMN05508935, SAMN0550981, SAMN0550982, SAMN0550983, SAMN0550984, SAMN0550985, SAMN0550986, SAMN0550987, SAMN0550988, SAMN0550989, and SAMN0550990. Code used for all analyses can be found at https://github.com/pmonnahan/EarlyLate.