A Comparison of Dose Metrics to Predict Local Tumor Control for Photofrin-mediated Photodynamic Therapy

Abstract

This preclinical study examines light fluence, PDT dose, and “apparent reacted singlet oxygen”, [¹O₂]_rx, to predict local control rate (LCR) for Photofrin-mediated photodynamic therapy (PDT) of radiation-induced fibrosarcoma (RIF) tumors. Mice bearing RIF tumors were treated with in-air fluences (50–250 J/cm²) and in-air fluence rates (50–150 mW/cm²) at Photofrin dosages of 5 and 15 mg/kg and a drug-light interval of 24 hours using a 630nm 1-cm diameter collimated laser. A macroscopic model were used to calculate [¹O₂]_rx and PDT dose based on in vivo explicit dosimetry of the drug concentration, light fluence, and tissue optical properties. PDT dose and [¹O₂]_rx were defined as a temporal integral of drug concentration and fluence rate, and singlet oxygen concentration consumed divided by the singlet oxygen lifetime, respectively. LCR was stratified for different dose metrics for 74 mice (66 + 8 control). Complete tumor control at 14 days was observed for [¹O₂]_rx ≥ 1.1 mM or PDT dose ≥ 1200 μMJ/cm² but cannot be predicted with fluence alone. LCR increases with increasing [¹O₂]_rx and PDT dose but is not well correlated with fluence. Comparing dosimetric quantities, [¹O₂]_rx outperformed both PDT dose and fluence in predicting tumor response and correlating with LCR.

INTRODUCTION

Photofrin-mediated photodynamic therapy (PDT) is approved by the US Food and Drug Administration (FDA) for the treatment of some malignant and pre-malignant conditions, such as esophageal cancer and non-small cell lung cancer (1–4). Photofrin is excited by exposure to light of a specific wavelength (usually at 400, 514, or 630 nm). Following the absorption of light, the photosensitizer undergoes a transition from its ground state (singlet state) into a relatively long-lived electronically excited state (triplet state) via a short-lived excited singlet state. The triplet can transfer its energy directly to ground-state oxygen (³O₂) to form singlet-state oxygen (¹O₂), which is thought to be responsible for cell death and contributes to the clinical benefits of PDT (5). Because of the high reactivity and short half-life of ¹O₂, only sub-cellular organelles within cells that are proximal to the area of the ¹O₂ production (area of photosensitizer localization) are directly affected by PDT (6, 7). Therefore, PDT destroys the disease in a way that causes significantly less generalized or secondary toxicities than other conventional treatments such as surgery, chemotherapy, and ionizing radiation.

An ideal dosimetric predictor for PDT efficacy is still elusive due to the dynamic changes and interactions of the key PDT components (fluence, drug concentration, and oxygen level) during treatment, which, to some extent, has hindered the clinical application of PDT. In most clinical and pre-clinical protocols, PDT dosimetry is still based on the administered photosensitizer dosage and the delivered light fluence under a range of fluence rates (ϕ) (8, 9). This method of clinical dosimetry does not take into account actual levels of photosensitizer uptake in the target tissue or, more importantly, variations in photochemical PDT oxygen consumption variation for different ϕ during PDT (10, 11). An earlier study demonstrated that these factors may be responsible for the poor predictive power of current methods in clinical dosimetry (10, 11). PDT dose, which can be expressed as a product of photosensitizer concentration and ϕ, measures the photon energy absorbed by the photosensitizer (12). This quantity may serve as a good predictor of outcomes in ³O₂-rich conditions. However, under hypoxic conditions, it is less accurate in predicting PDT efficacy because it does not consider the rate of PDT consumption of ³O₂ for different ϕ (13). The formation of reactive oxygen species is critical to PDT efficacy. For type I sensitizers, hydroxyl radicals (OH^•) appear to be the major cytotoxic element, but ¹O₂ is likely responsible for cellular killing and clinical outcomes for type II photosensitizers such as Photofrin. As the primary mediator of cell damage during Photofrin-PDT, ¹O₂ has gained special attention as a good dosimetric quantity based on either direct measurements or indirect modeling (14–17). This study is focused on the latter method due to the difficulties in directly measuring ¹O₂ in vivo during PDT delivery. We use a singlet oxygen explicit dosimetry (SOED) method to calculate the concentration of reacted singlet oxygen, [¹O₂]_rx, by using an empirical five-parameter model. Calculated [¹O₂]_rx is also compared with light fluence and PDT dose as dosimetric predictors for PDT. The tumor local control rate (LCR) is used as the treatment endpoint. Moreover, we provide Kaplan-Meier data analysis with in-depth statistical tests for the evaluation of the three dose metric quantities. To our knowledge, we are the first to establish the superiority of calculated [¹O₂]_rx as a predictor of outcome to Photofrin-PDT in vivo, compared to light fluence or PDT dose.

MATERIALS AND METHODS

In vivo treatment protocols

Radiation-induced fibrosarcoma (RIF) cells in logarithmic growth phase (30 μl of 1×10⁷ cells/ml concentration) were injected subcutaneously over the right shoulders of 6–8 week old female C3H mice (Charles River, Frederick, MD). Around 5–10 days after inoculation, when tumors reached ~3–5 mm in length, Porfimer Sodium (Photofrin©, Pinnacle Biologics, Chicago, Illinois) was injected at doses of 5 or 15 mg/kg via the tail vein. These doses of Photofrin were chosen to produce PDT doses that were well separated. At a 24 hour drug-light interval (optimized for survival) (18), PDT was performed by superficial irradiation of the tumor with a 630 nm laser (Biolitec AG., A-1030, Vienna) coupled to a microlens fiber to produce a collimated beam of 1-cm diameter on the tumor surface. A total in-air fluence of 50, 135, 200, or 250 J/cm² was delivered at in-air fluence rates (ϕ_air) of 50, 75, or 150 mW/cm². The “in-air fluence rate” is defined as the calculated irradiance determined by laser power divided by the treatment area. The “in-air fluence” was calculated by multiplying the “in-air fluence rate” by the treatment time. Mice were randomly assigned to various treatment groups. Immediately before and after PDT, the Photofrin fluorescence in the tumor was measured using a custom-designed multi-fiber probe (19). The multi-fiber probe was in physical contact with the tumor surface. The contact probe is composed of an array of optical fibers, one of which was connected to the 405 nm excitation light to measure fluorescence at detection fibers spaced at fixed locations from the source fiber. Collected spectra were imaged by a multi-channel CCD system and analyzed by a singular value decomposition (SVD) method (20). The contact probe collects fluorescence light only up to the depth of penetration of the UV excitation laser and the area of contact. The absorption coefficient (μ_a) and reduced scattering coefficient (μ_s′) of the tumor tissue was also obtained pre- and post-PDT using a two-catheter method (21). Tumor-bearing mice that received neither light irradiation nor Photofrin were used as controls. All procedures were approved by the Institutional Animal Care and Use Committee of University of Pennsylvania. Animal husbandry was provided by the Laboratory Animal Resources of the University of Pennsylvania in association with Assessment and Accreditation of Laboratory Animal Care (AALAC).

Determination of Photofrin concentration from the fluorescence measurements

Photofrin fluorescence spectra were measured using a multi-fiber spectroscopic contact probe (19) and were analyzed using singular value decomposition (SVD) fitting (20). The conversion between the best –fit value of the Photofrin component and in vivo Photofrin concentration was obtained by comparing the in vivo fluorescence with that of phantoms with known photosensitizer concentrations. An empirical correction factor was obtained from the phantom experiments and varying μ_a and μ_s′ (22). In separate experiments, the accuracy of the in vivo measurements were evaluated. Mice with tumors were administered Photofrin at a 24 hour drug-light interval and the interstitial photosensitizer concentration was measured with the multi-fiber probe. Immediately afterwards, tumors were excised and frozen. Tumors were later homogenized with Soluble (Perkin Elmer, Waltham, Massachusetts, United States) and their fluorescence was measured by a spectrofluorometer (FluoroMax-3; Jobin Yvon, Inc., Edison, New Jersey, United States). An excitation of 405 nm was used with an emission range from 630–750 nm, and photosensitizer concentration in tissue was calculated based on the increase in fluorescence resulting from the addition of a known amount of Photofrin to each sample after its initial reading. The correlation between the in vivo and ex vivo measurements was found to follow a linear fit (y=x) with goodness of R² = 0.99 (22).

Calculation of the tumor local control rate (LCR)

The width (a) and length (b) of the tumors were measured daily using a sliding caliper for up to 14 days post-PDT. The tumor volumes (V) were calculated using V= π×a²×b/6 (23). The raw tumor volumes were fitted to V₀e^kd for individual mouse (23). Since initial tumor volumes (V₀) at the time of treatment were not identical among mice (12 to 50 mm³), daily tracked tumor volumes were scaled relative to an initial normalized tumor volume of ~ 23 mm³ (the average of all initial tumor volume). This process provided for consistent comparisons among treatment groups. PDT was performed at small tumor volume to ensure complete treatment of the entire tumor (light can penetrate 3 – 5 mm depth), providing the potential for a curative response. To treat larger tumor volumes to complete cures would require interstitial delivery of light. This process provided for consistent comparisons among treatment groups. Tumors were randomly assigned to various treatment groups. A Kaplan–Meier curve for LCR was generated based on a tumor volume ≤ 50 mm³ and stratefied based on three different dosimetric metrics (fluence, PDT dose, and [¹O₂]_rx). A tumor volume of 50 mm³ was chosen as the endpoint because this volume enabled clear discrimination of tumor recurrence from treatment-induced inflammation in the two week period after PDT over which this study was conducted.

Calculation of the reacted singlet oxygen and PDT dose during PDT

The longitudinal distribution of ϕ for the 1-cm diameter field was determined using a Monte-Carlo (MC) simulation for a known in-air fluence rate and individual mouse tissue optical properties (22). The mean mouse tissue optical properties for the group was: μ_a = 0.9 cm⁻¹ and μ′_s = 8.4 cm⁻¹, which if used to replace the actual tissue optical properties will introduce ~10 % error in ϕ at 3 mm depth among different mice in the population (22). To obtain the corresponding temporal changes of Photofrin concentration ([S₀]), oxygen concentration ([³O₂]), and [¹O₂]_rx, the ϕ distribution and the measured photosensitizer concentration were passed to the following time (t)-dependent differential equations for a given treatment time point:

$$\frac{d[S_0]}{dt}+\left(\xi \sigma \frac{\varphi ([S_0]+\delta )[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\right)[S_0]=0,$$ (1)

$$\frac{d[{{}^{3}O}_2]}{dt}+\left(\xi \frac{\varphi [S_0]}{[{{}^{3}O}_2]+\beta }\right)[{{}^{3}O}_2]-g\left(1-\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2](t=0)}\right)=0,$$ (2)

$$\frac{d{[{{}^{1}O}_2]}_{rx}}{dt}-\left(\xi \frac{\varphi [S_0][{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\right)=0.$$ (3)

The definition and value of the specific PDT photochemical parameters (ξ, σ, β, δ, and g) are listed in Table 1. Initial oxygenation concentration ([³O₂]₀) is assumed to be 40 μM (13, 24). All calculations were performed using MATLAB R2015b (Mathworks®, Natick, Massachusetts, United States). More details of the calculation can be found elsewhere (17, 22). [¹O₂]_rx is determined using Eq. 3 at a depth of z = 3 mm. The PDT dose at z = 3 mm is calculated as:

$$D(Z)=\underset{0}{\overset{T}{\int }}\varphi (z,t)[S_0](t)dt$$ (4)

Table 1.

Photofrin photochemical parameters used in the macroscopic kinetic equations.

Parameter	Definition	Value	References
ξ (cm2s−1mW−1)	Specific oxygen consumption rate	3.7 ×10−3	(34, 35, 17)
σ (μM−1)	Specific photobleaching ratio	7.6 ×10−5	(17, 34)
β (μM)	Oxygen quenching threshold concentration	11.9	(34)
δ (μM)	Low concentration correction	33	(36)
g (μM/s)	Macroscopic oxygen maximum perfusion rate	0.76	(17)
[3O2]0 (μM)	Initial ground-state oxygen concentration	40	(37, 13, 24, 38)

For simplicity, we use the term “fluence” to refer to “in-air fluence” as a dosimetry quantity, and “PDT dose” and [¹O₂]_rx refer to PDT dose and [¹O₂]_rx calculated at z = 3 mm tumor depth, respectively, in the text.

Statistical Analysis

The association of light fluence, PDT dose, and [¹O₂]_rx with treatment efficacy was evaluated by Kaplan-Meier and statistical analyses; LCR was considered as the treatment endpoint. The Kaplan-Meier curves for LCR based on each PDT dose metrics group (fluence, PDT dose, and [¹O₂]_rx) were compared with the use of log-rank test. To explore how well the three dose metrics predict LCR at 7 and 14 days, the logistic regression procedure (25) was used with the dose metrics as continuous predictors. The goodness-of-fit (predictive power) for the logistic regression models were quantified by the max-rescaled generalized R² statistic (25, 26), which can be interpreted as the proportion of variations in LCR that is predicted by each dose metric. The overall predictive power of the three dose metrics was analyzed by the Cox proportional hazard model (27) with dose metrics treated as continuous predictors. The Cox model characterizes how well the dose metrics predict LCR over time from day 1 to day 14. The overall predictive power of the three dose metrics was also assessed by the max-rescaled generalized R² statistic of the corresponding Cox models. The marginal predictive powers of the three dose metrics were investigated by using each metric as the only predictor. We then estimated the multivariate associations by involving more than one dose metric into the Cox model. We tested the significance of one dose metric by controlling one or two other dose metrics, with the use of the Wald chi-square test. We also tested whether the survival probability could be better predicted by adding one or more dose metrics, based on the likelihood ratio tests. The analysis was conducted with the use of SAS software (version 9.4), and all p-values were two-sided. For the analyses p<0.05 level (95% confidence level) was considered statistically significant.

RESULTS

With the same Photofrin injected dose of 5 mg/kg, the uptake of Photofrin in tumors varied widely from 0.95 to 10.53 μM (3.54 μM median value). Mice that received a dose of 15 mg/kg Photofrin had tumors levels of Photofrin that ranged from 2.12 to 12.62 μM (7.08 μM median value). Variation of this magnitude is seen in the intraperitoneal tumors of human patients as well (28). Animals were assigned to four light fluence groups, and each group was comprised of 2–3 subgroups with different ϕ. Tables 2, 3, and 4 summarize the results when the mice were stratified by fluence, PDT dose, and [¹O₂]_rx, respectively.

Table 2.

In-air light fluence and in-air light fluence rate conditions used in each PDT treatment group.

Index	Fluence (J/cm2)	ϕair (mW/cm2)	PDT dose (μM J/cm2)	Photofrin (μM)	Photofrin variation† (μM)	[1O2]rx (mM)	[1O2]rx variation† (mM)	Variation count†
1	50	50	126.5	3.5	-	0.35	-	0 / 4
2		75	235.5	6.0	-	0.40	-	0 / 5
3		150	199.9	4.9	-	0.24	-	0 / 4
4	135	50	229.7	3.0	2.52 / 4.33*	0.66	0.45/0.91#	1 / 4
5		75	774.2	7.8	3.08 / 12.1*	0.93	0.27/1.25#	10 / 12
6		150	322.3	3.5	-	0.53	-	0 / 4
7	200	50	204.8	2.2	-	0.63	-	0 / 5
8		150	417.8	3.8	-	0.76	-	0 / 5
9	250	50	362.1	3.4	3.17 / 3.66*	1.03	0.97 / 1.09#	3 / 4
10		75	1380.1	5.8	1.88 / 12.6*	0.74	0.65 / 1.32#	8 / 10
11		150	393.0	3.1	2.45 / 5.32*	0.81	0.69 / 1.04#	2 / 9
	Control	0	0	0	-	0	-	0 / 8

^*Photofrin concentration in tumors with complete and partial response is significantly different, p<0.05.

^#[¹O₂]_rx concentration tumors with complete and partial response is significantly different, p<0.05

^†Variation is shown for (tumors with complete response) / (total number of tumors) at 14 days.

Table 3.

The amounts of PDT dose calculated for each PDT treatment condition.

PDT dose	[1O2]rx (mM)	In-air Fluence (J/cm2)	ϕair (mW/cm2)	Photofrin (μM)	Mice number
1200 μM J/cm2 < PDT dose	1.3-2-2	250	75	9.9–12.6	3
800<PDT dose≤1200 μM J/cm2	0.3–1.3	135	75	7.2–12.1	6
	1.3–1.8	250	75	5.3–7.0	2
400<PDT dose≤800 μM J/cm2	0.6–1.02	135	75	5.5–6.7	5
	0.8	200	150	4.7–4.9	2
	1.2–1.4	250	50	1.9–4.1	2
	0.9–1.09	250	150	3.3–6.9	5
PDT dose≤400 μM J/cm2	0.3–0.4	50	50	2.8–4.9	4
	0.4	50	75	4.3–7.5	5
	0.2–0.3	50	150	2.9–8.8	4
	0.5–0.9	135	50	2.0–4.3	4
	0.7	135	75	3.1	1
	0.5–0.6	135	150	3.0–3.8	4
	0.3–1.0	200	50	1.0–3.7	5
	0.6–0.75	200	150	2.7–3.5	3
	0.6–1.0	250	50	3.9–4.9	2
	0.6–0.8	250	75	1.9–2.7	5
	0.3–0.6	250	150	1.0–2.0	4

Table 4.

The amounts of reacted singlet oxygen concentration calculated for each PDT treatment condition.

[1O2]rx	PDT dose (μM J/cm2)	In-air Fluence (J/cm2)	ϕair (mW/cm2)	Photofrin (μM)	Mice number
1.1 mM≤[1O2]rx	977–1148	135	75	10.1–12.1	4
	418–530	250	50	1.9–4.1	2
	1555–1998	250	75	5.3–12.6	5
0.734≤[1O2]rx<1.1mM	324	135	50	4.3	1
	487–1029	135	75	5.5–7.2	5
	148–278	200	50	1.6–3.0	2
	390–579	200	150	3.5–4.9	3
	354	250	50	4.9	1
	254–308	250	75	2.4–2.7	3
	410–611	250	150	3.3–6.9	5
0.367≤[1O2]rx<0.734mM	166	50	50	0.4	1
	210–302	50	75	5.3–7.5	4
	155–239	135	50	2.0–3.0	3
	256–688	135	75	3.1–6.7	2
	262–358	135	150	2.9–3.8	4
	165–346	200	50	1.8–3.7	2
	276–309	200	150	2.7–2.9	2
	197	250	50	3.9	1
	199–332	250	75	1.9–2.1	2
	174–227	250	150	1.5–2.0	3
[1O2]rx<0.367mM	106–122	50	50	2.8–3.2	3
	165	50	75	4.3	1
	114–366	50	150	2.9–8.8	4
	974	135	75	9.1	1
	94	200	50	1.0	1
	101	250	150	1.0	1

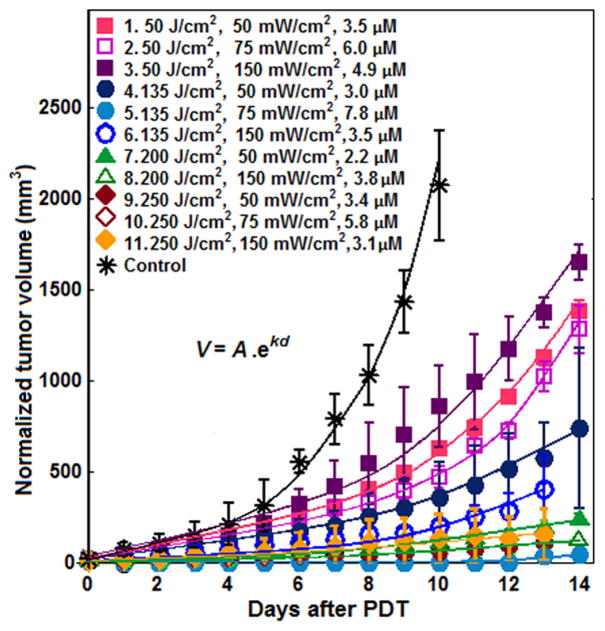
The raw tumor regrowth data for each PDT treatment and control group was fitted to an exponential function (V₀e^−kd) and then normalized to the mean intial mean volume, 23 mm³. The normalized regrowth data by multiplying all data by 23/V₀ are shown in Fig. 1.

Figure 1.

Exponential fitting of the normalized tumor volume over time after PDT. The index in the legend corresponds to that in Table 2. This figure has been modified from Ref. (22) with additional data.

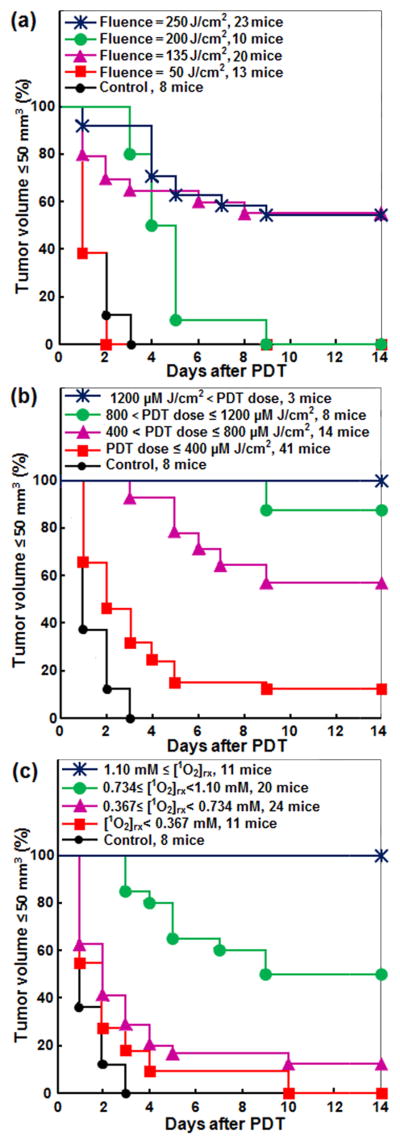
The association of light fluence, PDT dose, and [¹O₂]_rx, with treatment efficacy was evaluated by Kaplan-Meier analyses; LCR was considered as the treatment endpoint. As shown in Fig. 2(a), fluence was the poorest among these three metrics. Tumor control improved with a light fluence of 135, 250, 200 and 50 J/cm², in that order. Thus, light fluence did not well correlate with outcome. Figures 1(b) and 1(c) show the relationship of PDT dose and [¹O₂]_rx with tumor response; the mice were grouped into four ranges of calculated PDT dose and [¹O₂]_rx. As shown in these figures, LCR increased with an increase in PDT dose and [¹O₂]_rx. The log-rank tests showed significant differences among the stratified Kaplan-Meier curves for all dose metrics in Fig. 2, see statistics analysis summarized in Table 5.

Figure 2.

The impact of a) fluence, b) PDT dose at 3 mm tumor depth, and c) reacted singlet oxygen ([¹O₂]_rx) at 3 mm tumor depth on Kaplan-Meier curves of tumor local control rate (LCR) after Photofrin-mediated PDT. A normalized tumor volume ≤ 50 mm³ was used as the endpoint. The solid dark blue line with star symbols in (b) and (c) corresponds to the complete control of tumors.

Table 5.

Marginal and Multivariate Cox models (treating Fluence, PDT dose, and [¹O₂]_rx as continuous variables).

	DF	Estimated Coefficients			Adjusted R-square	Likelihood Ratio Tests
		Fluence	PDT dose	[1O2]rx		Null	F	P	O	F + P	F + O	P + O
Marginal models
1. Fluence	1	0.0084			24.14%	20.33
p-value		<.0001				<.0001
2. PDT dose	1		0.0041		42.95%	41.26
p-value			<.0001			<.0001
3. 1O2	1			2.8788	49.19%	49.76
p-value				<.0001		<.0001
Multivariate models
4. F + P	2	0.0044	0.0033		47.12%	46.83	26.50	5.57
p-value		.0019	.0008			<.0001	<.0001	.0183
5. F + O	2	0.0001		2.8874	49.19%	49.76	29.43		<0.01
p-value		.9824		<.0001		<.0001	<.0001		0.9822
6. P + O	2		0.0015	2.2747	51.84%	53.68		12.42	3.92
p-value			.0805	<.0001		<.0001		.0004	.0477
7. F + P + O	3	0.0006	0.0015	2.1459	51.88%	53.75	33.42	12.49	3.99	6.92	3.99	0.07
p-value		.7936	.0798	.0056		<.0001	<.0001	.0019	.1360	.0085	.0458	.7913

DF: degree of freedom; Null: the null model with no factors; F: model 1, Fluence; P: model 2, PDT dose; O: model 3, [¹O₂]_rx; F + P: model 4, Fluence + PDT; F + O: model 5, Fluence + [¹O₂]_rx; P + O: model 6, PDT dose + [¹O₂]_rx; F + P + O: model 7, Fluence + PDT dose + [¹O₂]_rx. Likelihood ratio tests compare the multivariate models to the models with the same but fewer factors. A small p-value means the model with more factors is significantly better than the model with fewer factors.

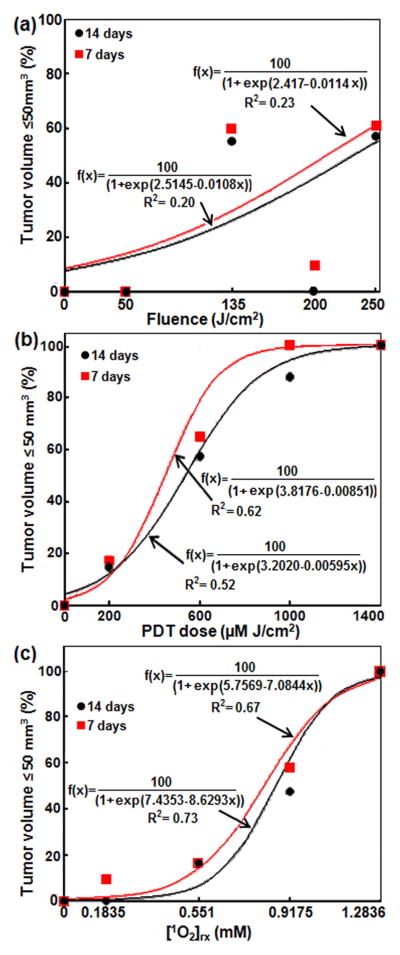
The LCR at 7 and 14 days were further plotted by grouping the three dose metrics into 5 or 6 groups in Fig. 3 to show the predictive power of each dosimetric quantity. The solid lines were fits to the data using a sigmoid curve (y = 100 / (1 + exp (b - c x))).

Figure 3.

Tumor local control rate (LCR) at 7 and 14 days versus (a) light fluence, (b) PDT dose at 3 mm tumor depth, (c) [¹O₂]_rx at 3 mm tumor depth. The solid lines are the sigmoid function (y=100/(1+ exp(b-cx)) for (b) and (c) fits, the resulting goodness of fits are R² = 0.20 (0.33), 0.52 (0.68), 0.72 (0.72) for light fluence, PDT dose at 3 mm, and [¹O₂]_rx at 3 mm for LCR at 14 (7) days, respectively.

DISCUSSION

The variation of the initial tumor volumes (12–55 mm³) between different tumors within the same treatment condition could introduce variations on local tumor control. This can be caused by tumor growth rate difference or can be caused by the variation of the starting date for PDT treatment for each mouse. To minimize these effects, we have fitted the tumor growth for each PDT treatment group of mice to an exponential fucntion (V₀e^−kd) and then normalized the initial tumor volume to the mean initial tumor volume (23 mm³) as shown in Fig. 1.

Based on a series of light fluences and ϕ, the effectiveness of Photofrin-mediated PDT on tumor LCR was investigated. Kaplan–Meier curves for LCR were chosen to assess Photofrin-mediated PDT treatment outcome because each dosimetrical condition exhibits a probability of treatment outcome, unlike what was found for some other photosensitizers where a more definitive outcome is observed (29). The Kaplan-Meier curves for Photofrin-mediated PDT found large variations in treatment response when mice were separated based on light fluence (Figs. 2a and 3a), which is a clear indication that light fluence alone is not predictive of PDT outcome. This conclusion is in agreement with that reported by others (8). However, some correlation between fluence and tumor response would likely emerge if the fluence range were increased. As indicated previously, PDT dose was better correlated to LCR than fluence (8). The correlation of [¹O₂]_rx with LCR indicated that when [¹O₂]_rx ≥ 1.1 mM, tumors exhibited a complete response (defined as a normalized tumor volume of ≤ 50 mm³ at 14 days after PDT). Two different administered doses of Photofrin were used in order to produce a range in the calculated PDT dose. In Figs. 1 (a) and 2(a), the LCR was better after treatment at fluence 135 J/cm² and fluence rate 75 mW/cm² compared to 200 J/cm², 50 and 150 mW/cm². This can be explained by greater photosensitizing drug uptake in the mice that went on to be treated at 135 J/cm² and 75 mW/cm², compared to those who were treated at 200 J/cm², 50 and 150 mW/cm², specifically the photosensitizer uptake happened to be 3 and 2 times higher than the other sets of experiments (see Tables 2–4). It is also in general 3 times higher than the average uptake of the entire mice.

The Cox proportional hazard models were fitted to quantify the overall predictive power of the three dose metrics by treating the dose metrics as continuous predictors of LCR over the whole time interval from day 1 to day 14. The results are shown in Table 5. Light fluence explained 24% of the variations in LCR over the whole time interval (R² = 0.2414). PDT dose explained 43% of the variations in LCR over the whole time interval (R² = 0.4295). [¹O₂]_rx explained 49% of the variations in LCR over the whole time interval (R² = 0.4919). These results indicate that, as a predictor of treatment outcome, [¹O₂]_rx is better correlated with tumor response than PDT dose, and PDT dose is better correlated with tumor response than is the fluence. The [¹O₂]_rx and the PDT dose are associated with less subject-to-subject variation in response. In multivariate models, the model combining fluence and PDT dose significantly outperforms the marginal models of the two dose metrics (p < 0.0001 for fluence and p = 0.0183 for PDT dose). Fluence is still a significant predictor (p = 0.0019) after controlling PDT dose. The model combining fluence and [¹O₂]_rx significantly outperforms the marginal model of fluence (p < 0.0001); but it is not significantly better than the marginal model of [¹O₂]_rx (p = 0.9822). Fluence is no longer a significant predictor (p = 0.9824) after controlling [¹O₂]_rx. The R² value of the model containing both fluence and [¹O₂]_rx is virtually the same as the marginal model of [¹O₂]_rx, which means light fluence adds no value to the prediction of survival probability if [¹O₂]_rx is given. The model combining PDT dose and [¹O₂]_rx significantly outperforms the marginal models of the two dose metrics (p = 0.0004 for PDT dose and p = 0.0477 for [¹O₂]_rx. But PDT dose is no longer a significant predictor (p = 0.0805) after controlling [¹O₂]_rx. The full model that contains all three dose metrics is significantly better than all the models without [¹O₂]_rx; but it is not significantly better than the marginal model of [¹O₂]_rx (p = 0.1360) or the bivariate model containing both PDT dose and [¹O₂]_rx (p = 0.7913). In the full model, fluence (p = 0.7936) and PDT dose (p = 0.0798) are not significant predictors after controlling [¹O₂]_rx (p = 0.0056).

The threshold value of PDT dose for achieving complete tumor control was 1200 μM J/cm² for Photofrin. This value is equivalent to 4.2 J/cm³ absorbed dose, calculated by multiplying the threshold value by the extinction coefficient of Photofrin. An absorbed dose of 4.2 J/cm³ for Photofrin is reasonably in agreement with 5.7, and 4.1 J/cm³ absorbed dose by 2-(1-Hexyloxyethyl)-2-devinylpyropheophorbide (HPPH) (30) and benzoporphyrin derivative monoacid ring A (BPD) (31), respectively (see Table 6). These values correspond to 13.4×10¹⁸, 19×10¹⁸, and 14.3×10¹⁸ photons/cm³ (calculated by dividing by the energy per photon) for Photofrin, HPPH and BPD, respectively. The PDT dose threshold behavior for our current results is larger than the 3.4×10¹⁸ photons/cm³ reported by others for Photofrin in vitro (32, 33). Although PDT dose accounts for both light fluence and tissue Photofrin level, it does not account for the oxygen dependence of singlet oxygen quantum yield and thus overestimates the production of [¹O₂]_rx in hypoxic conditions.

Table 6.

PDT dose and [¹O₂]_rx threshold for Photofrin, 2-(1-Hexyloxyethyl)-2- devinylpyropheophorbide (HPPH) (30) and benzoporphyrin derivative monoacid ring A (BPD) (31) photosensitizers.

Photosensitizers	ε† (μM−1cm−1)	λ‡ (nm)	PDT dose threshold (μM J cm−2)	Photosensitizer absorbed dose		[1O2]rx (mM)	Refs.
				(J/cm3)	(Photons/cm3)
Photofrin	0.0035	630	1200	4.2	13.4×1018	1.1	This study
HPPH	0.108	665	52.62	5.7	19 ×1018	1.2	(30)
BPD	0.078	690	52.94	4.1	14.3 ×1018	1.15	(31)

^†Extinction coefficient of the photosensitizer

^‡Wavelength of the excitation light

We also demonstrated that the threshold dose of [¹O₂]_rx to achieve complete tumor control was 1.1 mM for Photofrin. This value is comparable to the threshold of 1.2 mM and 1.15 mM to achieve tumor control for HPPH-PDT(30) and BPD-PDT (31), respectively (see Table 4). Our previous studies demonstrated that the threshold dose of [¹O₂]_rx to produce necrosis in the RIF tumor model was about 0.74 ± 0.25 mM for Photofrin-mediated PDT, 0.6 ± 0.1 for HPPH-mediated PDT (17, 13), 0.67 ± 0.13 for BPD-mediated PDT (29). However, it is likely that the mean values of [¹O₂]_rx for producing tumor cure is larger than that needed to induce tumor necrosis. These results show that mean [¹O₂]_rx at a 3 mm tumor depth is a good dosimetric quantity that combines the explicit dosimetry of light fluence and photosensitizer concentration, along with model calculation (Eqs. 1–3) of oxygen consumption during PDT.

The LCR at 7 and 14 days were further correlated with the three dose metrics in Fig. 3 to show the predictive power of each dosimetric quantity. Logistic regression models were fitted to LCR at 7 and 14 days with the three dose metrics as continuous predictors. Light fluence explained 23% of the variations in LCR at 7 days (R² = 0.2260) and 20% of the variations in LCR at 14 days (R² = 0.1976). PDT dose explained 62% of the variations in LCR at 7 days (R² = 0.6156) and 52% of the variations in LCR at 14 days (R² = 0.5210). [¹O₂]_rx explained 67% of the variations in LCR at 7 days (R² = 0.6666) and 73% of the variations in LCR at 14 days (R² = 0.7259). Based on the statistics analyses, the light fluence is not predictive of LCR (see Fig. 3a), while PDT dose (see Fig. 3b) and [¹O₂]_rx (see Fig. 3c) are correlated with LCR at both 7 days and 14 days; the two track each other very well. In comparisons of PDT dose and [¹O₂]_rx as dose metrics, [¹O₂]_rx predicts complete response at 14 days (R² = 0.7259) better than PDT dose (R² = 0.5210). When [¹O₂]_rx also is used as a dose metric, smaller light fluences are required to produce a tumor response than when PDT dose is used (for equivalent photosensitizer uptake) (see Tables 3 and 4).

One limitation of the current study is that the [¹O₂]_rx is calculated using Eqs. 1–3 rather than based on the actual measured tissue oxygen concentration during PDT. We anticipate improved prediction of LCR if the ³O₂ concentration variation during PDT can be incorporated directly into the [¹O₂]_rx determination.

CONCLUSIONS

The predictive ability of fluence, PDT dose, and [¹O₂]_rx as dosimetric quantities was evaluated by analyzing their relationships with LCR. Based on the outcomes of this study, [¹O₂]_rx is better than PDT dose, which in turn is better than light fluence, in predicting tumor control for Photofrin-mediated PDT. In addition, PDT dose requires a higher fluence than that predicted by [¹O₂]_rx for the same photosensitizer uptake to achieve a complete tumor response.

This preclinical study examines light fluence, PDT dose, and “apparent reacted singlet oxygen”, [¹O₂]_rx, to predict local control rate (LCR) for Photofrin-mediated photodynamic therapy (PDT) of radiation-induced fibrosarcoma (RIF) tumors. LCR was stratified for different dose metrics for 74 mice (66+8 control). Complete tumor control at 14 days was observed for [¹O₂]_rx ≥ 1.1mM or PDT dose ≥ 1200μMJ/cm² but cannot be predicted with fluence alone. LCR increases with increasing [¹O₂]_rx and PDT dose but is not well correlated with fluence. Comparing dosimetric quantities, [¹O₂]_rx outperformed both PDT dose and fluence in predicting tumor response and correlating with LCR.