Atomistic simulation of the growth of defect-free carbon nanotubes

The atomistic simulation of defect-free SWCNT growth is realized for the first time after 12 years of continuous effort.

Abstract

Atomistic simulation of defect-free single-walled carbon nanotube (SWCNT) growth is essential for the insightful understanding of the SWCNT's growth mechanism. Despite the extensive effort paid in the past two decades, the goal has not been completely achieved, due to the huge timescale discrepancy between atomistic simulation and the experimental synthesis of SWCNTs, as well as the lack of an accurate classical potential energy surface for large scale simulation. Here, we report atomistic simulations of defect-free SWCNT growth by using a new generation of carbon–metal potential and a hybrid method, in which a basin-hopping strategy is applied to facilitate the defect healing during the simulation. The simulations reveal a narrow diameter distribution and an even chiral angle distribution of the growth of SWCNTs from liquid catalyst, which is in agreement with most known experimental observations.

1. Introduction

Carbon nanotubes (CNTs) are promising for many potential applications, attributed to their unique cylindrical arrangement of the C atoms, and the consequently outstanding mechanical,^1,2 thermal, chemical, optical, and electronic properties.^3–6 Especially, single walled CNTs (SWCNTs) are considered as one of the most promising materials for large scale electronic circuits to replace silicon in the future.⁷ Thus, controllable syntheses of the desired semi-conductive SWCNTs, which are characterized by a pair of chiral indexes (n, m), are essential for many of these applications, such as for the synthesis of high performance electronic devices with a well-defined band-gap. However, due to the limited understanding of the CNT's growth mechanism, controllable syntheses of SWCNTs with desired structures have not been completely achieved, even after more than 20 years since the discovery of CNTs.⁸

In order to understand the CNT's growth mechanism, many theoretical studies have been dedicated to explore both the nucleation and the growth of SWCNTs on a catalyst particle surface.^9–15 Among them, atomistic simulations, including both molecular dynamic (MD) and basin-hopping (BH)^16,17 simulations, as well as their hybridizations,^18–20 have been broadly used. Various research groups have used empirical force fields (FFs),^21–32 density functional based tight binding (DFTB) approaches,^33–41 or density functional theory (DFT) based MDs to simulate the CNT growth.^42,43 Although great progresses have been achieved in the last decade, it is very difficult to grow a perfect SWCNT with atomistic simulations. Such difficulty may be attributed to: (i) the lack of high accuracy of the potential energy surface (PES), especially for the catalyst–carbon interactions in FFs; and/or (ii) the limited timescale of the atomistic simulations (i.e. from ps to ns), especially for the DFT based simulations. The DFT, DFTB, and FF based MD simulations can typically explore the real time evolution of CNT growth of a few ps, 100 ps and 10 ns, respectively, and FF can explore much larger model systems than the former two. On the other hand, the experimental timescale of CNT synthesis ranges from seconds to hours, which is 10⁹–10¹⁵ times longer than the affordable simulation timescales. Thus, it is a great challenge to bridge such a huge time gap, and a multi-scaled simulation methodology is necessary in order to simulate the growth of defect-free SWCNTs with well-defined chiralities.

In this study, we present an atomistic simulation of SWCNT growth on a nickel (Ni) cluster catalyst. To address the aforementioned difficulties, the C–Ni interactions were carefully fitted against DFT calculations, and a hybrid MD–BH multi-scaled strategy was adopted to actively heal the defects during the growth of SWCNTs. With these efforts, as well as exploring the optimized conditions of simulation, defect-free SWCNTs are successfully simulated for the first time, according to the authors' best knowledge. Based on the above efforts, the chiralities of the simulated SWCNTs were completely distinguished and assigned. In agreement with most known experiments, the simulated SWCNTs from a liquid catalyst particle clearly show diameter selection, but with an even chiral angle distribution from armchair to zigzag.^44–47

2. Computational details

Based on our previous studies,^{13,24,28–30,32} by carefully considering the C–Ni interactions under various environments (such as C clusters, including monomer, dimer, C chains of different lengths, and sp² hybridized graphitic islands on Ni surfaces; the dissolved C atom, the C dimer inside the Ni catalyst; the tilt angle dependent graphene edge–catalyst interaction, etc.), we fitted a large set of data basis calculated by the DFT method, and developed a new generation of C–Ni reactive empirical bond order (REBO) potential with 26 parameters (see ESI† for details). The tests with the newly developed PES successfully reproduced the correct stability order of various C clusters on a Ni (111) surface, and thus validated the accuracy of the PES. Such empirical PES allows us to simulate a relatively longer time (up to 10–100 ns) and a reasonably large system (up to 1000 atoms) in a reasonable CPU time (∼100–1000 CPU × hour for each trajectory of the SWCNT growth simulation).

Potential energy surface (PES)

A Ni particle is used as the catalyst in the simulation of the growth of SWCNTs, and the empirical PES of the model systems can be classified into the following three sections: (1) C–C interactions; (2) C–Ni interactions; and (3) Ni–Ni interactions. For the sake of simplicity, we just introduce the main characteristics of this newly developed PES, with the detailed descriptions and validations in the ESI.†

(1) The C–C interaction is based on the REBO2 potential⁴⁸ with modifications at the metal interface. To address the nature of C–metal interaction, the important screening effect on the C–C bond, which was firstly introduced by Martinez-Limia et al.,²² was considered. If a C–C bond is surrounded by metal atoms, it would be greatly weakened. The more the metal coordinates, the weaker the C–C bond. A parameter for the bond order for the coordinated Ni atoms around the C–C bond is adopted to modulate the C–C bond strength in different environments, in order to distinguish between C atoms far away from the Ni particle, C atoms on the Ni particle, and C atoms in the Ni particle.

(2) A variation of the REBO potential, motivated by the equations proposed by previous studies^22,29,49 is fitted against C–Ni interactions by DFT calculations. The key point of this newly developed C–Ni potential is that more detailed local environments have been included. A parameter is defined to modulate the C–Ni interactions according to the types of C atoms (e.g. C mono, C dimer, C chain, armchair C edge, zigzag C edge, and C wall, etc.) and the metal coordinates. Another parameter is employed to ensure that the edge atoms of graphene ribbon tend to stand perpendicularly on the Ni surface, according to recent DFT studies.^50,51 To take such an effect into account, we add an angle-dependent term into the C–Ni interaction, which calibrates the formation energies of the test structures to approach that calculated by DFT reasonably well, as shown in the ESI.†

(3) The Ni–Ni interaction of the metal cluster is modeled by the Sutton–Chen many-body potential,^52,53 which was demonstrated to model the Ni particle successfully.

Basin-hopping (BH) defects-healing strategy

Instead of overriding the energy barriers between the local energy minima via brute force MD simulation, the system finds the local energy minima by hopping between the basins in the PES randomly, and the acceptance (or rejection) of the new structure is determined by Metropolis criterion.⁵⁴ In our system, the trial move is operated by a random 90° rotation of an arbitrary sp² C–C bond on the C–Ni interfacial region, called Stone–Wales (SW) transformation,⁵⁵ through which the system tends to transform from a structure with higher energy to the one of local minimum in the PES. During this process, the topological defects produced near the open end of the tube, which raises the system energy, can be healed toward the lower energy structure. This method has already been successfully applied to simulate the coalescence of the encapsulated fullerenes constrained by an outer carbon nanotube. In the coalescence process, defects formed in the neck location of two fusing fullerenes can be healed efficiently, and a perfect inner tube is synthesized finally. Such a process is well known as the “peapod-derived double walled carbon nanotube”.^56,57

Hybridized molecular dynamic and basin-hopping (H-MD–BH) simulation

In the atomistic simulation, MD simulation is initialized with a bare Ni catalyst particle. The system was coupled to a Berendsen thermostat,⁵⁸ which is maintained at a temperature of 1300 K. Each MD step ran for 30 ps (for smaller catalyst particles Ni₁₉ and Ni₃₂) and 45 ps (for the larger catalyst particle Ni₅₅) at a time step of 0.5 fs. After each MD step, one C atom was added to the surface of the Ni particle, which mimicks the bare C atoms on the catalyst surface decomposed from the feedstock. After 30 C atoms were added, an alternative MD–BH strategy started to work at a temperature of 1300 K. The BH was carried out after every two atoms were added, corresponding to time intervals of 60 ps for smaller catalyst particles Ni₁₉ and Ni₃₂ and 90 ps for the larger catalyst particle Ni₅₅. To ensure that each C–C bond had the chance to be trial rotated, the number of trial moves was set to be 10 times the number of the total C–C bonds during SWCNT growth.

Definition of the chirality and chiral angle

Since the defect-free SWCNT can be simulated with the H-MD–BH method, the chirality of each SWCNT can be identified by counting the armchair and zigzag sites of the cutting edge of the SWCNT. The chiral angle θ is calculated by

θ = tan^–1(√3 × m/(2n + m)) 1

in which (n, m) is the chirality index of the SWCNT. In this work, the right and left handednesses are not distinguished. Therefore, the chiral angle of (m, n) is equivalent to the one of (n, m) within 0°–30°.

3. Results and discussion

Growth of defect-free SWCNTs

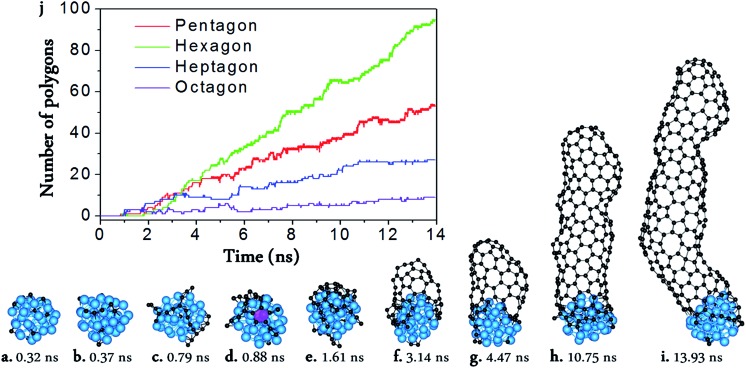
From Fig. 1, we can see the newly developed potential is capable of simulating the nucleation and growth of SWCNTs with fairly good quality, and comparable with those simulated by using higher level PESs such as TB,^16,17 DFTB,^33–41,59 or DFT^42,43 (Fig. 1a–i). On the other hand, it is notable that there are still many topological defects in the simulated SWCNT wall (Fig. 1j). This is expected because the defect healing at the SWCNT–catalyst interface needs to overcome a barrier of E _b ∼ 2.0–2.5 eV,⁶⁰ and thus the timescale for such an event to occur is estimated to be⁶⁰

τ ∼ 10^–13 × exp(E_b/kT) ∼ 10²–10⁴ μs 2

in which 10^–13 s^–1 is the attempt frequency, k is the Boltzmann constant, and T = 1300 K is a typical temperature of SWCNT growth. Based on eqn (2), a timescale from ms to s is required to simulate a perfect SWCNT with 100 polygons, which is 6–9 orders of magnitude longer than the affordable timescale of the current MD simulation. Therefore, a multi-scaled approach is necessary to simulate the growth of perfect SWCNTs.

Fig. 1. Molecular dynamic (MD) simulation of SWCNT growth from a Ni₃₂ catalyst surface. (a–i) Snapshots taken from the MD trajectory. (j) The numbers of the pentagons, hexagons, heptagons, and octagons vs. MD simulation time. The pink polygon in (d) is the pentagon which firstly appeared in the MD simulation.

In order to bridge such a huge gap between the affordable timescale of the MD simulation and that of the experimental SWCNT growth, we introduced a basin-hopping (BH) strategy to expedite the defect healing during the MD simulation.⁵⁴ Such a strategy allows the rotation of a randomly selected C–C bond at the CNT–catalyst interface and accepts the trial moves with the probability of

P = 1, if ΔE < 0 3-1

P = exp(–ΔE/kT), if ΔE > 0 3-2

where ΔE is the energy difference between the relaxed initial and final configurations and T is the temperature of the simulation (see methods and Fig. S1 in the ESI† for details). Such a strategy allows the system to be annealed to the configuration with a low SWCNT–catalyst interface formation energy. Because there is no information about the chiral structure of the SWCNT involved in the BH process and a low energy structure has a high probability of reaching that which should occur naturally, such a defect healing step is not expected to artificially bias the chirality distribution of the simulated SWCNTs, as evidenced in previous studies.^56,57,61

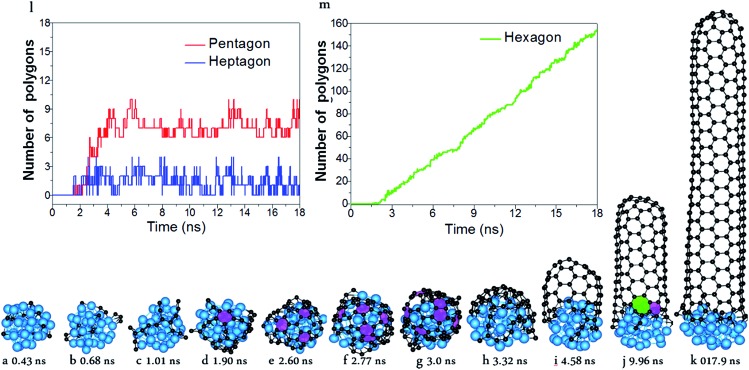
With the carefully parameterized PES and the hybrid atomistic simulation method, under the optimal conditions of simulation, the simulation of perfect SWCNT growth is possible. Fig. 2a–k show the snapshots taken from a H-MD–BH trajectory of the SWCNT growth simulation at a temperature of 1300 K. The Ni catalyst particle is a free standing Ni₃₂ in the liquid state, as can be evidenced by its shape variation. As described in the previous section, the H-MD–BH simulation starts with a MD simulation of a bare Ni₃₂ cluster, and C atoms are gradually added to the catalyst surface at the rate of 30 ps per atom, up to 30 C atoms. After which, the BH sampling of a stable SWCNT-catalyst interfacial configuration is performed by the addition of every 2 C atoms. The H-MD–BH simulation on the Ni₃₂ in Fig. 2 demonstrates the typical steps of SWCNT growth found in this study: i.e. (i) C atoms on the catalyst surface aggregate into dimers, trimers, and short C chains (Fig. 2a–c); (ii) C chains form small graphitic islands with one or several polygons (e.g. pentagons and hexagons, cf. Fig. 2d–f); (iii) small graphitic islands lift off the catalyst surface to form a cap on the catalyst surface (Fig. 2g and h); (iv) the graphitic cap grows to the diameter of the catalyst and becomes a short SWCNT (Fig. 2i); and (v) the short SWCNT grows longer and longer by incorporating more and more C atoms at the interface between its opening edge and the catalyst surface (Fig. 2j and k). Steps (i)–(iv) are nearly exactly the same as those shown in the MD simulations (Fig. 1a–g), while the elongation of a defect-free SWCNT in step (v) is achieved in this study only to our best knowledge. As can be clearly seen in Fig. 2i–k, all the polygons in the 4.5 nm long SWCNT are hexagons, and the wall has a pair of well defined chiral indexes of (6, 5).

Fig. 2. Simulated growth of a defect-free SWCNT by the multi-scaled H-MD–BH approach. (a–k) Snapshots taken during the simulation. (l) The numbers of pentagons and heptagons vs. simulation time. (m) The number of hexagons vs. simulation time. The pink and green polygons denote the pentagons and heptagon, respectively.

According to Euler's theorem, the cap of a SWCNT contains six pentagons exactly.⁶² Such a rule can be clearly seen in Fig. 2l, in which the number of pentagons varies from 6 to 9 and the number of heptagons varies from 0 to 3. As there is no pentagon or heptagon in the defect-free SWCNT wall, the pentagons and heptagons can only be formed near the edge of the SWCNT during the continuous addition of the C atoms to the Ni₃₂ cluster (Fig. 2i–k). During the H-MD–BH simulation, they are quickly healed because of their low stability, thanks to the BH process.

Defect healing

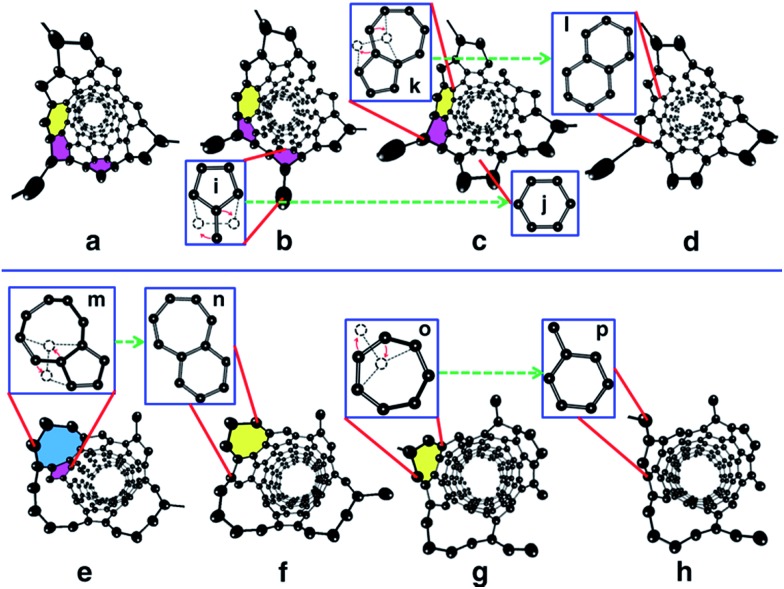
As comparing Fig. 1 and 2, it is obvious that efficient defect healing is crucial to achieve high quality SWCNTs in atomistic simulations. Previous studies have shown that the ring isomerization (or ring reconstruction), akin to the stepwise SW transformations in most cases, plays a significant role in healing the topological defects, e.g. pairs of pentagons and heptagons (5|7), octagons, etc. ^19,59,63 In the current H-MD–BH simulation, we found that the defects can be healed via either the MD simulation or the BH process. As shown in Fig. S9 in the ESI,† there are two typical cases for the healing of a pentagon during the MD simulation: (i) the breaking and reconnecting of C–C bonds via the attached dangling C atom; and (ii) direct insertion of a diffusing C atom to the pentagon. For case (i), the ring reconstruction plays a significant role in the defect healing, which is indeed equivalent to a SW transformation. Similarly, a heptagon can also be healed by bond reconstruction via an attached dangling C atom (Fig. S10 in the ESI†).

Fig. 3 shows the detailed atomistic process of typical defect healing during the H-MD–BH simulation of a (6, 5) SWCNT. It can be clearly seen that topological defects, such as pentagons, heptagons, octagons, and their pairs are frequently formed during the MD simulation when new C atoms are attached to the edge of the growing SWCNT's open end. A pentagon can be turned into a hexagon after a dangling C atom is attached to it (Fig. 3b and c); a heptagon can be transformed into a hexagon and a dangling atom (Fig. 3g and h); a pentagon and heptagon pair (5|7) can be healed by rotating a C–C bond on the outer shoulder of the heptagon (Fig. 3c and d); other large scale defects, such as octagons, can be healed by a few steps of bond rotations in the BH process. Through these typical healing processes, all the defects formed during the addition of C atoms are eventually healed, and a defect-free SWCNT wall with all hexagons is obtained with well-defined chirality.

Fig. 3. Atomistic process of the defect healing process observed in the H-MD–BH simulation. In the perspective view of the open end of the simulated SWCNT, the Ni₃₂ catalyst particle is removed for clarity. (a) A pentagon (pink) and 5|7 pair were produced during the incorporation of C atoms. (b) A dangling C atom was attached to the pentagon. The pentagons and heptagons (yellow) were healed during the BH processes shown in (c) and (d), respectively, with details illustrated as i → j and k → l. (e) A pentagon and octagon (blue) are formed during the MD simulation. The pentagon was healed by a C–C bond rotation and the adjacent octagon was consequently transformed into a heptagon, as shown in (f). The details are illustrated as (m → n). The left heptagon was turned into a hexagon by rotating a C–C bond (g → h) with the details shown as o → p.

We next consider the physical feasibility of the bond rotation at the SWCNT–catalyst interface during the BH process. It is well known that the energy barrier of rotating a C–C bond inside an sp² carbon network is E* = 5–9 eV.^64–67 On the other hand, for the defects at the edge of the SWCNT open end that attaches to the catalyst surface, E* is greatly reduced to 2.0–2.5 eV.⁶⁰ As estimated in eqn (2), the timescale for the defect healing is 10²–10⁴ μs, which is consistent with the SWCNT's growing rate of 100 μm s^–1 or 10^–4 nm ns^–1 achieved experimentally.⁶⁸ Therefore, instant defect healing at the SWCNT–catalyst interface during real SWCNT growth is feasible experimentally, and such healing is mimicked by the BH process, though not feasible for pure MD simulations at the current computational power. It is important to note that the defect healing procedure observed in the simulation is very similar to that explored in previous DFT studies,⁶⁰ which demonstrated that the healing process of pentagons, heptagons or their pairs is equivalent to a C–C bond rotation, while the bond rotation inside the SWCNT wall is not allowed. This also justifies that the BH strategy should not lead to unnatural bias to favor any chirality during the simulation of the SWCNT growth, as demonstrated in this study.

Formation of hexagons

As a consequence of the effective defect healing in the multi-scaled H-MD–BH simulation, the SWCNTs have a defect-free wall and an open end with only a few non-hexagonal rings. This allows us to examine the detailed process of C atom incorporation at different sites on the edge, such as AC-like or ZZ-like sites, which is of fundamental importance for understanding the growth rates of SWCNTs.^14,69

Fig. 4a–d and e–j present the processes of forming a new hexagon at an AC-like site and a ZZ-like site at the open end of an (8, 4) SWCNT, respectively. The formation of a new hexagon at an AC-like site is achieved by the addition of two C atoms. Firstly, a new pentagon is formed by a C atom addition (a); after which, a pentagon with a dangling C atom is formed by another C atom addition (c); thirdly, a hexagon is formed by rotating the C–C bond between the dangling C atom and one atom of the heptagon (d). On the other hand, the formation of a new hexagon at a ZZ-like site requires the continuous addition of three C atoms. Firstly, a dangling C atom is formed after the first C atom addition (f); after which, a dangling C2 dimer is formed after the addition of the second C atom (g); thirdly, a pentagon is formed, along with a dangling C atom, after the third C atom addition (h–i); finally, a new hexagon is formed via a C–C bond rotation (j). The process of forming a new hexagon at an AC-like site is exactly the same as that predicated by DFT calculations,⁶⁰ while the process of forming a hexagon on the ZZ edge is very similar to that proposed recently.⁷⁰

Fig. 4. Atomistic process of forming a new hexagon at an armchair-like site (a–d) and a zigzag-like site (e–j) of a simulated SWCNT growth.

Theoretically, it was predicated that forming a hexagon at an AC-like site is much easier than that at a ZZ-like site.^50,71,72 To verify the above predication, we counted the numbers of hexagons formed at ZZ-like and AC-like sites, respectively. It was found that 87.5% of hexagons are formed at AC-like sites and the remaining 12.5% are formed at ZZ-like sites. Thus, the current atomistic simulation agrees with the theoretical prediction very well.

Diameter and chiral angle distributions

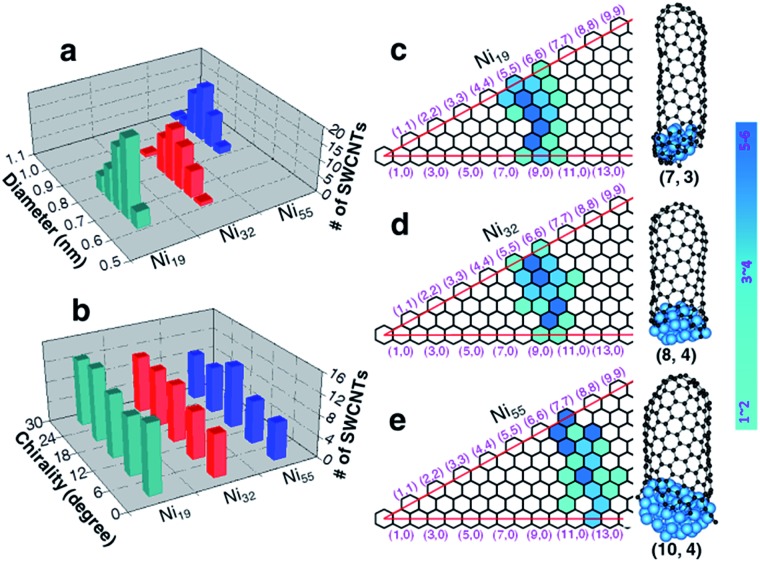
Apart from the defect-free (6, 5) SWCNT shown in Fig. 2, a large number of SWCNTs with different chiralities were also simulated (Fig. S2 in the ESI†). Fig. 5a shows the diameter distributions of the SWCNTs catalyzed by three different nickel particles (Ni₁₉, Ni₃₂ and Ni₅₅). The SWCNT diameters, growing on each nickel particle, show very narrow distributions, i.e., 0.71 ± 0.11 nm, 0.76 ± 0.14 nm, and 0.94 ± 0.14 nm, respectively, for Ni₁₉, Ni₃₂, and Ni₅₅. Such a narrow distribution indicates the strong correlation between the catalyst size and the SWCNT diameter for small catalyst particles, in good agreement with the tangent growth mode observed experimentally.⁷³

Fig. 5. Diameter and chiral angle distributions of the simulated SWCNTs grown from liquid catalysts at a temperature of 1300 K. Diameter (a) and chiral angle (b) distributions of the simulated SWCNTs formed on liquid Ni₁₉, Ni₃₂ and Ni₅₅ clusters. (c–e) The maps of chiral indexes of the simulated SWCNTs with three selected examples beside, catalyzed by liquid Ni₁₉, Ni₃₂ and Ni₅₅, respectively.

With the tangent mode of SWCNT growth, each SWCNT can reach its largest possible diameter and minimize the curvature energy of the tube wall. This is particularly important for the growth of small diameter SWCNTs from a small catalyst particle as used in this study (Fig. 5). Fig. 5b shows the chiral angle distributions of the simulated SWCNTs. For each catalyst size, there is no preference of chirality, as evidenced with the even chiral angle distributions. This is in agreement with the recent theoretical predication based on the kinetics of the addition of pentagons during the tube nucleation process.⁷⁴ The even chiral angle distributions with sharp diameter distributions can be seen vividly from the maps of the chiralities, as shown in Fig. 5c–e, for Ni₁₉, Ni₃₂, and Ni₅₅, respectively. Thus, for each diameter, the SWCNTs with all potential chiral angles have equal probabilities to be formed. Such even distribution of the chiral angles is in good agreement with many experimentally synthesized SWCNTs with mixed chiralities.^44,75–79

4. Conclusions

In conclusion, by a careful development of a new force field for Ni–C interactions and a multi-scaled approach of hybridizing MD and BH, the defect-free SWCNTs, with well-defined chiralities, are successfully grown from Ni catalyst particles by atomistic simulation. Detailed defect healing processes and the addition of carbon atoms during SWCNT growth are observed vividly in the simulation. The mechanism of SWCNT growth proposed by previous high level ab initio calculations is validated by the current simulation. The simulated SWCNTs from each catalyst particle possess a very narrow diameter distribution, which is in agreement with the tangent growth mode. The current simulation also demonstrates that all the potential SWCNTs of similar diameter have equal probabilities to be formed on the liquid catalyst particle, which results in an even chiral angle distribution of the synthesized SWCNTs. This is in agreement with most experimental observations, and shows that the chirality-selected growth of SWCNTs is very hard to achieve on liquid catalyst particles. Besides the growth of CNTs from Ni catalyst particles, the successful development of the new potential energy surface and the hybrid atomistic simulation method paves a way of deeply exploring the growth mechanism of nanocarbon materials (such as carbon nanotubes and graphene) from various catalyst particles or surfaces, such as Fe, Cu, Co, Au, Pt, Ru, Rh etc.