A scoring metric for multivariate data for reproducibility analysis using chemometric methods

Abstract

Process quality control and reproducibility in emerging measurement fields such as metabolomics is normally assured by interlaboratory comparison testing. As a part of this testing process, spectral features from a spectroscopic method such as nuclear magnetic resonance (NMR) spectroscopy are attributed to particular analytes within a mixture, and it is the metabolite concentrations that are returned for comparison between laboratories. However, data quality may also be assessed directly by using binned spectral data before the time-consuming identification and quantification. Use of the binned spectra has some advantages, including preserving information about trace constituents and enabling identification of process difficulties. In this paper, we demonstrate the use of binned NMR spectra to conduct a detailed interlaboratory comparison and composition analysis. Spectra of synthetic and biologically-obtained metabolite mixtures, taken from a previous interlaboratory study, are compared with cluster analysis using a variety of distance and entropy metrics. The individual measurements are then evaluated based on where they fall within their clusters, and a laboratory-level scoring metric is developed, which provides an assessment of each laboratory’s individual performance.

1 Introduction

Chemometrics is a field that refers to the application of a wide range of statistical and mathematical methods, including multivariate methods, to problems of chemical origin [1–3]. With the advance of analytical instrumentation in chemical metrology, an increasing amount of data can be generated which requires multiple approaches for extracting reliable information. This has required and enabled the development of improved analytical procedures for data analysis based on sound chemometric principles in order to reliably assess the properties of interest in a system under study.

In recent years, the importance of metrology in the world has grown significantly since its main focus is to provide reliability, credibility, universality and quality measurements. Since measurements are essential, directly or indirectly, in virtually all decision-making processes, the scope of metrology is immense, involving important areas of society such as industry, trade, health, safety, defense and the environment. It is estimated that about 4 % to 6 % of the gross domestic product of industrialized countries is dedicated to measurement [4]. In this context, the use of chemometrics in combination with metrology is a potential approach to the interpretation of data in decision making, providing improved industrial and technological development. One of the important metrological activities that can be highlighted is the participation and organization of interlaboratory quality assurance programs. Quality assurance includes interlaboratory studies used as an external evaluation tool and in the demonstration of the reliability of laboratory analytical results. It also serves to identify gaps in the analytical process and enable comparability improvement. Moreover, it is one of the items required for accreditation tests by ISO/IEC 17025: 2005 [5].

According to ISO 13528: 2015 [6] and ISO/IEC 17043 [7], there are several statistical tools to be used to assess the results of analytical laboratories participating in proficiency testing. Among them there are the Z-scores, Z′-scores, Zeta scores and E_n scores. The problem with these metrics is related to the fact that they can only be used for cases of univariate measurement results and have not been systematically extended to multivariate analyses. However, some studies have demonstrated efforts to analyze the quality of multivariate data. An example of this is in the field of metabolomics [8] in which principal components analysis (PCA) was used to evaluate data from an interlaboratory comparison. In other work [9], a metric called Qp-score is proposed to evaluate the performance of each laboratory for multivariate data. Other than these studies, there have been few attempts to perform interlaboratory comparisons on multivariate data. But even these studies have used spectral data to measure some property or set of properties and then determined standard univariate scores for these measurements. For instance, in Gallo et al. [9], the participating laboratories determined calibration curves for metabolite concentration with respect to nuclear magnetic resonance spectroscopy (NMR) spectral feature intensity and then determined a score from those curves. In Viant et al. [8], several significant features within each spectrum were identified and then univariate scores determined based on the intensities of those features. In each case, however, the scoring process reduces a vector of thousands of components to one possessing relatively few components, and it is still difficult to extract a comprehensive metric of “goodness” from this information.

Considering the lack of a multivariate metric in the ISO standards that address the subject, the objective of this study is to propose the application of algorithms, already known in the literature that can be used for the evaluation of multivariate data in proficiency tests. We re-examine the data collected by Viant, et al. [8], and extend their analysis by proposing a scoring metric that assumes a single value for each NMR spectrum, which can be further extended to a laboratory-level metric that can be used for quality control and analysis.

1.1 Brief statement of the interlaboratory comparison problem

The problem of laboratory-outlier detection in an intercomparison study can be expressed in the following way:

$$R\left(x,r,f\right)=T\left(x\right)+I\left(x,r,f\right)+\epsilon ,$$ (1)

where R is the measured response function, T is the underlying true value, I is some instrument function and epsilon is noise. R is a function of the experimental independent variables x (in this case, NMR chemical shifts and the NMR (static) field strength) but also depends on the replicate number r and the facility identifier f. This expression for R allows an explicit statement for how the response might vary based on the use of different measuring devices in different locations, and even run-to-run variability in the same device. The underlying truth T depends only on the independent variables, while I explicitly contains the variability among the measurements.

In the normal regression problem, I is treated as being part of the noise epsilon. For an interlaboratory study, however, the instrument function could actually contain a great deal of information about the individual laboratories that make the measurements.

The purpose of an interlaboratory comparison study is to identify those laboratories whose instrument function is sufficiently systematically different to indicate that those laboratories may be sampling from a different population. For instance, in the Viant et al. study [8], NMR spectra were taken at various magnetic field strengths. The individual spectra consist of magnetic field dependent features (chemical shifts) and magnetic field independent features (spin-spin couplings). As a result, spectra taken under different field strengths are not directly comparable. If the instrument function contains such systematic lab-to-lab variations, then, the performance of one laboratory relative to the others will be consistently different when compared across a range of many different values of the independent variables x, which in this case means many different samples.

It should be noted here that measurements taken of the same object at different laboratories by different analysts on different instruments are considered to be independent of each other, in the sense that there is no cross-communication between the different laboratories. Likewise, the measurements of different objects by the same laboratory will also be independent.

1.2 Multivariate metrics used for interlaboratory comparison

In chemometrics and information theory, there are several common metrics used for pattern recognition [10–16]. It is important to mention the Euclidean distance [17–20] and the Mahalanobis distance [21–26] as the most used, however, there are other metrics based on a probabilistic approach [27], for example, the Hellinger distance [28], the Kullback-Leibler divergence [29] and the Jensen-Shannon distance [30, 31]. All these metrics may be useful in metrological activities such as, for example, proficiency testing.

1.2.1 Similarity measures based on vector distance: Euclidian and Mahalanobis distance

The Euclidean distance is defined by

$$d_{\mathrm{E}}\left(\mathbf{x},\mathbf{y}\right)=\Vert \mathbf{x}-\mathbf{y}\Vert =\sqrt{{\left(\mathbf{x}-\mathbf{y}\right)}^T\left(\mathbf{x}-\mathbf{y}\right)}={\left[{\sum }_k{\left(x_k-y_k\right)}^2\right]}^{1/2},$$ (2)

where the x and y column vectors represent two spectra and x_k and y_k are the features of those spectra, with the sum taken over the elements of the vectors. The Euclidean distance gives greater weight to large differences between prominent features than to differences between small, but possibly clinically significant, features. However, it does not correct for correlation structures in the data. To resolve this issue, the Mahalanobis distance is often used, which is defined by

$$d_{\mathrm{M}}\left(\mathbf{x},\mathbf{y}\right)=\sqrt{{\left(\mathbf{x}-\mathbf{y}\right)}^{\mathrm{T}}{\mathbf{\sum }}^{-1}\left(\mathbf{x}-\mathbf{y}\right)}$$ (3)

where Σ is the covariance matrix which may be estimated in numerous ways.

1.2.2 Similarity measures based on probabilistic distance: Hellinger distance, Kullback-Leibler divergence, and the Jensen-Shannon distance

Alternatives to the Euclidean and Mahalanobis distances include metrics from information theory to analyze probability density functions. Interpreting an NMR spectrum in this way requires that the spectrum be non-negative and also that it integrate to unity. Under this interpretation, the spectrum indicates what fraction of the total oscillatory power is contained at each frequency. The metrics we discuss here are the Hellinger distance [28], the Kullback-Leibler (KL) divergence [29], and the Jensen-Shannon distance [30, 32–34]. The Hellinger distance between two spectra is defined by

$$d_{\mathrm{H}}\left(\mathbf{x},\mathbf{y}\right)=1-{\sum }_k\sqrt{x_k{y}_k}$$ (4)

and varies between 0 and 1. If d_H = 0, then x and y are identically equal, indicating similar performance of the two data sets from which x and y are obtained. If d_H = 1, x is zero everywhere that y is positive and vice versa, indicating a divergence of the two data sets. In terms of an interlaboratory comparison, d_H≪1 corresponds to similar performance between laboratories, while d_H ≈1 represents divergence in the results of the laboratories.

The KL divergence, sometimes termed the relative entropy, is defined by

$$d_{\text{KL}}(\mathbf{x},\mathbf{y})=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$ln2$}\right.{\sum }_k{x}_{k}ln\left(\frac{x_k}{y_k}\right).$$ (5)

The KL divergence is not symmetric, and so what is used here is the symmetrized KL (SKL) divergence, sometimes termed the Jeffreys divergence,

$$d_{\text{SKL}}\left(\mathbf{x},\mathbf{y}\right)=d_{\text{KL}}\left(\mathbf{x},\mathbf{y}\right)+d_{\text{KL}}\left(\mathbf{y},\mathbf{x}\right).$$ (6)

Unlike the Hellinger distance, the SKL divergence varies between 0 and positive infinity, with positive infinity corresponding to divergence between the laboratories. Furthermore, if an element of x or y is zero anywhere where the other is nonzero, the SKL divergence will diverge to infinity.

The SKL divergence is not a distance metric because it does not satisfy the triangle inequality, so as an alternative we will also use the Jensen-Shannon (JS) distance [35–37], defined by

$$d_{\text{JS}}\left(\mathbf{x},\mathbf{y}\right)=\sqrt{d_{\text{KL}}\left(\mathbf{x},\mathbf{m}\right)+d_{\text{KL}}\left(\mathbf{y},\mathbf{m}\right)}$$ (7)

where m is the arithmetic mean of x and y. Like the Hellinger distance, the JS distance varies between 0 and 1 and can be interpreted in the same way as the Hellinger distance.

The SKL divergence in particular is extremely sensitive to differences in small features, such as the presence of a feature in one spectrum and its absence in another. This behavior makes some sense in a metabolomics context, as the presence of even a trace compound would make a mixture completely different from a mixture that lacked that compound, and hence their spectra should be, in some sense, incomparably different.

As the JS and Hellinger distances vary between 0 and 1, we use here a hyperbolic transformation where d_hyp = ln[(1+d)/(1−d)]. In this transformation, the distances are treated as being the length of line segments in the Poincaré disk model of a hyperbolic space. Under this transformation, the distances vary between 0 and positive infinity, in the same manner as the SKL divergence and Mahalanobis distance, and thus all the distance metrics can be directly compared. All future references to the Hellinger and JS distances actually refer to distances under this hyperbolic transformation.

1.3 Expanded definition of the Z-score

In the ISO standards [6, 7], the Z-score is defined for a set of measurements first by fitting a normal distribution to that set of measurements, extracting a sample set mean, μ, and variance, σ². That is, for each measurement i whose value is x_i, the Z-score Z_i for each measurement is then calculated according to Z_i =(x_i − μ)/σ. If the data are well-approximated by a normal distribution, this method works well. For data that cannot be shown to follow a normal distribution, however, a more general theory is needed. For instance, the distance functions analyzed in this paper are strictly positive, and so an exponential or lognormal distribution may be more appropriate. Furthermore, arbitrarily small values of the distance functions are considered good, as opposed to the normal Z-score where small values are just as bad as large values. Consequently, a more general theory is needed.

In general, the cumulative distribution function for a probability distribution can be expressed as C = C(x;P), where P is a set of parameters that define the distribution. For instance, the normal and lognormal distributions have parameters μ and σ, while the exponential distribution has the parameter λ. Every probability distribution also has a standard form

$$C^{\ast }=C\left(Z_i;{\mathbf{P}}^{\ast }\right),$$ (8)

where P^* is the set of parameters under some standard conditions, such as with the normal distributions with mean and variance equal to unity. Then the generalized Z-score Z_i for a measured value x_i is

$$Z_i=C^{\ast -1}\left(C\left(x_i\right)\right),$$ (9)

where C^*−1 indicates the inverse function. For a single-tailed distribution such as a lognormal or exponential distribution, the Z-score for the α-confidence interval can be defined as Z_i = C^*−1(α). The Z-score corresponding to the median of the distribution is then Z_median = C^*−1(½), and the 95 % confidence interval is Z₉₅ = C^*−1(0.95).

1.4 Calculation of Z-scores for multivariate metrics

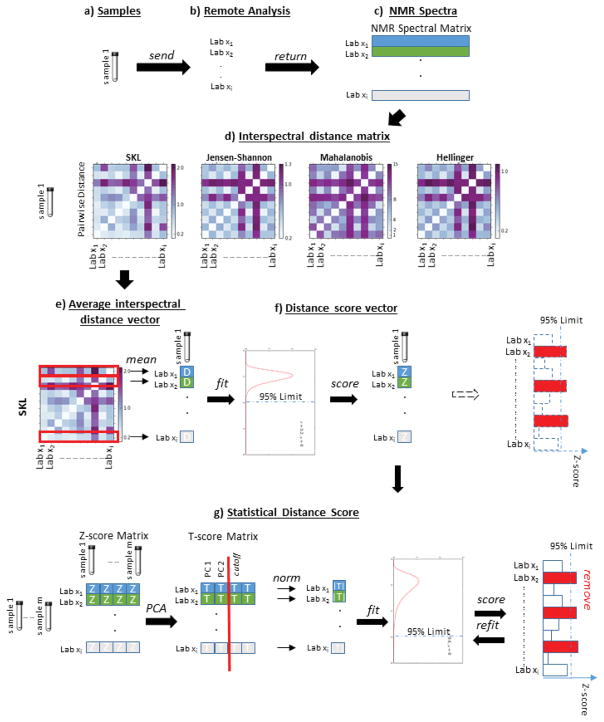
The sample-level Z-scores, Z_i, are calculated as follows, with the procedure summarized in Table 1 and Fig. 1. The spectra are first clustered in some manner, which results in a set of spectral clusters S. In the case of an interlaboratory study such as analyzed here, each cluster S_k consists of the multiple spectra of sample k provided by, for example, different laboratories. This is shown graphically in Fig. 1, panels a–c. Likewise, in an interlaboratory study, the spectra can also be clustered into a set of data sets A, where each data set A_i consists of the spectra taken by a particular, say, laboratory. Note that many interlaboratory studies include replication of samples in order to test the variability within each laboratory, while some laboratories might obtain multiple spectra for each sample under different conditions such as a different instrument or different settings on the same instrument. In this paper, a data set contains all spectra for a particular instrument with particular settings, while a spectral cluster contains all spectra for a material with a particular label, even if it is a replicate. Specifying the data set i and cluster k of a spectrum therefore serves to uniquely identify that spectrum.

Table 1.

Summary of scoring metric and consistency algorithm.

1. Calculate inter-spectral distances Dij,k (Fig. 1d)

2. Calculate the average diameter distances D̑i,k (Fig. 1e)

3. Fit D̑i,k to the chosen distribution Ck for each Lab xi (Fig. 1f)

4. Calculate Z matrix (Fig. 1g)

5. Perform PCA on Z (Fig. 1g)

6. Identify the L principal components (Fig. 1g)

7. Calculate projected distances ||Ti,L|| for each laboratory (Fig. 1g).

a. Fit ||Ti,L|| to the chosen distribution C̑

b. Calculate projected distance scores Z̑i

c. Remove data set i if Z̑i > Z̑95 and go to step 7a

Figure 1.

Overview of scoring and outlier detection procedure

Within each cluster S_k, the interspectral distance matrix D_k is determined, whose elements are

$$D_{ij,k}=d\left({\mathbf{s}}_{i,k},{\mathbf{s}}_{j,k}\right),$$ (10)

where s_i,k and s_j,k are spectra from Lab x_i and Lab x_j for cluster S_k, and d is the desired distance function. This is shown in Fig. 1d.

The average diameter distance D̑_i,k is defined as the average distance from spectrum s_i,k to the other spectra in cluster S_k, and is calculated as

$${\stackrel{⌢}{D}}_{i,k}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.{\sum }_j{D}_{ij,k},$$ (11)

where n is the cardinality of S_k. Note that, as D_k is symmetric, this is equivalent to both the row average and the column average. This is similar to the intercluster distance method used in the Unweighted Pair Group Method with Arithmetic Mean hierarchical clustering algorithm [38]. The D̑_i,k values were empirically observed to be lognormally distributed, and so are then fit to a lognormal distribution. The Z-score vector Z_i is calculated by Z_i,k = C^*−1(C_k(D̑_i,k)), where C_k is the cumulative distribution function after being fit to cluster k and C^* is the corresponding standard distribution function. Each individual Z_i,k is an indication of where the spectrum s_i,k lies with respect to the other members of cluster S_k. In the case of the lognormal distribution Z_i,k(½)=1 and Z_i,k(0.95)≈5, so a Z_i,k of 1 indicates that s_i,k lies closer the center of S_k than the median, and Z_i,k greater than about 5 indicates that s_i,k lies outside the 95% confidence interval of cluster S_k. It should be noted that the D̑_i,k values may take on other distributions depending on the application.

1.5 Calculation of laboratory-level Z-scores for outlier detection

The statistical analysis on the spectra still results in a k-vector of Z-scores for each laboratory, Lab x_i, and it is still necessary to generate a single number for each data set (laboratory). Because Z_i = 0 is an important measure, the Euclidean norm of a data set’s Z_i vector, ||Z_i||, provides a measure of that laboratory’s performance relative to the other laboratories. In order to identify patterns in how laboratories deviate from each other, dimensional reduction using PCA is also performed on the Z matrix. The PCA model is defined as T = ZP^T, where T is the matrix of PCA scores and P is the matrix of PCA loadings. The PCA model is then reduced by retaining the L most significant components, resulting in the reduced model ${\mathbf{T}}_L=\mathbf{Z}{\mathbf{P}}_L^{\mathrm{T}}$. For most of the metrics considered here, L = 2. We refer to ||T_i,L|| as the projected statistical distance, as it is the distance projected onto the PCA space, and use this number as the basis for comparing the datasets.

This PCA model can shed light on the instrument function by how many significant principal components it has. If the PCA model has many significant components, then the instrument function is essentially random and can be treated as a component of the noise (Eq x ). If the PCA model has few components, however, it means that the instrument function is not random. In this case, the measurements in some laboratory data sets are more frequently close to the consensus value than those of other data sets, and then there is a basis for identifying the distant data sets (laboratories) as outliers.

For each Lab x_i, we calculate ||T_i,L||, and then fit these statistical distances to a new distribution with distribution function C̑. This new distribution has a Z-score associated with it, which we call the projected statistical score, denoted Z̑_i and calculated using Z̑_k = C̑^*−1(C̑(||T_i,L)) As with the D̑_i,k values, the distribution function C̑ will need to be determined based on the application. Note also that C_k and C̑ may also be different distributions. Once the Z̑_i values have been computed, if any fall outside the 95 % confidence interval, the corresponding Lab x_i is considered as an outlier and removed from consideration. A new C̑ and corresponding Z̑_i values are then computed. This iterative process results in a consensus set of laboratory metrics that is self-consistent, thereby allowing a more precise specification of consensus than merely identifying the laboratory-outliers, as the ISO standards would direct.

2 Implementation Details

2.1 Data Sets

Two different sets of measurements were used in this study, which were obtained through the interlaboratory comparison exercise reported in Viant et al. [8] in which seven laboratories participated. In the exercise, each participating laboratory was sent one set of synthetic mixture samples and one set of biological-origin samples along with a detailed analysis protocol. Each laboratory obtained a one-dimensional ¹H NMR spectrum for each sample from both sets. Three of the laboratories performed measurements for two NMR field strengths, for a total of ten spectra for each sample. Four sets of spectra were obtained at an NMR field of 500 MHz, four at 600 MHz, and two at 800 MHz. These sets are the data sets A. The data set identifiers and the corresponding NMR field strengths are shown in Table 2. The spectra are reported as chemical shift frequencies in parts per million (ppm), with a range from 10.0 ppm to 0.2 ppm, with a region from 4.7 ppm to 5.2 ppm excluded due to water solvent suppression artifacts. The spectra are binned with a bin width of 0.005 ppm, for a total of 1860 variables in each spectrum. Due to additional water suppression artifacts apparent in the spectra, for this analysis, an additional region from 4.2 ppm to 4.7 ppm was excluded, after which the NMR spectra were renormalized.

Table 2.

Data set identifiers, corresponding NMR frequencies, and laboratory-outlier identifications for the synthetic samples

Data set identifier	NMR field strength (MHz)	Outlier
0115	600
0122	500
0258	600
0333	500
0711	600
0714	800	×
2861	500
7042	800	×
8865	500
9541	600	×

The set of synthetic data consists of six synthetic mixtures (S1–S6), each containing glucose, citrate, fumurate, glutamine, alanine and nicotinate in various concentrations. One mixture, S1, has six replicates, for a total of 11 samples and 110 spectra. The set of biological data consists of liver extracts from European flounder (Platichthys flesus) obtained from two different sampling locations, an unpolluted control site and a polluted site. Six samples were obtained from each site (BC1–BC6 for the control samples and BE1–BE6 for the polluted samples). One sample, BC1, has three replicates, for a total of 14 samples and 140 spectra. There are therefore 11 clusters of synthetic data and 14 of biological data.

Why these data were chosen is discussed in detail by Viant et al. [8], but, succinctly, the purpose was to compare the performance of the NMR spectroscopic methods using both synthetically derived mixtures with precisely defined composition and tissue extracts with highly variable or unknown composition. In this study, we compare the performance of the laboratory-outlier detection method using the synthetic mixtures and using the biological mixtures. Because of their simpler controlled composition, the synthetic mixtures were expected to provide a better basis for comparing the various laboratories.

2.2 Procedure and Software

In the original work of Viant et al. [8], a principal components analysis (PCA) was performed on both the synthetic data set and on the biological sample data set, excluding the replicates. In the case of the synthetic data set, a PCA model was derived that consistently differentiated among the various samples, without magnetic field dependence dominating the most significant principal components. For the biological samples, however, a PCA model using all spectra showed strong magnetic field dependence in the first principal component with notable class separation in the second (Figure S8, in Viant et al. [8]), so subsequent analysis was based on PCA models including only spectra from the same magnetic field strength.

In this work, therefore, the synthetic samples are used to conduct a quality assurance test in order to identify those data sets that may have problems with their workflow. The biological samples from these laboratories are removed from consideration in the PCA, and it is found that a PCA model is found that will consistently differentiate between the control and exposed samples. The algorithms used in this paper were implemented in Python, and all scripts are made available in the supporting information.

In this work, we regard “clusters” to be all of the spectra of a specific sample collected by each participating laboratory. For example, spectra from all of the S1a samples are treated as a cluster, and they are different clusters from the S1b and S2 samples, even though some samples are replicated of the others. Once the potentially outlier laboratory data sets have been flagged and removed, a PCA is conducted on the remaining biological spectra, showing that it is possible to separate the fish from the polluted site and those from the control site, independent of the magnetic field frequency.

The Mahalanobis distance requires some preprocessing because the NMR spectra are not full rank, and so the covariance matrix of a full data set is not well-conditioned. To address this issue, the inverse covariance matrix is calculated using the singular value decomposition pseudoinverse as implemented in Numerical Python (numpy.linalg.pinv), retaining singular values greater than 0.1 times the maximum singular value. The covariance matrix was calculated by calculating the variance-covariance matrix for each individual cluster and pooling them to estimate an overall covariance matrix for the entire set. It should be noted that the number of singular values to retain in the covariance matrix inversion is a free parameter, and changing it can have an effect on the final results.

3 Results and discussion

The results obtained through this study are presented in the following manner. In Sections 3.1 and 3.2, the methodology discussed in Sections 1.2 through 1.4 is presented in the context of the synthetic-mixture NMR spectra. These sections discuss the interspectral distance metrics and the methods for generating sample-level Z-scores within each cluster.

In Sections 3.3 and 3.4, the laboratory-level Z-scores are calculated and used for laboratory-outlier detection, as presented in Section 1.5. These sections discuss the use of principal components analysis to identify patterns in laboratory performance and of the scoring technique to rank the laboratories by their overall performance. This information allows us to determine which laboratories are similar enough to be comparable and which are not. As discussed in Section 1.2, there are many different distance metrics that can be chosen, and we do not know a priori which one is most appropriate. The identified outlier-laboratories differ somewhat based on which distance metric is used, and so it is not possible to make a single statement of which laboratories are outliers.

In Section 3.5, the results of the synthetic sample laboratory-outlier detection are used to analyze the biological-sample NMR spectra. As mentioned in Section 1, in the Viant, et al. study, it was not possible to develop a PCA model that was not dominated by magnetic field dependence. In this section, we show that the outlier detection method results in an improved separation and also in detection of a previously-unidentified feature that may be responsible for that separation.

Section 3.5 also includes a laboratory-outlier detection analysis on the biological samples. The outlier laboratories detected in this analysis were different from those detected by analyzing the synthetic samples and resulted in a less pronounced separation among the polluted-site and control-site animals. It was concluded, therefore, that using synthetic data as a filter adds valuable perspective in finding laboratory-outliers.

3.1 Similarity measures

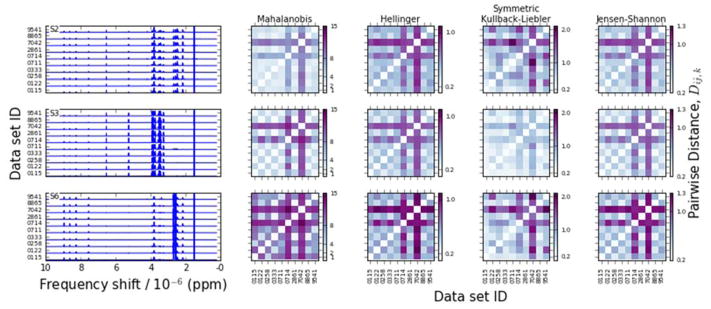
Figure 2 presents the NMR spectra for three synthetic samples, chosen to highlight the differences among the various distance metrics. The laboratories are labelled according to the identification numbers assigned to them in the Viant, et al. study [8]. A few patterns can be observed from the distance metrics. First, the Hellinger and the Jensen-Shannon distances universally indicate that the two spectra taken at 800 MHz are different from the others, without much discernable detail about other sets of spectra. This may simply mean that, because of an increase in the resolution of spectral information, the spectra at different magnetic field frequencies are not readily comparable. The Mahalanobis distance and SKL divergence detect that one of the labs, 9451, also exhibits some notable differences, although the Mahalanobis distance detects this difference only inconsistently. It should be noted that examining the figures in this way is inherently highly subjective, and that this analysis is intended only to draw high-level patterns that will later be examined with the more rigorous analysis to follow.

Figure 2.

NMR spectra (left) and pairwise interspectral distances (right) for three of the synthetic metabolite clusters (see Fig 1d).

3.2 Distance scoring

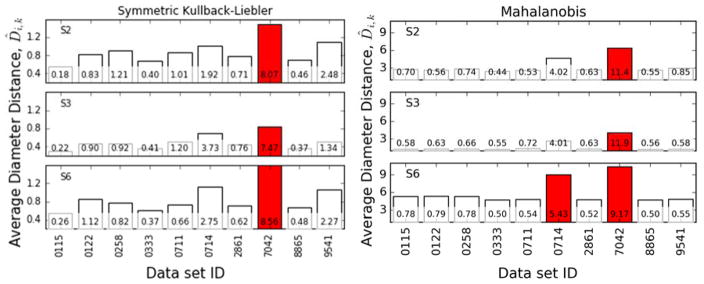
In order to produce a single number to classify the laboratories’ spectral consistency with the other members of the group, the average diameter distance D̑_i,k is calculated and then fit to a lognormal distribution. The lognormal distribution was chosen here based on a QQ comparison, which showed that the D̑_i,k values could be fit well by several distributions such as lognormal, χ, χ², or Γ distribution. We chose the lognormal distribution here because it is the maximum entropy distribution for a specified mean and standard deviation. We also tested the Γ distribution, which yielded the same set of laboratory-outliers.

The results of the lognormal distribution fits are shown in Fig. 3 for the SKL divergence and for the Mahalanobis distance. These figures show the D̑_i,k values and corresponding Z_ik values (Z-scores) for each of the 110 spectra in this data set. Those spectra with a Z_ik > 5.18 are labelled in the figure, meaning they lie outside the 95% confidence interval of the corresponding lognormal distribution C_k. The Mahalanobis distance identifies data set 7042 as a possible outlier among the data sets, but this is not consistent, and other sets have large Z_i for some spectra. The other measures consistently identify set 7042 as an outlier, and both the Hellinger and JS distance identify set 0714 as an occasional outlier. Visual inspection of the Z-scores can provide some guidance, but it is not sufficient to clearly or consistently identify laboratory-outlier data sets among the synthetic spectra, which is what motivates the principal components analysis on the Z-scores to follow.

Figure 3.

Average diameter distances (Eq. 8) for spectra from all data sets for three of the synthetic metabolite clusters, annotated with corresponding Z_i,k values (Eq. 10). Spectra that have a Z_i,k greater than 5 are marked in red. Distances and Z-scores are shown for (left) the SKL divergence and (right) the Mahalanobis distance

3.3 Principal components analysis on Z-scores matrix

In order to conduct the PCA, as described in Section 1.4, the Z-scores for the spectra in each Lab x_i are cast as a k-vector whose elements are the Z-scores for the NMR spectra in that set (Fig 1g). There are two limiting cases that this PCA would discriminate between. On the one hand, it is possible that some data sets contain spectra that are closer to the consensus value than the others, while also containing spectra that are farther from the consensus values than others. On the other hand, however, some data sets might consistently contain the spectra closest to the consensus value, while other sets consistently contain spectra far from the consensus value.

The PCA loadings calculated for all metrics are shown in Fig. 4, with the explained variance ratios included for each principal component. Recall from Section 1.4 that this PCA is conducted using the Z_i,k values, rather than on the NMR spectral data as would normally be expected for chemometric data. Consequently, the loadings seen in Fig. 4 will each be a laboratory performance vector similar to those presented in Fig. 3.

Figure 4.

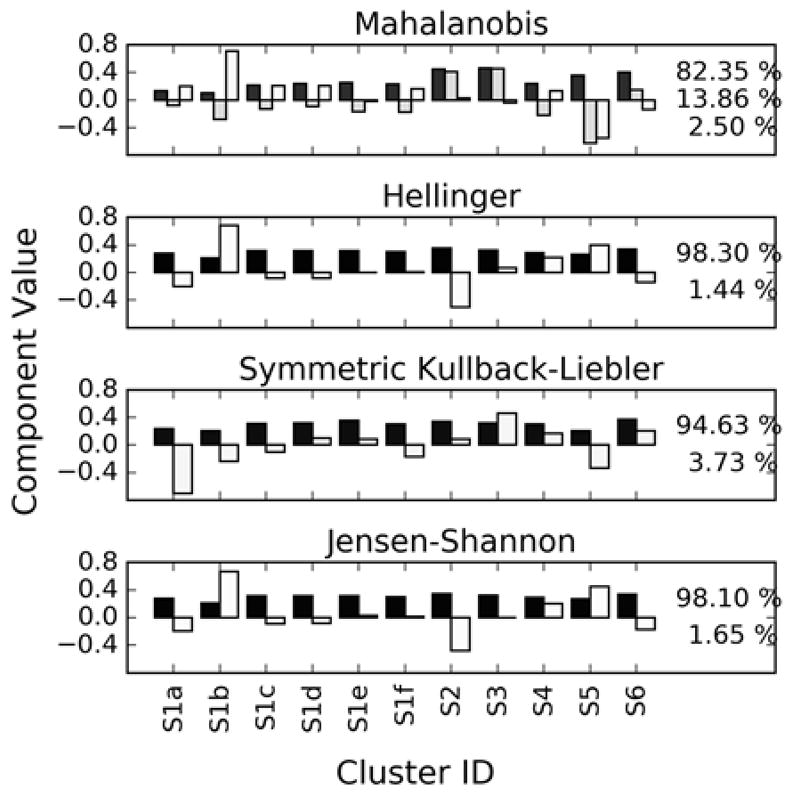
PCA loadings (P) shaded by explained variance fractions for the Z matrices (Z_i,k values). Black represents more explained variance, so the black bar is the first principal component. Plots are annotated with the explained variance fractions for the first L principal components. Note that, because this PCA is conducted on the Z_i,k values, each loading vector will appear as a laboratory performance vector similar to that in Fig. 3.

In the case of the probabilistic distance measures, the first principal component explains roughly 95 % of the variance, while the second component accounts for most of the remainder. Furthermore, the first component represents a roughly uniform increase or decrease in the Z-scores for all spectra in a given data set. This means that, for the most part, data sets contain spectra that are close to the consensus value or that are far from it, but not both. Any particular data set’s performance could then be assessed by its score along this single dimension.

The situation is less clear for the Mahalanobis distance. The first principal component explains only about 82 % of the variance among the Z-scores, and there are two other components that also explain roughly 15 % of the variance between them. Furthermore, the first component does not describe the uniform increase or decrease in the distance to the consensus of all a data set’s spectra. Rather, when the spectra are compared using the Mahalanobis distance, some data sets have one or two spectra that are far from the consensus while the rest are close. This result may be influenced by run-to-run variation in the individual laboratories that is captured by the Mahalanobis distance but not the other metrics.

3.4 Scoring on principal components analysis

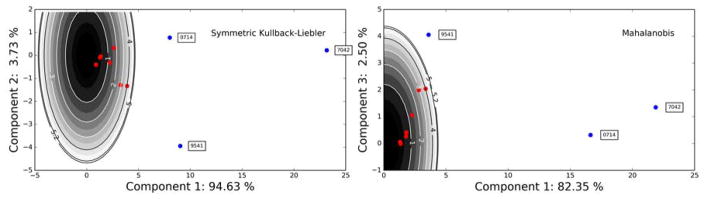
The PCA scores for each data set allow the projected statistical distance ||T_L,i|| to be calculated which is representative of each data set’s distance from consensus. For the Mahalanobis distance, ||T_L,i|| is determined using the first three components, and for the other metrics it is the first two. ||T_L,i|| is then fit to a lognormal distribution and the projected distance score Z̑_i is computed for each data set. Then, if any data set has a Z̑_i outside the 95 % confidence interval, the set with the largest Z̑_i is labelled as a laboratory-outlier and removed from consideration. The process is repeated until no data sets lie outside the 95 % confidence interval. Recall that, as discussed in Section 1.5, ||T_L,i|| is the distance of each laboratory from the point Z_i = 0 in the PCA space. Therefore, it measures how far each data set is from agreement with the consensus.

The results of this process are shown in Figs. 5 and 6. Figure 5 shows the ||T_L,i|| and corresponding Z̑_i values, while Fig. 6 shows the principal component scores for the labs along with contours of constant ||T_L||, in order to show the outliers. The sets identified as outliers are the two data sets taken at 800 MHz and one of the sets at 600 MHz, 9541. It should be noted that these three data sets were identified in the original Viant, et al. study [8] as being difficult to compare with the other data. The 800 MHz data contained information not present in the other data and data set 9541 exhibited peak shifting that made it difficult to compare with the other sets.

Figure 5.

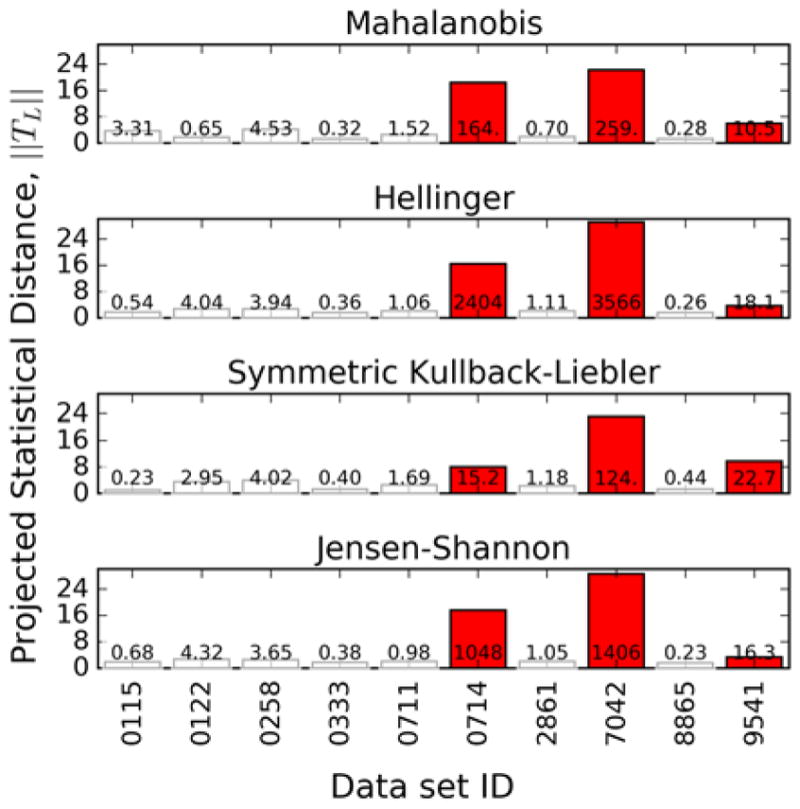
Projected statistical distance ||T_L,i|| calculated using each metric. Bars are annotated with their corresponding Z̑_i Outlier data sets are colored red.

Figure 6.

PCA scores for the Z matrix calculated using the SKL divergence and Mahalanobis distance, along with curves of constant ||T_L,i|| Note that, although the PCA is calculated using mean centering, the ||T_L,i|| values are calculated based on distance from Z_i = 0, as discussed in Sections 1.5 and 3.4. Outlier data sets are colored blue and labelled with the data set identifier. Inlier data sets are colored red and not annotated.

In the case of the Mahalanobis distance, the same outliers are detected. As can be seen in Fig. 6b, data set 9541 has a large score in the direction of the third principal component which is has a strong contribution to it being identified as an outlier. This principal component corresponds to a data set having spectra for samples S1a and S5 far from consensus, as shown in Fig. 4. Even without the contribution of this component, however, this data set is pushed very close to the 95 % confidence boundary.

3.5 Using synthetic sample data as a quality control measure for real data

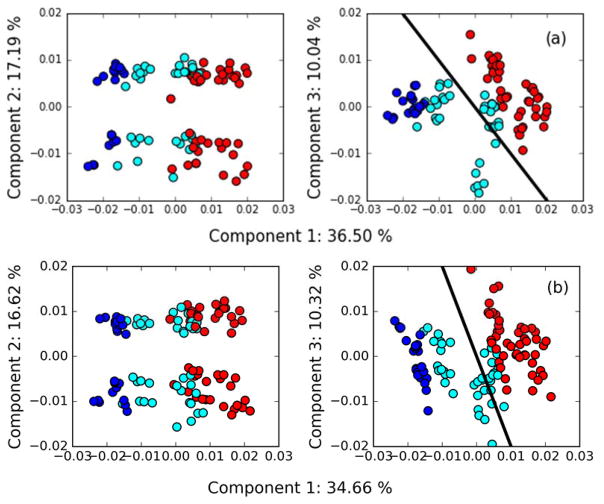
In the original Viant, et al. study [8], a PCA was conducted on the NMR spectra from both the synthetic samples and the biologically-obtained samples. It was possible to combine the synthetic-sample data across many platforms in a single analysis, but this proved to be impossible to do for the biological data without the results being dominated by magnetic field strength. In this study, we remove the data sets identified by our laboratory-outlier analysis and then conduct the PCA on the remaining data sets simultaneously. The results of this analysis are shown in Fig. 7. Two cases are considered. In both cases, the 800 MHz data sets are removed as outliers. In one case, set 9541 is also removed as an outlier based on the analysis using the laboratory-outlier detection methodology, and, in the other, only the 800 MHz spectra are considered as outliers based on the idea that these spectra should exhibit different chemical shift features, as discussed in Section 1. In both cases, the second principal component is a field-strength-dependent axis that carries little clinically relevant information (that is, it does not serve to separate the exposed-site fish from the control-site fish). A similar component was obtained by the PCA in Viant, et al. study [8] as the first principal component. However, when the first and third principal component scores are plotted, there is an evident separation between samples from fish in the polluted site and from the exposed site. This separation is comparable to that seen for a single data set, as was seen in the original study [8]. It should be noted that there is not a perfect separation between the two groups because of the complexities of biological systems.

Figure 7.

PCA scores and explained variance fractions for the biologically-obtained NMR spectra, after removal of outlier data sets identified using the synthetic mixtures, along with the approximate direction of separation indicated by the thick black lines. Samples from the control site are colored cyan and those from the polluted site are colored red. The dark blue points are the three biological samples BC1a, BC1b, and BC1c. Outlier data sets are removed based on results from (a) the outlier detection methodology in this work (see Table 2) and (b) removing only the 800 MHz spectra.

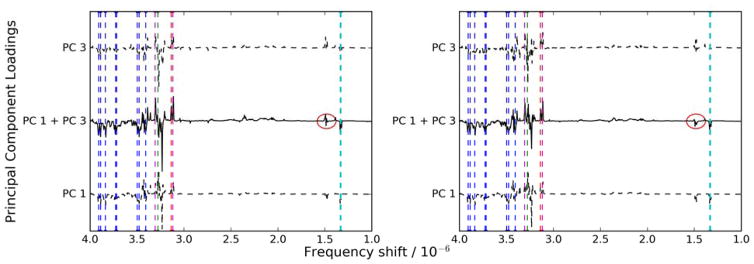
Because the separation between the animals from the two sampling sites is evident in both cases, it is worthwhile to examine the causes for separation in these two analyses. The two sampling sites are roughly split along the component 1/component 3 diagonal, so the NMR bins responsible for that separation are a linear combination of those components’ loadings. These loadings represent the “impacted direction” in the NMR space and are shown in Fig. 8, which also shows the significant bins identified by Viant, et al. [8]. In all cases, the PCA models show that exposed animals exhibit decreased levels of glucose and lactate and increased levels of three unidentified substances in their livers. However, in Fig. 8a, which shows the PCA model after data set 9451 has been removed, a small increase in another unidentified substance can be seen at a chemical shift of about 1.48 ppm. This bin was not identified in the Viant study, and it is also not readily visible in Fig. 8b, which shows the PCA model when this data set is not excluded. It is possible that the peak shifting issues that were observed with data set 9541 served to obscure this set of bins.

Figure 8.

Principal component loadings corresponding to the direction of separation in Fig. 7. Bins identified in the Viant study are marked with vertical dashed lines. Glucose is blue, lactate is cyan, and the three unknown metabolites are red, magenta, and green. The previously unidentified substance is circled in red. Outlier data sets are removed based on results from (a) the outlier detection methodology in this work (see Table 2) and (b) removing only the 800 MHz spectra.

It should be noted that the analysis performed here could have been applied to the biological spectra themselves in order to screen the data sets, rather than to the synthetic samples. The results of such an analysis are summarized rather than shown in detail, but they are as follows. When the SKL divergence is used on the biological samples, only one data set, 7042 at 800 MHz, is identified as an outlier. When the other metrics are used on the biological samples, both 800MHz sets are identified. It is impossible to draw any conclusions from the PCA results using the SKL divergence, and the PCA results using the other metrics are the same as the case shown in Fig. 7b.

The reason that more outlier data sets are detected, and more consistently, is due to the stark differences between the synthetic samples and the biological samples. The synthetic samples were made from known concentrations of a few particular metabolites with narrow and distinct features in their spectra. Consequently, differences among the spectra will appear prominently when examined using an information-theoretic analysis. The biological samples, on the other hand, are a mixture of thousands of potentially unknown and poorly characterized substances, and so differences among the spectra are more difficult to analyze.

Taken at face value, this conclusion would suggest that every NMR interlaboratory study would need to include a synthetic data set for quality control along with the biological samples under study. Such a procedure could make interlaberatory studies difficult to conduct, because it would effectively double the amount of effort needed to conduct the test. However, interlab studies often contain quality control replicates. For instance, in the Viant, et al. [8] study, the biological replicates were samples C1a, C1b, and C1c. As a middle ground that does not require two complete interlabs, we conduct the outlier detection analysis on these replicates. This would allow us to probe the instrument function directly, given that we know we are analyzing the same samples. The result is shown in Fig. 9, which shows the outliers detected by using the various metrics. Unlike the analysis of the synthetic samples, as shown in Fig. 4, the outliers detected in this way are not consistent across the metrics. Consequently, using these outputs of the algorithm, it is not possible to make an unequivocal statement of which laboratories are laboratory-outliers. It is possible, however, to say that the same laboratories are detected as possible laboratory-outliers the majority of the time. These results underscore the potential utility of using synthetic samples for quality control before conducting analysis on the more complex spectra obtained from biological samples, but also that it is possible to get similar results using quality control replicates of the biological samples as long as some care is taken.

Figure 9.

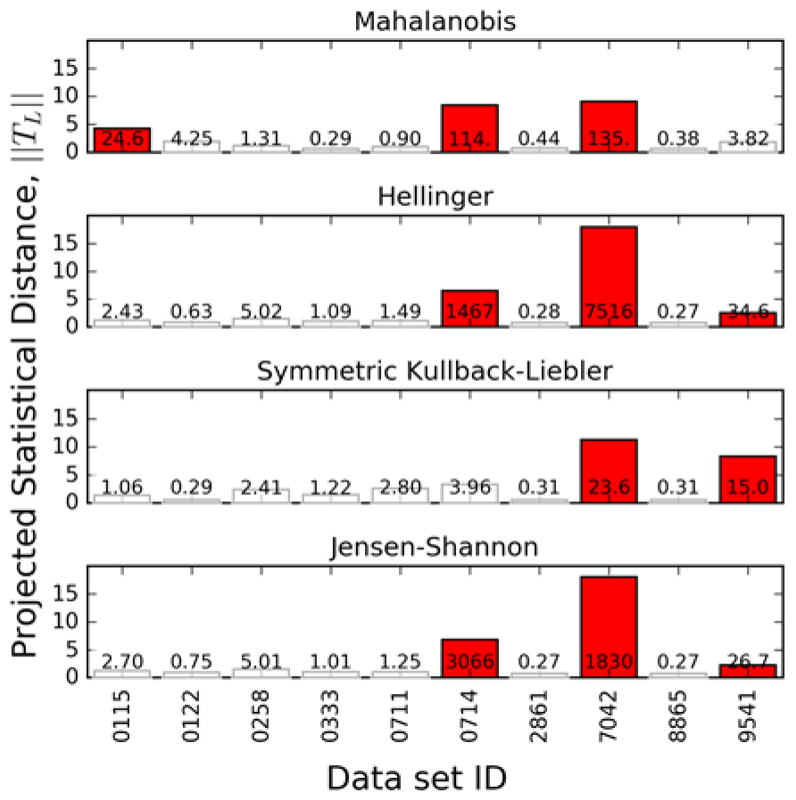
Projected statistical distance ||T_L,i|| calculated using each metric considering only the biological replicate samples C1a, C1b, and C1c. Bars are annotated with their corresponding Z̑_i Outlier data sets are colored red.

4 Conclusion

A two-stage quality control method for interlaboratory comparison was proposed and employed. In this method, the results from a mixture of known substances were used in order to screen for possible process problems, before an interlaboratory analysis was performed on samples of biological origin.

The quality control method was applied to nuclear magnetic resonance spectral data from an interlaboratory comparison study from literature. In this study, each data set included NMR spectra of synthetic mixtures and biological samples, thus enabling the synthetic samples to be used as a quality control measure on the biological samples. The biological samples consisted of one group of fish liver samples from a site exposed to a pollutant and one group from a control site. The method would be considered successful if it was able to separate the biological samples into an exposed and a control group when analyzed using principal components analysis.

Applying the quality control method to the synthetic mixtures proved to be an effective means of identifying difficulties in comparing data sets among the biological samples. Three data sets were identified as potential outliers. These were the same sets as were identified in the original study as exhibiting issues such as peak shifting and incomparable features. In the original study, these three data sets prevented a full interlaboratory analysis from being conducted. That is, the NMR spectra across all data sets could not be compared. Once these data sets were removed from consideration, a principal components analysis was able to separate the biological samples according to their exposure to pollutants. That the algorithm presented here is able to identify these data sets without expert intervention lends credence to its relevance to other studies.

In order to test whether the study of the synthetic mixtures is necessary, the method was applied to the biological samples only. In this case, the set of outliers was smaller, and the principal components analysis did not result in a clean separation between the exposed and control groups. This result underscores the utility of a set of simple mixtures as a means of process control, instead of needing to perform the analysis on the biological samples with their high chemical complexity. The spectrometric methods can easily identify process issues when using the synthetic samples with their highly-controlled compositions, but the complex and unknown composition of the biological samples serves to obscure any process issues that may arise. As a further test, the method was applied to only the biological replicate samples, and a result similar to using the synthetic samples was obtained. This means that using biological replicates for process control is possible, although the use of synthetic samples is still more robust.