The risk of mothers’ losing an only child in China

Abstract

China’s one-child policy has been quite successful in bringing down the fertility level and has produced a large number of one-child families, but their risk of losing the only child has not drawn enough attention. In this paper, using an extension of Goldman and Lord(1983)’s method to measure widowhood, we also use period life table data to examine age-specific and cumulative probabilities of mothers losing their only child. We find that a mother faces a probability of 14.94 percent of losing a son, and 12.21 percent of losing a daughter. As the age of first-time mothers increases, the probability of losing a child declines. Urban and rural mothers have different indices regarding the loss of children. Based on these findings we discuss the prospects for China’s one-child policy.

INTRODUCTION

In the early 1970s, China launched the so-called ‘later, longer, fewer’ population policy, because China’s government viewed rapid population growth as an impediment to expected economic growth. In 1980, China issued An Open Letter to All Members of the Communist Party and Communist Youth Leagueon the Issue of Controlling Population Growth, aimed at controlling the birth rate and population growth, boosting economic development, and improving living standards by adopting one-child policy. China’s one-child policy has been so successful in bringing down China’s total fertility rate (TFR) that after a period of fluctuation around replacement level in the 1980s, the TFR dropped below replacement level in the 1990s. Analysis of the 2000 census reveals that by 2000 the total fertility rate of China had dropped to 1.4–1.6 (Gu et al., 2007; Morgan et al., 2009; Cai, 2010). The strict one-child policy during the past 30 years and the low fertility level for the past 20 years have had broad effects on China’s economic and social development, as well producing effects on population growth, the distorted sex ratio at birth in a context of strong son preference and as a result the biased ratio between men and women, and the ratio between adult children and dependent elderly parents (Hesketh et al., 2005). In the mid-1980s, far-sighted demographers were already predicting that if the one-child policy were to achieve complete success, its subsequent side effects would become much more serious (Bongaarts and Greenhalgh, 1985; Greenhalgh and Bongaarts, 1987).

One of the most important issues that some Chinese families face is that of the only child.In the years 1971 to 1975, it is estimated that 5.41 percent of female births and 6.45 percent of male births in urban areas, and 0.48 percent of female births and 1.06 percent of male births in rural areas, were of only children. In the years 1976 to 1980, these figures rose to 26.55 percent, 31.55 percent, 2.00 percent, and 4.74 percent (Yang and Guo, 2000). However, with the full implementation of China’s birth control policy and the achievement of low fertility, the total number of only children has shown continuous and rapid growth. According to Wang (2011)’s estimate, there were 158.41 million only children aged 0 to 30 in 2005.Such a number implies that over40 percent of Chinese households have only one child. Even if some families currently with a very young only child may have a second child in the future, it can be asserted that over a third of all Chinese households may well end up with only one child (Wang, 2011).

The term ‘one-child family’ refers to a family which consists of the parents and an only child. Compared with a family that has two or more children, a family with one child faces a higher risk of becoming childless as a result of losing that child. Even though the child mortality rate is relatively low, considering the large number of one-child families, we cannot ignore the families facing such risks of losing children. In fact, the question of losing their child for one-child families aroused attention after the Wenchuan earthquake in 2008 in China (Gu and Cai, 2009), in which a death toll of over 80 thousand was estimated.

Accidents to children cause serious psychological trauma to relatives, and the influence of an accident to an only child is particularly significant for the whole family (Fenwick and Barresi, 1981). In general, government policies allow parents with an only child to give birth to another child if their child has a disease, disability or injury, or if he/she dies young. In fact, within China’s localized one-child policy, provincial Birth Planning Regulations do take into account the possibility of losing a child. For example, in Jiangsu’s Birth Planning Regulations, enacted in 1990, one exemption permitting a couple to have a second child is the death of the existing child (Cai, 2010). However, if the only child has a disease, disability or injury, and dies as an adult, it is quite difficult to remedy the situation by giving birth again as parents are older and may no longer be fertile. Therefore, an adult only child’s disability, injury, and death is devastating for the parents (Pan and Jiang, 2007).On June 5th 2012, over 80 parents who lost their only child gathered at the National Family and Birth Planning Commission of P.R.C. expressing their vulnerability after losing their only child, and their hope for financial reimbursement from governments, and more importantly, the hope of establishing a corresponding department to which those who complied with the national family planning policy but now unfortunately have lost their only child could turn to when needed².

Studies concerning Chinese only children were mainly focused on their behaviour and psychology (Poston and Falbo, 1990; Falbo and Poston, 1993; Falbo et al., 2005).Generally speaking, only children are advantaged in academic skills, and disadvantaged in social skills (Falbo et al., 2005). But insufficient attention has been paid to the risk of child losing. Falbo and Poston(1993) find that some only children do enjoy better nutrition and health advantages, but Mu(2009) finds that the risk of losing only children and subsequently ending up with no children is much higher when compared with families with more than one child.

In this paper, using life tables to analyze and estimate Chinese families’ chances of losing their child and other relevant indicators, we hope to provide a basis for the formulation of public policies concerning the death of the child in one-child families. The paper is divided into three parts; the first presents the methods and data used in the passage, the second presents the results, and the last is the conclusion and discussion.

METHOD

Generally fertility-related measures pertain to women, so it would be appropriate to consider losing a child from the point of view of a woman’s life cycle. In this article we calculate the mother’s probability of losing a child; it can also be calculated by the father’s probability of losing a child, which just requires changing the corresponding life table in the formula.

Myers (1959) uses the life table in his study to show the basic formula for calculating the probability of a male losing his spouse, but his calculation was based on the discrete age variable. Goldman and Lord (1983) made some improvements on Myers’ method, designing functions for measuring widowhood and related indicators with continuous age variable and conditional probability. Keyfitz and Caswell (2005) introduced methods for analyzing not only widowhood and related indicators, but also kinship relationships with life tables. In this paper, drawing on the generality of Goldman and Lord (1983) and Keyfitz and Caswell (2005)’s methods, we design formulas to calculate the probability of the female losing a child. The following is the brief introduction of the formulas.

Let l_m (t)and l_f (t)represent the life table probabilities of surviving from birth to exact age t , where superscripts m and f denote male and female, respectively. μ^m(t)and μ^f (t) denote the corresponding risk of dying at age t , where μ (t)= −l'(t) / l t (t). A female becomes a mother at the age x .We assume that a mother’s survivorship is independent of that of children; therefore the probability of losing a boy can be expressed as:

$$P_x^m={\int }_0^w\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)dt$$ (1)

Here t is the length of time from birth to death. w is the upper age limit in the definite integral and we assume the maximum age in the life table is a , so w = a−x. The probability of $\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)$ is the probability of the boy’s death after the mother and her son have both survived t years. It can be regarded as an age-specific probability for a mother to lose her child.

When we talk about a mother’s losing her child, we mean an “average” mother, without taking into consideration her age at childbirth. So we integrate the probabilities of a woman’s becoming a mother at age x, denoted by p(x) to get the ultimate probability for a mother to lose her child is:

$$P^m={\int }_0^w{\int }_{m_x}^{n_x}\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)p(x)\mathit{dxdt}$$ (2)

In which m_x is the minimum age when a female becomes a mother and n_x is the maximum age for becoming a mother. The p (x) is the probability distribution of mothers with an only child and ${\int }_{m_x}^{n_x}p(x)dx=1$. As far as the discrete age variable is concerned, p (x)is the proportion of women who are aged x at the birth of her only child. In the formula (2), ${\int }_{m_x}^{n_x}\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)p(x)dx$ removes the effect on the probability of child loss as a result of mothers’ giving birth at different ages. The formula denotes the probability of a mother’s losing her child when the child is aged t after both the mothers and her child have survived t years.

For a boy, the average age of his mother when the child is lost can be expressed as:

$${MA}^m=\frac{{\int }_0^w{\int }_{m_x}^{n_x}(x+t)\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)p(x)\mathit{dxdt}}{{\int }_0^w{\int }_{m_x}^{n_x}\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)p(x)\mathit{dxdt}}$$ (3)

The number of average years until a mother dies after losing her child, for a male can be expressed as:

$${MP}^m=\frac{{\int }_0^w{\int }_{m_x}^{n_x}{e}_{x+t}\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)p(x)\mathit{dxdt}}{{\int }_0^w{\int }_{m_x}^{n_x}\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)p(x)\mathit{dxdt}}$$ (4)

where e_x+t represents the remaining life expectancy at age x + t for females.

The formulas (2), (3) and (4) remove the age effect when a woman becomes a mother on the child loss indicator. If we are to examine corresponding indicators for a group when they become mothers at the age of x , we can simplify the formula (2) into the formula (1) and simplify the formulas (3) and (4) into the following formulas (5) and (6):

$${MA}_x^m=\frac{{\int }_0^w(x+t)\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)dt}{{\int }_0^w\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)dt}$$ (5)

$${MP}_x^m=\frac{{\int }_0^w{e}_{x+t}\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)dt}{{\int }_0^w\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)dt}$$ (6)

The above formulas apply only to the loss of a son. If it is a girl, one only needs to change the child data. For example, one can simply replace l_m(t), μ_m (t) with l_f (t), μ_f (t).

DATA

From the above it can be seen that the main data used in the article will be the life tables and ages at childbirth, which comes from China’s2000Population Census.

Life tables

The life tables are based on the 2000 population census which, generally speaking, was a successful census but nevertheless suffered from a serious problem, namely that the rate of underreporting is 1.81%. Although this rate is acceptable according to international standards, it is much higher than the 0.06% underreporting rate in the 1990 population census (Lavely, 2001; Walfish, 2001).Population deaths in the census indicate the number of people who died between November 1^st, 1999 and October 31^st, 2000. The data on the death rate are also questionable because of underreporting in death data (Li and Sun, 2003).

It is quite important to select life tables in the study. Banister and Hill (2004) provide life tables in their study, but their life tables are only for total population, not for urban and rural population. Li et al. (2005), analyze undercounting of deaths and adjust the data in China’s 2000 census, and present life tables for total, city, township, and rural population by sex, which we use here. We employ the eight tables here. Life expectancies for people of different residence are shown in Table 1.

Table 1.

Life expectancies at birth by residence in 2000 census

	Male	Female
Total	69.62	73.25
City	72.86	77.48
Township	71.28	76.17
Rural	68.19	71.54

Data Source, Li et al. (2005)

We must point out that since we are studying only children, in actual fact first order births, it would be better if we assumed life tables for first order births people. But due to limited data, we cannot obtain such life tables on first births.

Childbearing age

China’s legal minimum age for marriage is 22 years old for males and 20 for females. The 2000 census reveals that the average childbearing age is 24.83 if the childbearing age range falls between 15 and 49. The number of the first births given by mothers who are aged 20–29 years accounts for 91.2% of the total number of such births. The average childbearing age in this age group is 24.54. This article confines the national childbearing age to the 20–29 age group. The p (x) is the percentage of the first births given by females at the age of x of the total number of children born to mothers aged 20 – 29 years. As far as cities are concerned, the average childbearing age in cities is 26.13, if the childbearing age is limited between 15 and 49. The number of children born to females aged 21–30 years account for 90.3% of the total number of the first births. The average childbearing age for this age group is 25.78. As far as the township is concerned, the number of children born to females age 20–29 accounts for 92.19 percent of all first-order birth, and the average age at childbirth of the age group 24.26 years, and the age for all mothers giving first birth is 24.61. As far as the countryside is concerned, the average childbearing age in the countryside is 24.24, if the traditional concept of the childbearing age falls between 15 and 49. The number of children born to the population aged 19–28 years account for 92.16% of the total number of the first births. The average childbearing age is 23.84.

For the purpose of calculation convenience, this article limits the national child bearing age to the 20–29 age group. The p (x) is the percentage of the first child births given by females at the age of x of the total number of children born to mothers aged between 20 – 29 years, and we normalize these percentages ${\int }_{20}^{29}p(x)dx={\displaystyle \sum _{x=20}^{29}}{p}_x=1$. As in Chin there is a large discrepancy between rural and urban areas when it comes to childbearing, in terms of birth number and timing. Generally, urban females give birth later than their rural counterparts. In this paper we limit the childbearing age range to 21–30 for cities, 20–29 for township, and 19–28 for the countryside.

RESULTS

Age-specific probability of losing a child

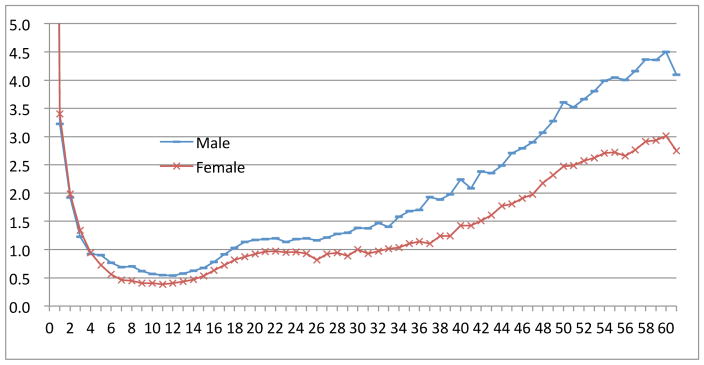
We refer to Figure 1 for age-specific probabilities of losing a child for a mother by age and sex of the child (as the probabilities of losing a child between birth and the age of one is too large to be reflected in Figure 1, we omit them from Figure 1, but Figure 2 can be taken as a reference). In the curve of the child’s age from 0 and 4, the age specific probability of losing a girl is higher than that for a boy. In a normal population without gender discrimination, biomedical factors are the main elements determining gender differentials in mortality levels in infant and early childhood (0–4 years old).There should be a normal level of ratio of the mortality rate for boys to that of girls (usually greater than 1), which reflects the biological gender differences in children’s mortality rates. Hill and Upchurch’s(1995) study, and Coale and Demeny’s western model life tables (Coale and Demeny, 1966) all show that the mortality rate for boys is higher than that for girls. But in China, the gender pattern of infant mortality is significantly different. From Li et al’s (2005) life table, the male infant mortality rate is 28.14 per thousand and that of females is 35.51 per thousand. Banister and Hill (2004) found a similar pattern and estimated that in 2000, China’s infant mortality rate for males was 22.66 per thousand and for females 33.51 per thousand. Some studies showed that in China the female’s mortality rate in the 1–4 age stage is 10% higher than the male’s, and the discrepancy is more obvious in the higher birth order, which reaches 15%. In particular, for the higher birth order children who were born in rural and have elder brothers and sisters, the discrepancy surprisingly reach up to 25%. In other words, for the parents who have already both a boy and a daughter in rural give birth to a girl, the chance of the girl’s death is 50% higher than that of a boy (Choe et al., 1995). This excess female child mortality is caused fundamentally by the strong son preference in traditional Chinese culture, and exacerbated by the government-guided family planning program and regulations (Li et al., 2004), still is usually a result of discrimination against girls in socioeconomic and health-related behavioural and environmental factors, such as nutrition, food and health care (Hill and Upchurch, 1995; Li et al., 2004). Those girls, who died from deliberate neglect(or referred to as active or passive infanticide) may be different from those dying of causes beyond the control of her parents, but they still caused trauma to her parents and relatives.

Figure 1.

Probability of losing a child for a mother by age and sex of the child (per thousand).

Figure 2.

Cumulative probability of losing a child for a mother by age and sex of the child (per thousand)

Biologically, females have a survival advantage over males at the same age. In Figure 1, this advantage begins to show after the child is 4 years old, as age-specific child-losing probability for a female child is lower than that for a male child. From Figure 1, for the most of the curve, if the child is a boy, the mother faces a greater likelihood of the child’s death. In usual situations, the age-specific death rate of males is higher than that of females, and this is reflected in most of the curve in Figure1.

It can be seen that the age-specific probability for a mother to lose her child decreases for boys aged 0 – 12 years as well as for girls aged 0 – 11 years before it gradually increases. When a child reaches the age of 20, the age-specific probability for a mother to lose a child is 1.17 per thousand for boys and 0.92 per thousand for girls. When a child reaches the age of 40, the age-specific probability for a mother to lose a child is 2.24 per thousand for boys and 1.43 per thousand for girls.

Cumulative probability of losing a child

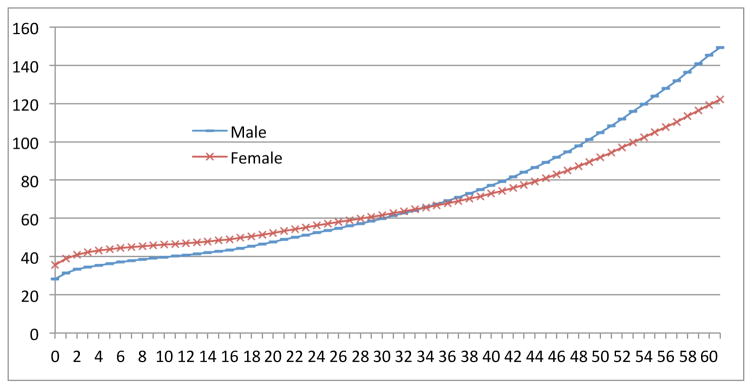
Figure 2 shows the cumulative probability of losing a child for a mother by age and sex of the child. Eventually the risk of losing a male child for a mother is 14.94 percent, while that for a female child is 12.21 percent. Before the child’s age of 36, the cumulative probability of losing a girl is higher than that of losing a boy, which results from the huge discrepancy when the child is 0–4 years old. After the child’s age of 36, the cumulative probability of losing a boy is higher than that of losing a girl. At the child’s age of 30, the cumulative probabilities are 59.92 per thousand and 61.73 per thousand for a male and female child respectively. At the age of 40, the probabilities rise to 77.17 per thousand and 72.94 per thousand. At the age of 50, the probabilities increase to 104.83 per thousand and 91.93 per thousand.

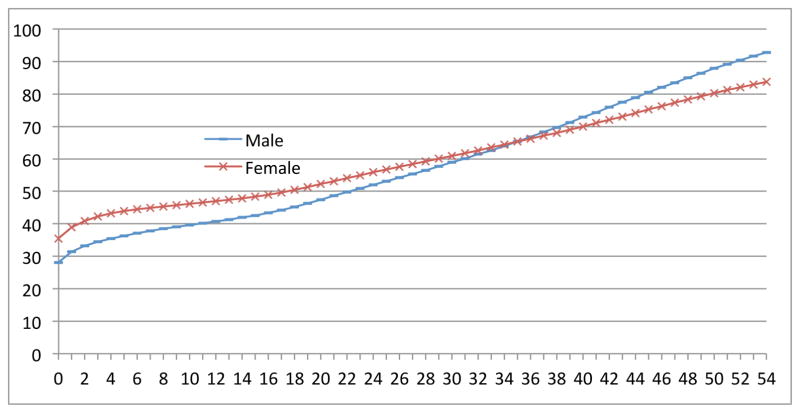
If a mother loses a child at younger age, say when the child is below 20 and she herself in 40s, she may have a chance to have another biological child. But if she loses the child when the child is over 20, she may lose such replacement chance. Besides Figure 2, we provide a figure of cumulative probabilities for mothers who begin their motherhood at 36. We can see that cumulative probabilities is lower than that in Figure 2.

Sensitivity analysis of effect of the age at which motherhood begins on indices

As Table 2 shows, the age at which a female becomes a mother has an influence on the indices of losing a child. During the increase of this age from 20 to 36, the probability of losing a boy falls from 16.61 percent to 9.27 percent, and the probability of losing a girl falls from 13.34 percent to 8.37 percent. However, the change in the age at which a female becomes a mother has little effect on the average age of losing a child and the average years spent until a mother dies after losing her child.

Table 2.

Effect of mother’s age at childbirth on indices of child loss

Age	Cumulative probability of losing a child (%)		Average age at losing a child (years)		Years survived after losing a child
	Male child	Female child	Male child	Female child	Male child	Female child
20	16.61	13.34	54.90	49.70	26.63	31.14
22	15.83	12.81	55.91	50.66	25.94	30.44
24	14.98	12.24	56.73	51.44	25.41	29.89
26	14.08	11.63	57.37	52.05	25.02	29.46
28	13.18	11.02	57.86	52.54	24.72	29.10
30	12.11	10.29	57.73	52.47	24.80	29.09
32	10.99	9.54	57.12	52.02	25.15	29.29
34	10.06	8.90	56.72	51.83	25.34	29.28
36	9.27	8.37	56.50	51.85	25.37	29.09
Total	14.94	12.21	56.56	51.30	25.53	29.99

Total is derived with formulas 2, 3 and 4; others are derived with formulas 1, 5 and 6.

Formula (1) reveals that when a mother’s age increases from a relatively young age (e.g.: 20 years old), w , the upper age limit in the definite integral which is w = a−x as defined decreases, so the cumulative probability of losing a child usually decreases. It still means that as the age at childbearing increase, the risk of the mother dying before the child rises (as the probability for a mother to predecease her child is the complementary probability of $P_x^m$ defined Formula (1)).

As for the difference in the mean age for the mother at the loss of a boy and a girl, we can see from Formula (5) that the age at child loss is actually a weighted average of x + t, and the weights are $\frac{l^f(x+t)}{l^f(x)}\frac{l^m(t)}{l^m(0)}{\mu }^m(t)$ for a boy and $\frac{l^f(x+t)}{l^f(x)}\frac{l^f(t)}{l^f(0)}{\mu }^f(t)$ for a girl. From the discussion above we know female children have excess mortality compared their male counterparts, so a higher proportion of girls who die at very young ages when their mother are still very young depresses the mean age of mothers at losing a female child.

Formula (5) still reveals that the child loss age can be attributed to a combination of several factors: the age-specific probability of losing a child, a mother’s age x and the cumulative probability of losing a child. For a male child, the age for a mother at child loss don’t change significantly with the increase in age at motherhood.

Rural-urban difference in child losing indices

With the implementation of China’s family planning policy, there are more and more only children in urban and rural areas. There is a big difference between urban and rural areas in terms of social and economic development, as well as in the allocation of health resources(Zhang and Kanbur, 2005). In 2010, the gap of per capita disposable income between urban and rural areas is 3.23 to 1, making it one of the largest urban-rural gaps worldwide (Wang and Zhu, 2011). The large gap between urban and rural areas leads to different health results and mortality rates, with the rural population at a great disadvantage. Table 3 shows the difference in indices of the loss of children between cities, township and rural areas. Mothers in rural areas have a much higher risk of losing a child than their counterparts in towns and cities, and their average age when losing a child is lower than that for urban mothers. But due to their shorter life expectancy at birth, observed in Table 3, the remaining life expectancy for mothers from rural areas after the death of their only child is almost the same as their urban counterparts.

Table 3.

Urban-rural difference in indices of child loss

	Cumulative probability of losing a child (%)		Average age at losing a child (Years)		Years survived after losing a child
	Male child	Female child	Male child	Female child	Male child	Female Child
City	11.27	8.09	59.39	55.03	24.90	28.74
Township	13.69	9.84	59.02	53.39	24.89	29.83
Rural	17.02	14.17	55.81	50.74	25.42	29.67

Data are derived with formulas 2, 3 and 4

CONCLUSIONS AND DISCUSSIONS

Because of the increase in the proportion and total number of one-child families, [Chinese] society as a whole has become concerned about the growth and development of only children, as well as related phenomena and problems concerning them, and only-child and related issues are receiving more and more attention from researchers. Once there is an accident to the only child, it affects the economic interests of family members, threatens the safety of family property, and also affects the family culture, genetic heritage, and also, to some degree, harms the emotions dependent on blood and marriage (Pan and Jiang, 2007). If the child dies at an early age when the parents are still young, they can give birth to another child in compensation. However, if the parents are older when the child dies, it is more difficult to have another child. One-child families are more afraid of losing a child later in their life-cycle. The survival risks which appear in the early life-cycle can be dispelled by compensatory fertility, but survival risks which appear in the later stages of the life-cycle mean the possibility of compensatory fertility is lost because the parents are older. The loss of a child in middle age would fully affect the material and emotional life of one-child families.

Through the above analysis, the main findings are as follows:

Firstly, because of the preference for sons in China, there is a higher probability of girls’ mortality than that of boys during infancy. Therefore, the mother’s age-specific probability of losing a girl is higher than that of losing a boy when the children are 0–4 years old. But after the age of 5, the age-specific probability of losing a son is higher than that of losing a daughter.

Secondly, the cumulative probability of losing a child increases as the age of the child increases. At the child’s age of 30, the cumulative probabilities are 59.92 per thousand and 61.73 per thousand for a male and female child respectively. At the age of 40, the probabilities rise to 77.17 per thousand and 72.94 per thousand. The probability of losing a child (a son or a daughter), namely the cumulative probability of children dying before their parents, is 14.94 percent for a son and 12.21 percent for a daughter.

Thirdly, we can see that with the increase in the age at childbirth, the cumulative probability of losing a child declines, and the average age at losing a child first increases and then declines, but generally the average age at losing a child does not change much, nor do the years survived after losing a child.

Finally, there is also a difference between the probability of losing a child in urban and rural areas. The risk of losing a child in rural areas is higher than in urban areas, and the average age at which mothers lose their child is lower. Still, as the age range at childbirth is the same for the population in townships as it is for the total population, and the population in townships enjoys a lower mortality level and higher life expectancy, we can see that as the mortality level decreases, the probability of losing a child also decreases, and the age at child loss increases.

One may be concerned with the years survived for a woman after she loses her only child. For only-child families, a woman’s family members include her husband and her son. The average age at losing an only son for a woman is 56.56 years, and that for losing an only daughter is 51.30 years. Let us examine the probability of losing her husband. According to Jiang et al. (2012)’s study, a woman at age 60 faces the cumulative probability of 0.2 of losing her husband, and at 70, she faces a probability of 0.4. So after losing her child, she has a probability of 0.8 of living with her husband(without taking into account divorce or separation), and at age 70, there is a 60 percent possibly of living with her husband.

One may argue that even if a woman has more than one child, she still faces the probability of losing children. But she will undeniably face a much lower probability of having no children. From Figure 2 we can see that when the child is 30, the cumulative probability of losing a child is 6 percent. But if a woman has two children, then at the children’s age 30, the probability of having no children for a woman is less than 3.6 per thousand. (We roughly estimate that the probability of having one child is 0.94, and having two children is two independent events, thus the probability of having no children is 1-(0.94+0.94–0.94×0.94)).

As the proportion and number of one-child families is increasing, some scholars have analyzed the feelings of parents of only children towards the child’s safety. If a car accident happens on a bustling city street, and the injured person is a child, when the parents of an only child hear such news, they normally show anxiety, agitation, and cannot control their emotions. Even if their child is not hurt, they would have a feeling of insecurity with some kind of external stimulus (Lin and Zhang, 2001). This sense of insecurity in the context of Chinese culture will become especially strong because the death of offspring is the most unacceptable thing in the tradition of “family first”. The fear of remaining childless makes ‘incomplete’ family-planning families caused by the death of the only child hold a grudge against society, as they attribute their childlessness to the one-child policy(Mu, 2009). As many elderly people depend on their adult children for old age support, being without a surviving child will certainly leave those child-losing parents in a dilemma in their old age. In fact, the Chinese government has paid attention to the issue of old age support and the other needs of such parents. In China’s 11th Five-Year Guidelines for National Economy and Social Development released in 2006, it is stated that a support system should be established for those only child families whose only child dies or is disabled. And in the Law of the People's Republic of China on Population and Family Planning, it is stipulated that local governments should assist those parents whose only child is dead or disabled, on the condition that those parents are to give up a second birth and not to adopt one child (Huang, 2009). But the assistance obtained from local governments is far from enough. There have been some family-planning families who have demanded compensation from the government, due to their loss of an only child. If the resentment cannot be resolved, and the compensation requests cannot be met and satisfied quickly, this would pose a threat to social harmony and stability (Mu, 2009).

The one-child policy, which has been widely criticized around the world and has damaged China’s international image (Zeng, 2007), is perhaps the most ambitious family planning policy in the world. The current fertility policy requires about 63% of families to have only one child (Gu et al., 2007).In the 2009 World Population Data Sheet offered by the USA Population Reference Bureau, China’s total fertility rate was 1.6, while some scholars estimate that it is currently between 1.4 and 1.6, and it may drop to 1.4 in 2020 (Morgan et al., 2009).The preliminary results of China’s latest census in 2010 indicate an approximate but low fertility rate, below 1.5(Hvistendahl, 2011).Although China is not yet ready to give up the current birth policy, there are more and more appeals for the relaxation or termination of such a policy. During meetings of China’s NPC (National People’s Congress, the highest organ of State power of the People's Republic of China. Its main functions and powers include formulation of laws, delegating authority, policy formulation, and supervision of other governing organs) and CPPCC (Chinese People's Political Consultative Conference, a political advisory body in the People's Republic of China) in March 2011, many deputies to the two organizations and scholars debated the one-child policy and stirred up considerable controversy in society. Administrative control of personal decisions about fertility has generated and will continue to generate an increasing array of problems, and now the policy faces severe challenges (Peng, 2011). Less restrictive policies are realistic alternatives whose consequences are likely to be socially and economically positive for the nation. In the 1980 Open Letter, it is stated that the one-child policy is for one generation. Now, after 30 years of strict implementation, it is time to consider adjusting the policy.

Still the paper has some drawbacks which may affect our results. One of them is the assumption of the independence of mother’s and child’s mortality. We in fact know that in general the hereditary and socioeconomic factors make children’s life expectancy to be correlated with that of their mothers and that the loss of a relative induces stress in individuals, thereby harming their health, but due to the lack of life tables for people who have lost their child, we have to use life tables without distinguishing whether the population used to calculate the life tables have lost their child or not. And we limit the childbearing age to a small range around peak childbearing age; this lowers the age at childbearing, and will lower the cumulative probability of losing a child.

Figure 3.

Cumulative probability of losing a child for a mother by age and sex of the child (per thousand), motherhood age 36