Abstract
Objective
In glioblastoma, the crosstalk between vascular endothelial cells (VECs) and glioma stem cells (GSCs) has been shown to enhance tumor growth. We propose a multiscale mathematical model to study this mechanism, explore tumor growth under various initial and microenvironmental conditions and investigate the effects of blocking this crosstalk.
Methods
We develop a hybrid continuum-discrete model of highly organized, vascularized tumors. VEC-GSC crosstalk is modeled via VEGF production by tumor cells and by secretion of soluble factors by VECs that promote GSC self-renewal and proliferation.
Results
VEC-GSC crosstalk increases both tumor size and GSC fraction by enhancing GSC activity and neovascular development. VEGF promotes vessel formation, and larger VEGF sources typically increase vessel numbers, which enhances tumor growth and stabilizes the tumor shape. Increasing the initial GSC fraction has a similar effect. Partially disrupting the crosstalk by blocking VEC secretion of GSC promoters reduces tumor size but does not increase invasiveness, which is in contrast to anti-angiogenic therapies, which reduce tumor size but may significantly increase tumor invasiveness.
Significance
Multiscale modeling supports the targeting of VEC-GSC crosstalk as a promising approach for cancer therapy.
Index Terms: Mathematical Model, Feedback Regulation, Brain Tumors, Cancer Stem Cells, Cancer Therapies
I. Introduction
Glioblastoma (grade IV glioma, GBM) is one of the most aggressive and deadly brain tumors causing over ten thousand deaths each year in the United States [16, 72]. The median patient survival for GBM is approximately 15 months, according to the American Brain Tumor Association [34]. It remains a challenge to eradicate GBM because of its highly vascularized, heterogeneous, and invasive nature [1].
In recent years, the heterogeneity of GBM has been extensively studied [9]. The glioma stem cell (GSC) hierarchy has been found to play a crucial role in tumor development and therapy resistance [68]. For example, tumors with high GSC population are more aggressive than tumors with low or no GSCs [6]. Further, as noted in [6], GSCs have three main characteristics. They are multipotent (differentiate into the other cell types), are able to self-renew (give rise to cells with the same characteristics) and produce tumors when implanted in animal models. It is also believed that GSCs are responsible for resistance to radiotherapy and chemotherapy [23]. However, there are limited experimental studies that identify different tumor cell lineages in GBM progression [14, 51]. In this study, we develop and investigate a mathematical model to provide a better understanding of GSC dynamics in tumor progression.
In healthy brain, it has been observed that the microenvironment of the neural stem cells (NSCs) is important in maintaining their stemness. In particular, vascular endothelial cells (VECs) secrete factors that stimulate the self-renewal and proliferation of NSCs, and NSCs are found close to capillaries [61, 65, 70]. This crosstalk between the NSC niche and capillaries motivated similar studies in glioma. For example, [11] found that Nestin+/CD133+ cells, which are believed to be GSCs, are located closer to the capillaries, and GSCs cocultured with VECs exhibit increased proliferation and self-renewal. In addition, GSCs respond to signals present in the secretome of VECs, indicating that GSCs do not require direct contact with VECs [11].
Several molecules are believed to control the crosstalk. These include endothelial Nitric Oxide that activates Notch signaling between adjacent VECs and GSCs and regulates the proliferation of the GSCs [13, 24, 80]. Also implicated is the Hedgehog (HH) pathway, which is involved in maintaining the stem-ness of somatic cells [54]. Sonic hedgehog ligand (Shh) is secreted by VECs and activates the HH pathway in GSCs, which regulates their self-renewal and proliferation [76]. The mTOR pathway has also been shown to maintain GSCs in the presence of VECs [30]. These pathways can be targeted by possible anti-tumor therapies. For example, blocking the mTOR or Hedgehog pathway has been shown to reduce the self-renewing GSC population and tumor size, via blocking of the crosstalk between VECs and GSCs [30, 76].
Numerous mathematical models have been developed to study tumor growth and its response to treatment [19]. For example, [36] reviewed theories of tumor vasculature and simulated random vessel network generation algorithms, tumor-vasculature interaction via growth factors and oxygen, and interstitial fluid flows. In [37], a data-based model was used to validate the structural link between metastatic emission and primary tumor size. In [62], a hybrid cellular automation was developed to investigate the effects of metabolic heterogeneity on tumor progression. Diffusible cytotoxic treatments (e.g. chemotherapy) and antiangiogenic therapy may increase metabolic aggressiveness. In addition, hybrid continuum-discrete models have been developed to model angiogenesis and vessel networks [2, 28, 53]. Ref. [31] revealed that acute and fractionated irradiation results in GSC enrichment, which contributes to accelerated repopulation after irradiation, and reprogramming of non-cancer stem cells back to a cancer stem cell state [32].
In this paper, we develop a 3D hybrid continuum-discrete model of GBM by accounting for cancer cell lineages (collections of progressively more differentiated cancer cells) and feedback among the different cell types, following the continuum model in [78]. We account for tumor-induced neovascularization, using the discrete model in [28], and incorporate crosstalk between GSCs and VECs via pro-angiogenic factors secreted by tumor cells and factors secreted by VECs that promote GSC self-renewal and proliferation. We consider the effects of different VEGF sources on tumor progression and neovascularization. Since GSCs play an important role in tumor progression, we vary the initial GSC fraction and study tumor response. Then, we investigate the effects when the crosstalk is partially disrupted and when angiogenesis is blocked. Lastly, we relate our results to experimental findings and discuss future work.
II. Methods
A. Continuum tumor growth model
We adapt the three-dimensional multispecies tumor mixture model described in [28, 74, 78], where tumor cells are tightly packed and cell species are modeled as volume fractions. Let φGSC, φGCP, φGTD, φD and φH be the volume fractions of GSCs, committed progenitor GBM cells (GCPs), terminally differentiated GBM cells (GTDs), dead GBM cells and host tissue respectively. The total fraction of tumor cells is φT = φGSC + φGCP + φGTD + φD. We assume that the fractions of solid region φS = φT + φH and interstitial water (φW) are constant and add up to 1. The volume fractions of the cells are normalized by φs.
The volume fractions satisfy the mass conservation equation
| (1) |
where i = GSC, GCP, GTD, D or T, and Ji is a mass flux. The term ▽ · (uφi) models passive cell movement (advection); u is the mass-averaged velocity of solid components defined by Darcy’s law: u = –▽p + F, where F models cell adhesion and p is the solid pressure created by tumor cell proliferation. See Sec. S1 in Supplemental Materials for further details. Our choice of u represents passive cell movement from high to low pressure.
B. Tumor cell species and lineage relationships
Following [78], we assume that the proliferation rates of GSCs and GCPs are proportional to the nutrient concentration n, which is nondimensionalized such that n = 1 in the well-vascularized tissue and n ≤ 1 in the tumor. GSCs and GCPs self-renew with probabilities p0 and p1 respectively. GTDs do not proliferate and die at a constant rate (e.g. apoptosis). Because the proliferation rate is proportional to nutrient level, the effective death rate (death rate minus proliferation rate) increases in regions where there are fewer nutrients, which mimics the effects of necrosis. Dead cells are lysed into water. The mass exchange terms for tumor cells are
| (2) |
Here and are the mitosis rates of GSCs and GCPs respectively. is the apoptosis rate of GTDs, and is the lysis rate of dead cells. The mass exchange term of total tumor is the sum of Eq. (2) and accounts for GSC and GCP proliferation as well as cell lysis:
| (3) |
C. Angiogenesis
We adapt the angiogenesis model in [28], which was inspired by earlier work [2]. This model generates a vascular network stimulated by soluble angiogenic regulators (e.g. vascular endothelial growth factor, VEGF [5, 69]), which we model using a single variable CV that represents the total concentration of pro-angiogenic factors (henceforth referred to as VEGF). In particular,
| (4) |
where DV, dV and SV are the diffusivity, natural decay and production rates of VEGF respectively. For example, VEGF may be produced by viable cells (whose volume fraction is φV = φGSC + φGCP + φGTD = φT – φD) in regions of hypoxia [42, 55]. This can be modeled as SV = PVH(ñ–n)(φT – φD), where pV is production rate, H(x) is the Heaviside function (H(x) = 1 when x > 0 ; H(x) = 0 otherwise), and ñ is the hypoxia threshold that viable cells (φT – φD) produce VEGF when the nutrient level n < ñ. Other sources of VEGF are considered in Sec. III. B.
Vessel sprout sites are selected at a constant probability once the VEGF concentration is higher than a threshold in a region a short distance away from the tumor. This simulates endothelial cells proliferating and forming vessels towards the VEGF tumor gradient [42]. The tip endothelial cell of a capillary moves in circular random walk and so the vessel network is independent of the computational grid for tumor cells. At each time step, the tip cell has a fixed probability to divide into two leading endothelial cells that continue to develop into new vessels. Once a tip cell crosses the path of another vessel, the two vessels may connect (anastomose) and form loops, and begin to deliver cell substrates, e.g. nutrients to the tumor [3]. Such vessels are termed “functional.” The contribution from all vessel segments that supply cell substrates is integrated to obtain the effective vascular density. Further, when the solid pressure created by tumor cell proliferation exceeds a threshold at a specific location, nearby vessels are shut down (with a certain probability) [39] by removing them from the vascular network and any associated vessel loops will discontinue nutrient delivery.
D. Cell Substrates and Feedback Regulation
We assume that the nutrient concentration n satisfies a quasi-steady state equation, because nutrient diffusion (minutes) occurs significantly faster than cell proliferation (days). Nutrients are produced by pre-existing vessels in the host tissue and functional (anastomosed) vessels [3]. Cells uptake nutrients at potentially different rates. In particular,
| (5) |
where Dn is the diffusivity, dn is the natural decay rate, , and are the uptake rates by GSCs, GCPs and GTDs respectively. The function Q(φT) ≈ 1 – φT approximates the characteristic function of the host tissue, see [73]. and are the nutrient supply rates from the pre-existing and functional neo-vessels (ρFV) respectively. n̄ is the nutrient concentration in the vessels.
The self-renewal fraction of GSCs and GCPs are controlled by various soluble signaling factors. We assume that GTDs produce negative feedback regulators CT1 on GSC self-renewal and CT2 on GCP self-renewal. Frequently, these are members of the TGF-β superfamily, which are known to diffuse over long ranges. For example, bone morphogenetic proteins (BMPs) inhibit the self-renewal of stem-like cells in GBM [59]. In addition, we follow [78] and account for a self-renewal promoter CW (e.g. Wnt [4]) and its inhibitor CWI (e.g. Dkk [35, 49] in the case of Wnt). Both CW and CWI are produced by GSCs [44] and their production rates are proportional to the nutrient concentration. We use a generalized Gierer-Meinhardt model described in [78] for CW and CWI. See Sec. S2 in Supplemental Materials for details.
E. Crosstalk
In brain tumors, primary human endothelial cells (pHVECs) are found to help maintain the cancer stem cell pool through soluble factors, and increase the size of tumor spheres by up to five-times larger [11], suggesting positive feedback from pHVECs to stem cells. The mechanisms include Notch signaling [40], endothelial Nitric Oxide [22] and Hedgehog pathway by diffusion [76]. Here, we investigate the combined effect of these mechanisms, and assume that the vasculature produces a soluble cell substrate F whose concentration is CF:
| (6) |
where ▽ ·(uw CF) models the advection with the interstitial water, DF and dF are the diffusivities and natural decay respectively. pF, is the production rate from neovessels (ρV), C̅F is the concentration near the vessels. The factor F is assumed to represent the concentration of all VEC secreted GSC promoters.
We assume that CF promotes both GSC proliferation and self-renewal [22, 76]. We thus take the GSC mitosis rate to be
| (7) |
where is the base proliferation rate, is the positive feedback gain by CF and is the maximum fold change. Next, we incorporate the positive feedback by CF and CW, and negative feedback by CT1 on GSC self-renewal. Following [46, 78], we take a mixed feedback model
| (8) |
Here and are the minimum and maximum levels of GSC self-renewal respectively. and are the positive feedback gains by CF and CW respectively. ψ0 is the negative feedback gain by CT1. The self-renewal probability of GCPs is defined analogously without the feedback from CF :
| (9) |
III. Results
We now solve the model to study tumor progression and its response to treatment. The tumor begins as a perturbed avascular spheroid that, unless stated otherwise, consists of uniformly distributed 10% GSCs, 25% GCPs, 60% GTDs and 5% dead cells. All parameters are listed in Table S1 in Supplementary Materials.
A. VEC-GSC crosstalk promotes stem cell proliferation
At early stages, GSCs self-organize and clusters emerge at tumor boundary (Fig. 1A, red; Fig. 1B) as an effect of a Turing-type pattern formation of the self-renewal promoter and its inhibitor. While the tumor grows these GSC clusters stay near the tumor boundary, which was also observed in vivo [15, 71] and in vitro [67]. Dead cells concentrate at the tumor center, where the nutrient level is lowest and tumor cells are hypoxic (see Fig. S1 (C-D) in Supplemental Materials). Blood vessels sprout (red dots) near the tumor boundary around T = 40, then grow and anastomose into functional vessels (blue lines) that are connected to host vasculature and supply nutrients to the tumor. This neovascularization near the tumor-brain interface has been observed clinically [7]. Consequently, tumor cell proliferation is enhanced and the tumor size grows rapidly. Interestingly, the evolution of the GCPs is non-monotone; the GCP fraction reaches a minimum around T=50 (Fig. 1A and Fig. S4 (blue) in Supplementary Materials). This occurs because around this time GSC self-renewal is enhanced by VEC-GSC crosstalk, p0 at the center begins to increase over 0.5 due to positive feedback F secreted by VECs (Fig. 1C). This decreases the replenishment of the GCP population by differentiating GSCs and so GCP numbers decrease due to their differentiation to GTDs (note that the maximum GCP self-renewal , see Table S1 in Supplemental Materials). As a result, a new GSC cluster emerges at the tumor center, which was also observed in [60], and the GSC fraction in the tumor increases (Fig. 1B, Fig. 2B, blue). We note that high p0 regions are colocalized with functional vessels, which are mainly present at the tumor center (Fig 1C). These high p0 regions increase solid pressure at the tumor center, which results in tumor cells moving outwards from the hypoxic core (see Fig. S2 in Supplemental Materials).
Fig. 1.
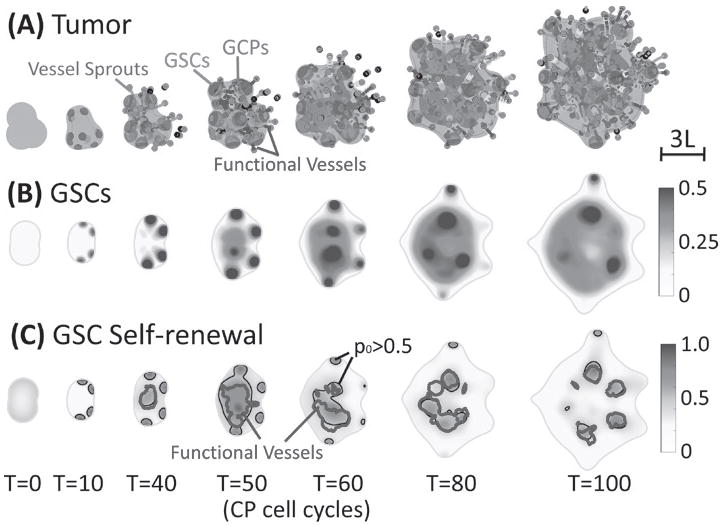
VEC-GSC crosstalk promotes GSC proliferation and self-renewal. (A) Time evolution of tumor (φT = 0.5 surface, blue), GSCs (φGSC = 0.3 surface, red), GCPs (φGCP = 0.25 surface, green) and neovasculature (red dots: sprout initiation points; grey: sprouts, blue: functional vessels). At early stages, GSC clusters form near the tumor boundary and fingers develop. Angiogenesis starts around T =39, after which a large GSC cluster forms at the center of tumor due to VEC-GSC crosstalk. (B) 2D slices of GSCs (at z =-1). At T=5, GSC clusters begin to emerge near tumor boundary. (C) 2D slices of the GSC self-renewal probability p (at z=-1) 0 shown together with the p0 = 0.5 (black) and functional vessel density ρFV = 20 (blue) FV contours. In the tumor interior, the functional vessels are colocalized with GSC clusters with p0 > 0.5.
Fig. 2.
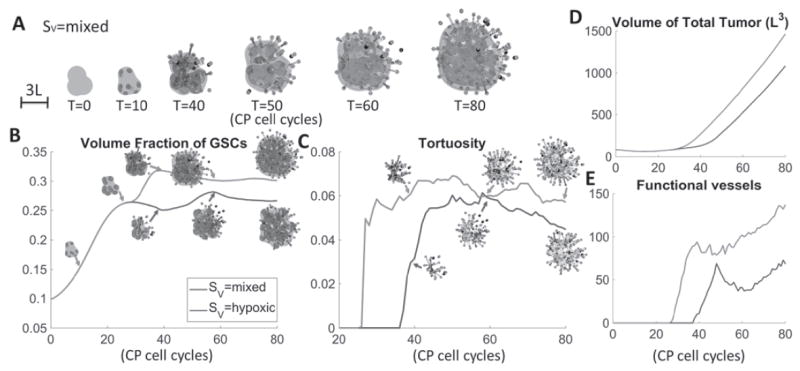
VEGF sources affect tumor and vasculature characteristics. (A) Time evolution of tumor with mixed VEGF production, i.e. SV = pVH(ñ – n)(φT – φD) + pV (φSC + φCP) Blue: tumor boundary; red: GSCs; green: GCPs. Red dots: sprout initiation points; grey: sprouts, blue: functional vessels. (B) Time evolution of GSC fractions; (C) vessel tortuosity; (D) total tumor volume and (E) numbers of functional vessels with indicated VEGF sources. Insets in (B) show GSCs (red) in the tumor (blue). Insets in (C) show the vessel network. When GSC/GCPs produce twice as much VEGF as other cells (red curves), the tumor has larger size, GSC fraction and more spherical shape. The vessels are generated earlier and more tortuous. At late stages, vessel crushing takes place in all tumors leading to saturation in vessel tortuosity.
B. VEGF sources affect tumor and vasculature characteristics
Next, we study the effects of different VEGF sources on the tumor and vasculature. To quantify the tumor shape, we use the shape factor: , where S and V are the surface area and volume of the tumor respectively. Note that a sphere has shape factor equal to one. To quantify the vessel network, we use the tortuosity of the vessel network (following [75]), as well as the total number of vessels and the number of functional vessels. In Fig. 1, VEGF is produced by hypoxic tumor cells, that is, SV = pVH (ñ – n)(φT – φD) is used in Eq. (7), as described earlier. The tumor volume grows rapidly once angiogenesis starts around T=37 (Fig. 2A, blue). The volume fraction of GSCs increases slightly after this (Fig. 2B, blue) due to enhanced GSC proliferation and self-renewal because of increased nutrients and positive feedback from VECs. After T=60, the fraction reaches a maximum and stabilizes. We will discuss this in the next section. The tumor remains roughly spherical with shape factor approximately equal to one (Fig. 2C, blue) although the growth of fingers at late times increases the shape factor. The total number of vessels steadily increases (Fig. 2F, blue), consistent with the fairly steady increase in VEGF production (Fig. 2G, blue). However, the number of functional vessels also reaches a maximum shortly after angiogenesis is initiated (Fig. 2E, blue) and before increasing at late times. The non-monotone dynamics of the number of functional vessels is due to the crushing of vessels by high pressure resulting from rapid cell division (see Fig. S5 in Supplementary Materials), which is consistent with experimental observations [52, 66]. Vessel crushing also causes the tortuosity of the vascular system to saturate (Fig. 2D, blue).
It has been believed that hypoxic tumor cells secrete angiogenic proteins that promote tumor vascularization, as modeled above. However, [5] observed that tumors initiated with stem-like glioma cells are more vascularized and aggressive. Under normoxic conditions, only GSCs secrete angiogenic factors, e.g. VEGF. However, non-GSCs also secrete VEGF under hypoxic conditions. In particular, GSCs were found to secrete more than twice as much angiogenic factors than non-GSCs. To model this mixed VEGF production, we take SV = pVH (ñ – n)(φT – φD) + pV (φSC + φCP), where we assume that GCPs and GSCs behave similarly with respect to VEGF production. Compared to Fig. 1, the tumor with mixed SV grows faster (Fig. 2A, red versus blue), has larger GSC fraction (Fig. 2B), is more compact (Fig. 2C), has more tortuous vessels (Fig. 2D), and more vessels generally (Figs. 2E and F) and generates larger amounts of VEGF (Fig. 2G). This is consistent with [5]. In a migration and tube formation assay with endothelial cells using conditioned media from CD133+ (GSC) and CD133- cells, the authors observed larger tumor size and higher total vessel length with CD133+ conditioned media. Moreover, higher microvessel densities were observed in GSC orthotopic xenograft tumors in mice compared with non-GSC tumors, indicating that GSCs recruited higher number of VECs, which is correlated with the amount of VEGF secreted.
Accordingly, neovascularization starts earlier, which is consistent with [50]. In this case, the tumor is vascularized around T=25, compared to T=37 for hypoxic production of VEGF. Interestingly, because nutrients are supplied into the tumor interior, the GSC clusters originally at the tumor boundary move inwards and merge with the central GSC cluster. As a result, finger development is suppressed and the tumor acquires a nearly spherical shape. In contrast, the tumor in Fig. 1 still has fingers at late stages that continue to develop.
After the tumors are vascularized, they all grow roughly at the same speed (Fig. 2A). The vessels are less tortuous compared to both the mixed and hypoxic VEGF sources because most vessels are directed towards GSC clusters. This also results in less pressure-induced vessel crushing, as seen by the steady increase of functional vessels at later times (Fig. 2E, green). The shape factor is increased compared to the tumor with mixed Sv due to fingers on the tumor surface (Fig. 2A). The tumor is less invasive (smaller shape factor) than the hypoxic case (Fig. 2C). This is consistent with previous evidence that shape and invasiveness may be related in glioblastoma [7, 29, 58]. In addition, experimental works have shown that aggressive glioblastoma tumors are characterized by unstable morphologies, including the formation of invasive fingers [8, 45].
Overall, we observe that the larger VEGF production results in vascularization of the tumor at an earlier time and that GSC fraction and the number of vessels at early times are correlated with the amount of VEGF. In addition, tumor sizes correlate with the number of functional vessels [25, 56]. Finally, the tumor with mixed VEGF sources has most tortuous vessels among the VEGF sources we tested, which is consistent with experimental results when VEGF is overexpressed [10, 27].
C. Higher initial GSC fractions increase tumor sizes and vessel numbers
An in vitro and in vivo study in [26] showed the differences in GBM growth and vasculature between low and high numbers of GSCs. We now take the tumor in Fig. 1 and change the initial GSC fraction to 30%, 50%, 70% and 90%. We take the extra portions first from GTDs, then from dead cells and finally from GCPs as necessary. For example, the tumor that starts with 50% GSCs has 25% GCPs, 20% GTDs (reduced) and 5% dead cells. The tumor with 90% GSCs has 10% GCPs and no GTDs/dead cells initially. Cell distributions are still homogeneous in space initially. We assume that VEGF is produced by hypoxic cells (e.g. SV = pVH(ñ – n)(φT – φD) ) for all cases. The tumor morphologies and cell and vessel distributions are shown in Fig. 3A. While the initial sizes are the same, tumors starting from higher GSC fractions grow more rapidly. In [26], the authors observed larger tumors with more initial GSCs both in vitro and in vivo. The center GSC cluster forms earlier, and connects to GSC clusters near the boundary as it grows. These GSC clusters no longer develop into fingers. Consequently, the tumors with large GSC initial fractions are more compact and the shape factor is smaller (see Fig. S7 (B) in Supplemental Materials).
Fig. 3.
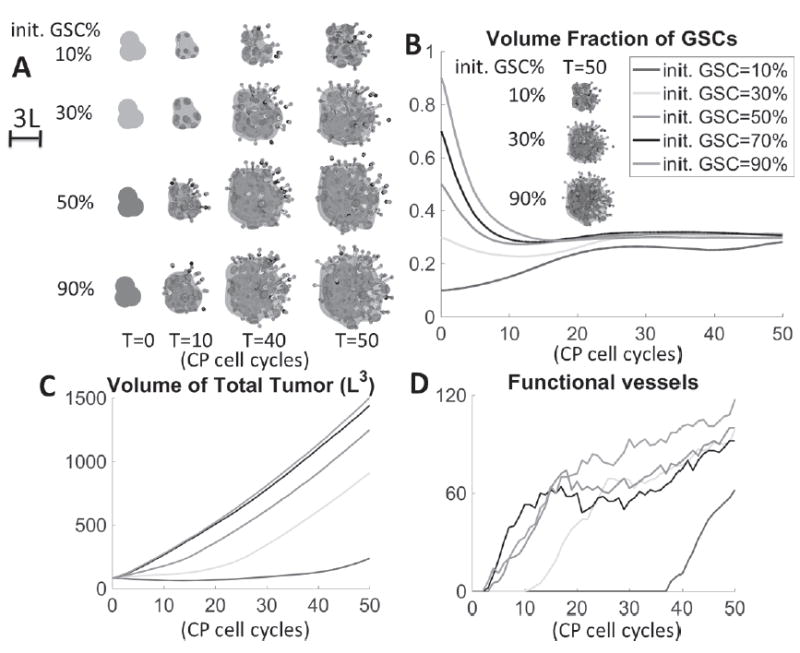
Higher initial GSC fractions increase tumor sizes and vessel numbers. (A) Evolution of tumors with different initial GSC fractions at indicated times. A large GSC cluster emerges earlier in tumors with higher initial GSC fraction. (B) As time evolves, the GSC fraction in all cases converges to approximately 30% despite different tumor sizes and initial GSC fractions. Insets show GSC distributions in tumors with 10%, 30% and 90% initial GSCs. (C) Higher initial GSC fractions result in larger tumor sizes. (D) The number of functional vessels. Angiogenesis begins earlier in tumors with higher initial GSC fraction. The 50%, 70% and 90% tumors generate functional vessels around the same time, and the functional vessel numbers evolve similarly, suggesting that the positive feedback from VEC-GSC crosstalk has saturated. The GSC fractions tend to converge to about 30% for all tumors, regardless of size, which reflects the fact that at the later stages of vascularization, the number of functional vessels is roughly independent of the initial GSC fraction and instead regulated by mechanical and chemical feedback signaling.
An interesting observation is that the GSC fraction in all cases converges to approximately 30% as time evolves, regardless of tumor size and initial GSC fraction (Fig. 3C). This suggests that the GSC fractions are regulated by feedback from GTDs and VEC-GSC crosstalk, which in part is regulated by mechanical feedback. For instance, the number of functional vessels saturates at roughly similar values across all tumor cases. This is due to vessel crushing and reflects regulation by mechanical pressure. Tumors with mixed VEGF sources in Fig. 2 behave similarly (see Fig. S8 in Supplemental Materials). However, by changing the vascular model parameters, e.g., making the sprouting probability continuously dependent on VEGF concentration and varying the pressure threshold at which crushing occurs, the limiting GSC fractions can be altered (see Fig. S9 in Supplemental Materials). See also the Supplementary Materials (Fig. S6) for the dynamics of the GCP and GTD fractions.
As for the vasculature, larger initial GSC fractions increase VEGF production (see Fig. S7 in Supplemental Materials), which advances vessel formation (except that the 90% and 70% cases are vascularized at the same day) and results in more functional vessels (Fig. 3E). This is consistent with [5, 26], where tumors with more GSCs expressed significantly more VEGF both in vitro and in vivo, which is directly correlated with the number of vessels in the tumor. In [26], more initial GSCs also result in higher perfused microvessel densities (functional vessels). Vessel crushing takes place in tumors with more than 30% initial GSCs, which stabilizes the number of functional vessels. Consequently, the evolution of vessel numbers is not monotonic with the amount of VEGF. The dynamics is similar in tumors with 70% or 90% initial GSCs, which suggests that the feedback from crosstalk has saturated.
D. Partially disrupting VEC-GSC crosstalk reduces tumor volume without significantly increasing invasiveness
In experiments, a number of mechanisms have been found to partially disrupt VEC-GSC crosstalk. For example, previous work [30] revealed that VECs maintain GSC activities through mTOR, and that spheroid growth can be reduced by pharmacological inhibition and RNA interference with this pathway. Reference [76] also showed that VECs provide Shh to activate the Hedgehog pathway, thereby promoting GSC properties. On the other hand, VECs with Shh knockdown fail to activate the Hedgehog pathway and promote GSCs. To model this type of treatment, we take the tumor in Fig. 1 as the Control and test the effects of partially disrupting VEC-GSC crosstalk by blocking VEC secretion of the GSC promoter F. Recall that in Control, functional vessels release feedback factors F that enhance GSC proliferation and self-renewal. As a result, the effective GSC mitosis rate is higher and the tumor has a large GSC cluster at the tumor center (Fig. 4F, top row). However, when the VEC secretion of F is blocked (or F is de-activated), only the self-renewal promoter CW exerts positive feedback on p0. Since CW colocalizes at GSC clusters, the effective mitosis rate at other locations are greatly reduced (Fig. 4F, middle row). Thus, in the treated case, the large GSC cluster at tumor center no longer forms. Consequently, both the tumor volume and the GSC fraction are reduced significantly compared to Control (Figs. 4A, B; green vs blue). In particular, the tumor volume is reduced by 77% at T=100 (see Fig. S12 in Supplemental Materials). This behavior is consistent with experimental results. For example, the self-renewing GSC population and the tumor size are reduced when inhibiting or interfering with the mTOR pathway [30]. In addition, inhibition of Hedgehog signaling in VECs also hampers the self-renewal and proliferation of the GSCs, and produces smaller tumors [76]. Importantly, the shape factor is not significantly increased from that for the Control (Fig. 4C), which suggests that this treatment does not increase tumor invasiveness. This can be explained as follows.
Fig. 4.
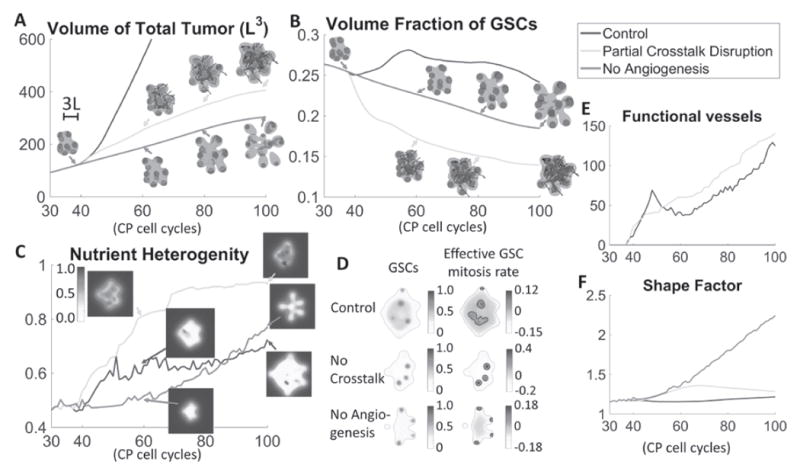
Treatment of vascularized GBM. (A) Time evolution of total tumor volumes. Treatments that partially disrupt VEC-GSC crosstalk by blocking VEC secretion of the GSC promoter F (green) or angiogenesis (red) reduce tumor size compared to Control (blue, tumor from Fig. 1). (B) Blocking angiogenesis prevents the formation of a GSC cluster at the tumor center and reduces the GSC fraction. Blocking VEC-GSC crosstalk removes the positive feedback on GSC self-renewal and further reduces GSC fraction. (C) Time evolution of average nutrient concentration in the tumor. Insets show slices of the nutrient distribution at the tumor center. (D) Slices of GSC mitosis rate at T=80 for the indicated tumors. Green: tumor boundary. Black: contours of . Blocking the crosstalk reduces the effective GSC mitosis at the tumor center, and GSC clusters are located off the tumor boundary due to higher nutrient levels at the center (see insets in (C)). (E) Between T=50 and T=60 in Control, pressure-induced vessel crushing reduces functional vessels, which recover after T=60. The functional vessels in tumors with VEC-GSC crosstalk blocked steadily increases. (F) Blocking angiogenesis promotes finger development and significantly increases the tumor shape factor. Blocking the VEC-GSC crosstalk increases the shape factor at early times. At later times, GSC clusters are located closer to tumor center and fingers cease to grow, which reduces the shape factor.
In Control, GSC proliferation at the center creates excessive solid pressure that induces vessel crushing (see Fig. S13 in Supplemental Materials). As a result, the number of functional vessels decreases between T=45 and T=60 (Fig. 4E, blue). Nutrient production also decreases, which stabilizes the average nutrient concentration in the tumor (Fig. 4D, blue), calculated as . In contrast, when the VEC secretion of F is blocked, the solid pressure is much lower, vessels rarely crush and the number of functional vessels increases steadily (Fig. 4E, green). This brings more nutrients to the tumor (Fig. 4D, green) enabling GSCs to proliferate faster and be located more in the tumor interior rather than at the tumor boundary, which is the case at early times. Consequently, at late times, finger growth is suppressed, the tumor becomes more compact and its shape factor approaches that of the Control. Note that the shape factor does increase between T=40 and T=60 during the early stages of angiogenesis before there is significant nutrient delivery through the neovasculature.
Next, we block angiogenesis in the model. Effectively, this removes the positive feedback on tumor cell proliferation from nutrients released by functional vessels. The tumor volume is further reduced (Fig. 4A, red) by 83% at T=100 (see Fig. S12 in Supplemental Materials). Starting from T=40, GSC clusters near the boundary begin to develop fingers. Since few nutrients penetrate the tumor and the nutrient level is now highest at tumor boundary, the GSC clusters remain at the tumor boundary and promote the growth of invasive fingers, which are much more pronounced than the invasive tumors and significantly increase the shape factor (Fig. 4C, red). At late stages (T~100), these fingers grow into multifocal tumors, indicating greater tumor invasiveness. The GSC fraction is also higher than the tumor with partially disrupted VEC-GSC crosstalk because the tumor is smaller and GSCs are located at the tips of fingers where there is ample nutrient, which increases GSC proliferation and self-renewal. Further, in the tumor interior, the nutrient levels are low, which reduces cell proliferation (Fig. 4F, bottom row). Overall, our results are consistent with [11], where antiangiogenic therapy (e.g. bevacizumab) depletes tumor vasculature, reduces GSCs and inhibits tumor growth. In addition, it is well known that GBM becomes more invasive after bevacizumab treatment [20], and even forms multifocal tumors in some cases [41]. Previous mathematical models that did not distinguish between tumor cell types also showed increased morphologic instability following antiangiogenic therapy [17].
IV. Discussion
In this paper, we have developed and investigated a hybrid continuum-discrete multispecies model of GBM growth. We modeled feedback interactions among GSCs, GCPs, GTDs, VECs and the neovascular network. The cells and cell substrates are treated as continuum, and the vasculature is composed of discrete VECs. Nutrient delivery from the vasculature enhances tumor cell proliferation. VEC-GSC crosstalk is mediated by a VEC-secreted soluble factor that promotes GSC mitosis and self-renewal. Tumor cells may secrete VEGF and promote vessel formation, whereas excessive solid pressure created by tumor cell proliferation causes vessels to be crushed, which limits perfusion. Although we presented the results corresponding to one set of parameters (Table S1, Supplementary Materials), the model behavior we observe is characteristic of that obtained across a wide range of parameters.
Our continuum model does not track the migration of individual cells. We have assumed passive cell movement, i.e. from high to low solid pressure. Active cell movements have been studied previously, e.g. [7, 28] incorporated chemotaxis and haptotaxis that led to increased budding and fingering of tumors. Future work will investigate these effects in the models considered here.
The parameters we chose (see Table S1 in the supplemental material) originate from either experimental data or previous numerical studies. Results are qualitatively similar for a wide range of parameter choices. For example, tumors with enhanced GSC mitosis or self-renewal are larger and more invasive. On the other hand, inhibiting GSC properties suppresses the patterning and may stabilize tumor growth. In addition, reducing the lysis rate results in larger tumors but smaller GSC fractions, since GSCs are located sparsely in clusters. Larger lysis rates tend to create multifocal tumors as lysis removes cells at finger necks. The tumor behavior is similar as long as pmin < 0.5 and pmax > 0.5 [46].
GSC spatiotemporal patterning plays an important role in tumor invasion. During the avascular stage of growth, our model shows that GSCs cluster near the tumor boundary and develop into invasive fingers. Similar results have been observed previously in both experiments [15, 67, 71] and modeling studies [78]. After neovascularization, positive feedback factors from VECs, combined with increased nutrient levels, result in the formation of GSC clusters in the tumor interior in addition to those at the boundary. This is also consistent with experiments. For example, in [60] the authors found that GSCs are mainly localized in the inner core and intermediate regions of tumor. Consequently, the VEC-GSC crosstalk enhances tumor growth and increases GSC fractions, which is consistent with [5, 11]. This leads to more uniform cell proliferation within the tumor and as a result, the tumors tend to grow in compact shapes.
We note that the mechanism used to generate vessels is highly simplified: vessel sprouts are generated randomly once VEGF concentration is above a threshold. In Fig. S9, we investigated a different sprouting mechanism in which the probability of vessel generation is proportional to the VEGF concentration. This affects both the GSC fractions and vessel densities. In particular, GSC fractions increase significantly once the tumors become vascularized. This suggests that GSC fractions can be altered by the vascular sensitivity to VEGF through positive feedback factors secreted by VECs. In future work we will further investigate the details of these interactions on vessel sprouting and the growth of vascularized tumors.
We have also worked from the assumption that VEGF diffuses freely across the tumor. In practice, GBM vessels are highly dysfunctional, which makes penetration of the GBM by nutrients difficult, leading to formation of a nutrient-poor and hypoxic core [21]. Vessel dysfunction could also restrict the effect of crosstalk at the tumor core. In our simulations, tumors also form a hypoxic core, although there are a few functional vessels located inside the tumor.
It is typically assumed that hypoxic tumor cells release VEGF to promote vessel formation and gain access to nutrients [42, 55]. However, there is also evidence that GSCs and GCPs may be more involved in VEGF production [5]. Our model accounts for both scenarios, and shows that the latter case results in larger amounts of VEGF, and consequently more vessels and a larger tumor volume, which are both consistent with [5]. We also find that larger amounts of VEGF advance the time of neovascularization as observed in [50]. In addition, vessels are more tortuous with increasing amounts of VEGF, which is also consistent with experiments [10, 27]. It is thought that an excess of VEGF impairs vessel development giving rise to tortuous vessels [63]. At later stages of growth, vessels may be crushed and stops functioning due to proliferation-induced pressure forces [39], which can lead to a non-monotone evolution of vessel distributions. Our results suggest that the amount of VEGF is correlated with tumor volume and the number of vessels. We also predict that tumors with larger amounts of VEGF grow in more compact shapes. Although the effects on tumor growth of overexpression of VEGF and its isoforms is incompletely understood, there is evidence that in some cases this overexpression may promote more compact tumor growth [38, 47].
Due to the importance of GSCs in tumor progression, their initial fraction is expected to affect the characteristics of tumor and vasculature. We have shown that tumors with higher GSC fractions grow larger in size and have larger amounts of vessels, consistent with [26]. However, GSC fractions converge to a common value as time evolves regardless of the tumor size and initial GSC fraction. This unexpected result suggests that GSC fractions are regulated by a complex interplay of mechanical and chemical signaling mechanisms. Previous work [78] showed that in avascular tumors, varying the level of negative feedback on GSC self-renewal has little effect on the fraction.
Our results confirm that anti-angiogenic therapy, modeled as removing the tumor vasculature and preventing further neovascularization, effectively reduces tumor size [11], but risks increased tumor invasion [20, 41]. Although hypoxia may select for cells that have a more aggressive, migratory phenotype [43], we find that morphological changes and invasive fingering are a natural consequence of blocking angiogenesis by disrupting both VEC-GSC crosstalk and nutrients supplied from vessels. Avascular tumors can develop invasive fingers by increasing their surface area to gain access to nutrients in the host [17, 18]. While shape and invasiveness may not necessarily be correlated, there is evidence that in glioblastoma they may be related. We refer to [7, 28, 58] that link tumor shape with invasiveness.
Angiogenesis restrains tumor invasion through nutrients supplied from functional vessels, which results in more uniform cell proliferation and faster growth as a tradeoff [12, 57]. On the other hand, partially disrupting the VEC-GSC crosstalk by blocking secretion of GSC promoters also reduces tumor size very effectively, which has been observed in [30, 76]. However, unlike anti-angiogenic therapy, this partial disruption does not significantly increase the potential for invasiveness. Thus, this modeling study supports the experimental findings [33, 48, 64, 77, 79] that targeting VEC-GSC crosstalk may be a promising direction for anti-cancer treatment.
V. Conclusion
We have developed and studied a 3D hybrid mathematical model of glioblastoma growth that accounts for cancer cell lineages containing cancer stem cells, committed progenitor cells and post-mitotic terminally differentiated cells, as well as vascular endothelial cells and a tumor-induced neovascular network. Feedback signaling between tumor cells and vasculature regulates their dynamics. Our studies show how the tumor and vascular development depend on feedback regulation. For instance, crosstalk between cancer stem cells and vascular endothelial cells, via pro-angiogenic factors secreted by tumor cells and VEC-secreted factors that upregulate GSC proliferation and renewal, is shown to promote cancer stem cell self-renewal and proliferation, resulting in large tumors with tortuous neovascular networks. Targeting this crosstalk may hold promise as a novel anti-cancer therapy.
Supplementary Material
Acknowledgments
The authors thank Arthur Lander, Hamed Youssefpour and Marian Waterman for useful discussions. This work is supported in part by the National Science Foundation Division of Mathematical Sciences (HY, JSL), a UC-MEXUS fellowship (MRL), a Miguel Velez fellowship at UCI (MRL) the National Institutes of Health through grants U54CA143907 (HBF), R01HL60067 (CCWH), P50GM76516 for the Center of Excellence in Systems Biology at the University of California, Irvine. JSL and CCWH receive support from the Chao Family Comprehensive Cancer Center at University of California, Irvine through an NCI Center Grant Award, P30CA062203.
Contributor Information
H. Yan, Department of Mathematics, University of California, Irvine
M. Romero-López, Department of Biomedical Engineering, University of California
H.B. Frieboes, Department of Bioengineering, and the James Brown Cancer Center, University of Louisville
C.C.W. Hughes, Department of Biomedical Engineering, the Department of Molecular Biology and Biochemistry and the Chao Comprehensive Cancer Center, University of California
J.S. Lowengrub, Department of Mathematics, the Department of Biomedical Engineering, the Center for Complex Biological Systems, and the Chao Comprehensive Cancer Center, University of California, 540H Rowland Hall, Irvine CA 92697.
References
- 1.Alves TR, et al. Glioblastoma cells: a heterogeneous and fatal tumor interacting with the parenchyma. Life Sci. 2011;89(15-16):532–9. doi: 10.1016/j.lfs.2011.04.022. [DOI] [PubMed] [Google Scholar]
- 2.Anderson AR, Chaplain MA. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Biol. 1998;60(5):857–99. doi: 10.1006/bulm.1998.0042. [DOI] [PubMed] [Google Scholar]
- 3.Augustin HG. Tubes, branches, and pillars: the many ways of forming a new vasculature. Circ Res. 2001;89(8):645–7. [PubMed] [Google Scholar]
- 4.Bailey JM, et al. Cancer metastasis facilitated by developmental pathways: Sonic hedgehog, Notch, and bone morphogenic proteins. J Cell Biochem. 2007;102(4):829–39. doi: 10.1002/jcb.21509. [DOI] [PubMed] [Google Scholar]
- 5.Bao S, et al. Stem cell-like glioma cells promote tumor angiogenesis through vascular endothelial growth factor. Cancer Res. 2006;66(16):7843–8. doi: 10.1158/0008-5472.CAN-06-1010. [DOI] [PubMed] [Google Scholar]
- 6.Bayin NS, et al. Glioblastoma stem cells: Molecular characteristics and therapeutic implications. World J Stem Cells. 2014;6(2):230–8. doi: 10.4252/wjsc.v6.i2.230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bearer EL, et al. Multiparameter computational modeling of tumor invasion. Cancer Res. 2009;69(10):4493–501. doi: 10.1158/0008-5472.CAN-08-3834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bello L, et al. Combinatorial administration of molecules that simultaneously inhibit angiogenesis and invasion leads to increased therapeutic efficacy in mouse models of malignant glioma. Clin Cancer Res. 2004;10(13):4527–37. doi: 10.1158/1078-0432.CCR-04-0194. [DOI] [PubMed] [Google Scholar]
- 9.Bonavia Rudy, et al. Heterogeneity Maintenance in Glioblastoma: A Social Network. Cancer Research. 2011;71(12):4055–60. doi: 10.1158/0008-5472.CAN-11-0153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bullitt Elizabeth, et al. Vessel Tortuosity and Brain Tumor Malignancy: A Blinded Study. Academic radiology. 2005;12(10):1232–40. doi: 10.1016/j.acra.2005.05.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Calabrese C, et al. A perivascular niche for brain tumor stem cells. Cancer Cell. 2007;11(1):69–82. doi: 10.1016/j.ccr.2006.11.020. [DOI] [PubMed] [Google Scholar]
- 12.Casanovas O, et al. Drug resistance by evasion of antiangiogenic targeting of VEGF signaling in late-stage pancreatic islet tumors. Cancer Cell. 2005;8(4):299–309. doi: 10.1016/j.ccr.2005.09.005. [DOI] [PubMed] [Google Scholar]
- 13.Charles N, et al. Perivascular nitric oxide activates notch signaling and promotes stem-like character in PDGF-induced glioma cells. Cell Stem Cell. 2010;6(2):141–52. doi: 10.1016/j.stem.2010.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen R, et al. A hierarchy of self-renewing tumor-initiating cell types in glioblastoma. Cancer Cell. 2010;17(4):362–75. doi: 10.1016/j.ccr.2009.12.049. [DOI] [PubMed] [Google Scholar]
- 15.Cheng L, et al. Elevated invasive potential of glioblastoma stem cells. Biochem Biophys Res Commun. 2011;406(4):643–8. doi: 10.1016/j.bbrc.2011.02.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Clarke J, et al. Recent advances in therapy for glioblastoma. Arch Neurol. 2010;67(3):279–83. doi: 10.1001/archneurol.2010.5. [DOI] [PubMed] [Google Scholar]
- 17.Cristini V, et al. Morphologic instability and cancer invasion. Clin Cancer Res. 2005;11(19 Pt 1):6772–9. doi: 10.1158/1078-0432.CCR-05-0852. [DOI] [PubMed] [Google Scholar]
- 18.Cristini V, et al. Nonlinear simulation of tumor growth. J Math Biol. 2003;46(3):191–224. doi: 10.1007/s00285-002-0174-6. [DOI] [PubMed] [Google Scholar]
- 19.Cristini V, Lowengrub JS. Multiscale modeling of cancer: An integrated experimental and mathematical modeling approach. Cambridge, UK: Cambridge University Press; 2010. [Google Scholar]
- 20.de Groot JF, et al. Tumor invasion after treatment of glioblastoma with bevacizumab: radiographic and pathologic correlation in humans and mice. Neuro Oncol. 2010;12(3):233–42. doi: 10.1093/neuonc/nop027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dimberg A. The glioblastoma vasculature as a target for cancer therapy. Biochem Soc Trans. 2014;42(6):1647–52. doi: 10.1042/BST20140278. [DOI] [PubMed] [Google Scholar]
- 22.Eyler CE, et al. Glioma stem cell proliferation and tumor growth are promoted by nitric oxide synthase-2. Cell. 2011;146(1):53–66. doi: 10.1016/j.cell.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eyler Christine E, Rich Jeremy N. Survival of the Fittest: Cancer Stem Cells in Therapeutic Resistance and Angiogenesis. Journal of Clinical Oncology. 2008;26(17):2839–45. doi: 10.1200/JCO.2007.15.1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fan X, et al. NOTCH pathway blockade depletes CD133-positive glioblastoma cells and inhibits growth of tumor neurospheres and xenografts. Stem Cells. 2010;28(1):5–16. doi: 10.1002/stem.254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Folkins C, et al. Anticancer therapies combining antiangiogenic and tumor cell cytotoxic effects reduce the tumor stem-like cell fraction in glioma xenograft tumors. Cancer Res. 2007;67(8):3560–4. doi: 10.1158/0008-5472.CAN-06-4238. [DOI] [PubMed] [Google Scholar]
- 26.Folkins C, et al. Glioma tumor stem-like cells promote tumor angiogenesis and vasculogenesis via vascular endothelial growth factor and stromal-derived factor 1. Cancer Res. 2009;69(18):7243–51. doi: 10.1158/0008-5472.CAN-09-0167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Folkman Judah. Incipient Angiogenesis. Journal of the National Cancer Institute. 2000;92(2):94–95. doi: 10.1093/jnci/92.2.94. [DOI] [PubMed] [Google Scholar]
- 28.Frieboes HB, et al. Three-dimensional multispecies nonlinear tumor growth-II: Tumor invasion and angiogenesis. J Theor Biol. 2010;264(4):1254–78. doi: 10.1016/j.jtbi.2010.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Frieboes HB, et al. Computer simulation of glioma growth and morphology. Neuroimage. 2007;37(Suppl 1):S59–70. doi: 10.1016/j.neuroimage.2007.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Galan-Moya EM, et al. Secreted factors from brain endothelial cells maintain glioblastoma stem-like cell expansion through the mTOR pathway. EMBO Rep. 2011;12(5):470–6. doi: 10.1038/embor.2011.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gao X, et al. Acute and fractionated irradiation differentially modulate glioma stem cell division kinetics. Cancer Res. 2013;73(5):1481–90. doi: 10.1158/0008-5472.CAN-12-3429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gao X, et al. A proposed quantitative index for assessing the potential contribution of reprogramming to cancer stem cell kinetics. Stem Cells Int. 2014;2014:249309. doi: 10.1155/2014/249309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gilbertson RJ, Rich JN. Making a tumour’s bed: glioblastoma stem cells and the vascular niche. Nat Rev Cancer. 2007;7(10):733–6. doi: 10.1038/nrc2246. [DOI] [PubMed] [Google Scholar]
- 34.Girvan AC, et al. Glioblastoma treatment patterns, survival, and healthcare resource use in real-world clinical practice in the USA. Drugs Context. 2015;4 doi: 10.7573/dic.212274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gregory CA, et al. The Wnt signaling inhibitor dickkopf-1 is required for reentry into the cell cycle of human adult stem cells from bone marrow. Journal of Biological Chemistry. 2003;278(30):28067–78. doi: 10.1074/jbc.M300373200. [DOI] [PubMed] [Google Scholar]
- 36.Rieger H, Fredrich T, Welter M. Physics of the tumor vasculature: Theory and experiment. Eur Phys J Plus. 2016;131(31) [Google Scholar]
- 37.Hartung N, et al. Mathematical modeling of tumor growth and metastatic spreading: validation in tumor-bearing mice. Cancer Res. 2014;74(22):6397–407. doi: 10.1158/0008-5472.CAN-14-0721. [DOI] [PubMed] [Google Scholar]
- 38.Herve MA, et al. Overexpression of vascular endothelial growth factor 189 in breast cancer cells leads to delayed tumor uptake with dilated intratumoral vessels. Am J Pathol. 2008;172(1):167–78. doi: 10.2353/ajpath.2008.070181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Holash J, et al. Vessel cooption, regression, and growth in tumors mediated by angiopoietins and VEGF. Science. 1999;284(5422):1994–8. doi: 10.1126/science.284.5422.1994. [DOI] [PubMed] [Google Scholar]
- 40.Hovinga KE, et al. Inhibition of notch signaling in glioblastoma targets cancer stem cells via an endothelial cell intermediate. Stem Cells. 2010;28(6):1019–29. doi: 10.1002/stem.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Iwamoto FM, et al. Patterns of relapse and prognosis after bevacizumab failure in recurrent glioblastoma. Neurology. 2009;73(15):1200–6. doi: 10.1212/WNL.0b013e3181bc0184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jain RK. Molecular regulation of vessel maturation. Nat Med. 2003;9(6):685–93. doi: 10.1038/nm0603-685. [DOI] [PubMed] [Google Scholar]
- 43.Joseph JV, et al. Hypoxia enhances migration and invasion in glioblastoma by promoting a mesenchymal shift mediated by the HIF1alpha-ZEB1 axis. Cancer Lett. 2015;359(1):107–16. doi: 10.1016/j.canlet.2015.01.010. [DOI] [PubMed] [Google Scholar]
- 44.Klaus A, Birchmeier W. Wnt signalling and its impact on development and cancer. Nat Rev Cancer. 2008;8(5):387–98. doi: 10.1038/nrc2389. [DOI] [PubMed] [Google Scholar]
- 45.Kunkel P, et al. Inhibition of glioma angiogenesis and growth in vivo by systemic treatment with a monoclonal antibody against vascular endothelial growth factor receptor-2. Cancer Res. 2001;61(18):6624–8. [PubMed] [Google Scholar]
- 46.Lander AD, et al. Cell lineages and the logic of proliferative control. PLoS Biol. 2009;7(1):e15. doi: 10.1371/journal.pbio.1000015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lederle W, et al. Platelet-derived growth factor-B normalizes micromorphology and vessel function in vascular endothelial growth factor-A-induced squamous cell carcinomas. Am J Pathol. 2010;176(2):981–94. doi: 10.2353/ajpath.2010.080998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lee E, et al. Crosstalk between cancer cells and blood endothelial and lymphatic endothelial cells in tumour and organ microenvironment. Expert Rev Mol Med. 2015;17:e3. doi: 10.1017/erm.2015.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lee N, et al. A potential role for Dkk-1 in the pathogenesis of osteosarcoma predicts novel diagnostic and treatment strategies. British Journal of Cancer. 2007;97(11):1552–59. doi: 10.1038/sj.bjc.6604069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Li Z, et al. Hypoxia-inducible factors regulate tumorigenic capacity of glioma stem cells. Cancer Cell. 2009;15(6):501–13. doi: 10.1016/j.ccr.2009.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ligon KL, et al. Olig2-regulated lineage-restricted pathway controls replication competence in neural stem cells and malignant glioma. Neuron. 2007;53(4):503–17. doi: 10.1016/j.neuron.2007.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lunt Sarah Jane, et al. Interstitial fluid pressure in tumors: therapeutic barrier and biomarker of angiogenesis. Future Oncology. 2008;4(6):793–802. doi: 10.2217/14796694.4.6.793. [DOI] [PubMed] [Google Scholar]
- 53.McDougall SR, et al. Mathematical modelling of flow through vascular networks: implications for tumour-induced angiogenesis and chemotherapy strategies. Bull Math Biol. 2002;64(4):673–702. doi: 10.1006/bulm.2002.0293. [DOI] [PubMed] [Google Scholar]
- 54.Merchant AA, Matsui W. Targeting Hedgehog--a cancer stem cell pathway. Clin Cancer Res. 2010;16(12):3130–40. doi: 10.1158/1078-0432.CCR-09-2846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Minchenko A, et al. Hypoxic stimulation of vascular endothelial growth factor expression in vitro and in vivo. Lab Invest. 1994;71(3):374–9. [PubMed] [Google Scholar]
- 56.Oka N, et al. VEGF promotes tumorigenesis and angiogenesis of human glioblastoma stem cells. Biochem Biophys Res Commun. 2007;360(3):553–9. doi: 10.1016/j.bbrc.2007.06.094. [DOI] [PubMed] [Google Scholar]
- 57.Paez-Ribes M, et al. Antiangiogenic therapy elicits malignant progression of tumors to increased local invasion and distant metastasis. Cancer Cell. 2009;15(3):220–31. doi: 10.1016/j.ccr.2009.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Pham K, et al. Predictions of tumour morphological stability and evaluation against experimental observations. J R Soc Interface. 2011;8(54):16–29. doi: 10.1098/rsif.2010.0194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Piccirillo SG, et al. Bone morphogenetic proteins inhibit the tumorigenic potential of human brain tumour-initiating cells. Nature. 2006;444(7120):761–5. doi: 10.1038/nature05349. [DOI] [PubMed] [Google Scholar]
- 60.Pistollato F, et al. Intratumoral hypoxic gradient drives stem cells distribution and MGMT expression in glioblastoma. Stem Cells. 2010;28(5):851–62. doi: 10.1002/stem.415. [DOI] [PubMed] [Google Scholar]
- 61.Ramírez-Castillejo C, Sánchez-Sánchez F, Andreu-Agulló C, Ferrón SR, Aroca-Aguilar JD, Sánchez P, Mira H, Escribano J, Fariñas I. Pigment epithelium-derived factor is a niche signal for neural stem cell renewal. Nat Neurosci. 2006;9(3):331–9. doi: 10.1038/nn1657. [DOI] [PubMed] [Google Scholar]
- 62.Robertson-Tessi M, et al. Impact of metabolic heterogeneity on tumor growth, invasion, and treatment outcomes. Cancer Res. 2015;75(8):1567–79. doi: 10.1158/0008-5472.CAN-14-1428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Saaristo Anne, et al. Adenoviral VEGF-C overexpression induces blood vessel enlargement, tortuosity, and leakiness but no sprouting angiogenesis in the skin or mucous membranes. The FASEB Journal. 2002;16(9):1041–49. doi: 10.1096/fj.01-1042com. [DOI] [PubMed] [Google Scholar]
- 64.Sharma A, Shiras A. Cancer stem cell-vascular endothelial cell interactions in glioblastoma. Biochem Biophys Res Commun. 2016;473(3):688–92. doi: 10.1016/j.bbrc.2015.12.022. [DOI] [PubMed] [Google Scholar]
- 65.Shen Q, et al. Endothelial cells stimulate self-renewal and expand neurogenesis of neural stem cells. Science. 2004;304(5675):1338–40. doi: 10.1126/science.1095505. [DOI] [PubMed] [Google Scholar]
- 66.Simonsen Trude G, et al. High Interstitial Fluid Pressure Is Associated with Tumor-Line Specific Vascular Abnormalities in Human Melanoma Xenografts. PLoS ONE. 2012;7(6):e40006. doi: 10.1371/journal.pone.0040006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Sottoriva A, et al. Cancer stem cell tumor model reveals invasive morphology and increased phenotypical heterogeneity. Cancer Res. 2010;70(1):46–56. doi: 10.1158/0008-5472.CAN-09-3663. [DOI] [PubMed] [Google Scholar]
- 68.Tabatabai Ghazaleh, Weller Michael. Glioblastoma stem cells. Cell and Tissue Research. 2011;343(3):459–65. doi: 10.1007/s00441-010-1123-0. [DOI] [PubMed] [Google Scholar]
- 69.Takano S, et al. Concentration of vascular endothelial growth factor in the serum and tumor tissue of brain tumor patients. Cancer Res. 1996;56(9):2185–90. [PubMed] [Google Scholar]
- 70.Tavazoie M, et al. A specialized vascular niche for adult neural stem cells. Cell Stem Cell. 2008;3(3):279–88. doi: 10.1016/j.stem.2008.07.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Vlashi E, et al. In vivo imaging, tracking, and targeting of cancer stem cells. J Natl Cancer Inst. 2009;101(5):350–9. doi: 10.1093/jnci/djn509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wilson TA, et al. Glioblastoma multiforme: State of the art and future therapeutics. Surg Neurol Int. 2014;5:64. doi: 10.4103/2152-7806.132138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Wise SM, et al. An Adaptive Multigrid Algorithm for Simulating Solid Tumor Growth Using Mixture Models. Math Comput Model. 2011;53(1-2):1–20. doi: 10.1016/j.mcm.2010.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Wise SM, et al. Three-dimensional multispecies nonlinear tumor growth--I Model and numerical method. J Theor Biol. 2008;253(3):524–43. doi: 10.1016/j.jtbi.2008.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Xiangxin Zhu, Max Welling, Fang Jin, John Lowengrub. Predicting Simulation Parameters of Biological Systems Using a Gaussian Process Model. Stat Anal Data Min. 2012;5(6):509–22. doi: 10.1002/sam.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Yan GN, et al. Endothelial cells promote stem-like phenotype of glioma cells through activating the Hedgehog pathway. J Pathol. 2014;234(1):11–22. doi: 10.1002/path.4349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Ye J, et al. The cancer stem cell niche: cross talk between cancer stem cells and their microenvironment. Tumour Biol. 2014;35(5):3945–51. doi: 10.1007/s13277-013-1561-x. [DOI] [PubMed] [Google Scholar]
- 78.Youssefpour H, et al. Multispecies model of cell lineages and feedback control in solid tumors. Journal of theoretical biology. 2012;304:39–59. doi: 10.1016/j.jtbi.2012.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Zeng Q, et al. Crosstalk between tumor and endothelial cells promotes tumor angiogenesis by MAPK activation of Notch signaling. Cancer Cell. 2005;8(1):13–23. doi: 10.1016/j.ccr.2005.06.004. [DOI] [PubMed] [Google Scholar]
- 80.Zhu TS, et al. Endothelial cells create a stem cell niche in glioblastoma by providing NOTCH ligands that nurture self-renewal of cancer stem-like cells. Cancer Res. 2011;71(18):6061–72. doi: 10.1158/0008-5472.CAN-10-4269. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


