Abstract
Non-invasive optoacoustic mapping of temperature in tissues with low blood content can be enabled by administering external contrast agents. Some important clinical applications of such approach include temperature mapping during thermal therapies in a prostate or a mammary gland. However, the technique would require a calibration that establishes functional relationship between the measured normalized optoacoustic response and local tissue temperature. In this work, we investigate how a key calibration parameter – the temperature of zero optoacoustic response (T0) – behaves in different environments simulating biological tissues augmented with either dissolved or particulate (nanoparticles) contrast agents. The observed behavior of T0 in ionic and molecular solutions suggests that in-vivo temperature mapping is feasible for contrast agents of this type, but requires knowledge of local concentrations. Oppositely, particulate contrast agents (plasmonic or carbon nanoparticles) demonstrated concentration-independent thermal behavior of optoacoustic response with T0 defined by the thermoelastic properties of the local environment.
Abbreviations: GNR, Gold nanorods; NIR, Near-infrared; NP, Nanoparticles; MRI, Magnetic resonance imaging; OA, Optoacoustic; ROI, Region of interest; SNR, Signal-to-noise ratio; SOS, Speed of sound; ThOR, Thermal (temperature-dependent) optoacoustic response; USI, Ultrasound imaging
Keywords: Photoacoustic, Optical contrast agents, Temperature monitoring, Optoacoustic imaging
1. Introduction
The manipulation of tissue temperature has been used for many years for clinical applications that benefit patients with a variety of diseases, including cancer [1], [2]. Thermal therapy is a promising way to improve cancer treatment, but it is largely an experimental technique with few clinically approved applications [3], [4], [5], [6]. High-efficacy thermal therapy would provide destruction of the targeted lesion, while preventing damage to adjacent healthy tissues. Therefore, significant research efforts are aimed at developing a more effective and safe thermal therapeutic equipment enhanced with temperature image guidance.
The ideal image-guiding system for a thermal therapy should provide real-time visualization of the temperature changes in the target tissue, be compatible with the used therapeutic equipment, convenient in operation, and should not drive the cost of the entire instrument prohibiting its commercialization. Optoacoustic (OA) thermometry demonstrated feasibility for those required characteristics by providing real-time noninvasive imaging of temperature distribution in vascularized tissue-mimicking phantoms with high spatial (<1 mm) resolution [7], [8], [9]. The OA thermometry also benefits from relatively low cost as compared to magnetic resonance imaging (MRI), which was also attempted for temperature monitoring [10], [11], and its compatibility with ultrasound imaging (USI), which is a current clinical standard for real-time monitoring of thermal ablative therapies [12], [13].
Optoacoustic effect, also known as photoacoustic effect, is generated in biological tissues upon absorption of short pulses of optical energy. Typically, nanosecond-range pulses produced by a Q-switched laser and surface fluence on the order of mJ/cm2 are required to generate detectable OA pressure waves in deep biological tissues [14], [15]. OA detection could be performed by a clinical ultrasound probe modified for a triggered receive mode, or, more optimally, by using dedicated ultra-wideband optoacoustic sensors and electronics [16].
The amplitude of a generated OA pressure wave, p, can be expressed as [14], [15]:
| (1) |
with the local optical fluence F, optical absorption coefficient μa, and the dimensionless Grüneisen parameter Γ representing thermoelastic efficiency of the medium. Grüneisen is a multicomponent parameter that gets contributions from the volumetric thermal expansion coefficient (β), the speed of sound (SOS) for longitudinal waves (Vl), and the specific (per mass) heat capacity at constant pressure (Cp). The change of Grüneisen parameter on temperature may be presented as:
| (2) |
Water is a ubiquitous component of a live organism. In humans it constitutes up to 50–75% of body mass [17]. Thermodynamic characteristics contributing to Grüneisen parameter of water were well studied for the physiological range of temperatures [0,40] °C. The contribution of each thermodynamic characteristic to the rate of change of Grüneisen parameter of water per degree of temperature in the physiological range can be summarized as following [18]:
| (3) |
| (4) |
| (5) |
| (6) |
The first number in parenthesis corresponds to T ≈ 0 °C, just prior to freezing. The last number in parenthesis corresponds to T = 40 °C. In water, changes of Vl and Cp with temperature are negligible as compared to the temperature-dependent behavior of β. Therefore, it is widely considered that linear thermal behavior of optoacoustic response, which is observed in aqueous solutions within the physiologic range of temperatures, follows the temperature dependence of the thermal expansion coefficient [19], [20]. Consequently, the amplitude of a measured OA signal replicates the temperature-dependent behavior of the local thermal expansion coefficient, which constitutes the fundamental concept of OA temperature monitoring [21], [22]. Recently, the phenomenon was studied extensively using inorganic compounds [23], tissue simulating phantoms [7], [8], [24], [25], and biological samples [26], [27], [28], [29], [30], [31]. OA thermometry was also attempted on single cells in a microscopy mode [32], [33] and some nonlinear effects were investigated [34], [35].
Our group showed images of transition through zero optoacoustic response in samples of mammalian blood [30]. Those studies also demonstrated that the temperature of zero optoacoustic response (T0) is invariant with dilution of blood, but decreases linearly as a function of concentration in control hemoglobin solutions as it was also found for ionic salts [23]. The phenomenon was explained by a unique compartmentalization of hemoglobin inside a stable cytoplasmic environment of erythrocytes and allowed for establishing accurate hematocrit-independent calibration of normalized optoacoustic response in vascularized tissues. The proposed optoacoustic temperature mapping technique included two steps: (1) obtain the OA reference frame including the region of interest at a known temperature, (2) normalize a subsequent OA frame to the reference frame and use the calibration OA(T) equation to convert the normalized frame to the temperature map. The method showed accuracy as high as ±1 °C for temperatures below 0 °C and average accuracy of ±3 °C for the entire interrogated range of temperatures between 40 °C and −16 °C [7].
However, in vivo applicability of the temperature mapping technique, which is based on the optical absorption of red blood cells, is limited to highly vascularized biological tissues [9]. The technique cannot be efficiently used for monitoring thermal therapies in most of the glandular, adipose, and other tissues with reduced blood perfusion. Significant recent advancements in development of biocompatible OA contrast agents [36], [37] may help to solve that problem. There are OA contrast agents that have been selectively tailored for enhanced temperature-dependent OA response [33], [38]. There are also biocompatible dyes, like the FDA approved indocyanine green (ICG), which may be injected into a body either as an aqueous solution or being encapsulated into liposomes and erythrocyte ghosts creating sensitive OA contrast agents [33], [39], [40]. Upon delivery of such constructs to tissues, which normally do not absorb well near-infrared (NIR) light, the OA temperature monitoring may become enabled.
However, there is still a major problem related to the fact that the calibration for temperature monitoring is heavily dependent on the medium that generates OA response. The OA contrast agents loaded to different types of tissue with significant variations in local concentrations will likely behave very differently from the invariant relationship demonstrated by blood. In this work we study various scenarios by using different types of contrast agents to enable OA temperature monitoring in media that naturally do not absorb light. Ionic solutions and suspensions of nanoparticles with various compositions and concentrations are experimentally investigated for the produced temperature-dependent OA response. We focus on the analysis of T0, which is a key calibration parameter contributing to the accuracy of the temperature mapping technique.
2. Materials and methods
OA imaging provides a handy visual tool for determination of the temperature of zero optoacoustic response (T0), when the OA effect in a studied sample switches from optically induced thermal expansion to compression. OA imaging also enables efficient parallel testing of multiple samples, which can be simultaneously imaged and analyzed without any crosstalk.
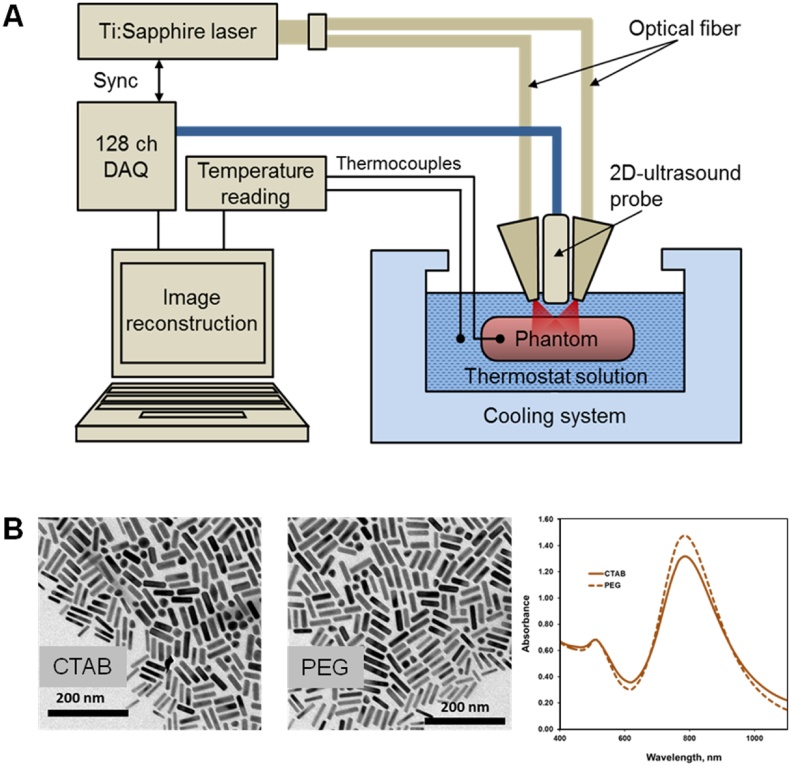
The detailed description of the experimental setup (Fig. 1A) can be found in Ref. [23], [41]. It utilizes a real-time two-dimensional laser optoacoustic imaging system (LOIS-2D, TomoWave Laboratories, Houston, TX) with a 5-MHz central frequency 128-channel linear ultrasound probe (L5, Acuson, CA). The Ti-Sapphire laser unit produced NIR pulses with duration of 6 ns and energy of 16 mJ at a pulse repetition rate of 10 Hz. Two laser emitting bars attached on both sides of the ultrasound probe had rectangular output apertures of 1.5 mm × 50 mm each with the long sides oriented parallel to the linear array of ultrasound transducers. The laser bars were tilted to converge the output laser radiation within the interrogated region of the imaging plane. Laser fluence of 2 mJ/cm2 was measured at a distance of 20 mm from the ultrasound detector. The laser output was tuned to the wavelength of either 800 nm or 760 nm in order to obtain sufficient optical absorption in the aqueous solutions and adequate signal-to-noise ratio (SNR) on the OA images [42], [43]. Optoacoustic imaging was performed in the backward mode [44] and reconstructed using the filtered back projection algorithm [45], [46]. Plastic tubes with thin optically transparent walls were filled with optically absorbing samples and placed orthogonally to the imaging plane at two levels: 15 mm and 22 mm from the optoacoustic probe such that cross-sections of the tubes were observed on the images. Optoacoustic data were acquired with 30 s or 120 s intervals and averaged over 64 laser pulses. The detailed description of the signal processing can be found in Ref. [23]. Automatic adjustment of SOS was implemented to minimize defocusing of the OA image caused by the thermal changes in the coupling medium [42], [47]. A linear grayscale palette was used for display of all optoacoustic images. The palette was autoscaled for the first frame acquired at 20 °C and the limits were fixed for all the subsequent frames. To obtain a quantitative metric of the OA response (local pressure generated from the absorption of laser pulses), the statistical median of the reconstructed OA image matrix was evaluated inside the region of interest (ROI), which was selected manually and contained one of the studied samples. Using a median estimate of the OA image matrix allowed a 6-fold reduction in the root-mean-square noise (RMSN) as compared to an OA sensing technique [23]. A thermostat provided cooling up to −21 °C at a rate of 0.1–0.2 °C/min. Temperature was measured at 5-s intervals using fine-gauge thermocouples placed inside and outside the tubes and logged by the data acquisition module (OM-DAQ-USB-2401, Omega, Stamford, CT) with precision of 0.01 °C. Aqueous solution of NaCl 23 wt% (freezing temperature about −21 °C) or 40% Ethanol (freezing temperature about −29 °C) were employed as acoustic coupling media in experiments below the freezing point of water.
Fig. 1.
A. Schematics of the experimental setup. Latched light bar illuminators, ultrasound probe, and multi-tube phantom frame with sample tubes oriented orthogonally to imaging plane, all are placed inside a thermostat filled with a coupling liquid. B. TEM images of GNRs before (suspension of GNRs in 10 mM CTAB) and after pegylation (PEG) and their normalized UV–Vis spectra.
Thin-walled (0.051 mm) polytetrafluoroethylene (PTFE) tubes (Sub-Lite-Wall Tubing, Zeus, Orangeburg, SC) with the inner diameter of 0.635 mm were filled with the studied liquid samples. Aqueous solutions were prepared using salts of CuSO4*5H2O, NiSO4*6H2O, and NaCl (Sigma Aldrich, St Louis, MO) in distilled water. Custom-made aqueous suspensions of pegylated gold nanorods (GNR) were utilized as contrast agents for OA imaging of non-absorbing aqueous media. Powdered carbon black – low-structured hydrophobic particles with mean size of 25 nm and ratio of external surface area to the total surface area as 206/270 m2/g (Raven 2500, Columbian Chemicals, Centerville, LA) – were used as contrast agents for OA imaging of non-absorbing non-aqueous media such as mineral oil (Aegis Sciences Co., Nashville, TN). Surface modified ink carbon particles suspended in water (Higgins Eternal, Chartpak Inc, Leeds, MA) were used in control experiments.
Previously, we described the general strategy for synthesis of GNR and their stabilization with thiol-terminal PEG [48], [49], [50]. Using the same protocol we synthesized pegylated GNR with maximum of the localized surface plasmon resonance (LSPR) near 800 nm (Fig. 1B). GNR were characterized by UV–vis spectra, which were obtained using poly(methylmethacrylate) cuvettes (1 cm optical path) on a Thermo Scientific Evolution 201 spectrophotometer. Transmission electron microscopy (TEM) was performed with a JEOL-1230 (JEOL) instrument operating at 80 kV. Evaluation of GNR size distribution was performed by analysis of TEM images using ImageJ software (National Institutes of Health). The concentration of GNR in the tested solutions was controlled by measuring optical absorbance at the wavelength of 800 nm. We used 3 different concentrations of GNR in water, which resulted in the measured OD 0.5, 1.0, and 1.5 cm−1 at 800 nm. Mineral oil samples contrasted by carbon particles had OD 0.2 cm−1 and 0.6 cm−1 at 800 nm.
3. Results and discussion
It is considered that T0 measured with the OA imaging technique for an optically absorbing aqueous solution coincides with the temperature of maximum density of that solution − a point at which the thermal expansion coefficient becomes nil [51] and, therefore, no stress can be generated from the absorbed electromagnetic energy. Most substances typically increase their density with decreasing temperature. Water, however, is a unique matter with its density gradually increasing while temperature is decreasing, then reaching the point of maximum density and reversing the trend. The water anomaly appears as the maximum density at 3.98 °C [52], and results in a negative thermal expansion coefficient for the range between the temperature of maximum density and the freezing point at 0 °C. Experimental and theoretical results indicate that the explanation of the maximum density phenomenon in water is related to hydrogen-bond interaction between water molecules [53], [54], [55], [56]. The basic assumption is the existence of local structural fluctuations in the tetrahedrally-coordinated hydrogen-bond network. Some of those fluctuations produce domains with thermodynamic behavior of high density liquid, which predominates at higher temperatures. Other fluctuations produce domains with thermodynamic behavior of low density liquid, in which hydrogen-bonds cluster and form a more open, “ice-like” structure. Competition between these two local forms of hydrogen-bond network is manifested as the thermodynamic anomaly of water [51].
The majority of dissolved substances depress the temperature of maximum density of water, obeying the Despretz law [57], [58]:
| (7) |
where T0 is the temperature of maximum density of an aqueous solution, is the temperature of maximum density of pure water, KD is the Despretz constant that depends on the additive’s thermodynamic properties, and C is the concentration of additive. The shift ΔQD = −T0 in the temperature of maximum density is frequently expressed as ΔQD = KDmm, where m is the molality of the dissolved substance [58]. For diluted aqueous solutions, molality (m) can be numerically approximated by molar concentration (CM) expressed in moles/liter; therefore, ΔθD≈KDM·CM. For blood, ΔθD is almost 18 °C and is determined by the intracellular concentration of hemoglobin (about 5.3 mM), resulting in the Despretz constant of KDM(Hb) ≈ 3.4 × 103 °C/M [30].
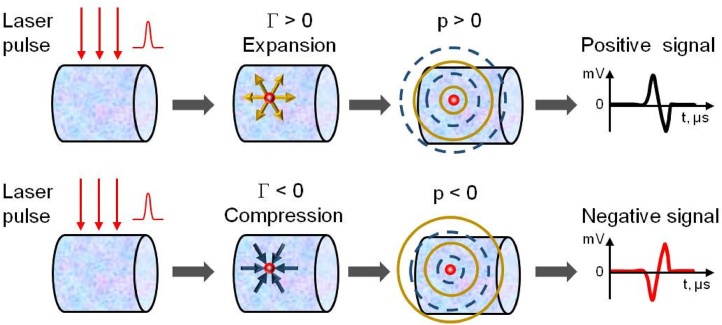
Transition of a sample through the point of maximum density is manifested by the change of polarity for measured OA signals, as depicted in Fig. 2 and explained in Fig. 3. The OA signals measured by all transducers of the ultrasound probe are used in the tomographic reconstruction, producing an image of the sample’s cross-section with a contrast defined by the magnitude and polarity of individual coherently added OA signals. At first, the deposited laser energy produces a quick increase of temperature inside an absorbing sample. If the thermal expansion coefficient (β) and by extension Grüneisen parameter (Γ) of the sample are positive, the temperature increase results in expansion of the constitutive substance. In that case, the optoacoustic pressure wave generated by adiabatic expansion of the medium propagates and is being detected with a rising front (top panel of Fig. 3). Such signals produce OA images of the samples with positive contrast (e.g. Sample 2 in Fig. 3A and B). When β is negative, deposition of the optical energy leads to adiabatic compression, and the propagating pressure wave is registered with a falling front (bottom panel of Fig. 3). Such signals produce OA images of the samples with negative contrast (e.g. Sample 2 in Fig. 2D–F). If the thermal expansion coefficient β = 0, the OA effect is not produced (e.g. Sample 2 in Fig. 2C), as the laser energy deposition into the optically absorbing material does not result in any detectable generation of stress. At this point, the excessive thermal energy is spend on rearrangement of the unique hydrogen-bond network found in water and water-based solutions (high density liquid and low density “ice-like” liquid) and does not produce any mechanical work required for generation of OA waves.
Fig. 2.
Optoacoustic images of four tubes (cross-sectional views) filled by CuSO4*5H2O solutions with the following concentrations: 1–0.06 M; 2–0.24 M; 3–0.36 M; and 4–0.48 M. Acoustic coupling medium is NaCl 23 wt% solutions with freezing point of −21 °C. Directions of optical illumination and detection of optoacoustic waves coincide (reflection mode) and are shown by an open arrow (A). OA response was estimated for each sample in the selected ROI, marked by dashed circles (B-F). Image intensity of samples decreases for lower temperatures [23]. At the point of zero OA response (maximum density) for a particular sample, the image of that sample disappeared in the background (as indicated by solid arrows). Change of OA image contrast corresponds to the change of the Grüneisen parameter. A linear grayscale palette was autoscaled for the first frame acquired at 20 °C and the limits were fixed for all the subsequent frames. Video is provided.
Fig. 3.
Optoacoustic phenomenon for positive and negative Grüneisen parameters (G). It depends on the thermal expansion coefficient (β), optical absorption coefficient (μa), and fluence (F), and can be observed during both expansion (positive β) and compression (negative β) of the optically absorbing medium. According to response of the medium to instant heating, a pressure wave will be generated in its positive or negative phase.
First, we investigated temperature-dependent OA response near the point of maximum density in ionic aqueous solutions. Fig. 2 demonstrates a series of OA images acquired from the cupric sulfate samples of four different concentrations while temperature was systematically decreased. The laser fluence in our setup was decreasing in the direction from the top to the bottom of each presented image due to natural divergence out of the fiber bundle termini. At the wavelength of 800 nm, cupric sulfate solution absorbs laser light, and the OA response increases proportionally to the concentration and the local fluence (white circles on a gray background in Fig. 2A). About 350 OA frames were acquired and automatically analyzed during the gradual temperature decrease from +20 to −10 °C. Fig. 2B presents the frame acquired at the temperature of 2.7 °C showing that the Sample 1 of cupric sulfate solution with molar concentration CM = 0.06 M became completely indistinguishable from the background. It can be seen on Fig. 2C that the vanished Sample 1 re-appears again, but its contrast is now reversed (sample image changes from white to black) indicating that Grüneisen parameter has switched from a positive to a negative value. The other three images of the samples pass through the same sequence of contrast transformations, but at different temperatures corresponding to the zero of thermal expansion in each sample solution.
As any other imaging modality, optoacoustic imaging is not free of effects of noise, limited detection characteristics of the hardware, and image artifacts. Signal processing that is typically applied in optoacoustic tomography is designed to improve contrast-to-noise ratio. However, it also may create some overshoot artifacts at the sharp boundaries of the samples revealed as a narrow opposite-contrast ring (or an arc) around the sample image (Fig. 2). Limited bandwidth and directivity of ultrasound transducers distort the received pressure signals, which are naturally ultrawide-band [16]. Reconstruction of the distorted pressure signals may produce small areas of erroneous contrast around the samples. Finally, limited view aperture of the linear probe provides incomplete tomographic data. Reconstruction of such data results in image artifacts, including distortions of the contrast at the boundary of the sample. Our estimates of the OA response were limited to the interior portion of the sample image at all times. Therefore, the potential boundary artifacts, mentioned above, did not propagate to the analyzed median values.
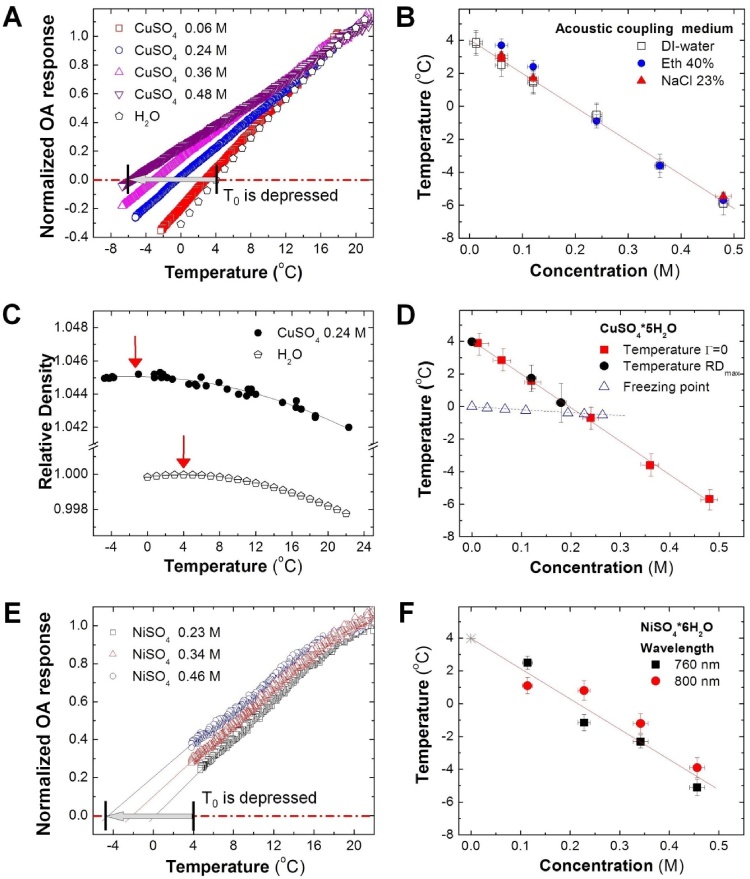
To evaluate the decrease in the value of temperature of maximum density in samples of cupric sulfate solutions, the estimated OA response was normalized at the initial temperature (19 °C) and plotted as a function of temperature (Fig. 4A). For comparison, the normalized value of the Grüneisen parameter for pure water was calculated from the data of the thermal expansion coefficient, SOS, and specific heat capacity [18] and provided on the same graph. The graph clearly shows that addition of cupric sulfate salt causes depression in the measured T0. Linear fit of the OA response versus temperature profiles for each sample provides accurate estimates for the temperatures of maximum density of the cupric sulfate solutions at different concentrations. Our experiments confirmed that the same T0 is observed during both cooling and heating of samples without any hysteresis. Linear fit for ΔθD vs CM results in the Despretz constant of KDM(CuSO4*5H2O) = 20.3 ± 0.3 °C/M (R2 = 0.997).
Fig. 4.
A. Temperature dependence of the normalized OA response for optically absorbing CuSO4*5H2O solutions and calculated normalized Grüneisen parameter (Γ) of pure water [17]. Dash-dotted line shows the level of zero OA response. B. Temperatures of maximum density for the studied cupric sulfate samples, where OA response is equal to zero, as a function of concentration; measurements were performed using various acoustic coupling media; C. Relative density measured with a hydrometer as a function of temperature [30] for 0.24 M solution of cupric sulfate (closed circles) and water (open circles); Data were fit with a parabolic function to obtain the temperatures of maximum relative density (RDmax) as indicated by the red arrows. D.T0 and RDmax and the freezing temperature measured for different concentrations of CuSO4[17]. E. Temperature dependence of the normalized OA response for optically absorbing solutions of nickel sulfate. F. The temperature of maximum density measured by the OA imaging technique (T0) as a function of nickel sulfate concentration; data are shown for two different laser wavelengths utilized for OA excitation.
We also validated that the medium used to enable propagation of OA waves from the studied samples to the ultrasound probe did not affect the measurements of T0. Three different types of acoustic coupling medium including deionized (DI) water, ethanol, and NaCl (23 wt%) solution were employed. SOS increases with temperature in NaCl solution as well as in pure DI-water [18]. On the contrary, in ethanol solution SOS decreases with temperature [18]. Our SOS automatic adjustment procedure, that involves finding maximum of the correlation function for the reconstructed image and the template sub-image of a sample in a frame-by-frame sequence, worked well to accurately capture those significant SOS differences and allowed for reconstruction of the sample images without visible distortions. The values of T0 were found to be consistent for all the tested acoustic coupling media (Fig. 4B).
In the control experiment, we directly measured the temperature of maximum relative density for cupric sulfate solutions, using a hydrometer [30]. The relative density data was fit with a parabolic function, providing maxima that coincided with T0, evaluated by the analysis of optoacoustic images (Fig. 4C and D).
Next, we evaluated T0 as a function of concentration for an aqueous ionic solution of nickel sulfate. Optoacoustic waves were induced in the samples using laser irradiation at 800 nm, the same wavelength that was used in the experiments on CuSO4 solutions. The molar extinction of NiSO4*6H2O in water was measured ε800nm = 1.02 ± 0.04 M−1cm−1, R2 = 0.993. To increase the experimental sensitivity and decrease susceptibility to fluctuations of laser fluence [42] we also measured temperature-dependent OA response using a different optical excitation wavelength of 760 nm where ε760nm = 1.83 ± 0.09 M−1cm−1, R2 = 0.991. The normalized OA response versus temperature graphs are presented in Fig. 4E, and the relationship of the estimated T0 with respect to the salt concentration is shown in Fig. 4F. The results are consistent for both excitation wavelengths with the measurement errors confined within 10–15%. Similar to the cupric sulfate solutions, the temperature T0 of maximum density for the nickel sulfate solutions decreases with increasing concentration of the salt. Linear fit for ΔθD vs CM results in the Despretz constant of KDM(NiSO4*6H2O) = 19.5 ± 0.8 °C/M (R2 = 0.989). The Despretz constants KDM for cupric sulfate and nickel sulfate were found almost equal (different by about 4% and within the margins of experimental error). On the other hand, Despretz constants for the sulfate salts are about 170 times smaller than the Despretz constant of hemoglobin evaluated from the T0 of whole blood. The interpretation of the Despretz constant is not straightforward and known to be dependent on charge, size and shape of ions [58], [59]. At low concentrations (0–0.3 mol/kg) of ions, the Despretz constant can be rationalized through the linear dependence of KDM on the ionic radii. In water, molecules of nickel sulfate and cupric sulfate dissociate into identical anions with radii r(SO42−) = 170 pm and cations of comparable radii: r(Ni2+) = 69 pm, r(Cu2+) = 73 pm. Therefore, it is expected that both salts will produce similar effects on the hydrogen-bond network in aqueous solutions, resulting in a similar thermodynamic behavior and Despretz constants. The molecule of hemoglobin has a tetrameric structure, which contains 574 amino acid residues, and the radius of the molecule is equal to 2.5 nm (or 2500 pm). This molecule is about 35 times bigger than the ions of nickel (2+) and copper (2+) and 15 times bigger than the sulfate ions. However, the relationship between KDM and ionic radii cannot be extrapolated to multi-domain protein molecules of hemoglobin, which are packed inside erythrocytes at extreme concentrations. The hemoglobin molecule has a complex distribution of surface electrical charge and thermodynamic macro effects contributing to the Despretz constant should be considered through the entire prism of hydrophobic, electrostatic and hydrogen-bond interactions [59].
OA response can be efficiently induced in weekly-absorbing media using contrast agents, such as plasmonic metal nanoparticles (NPs) or carbon black particles [19], [37], [60]. Those particles do not dissolve in water, but can form a highly-dispersed suspension. Following the absorption of optical energy, NPs rapidly transfer heat to the surrounding medium generating OA waves [60]. In the next set of experiments we studied the effects of NP concentration on the temperature of maximum density T0.
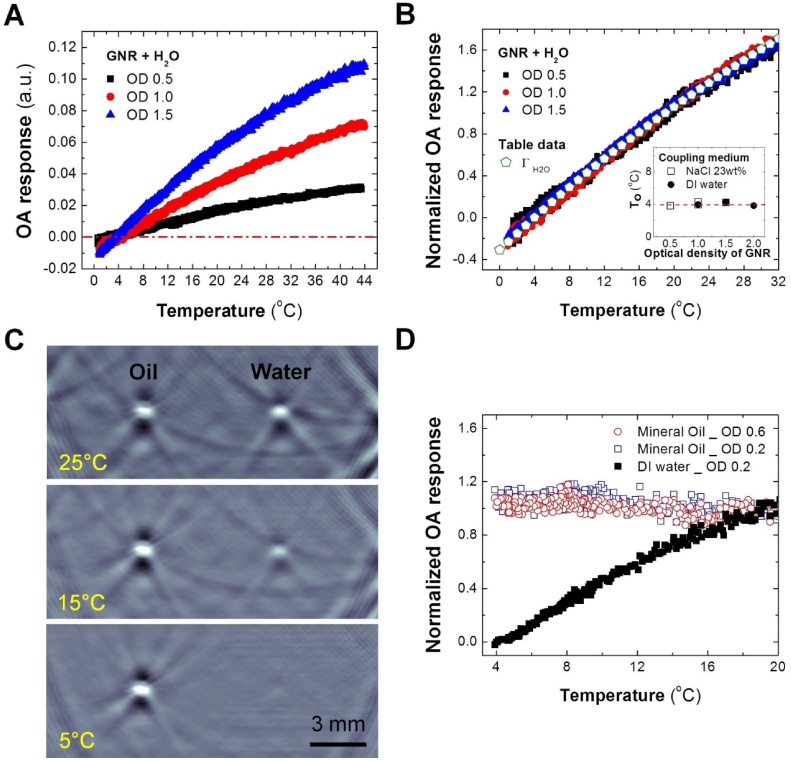
Fig. 5A shows OA response as a function of temperature for different concentrations of GNR suspended in water (concentrations are expressed in terms of measured optical density, OD). Fig. 5B demonstrates that the normalized temperature-dependent OA response is identical for all the concentrations of GNR and replicates the relationship for the Grüneisen of water. The data analysis shows that the temperature of maximum density (T0) in a suspension of GNR does not vary with concentration and is equal to that of pure water (inset graph on Fig. 5B). OA measurements of T0 in aqueous solutions all demonstrated linear dependence for a wide range of concentrations following well the Despretz’s law (Figs. 4 B, F, and 6 B). On the other hand, temperature dependent OA response in aqueous suspensions of NPs represented the temperature function of the Grüneisen of water, independent of NP concentration.
Fig. 5.
A. Temperature dependence of the OA response for pure water contrasted by GNR coated with PEG. Three concentrations of GNR presented with optical density (OD) at 800 nm: 0.5 cm−1, 1.0 cm−1, and 1.5 cm−1. B. The normalized OA response of GNR suspensions as compared to the calculated and normalized Grüneisen parameter (Γ) of pure water. The inlet shows the measured T0 as a function of GNR optical density. C. Optoacoustic images show cross sections of two tubes filled with liquids contrasted by carbon particles: left – mineral oil, right – pure water. Acoustic coupling was provided by water. D. Normalized (19 °C) OA response as a function of temperature for oil and water contrasted by carbon particles. Mineral oil results are depicted by open circles, pure water – solid squares.
Fig. 6.
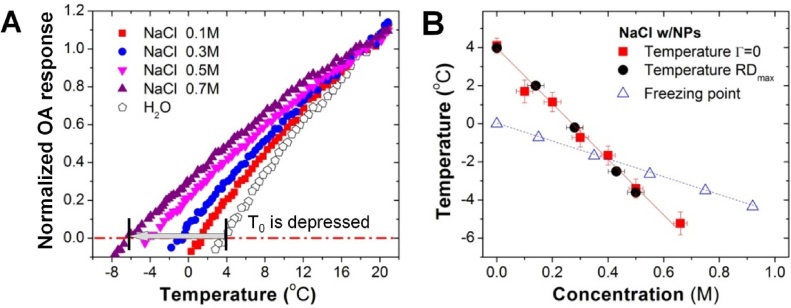
A. Temperature dependence of the normalized OA response for non-absorbing NaCl solutions augmented by plasmonic nanoparticles (NPs) and DI-water contrasted with carbon NPs. B. The temperature of Γ = 0 for the sodium chloride as a function of concentration; the temperature of RDmax according to seawater data; and the freezing temperature for sodium chloride solutions [18].
Prost et al. [35] theoretically predicted and Simandoux et al. [34] observed peculiar nonlinearity of OA response in aqueous suspensions of plasmonic nanoparticles, which showed a non-zero OA response detected in the high-frequency range (using a photoacoustic microscope equipped with a 20 MHz transducer) while the bulk suspension was at the equilibrium temperature of maximum density. Our setup was equipped with an ultrasound detector with a 5-MHz central frequency, which could be too low to observe any nonlinear deviation in the signals from the suspensions of GNRs as predicted [35].
We also investigated temperature dependent OA response of a non-aqueous liquid enhanced with suspension of optically absorbing NPs. Fig. 5C and D, demonstrate OA images and a graph showing behavior of mineral oil samples enhanced with carbon black particles vs. another sample with optically contrasted water. The normalized OA response of oil samples with two different concentrations of carbon nanoparticles show identical behavior in the interrogated range of temperatures (Fig. 5D). While contrast of the OA images of the oil sample remain independent of the local temperature, contrast of the OA image of the water sample decreases until the sample completely vanishes into the background (Fig. 5C). It is known that mineral oil and other types of oil are characterized by weak dependence of thermal expansion coefficient on temperature. Recent meticulous measurements in silicone oil demonstrated that the thermal expansion coefficient increased only by 6.3% when the temperature increased from 20 to 90 °C [61].
Previously, Chen et al. [19] analytically estimated that at 20 °C, up to 99% of OA pressure generated by a gold nanosphere inside the aqueous medium would be defined by the thermoelastic characteristics of the medium, and only about 1% by those of the nanoparticle. They also provided qualitative experimental demonstration that OA response of particulate contrast agents frequently depends on the thermodynamic characteristics of the immediate nanoparticle environment. The authors of [19] reported good qualitative resemblance of the relationships between the measured amplitudes of OA signals and temperature for the samples of pure silicon oil and silicon oil enhanced with gold nanospheres, indirectly supporting the original hypothesis. Our current results provided additional evidence that different types (gold and carbon) and concentrations of nanoparticles would not change temperature dependent behavior of the OA response of their colloids (see Fig. 5B and D).
The fact that suspensions of NPs maintain the temperature dependent OA response of a pure medium independent on the concentration of NPs has far going consequences for contrasted OA monitoring of temperature. It’s true that NPs used as temperature sensors in biological tissues which otherwise weakly absorb optical radiation, will require the environment-dependent calibration. Furthermore, it seems that reliable temperature monitoring is only possible in the water-rich tissues, which provide significant sensitivity for the technique. However, a big advantage of such contrasted temperature mapping approach would be in fact that the calibration will remain valid invariably with the local concentration of such NPs as long as it does not significantly change in a time course of temperature monitoring.
The fact that suspensions of NPs demonstrate temperature-dependent OA response of the medium itself could be further utilized to study transparent media other than water. To exemplify this statement, solutions of NaCl that do not absorb electromagnetic radiation in the near-infrared (NIR) optical range were optically contrasted with GNR. The graphs of temperature dependence of OA response for sodium chloride samples and DI water are presented in Fig. 6A. The temperature function of OA response measured in water contrasted with NPs coincides with the calculated Grüneisen parameter Γ(T). The accuracy of the temperature of maximum density estimated using the OA imaging technique was ±0.2 °C (Fig. 6B). The shift in the temperature of maximum density with respect to the concentration of NaCl solution measured by OA imaging technique (Fig. 6B) is consistent with the published data for seawater [18]. Linear fit for ΔθD vs CM results in the Despretz constant of KDM(NaCl) = 14.4 ± 0.5 °C/M (R2 = 0.994), consistent with the previously reported data [58]. The ionic radii r(Na+) = 97 pm and r(Cl−) = 181 pm. However, KDM of NaCl solution cannot be directly compared to the estimated KDM of sulfates, since the dissociated ions of those two salts have different ionic charges.
In addition to non-invasive temperature mapping, the OA imaging technique can be also conveniently used to measure the temperature of maximum density in optically transparent or opaque aqueous solutions. Due to low probability of heterogeneous ice nucleation in a small volume of each experimental sample, the OA imaging technique allows interrogation of T0 even below the freezing point of the studied solution (Figs. 4 D and 6 B).
4. Conclusion
In this work we demonstrated feasibility of OA temperature monitoring in tissue with low blood content exploiting exogenous contrast agent and the calibration method based on relationship between the measured temperature of zero Gruneisen parameter and soluble content of water-rich tissue. The calibration might vary depending on the type and local concentration of the contrast agent. In experiments on ionic solutions, we rigorously demonstrated that the relationship describing normalized OA response as a function of temperature depends on the concentration of electrolyte. The shift in the temperature of zero Grüneisen parameter in aqueous solutions is consistent with the shift in the temperature of maximum density and obeys the Despretz law for maximum density. However, using this type of contrast agents in vivo requires knowledge of local concentration of the administered contrast agent. On contrary, the normalized optoacoustic response of particulate contrast agents such as plasmonic or carbon nanoparticles does not depend on its local concentration and represents temperature-dependent optoacoustic response of the tissue itself. Particulate contrast agents suspended in mineral oil did not reveal detectable change in optoacoustic response as a function of temperature, suggesting that the current technique of the optoacoustic temperature mapping may not be applicable for adipose and other types of tissue with low water content. However, in water-rich soft tissue, optically contrasted nanoparticles should be more accurate temperature sensors as compared to water soluble chemicals and macromolecules. These findings provide an important step towards future non-invasive temperature monitoring in variety of low absorbing water-based biological tissues.
Author contributions
E.P. designed, performed, processed, and analyzed the imaging experiments. A.L. synthesized GNR and guided the experiments with GNR. A.O. participated in the strategic planning of the research. S.E. was the principal investigator of the research, developed algorithms and software on image reconstruction and temperature mapping. All authors contributed to writing of the manuscript.
Conflict of interest statement
The authors declare that there are no conflicts of interest between the business of Tomowave Laboratories, Inc. and the research presented in this article.
Acknowledgements
This work was supported in part by National Institutes of Health (National Cancer Institute) grant 1R43CA177148. We thank Professor Anatoly B. Kolomeisky from the Department of Chemistry, Rice University, Houston, TX, who assisted with the discussion of the observed decrease in the temperature of maximum density.
Biographies

Elena Petrova received her PhD from Lomonosov Moscow State University, Russia with a major in Physics. In her thesis she studied physical processes during formation of kidney stones, she proposed two new types of inhibitors of kidney crystals growth and explained the associated molecular mechanisms. The results were published as a book. During internship in Tohoku University, Japan Dr. Petrova investigated aggregation of glycoside hydrolases. She studied molecular biopolymerization in blood disorders as sickle cell anemia and malaria. In TomoWave Laboratories Inc. Dr. Petrova developed optoacoustic temperature mapping and proposed to employ erythrocytes as a universal optoacoustic temperature sensor. She has 20 peer-review publications, 1 book, and 1 patent. Her scientific interests include the development of biomedical imaging techniques, functional optoacoustics, physicochemical properties of solutions, crystallization, and phase transitions.

Anton Liopo is a former lead scientist of TomoWave Laboratories Inc. Houston, TX, USA, where he created several novel contrast agents, such as gold nanorods with plasmon resonance from 650 nm to 1500 nm and various polymeric nanoparticles. Dr. Liopo has 25 years of experience in biochemistry of bioactive compounds, human and animal physiology and investigation of the structural and functional changes of cells membrane. In the past 10 years his research emphasis was on advancement of optoacoustic imaging technology with new contrast and optical clearing agents. He served as a committee member for a number of international conferences. Dr. Liopo has more than 75 publications in peer-reviewed journals and proceedings of international conferences, 2 books and 2 book chapters.

Alexander A. Oraevsky has over 25 years experience managing research and development laboratories in academia and small businesses. He is a pioneer in the field of biomedical optoacoustics. Alexander received his initial training in physics and mathematics from the Moscow Physical and Engineering Institute in Moscow, Russia and obtained a doctorate in laser spectroscopy and laser biophysics from the USSR Academy of Sciences in 1986. Presently Dr. Oraevsky is the holder of 20 patents, has published 10 book chapters and over 250 scientific papers dealing with novel laser technologies applicable in biology and medicine.

Sergey A. Ermilov received his PhD in bioengineering from Rice University, Houston, Texas. His scientific interests are focused on development of biomedical optical and optoacoustic imaging technologies. His specific areas of expertise include theoretical aspects, computer modeling, signal and image processing, and image reconstruction.
Footnotes
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.pacs.2017.06.002.
Appendix A. Supplementary data
The following are Supplementary data to this article:
References
- 1.Chu K.F., Dupuy D.E. Thermal ablation of tumours: biological mechanisms and advances in therapy. Nat. Rev. Cancer. 2014;14:199–208. doi: 10.1038/nrc3672. [DOI] [PubMed] [Google Scholar]
- 2.Repasky E.A., Evans S.S., Dewhirst M.W. Temperature matters! and why it should matter to tumor immunologists. Cancer Immunol. Res. 2013;1(4):210–216. doi: 10.1158/2326-6066.CIR-13-0118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mohammed A., Miller S., Douglas-Moore J., Miller M. Cryotherapy and its applications in the management of urologic malignancies: a review of its use in prostate and renal cancers. Urol. Oncol. 2014;32(39):e19–e27. doi: 10.1016/j.urolonc.2013.04.004. [DOI] [PubMed] [Google Scholar]
- 4.Hsiao Y.-H., Kuo S.-J., Tsai H.-D., Chou M.-C., Yeh G.-P. Clinical application of high-intensity focused ultrasound in cancer therapy. J. Cancer. 2016;7:225–231. doi: 10.7150/jca.13906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Siva S., Ellis R.J., Ponsky L., The B.S., Mahadevan A., Muacevic A., Staehler M., Onishi H., Wesall P., Nomiya T., Lo S.S. Consensus statement from the international radiosurgery oncology consortium for kidney for primary renal cell carcinoma. Future Oncol. 2016;12:637–645. doi: 10.2217/fon.16.2. [DOI] [PubMed] [Google Scholar]
- 6.Baust J.G., Bischof J.C., Jiang-Hughes S., Polascik T.J., Rukstalis D.B., Gage A.A., Baust J.M. Re-purposing cryoablation: a combinatorial ‘therapy' for the destruction of tissue. Prostate Cancer Prostatic Dis. 2015;18(2):87–95. doi: 10.1038/pcan.2014.54. [DOI] [PubMed] [Google Scholar]
- 7.Petrova E., Liopo A., Nadvoretskiy V., Ermilov S. Imaging technique for real-time temperature monitoring during cryotherapy of lesions. J. Biomed. Opt. 2016;21(11):116007. doi: 10.1117/1.JBO.21.11.116007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ke H., Tai S., Wang L.V. Photoacoustic thermography of tissue. J. Biomed. Opt. 2014;19:26003. doi: 10.1117/1.JBO.19.2.026003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Petrova E.V., Motamedi M., Oraevsky A.A., Ermilov S.A. In vivo cryoablation of prostate tissue with real-time optoacoustic monitoring. Proc. SPIE Photons Plus Ultrasound: Imaging Sens. 2016;9708:97080G. [Google Scholar]
- 10.Rieke V., Pauly K.B., thermometry M.R. J. Magn. Reson. Imaging. 2008;27:376–3390. doi: 10.1002/jmri.21265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yuan J., Mei C.S., Panych L.P., McDannold N.J., Madore B. Towards fast and accurate temperature mapping with proton resonance frequency-based MR thermometry. Quant. Imaging Med. Surg. 2012;2(1):21–32. doi: 10.3978/j.issn.2223-4292.2012.01.06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sankineni S., Wood B.J., Rais-Bahrami S., Walton Diaz A., Hoang A.N., Pinto P.A., Choyke P.L., Türkbey B. Image-guided focal therapy for prostate cancer. Diagn. Interv. Radiol. 2014;20:492–497. doi: 10.5152/dir.2014.14134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Miller N.R., Bamber J.C., Meaney P.M. Fundamental limitations of noninvasive temperature imaging by means of ultrasound echo strain estimation. Ultrasound Med. Biol. 2002;28:1319–1333. doi: 10.1016/s0301-5629(02)00608-7. [DOI] [PubMed] [Google Scholar]
- 14.Oraevsky A.A., Karabutov A.A. Optoacoustic tomography. In: Vo-Dinh T., editor. Biomedical Photonics Handbook. CRC Press Boca Raton; London, New York, Washington, DC: 2003. pp. 34/1–34/34. [Google Scholar]
- 15.Wang L.V., Hu S. Photoacoustic tomography: in vivo imaging from organelles to organs. Science. 2012;335(6075):1458–1462. doi: 10.1126/science.1216210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Andreev V.G., Karabutov A.A., Oraevsky A.A. Detection of ultrawide-band ultrasound pulses in optoacoustic tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2003;50(10):1383–1390. doi: 10.1109/tuffc.2003.1244756. [DOI] [PubMed] [Google Scholar]
- 17.Watson P.E., Watson I.D., Batt R.D. Total body water volumes for adult males and females estimated from simple anthropometric measurements. Am. J. Clin. Nutr. 1980;33(1):27–39. doi: 10.1093/ajcn/33.1.27. [DOI] [PubMed] [Google Scholar]
- 18.93rd ed. CRC Press Boca Raton; 2012. CRC Handbook of Chemistry and Physics. [Google Scholar]
- 19.Chen Y.S., Frey W., Aglyamov S., Emelianov S. Environment-dependent generation of photoacoustic waves from plasmonic nanoparticles. Small (Weinheim an der Bergstrasse Germany) 2012;8(1):47–52. doi: 10.1002/smll.201101140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gusev V.E., Karabutov A.A. American Institute of Physics; New York: 1993. Laser Optoacoustics; p. 136. [Google Scholar]
- 21.Esenaliev R.O., Karabutov A.A., Motamedi M., Oraevsky A.A. Real-time optoacoustic monitoring of photothermal laser-tissue interactions. Proc. SPIE. 1999;3601:268–274. [Google Scholar]
- 22.Larina I.V., Larin K.V., Esenaliev R.O. Real-time optoacoustic monitoring of temperature in tissues. J. Phys. 2005;38(15):2633–2639. [Google Scholar]
- 23.Petrova E., Ermilov S., Su R., Nadvoretskiy V., Conjusteau A., Oraevsky A. Using optoacoustic imaging for measuring the temperature dependence of Gruneisen parameter in optically absorbing solutions. Opt. Express. 2013;21:25077–25090. doi: 10.1364/OE.21.025077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pramanik M., Wang L.V. Thermoacoustic and photoacoustic sensing of temperature. J. Biomed. Opt. 2009;14(5):054024. doi: 10.1117/1.3247155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Soroushian B., Whelan W.M., Kolios M.C. Study of laser-induced thermoelastic deformation of native and coagulated ex-vivo bovine liver tissues for estimating their optical and thermomechanical properties. J. Biomed. Opt. 2010;15(6):065002. doi: 10.1117/1.3517455. [DOI] [PubMed] [Google Scholar]
- 26.Shah J., Park S., Aglyamov S., Larson T., Ma L., Sokolov K., Johnston K., Milner T., Emelianov S.Y. Photoacoustic imaging and temperature measurement for photothermal cancer therapy. J. Biomed. Opt. 2008;13(3):034024. doi: 10.1117/1.294036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nikitin S.M., Khokhlova T.D., Pelivanov I.M. Temperature dependence of the optoacoustic transformation efficiency in ex vivo tissues for application in monitoring thermal therapies. J. Biomed. Opt. 2012;17(6):061214. doi: 10.1117/1.JBO.17.6.061214. [DOI] [PubMed] [Google Scholar]
- 28.Brinkmann R., Koinzer S., Schlott K., Ptaszynski L., Bever M., Baade A., Luft S., Miura J., Birngruber R. Real-time temperature determination during retinal photocoagulation on patients. J. Biomed. Opt. 2012;17(6):061219. doi: 10.1117/1.JBO.17.6.061219. [DOI] [PubMed] [Google Scholar]
- 29.Yao D.-K., Wang L.V. Measurement of grüneisen parameter of tissue by photoacoustic spectrometry. Proc. SPIE. 2013;8581 858138-1. [Google Scholar]
- 30.Petrova E.V., Oraevsky A.A., Ermilov S.A. Red blood cell as a universal optoacoustic sensor for non-invasive temperature monitoring. Appl. Phys. Lett. 2014;105:094103. doi: 10.1063/1.4894635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang B., Emelianov S. Thermal intravascular photoacoustic imaging. Biomed. Opt. Express. 2011;2(11):3072–3078. doi: 10.1364/BOE.2.003072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gao L., Wang L., Li C., Liu Y., Ke H., Zhang C., Wang L.V. Single-cell photoacoustic thermometry. J. Biomed. Opt. 2013;18(2):026003. doi: 10.1117/1.JBO.18.2.026003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gao L., Zhang C., Li C., Wan L.V. Intracellular temperature mapping with fluorescence-assisted photoacoustic-thermometry. Appl. Phys. Lett. 2013;102:193705. doi: 10.1063/1.4807140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Simandoux O., Prost A., Gateau J., Bossy E. Influence of nanoscale temperature rises on photoacoustic generation: discrimination between optical absorbers based on thermal nonlinearity at high frequency. Photoacoustics. 2015;3(1):20–25. doi: 10.1016/j.pacs.2014.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Prost A., Poisson F., Bossy E. Photoacoustic generation by a gold nanosphere: from linear to nonlinear thermoelastics in the long-pulse illumination regime. Phys. Rev. B. 2015;92:115450. [Google Scholar]
- 36.Li W., Chen X. Gold nanoparticles for photoacoustic imaging. Nanomedicine. 2015;10(2):299–320. doi: 10.2217/nnm.14.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liopo A.V., Oraevsky A.A. Nanoparticles as contrast agents for optoacoustic imaging. In: Berezin M., editor. Nanotechnology for Biomedical Imaging and Diagnostics: from Nanoparticle Design to Clinical Applications. John Wiley and Sons; NJ, USA: 2015. pp. 111–149. [Google Scholar]
- 38.Yoon S.J., Murthy A., Johnston K.P., Sokolov K.V., Emelianov S.Y. Thermal stability of biodegradable plasmonic nanoclusters in photoacoustic imaging. Opt. Express. 2012;20(28):29479–29487. doi: 10.1364/OE.20.029479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jung B., Anvari B. Virus-mimicking optical nanomaterials: near infrared absorption and fluorescence characteristics and physical stability in biological environments. ACS Appl. Mater. Interfaces. 2013;5(15):7492–7500. doi: 10.1021/am401800w. [DOI] [PubMed] [Google Scholar]
- 40.Luke G.P., Yeager D., Emelianov S.Y. Biomedical applications of photoacoustic imaging with exogenous contrast agents. Ann. Biomed. Eng. 2012;40(2):422–437. doi: 10.1007/s10439-011-0449-4. [DOI] [PubMed] [Google Scholar]
- 41.Zalev J., Herzog D., Clingman B., Miller T., Kist K., Dornbluth N.K., McCorvey B.M., Otto P., Ermilov S., Nadvoretsky V., Conjusteau A., Su R., Tsyboulski D., Oraevsky A. Clinical feasibility study of combined optoacoustic and ultrasonic imaging modality providing coregistered functional and anatomical maps of breast tumors. Proc. SPIE. 2012;8223:82230A. [Google Scholar]
- 42.Petrova E.V., Ermilov S.A., Su R., Nadvoretskiy V.V., Conjusteau A., Oraevsky A.A. Temperature dependence of Grüneisen parameter in optically absorbing solutions measured by 2D optoacoustic imaging. Proc. SPIE. 2014;8943:89430S. doi: 10.1364/OE.21.025077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Petrova E.V., Vorontsova M.A., Manomenova V.L., Rashkovich L.N. Some properties of alpha-NiSO4.6H2O water solution. Crystallogr. Rep. 2011;57:234–2239. [Google Scholar]
- 44.Karabutov A.A., Savateeva E.V., Podymova N.B., Oraevsky A.A. Backward mode detection of laser-induced wide-band ultrasonic transients with optoacoustic transducer. J. Appl. Phys. 2000;87(4):2003–2014. [Google Scholar]
- 45.Kruger R.A., Liu P., Fang Y.R., Appledorn C.R. Photoacoustic ultrasound (PAUS)?reconstruction tomography. Med. Phys. 1995;22(10):1605–1609. doi: 10.1118/1.597429. [DOI] [PubMed] [Google Scholar]
- 46.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. 2005;71(1 Pt 2):016706. doi: 10.1103/PhysRevE.71.016706. [DOI] [PubMed] [Google Scholar]
- 47.Oruganti T., Petrova E., Oraevsky A.A., Ermilov S.A. Speed of sound and acoustic attenuation of compounds affected during optoacoustic monitoring of thermal therapies measured in the temperature range from 5°C to 60°C. Proc. SPIE. 2015;9323:932331. [Google Scholar]
- 48.Liopo A.V., Wang S., Derry P.J., Oraevsky A.A., Zubarev E.R. Seedless synthesis of gold nanorods using dopamine as a reducing agent. RSC Adv. 2015;5:91587–91593. [Google Scholar]
- 49.Liopo A.V., Conjusteau A., Chumakova O.V., Ermilov S.A., Su R., Oraevsky A.A. Highly purified biocompatible gold nanorods for contrasted optoacoustic imaging of small animal models. Nanosci. Nanotechnol. Lett. (Print) 2012;4(7):681–686. doi: 10.1166/nnl.2012.1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Liopo A.V., Conjusteau A., Konopleva M., Andreeff M., Oraevsky A.A. Laser nanothermolysis of human leukemia cells using functionalized plasmonic nanoparticles. Nano Biomed. Eng. 2012;4(2):66–75. doi: 10.5101/nbe.v4i2.p66-75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mallamace F., Corsaro C., Stanley H.E. A singular thermodynamically consistent temperature at the origin of the anomalous behavior of liquid water. Sci. Rep. 2012;2:993. doi: 10.1038/srep00993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cawley M.F., McGlynn D., Mooney P.A. Measurement of the temperature of density maximum of water solutions using a convective flow technique. Int. J. Heat Mass Transf. 2006;49:1763–1772. [Google Scholar]
- 53.Franks F. Volume 4: Aqueous Solutions of Amphiphiles and Macromolecules. Plenum; New York: 1978. Water: a comprehensive treatise. [Google Scholar]
- 54.Poole P.H., Sciortino F., Essmann U., Stanley H.E. Phase behavior of metastable water. Nature. 1992;360:324–328. [Google Scholar]
- 55.Cho C.H., Singh S., Robinson G.W. An explanation of the density maximum in water. Phys. Rev. Lett. 1996;76(10):1651–1654. doi: 10.1103/PhysRevLett.76.1651. [DOI] [PubMed] [Google Scholar]
- 56.Dinga Y., Hassanalia A.A., Parrinelloa M. Anomalous water diffusion in salt solutions. Proc. Natl. Acad. Sci. 2014;111(9):3310–3315. doi: 10.1073/pnas.1400675111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Despretz M.-C. Recherches sur le maximum de densité de l’eau et des dissolitions aqueoses. Ann. Chem. Phys. 1839;70:49–81. [Google Scholar]
- 58.Kaulgud M.V., Pokale W.K. Measurement of the temperature of maximum density of aqueous solutions of some salts and acids. J. Chem. Soc. Faraday Trans. 1995;91(6):999–1004. [Google Scholar]
- 59.Tariq M., Esperança J.M.S.S., Soromenho M.R.C., Rebeloa L.P.N., Canongia Lopes J.N. Shifts in the temperature of maximum density (TMD) of ionic liquid aqueous solutions. Phys. Chem. Chem. Phys. 2013;15:10960–10970. doi: 10.1039/c3cp50387a. [DOI] [PubMed] [Google Scholar]
- 60.Egerev S., Ermilov S., Ovchinnikov O., Fokin A., Guzatov D., Klimov V., Kanavin A., Oraevsky A.A. Acoustic signals generated by laser-irradiated metal nanoparticles. Appl. Opt. 2009;48(7):C38–C45. doi: 10.1364/ao.48.000c38. [DOI] [PubMed] [Google Scholar]
- 61.Romano M.R., Romano V., Mauro A., Angi M., Costagliola C., Ambrosone L. The effect of temperature changes in vitreoretinal surgery. Transl. Vis. Sci. Technol. 2016;5:4. doi: 10.1167/tvst.5.1.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.