Abstract
In this study, milling recovery, head rice yield, degree of milling and whiteness were utilized to characterize the milling quality of Tarom parboiled rice variety. The parboiled rice was prepared with three soaking temperatures and steaming times. Then the samples were dried to three levels of final moisture contents [8, 10 and 12% (w.b)]. Modeling of process and validating of the results with small dataset are always challenging. So, the aim of this study was to develop models based on the milling quality data in parboiling process by means of multivariate regression and artificial neural network. In order to validate the neural network model with a little dataset, K-fold cross validation method was applied. The ANN structure with one hidden layer and Tansig transfer function by 18 neurons in the hidden layer was selected as the best model in this study. The results indicated that the neural network could model the parboiling process with higher degree of accuracy. This method was a promising procedure to create accuracy and can be used as a reliable model to select the best parameters for the parboiling process with little experiment dataset.
Keywords: Artificial neural network, K-fold cross validation, Parboiling, Rice
Introduction
Rice (Oryza sativa L.) is one of the main foods for more than half of the world’s population and the demand for increasing the production is particularly urgent (Nasirahmadi et al. 2014a; Amanullah and Inamullah 2016). To compensate the increasing demand of rice, reducing the losses of post-harvest processing is one of the feasible ways. Parboiling can be introduced as an optional processing operation to enhance the quality and decline processing losses of rice which includes different steps, i.e. soaking in (hot/cold) water, steaming with hot vapor and drying process (Nasirahmadi et al. 2014a). Rice milling process can be subjected to dehusking of paddy which results in brown rice, and removing the bran from the kernel by polishing the brown rice to yield white rice. Color is an important factor influencing the rice price and the amount of polishing can effect on rice color (Mohapatra and Bal 2007). Milling recovery (MR) and head rice yield (HRY) are defined as the percentages of total milled rice (broken + head) and head rice based on the paddy weight, respectively (Pan et al. 2007). Head rice is expressed as milled kernels that their length are ¾ or more than the original kernel’s length. Degree of milling (DOM) is defined as the extent of bran removal from brown rice. This parameter is an essential factor to estimate the nutritional value of rice including the amount of protein, vitamins, and minerals. Milling quality (MQ) is an important factor which affects the economic value of rice, while there is not a specific definition for that (Nasirahmadi et al. 2014a). In this Study MQ has been defined as a function of MR, HRY, DOM and Whiteness based on (Nasirahmadi et al. 2014a).
Artificial neural network (ANN) is a robust tool for modeling of food process (Omid et al. 2009; Behroozi-Khazaei et al. 2013). However, it needs a good (enough) database for training and validation. When there is a poor (little) database, especially in postharvest processing in agriculture product, modeling with ANN is challengeable due to experiment costs or time limits. In this condition, data division, training, initial weights and biases of the ANN effect on precision and accuracy of the model. Two methods could be proposed for solving the challenge: (1) generating synthetic samples from original dataset using different approaches. Examples of different methods have been used by researchers are: mega-trend-diffusion technique by Li et al. (2007), bootstrap method by Chao et al. (2011), and multivariate normal technique by Kato et al. (2012). Their results indicated that learning accuracy of the ANN was enhanced and the constructed model had good reliability. Furthermore, Li et al. (2014) employed gene expression programming to provide a procedure to generate related virtual samples with non-linearity. (2) A particular train-validation-test procedure. The performance is measured by an accuracy on K-fold cross validation. Some researchers were used K-fold cross validation for training of the ANN for increasing the reliability of the model, e.g. Gitifar et al. (2013) for modeling of sugarcane bagasse and Rudiyanto et al. (2016) in predicting of the depth and carbon stocks.
The ANN has been widely used in rice based research. To predict the presence or absence of flamingo damages of rice paddies, a multilayer feed-forward neural network was used by Tourenq et al. (1999). In another research, an ANN model was developed for paddy drying to obtain energy consumption, final moisture content, kernel cracking, moisture removal rate, drying intensity and water mass removal rate (Zhang et al. 2002). In their research, 22 dataset was used (20 for training and 2 for testing). The reported model didn’t have good reliability for prediction and optimizing of the process. Compressive strength properties of parboiled paddy and milled rice have been predicted using ANN by Nasirahmadi et al. (2014b). The results indicated that the model could predict the properties with high correlations and low mean square errors. Furthermore, with ANN the optimum frozen condition of cooked rice has been predicted by Kono et al. (2016). It was shown that the ANN models predicted the sensory evaluation scores with high accuracy.
In the literature, there is a little information for creating the accuracy and reliable model in post-harvest processing of agricultural products based researches when the dataset is small. So, the main objectives of this study were to develop a precision model for the MQ of rice in parboiling condition based on ANN and Multivariate regression (MVR) as a function of MR, HRY, DOM and Whiteness. Also for developing the good accuracy and reliability of the ANN, K-fold cross validation method was applied.
Materials and methods
An Iranian rice variety (Tarom) was used in this study and the moisture of paddy was determined by hot air oven. Around 5 g of the paddy sample with three replications was kept at 105 °C for 24 h (Mohapatra and Bal 2007), and then the moisture content was measured and expressed as wet basis. The paddy rice grains were soaked in the water at 25, 50 and 75 °C for 48, 6 and 3 h, respectively. The samples were then completely drained until there was no free water. For each soaking temperature the paddy samples were steamed for 10, 15 and 20 min at 100 °C and atmospheric pressure. Parboiled paddy samples were left in the laboratory on the mats for 48 h, the moisture content of samples was round 15% (w.b). The samples were then dried in a standard hot air oven at 35–40 °C for 24–48 h, until achieving 12, 10 and 8% of moisture content (w.b) levels.
Using a laboratory rubber roll type rice husker (ST 50, Yanmar, Japan) three sub-samples (500 g) of parboiled paddy were taken and dehusked at three mentioned moisture content levels and result in brown rice. The whole brown rice kernels were milled using a laboratory friction and abrasion vertical type whitener (VP-31, Yamamoto, Japan). The head rice and broken kernels were separated using a laboratory rice grader (TRG 058, Satake, Japan). The degree of Whiteness of milled rice samples was measured with a laboratory Whiteness meter (C-300-3, Kett Electronic, Japan). MR, HRY and DOM based on paddy weight were determined as the following (Gujral et al. 2002; Pan et al. 2007; Bello et al. 2015):
| 1 |
| 2 |
| 3 |
where W t(g) is the weight of total rice (head + broken) after milling, W d (g) is the weight of head rice after milling, W b(g) is the weight of brown rice and W p (g) is the weight of paddy.
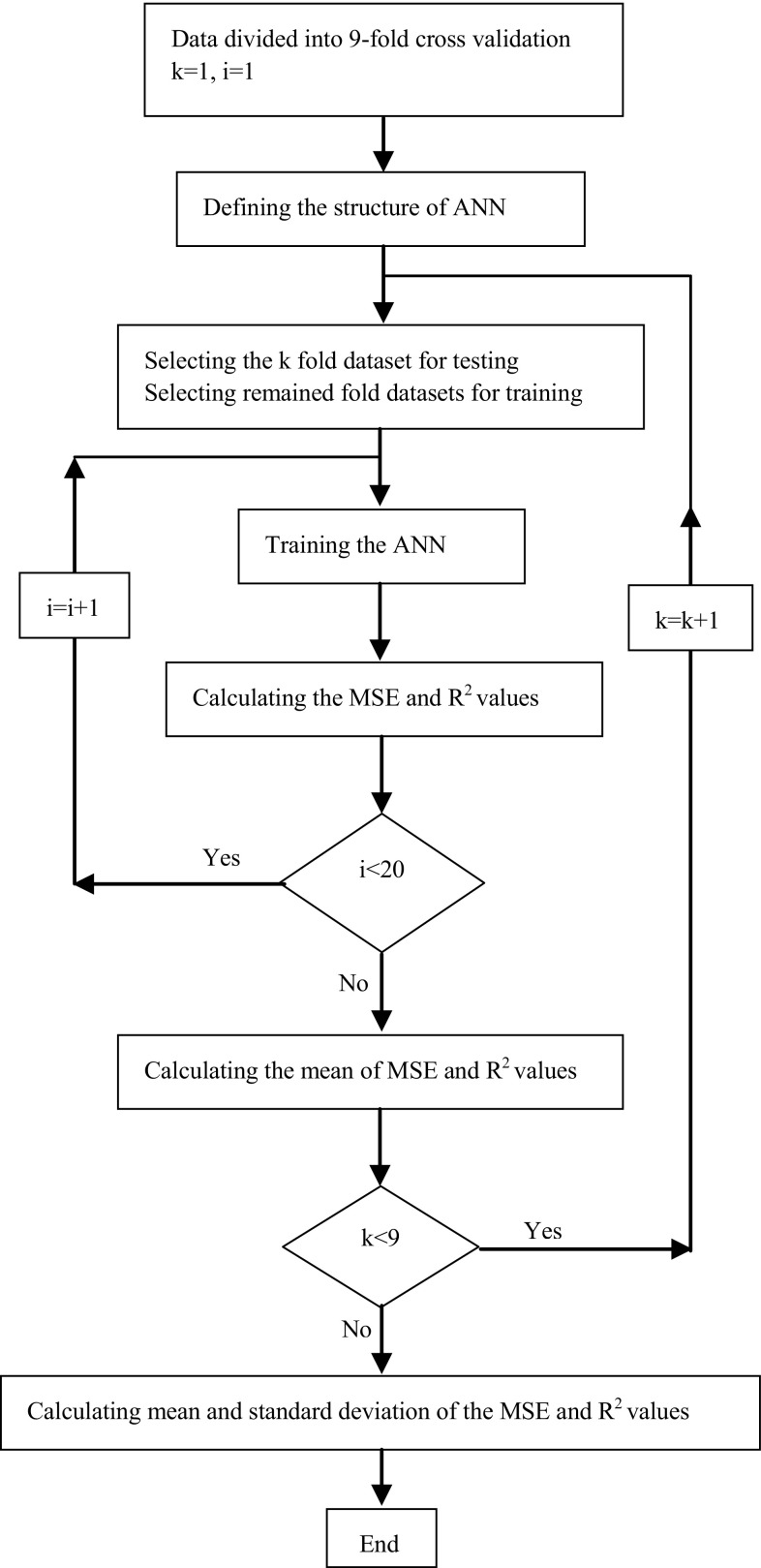
Feed-forward neural networks are the most popular architectures due to the flexibility of architecture and good representational capabilities (Shrivastav and Kumbhar 2011; Salehi et al. 2011; Motavali et al. 2013; Nasirahmadi et al. 2017). ANN model contains an input layer, an output layer and one or more hidden layers. The number of neurons in the input and output layers are equal to the number of input (independent) and output (dependent) variables. The ANN structures employed for modeling the MQ and parboiling process of the rice had three input variables i.e. soaking temperature, steaming time and moisture content. The output variables of the ANNs were MR, HRY, DOM and Whiteness. The number of hidden layers and their neurons is an important and crucial stage in the design of any ANN which depends on the complexity of the problem. The topology of the network was selected by trial and error method (Nasirahmadi et al. 2017). The other parameters of network also affect the network training process. These parameters are the weights of the connection between neurons and bias for each neuron in the hidden and output layers as well as transfer function in the hidden layers. These parameters are updated through a training procedure, with the aim of minimizing the difference between the network’s outputs and the target values. However, the response of the network strongly depends on the initial value of these parameters. Normally, the initial values of these parameters were selected randomly. Another way to remove the effect of initial weights on the ANN performance is the ensemble runs. This method includes repeating of a certain number of times (usually 20–30) and new random choices of initial weights (Pasini and Modugno 2013; Pasini 2015). In this study, the ensemble runs of the ANN by 20 repeating were used. The ANN training algorithm (Fig. 1) was developed in MATLAB® (the Mathworks Inc., Natick, MA, USA) software.
Fig. 1.
Schematic of the training process of the ANN
In this study 81 datasets (3 levels of soaking temperature × 3 levels of steaming temperature × 3 levels of final moisture content × 3 replications) were available. In the K-fold cross validation, th high value of K reduces the variance but increseas the computational time. In addition, the K with low value leads to an increase in the variance value. In this study, the datasets were divided into ninefold cross validation. For each K fold, K-1 folds are used for training and the remaining values utilized for testing (Stegmayer et al. 2013). Then the average mean square error (MSE) and regression coefficient (R2) of all K trials are computed as:
| 4 |
| 5 |
The advantage of this method is that every data point needs to be in a test set exactly once, and needs to be in training set K − 1 times.
In this study, feed forward ANN with back-propagation training algorithm was used. In order to obtain an ANN with the best performance, Bayesian Regularization (BR) algorithm was utilized. This algorithm is suitable for training small database and does not need validation dataset (Demuth and Beale 2003). As a result, the database was divided into two sets, i.e. training and testing. In order to avoid over-fitting during the training process, the BR algorithm applied as a modifier in performance function, which is normally chosen tbe the sum of squares of the network errors on the training set. Using the modified performance function causes the network to have smaller weights and biases. Moreover it forces the network response to be smoother with less over-fitting problems (Demuth and Beale 2003). However, the network must be trained for a sufficient number of iterations to ensure convergence. Therefore, 1000 epoch was used for training in this sutdy. The hyperbolic tangent sigmoid transfer function in the hidden and purlin transfer function in the output layer were applied. Due to the different ranges of each input and output, the input and output datasets were normalized and imposed between [-1, 1] with mapminmax function in the MATLAB®. After selecting the best network, this structure has been trained with Logsig transfer function for evaluating the transfer function on the ANN accuracy.
Beside the ANN a mathematical regression model was also adopted for modeling of rice parboiling process variables in this study. Since there is a large number of variable influences the quality of the parboiled rice, some mathematical models are needed to represent the process. However, these models have to be developed using only significant parameters influencing the parboiling process rather than including all the parameters. MVR with three-variables (soaking temperature (X1), steaming time (X2), and moisture content (X3)), was adopted to determine the effects of the independent variables on the MQ variables. The experimental data obtained from experiments can be represented in the form of the following Eq. (6):
| 6 |
B1, B2,…, B9 are the coefficients of the model. MVR analysis was carried out on the data using MATLAB® software.
Results and discussion
The experiment data indicated that the maximum and minimum values for MR (75.63 and 68.58%), for HRY (65.68 and 45.74%), for DOM (6.01 and 4.81%) and for Whiteness (24.83 and 20.76) were observed, respectively. Other researchers showed that soaking temperature and steaming time (Nasirahmadi et al. 2014a; Danbaba et al. 2014; Leethanapanich et al. 2016) and final moisture content (Nasirahmadi et al. 2014a) had significant effect on the MQ variables. So, in this paper, the soaking temperature, steaming time and moisture content were taken as the dependent/input parameters, where MR, HRY, DOM and Whiteness assumed as independent/output parameters. The MVR and ANN were used for modeling of the MQ variable based on effective parameters on parboiling process.
The MVR model coefficients, P value of each coefficient, R2 and MSE of each MQ were represented in Table 1.
Table 1.
The results of the regression analysis and corresponding P value of second order polynomial model
| Model term | MR | HRY | Whiteness | DOM | ||||
|---|---|---|---|---|---|---|---|---|
| Coefficient | P value | Coefficient | P value | Coefficient | P value | Coefficient | P value | |
| B0 | 79.941 | 0.000 | 82.850 | 0.000 | 30.2480 | 0.000 | 3.1104 | 0.002 |
| B1 | −0.093 | 0.071 | −1.344 | 0.000 | 0.16215 | 0.000 | 0.0485 | 0.000 |
| B2 | 0.685 | 0.032 | −0.769 | 0.116 | −0.09129 | 0.590 | 0.0561 | 0.239 |
| B3 | −2.056 | 0.075 | 2.077 | 0.240 | −1.95880 | 0.002 | 0.1561 | 0.365 |
| B4 | −0.005 | 0.000 | 0.013 | 0.000 | 0.00131 | 0.054 | −0.0001 | 0.501 |
| B5 | 0.011 | 0.000 | −0.003 | 0.585 | −0.00061 | 0.716 | −0.0013 | 0.005 |
| B6 | 0.033 | 0.038 | 0.008 | 0.732 | −0.00138 | 0.868 | 0.0010 | 0.671 |
| B7 | 0.0007 | 0.040 | 0.011 | 0.000 | −0.00194 | 0.000 | −0.0003 | 0.000 |
| B8 | −0.015 | 0.078 | 0.022 | 0.104 | 0.00052 | 0.913 | −0.0033 | 0.013 |
| B9 | 0.029 | 0.595 | −0.156 | 0.069 | 0.09768 | 0.001 | −0.0015 | 0.854 |
| R2 | 0.757 | – | 0.930 | – | 0.710 | – | 0.764 | – |
| MSE | 0.876 | – | 2.073 | – | 0.252 | – | 0.020 | – |
The P value was used to investigate the significance of each coefficient. Smaller P value denotes greater significance of the corresponding coefficient (Lee and Wang 1997). The result of this table showed that the proposed model with MVR could predict the MR, HRY, DOM and Whiteness with R2 of 0.75, 0.93, 0.71 and 0.76 and MSE values of 0.87, 2.07, 0.25 and 0.02, respectively.
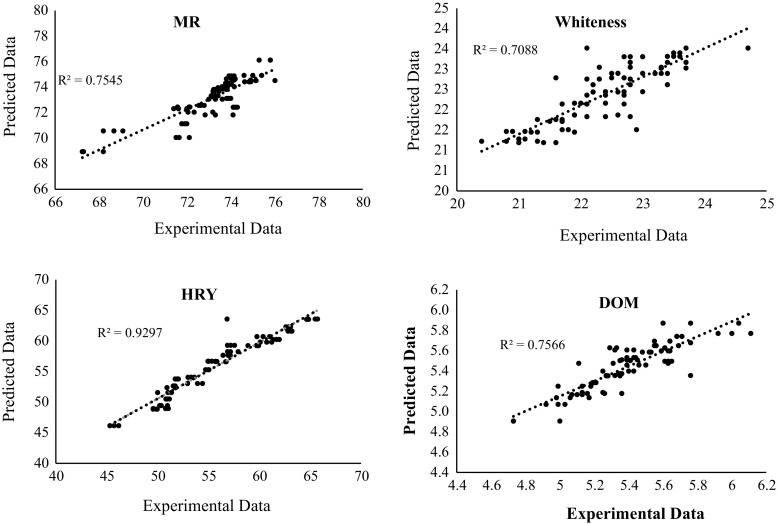
The predicted all data (train and test) versus the actual data were plotted in Fig. 2. These results indicated the model could predict HRY with high enough R2 (0.92) value, while other MQ variables i.e. MR (0.75), DOM (0.75) and Whiteness (0.78) were not properly predicted by the model. The results of Danbaba et al. (2014) for modeling of the HRY also showed that the second order polynomial could predict the HRY with suitable accuracy (R2 = 0.97).
Fig. 2.
Experimental data versus predicted data (train and test) by the MVR
The ANN was accomplished using the training and test datasets. In the ANN model, the soaking temperature, steaming time and moisture content were taken as the input parameters, where MR, HRY, DOM and Whiteness assumed as output parameters. Therefore, The ANN used here had 3 neurons in the input layer and 4 neurons in the output layer. The number of neurons in the hidden layer was determined by trial and error method. The MSE and R2 values at different number of neurons in the hidden layer were illustrated in Table 2. The optimal ANN model should have the lowest MSE value and highest R2 value. As can be seen in the table (marked in bold), the structure with 18 neurons in hidden layer amongst the networks with one hidden layer had the best results. The structure has predicted the MQ variables with MSE of 0.23 and 0.53 and R2 of 0.88 and 0.84 for training and testing process, respectively. Also between the networks with two hidden layers, the structure with 12 neurons (marked in bold in Table 2) in the first and second layer with MSE of 0.23 and 0.53 and R2 of 0.87 and 0.84 for training and testing process, respectively, had the best results. The results of the best structure with Logsig transfer function in the hidden layers were illustrated in Table 2. By comparing the results obtained in the table, the ANN structure with Tansig transfer function in hidden layers had better results than Logsig transfer function. Therefore, the network with one hidden layer, 18 neurons and Tansig transfer function in the hidden layer was selected as the best model in this study.
Table 2.
The MSE and R2 values at different number of neurons with Tansig function in the hidden layer
| Num. of neurons in the hidden layer | Transfer function | MSE | R2 | ||
|---|---|---|---|---|---|
| Train | Test | Train | Test | ||
| 3 | Tansig | 0.7260 ± 0.056 | 0.9920 ± 0.621 | 0.6839 ± 0.006 | 0.7157 ± 0.056 |
| 6 | Tansig | 0.3880 ± 0.060 | 0.7350 ± 0.680 | 0.7956 ± 0.006 | 0.7814 ± 0.040 |
| 9 | Tansig | 0.2772 ± 0.060 | 0.6063 ± 0.712 | 0.8484 ± 0.005 | 0.8184 ± 0.033 |
| 12 | Tansig | 0.2387 ± 0.057 | 0.5451 ± 0.732 | 0.8744 ± 0.005 | 0.8412 ± 0.030 |
| 15 | Tansig | 0.2334 ± 0.057 | 0.5392 ± 0.734 | 0.8800 ± 0.006 | 0.8313 ± 0.027 |
| 18 | Tansig | 0.2332 ± 0.057 | 0.5340 ± 0.735 | 0.8809 ± 0.005 | 0.8434 ± 0.027 |
| 21 | Tansig | 0.2332 ± 0.057 | 0.5396 ± 0.735 | 0.8809 ± 0.006 | 0.8410 ± 0.028 |
| 3-3 | Tansig | 0.4468 ± 0.085 | 0.7092 ± 0.628 | 0.7800 ± 0.007 | 0.7354 ± 0.051 |
| 6-6 | Tansig | 0.2339 ± 0.058 | 0.5482 ± 0.733 | 0.8591 ± 0.006 | 0.8253 ± 0.032 |
| 9-9 | Tansig | 0.2307 ± 0.056 | 0.5370 ± 0.735 | 0.8751 ± 0.006 | 0.8397 ± 0.033 |
| 12-12 | Tansig | 0.2300 ± 0.056 | 0.5346 ± 0.737 | 0.8764 ± 0.006 | 0.8423 ± 0.032 |
| 15-15 | Tansig | 0.2297 ± 0.056 | 0.5349 ± 0.736 | 0.8770 ± 0.006 | 0.8410 ± 0.032 |
| 18 | Logsig | 0.2342 ± 0.058 | 0.5350 ± 0.745 | 0.8787 ± 0.006 | 0.8408 ± 0.027 |
| 12-12 | Logsig | 0.2320 ± 0.056 | 0.5356 ± 0.737 | 0.8727 ± 0.006 | 0.8386 ± 0.032 |
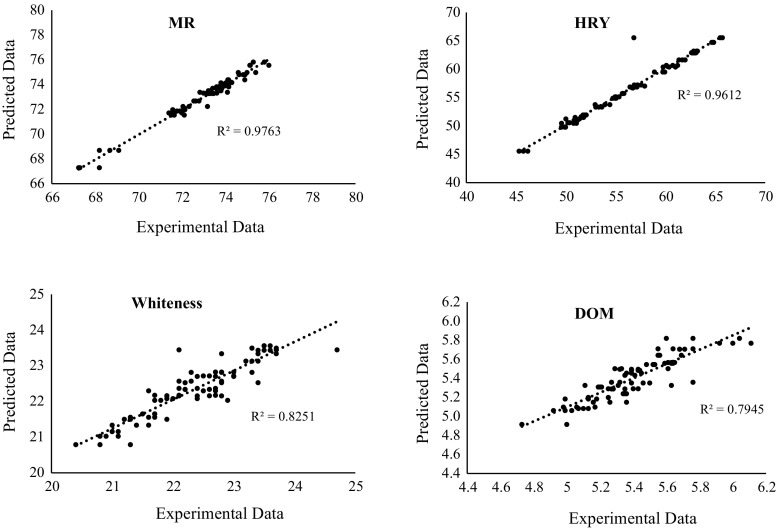
The MSE and R2 values for training and testing data of each output for the ANN with 18 neurons in hidden layer were showed in Table 3. According to the table the MR, HRY, Whiteness and DOM can be predicted with R2 of 0.93, 0.94, 0.72 and 0.77 and MSE values of 0.18, 1.69, 0.25 and 0.02, respectively in the test process of the ANN model. These results indicated that the ANN has higher accuracy than the MVR model. The predicted all data (test and train) along with the experimental data with the best structure of the ANN was showed in Fig. 3. Here, the R2 shows almost more predictability for all MQ features i.e. MR (R2 = 0.97), Whiteness (R2 = 0.82), HRY (R2 = 0.96) and DOM (R2 = 0.79). The lower value for Whiteness and DOM for both models could be for higher distributions of raw (experimental data) which were used in the models. The differences in DOM values could be related to the changes in shape and hardness of rice grains which normally affect the DOM of rice during the milling process (Singh et al. 2000). Furthermore, the hardness of rice during the parboiling process is associated with amylose and amylopectin (Pal et al. 2016) and the shape of samples may change when the rice grains are soaked or steamed. Color of rice samples during the parboiling process is affected by the factors like time and temperature of soaking and steaming, and the methods samples were dried (Lv et al. 2009). Whiteness of rice generally changes with changing in chalkiness of rice grains (Singh et al. 2014), however in this study the chalkiness of samples was not measured. So, the differences is in the data could be related to changes in chalkiness of samples. The highest value of R2 and lowest value of MSE for each MQ variables (Table 3) have indicated that the K-fold cross validation and the ANN model can be used for modeling and predicting of quality parameters of parboiling rice. Therefore, the obtained model of the ANN can be used for optimization of the parboiling process. Parboiling as an effective tool for reduction of losses in rice milling process can be mixed with ANN models to enhance the efficiency of rice post-harvest processes. By 2025 the production countries will need 70% more rice (Amanullah and Inamullah 2016), while due to water and population crises the rice farms may decline in the next decades. It has been explained how rice milling and parboiling process are limited by different parameters. For this reason, it is important to perform good controls before rice are processed in post-harvest sectors. The proposed approach is based on the combination of the MQ features in parboiling process and a classifier that has been developed on the experiment data. So applying the model with high accuracy to enhance rice milling output both in parboiled and non-parboiled process is crucial.
Table 3.
The MSE and R2 values for performance of the ANN with 18 neurons in hidden layer
| MQ variables | MSE | R2 | ||
|---|---|---|---|---|
| Train | Test | Train | Test | |
| MR | 0.0739 ± 0.006 | 0.1839 ± 0.019 | 0.97673 ± 0. 001 | 0.9341 ± 0.052 |
| HRY | 0.7058 ± 0.225 | 1.6912 ± 0.216 | 0.9729 ± 0.004 | 0.9440 ± 0.083 |
| Whiteness | 0.1354 ± 0.015 | 0.2582 ± 0.033 | 0.8221 ± 0.012 | 0.7279 ± 0.050 |
| DOM | 0.0178 ± 0.002 | 0.0232 ± 0.100 | 0.7610 ± 0.013 | 0.7782 ± 0.022 |
Fig. 3.
Experimental data versus predicted data (train and test) by the ANN
Conclusion
In this study, the possibility of application of the ANN approach with K-fold cross validation along with the MVR to create reliable model of parboiling process of an Iranian rice variety with small dataset was investigated. The soaking temperature, steaming time and moisture content were taken as the input parameters, however the MR, HRY, DOM and Whiteness were selected as output parameters. Results indicated that the ANN had better modeling results than the MVR. The best structure of the ANN had 18 neurons in hidden layer with Tansig transfer function in the hidden layer. In addition, the high R2 and low MSE values for the MR variable, showed that the ANN model with K-fold cross validation training method can adequately predict the MR and HRY but not good accuracy for prediction of the Whiteness and DOM. To obtain better accuracy of these parameters, more experimental data need to be gathered and other modeling methods e.g. adaptive network based fuzzy inference system and support vector regression can be tested.
References
- Amanullah, Inamullah Dry matter partitioning and harvest index differ in rice genotypes with variable rates of phosphorus and zinc nutrition. Rice Sci. 2016;23(2):78–87. doi: 10.1016/j.rsci.2015.09.006. [DOI] [Google Scholar]
- Behroozi-Khazaei N, Tavakoli Hashjin T, Ghassemian H, Khoshtaghaza MH, Banakar A. Applied machine vision and artificial neural network for modeling and controlling of the grape drying process. Comput Electron Agric. 2013;98:205–213. doi: 10.1016/j.compag.2013.08.010. [DOI] [Google Scholar]
- Bello MO, Loubes MA, Aguerre RJ, Tolaba MP. Hydrothermal treatment of rough rice: effect of processing conditions on product attributes. J Food Sci Technol. 2015;52(8):5156–5163. doi: 10.1007/s13197-014-1534-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao GY, Tsai TI, Lu TJ, Hsu HC, Bao BY, Wuc WY, Lin MT, Lu TL. A new approach to prediction of radiotherapy of bladder cancer cells in small dataset analysis. Expert Syst Appl. 2011;38(7):7963–7969. doi: 10.1016/j.eswa.2010.12.035. [DOI] [Google Scholar]
- Danbaba N, Nkama I, Badau MH, Ukwungwu MN, Maji AT, Abo ME, Hauwawu H, Fati KI, Oko AO. Optimization of rice parboiling process for optimum head rice yield: a response surface methodology (RSM) approach. Int J Agric For. 2014;4(3):154–165. [Google Scholar]
- Demuth H, Beale M. Neural network toolbox for matlab user guide version 4.1. Natick: The Mathworks Inc; 2003. [Google Scholar]
- Gitifar V, Eslamloueyan R, Sarshar M. Experimental study and neural network modeling of sugarcane bagasse pretreatment with H2SO4 and O3 for cellulosic material conversion to sugar. Bioresour Technol. 2013;148:47–52. doi: 10.1016/j.biortech.2013.08.060. [DOI] [PubMed] [Google Scholar]
- Gujral HS, Singh J, Sodhi NS, Singh N. Effect of milling variables on the degree of milling of unparboiled and parboiled rice. Int J Food Prop. 2002;5(1):193–204. doi: 10.1081/JFP-120015601. [DOI] [Google Scholar]
- Kato L, Panigrahi S, Doetkott C, Chang Y, Glower J, Amamcharla J, Logue C, Sherwood J. Evaluation of technique to overcome small dataset problems during neural network based contamination classification of packaged beef using integrated olfactory sensor system. LWT Food Sci Technol. 2012;45:233–240. doi: 10.1016/j.lwt.2011.06.011. [DOI] [Google Scholar]
- Kono S, Kawamura I, Araki T, Sagara Y. ANN modeling for optimum storage condition based on viscoelastic characteristics and sensory evaluation of frozen cooked rice. Int J Refrig. 2016;65:218–227. doi: 10.1016/j.ijrefrig.2015.10.009. [DOI] [Google Scholar]
- Lee CL, Wang WL. Biological statistics. China: Science Press; 1997. [Google Scholar]
- Leethanapanich K, Mauromoustakos A, Wang YJ. Impacts of parboiling conditions on quality characteristics of parboiled commingled rice. J Cereal Sci. 2016;69:283–289. doi: 10.1016/j.jcs.2016.04.003. [DOI] [Google Scholar]
- Li DCh, Hsu HCh, Tsai T, Lu TJ, Hu S. A new method to help diagnose cancers for small sample size. Expert Syst Appl. 2007;33(2):420–424. doi: 10.1016/j.eswa.2006.05.028. [DOI] [Google Scholar]
- Li DC, Lin LS, Peng LJ. Improving learning accuracy by using synthetic samples for small datasets with non-linear attribute dependency. Decis Support Syst. 2014;59:286–295. doi: 10.1016/j.dss.2013.12.007. [DOI] [Google Scholar]
- Lv B, Li B, Chen S, Chen J, Zhu B. Comparison of color techniques to measure the color of parboiled rice. J Cereal Sci. 2009;50(2):262–265. doi: 10.1016/j.jcs.2009.06.004. [DOI] [Google Scholar]
- Mohapatra D, Bal S. Effect of degree of milling on specific energy consumption, optical measurements and cooking quality of rice. J Food Eng. 2007;80(1):119–125. doi: 10.1016/j.jfoodeng.2006.04.055. [DOI] [Google Scholar]
- Motavali A, Najafi GH, Abbasi S, Minaei S, Ghaderi A. Microwave–vacuum drying of sour cherry: comparison of mathematical models and artificial neural networks. J Food Sci Technol. 2013;50(4):714–722. doi: 10.1007/s13197-011-0393-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasirahmadi A, Emadi B, Abbaspour-Fard MH, Aghagolzade H. Influence of moisture content, variety and parboiling on milling quality of rice grains. Rice Sci. 2014;21(2):116–122. doi: 10.1016/S1672-6308(13)60169-9. [DOI] [Google Scholar]
- Nasirahmadi A, Abbaspour-Fard M, Emadi B, Behroozi-Khazaei N. Modelling and analysis of compressive strength properties of parboiled paddy and milled rice. Int Agrophys. 2014;28(1):73–78. doi: 10.2478/intag-2013-0029. [DOI] [Google Scholar]
- Nasirahmadi A, Hensel O, Edwards SA, Sturm B. A new approach for categorizing pig lying behaviour based on a Delaunay triangulation method. Animal. 2017;11(1):131–139. doi: 10.1017/S1751731116001208. [DOI] [PubMed] [Google Scholar]
- Omid M, Baharlooei A, Ahmadi H. Modeling drying kinetics of pistachio nuts with multilayer feed-forward neural network. Dry Technol. 2009;27(10):1069–1077. doi: 10.1080/07373930903218602. [DOI] [Google Scholar]
- Pal P, Singh N, Kaur P, Kaur A, Singh Virdi AS, Parmar N. Comparison of composition, protein, pasting, and phenolic compounds of brown rice and germinated brown rice from different cultivars. Cereal Chem. 2016;93(6):584–592. doi: 10.1094/CCHEM-03-16-0066-R. [DOI] [Google Scholar]
- Pan Z, Amaratunga KSP, Thompson JF. Relationship between rice sample milling conditions and milling quality. Trans ASABE. 2007;50(4):1307–1313. doi: 10.13031/2013.23607. [DOI] [Google Scholar]
- Pasini A. Artificial neural network for small dataset analysis. J Thorac Dis. 2015;7(5):953–960. doi: 10.3978/j.issn.2072-1439.2015.04.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasini A, Modugno G. Climatic attribution at the regional scale: a case study on the role of circulation patterns and external forcings. Atmos Sci Lett. 2013;14:301–305. doi: 10.1002/asl2.463. [DOI] [Google Scholar]
- Rudiyanto Minasny B, Setiawan BI, Arif C, Saptomo SK, Chadirin Y. Digital mapping for cost-effective and accurate prediction of the depth and carbon stocks in Indonesian peatlands. Geoderma. 2016;272:20–31. doi: 10.1016/j.geoderma.2016.02.026. [DOI] [Google Scholar]
- Salehi H, ZeinaliHeris S, KoolivandSalooki MK, Noei SH. Designing a neural network for closed thermosyphon with nanofluid using a genetic algorithm. Braz J Chem Eng. 2011;28:157–168. doi: 10.1590/S0104-66322011000100017. [DOI] [Google Scholar]
- Shrivastav S, Kumbhar BK. Drying kinetics and ANN modeling of paneer at low pressure superheated steam. J Food Sci Technol. 2011;48(5):577–583. doi: 10.1007/s13197-010-0167-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh N, Singh H, Kaur K, Bakshi MS. Relationship between the degree of milling, ash distribution pattern and conductivity in brown rice. Food Chem. 2000;69(2):147–151. doi: 10.1016/S0308-8146(99)00237-X. [DOI] [Google Scholar]
- Singh N, Paul P, Virdi AS, Kaur P, Mahajan G. Influence of early and delayed transplantation of paddy on physicochemical, pasting, cooking, textural, and protein characteristics of milled rice. Cereal Chem. 2014;93(6):389–397. doi: 10.1094/CCHEM-09-13-0193-R. [DOI] [Google Scholar]
- Stegmayer G, Milone DH, Garran S, Burdyn L. Automatic recognition of quarantine citrus diseases. Expert Syst Appl. 2013;40(9):3512–3517. doi: 10.1016/j.eswa.2012.12.059. [DOI] [Google Scholar]
- Tourenq C, Aulagnier S, Mesléard F, Durieux L, Johnson A, Gonzalez G, Lek S. Use of artificial neural networks for predicting rice crop damage by greater flamingos in the Camargue. Ecol Model. 1999;120:349–358. doi: 10.1016/S0304-3800(99)00114-3. [DOI] [Google Scholar]
- Zhang Q, Yang XS, Mittal GS, Yi S. Prediction of performance indices and optimal parameters of rough rice drying using neural networks. Biosyst Eng. 2002;83(3):281–290. doi: 10.1006/bioe.2002.0123. [DOI] [Google Scholar]