The Neural Basis for Sleep Regulation - Data Assimilation from Animal to Model

Abstract

Sleep is important for normal brain function, and sleep disruption is comorbid with many neurological diseases. There is a growing mechanistic understanding of the neurological basis for sleep regulation that is beginning to lead to mechanistic mathematically described models. It is our objective to validate the predictive capacity of such models using data assimilation (DA) methods. If such methods are successful, and the models accurately describe enough of the mechanistic functions of the physical system, then they can be used as sophisticated observation systems to reveal both system changes and sources of dysfunction with neurological diseases and identify routes to intervene. Here we report on extensions to our initial efforts [1] at applying unscented Kalman Filter (UKF) to models of sleep regulation on three fronts: tools for multi-parameter fitting; a sophisticated observation model to apply the UKF for observations of behavioral state; and comparison with data recorded from brainstem cell groups thought to regulate sleep.

I. Introduction

Sleep is part of a fundamental biological cycle that is coupled into every aspect of body function from behavior and information processing to metabolic storage and release. The association between sleep disruption and abnormal brain function was noted by Emil Kraepelin in 1883 in his psychiatry textbook [2], [3].

Disruption of sleep destabilizes physiology and promotes a range of pathologies (reviewed in [2]). Likewise, its dynamics correlate with symptoms of many neurological and mental health diseases such as epilepsy [4]–[7], schizophrenia [8], [9], and a range of childhood psychiatric disorders such as attention deficit hyperactivity, mood, and anxiety disorder [10]. And most recently, the mechanisms coupling sleep disruption to Alzheimer’s disease (AD) have come under focus with the hypothesis that sleep disruption alters the brain’s ability to clear amyloid beta, while the buildup of amyloid plaques contributes to the development of AD and its co-morbid sleep disruption [11], [12].

Sleep and wake are highly complex dynamical states that arise from interactions of multiple brain regions, neurotransmitter systems, modulatory hormones, subcellular circadian clocks, as well as cognitive and sensory systems. It is hypothesized that the stabilization of sleep-wake cycles may be a means to treat aspects of psychiatric and neurodegenerative diseases (see for example: [2]). But to do so in a minimally invasive, targeted fashion requires accurate models of the relevant dynamics, and is further constrained by the ability to observe the destabilized dynamics.

Additionally, if we understand and can observe the dynamics of the brain networks that regulate sleep, then we can identify its coupling to the symptoms associated with neurological diseases, and develop interventions.

An observation and control system for sleep regulation can be understood as a particular embodiment of a general neural prosthetic, as illustrated in Fig. 1. A sensor and stimulation layer connects to the system and may be mediated by, among others, electrical, optical, chemical or mechanical sensors, where the system is defined by the brain and body and likely the environment. The sensors signals are transduced and converted to typically digital electrical signals. Signal processing is applied to convert the sensor data, which not only may represent sensation at many different space scales of the system but also can be presented at vastly different rates, into salient features. These features are handed to a Decision Process subunit that converts the incoming data into control output signals based on some control objective.

Fig. 1. General Structure of a Neural Prosthetic.

The control output is then passed back through instrumentation and stimulation interfaces to modify the system. Stimulation systems in this very general sense would be any modality that would actuate changes in the system, including direct modification of brain activity through electrical, optical mechanical or pharmacological means, indirect input through normal sensory modalities such as sound or touch, direct or indirect actuation of muscle or assistive technology, or modification of the environment.

A critical element of our articulation of this system is that the Decision Process relies on some inherent model of the system, as illustrated in Fig. 1. Such models can be - and often are - data driven models which rely on previous observations and applications of control output to define both what the current system state is and what control outputs will optimally achieve the control objective.

Alternatives include dynamical models that embody at some level of specificity our understanding of the mechanisms that govern the real system’s dynamics. For control purposes, it is established from a fundamental theoretical basis that the optimal regulator of a system is a model of the system [13]. This would imply that the best model to use is one that matches the system’s physics.

The use of mechanistic models also has the potential to allow a control system to extend its capacity or utility for system states that it hasn’t yet observed. In the case of neural prosthetics, and especially for applications to neurological diseases, the system is not only continually changing, but it is highly patient-specific. Therefore data driven models may not embody the specific dynamics of the subject without extensive retraining. But in the case of mechanistic-based controllers, the process of fitting the model parameters to the observations allows potential identification of the root mechanisms of the disease which might not otherwise be known, and therefore opens new avenues for minimally invasive and optimal patient specific interventions.

Another major consideration in the engineering of observation and control systems is a matter of cost of particular measurements. This is particularly critical in the design of neural prosthetics, where not only are there financial costs to instrumenting brain, and medical risks associated with invasive measures, but where particular interfaces - and in particular penetrating electrodes or other probes - displace and irreversibly damage the subject of the measurements.

Data assimilation is an iterative prediction-correction scheme that synchronizes a computational model to observed dynamics, allows one to reconstruct model variables from incomplete, noisy observations, and provides for forecasting of future states.

We assert that data assimilation methods, coupled with dynamical models that embody the governing mechanisms of brain state, will allow for more robust neural prosthetic controllers. We further hypothesize that once such methods are used to validate the models they utilize, which will involve expensive measures of the variables embodied in the models, that they can be scrutinized to identify the least-costly measures that will allow sufficient observation to achieve the desired levels of control.

II. Sleep Modeling and Data Assimilation

The field of sleep research has a history of using mathematical models to frame understanding of both sleep homeostasis and circadian influences. One of the striking elements about the sleep-wake regulatory system (SWRS) is that it induces what are believe to be distinct, non-overlapping brain states.

Early models include the Reciprocal Interaction model for the transitions between REM and NREM sleep [15] and the Two- Process model for homeostatic sleep drive / circadian pacemaker interactions [16]. Each of these models had significant impact as conceptual models that guided experimental investigations and provided a context for interpreting experimental results. Based on more recent results, physiologically based mathematical models have been developed to provide quantitative underpinnings for the classical and more recent conceptual models of sleep regulation [14], [17]–[20]. Broadly speaking, these models utilize interacting elements that represent neuronal population groups.

The model developed by Diniz-Behn and Booth [14] and adopted by us [1], is illustrated in Fig. 2.a. Each oval represents a cell group whose steady-state output firing rate is a sigmoidal function of its input, and the dynamics follow first order kinetics. The input to each group is mediated by excitatory or inhibitory neurotransmitters from other groups, and a function of their firing rates. The governing nonlinear equations can be found in [1].

Fig. 2. Sleep-Wake Regulatory Model.

The network model is taken from [1], [14]. 2a Network Model structure, adapted from [1]. 2b Example dynamics of the model. System state, illustrated by the hypnogram in the upper trace, is determined from the dominant cell group activity - if the REM active group is active, then the state is in REM, otherwise if the WAKE active groups are high it is AWAKE, otherwise it is in NREM.

In earlier work we demonstrated an Unscented Kalman Filter (UKF) based toolkit as applied to models of the Sleep-Wake-Regulatory system [1]. In particular, we used model-generated data as ground truth, and demonstrated the ability to reconstruct full model state from noisy measurements of a subset of the model variables, methods of optimizing the DA computation, and assessing which variables or variable-combinations provided suitable reconstruction of state through an empirical observability coefficient (EOC).

In addition, we demonstrated that, in principle, model parameters could be individually fit to optimize the reconstruction and that converged to those of the data generator. Such parameter fitting is critical for neural prosthetics in part because of a lack of a-priori knowledge of the correct or best parameters for any brain, and in part because of the inherent non-stationarity of biological systems. Finally, we demonstrated that with a rather naive observation model, we could reconstruct model state from the hypnogram, which is the time series of classified state of vigilance.

III. RESULTS

Here we extend upon our previous results on three fronts: First, we have implemented scheme that allows for simultaneous fitting of multiple parameters. Second, we have made a more sophisticated observer model for UKF-based DA of hypnogram data that allows for better reconstruction of model variables. And third, we present the first application of this technique to observe the SWRS of a freely behaving chronically implanted animal.

A. Improved Multiparameter Fitting

Our original parameter estimation method [1] is an iterative reconstruction - multiple step shooting method not unlike that described by Voss, et. al [22]. In our initial implementation, we first used the UKF with fixed parameters to reconstruct and smooth estimated state space for a sufficient period of the dynamics. We then seeded the model with initial conditions on the reconstructed space, and measured how fast they diverged away from the reconstructed trajectory. Recall that the UKF is an iterative prediction-correction scheme, and this divergence, which is illustrated in the upper two rows of Fig. 3a, results from not correcting these dynamics.

Fig. 3. Multiple-Parameter Estimation.

(a) Illustration of the Levenberg-Marquardt algorithm [21]. For parameter small, the approach follows a Gauss-Newton methodology, otherwise it follows a Gradient-Descent approach. This serves to accelerate convergence close to the minimum of the cost function. (b) Output of the multi-parameter fitting algorithm.

We then minimized the mean-square divergence through a random walk in parameter offsets. By iterating between trajectory reconstruction and least-squares fitting, we achieve an expectation-maximization fitting algorithm.

This method has some advantages over other DA approaches that update the parameters in parallel with state estimation. The first is that by averaging over a longer time, this method better separates the system dynamics from parameter variations and better achieves the ideal that parameters, if not fixed, should vary on time scales slower than the dynamical variables. It also addresses instabilities that arise when the parameters of interest only affect the dynamics in select regions of state space.

The current version suitable for estimation of multiple parameters simultaneously is an extension of this multiple shooting method. Here the shooting method utilizes a full estimation step that minimizes the square divergence between the reconstructed trajectory and the dynamics. In particular we apply the least-squares fitting approach for nonlinear dynamics developed by Marquardt [21].

Nonlinear least squares methods involve an iterative improvement to parameter values in order to minimize the sum of the squares of the errors between the function and the measured data points. The Levenberg-Marquardt curve-fitting method is a combination of two minimization methods (Fig. 3a): the gradient descent method and the Gauss-Newton method. In the gradient descent method, the sum of the squared errors is reduced by updating the parameters in the steepest-descent direction. In the Gauss-Newton method, the cost function - the sum of the squared errors - is reduced by assuming the least squares function is locally quadratic, and finding the minimum of the quadratic.

The Levenberg-Marquardt method acts as a gradient-descent method when the parameters are far from their optimal value, and as a Gauss-Newton method when the parameters are close to their optimal value. In detail, it is tuned via the parameter λ, which is adjusted on an iteration by iteration basis based on the total cost function value.

The performance of our parameter estimation method is illustrated in Fig. 3b. Parameter estimation is performed by minimizing the cumulative divergence between short model-generated trajectories and UKF-reconstruction. In practice, the minimization step is applied to UKF-reconstructed trajectories that are at least one sleep-wake cycle long in order to sample the state space. Additionally, the short trajectories are set such that they are long enough for parameter differences to cause significant divergence between model-generated trajectories and UKF-reconstructed dynamics.

Shown in the upper two rows of Fig. 3b are the divergences of model-generated trajectories from the reconstructed state trajectory for two state variables. As the fitting progresses in time (latter columns), the dynamics track better. In the lower panels are shown the simultaneous changes in the three parameters being estimated (upper panel), the cost function (second panel), and reconstruction error values for the two variables in the upper panels.

B. Observation model from Hypnogram

One of the major challenges for observing the SWRS in detail in living animals is that the cell groups that perform this regulation are small and deeply embedded in the brainstem. Therefore directly measuring them with invasive probes is challenging and often highly damaging to delicate systems that are critical for organism survival. It is therefore advantageous to observe these dynamics through the DA tools using less invasive / less costly measurements.

One approach that we introduced in [1] was to invert the classified SOV time series into estimates of the cell group firing rates. In particular, we utilized the SOV-dependent median firing rate value as the inversion. Although this worked, the fidelity from the ground-truth data was large, and some of the finer features of the dynamics were not well-reconstructed.

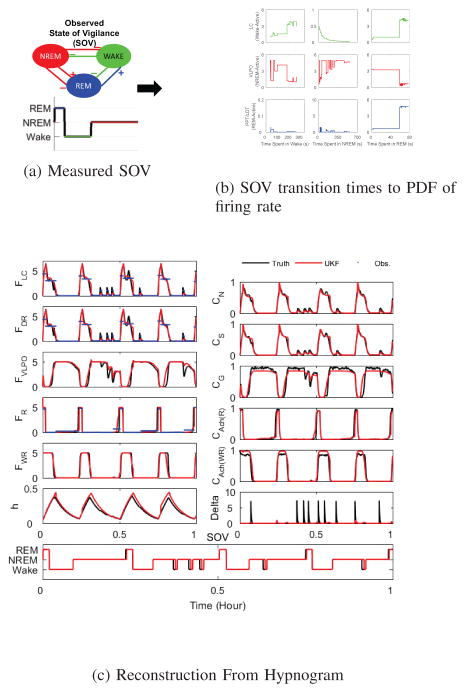
Here we extend this inversion to include information about time since the last state transition. In particular, we use model generated data to create distributions of firing rates as a function of time since transition into each SOV. The means of these distributions over time, shown for three firing rate variables for each SOV in Fig. 4b, along with their variance, are used to translate the SOV as a function of time into probability of firing rate, which is handed to the UKF for each observation time.

Fig. 4. Reconstruction From Hypnogram.

(a) From observations of behavioral SOV is determined the hypnogram and the transition times between state. (b) From model generated data, the probability of firing rate is determined as a function of state and time since state change. (c) This SOV/hypnogram to firing rate probability is used as the observation function in the UKF reconstruction, shown here also for model generated data. Note that even brief awakenings are well-reconstructed.

Shown in the various panels in Fig. 4c are these input values (blue traces), the UKF reconstructed values (red traces), and the ground truth (black traces). In all cases except for the random thalamic input noise δ the reconstruction is good. In the lowest panel is shown the hypnogram generated from the reconstructed state space, and the original ground truth generated hypnogram. Note that even the brief awakenings are well represented by the reconstructed dynamics.

C. Reconstruction of SWRS Dynamics from Live Animals

To date, all the results shown have been reconstruction of model generated data. One of the major challenges is to apply this to real biological systems for which even the validity of the model is in question.

Here we report some of the first results in applying these methods to data collected from living brain. The details of the experiments will be documented in the future, but are summarized here.

Experimental Methods

All protocols and procedures were approved by the Animal Care Committee of the Pennsylvania State University, University Park, and all experiments were performed in accordance with relevant guidelines and regulations. Rats were implanted with microwire bundles of electrodes in brainstem targets including the pedunculopontine tegmental (PPT) and dorsal raphe (DR) nuclei, with hippocampal depth, and cortical screw electrodes. After 1–2 weeks recovery, animals were connected to a recording system and microwire bundles advanced until clear unit recordings were apparent. Animals were then returned to their home-cage and monitored for periods of 1–5 hours.

Recordings were then analyzed as follows: Combinations of hippocampal and cortical field potentials along with head acceleration were used to score state of vigilance [23]. Separately, microwire depth electrodes were analyzed to extract unit firing events using standard software packages (NeuroExplorer and Offline Sorter, Plexon inc, Dallas Tx). Units were further identified as separable single units, or non-separable multi-units, and their firing rates computed over time.

Experimental Results

Shown in Fig. 5 are the results from applying the methods described in Sec. III-B. In particular, the hippocampal and cortical recordings were used to classify the SOV for the animal as shown in upper panel of Fig. 5. We then passed this hypnogram (Fig. 4a) through the inversion observation model (Fig. 4b) to reconstruct SWRS state. The REM-active firing rates in the PPT from this reconstruction are shown in the lower panel of Fig. 5(red trace), along with the multi-unit firing rates simultaneously measured from the PPT (black).

Fig. 5. In Vivo Hypnogram to PPT Firing Rate.

For data acquired

Because the PPT firing rate was not used in the original classification of the animal’s SOV, it serves as an independent measure from the reconstructed state. The correspondence is reasonably good, and accurately predicts the onset of firing rate increases. We are currently repeating this process across multiple animals and recordings to investigate how well these models correspond to actual cell group dynamics.

IV. Conclusion

We have outlined here a novel paradigm for neural prosthetics that utilizes data assimilation and mechanistic based models as observers of brain state. We have demonstrated this method computationally and in experiment for observing the sleep-wake regulatory system (SWRS) which is comprised of brain-stem related cell groups.