Self-Grouping Multi-Network Clustering

Abstract

Joint clustering of multiple networks has been shown to be more accurate than performing clustering on individual networks separately. Many multi-view and multi-domain network clustering methods have been developed for joint multi-network clustering. These methods typically assume there is a common clustering structure shared by all networks, and different networks can provide complementary information on this underlying clustering structure. However, this assumption is too strict to hold in many emerging real-life applications, where multiple networks have diverse data distributions. More popularly, the networks in consideration belong to different underlying groups. Only networks in the same underlying group share similar clustering structures. Better clustering performance can be achieved by considering such groups differently. As a result, an ideal method should be able to automatically detect network groups so that networks in the same group share a common clustering structure. To address this problem, we propose a novel method, ComClus, to simultaneously group and cluster multiple networks. ComClus treats node clusters as features of networks and uses them to differentiate different network groups. Network grouping and clustering are coupled and mutually enhanced during the learning process. Extensive experimental evaluation on a variety of synthetic and real datasets demonstrates the effectiveness of our method.

I. Introduction

Network (or graph) clustering is a fundamental problem to discover closely related objects in a network. In many emerging applications, multiple networks are generated from different conditions or domains, such as gene co-expression networks collected from different tissues of model organisms [1], social networks generated at different time points [2], etc. These applications drive the recent research interests to joint clustering of multiple networks, which has been shown to significantly improve the clustering accuracy over single network clustering methods [3].

The key superiority of multi-network clustering methods is to leverage the shared clustering structure across all networks, since a consensus clustering structure is more robust to the incompleteness and noise in individual networks. For example, multi-view network clustering methods [3]–[5] work on multiple representations (views) of the same set of data objects. Different views can provide complementary information on the underlying data distribution. Multi-domain network clustering [6], [7] integrates networks of different sets of objects, and uses mappings between objects in different networks to penalize inconsistent clusterings.

To be successful, the existing multi-network clustering methods typically assume different networks share a consensus clustering structure. This very basic assumption, however, is too simplified to real-world applications. Consider an important bioinformatics problem, the gene co-expression network clustering [1]. In a gene co-expression network, each node is a gene and an edge represents the functional association between two connected genes. To enhance performance, we can use multiple gene co-expression networks collected in different tissues. Recent studies show that genes have tissue-specific roles and form tissue-specific interactions [8]. The same set of genes may form a cluster (e.g., a functional module) in similar tissues but not in others. Thus we cannot assume that gene co-expression networks from different tissues form similar clustering structures.

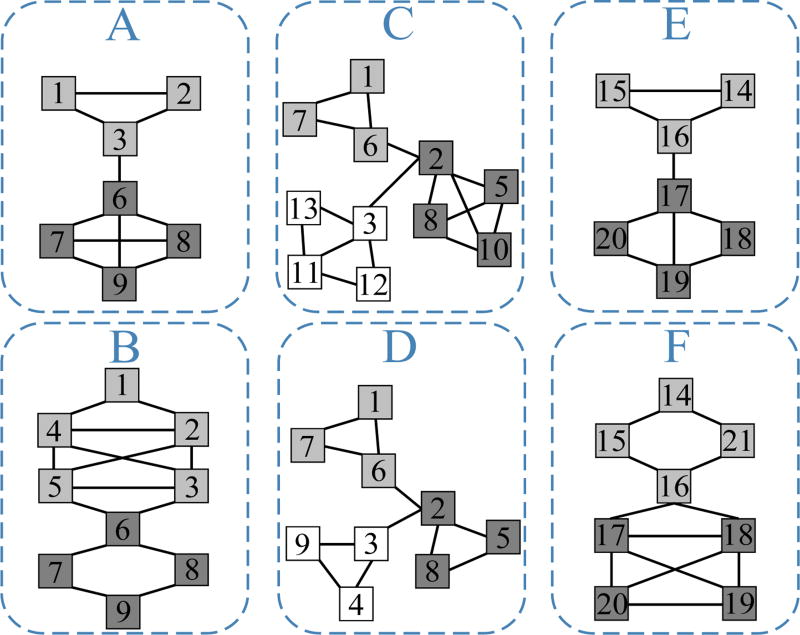
In this paper, we study a novel and generalized problem where we cannot simply assume the given networks share a consensus clustering structure. Consider the six networks in Fig. 1, they may represent gene co-expression networks from different tissues. Clearly, they do not share a common clustering structure. For example, nodes {1, 2, 3} form a cluster in network A but are in three different clusters in network C. However, by a visual inspection, we can partition these networks into three groups, i.e., {A, B}, {C, D} and {E, F}, since {A, B} share an underlying clustering structure, and so do {C, D} and {E, F}. This is practically reasonable. For example, a set of similar tissues can share many similar gene clusters. As another example, consider the co-author networks of different research areas [9]. Similar areas usually attract many similar author clusters (e.g., research sub-communities). Thus an ideal method to cluster this collection of networks should be able to (1) automatically detect network groups s.t. networks in the same group share a common clustering structure, and (2) enhance clustering accuracy by group-wise consensus structures.

Fig. 1.

An example of six networks. These networks can be grouped into {A, B}, {C, D} and {E, F} according to their clustering structures.

However, real-life networks are often diverse, noisy and incomplete. Even a group of similar networks may not have exactly the same clustering structure. Instead, they may only share a subset of their clusters and the shared clusters may only partially match. In Fig. 1, networks {C, D} only share two clusters {1, 7, 6} and {2, 5, 8}, and other nodes are irrelevant. Therefore, to effectively group together some networks, an ideal method should identify a subset of clusters that are common among these networks. This is a novel and non-trivial challenge. The existing multi-network clustering methods either assume all clusters are common [3]–[5] or simply enhance common clusters without identifying them [1], [6], [7] thus cannot tackle this problem.

In this paper, we propose a novel method ComClus to address these challenges. ComClus is novel in combining metric learning [10] with non-negative matrix factorization [11]. Briefly, ComClus treats node clusters as features of networks and group together networks sharing the same feature subspace (i.e., a common subset of clusters). In ComClus, network grouping and common cluster detection are coupled and mutually enhanced during the learning process. Correctly grouping networks sharing a common clustering structure can resolve ambiguities hence refine common cluster detection. Correct detection of common clusters reduces the possibility that a network goes to the wrong group. Experimental results on both synthetic and real-life datasets suggest the effectiveness of the proposed method.

II. Related Work

Several approaches have been developed for multi-network clustering. Multi-view clustering is among the most popular ones [3]–[5]. In these methods, views can be either networks or data-feature matrices of the same set of objects. Recent methods on multi-domain network clustering [6], [7] integrate networks of different sets of objects by cross-network object mapping relationships. Ensemble clustering [12] does not simultaneously clustering multiple data views, but aims to find an agreement of individual clustering results. All these methods simplify an assumption that multiple networks or views share a consensus clustering structure.

Multiple networks can also be represented by the tensor model. However, existing tensor decomposition methods, such as CP and Tucker decompositions [13], are good for co-clustering multiple matrices, but are not designed for network data where two modes of the tensor are symmetric. Moreover, tensor decomposition also limits all networks to share a single common underlying clustering structure.

Some methods detect communities in multi-layer networks [2], [14]. Each layer is a distinct network. The same set of objects are represented by different layers. These approaches aim to identify communities that are consistent in some layers, not to enhance clustering accuracy by using consensus. Thus they have a different goal from us (and the approaches mentioned above) and cannot be applied to solve our problem.

In [1], the authors developed a method, NoNClus, to cluster multiple networks with multiple underlying clustering structures. Our work differs markedly from [1]. [1] studies a different problem: to enhance clustering accuracy by using the network group information that is already known. In practice, however, such network group information may not be available beforehand. Thus NoNClus can neither identify common clusters among networks nor group networks by their different clustering structures.

III. The Problem

Let 𝒜 = {A⁽¹⁾, ..., A^(g)} be the g given member networks. Each network is represented by its adjacency matrix ${\mathbf{A}}^{(i)}\in {\mathbb{R}}_{+}^{n_i\times n_i}$, where n_i is the number of nodes in A⁽ⁱ⁾. Moreover, 𝒱⁽ⁱ⁾ represents the set of nodes in A⁽ⁱ⁾, ℐ^(ij) = 𝒱⁽ⁱ⁾ ∩ 𝒱^(j) represents the set of common nodes between A⁽ⁱ⁾ and A^(j).

A network group 𝒜^(p) is a subset of 𝒜 such that networks in 𝒜^(p) share a common underlying clustering structure. In this paper, we consider each network to belong to one group. That is, if there are k network groups, then ${\cup }_{p=1}^k{𝒜}^{(p)}=𝒜$, and for any p ≠ q, 𝒜^(p) ∩ 𝒜^(q) = ∅. In Fig. 1, the six networks can be grouped as {A, B}, {C, D} and {E, F}.

The member networks in the same group share a set of common clusters. These clusters are used as features to characterize each network group and distinguish one group from another. In Fig. 1, the common clusters of network group {C, D} are clusters {1, 7, 6} and {2, 5, 8}.

Our goal is to simultaneously grouping and clustering the given member networks ${\{{\mathbf{A}}^{(i)}\}}_{i=1}^g$, such that (1) the member networks are partitioned into k groups with each group sharing a common set of clusters; and (2) the common clusters in each group are identified and their accuracies are enhanced. Note that we focus on finding non-overlapping clusters, which is also the common setting of the existing multi-view (domain) network clustering methods [1], [3]–[7].

IV. The Comclus Algorithm

In this section, we introduce ComClus, a novel subspace NMF method that incorporates metric learning [10] with NMF to learn cluster-level features for simultaneously grouping and clustering different member networks.

A. Preliminaries

Non-negative matrix factorization (NMF) [15] is widely used for clustering. We adopt the symmetric version of NMF (SNMF) [11] as the basic approach for clustering a single network, which minimizes the following objective function

$${ℒ}_G(\mathbf{V})=\sum _{i,j=1}^g{({\mathbf{G}}_{ij}-{\mathbf{v}}_{i\ast }{\mathbf{v}}_{j\ast }^T)}^2={\Vert \mathbf{G}-{\mathbf{V}\mathbf{V}}^T\Vert }_F^2$$ (1)

where ‖ · ‖_F is the Frobenius norm, ${\mathbf{v}}_{i\ast }\in {\mathbb{R}}_{+}^{1\times k}$ is a k-dimensional latent vector of node i, and $\mathbf{V}={[{\mathbf{v}}_{1\ast }^T,\dots ,{\mathbf{v}}_{g\ast }^T]}^T$ is the factor matrix of G. An entry V_ij indicates to which degree the node i belongs to the cluster j.

B. Clusters as Network Features

In the next, we develop a subspace SNMF method to learn the set of clusters that can be used as features to characterize each member network in ${\{{\mathbf{A}}^{(i)}\}}_{i=1}^g$. Let $𝒱={\cup }_{i=1}^g{𝒱}^{(i)}$ be the global set of nodes in all member networks. In the SNMF, i.e., Eq. (1), each node i is represented in a k-dimensional latent space by v_i* for a single network. Given multiple networks ${\{{\mathbf{A}}^{(i)}\}}_{i=1}^g$, we aggregate their latent spaces into a single global h-dimensional latent space, where h is the number of latent dimensions. Then for each node x in 𝒱, we represent it by a global latent vector ${\mathbf{u}}_{x\ast }\in {\mathbb{R}}_{+}^{1\times h}$.

In Eq. (1), each entry G_ij is approximated by the inner product between v_i* and v_j*, where the full spaces of the k-dimensional latent vectors v_i* and v_j* are used for approximation. In our method, when approximating an entry ${\mathbf{A}}_{xy}^{(i)}$ in one member network A⁽ⁱ⁾, we only use a subspace of the global h-dimensional u_x* and u_y*.

Specifically, for each network A⁽ⁱ⁾, we define a metric vector ${\mathbf{w}}^{(i)}\in {\mathbb{R}}_{+}^{h\times 1}$ whose entry ${\mathbf{w}}_p^{(i)}$ indicates the importance of the global latent dimension p to network A⁽ⁱ⁾. Therefore, when we approximate an entry ${\mathbf{A}}_{xy}^{(i)}$, we use ${\mathbf{u}}_{x\ast }\text{diag}({\mathbf{w}}^{(i)}){\mathbf{u}}_{y\ast }^T$, where diag(w⁽ⁱ⁾) is a diagonal matrix with the diagonal vector as w⁽ⁱ⁾. Let ${\mathbf{D}}_W^{(i)}=\text{diag}({\mathbf{w}}^{(i)})$, using square loss function, we can collectively approximate A⁽ⁱ⁾ by minimizing

$${ℒ}_i({\{{\mathbf{u}}_{x\ast }\}}_{x=1}^{n_i},{\mathbf{D}}_W^{(i)}=\sum _{x,y=1}^{n_i}{({\mathbf{A}}_{xy}^{(i)}-{\mathbf{u}}_{x\ast }{\mathbf{D}}_W^{(i)}{\mathbf{u}}_{y\ast }^T)}^2$$ (2)

In general, different networks can have different node sets 𝒱⁽ⁱ⁾, thus have different sizes. Let n = |𝒱|. We define for each network A⁽ⁱ⁾ a mapping matrix O⁽ⁱ⁾ ∈ {0, 1}^n_i×n s.t. O⁽ⁱ⁾(x, y) = 1 iff node x in 𝒱⁽ⁱ⁾ and node y in 𝒱 represent the same object. Let $\mathbf{U}={[{\mathbf{u}}_{1\ast }^T,\dots ,{\mathbf{u}}_{n\ast }^T]}^T\in {\mathbb{R}}_{+}^{n\times h}$ be a global latent factor matrix, we can obtain the matrix form of Eq. (2)

$${ℒ}_i(\mathbf{U},{\mathbf{D}}_W^{(i)})={\Vert {\mathbf{A}}^{(i)}-({\mathbf{O}}^{(i)}\mathbf{U}){\mathbf{D}}_W^{(i)}{({\mathbf{O}}^{(i)}\mathbf{U})}^T\Vert }_F^2$$ (3)

Then for all member networks, we have

$${ℒ}_A(\mathbf{U},{\{{\mathbf{D}}_W^{(i)}\}}_{i=1}^g)=\sum _{i=1}^g{ℒ}_i(\mathbf{U},{\mathbf{D}}_W^{(i)})$$ (4)

In Eq. (4), all member networks share the same latent factor matrix U. When approximating A⁽ⁱ⁾, a sub-block of U is used. Fig. 2 illustrates the idea. In this process, O⁽ⁱ⁾ selects the rows of U for A⁽ⁱ⁾, which corresponds to the selection of node set 𝒱⁽ⁱ⁾ from 𝒱. ${\mathbf{D}}_W^{(i)}$ selects the columns of U for A⁽ⁱ⁾, which corresponds to the selection of latent subspace. Therefore, if two networks A⁽ⁱ⁾ and A^(j) share many nodes, they will have large overlap in the rows of U. If A⁽ⁱ⁾ and A^(j) further show similar clustering structures, it is highly possible that they will share similar columns in U, i.e., similar ${\mathbf{D}}_W^{(i)}$ and ${\mathbf{D}}_W^{(j)}$. This is because using similar sub-blocks of U would achieve good approximations for both A⁽ⁱ⁾ and A^(j) at this time. On the other hand, if A⁽ⁱ⁾ and A^(j) have dissimilar clustering structures, using similar subspaces of U (i.e., similar sub-blocks of U) to approximate both A⁽ⁱ⁾ and A^(j) will result in large loss function value. By minimizing ℒ_A, ${\mathbf{D}}_W^{(i)}$ and ${\mathbf{D}}_W^{(j)}$ then tend to lie in separate subspaces of U.

Fig. 2.

An illustration of the subspace-based SNMF for two networks.

In Eq. (1), the latent dimensions (i.e., columns) of V represent clusters of nodes. Thus in our subspace SNMF, the columns of U represent latent clusters. Each w⁽ⁱ⁾ (recall ${\mathbf{D}}_W^{(i)}=\text{diag}({\mathbf{w}}^{(i)})$) is a cluster-level feature vector where an entry ${\mathbf{w}}_p^{(i)}$ indicates the selection the p^th latent cluster for network A⁽ⁱ⁾. Therefore, w⁽ⁱ⁾ carries the clustering structure information of network A⁽ⁱ⁾ and can be used as a feature for network grouping.

C. Regularization on Network Node Sets

In this section, we develop a regularizer to encode the similarity between node sets of different networks. The intuition is based on the following observation. Let us consider a special case when two networks A⁽¹⁾ and A⁽²⁾ share few or no nodes, which makes O⁽¹⁾ and O⁽²⁾ different. Their selected sub-blocks from U will have few overlap and be separated vertically. Using the example in Fig. 2, in this case, U⁽²⁾ may lie vertically below U⁽¹⁾. At this time, A⁽¹⁾ and A⁽²⁾ can be well approximated by the two different sub-blocks of U no matter w⁽¹⁾ and w⁽²⁾ are similar or not. Thus it is likely that w⁽¹⁾ and w⁽²⁾ are similar while O⁽¹⁾ and O⁽²⁾ are different. However, this is counterintuitive since two networks having few common nodes should be considered dissimilar and we expect them to have dissimilar structural feature vectors w⁽¹⁾ and w⁽²⁾. To address this issue, we employ the regularization on the network node set similarity. The details are shown in the following.

We measure the similarity between w⁽ⁱ⁾ and w^(j) by their inner product (w⁽ⁱ⁾)^Tw^(j). To penalize the similarity when A⁽ⁱ⁾ and A^(j) share few nodes, we propose the following penalty function.

$${ℒ}_{\mathrm{\Phi }}({\{{\mathbf{w}}^{(i)}\}}_{i=1}^g)=\sum _{i,j=1}^g{\mathbf{\Phi }}_{ij}{({\mathbf{w}}^{(i)})}^T{\mathbf{w}}^{(j)}$$ (5)

where Φ_i,j is the penalty strength on (w⁽ⁱ⁾)^Tw^(j). A proper Φ_i,j should have a high value when |ℐ^(ij)| is small and a low value when |ℐ^(ij)| is large. We use a logistic function¹ as following to measure the penalty strength.

$${\mathbf{\Phi }}_{ij}=\{\begin{array}{cc}\frac{1}{1+e^{-\lambda +2\lambda \text{Jaccard}({\nu }^{(i)},{\nu }^{(j)})}}& i\ne j\\ 0& i=j\end{array}$$ (6)

where $\text{Jaccard}({𝒱}^{(i)},{𝒱}^{(j)})=\frac{|{𝒱}^{(i)}\cap {𝒱}^{(j)}|}{|{𝒱}^{(i)}\cup {𝒱}^{(j)}|}$, λ is a parameter that can be set to log(999) s.t. Φ_i,j ∈ [10⁻³, 1 − 10⁻³].

Let $\mathbf{W}=[{\mathbf{w}}^{(1)},{\mathbf{w}}^{(2)},\dots ,{\mathbf{w}}^{(g)}]\in {\mathbb{R}}_{+}^{h\times g}$ and $\mathbf{\Phi }\in {\mathbb{R}}_{+}^{g\times g}$ whose (i, j)^th entry is Φ_i,j. Then we have

$${ℒ}_{\mathrm{\Phi }}({\{{\mathbf{w}}^{(i)}\}}_{i=1}^g)={ℒ}_{\mathrm{\Phi }}(\mathbf{W})={\Vert \mathbf{\Phi }○({\mathbf{W}}^T\mathbf{W})\Vert }_1$$ (7)

where ○ is the entry-wise product, and ‖ · ‖₁ is the ℓ₁ norm.

D. Network Grouping

In order to assign member networks into k groups while detecting common clusters within each network group, we define k centroid vectors ${\{{\mathbf{s}}^{(j)}\}}_{j=1}^k$, where ${\mathbf{s}}^{(j)}\in {\mathbb{R}}_{+}^{h\times 1}(1\le j\le k)$. Member networks in the same group share the same centroid vector. That is, if network A⁽ⁱ⁾ belongs to group 𝒜^(j), we want to minimize the difference ${\Vert {\mathbf{w}}^{(i)}-{\mathbf{s}}^{(j)}\Vert }_F^2$. Therefore, s^(j) represents the consistent cluster feature subspace of member networks in group 𝒜^(j) and large entries in s^(j) indicate the shared latent dimensions, i.e., common clusters, in group 𝒜^(j).

Let v_i* ∈ {0, 1}^1×k be the group membership vector of A⁽ⁱ⁾, i.e., v_ij = 1 iff A⁽ⁱ⁾ ∈ 𝒜^(j), let S = [s⁽¹⁾, ..., s^(k)], we can collectively minimize the difference between the cluster feature vectors and centroid vectors by minimizing

$${ℒ}_R(\mathbf{S},{\{{\mathbf{v}}_{i\ast }\}}_{i=1}^g,{\{{\mathbf{w}}^{(i)}\}}_{i=1}^g)=\sum _{i=1}^g{\Vert {\mathbf{w}}^{(i)}-\mathbf{S}{\mathbf{v}}_{i\ast }^T\Vert }_F^2$$ (8)

Equivalently, let $\mathbf{V}={[{\mathbf{v}}_{1\ast }^T,\dots {\mathbf{v}}_{g\ast }^T]}^T$, we have

$${ℒ}_R(\mathbf{S},\mathbf{V},\mathbf{W})={\Vert \mathbf{W}-{\mathbf{\text{SV}}}^T\Vert }_F^2$$ (9)

Eq. (9) can be explained as a co-clustering of W by NMF [15], [16]. Thus we can relax the {0, 1} constraint on V s.t. $\mathbf{V}\in {\mathbb{R}}_{+}^{g\times k}$ to avoid the mixed integer programming [17], which is difficult to solve. Then an entry V_ij indicates to which degree A⁽ⁱ⁾ belongs to network group 𝒜^(j).

E. The Unified Model

Combining the loss function of subspace SNMF in Eq. (4), the penalty function in Eq. (7) and the loss function of network grouping in Eq. (9), we obtain a unified objective function for simultaneous multi-network grouping and clustering.

$$ℒ(\mathbf{U},\mathbf{V},\mathbf{S},\mathbf{W})={ℒ}_A(\mathbf{U},{\{{\mathbf{D}}_W^{(i)}\}}_{i=1}^g)+\alpha {ℒ}_{\mathrm{\Phi }}(\mathbf{W})+\beta {ℒ}_R(\mathbf{S},\mathbf{V},\mathbf{W})$$ (10)

where α and β are two parameters controlling the importances of the penalty function and network grouping, respectively. Note that W and ${\{{\mathbf{D}}_W^{(i)}\}}_{i=1}^g$ are two different representations of the same variables, we keep both of them in our algorithm.

Formally, we forlumate a joint optimization problem as

$$\underset{\mathbf{U},\mathbf{V},\mathbf{S},\mathbf{W}}{\text{min}}ℒ(\mathbf{U},\mathbf{V},\mathbf{S},\mathbf{W})+\rho ({\Vert \mathbf{V}\Vert }_1+{\Vert \mathbf{U}\Vert }_1+{\Vert \mathbf{S}\Vert }_1)$$

$$\mathrm{s}.\mathrm{t}.\mathbf{U}\ge 0,\mathbf{V}\ge 0,\mathbf{S}\ge 0,$$ (11)

$$\mathbf{W}\ge 0,{\mathbf{D}}_W^{(i)}=\text{diag}({\mathbf{w}}^{(i)}),\forall 1\le i\le g$$

In Eq. (11), we also add ℓ₁ norms on U, V and S to provide the option on sparseness constraints. This can be useful when nodes (member networks) do not belong to many clusters (network groups) [16] and each network group do not have many common clusters. ρ is a controlling parameter. Intuitively, the larger the ρ the more sparse the {U, V, S}.

V. Learning Algorithm

Since the objective function in Eq. (11) is not jointly convex, we take an alternating minimization framework that alternately solves U, V, S and W until a stationary point is achieved. For the details, please refer to an online Supplementary Material².

Cluster Membership Inference

After obtaining U, V, S, and W, we can infer the network group of A⁽ⁱ⁾ by j^* = arg max_j V_ij . We can infer the cluster membership of node x in A⁽ⁱ⁾ by $p^{\ast }={\text{arg max}}_p{({\mathbf{O}}^{(i)}{\mathbf{\text{UD}}}_W^{(i)})}_{xp}$. Also, for a node x, we can infer its membership to a common cluster shared in network group j by p^* = arg max_p (Udiag(s^(j)))_xp. More uniquely, we can sort the values in s^(j) in descending order to identify the most common clusters in network group j.

VI. Experimental Results

Simulation Study

We first evaluate ComClus using synthetic datasets. The member networks are generated as follows. Suppose we have k network groups. For each network group, we first generate an underlying clustering structure with d_c clusters (30 nodes per cluster). The k underlying clustering structures have the same set of nodes but different node cluster memberships. Then member networks are generated from each underlying clustering structure. Based on an underlying clustering structure, each member network is appended with d_n irrelevant (“noisy”) clusters (30 nodes per cluster). The noisy clusters of different networks may have different nodes.

Fig. 3(a) shows an example using d_c = 3 and d_n = 3, where non-zero entries are set to 1. To embed noises, we randomly flip ω₀ fraction of 1 in the matrix to 0 and ω₁ fraction of 0 to 1. To generate member networks with different sizes, we randomly remove or add ε fraction of nodes in the previous matrix. ε follows normal distribution with mean μ and standard deviation σ and its value is set between 0 and 1. An example member network with 193 nodes generated using ω₀ = 80%, ω₁ = 5%, μ = 0.1, σ = 0.05 is shown in Fig. 3(b).

Fig. 3.

Synthetic dataset generation, shown by network adjacency matrices.

Using this generation process, we generate two types of synthetic datasets, both have k = 5 network groups where each group has 10 networks (thus 50 networks in total). In the first dataset, d_c = 6 and d_n = 0. All member networks have the same set of 180 nodes. ω₀ and ω₁ are set to 80% and 5% respectively to simulate noise. We refer to this dataset as SynView dataset. In the second dataset, d_c = 3 and d_n = 3. To simulate noise, we set ω₀ = 80%, ω₁ = 5%, μ = 0.1, σ = 0.05. Thus different networks have different node sets and sizes. We refer to this dataset as SynNet dataset.

We compare ComClus with the state-of-the-art methods, including (1) SNMF [11]; (2) Spectral clustering (Spectral) [18]; (3) Multi-view pair-wise co-regularized spectral clustering (PairCRSC) [3]; (4) Multi-view centroid-based co-regularized spectral clustering (CentCRSC) [3]; (5) Multi-view co-training spectral clustering (CTSC) [5]; (6) Tensor factorization (TF) [13]; (7) multi-domain co-regularized graph clustering (CGC) [6]; and (8) NoNClus [1].

SNMF and spectral clustering methods can only be applied on single networks. PairCRSC, CentCRSC, CTSC and TF can only be applied on SynView dataset. CGC is a recent multi-domain graph clustering method that can be applied on SynNet dataset. NoNClus can be applied on SynNet dataset given that the similarity between networks is available. Thus, we generate a similarity matrix for the 50 member networks using the same method described above by setting ω₀ = 80%, ω₁ = 5%, μ = 0, σ = 0. The generated similarity matrix allows to partition member networks into 5 groups.

The accuracies of common clusters are evaluated using both normalized mutual information (NMI) and purity accuracy (ACC), which are standard evaluation metrics. Table I shows the averaged results of different methods over 100 runs. The NMIs and ACCs are averaged over all member networks. The parameters are tuned for optimal performance of all methods.

TABLE I.

Clustering accuray on synthetic datasets.

Method	SynView dataset		SynNet dataset
	NMI	ACC	NMI	ACC
SNMF	0.4853	0.6900	0.3391	0.7659
Spectral	0.4723	0.6698	0.3145	0.7408
PairCRSC	0.3280	0.5437	−	−
CentCRSC	0.6541	0.8155	−	−
CTSC	0.4604	0.6587	−	−
TF	0.4803	0.5431	−	−
CGC	0.1291	0.3322	0.4498	0.7625
NoNClus	0.5572	0.7320	0.3824	0.7454
ComClus	0.9764	0.9766	0.8605	0.9896

From Table I, we observe that ComClus achieves significantly better performance than other methods on both datasets. The multi-view/domain clustering methods, Pair-CRSC, CentCRSC, CTSC, TF and CGC, assume all member networks share the same underlying clustering structure thus are not able to handle these datasets. NoNClus differentiates network clustering structures completely based on the similarity between member networks, which makes it sensitive to the noise in the similarity matrix. In contrast, ComClus is able to automatically group networks based on their shared clusters and use the grouping information to further improve the clustering of individual networks.

20Newsgroup Dataset

Next we evaluate ComClus using the 20Newsgroup dataset³. We use 12 news groups of 3 categories, Comp, Rec and Talk⁴, corresponding to 3 underlying clustering structures, each with 4 clusters (news groups). In this study, we generate 10 member networks from each category. Thus there are 30 member networks forming 3 groups corresponding to the 3 categories. Each member network contains randomly sampled 200 documents from the 4 news groups (50 documents from each news group) in a category. The adjacency matrix of documents is computed based on cosine similarity between document contents.

The common nodes in different member networks are generated as follows. For any two member networks from the same category, a document in one network is randomly mapped to a document with the same cluster label (e.g., comp.graphics) in another network. For any two member networks from different categories, the documents are randomly mapped with one-to-one relationship. We vary the ratio of common nodes, γ, from 0 to 1 to evaluate its effects.

For comparison, the single network clustering methods SNMF and Spectral clustering are performed on individual member networks. The widely used k-means clustering [19] is also selected as a baseline method, it is applied on the original document-word matrix instead of the network data. Note that multi-view clustering methods PairCRSC, CentCRSC, CTSC, and TF cannot be applied here since they require full mapping of nodes between networks. We omit CGC since it is very slow on tens of networks. To apply NoNClus, we calculate the cosine similarity between the overall word frequencies of member networks.

Fig. 4 shows the averaged NMI and ACC of different methods over 100 runs. In general, ComClus achieves better performance than other methods. Note ComClus is better than NoNClus although NoNClus uses the high quality similarity information between member networks. This shows the importance to group and cluster multiple networks simultaneously. The blue dotted curve in Fig. 4 shows that ComClus achieves increased NMI and ACC of network grouping as more common nodes are added. This confirms that better common cluster detection enhances network grouping.

Fig. 4.

Performance on 20Newsgroup dataset with various common node ratio. The blue dotted curve shows the grouping performance of ComClus.

Reality Mining Dataset

In this section, we evaluate ComClus on the MIT reality mining proximity networks [20]. From the original dataset, we obtain 371 proximity networks about 91 subjects (e.g., faculties, staffs, students). Each of the network is constructed in one day between July 2004 and July 2005. In a proximity network, any pair of subjects are linked if their phones detect each other (within certain distance) at least once in that day.

As analyzed in [20], subjects have different roles during work and out of campus, which reflects in different subject clusters (e.g., working groups or social communities) in in- and off-campus. As suggested by [20], we separate each of the 371 proximity networks by time 8 p.m. to obtain two groups of networks for in- and off-campus, respectively.

Since many proximity networks are very sparse without obvious structures, we take two steps to process them. First, we extract networks from September to December 2004, which generally has more data collected than other periods. Then we aggregate the networks by month. Finally we have dataset RM-month: 8 proximity networks, 4 of them are in-campus and 4 of them are off-campus.

Next we evaluate ComClus to see if it can (1) automatically group in (off)-campus networks together; and (2) enhance common subject clusters in in (off)-campus networks.

First, in our results, we observe ComClus correctly groups in-campus and off-campus networks. To evaluate the subject clusters in in-campus networks, we use the ground truth from the dataset, which indicates the subjects’ affiliations, i.e., MIT media lab or business school. The averaged NMIs (over all in-campus networks) of different methods are shown in Table II. Here NoNClus is omitted because network similarity is not available in this dataset. For spectral based methods, we report the best results, which is given by CTSC. As can be seen, ComClus exactly discovers the subject clusters in incampus networks, while none of the baseline methods can achieve this accuracy. This shows the importance to group networks and enhance clustering by group-wise consensus. For off-campus networks, since there is no ground truth, we use internal density [21] as the cluster quality measure. As shown in Table II, ComClus achieves the best averaged density, which indicates its capability to discover meaningful clusters in off-campus networks. These results imply that subjects may have different communities during and after work.

TABLE II.

Performance on RM-month dataset.

Measure	SNMF	CTSC	CGC	TF	ComClus
NMI	0.7278	0.8705	0.9083	0.9066	1.0000
Density	0.2019	0.1822	0.1702	0.1852	0.2253

VII. Conclusion

In this paper, we generalize the existing multi-network clustering methods to consider network groups and use group-wise consensus to enhance clustering accuracy. We treat node clusters as features of networks and propose a novel method ComClus to infer the shared cluster-level feature subspaces in network groups. ComClus is not only able to simultaneously group networks and detect common clusters, but also mutually enhance the performance of both procedures. Extensive experiments on synthetic and real datasets demonstrate the effectiveness of our method.