Monocular and Binocular Smooth Pursuit in Central Field Loss

Abstract

Macular degeneration results in heterogeneous central field loss (CFL) and often has asymmetrical effects in the two eyes. As such, it is not clear to what degree the movements of the two eyes are coordinated. To address this issue, we examined smooth pursuit quantitatively in CFL participants during binocular viewing and compared it to the monocular viewing case. We also examined coordination of the two eyes during smooth pursuit and how this coordination was affected by interocular ratios of acuity and contrast, as well as CFL-specific interocular differences, such as scotoma sizes and degree of binocular overlap. We hypothesized that the coordination of eye movements would depend on the binocularity of the two eyes. To test our hypotheses, we used a modified step-ramp paradigm, and measured pursuit in both eyes while viewing was binocular, or monocular with the dominant or non-dominant eye. Data for CFL participants and age-matched controls were examined at the group, within-group, and individual levels. We found that CFL participants had a broader range of smooth pursuit gains and a significantly lower correlation between the two eyes, as compared to controls. Across both CFL and control groups, smooth pursuit gain and correlation between the eyes are best predicted by the ratio of contrast sensitivity between the eyes. For the subgroup of participants with measurable stereopsis, both smooth pursuit gain and correlation are best predicted by stereoacuity. Therefore, our results suggest that coordination between the eyes during smooth pursuit depends on binocular cooperation between the eyes.

1. Introduction

Central field loss (CFL) due to diseases such as macular degeneration presents a complex challenge, as well as a unique opportunity, to look at how damage to the retina affects vision and oculomotor behaviors. The pattern of vision loss in CFL is highly heterogeneous. For a given eye, the degree of disease progression, the exact shape and distribution of the damage (scotoma), and placement of the preferred retinal locus (PRL) vary tremendously across individuals with CFL (Fletcher & Schuchard, 1997). Previous literature has shown that looking at this array of characteristics is important for understanding visual performance in this population (Fletcher & Schuchard, 2006). In a recent paper we looked at how these characteristics affect smooth pursuit in individuals with CFL (Shanidze, Fusco, Potapchuk, Heinen, & Verghese, 2016) during monocular viewing. However, changes in monocular versus binocular gaze have been shown previously (Kabanarou et al., 2006), and the problem is further complicated by differences in scotoma and PRL characteristics between eyes for a given individual. Some individuals exhibit overlapping scotomata and PRLs that are placed symmetrically, which result in a binocular scotoma that closely resembles the scotomata in each eye. Others develop the disease in one eye and the other eye is able to compensate for the majority of the visual field loss. Most often, however, individuals with CFL have an intermediate situation where each eye has some degree of field loss that is partially overlapping between the two eyes, but even the degree of overlap can vary, depending on the number and placement of the PRLs in each eye (Tarita-Nistor, González, Markowitz, & Steinbach, 2006). These losses in foveal vision result in oculomotor behaviors that are distinct from the fovea-based, symmetric, binocular vision-driven behaviors that have been studied in human and non-human primates for decades previously.

This continuum of differences in patterns of vision loss presents a challenge to understanding behaviors that are normally binocular and may rely on the use of the central retina and specifically the fovea, such as smooth pursuit. Smooth pursuit is used to stabilize a moving stimulus on the retina and in the case of a spot stimulus, the fovea closely tracks the moving target (for review see Krauzlis, 2004). As such, in individuals with normal vision, smooth pursuit eye movements are likely conjugate during binocular tracking in the fronto-parallel plane, with the foveas of both eyes following the object of interest. It is not clear how this behavior might change if the fovea in either, or both eyes is no longer available and the new PRLs may not be in retinal correspondence. A simple hypothesis would be that smooth pursuit would be driven entirely by the dominant, or better eye. However, individual differences in this population complicate this interpretation – the definition of a “better” eye may change depending on the task at hand. For example, an individual with a ring-shaped scotoma may use the eye with higher acuity for reading, but may use the other eye for more global processing. Another possibility is that both eyes are utilized for pursuing a moving target, with each eye compensating for physiological limitations on the other’s movement; because PRL location can be highly eccentric, the eye may be limited in how much it can move in the orbit and therefore both eyes may be necessary to follow the target, taking over at different parts of the trajectory.

In this study, we examined characteristics of binocular smooth pursuit eye movements in response to a single spot target moving in the fronto-parallel plane. We examined binocular and monocular viewing in individuals with central field loss and age-matched controls with healthy vision. We hypothesized that participants with CFL would have reduced coordination between the two eyes during monocular and binocular viewing, as compared to controls, with the dominant eye driving the smooth pursuit behavior. To test our hypotheses, we used several levels of analysis, starting by comparing CFL and control participants, then examining trends within the CFL group, and finally looking at individual differences on a participant-by-participant basis. Consistent with our hypothesis, we found reduced correlation in the movement of the two eyes in CFL individuals, as compared to controls, that was especially evident during viewing with the non-dominant eye. Smooth pursuit gains were also affected across viewing conditions, with worst gains and highest gain discrepancies between the two eyes occurring during non-dominant eye viewing. Participants’ ratio of contrast sensitivity between the eyes and stereoacuity had significant effects on both between-eye correlations and monocular smooth pursuit gains.

2. Materials and Methods

2.1 Participants

All research was performed in accordance with the Declaration of Helsinki and was approved by the Institutional Review Board of the Smith-Kettlewell Eye Research Institute. We recruited 7 participants with central field loss (ages: 52–91, 4 males) and 4 controls (ages: 70–84, 1 male). All participants provided informed consent. All controls had no vision or eye movement disorders. All CFL participants had macular degeneration (6 with age-related macular degeneration and 1 with Stargardt’s disease, P2) in one or both eyes. One CFL participant also had a history of strabismic amblyopia, with a dominant fellow eye (P5, Table 1).

Table 1.

Participant demographics: Dx – Diagnosis (CFL Status), CS – contrast sensitivity, SA – stereoacuity, B – binocular, D – dominant eye, ND – non-dominant eye, R – right, L – left

ID	D Eye	Age	Sex	Dx	logMAR Acuity (D)	Acuity (D/ND)	MARS CS (D)	MARS CS (D/ND)	SA (arcmin)	Fixational Stability (D)	Fixational Stability (D/ND)	Scotoma Area (D/ND)	Scotoma Overlap (B/D)
P1	R	73	M	AMD	1.3	0.097	1.05	1.4	10	0.5	0.455	1.08	0.67
P2	R	52	M	JMD	−0.1	0.000	1.6	1.08	5	0.8	1.333	1.10	0.78
P3	R	71	M	AMD	0.1	1.000	1.8	1.15	>30	1	0.714	0	—
P4	R	87	F	AMD	0.7	0.302	0.88	0.66	>30	0.6	0.545	1.60	0.22
P5	L	91	M	AMD	0.1	4.805	1.2	2.88	>30	0.3	0.057	0.52	0.61
P6	L	84	F	AMD	0.6	0.574	1.02	2.13	13.33	0.4	0.235	0.53	0.41
P7	R	87	F	AMD	0.2	0.097	1.08	1.35	>30	1.3	1.000	3.14	0.26
C1	L	84	F	Control	−0.1	0.097	1.72	0.93	0.67	0.1	1.000	—	—
C2	L	70	F	Control	0.0	0	1.72	1.02	0.67	0.1	2.000	—	—
C3	R	73	F	Control	−0.1	0.097	1.76	1.00	0.1	0.1	1.000	—	—
C4	L	74	M	Control	0.1	0	1.76	1.00	1	0.05	0.500	—	—

Prior to testing, all participants were assessed using a standard battery of tests to calculate their acuity, contrast sensitivity, and stereoacuity. Scotomata were mapped monocularly using standard microperimetry approaches in the scanning laser ophthalmoscope (Optos OCT/SLO) and fixational stability was measured as the 68% bivariate contour ellipse area (Steinman, 1965) during a 10-second fixation task. To estimate binocular scotoma areas, we used an in-house algorithm (Ghahghaei & Walker, 2016) that allowed us to combine the monocular maps using the optic disc and the foveal pits (if available from the OCT) or an estimate of the foveal location based on normative data of foveal location from the center of the optic disc (Kabanarou et al., 2006). The amount of scotoma overlap was estimated statically for straight ahead gaze. Ocular dominance was assessed using Miles’ “hole-in-the-hand” method (Roth, Lora, & Heilman, 2002).

2.2 Equipment

Participants were seated 1 meter away from a CRT monitor. Each participant’s head was restrained comfortably in a chin and forehead rest, and eye movements were recorded using an Eyelink 1000 infrared eye tracker, placed in the table-top configuration, to allow for binocular tracking. Data were sampled at 1000 Hz. During experimental blocks with monocular viewing, participants wore an opaque eye patch (transparent to infrared) over the non-viewing eye. Calibration was performed at the beginning of each block, which consisted of 90 trials of the same viewing condition: binocular, monocular left, and monocular right.

2.3 Smooth Pursuit

For each trial, participants viewed a 1° white annulus (0.2° black center) that appeared in the center of a black screen, and were asked to follow a target that moved in a modified step-ramp paradigm (Rashbass, 1961). Participants initiated each trial with the press of the space bar. Trial onset was gaze-contingent, requiring the participant to fixate within 3–5° of screen center (to allow for fixational instability due to CFL participants’ eccentric viewing) for 0.3 seconds plus a random delay period between 500 and 1000 milliseconds. Once fixation was acquired for a requisite amount of time, the central target disappeared and reappeared at one of six possible locations, 6° from center. The target then moved in the opposite direction of the initial step (0°, 90°, 135°, 180°, 270°, 315°) for 12°, moving through screen center. Targets moved at one of three possible velocities (5, 10, 15 °/s), and each velocity and trajectory combination was repeated 5 times, for a total of 90 trials for each viewing condition (binocular, dominant and non-dominant eye). Eye movement recordings were always binocular, regardless of viewing condition. Velocity and trajectory combinations were randomized within each block. Eye movement and stimulus data were saved for offline analysis.

2.4 Data Analysis

Raw eye position data was filtered with a 2-pole Butterworth non-causal filter (cutoff = 50Hz) prior to analysis. Saccades were detected offline when eye velocity exceeded 40°/s, or variance exceeded 150 (°/s)². All velocity traces where a saccade was detected in the last 150 ms were then visually inspected and those where saccades or blinks were present were rejected for future gain analysis.

Due to poor fixation (and overall eye) stability in the CFL participant population, standard methods to differentiate the eye position signal to obtain eye velocity (and therefore smooth pursuit gain) were too noisy. Instead, a linear fit approach was used on the horizontal and vertical eye movement position traces to calculate velocity. CFL participants rarely maintained a consistent velocity throughout the smooth pursuit trial, often showing variation during the epoch conventionally defined as the steady-state interval of pursuit. Therefore, we used the last 150 ms of the eye movement trace to obtain a linear fit to horizontal and vertical eye position (Figure 1). We chose this time point and duration to account for variability in position and velocity within trials and to have comparable time periods between the two eyes and viewing conditions. Furthermore, because targets always moved across the same 12° distance, we wanted to ensure that even for the fastest velocity we were able to capture velocity after pursuit onset, even accounting for long latencies often seen in the CFL participants (up to 0.6 seconds, Shanidze et al., 2016). The values obtained using this analysis were consistent with those obtained using a traditional, velocity-based gain estimation approach (Figure S1 in Supplementary Materials).

Figure 1.

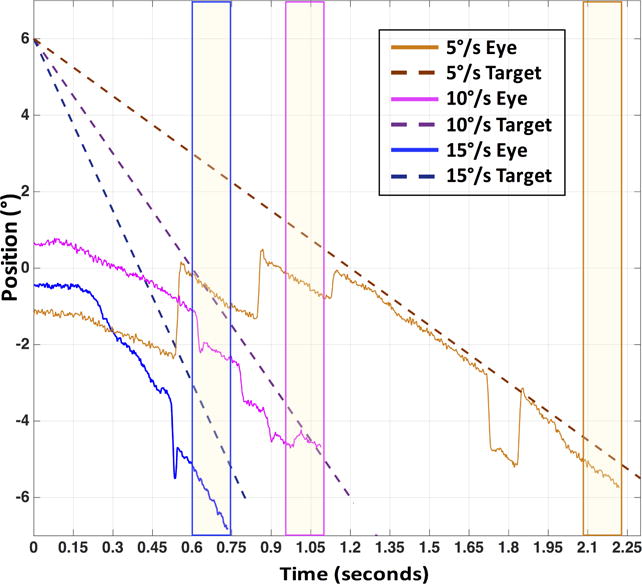
Example horizontal eye (solid) and target (dashed) position traces for P2 for a target moving in the 180° direction (to the left) at 5, 10 and 15°/s. Yellow vertical bars represent 150 millisecond segments within which gain was calculated

2.4.1 Gain

Gain was calculated as the ratio of the slope of the linear fit to target velocity. The XY slope was calculated as the square root of the sum of squares of the individual horizontal and vertical slopes. Median gain values of each set of 5 identical trials were used for all subsequent analysis. For further analyses, for each participant and velocity, we found the target direction during binocular viewing where gain was closest to 1 (indicating best pursuit for a given participant). Gains for corresponding directions were used for monocular viewing trials.

2.4.2 Inter-eye Correlation

To quantify similarity in eye movements between the two eyes, we also performed a cross-correlation between the two eyes for the movement portion of the trial (entire trace in Figure 1). Horizontal and vertical components of the eye movement signal were correlated separately and all correlations were performed across the entire movement portion of the trial, on a trial-by-trial basis. As the maximum correlation typically occurred at a lag of 0 (77% of all trials, Figure S2 in Supplementary Materials), we characterized the correlation by the Pearson correlation coefficient, calculated when the two eye traces are not offset in time relative to each other (lag = 0). For further analysis (see section 2.5 of Methods below), we determined the target direction with the lowest Pearson correlation coefficient for each velocity and viewing condition (indicating highest discrepancy between the two eyes). This minimum inter-eye correlation value was then used as the response variable in the linear mixed-effects model.

2.5 Statistical analysis

We used linear mixed-effects models to model the dependent variables of best smooth pursuit gain across target directions and minimum inter-eye correlation coefficients (worst correlation). Across all participants, we analyzed the effect of patient-specific independent variables (age, CFL status, stereoacuity, scotoma overlap in the two eyes relative to scotoma area in the dominant eye, and interocular ratios, D/ND, of: acuity, contrast sensitivity, fixational stability, scotoma size) and trial-specific independent variables (viewing condition and eye, speed, as well as direction components – horizontal and vertical – of smooth pursuit for correlation models). Categorical variables (viewing condition, CFL status) were separated into dichotomous variables based on their values (e.g., viewing condition and eye resulted in Binocular D, Binocular ND, Dominant, and Non-Dominant – note, non-viewing eyes were excluded). Dummy coding was used for the categorical variables with the first group being treated as the reference group.

A subset of the CFL participants in this study did not have measurable stereopsis. Previous work has shown differences in behavior between CFL participants with and without stereopsis (Verghese, Tyson, Ghahghaei, & Fletcher, 2016); thus, we created two sets of linear mixed-effects models: one using all patients (N=11) and excluding stereoacuity as a predictor variable, and another excluding patients without measurable stereopsis and including stereoacuity as a variable (N=7).

In both sets, we used stepwise model selection with forward and backward forms to guide the selection of fixed effect terms to include in the model. The stepwise approach adds and removes potential terms by comparing the fit of the resulting models using their Bayes Information Criterion (BIC) value. For both the correlation and gain models, we included random-effects of intercept for participant and viewing condition grouped by participant. The resulting formulas were:

All participants:

$${\text{Correlation}}^{~}In{t}_F+\text{CS}\text{ratio}+{\text{Dx}}^{\ast }\text{Direction}\text{Component}+\left(In{t}_R+\text{Viewing}|\text{Participant}\right)$$ (1)

$${\text{Gain}}^{~}In{t}_F+\text{CS}\text{ratio}+\left(In{t}_R+\text{Viewing}|\text{Participant}\right)$$ (2)

Participants with stereoacuity:

$${\text{Correlation}}^{~}In{t}_F+\text{Dx}+\text{Stereoacuity}+\left(In{t}_R+\text{Viewing}|\text{Participant}\right)$$ (3)

$${\text{Gain}}^{~}In{t}_F+\text{Stereoacuity}+\left(In{t}_R+\text{Viewing}|\text{Participant}\right)$$ (4)

To monitor multicollinearity between the variables in the models, we calculated the variance inflation factor (VIF) of the terms in each of the models. All computed VIFs were < 5, indicating insufficient multicollinearity.

3. Results

3.1 Pursuit Gain

We observed variability in pursuit gains across velocities and viewing conditions in CFL participants that was not present in controls. Figure 2 summarizes overall gain distributions across all controls and CFL participants. Although there was no mean difference in the majority of conditions between smooth pursuit gains in CFL participants and controls, there was a marked increase in variability during monocular for the CFL population, with gains dipping as low as 0.05 (indicating no pursuit) for CFL.

Figure 2. Summary of smooth pursuit gains across different target velocities and viewing conditions (marked above).

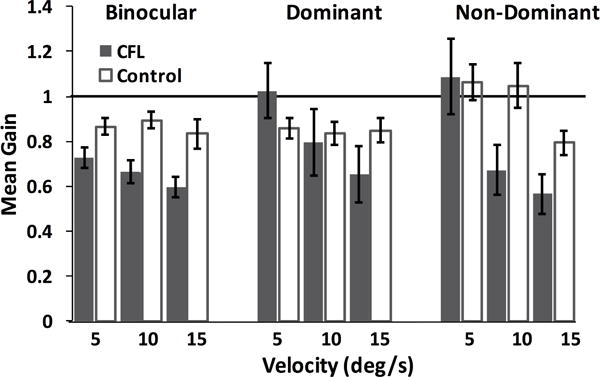
Error bars represent standard error. The horizontal line marks a gain value of 1.

To quantify these differences, we performed a 3-way ANOVA, taking participant group, viewing condition and velocity into account as independent variables. The analysis revealed a significant effect of participant type (F(1, 559) = 8.44, p = 0.004, η_p² = 0.015) and velocity (F(2, 559) = 7.13, p = 0.001, η_p² = 0.025). A post-hoc Tukey-Kramer comparison showed that for CFL participants, gains for the non-dominant viewing condition were different for 5 vs. 15 deg/s target velocities: gains for 15 deg/s targets were significantly lower than those for 5 deg/s targets for binocular and non-dominant viewing conditions. For controls, there was no difference between viewing conditions or target velocities. Across participant type, control gains during non-dominant viewing of 5 deg/s targets were significantly higher than CFL participants’ gains during binocular viewing for 10 and 15 deg/s targets, as well as during non-dominant viewing of 15 deg/s targets (p < 0.05).

As is evident from Figure 2, participants had a similar pattern of performance for all three velocities tested. However, due to the long latency of smooth pursuit in CFL participants and the short duration of target motion in the 15°/s condition, there was only a small proportion of the trials where smooth pursuit behavior was evident throughout the 150 ms measurement period. Therefore, we present data only for the 5 and 10°/s trials for the rest of the analysis.

In our previous work, we showed that for monocular viewing, smooth pursuit gain depends on the direction of target motion relative to scotoma location (Shanidze et al., 2016). Therefore, some of the variability that we see in gains across trials may be due to changes across trajectory direction and not simple trial-to-trial variation. Because the specific combination of trajectory direction and scotoma orientation is different for every CFL participant (and sometimes between eyes) depending on the specifics of that participant’s scotoma characteristics, we were not able to treat trajectory direction as just another analysis dimension across all CFL participants. Instead, we chose to look at the trajectory direction that provides the gain closest to 1 for each CFL participant under binocular viewing and compare those to an analogous metric in controls (where across-direction variation was significantly lower). Therefore, we found the direction with the best gains for the dominant eye during binocular viewing and analyzed gains for that direction for subsequent analysis of all viewing conditions (Figure 3).

Figure 3.

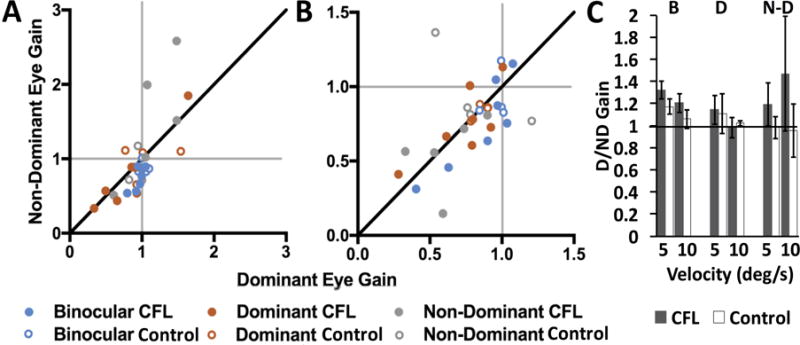
Best gain distributions for 5°/s (A) and 10°/s (B) trials for CFL participants (filled circles) and controls (open circles). Thin gray lines in A & B indicate gain = 1; thick black lines are the lines of equality. Colors represent viewing conditions (note difference in x and y scales). (C) Mean best gain ratios across viewing conditions (labeled above) and velocities. Horizontal black line in C indicates D/ND gain ratio = 1. Error bars represent standard error.

To assess similarity in pursuit between the two eyes in the best-gain direction, we plot best gains of the dominant versus non-dominant eye for each viewing condition, for CFL and control participants in Figures 3A and B. Consistent with data in Figure 2, across all viewing conditions, best gains of control participants are more tightly clustered around 1, while for CFL participants even pursuit gains at the optimized target direction had an extensive range (0.15–2.13 for the viewing eye). Additionally, there are notable differences between dominant and non-dominant eye gains. Figure 3C plots the mean ratios of the dominant to non-dominant eye gains for each viewing condition, i.e., the mean of dominant to non-dominant (D/ND) ratios for each group of points in A and B. For CFL participants, ratios between gains of the two eyes were significantly greater than 1 for both target speeds during binocular viewing (one-sample t-test, 5°/s: t(6) = 4.12, p = 0.006, d = 1.56; 10°/s: t(6) = 2.49, p = 0.047, d = 0.94). This effect was not present for controls during binocular viewing or for either group for monocular viewing conditions.

When we looked at gains closest to 1 for each viewing condition, the gains ranged between 0.31 and 1.20 for 10°/s targets and 0.63 and 1.05 for 5°/s targets. These numbers indicate that for some CFL participants, certain viewing conditions produced smooth pursuit velocities that corresponded to, at best, 0.3 gain.

We wanted to examine whether specific characteristics of the CFL participants’ field loss, such as the correspondence between the scotomata in the two eyes, affected the gain for the two eyes. Thus, we constructed a linear mixed-effects regression model that tested metrics listed in Table 1. The model was first constructed based on the entire participant population, but excluding stereopsis as a possible predictor variable. Using this approach, we found that the ratio of contrast sensitivity between the two eyes was the only significant predictor variable. However, when we included stereoacuity as a possible predictor (thereby excluding participants P3, P4, P5 and P7), we found that a model that relied only on stereoacuity was best (Table 2).

Table 2.

Linear model for gain. Model predictors for gains closest to 1. CS: contrast sensitivity; SA: stereoacuity. All participants: R² = 0.357; Participants with stereopsis: R² = 0.503.

All Participants (N = 11)					Participants with Stereopsis (N = 7)
	Estimate	SE	p	df		Estimate	SE	p	df
Fixed Effects					Fixed Effects
InterceptF	1.067	0.073	<0.001	84	InterceptF	0.967	0.041	<0.001	54
CS Ratio	−0.157	0.051	0.003	84	SA	−0.017	0.008	0.009	54
Random Effects					Random Effects
InterceptR	0.064				InterceptR	0.078
Viewing|Participant					Viewing|Participant
Binocular	0.057				Binocular	0.091
Dominant	0.024				Dominant	0.075
Non-Dominant	0.291				Non-Dominant	0.337

3.2. Inter-eye Correlation

To determine the degree of movement similarity between the two eyes throughout each trial, we performed a cross-correlation between the two eye position signals for the duration of these trials. Overall, we saw a significant decrease in correlation in CFL participants that was not evident in controls. For both horizontal and vertical components of motion, there was a significant difference in the mean value of the Pearson’s correlation coefficient between CFL and control participants at both 5 and 10°/s. To analyze these data, we looked at between-eye correlations for target directions where the corresponding component of target motion was present (vertical, horizontal); for correlations of the horizontal component of motion we looked at trajectories that had a horizontal component (0°, 135°, 180°, 315°) and for the vertical motion correlations we looked at trials where target trajectories had a vertical component (90°, 135°, 270°, 315°). Comparing correlation coefficients for participants with CFL and controls yielded the following results (2-factor ANOVA with Tukey correction for multiple comparisons):

Table 3 summarizes a significantly lower level of correlation between the two eyes in CFL versus control participants for both 5 and 10°/s targets. Furthermore, in the horizontal dimension, unlike controls, participants with CFL showed a significantly lower correlation in the non-dominant eye viewing condition than dominant or binocular (5°/s: mean_CFL = 0.886 vs. mean_Cont = 0.993, F(2,18)=9.22, p = 0.002, η_p² = 0.506 & 10°/s : mean_CFL = 0.872 vs. mean_Cont = 0.990, F(2,18)=5.71, p = 0.012, η_p² = 0.388; interaction terms of the 2-factor ANOVA in Table 3). Figure 4 shows the correlation coefficients for the four conditions in Table 3. The figure clearly illustrates consistent, near-perfect correlation between the eyes of control participants, as indicated by the black horizontal line at the top of each panel. Correlation is significantly decreased for CFL participants across all viewing conditions. To ensure that the observed decrease in correlation was not due to a decrease in pursuit velocity on those trials, we looked at correlation coefficients as a function of gain across all velocities and participants and found no significant relationship for horizontal or vertical correlations (linear regression, R² = 0.08, F(1,18)=1.52, p = 0.23 and R² = 0.16, F(1,17)=3.22, p = 0.09, respectively). We did see an overall trend where pursuit directions that were the most affected (farthest from gain=1) tended to have some of the worse correlations, on a participant-by-participant basis.

Table 3.

Comparison of Pearson’s correlation coefficients for inter-eye position, for CFL and control participants, for all three viewing conditions; p-values in bold represent significant difference in correlation coefficient means.

			Horizontal Component				Vertical Component
Vel	Factor	Condition	Mean	F-stat	p-value	ηp2	Mean	F-stat	p-value	ηp2
5°/s	Participant Type	CFL Control	0.947 0.994	F(1,18) = 20.91	<0.001	0.537	0.903 0.989	F(1,18) = 30.30	<0.001	0.627
10°/s	Participant Type	CFL Control	0.939 0.992	F(1,18) = 15.55	0.001	0.463	0.876 0.980	F(1,18) = 18.69	<0.001	0.509
5°/s	Viewing Condition	Binocular Dominant Non-Dominant	0.990 0.983 0.939	F(2,18) = 9.63	0.001	0.506	0.967 0.953 0.919	F(2,18) = 3.39	0.056	—
10°/s	Viewing Condition	Binocular Dominant Non-Dominant	0.981 0.974 0.901	F(2,18) = 6.65	0.007	0.388	0.958 0.926 0.900	F(2,18) = 1.93	0.175	—

Figure 4.

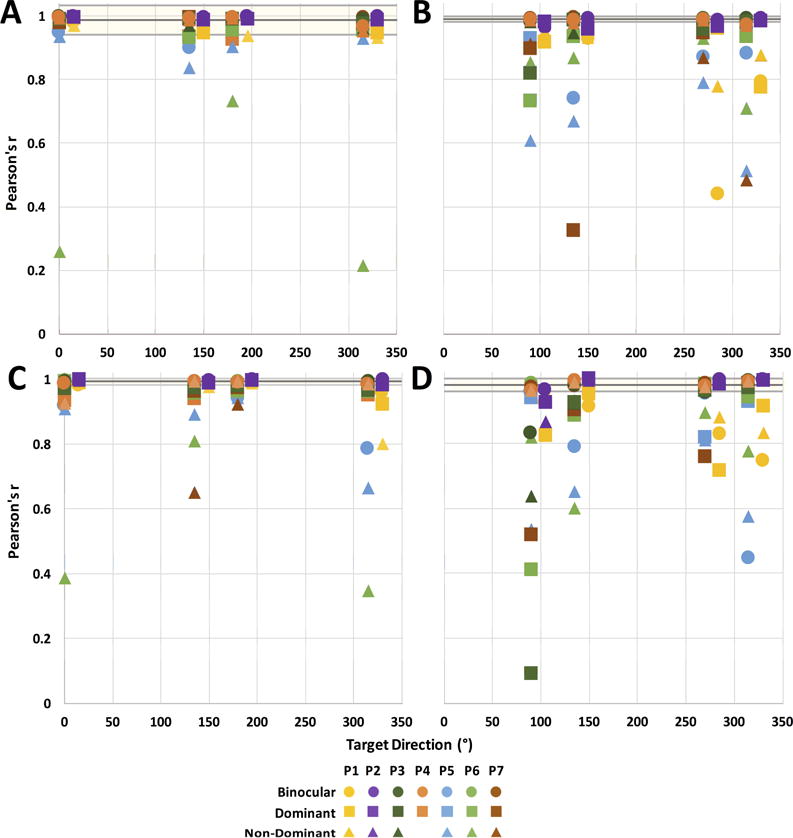
Pearson correlation coefficients for inter-eye positions during 5°/s (A, B) and 10°/s (C, D) target motion. Correlations between horizontal (A, C) and vertical (B, D) eye positions are shown separately. Black and gray horizontal lines represent the mean and standard deviation of controls’ correlation coefficients across all target directions for the given velocity and motion dimension. CFL participants P1 and P2 are plotted at a +15° horizontal offset from the rest of participants for clarity.

Two of our CFL participants (P1 and P2) have large, overlapping scotomas in the two eyes that correspond to an analogous binocular scotoma, as estimated by a tangent screen test that maps the binocular scotoma (Verghese & Janssen, 2015; Janssen & Verghese, JOV, in press). These participants also have measurable (coarse) stereoacuity (Table 1). When we examined correlation coefficients for these two participants separately (Figure 4, offset values), we found that they had overall higher correlations between the two eyes across all viewing conditions, than the other CFL participants, although still lower than controls (Table 4). To examine this result further, we compared mean Pearson correlation coefficients, averaged across trajectories for each velocity and eye-movement direction component, across the three groups (P1–P2 vs. P3–P7 vs. C1–C4, see Table 4 for across-viewing condition averages). We found a significant difference between groups (Friedman test, chi-square = 8.0, p = 0.005). Subsequently, we used Dunn’s multiple comparisons test, and found that there was a significant difference between P3–P7 and C1–C4 groups (p = 0.014), but not P1–P2 and C1–C4 (p = 0.472).

Table 4.

Mean Pearson’s correlation coefficients across participant groups (P3–P7 – intermediate scotoma overlap; P1 & P2 – large scotoma overlap; C1–C4 – controls).

	5°/s		10°/s
	Horizontal	Vertical	Horizontal	Vertical
P3–P7	0.939±0.148	0.898±0.147	0.930±0.133	0.861±0.190
P1 & P2	0.980±0.021	0.920±0.122	0.980±0.042	0.923±0.082
C1–C4	0.987±0.045	0.989±0.009	0.992±0.010	0.980±0.020

Next, we wanted to understand what changes in visual function due to CFL might contribute to reducing the amount of correlation between the two eyes. Having shown previously that target direction affects smooth pursuit eye movements in CFL, we chose to examine the target direction that yielded the greatest discrepancy between the two eyes (lowest correlation), for each participant, velocity and viewing condition. Using a linear model approach (as described in Section 2.5 of Methods), we found several significant factors (Table 5).

Table 5.

Linear model results for minimum correlation of inter-eye position. Dx: diagnosis, CS: contrast sensitivity, DirComp: eye-movement direction component, SA: stereoacuity; All participants: R² = 0.504; Participants with stereopsis: R² = 0.619.

All Participants (N = 11)					Participants with Stereopsis (N = 7)
	Estimate	SE	p	df		Estimate	SE	p	df
Fixed Effects					Fixed Effects
InterceptF	1.082	0.043	<0.001	123	InterceptF	1.113	0.046	<0.001	81
Dx	−0.006	0.037	0.874	123	Dx	−0.120	0.046	0.010	81
CS Ratio	−0.105	0.023	<0.001	123	SA	−0.029	0.005	<0.001	81
Dir Component	−0.135	0.028	<0.001	123
Dx:DirComp	0.136	0.046	0.004	123
Random Effects					Random Effects
InterceptR	0.062				InterceptR	0.098
Viewing|Participant					Viewing|Participant
Dominant	0.119				Dominant	0.086
Non-Dominant	0.156				Non-Dominant	0.188

When we examined the entire participant population, without taking stereopsis into account, we found that participant diagnosis (CFL vs. Control) and ratio of contrast sensitivities of the two eyes contributed significantly to predicting inter-eye correlation. Eye movement direction also played a significant role, consistent with our observation that inter-eye correlations were significantly lower for vertical eye movements than horizontal (Figure 4, compare A & C to B & D). Additionally, an interaction between diagnosis and eye-movement direction component suggests that participants with CFL exhibit higher decorrelation of the two eyes in the vertical direction than controls (gray horizontal bars in Figures 4B & D). When taking stereopsis into account, the model indicated that both stereoacuity and diagnosis significantly contributed to predicting inter-eye correlation. It is interesting to note that with stereoacuity present, the model became simpler and more effective (higher R²). This outcome suggests that participants with limited degree of retinal overlap do not maintain conjugacy between the two eyes to the same extent as controls. Interestingly, the ratio of fixational stability of the two eyes did not improve the linear model for the entire population, despite its potential relationship to binocularity, or the degree of similarity between fixational stability of the two eyes (Irsch, Geary, Tian, & Guyton, 2014).

3.3. Across-Participant Variations in Pursuit Strategy

Figure 5 shows a typical set of eye position traces for 5 trials of identical target motion (10 °/s, at 135° and 315° target directions) for participants P1 and P2. Both participants have large, overlapping scotomas in the two eyes, and similar PRLs in the two eyes, which result in a binocular scotoma in the upper right for P1 and in the upper visual field for P2 (see insets in Figure 5 for rough diagrams, Supplementary Materials, Table S1 and P4 & P6 in Table 1 of Shanidze et al., 2016 for perimetry maps). However, the two exhibit very different pursuit strategies for targets that are heading towards (315°) and away (135°) from their scotomas. For P1, when the target is heading out of the scotoma (top left), the participant is able to pursue the target (although note variability across trials). However, when the target is moving towards the scotoma, the participant consistently fails to acquire and pursue the target, possibly because it disappears within his scotoma before he is able to initiate smooth pursuit. P2, on the other hand, is able to pursue targets heading toward his scotoma with excellent gains. However, when the target starts its smooth motion within his scotoma (bottom left), P2 does not initiate pursuit until the target has crossed the center point, and then his pursuit is saccadic, with pursuit velocities exceeding those of the target (e.g., magenta trace). One possible explanation is the difference in ages between the two participants. Smooth pursuit has been shown to be impaired in senescence (Spooner, Sakala, & Baloh, 1980), suggesting that P1 may not be able to initiate pursuit quickly enough when the target moves towards the scotoma, while P2 can quickly initiate pursuit when the target is visible at the start of its trajectory. However, age is unlikely to be a factor in P2’s strategy when the target starts its trajectory in the scotoma. Here, the participant is more likely to be waiting for the target to appear in the center of the screen.

Figure 5. Raw position traces for P1 and P2.

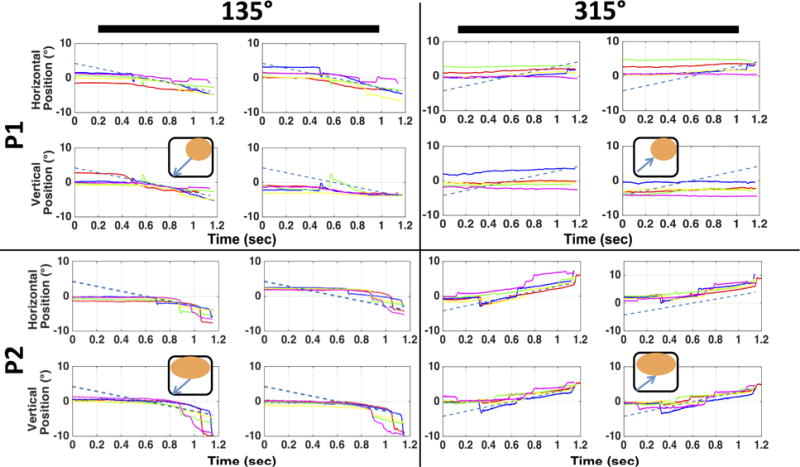
Data in each pane shown for 5 trials in the 10°/s velocity conditions, for targets moving at 135° (left two columns) and 315° (right two columns). Each group of four shows horizontal and vertical components (rows) of eye position for the left and right eyes (columns). Dashed blue line: target position. Insets: orange ovals – binocular scotoma, black outline – visual field, blue arrows: target motion.

The relationship between binocular scotoma location and target direction is evident for participants with large binocular overlap and compact lesions; however, the majority of individuals with CFL have a more complicated pattern of retinal lesions. Figure 6A illustrates P1’s response gains for all target directions tested. There is a clear modulation in gain dependent on target trajectory, with gains being lowest for targets moving towards the participant’s scotoma and highest for targets moving away from the scotoma and having least interaction with it (down: 90° and right-to-left: 180°). Importantly, this pattern is consistent between binocular and dominant eye viewing (compare orange and blue dots).

Figure 6.

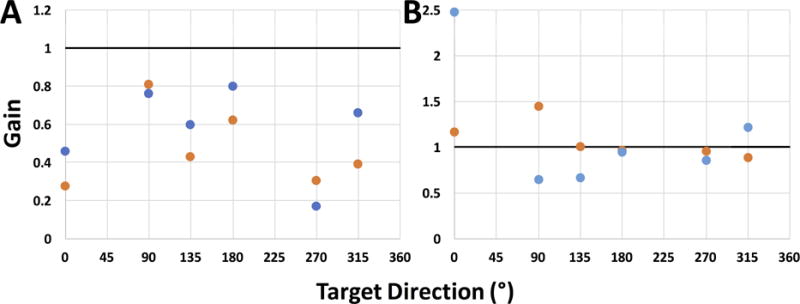
Smooth pursuit gains in response to 10 °/s target motion across all target directions during binocular (orange circles) and dominant eye viewing (blue circles) conditions for participants P1 (A) and P4 (B). Dominant (right) eye shown for both participants. Note difference in y-axis scale between the two plots.

Data are more difficult to interpret for participant P4 (Figure 6B), whose scotoma is more disperse and who has very little amount of binocular overlap (see Table S1 in Supplementary Materials). In the case of P4, gains during binocular viewing are closer to 1 (suggesting a more consistent placement of the eyes on target). Furthermore, gains during binocular viewing tend to be more consistent, suggesting less influence of scotoma placement in either eye. Overall, there is a greater difference in gains between viewing conditions for P4 than P1 (especially note difference in scale between the two plots).

Differences in pursuit strategy are an important consideration when looking at oculomotor function in this population (Liu, Keith, & Bolding, 2016). In the example of compact, binocular scotomas, as is the case for participants P1 and P2, a descriptive analysis of each individual strategy may be possible. However, the problem becomes more complex with more complicated scotoma profiles and differences in binocular overlap.

4. Discussion

In this study, we looked at smooth pursuit eye movements in individuals with central field loss during binocular and monocular viewing. In the experiment, we had two major goals: (1) quantify smooth pursuit in CFL participants during binocular viewing and compare it to the monocular case and (2) examine changes in the coordination of the two eyes during smooth pursuit of a stimulus moving in the fronto-parallel plane.

4.1 Gain

First, we showed that although on the whole, individuals with CFL could pursue targets moving between 5 and 15°/s, they had a much higher variability in gains compared to controls, with instances of eye velocity significantly higher or lower than target velocity. Both of these scenarios are disadvantageous for visualizing the target, as both lead to an increase in retinal slip. Control participants tended to have gains closer to one. This observation is further illustrated in Figure 3, where best (least retinal slip) gains are plotted for each participant. Control gains (open circles) are clustered near 1, whereas best gains for CFL participants are dispersed much more widely. On average, however, we did not find a significant difference between the best gains of participants with and without CFL.

When we examined gains across all target directions, we found gains to be significantly lower for CFL participants than controls (Figure 2). This finding is in agreement with our earlier study of monocular pursuit, where we showed that CFL participants had significantly lower gain than did controls for target velocities of 6°/s. The agreement between the two sets of results is notable not only because this study extends the finding to binocular pursuit, but also because in the previous study, we calculated velocity by differentiating the position data and compared gains during periods of longest continuous velocity for each trial. We could not apply those methods to the current analysis of binocular pursuit because periods of continuous gain were not consistent between the two eyes. Furthermore, differentiation of eye position signals yielded noisy velocity traces. Instead, we computed gain using a linear fit at the end of each trial, when controls’ gain would have reached the lower steady state velocity (Robinson, Gordon, & Gordon, 1986) or CFL gain may have been at its highest, as the participants had the maximum time to find the target and begin pursuit.

An important distinction between CFL and control participants’ overall gains, is that target velocity had an effect on CFL gain during binocular and non-dominant viewing. This effect was not present in control gains. This finding suggests that CFL participants’ reliance on the two eyes may change depending on the speed of target motion. Specifically, input from the non-dominant eye appears insufficient to effectively drive pursuit at higher target velocities.

Another key finding regarding CFL participants’ use of the two eyes is illustrated in Figure 3. Whereas control participants did not show a difference in pursuit gains between the two eyes during pursuit under binocular or monocular viewing conditions, CFL participants’ gains in the two eyes were more similar during monocular than during binocular viewing. The data suggests that during monocular viewing, CFL participants likely relied on the information from the viewing eye and the non-viewing eye followed at a similar velocity. However, when viewing was binocular, the two eyes moved more independently of each other, possibly due to asymmetric visual function in the two eyes.

The significance of differences between the two eyes is emphasized further with our linear model analysis of gain. When considering all our participants together, we found that the ratio of contrast sensitivities between the dominant and non-dominant eyes was a significant predictor of optimal gain. When we repeated the regression analysis for those participants who had measurable stereopsis with stereoacuity as a possible factor, we found that stereoacuity alone was the best predictor of optimal gain. These outcomes suggest that the effectiveness of the dominant eye, as well as the availability of the image in both eyes, are important for pursuit performance, even when the target moves entirely in the fronto-parallel plane.

In future studies, it will be of interest to test target motion in depth and to manipulate the task to make visualization of the target an important component by asking observers to detect a letter on the moving target. These approaches will further probe the interaction between smooth pursuit performance and effects of CFL on functional vision.

In addition to the changes in performance related to the characteristics of a particular eye with CFL, changes in strategy are an important factor to consider on a participant-by-participant basis (Figure 5). These variations in strategy are less evident in controls who have a lifetime of experience pursuing moving objects with their central retina. For CFL participants, however, their particular strategies may depend not only on the field loss itself, but other factors, such as age or experience. This kind of variability has been shown in PRL formation (Fletcher & Schuchard, 1997), and in the ability to use the PRL as an oculomotor reference (White & Bedell, 1990). In our SLO experiments, we were able to visualize the target trajectory directly on the retina of the viewing eye and describe in detail a participant’s performance on a given trial (Shanidze et al., 2016). Using an eyetracker allows us to monitor binocular eye movements in this study, but does not allow us to map target location relative to the binocular scotoma, which is likely to change during pursuit from the map acquired during static viewing. Section 3.3 in this paper provides a limited measure of this individual-level analysis for the relatively simple case of participants who have large, compact overlapping scotomas and symmetrically placed fixational PRLs. Figure 5 illustrates an example of differences in pursuit strategy between two individuals with almost completely overlapping scotomata in the two eyes, but different set of experiences, age and stated pursuit strategies. Whereas P1 expressed a desire to “catch and follow” the stimulus as quickly as possible and an unwillingness to miss any part of the stimulus, P2 described his strategy as wanting to be “efficient” and making sure that he can always visualize the target where he knows to expect it – at screen center.

4.2. Inter-Eye Correlation

To address our second goal, we looked at the correlation between the two eyes in CFL and control participants throughout the smooth pursuit trial, during both binocular and monocular viewing. Here, again, we saw important differences between the two groups. Most notable was the relatively reduced correlation between the two eyes in CFL. In all viewing conditions, we saw markedly lower correlations in participants with CFL, as compared to controls. This finding is intriguing, as it suggests that binocular coordination of the two eyes may be disrupted with an asymmetrical loss of the visual field between the two eyes. Conjugate eye movements are commonly viewed as being highly coordinated, driven by a common neural command. Without this tight coupling, binocular vision would be difficult to maintain during eye movements (reviewed in King, 2011). However, in a population where binocular vision is naturally disrupted, this tight coupling may become moot, or even disadvantageous. This observation is further supported by the outcomes of our linear models, where stereoacuity played a significant role for both inter-eye correlation and gain. This line of reasoning is further supported by the observation that participants who had good binocular correspondence between the PRLs and scotomas in the two eyes (P1 and P2) had higher between-eye correlations and a degree of conjugacy close to that of controls.

4.3. Summary and Conclusion

In our study, we examine the interaction between CFL’s effects on visual and binocular function and performance on a smooth pursuit task during binocular and monocular viewing. In modeling our outcome variables of gain and inter-ocular correlation, we found that the interocular ratio of contrast sensitivity and stereoacuity played a significant role. This finding is consistent with studies by Legge and Gu (1989) who showed that stereoacuity is very sensitive to the interocular contrast ratio, and with Schneck et al. (2010), who showed that contrast sensitivity is a better indicator of binocular (relative to monocular) visual function in the elderly, than is high contrast visual acuity. Our results are also consistent with that of Tarita-Nistor et al. (2006), who showed that interocular acuity ratio did not predict binocular function in CFL: interocular acuity ratios were similar in age-matched controls and in CFL participants. It is interesting to note that in both versions of the models – those for the entire participant population and those for individuals with measurable stereoacuity – gain and correlation both relied on contrast sensitivity for the former model and stereoacuity for the latter. This finding suggests a link between performance on the pursuit task (gain) and interocular coordination (correlation), consistent with the effects of viewing condition illustrated in Figure 2.

A recent study that investigated optokinetic nystagmus (OKN) in a nonhuman primate model of strabismus found that OKN eye movements in both eyes could be driven by the strabismic eye (S. Agaoglu, Agaoglu, & Das, 2015), albeit at lower gains. Our results suggest that this tight coupling between the two eyes may not occur in CFL during smooth pursuit. Importantly, OKN does not require foveal stimulation, unlike smooth pursuit of a small spot stimulus (Abadi, Howard, Ohmi, & Lee, 2005). Consistent with our observations, Agaoglu and colleagues’ data suggests smooth pursuit was not as tightly coupled between the two eyes during monocular viewing in the two exotropic animals. It is important to note that all of our participants had static intraocular misalignments of less than 3° (median = 0.706, maximum: 2.098°, P1, binocular viewing), measured during the fixation segments of our trials. These values are not large enough to be thought clinically relevant, which is usually considered to be greater than 4 diopters (5.25°). Furthermore, previous studies have shown that vection and OKN are not affected in individuals with CFL of less than 20° (Tarita-Nistor, González, Markowitz, Lillakas, & Steinbach, 2008; Valmaggia, Charlier, & Gottlob, 2001) possibly due to a filling-in phenomenon (Valmaggia & Gottlob, 2002). Consequently, changes in visual field between monocular and binocular viewing in these individuals may not affect OKN responses, where filling in does not interfere with the motion stimulus. In smooth pursuit, however, monocular viewing could provide a very different experience with the motion stimulus than binocular viewing. Therefore, any behavioral changes elicited by a switch to monocular viewing may lead to decrements in pursuit performance (see Figure 3). This idea is further supported by our observations that two participants (P1 & P2) who did not have a large change in intact visual field between binocular or monocular viewing also tended to have a higher correlation between the eyes under monocular viewing conditions. This explanation is particularly interesting in the context of monocular control of eye movements (King, 2011), where visual feedback may have different effects on the viewing and non-viewing eyes’ motor program on a given pursuit trial.

It is perhaps surprising that we did not find a significant effect of scotoma or PRL overlap on either of the two outcome measures. One possibility is that these metrics alone cannot determine pursuit behavior but must be considered in the context of other aspects of the disease, such as retinal health near the PRL or compactness of the scotoma (especially binocular scotoma). Another possibility, however, is that the metrics we provide are insufficient, in that most of them (such as scotoma overlap) are measured or calculated for static viewing and are not representative of the dynamic changes in the visual field during eye movements. This observation is particularly important to consider given that majority of clinical measurements made in this patient populations are static.

The results of this study provide an analysis of oculomotor function in the context of macular degeneration, which results in highly heterogeneous patterns of vision loss. In addition to laying the groundwork for further research into oculomotor strategies in the CFL population, we show that disconjugate eye movements in the fronto-parallel plane are generated when binocular alignment is disrupted.