Simple Fully Nonlocal Density Functionals for Electronic Repulsion Energy

Abstract

From a simplified version of the mathematical structure of the strong coupling limit of the exact exchange-correlation functional, we construct an approximation for the electronic repulsion energy at physical coupling strength, which is fully nonlocal. This functional is self-interaction free and yields energy densities within the definition of the electrostatic potential of the exchange-correlation hole that are locally accurate and have the correct asymptotic behavior. The model is able to capture strong correlation effects that arise from chemical bond dissociation, without relying on error cancellation. These features, which are usually missed by standard density functional theory (DFT) functionals, are captured by the highly nonlocal structure, which goes beyond the “Jacob’s ladder” framework for functional construction, by using integrals of the density as the key ingredient. Possible routes for obtaining the full exchange-correlation functional by recovering the missing kinetic component of the correlation energy are also implemented and discussed.

The widespread success of Kohn–Sham density-functional theory (KS DFT)¹⁻⁴ across various chemical and physical disciplines has been also accompanied by spectacular failures,² reflecting fundamental issues in the present density functional approximations (DFAs) for the exchange–correlation (XC) functional. Well-known examples are the paradigmatic case of the dissociation curves of the H₂ and H₂⁺ molecules.^2,5 The usual DFA approach to construct XC functionals consists in making an ansatz in terms of “Jacob’s ladder” ingredients:^4,6−8 the local density, its gradient, its laplacian, and/or KS kinetic energy density, up to occupied and virtual KS orbitals. While this strategy has been very successful for moderately correlated systems (see, e.g., refs (3, 4, and 9−11).), it has failed so far when correlation effects become important (e.g., in stretched bonds, but also at equilibrium gemoetries when partially filled d and f subshells are present). This fact suggests that a different approach to DFAs is needed to address the problem of strong correlation.^2,3,12−14

The strong-interaction limit of DFT¹⁵⁻¹⁸ provides information on how the exact XC functional depends on the density in a well-defined mathematical limit, which is relevant for strong correlation. The thorough explorations of this limit reveal a mathematical structure totally different from that of Jacob’s ladder ingredients. Instead of the local density, density derivatives, or KS orbitals, in this limit we see that certain integrals of the density play a crucial role, encoding highly nonlocal information,¹⁵⁻¹⁷ embodied in the so-called strictly correlated electrons (SCE) functional.¹⁵⁻¹⁷ This functional appears to be well-equipped for solving long-standing DFAs problems: it is self-interaction free, it captures the physics of charge localization due to strong correlation without resorting to symmetry breaking,¹⁹⁻²¹ and its functional derivative displays (in the low-density asymptotic limit) a discontinuity on the onset of fractional particle number.²² Despite these appealing features, there are two main obstacles to the routine use of the SCE functional: its availability is restricted to small systems^16,23 and its energies are way too low for most of physical and chemical systems.^19,23−25 The nonlocal radius (NLR) functional,²⁶ and the newer shell model²⁷ are inspired to the SCE functional form and retain only some of its nonlocality. They are readily available,²⁷ but, being approximations to the SCE functional, their energies are also too low with respect to those of chemical systems.^26,27 The information encoded in the SCE functional or its approximations can be combined with the complementary information from the weak coupling limit. This has been recently used for constructing XC functionals from a local interpolation along the adiabatic connection.^14,27−29 Although this approach is promising for treating strong correlation within the realm of DFT,¹⁴ it can still easily overcorrelate (for example for stretched bonds it overcorrelates the fragments), again because the SCE (exact or approximate) quantities are often far from the physical ones.²⁹

Nonetheless, the way in which the information encoded in the density is transfomed into an electron–electron repulsion energy in the SCE functional is very intriguing, with many physical appealing features.^16,30−32 Motivated by this observation, in this letter we use the SCE mathematical structure to devise a new way to design fully nonlocal approximate density functionals for the electronic interaction energy at the physical coupling strength. Capturing the main structural motives of the SCE functional, we preserve many of its appealing features, but with repulsion energies that are much closer to those of physical systems. Moreover, besides accurate total repulsion energies, our model provides energy densities within the definition of the electrostratic potential of the XC hole that are also locally very close to exact ones, making it an ideal tool for the development of functionals that use the exact exchange energy density, like hyperGGA’s³³⁻³⁶ or local hybrids.^37,38 In other words, it is known^33,35,39,40 that in order to use the exact exchange energy density, we need a fully nonlocal correlation functional compatible with it. It is the purpose of this work to provide a new strategy to build this fully nonlocal functional at a computational cost similar to the one of the exact exchange energy density.

In order to explain our construction, we have to first quickly review some basic DFT equations. An exact expression for the XC energy can be obtained from the density-fixed adiabatic connection formalism (AC):^41,42

1

where W_λ[ρ] is the global (i.e., integrated over all space) AC integrand:

2

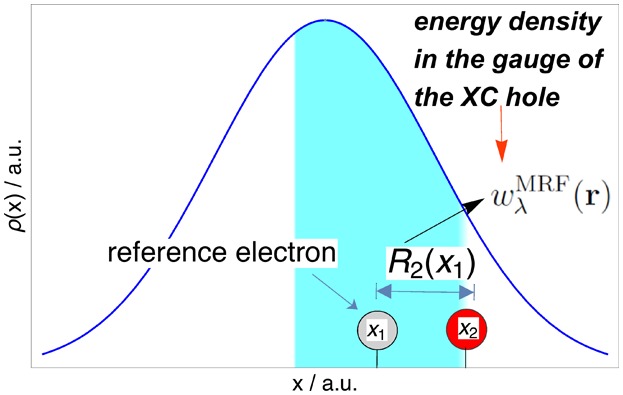
The wave function Ψ_λ[ρ] depends on the positive coupling constant λ and minimizes ⟨T̂ + λV̂_ee⟩, while integrating to ρ(r), the density of the physical system (λ = 1). This way, AC links the KS non-interacting state described by Ψ₀[ρ] and the physical state described by Ψ₁[ρ]. It also further connects the physical and the SCE state, i.e., the state of perfect electron correlation, corresponding to the limit λ → ∞. The XC energy densities along the adiabatic connection (i.e., position-dependent quantities w_λ(r) that integrate to W_λ[ρ] when multiplied by the density) are not uniquely defined and therefore we have to be specific on their gauge.^{14,29,43−45} A physically sound gauge often considered in DFT is the one of the electrostatic potential of the XC hole.^14,34,35,46 Within this gauge we can express the λ-dependent energy density in terms of the corresponding spherically averaged XC hole^14,34,35,47h_xc^λ(r, u) obtained from |Ψ_λ[ρ]|²,

3

where u = |r – r′| is the distance from a reference electron at r. In the SCE (λ→ ∞) limit the energy density w_λ(r) in the gauge of eq 3 has the exact form⁴⁸

4

where v_H(r) is the Hartree potential and the comotion functionsf_i([ρ]; r) are nonlocal functionals of the density that give the positions of the remaining N – 1 electrons when one electron is at position r.^15,16,32 From eq 4 we see that in the λ → ∞ limit the energy density w_∞(r) is fully determined by the distances R_i^SCE([ρ]; r) = |r–f_i([ρ]; r)| between a reference electron in r and the remaining N – 1 ones. For example, in the case of one-dimensional systems, the distances R_i([ρ]; x) can be constructed exactly^15,49 from the equations (with i = 2, ..., N)

5

which can be solved in terms of the function N_1D(x) = ∫_–∞^xρ(x′) dx′ and its inverse N_1D(y).^15,19,30 We see that in this limit each electron is separated by the closest one by a piece of density that integrates exactly to 1 (in other words, fluctuations are totally suppressed in the limit of extreme correlation), with the key ingredient being the amount of expected electrons between two electronic positions.

In this work we propose a way to generalize the SCE form of eq 4 by using λ-dependent distances (or “radii”) R_i^λ([ρ]; r) that will take into account the effect of fluctuations, which are not as suppressed as in the extreme SCE case. Thus, our “multiple-radii functional” (MRF) energy density reads as

6

As we shall see, we will determine the R_i^λ([ρ]; r) by using a simplified version of the same kind of integrals of the density that appear in the SCE limit, introducing the average effect of fluctuations by reducing the amount of expected charge between two electronic positions. Before coming to the details of the R_i([ρ]; r) construction, we remark that eq 6 can be also derived from the following model for the spherically averaged pair-density

7

where δ is the Dirac delta function. Given that the model of eq 7 is properly normalized, the corresponding λ-dependent XC hole satisfies the sum rule, integrating to −1 electron.

We now turn to the construction the radii R_i^λ([ρ]; r). Motivated by the structure of eq 5, and similarly to the recent nonlocal approximations for the SCE functional for three-dimensional systems,^26,27 we introduce the spherically averaged density ρ̃(r, u) around a position r,

8

and the function N_e(r, u),

9

These functions have been studied and efficiently implemented by Ernzerhof and co-workers.^27,28,51 We now want to find a physical approximation for the crucial quantities

10

which give the expected number of electrons in a sphere of radius R_i^λ(r) centered at the reference electron in r. We notice at this point that in an inhomogeneous system, even one-dimensional, it is not possible to write the exact SCE radii explicitly in terms of the function N_e(r, u) obtained by spherically averaging the density around a reference electron in r as in eq 8. An exception is an homogeneous 1D system, in which ν₂ = ν₃^SCE = 2, ν₄ = ν₅^SCE = 4, etc.

At the physical interaction strength λ = 1, we expect a situation in which this extreme correlation is reduced, with all the ν_i close to i – 1. To illustrate this fact, we consider first an N = 2 system, for which we have only one radius, R₂^λ, which from eq 6 will be equal to

11

showing that, for N = 2, R₂^λ(r) is the screening length associated with the Hartree-exchange-correlation potential when its response part is removed.⁵²⁻⁵⁴ Given that for two-electron systems highly accurate w_λ(r) have been computed,^14,50 we can use eq 11 to obtain the “exact” R₂(r). In Figure 1 we show the corresponding ν₂^λ(r) for the hydride ion at λ = 0, λ = 1, and λ → ∞. We clearly see that, in the physical system, ν₂(r) is much closer to 1 than in the SCE extreme case, which allows for much larger numbers ν₂^∞(r), becoming equal to 2 at the nucleus, as in the homogeneous 1D solution.

Figure 1.

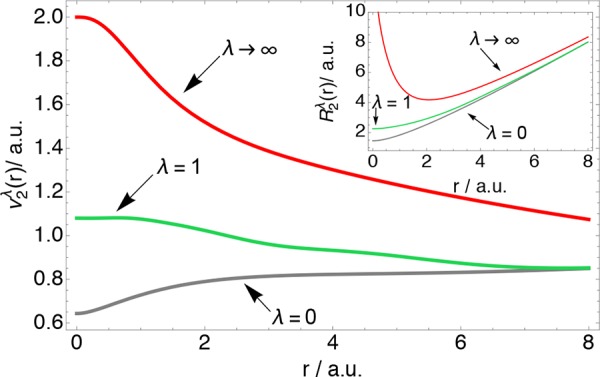
ν₂^λ(r) quantity of eq 10 and the corresponding R₂(r) radius at different coupling strengths for the hydride ion obtained from eq 11 using accurate xc energy densities w_λ(r) from refs (14 and 50)

It is clear that there are several ways to define approximations for ν_i^λ(r), using different ingredients. Here, our aim is to show that already very simple approximations can yield rather accurate results, and we focus on the physical λ = 1 case. As said, we expect that ν₂(r) ≈ 1, ν₃^λ = 1(r) ≈ 2,..., and we write

12

yielding for the radii R_i^λ = 1(r) the equations

13

with σ_i(r) being the fluctuation function, which can push away or bring closer the ith electron to the reference one with respect to the expected distance a_i(r) = N_e^–1(r, i – 1). In this first model, we consider only the case in which the ith electron is pushed further, because for this case we can use again the mathematical structure of the SCE functional as a guide. More general models will be explored in future works. From the SCE theory for spherically symmetric systems,^16,32 we know that the derivative of the radial comotion function f_i(r) at point r is inversely proportional to 4πf_i(r)²ρ(f_i(r)). We thus introduce the quantity S_i(r)

14

which, in analogy to the SCE structure, provides information on the derivative of the R_i¹(r) at σ_i = 0. When S_i(r) is small, the derivative of the R_i(r) will be very large, and we expect the electron to be pushed further, with σ_i approaching the average value 1/2 (which is exactly in between two expected positions). When S_i(r) is large, the derivative of R_i(r) is very small, and we expect it to stay close to σ_i = 0 (or even become slightly negative, a possibility not considered here). Thus, for constructing the MRF functional at the full coupling strength, hereinafter the MRF-1 functional, W₁[ρ] = ∫ρ(r)w₁^MRF(r)dr, we use a simple Gaussian ansatz

15

where b = 5 has been chosen to optimize the He atom W₁[ρ]. Equations 6, 8, 9, and 12–15 completely define w₁^MRF(r).

In Table 1 we compare W₁[ρ] obtained with the MRF-1 model with corresponding reference values (full-CI/CCSD), PBE, and SCE ones (W_∞[ρ]) for several closed-shell atomic (ionic) systems evaluated on accurate (CCSD/full-CI) densities. The PBE values have been obtained by using the scaling relation,^58,59 with ρ_γ(r) = γ³ρ(γ r),

16

From Table 1 we can see that our model, even with the very simple ansatz for σ_i(r) of eq 15, gives repulsion energy much closer to the physical ones with respect to SCE. Their quality is comparable to that of PBE, with MAE somewhat smaller (0.17 au vs 0.24 au). The purpose here is not to reach high accuracy (which requires optimization and further studies of the R_i), but to show that functional approximations based on modeling the quantity σ_i(r) is a very promising strategy, because already a primitive nonoptimized model performs very well. Even more interesting than the global W₁^MRF[ρ] values are the energy densities: in Figure 2 we compare w₁(r) with the reference w₁(r) for the neon atom (top panel) and the hydride ion (bottom panel). We also show w₁(r) obtained with the LDA functional from the PW92 parametrization,^57,60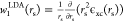. We see that w₁^MRF(r) is in good agreement with the reference w₁(r) in the case of Ne, but also in the more correlated case^14,48 of H^–, again improving dramatically with respect to SCE. 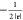From the insets of the same figure, we can see that the local error of our model is very small, vanishing for large r due to the correct asymptotic behavior, arising from the proper normalization of eq 7. The availability of DFAs energy densities in this gauge is rather limited, and beyond LDA it is restricted to few approximations^61,62 to the exchange energy density (ϵ_x(r) = w₀(r)). For instance, the gauge incompatibility⁶³ of the generalized gradient approximation (GGA) exchange energy densities and the exact ϵ_x(r), which is in the gauge of eq 3, has been a major hurdle for the development of local hybrid DFAs.^37,38

Table 1. Atomic (Ionic) Repulsion Energies W₁[ρ] Obtained by the MRF-1 Model and PBE Compared to Reference W₁[ρ], Obtained with the Gamess-US Package⁵⁵ Using Full-CI (for the First Four Systems) and CCSD Wavefunctions (Other Systems)^a.

atom/ion	reference	MRF-1	PBE	SCE
He	–1.1029	–1.1844	–1.1047	–1.4982
H–	–0.4532	–0.4681	–0.4413	–0.5689
Be	–2.8341	–2.8044	–2.8430	–4.0195
Li–	–1.9462	–2.1170	–1.9617	–2.7308
F–	–10.889	–10.741	–10.997	–16.940
Ne	–12.765	–12.823	–12.876	–20.041
Mg	–16.701	–16.365	–16.913	–26.709
Cl–	–28.89	–28.48	–29.19	–47.26
Ar	–31.35	–31.19	–31.68	–51.49
Ca	–35.60	–35.92	–36.85	–60.34
MAE	-	0.17	0.24	-

^aThe aug-cc-pCVXZ basis set of Dunning⁵⁶ has been used (X = 6 for He and H^–, X = 5 for F^– and Ne, X = T for Be and Li^– and X = Q for the other atoms). The SCE values W_∞[ρ] computed from the same densities are also reported.

Figure 2.

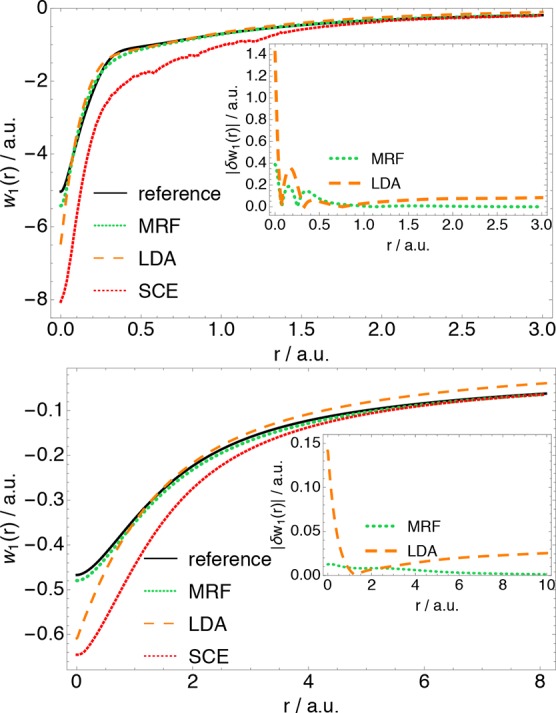
Energy densities at full coupling strength w₁(r) as a function of distance from the nucleus, r/a.u., obtained from the present model (MRF), from the local-density approximation (LDA),⁵⁷ and from the strictly correlated electrons functional (SCE), all evaluated on accurate densities, for Ne (upper panel) and H^– (lower panel). The reference w₁(r) are obtained at the full-CI and CCSD level of theory, as in refs (14 and 48), by using the aug-cc-pCVTZ and aug-cc-pV6Z basis sets⁵⁶ for Ne and H^–, respectively. Insets show the absolute error of approximate energy densities, δw₁(r) = w₁ – w₁^apx(r).

The main point of introducing the full nonlocal dependence is of course to treat static and strong correlation. In Figure 3 we show the energy density w₁^MRF(r) for the H₂ molecule at different bond lengths L_b along the internuclear axis, compared with accurate ones from ref (14). For comparison, we also show w₁(r) obtained from the interpolation model of Liu and Burke (LB)⁶⁴ applied to energy densities, with the exact w₀(r), w₀(r), and w_∞(r) as input ingredients.¹⁴ As we can see from Figure 3, in the equilibrium region the MRF-1 energy densities are still somewhat lower than the reference ones, whereas the LB is highly accurate, as it is also the case with atoms.^14,29 However, we can also see that in the stretched case (L_b = 10 au) the MRF-1 energy densities are very accurate, even more accurate than the LB interpolated ones, whose error is already small (note again that they use the exact w₀(r), w₀^′(r) and w_∞(r) as input for the interpolation). While in the stretched H₂ molecule the static correlation effects are dominant, at intermediate bond lengths, around L_b ∼ 5.0 au, there is a subtle interplay between dynamic and static correlation effects.²⁹ This region can be even more challenging for DFAs than the stretched case, given that certain DFAs that dissociate H₂ correctly fail in this scenario yielding a positive “bump” (see, e.g., refs (14 and 65−67)). We can see that the MRF-1 energy densities are very accurate at L_b = 5.0 au, hardly distinguishable from the reference ones.

Figure 3.

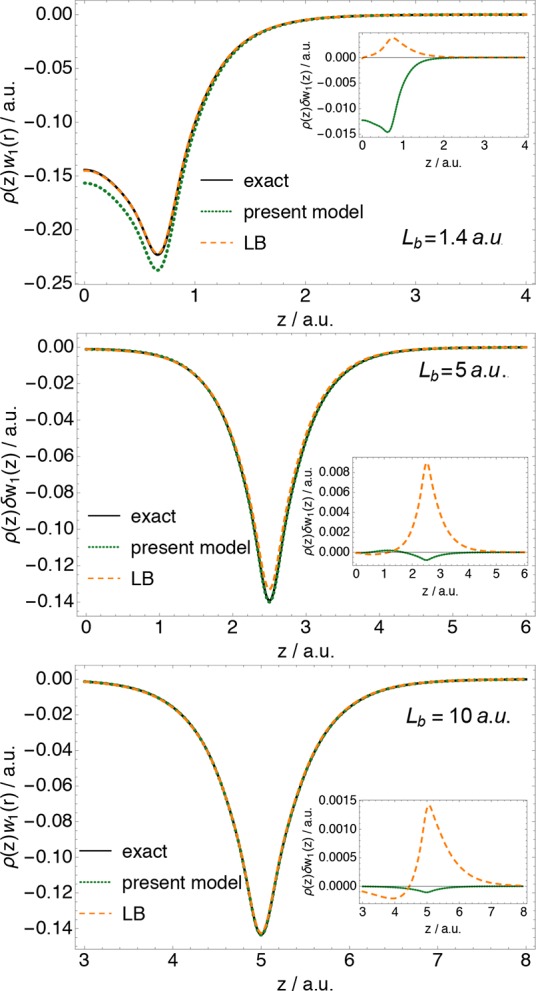
Energy densities at full coupling strength as a function of the distance from the bond midpoint z along the internuclear axis for the H₂ molecule at different bond-lengths L_b obtained with MRF-1 using accurate FCI/aug-cc-pCVTZ densities. Reference energy densities and those obtained with the LB local interpolation scheme are from ref (14).

In Figure 4 we show the dissociation curve for the H₂ molecule obtained using the MRF-1 functional evaluated on the accurate FCI/aug-cc-pCVTZ densities. We can see that around equilibrium MRF-1 underestimates the total energy, because it misses the positive kinetic correlation component T_c[ρ] and slightly underestimates the exact W₁[ρ], as already shown in Figure 3. Despite missing T_c[ρ], MRF-1 dissociates H₂ correctly, because T_c[ρ] vanishes as the H₂ dissociates into atoms. To recover the missing T_c[ρ] component, one can combine W₁^MRF[ρ] with the quantities from the weak coupling limit, namely, W₀[ρ] and W₀[ρ], to interpolate W_λ[ρ] and thus obtain E_xc[ρ]. For this purpose, we employ a very simple interpolation form, the two-legged representation,^14,29,68 which has recently been used to construct a tight lower bound to correlation energies.²⁹ This form reads as

17a

17b

As in this work, we use W₁^MRF[ρ] as an approximation to W₁[ρ], we call this approach the “2-leg MRF”, and from Figure 4 we can see that it substantially improves the MRF-1 energies. In this case very similar results are obtained if we do the interpolation on the energy densities rather than on integrated quantities. Besides dissociating correctly H₂, the dissociation of H₂ is also correctly described within the MRF-1 and 2-leg MRF approaches, because our model of eq 7 is equal to 0 for all N = 1 systems.

Figure 4.

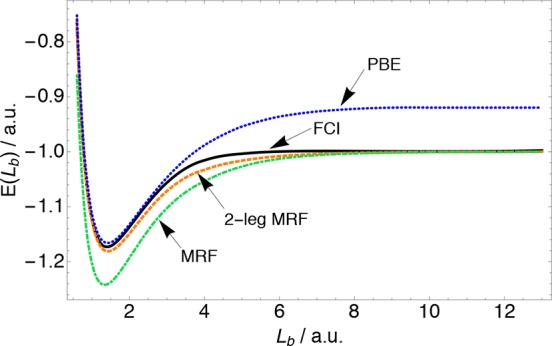
H₂ molecule dissociation curve as a function of the internuclear distance L_b/a.u. obtained with the MRF-1 and 2-leg MRF approaches presented in this work, compared to restricted PBE and FCI. All the curves have been obtained using the aug-cc-pCVTZ basis set.⁵⁶

Finally, one may wonder if the MRF would encounter problems for extended systems. As a paradigmatic example, we consider the uniform electron gas (UEG) with density 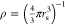, for which N_e(r, u) = N_e(u) = u³/r_s³ and N_e(i – 1) = r_s(i – 1)^1/3. Then, by using the model pair density of eq 7, we obtain w₁^MRF(r_s) = w̃(r_s)/r_s with

18

where σ_i(r_s) is given by eq 15 and, from eq 14, S_i = 3(i – 1)^2/3/r_s. This expression has a fast N → ∞ convergence and when σ_i = 0 can be evaluated in closed form. It yields reasonable values for the UEG, with a maximum relative error of 23%. The function w̃(r_s) of eq 18 has the same qualitative behavior of the exact one: it is monotonically decreasing with r_s, bounded between the two limting values w̃(0) = −0.487 and w̃(∞) = −0.7564, not so far (considering the simplicity of the model for σ_i(r_s)) from the exact ones, 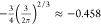and ≈ – 0.876, respectively (this latter value is currently a matter of discussion, see refs (69 and 70)). The UEG also illustrates the physics of the model: when r_s → 0 (weak correlation) σ_i≥2 → 0, while when r_s → ∞ (strong correlation), σ_i ≠ 0 for i larger and larger (long-range fluctuations become more and more important). It also suggests that for extended systems the explicit functional can be confined to a set i < i_max, and the rest can be resummed. The value i_max is determined by correlation (for example, in the UEG it is automatically determined by σ_i(r_s)).

In summary, we have proposed a strategy to build fully nonlocal DFAs inspired by the mathematical structure of the exact XC functional in the strong coupling limit, reducing the problem to the construction of the fluctation function σ_i(r) in terms of S_i(r) of eq 14. Already an extremely simple model such as the one of eq 15 is locally accurate, it is able to dissociate correctly the H₂ and H₂⁺ molecules, and gives very reasonable results for the uniform electron gas. We thus believe that the nonlocal structure of our functional, which goes beyond the Jacob’s ladder framework, opens up new perspectives for the development of XC functionals able to tackle strong correlation. Although the functional is highly nonlocal, it can be obtained at a computational cost comparable to that of the NLR and shell functionals, which have been recently implemented in a very efficient way.²⁷ Many strategies to improve the accuracy can be pursued: the inclusion of kinetic correlation through interpolation along the adiabatic connection (as in Figure 4); trying to model directly the λ-dependence of σ_i; the generalization to noninteger number of electrons²² and spin densities; improving the accuracy for the UEG, and adding the dependence on the gradient of S_i(r). The functional can also be readily applied to other dimensionalities, e.g., electrons confined in quasi-1D and quasi-2D geometries, for which the SCE approach has already proven very useful.^19,20 It can be also applied to other isotropic interactions, such as the error function used in range separation⁵ but also effective interactions for ultracold quantum gases.²¹

The authors declare no competing financial interest.