New dental implant selection criterion based on implant design

Abstract

Objective:

A comparative study between threaded and plain dental implant designs was performed to find out a new criterion for dental implant selection.

Materials and Methods:

Several dental implant designs with a systematic increase in diameter and length were positioned in a cylindrical-shaped bone section and analyzed using finite element method. Four loading types were tested on different dental implant designs; tension of 50 N, compression of 100 N, bending of 20 N, and torque of 2 Nm, to derive design curves.

Results:

Better stress distribution on both spongy and cortical bone was noted with an increase in dental implant diameter and length. With the increase in dental implant side area, a stress reduction in the surrounding bones was observed, where threaded dental implants showed better behavior over the plain ones.

Conclusions:

Increasing value of ratio between dental implant side area and its cross-sectional area reduces stresses transferred to cortical and spongy bones. The use of implants with higher ratio of side area to cross-section area, especially with weak jaw bone, is recommended.

INTRODUCTION

Dental implants can be considered the most attractive treatment option for the replacement of missing teeth. In clinical situations of a missing single tooth bounded by healthy nonrestored teeth, restoration of the dental space by a dental implant is considered ideal as it preserves the intact teeth and prevents using additional natural teeth as abutments.[1,2]

It is well known that success of dental implants is multifactorial and depends on many factors such as bone quality and quantity, surgical and prosthetic techniques, prosthetic construction, and nature of functional load applied to dental implants.[3]

A primary indicator for success of dental implants is osseointegration or direct implant–bone contact. Successful osseointegration is an indication of favorable response of surrounding bone to insertion of the dental implant. However, long-term successful osseointegration of dental implants into jaw bones is highly related to precise biomechanical placement of implants and its superstructure. Ideally, the dental implant and its prosthetic superstructure should be positioned and designed to transfer functional load in an even way to the supporting bone. On the contrary, overloading of an implant or unbalanced distribution of load may lead to failure of bone healing and hence failure of the implant treatment.[3,4] Understanding the elements that control the stresses transferred through dental implants can be crucial in minimizing the risk factors for failure of dental implant therapy. The literature indicates that factors such as implant surface topography, implant surface roughness, bone–implant interface, implant design, length and diameter of the implant, site geometrical characteristics, and properties of the supporting bone are important factors on load transfer mechanism and implant–bone response.[4,5] Proper analysis of such factors may help in improving design of implant features to reduce the amount of harmful stresses transferred to the supporting tissues and this in turn could enhance the long-term successful outcome of implant treatment.[6]

While clinical evaluation of stresses generated on a dental implant is quite difficult task and simulation of mechanical forces distribution upon human bone tissue is very complex issue, the finite element method provides a reliable way to estimate stress distribution on implant system in relation to the type of prosthetic assembly used.[7] Finite element analysis (FEA) has been considered in solving challenging geometric problems, for which it is very hard to achieve an analytical explanation. This method was considered to investigate the mechanical aspects of biomaterials and human tissues that cannot be measured in vivo. During the last 30 years, the FEA has been widely used to estimate the effect of stress on dental implants and adjacent bone.[8,9]

Research findings indicated that the placement of implants in bone with adequately thick cortical bone and high density will reduce both, implant micro-movement and stress concentration that consequently increase implant stabilization and tissue integration.[10] It was also found that in situations of normal bone conditions, implant length and diameter were found to be insignificant factors for its success. On the contrary, in cases of poor bone quality, increasing implant length and diameter is highly recommended to reduce the stresses generated on jaw bone during normal occlusion.[10,11] In this research, plain and threaded implants covering wide range of diameters and lengths were examined by finite element method to find out simple and accurate criterion for selecting implants that reduce stresses transferred to jaw bones.

MATERIALS AND METHODS

Set of fifty finite element models covering a wide range of implant diameters and lengths was subjected to different types of masticatory forces. The geometric models generation in this study was based on the development of similar ones for implants fixed to an edentulous mandible.[12,13,14,15] That the bone geometry was simplified and simulated as two coaxial cylinders, the inner one represents the spongy bone with 14 mm diameter and 22 mm height, that filling the internal cylindrical space of the other cylinder (shell of 1 mm thickness) that represents cortical bone (outer diameter of 16 mm and its height of 24 mm). Two sets each of 25 different implant designs used in this study covering the diameter range from 3.5 to 6.0 mm and length range from 9.0 to 13.0 mm. The 25 plain implants were simply modeled by cylinders with partially reduced diameter by 1.0 mm; in addition, thread thickness was cut from reduced diameter part to produce the 25 threaded implants models. Each implant was subjected to four different loading conditions; tension at 50 N, compression at 100 N, bending at 20 N, and torque at 2 Nm. Meanwhile, loading was applied on the top middle node of each implant assembly in the studied models [Figure 1].

Figure 1.

One finite element model and sample of its results

Torque was generated using two forces equal in magnitude and opposite in direction, applied on the diameter of implant head. The base of finite element models set was fixed which defined the boundary condition.[12,13,14,16] Table 1 lists the material properties used in the analysis where all materials were assumed to be isotropic, homogeneous, and linearly elastic.

Table 1.

Properties of the used materials

Brick element “SOLID45” has three degrees of freedom as translations in the global directions[16] and was used for meshing all models on the finite element package ANSYS version 9 (ANSYS Inc., Canonsburg, PA, USA). The solid modeling and finite element linear static analyses were performed on a personal computer, Intel Pentium IV, processor 2.8 GHz, 1.0 GB RAM.

RESULTS

Four runs on each of the fifty models were executed simulating the four loading conditions prescribed for this study. Because of the great number of models and load cases utilized, graphical comparisons were considered on cortical bone. Design equations and curves were obtained using least square method.

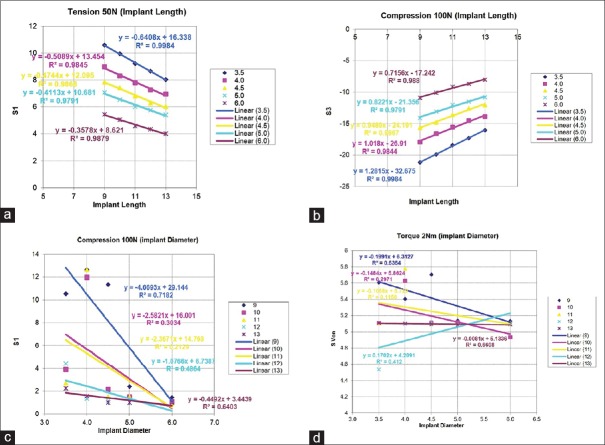
Such scheme was done twice, one time for the plain implant design while the other one for the threaded implant one. Effects of increasing implant length and diameter on implant side area to cross-sectional area are illustrated [Figure 2a and b]. Where increasing implant length increases the ratio of implant side area to cross-sectional area (cross-section area is fixed) while increasing implant diameter has the opposite effect (linearly increase side area and quadratic increase cross-section area). Figure 3 illustrates samples from cortical bone maximum values of principal stresses under different load cases. Trends of fitting lines indicate combined relation between implant length and diameter with bone stresses. That may prove the possibility of using the new criterion (ratio of implant side area to cross-sectional area) for plain or threaded types of implants.

Figure 2.

(a) Effect of increasing implant length on the ratio of side area to cross-sectional area, (b) Effect of increasing implant diameter on the ratio of side area to cross-sectional area

Figure 3.

Threaded implant behaviors improve with increasing implant length on cortical bone: (a) Maximum tensile stress under 50N tension loading, (b) Maximum compressive stress under 100 N compression loading. Plain implant shows minor improvement with increasing implant diameter on cortical bone: (c) Maximum tensile stress under 100 N compression loading, (d) Maximum Von Mesis stress under 2 Nm torque loading

DISCUSSION

Stress distribution around dental implants or around the peri-implant bone tissue is one of the controversial issues in current dental implants literature.[14] Clinicians and researchers appreciate the importance of even and well-designed stress distribution on the long-term clinical success of dental implants. The material of construction of the dental implant may play an important role in this context. The main problems related to this issue are related to the material composition and fatigue of implants during masticatory cycles.[7]

Back to previous studies;[12,13,14] it was found that increasing implant diameter has a minor effect on bone stress distribution and has a slight effect on bone stresses values, especially with wide implants, i.e., it goes toward stabilization. On the other hand, increasing the implant length dramatically affect bone stresses values. For plain implants, the side area is linearly related to both implant diameter and length. Thus, the wider range of implant length increases its effect by increasing side area and its ratio to the constant cross-section area. This finding matches previous conclusion of having less effect of increasing implant length as the implant diameter is fairly large.[12]

Meanwhile, an increase in the threaded implant length will have larger effect on side area and its ratio to cross-section area (do not change with implant length) due to the serrations on implant side; with large implant diameters, the effect of increased implant length will be reduced.[14]

Demonstrating stress distribution and deformations of different plain/threaded dental implant designs on surrounding bone and correlating these values to implant length and diameter were considered as most effective parameters on stresses distribution in many investigations.[12,13,14,16] The purpose of this investigation was to provide an analysis among different geometric configurations of implants and to analyze their behavior in terms of biomechanics. Actual situations observed in clinical studies can be simulated in study models by simply considering the bone to be homogeneous, of linear elasticity, muscle action being symmetric and the load being static. Under such circumstances, the model results can be very close to actual situations observed in clinical studies.[6,17,18]

As presented in Figure 2a, it can be proven mathematically for the used implant type and design that whatever the implant diameter; any increase in the implant length between 9 and 13 mm will result in gradual increase of the ratio of side area to cross-section area up to 66.6% and 76.2% for plain implant and threaded one, respectively. On the other hand, comparing this ratio for plain with threaded implants indicated that whatever the implant diameter; increasing implant length from 9 mm to 13 mm reduced the superiority of threaded implant over the plain one by 3%. Similar finding can be obtained from Figure 2b but in the opposite direction.

Despite the limitations of this study, it was proven that implant length (side area) and diameter, placement site, and crestal bone geometry have the greatest effect on the load transmission mechanisms. Even with changing implant diameter or length, the pattern of stress distribution did not change between different utilized implants. On the other hand, stress values may greatly differ if the implant diameter and/or length were changed.[12]

In this study, maximum concentration of stresses was found in the area of contact between the bone and the implant. Furthermore, it can be noted that large distribution of mechanical stresses occurs where the bone is in contact with the implant. Previous studies revealed that when the maximum stress concentration occurs in the cortical bone, it is confined to the area adjacent to the implant; while when the maximum stress concentration occurs in the cancellous bone, it affects the apical area of the implant.[7]

Stress peaks at the cortical bone depend on implant diameter while implant length is the main determinant of the stress values and its distribution at bone–implant interface. Thus, to control bone overloading and to improve the implant stress-based biomechanical performance, implant diameter proved to be a design parameter which is more effective than implant length.[6,19]

Nevertheless, wide diameter implants (5–6 mm) behavior was not greatly affected by increasing its length. On the other hand, small diameter implants’ behaviors were enhanced to great extent by increasing implant length (increasing side area). Therefore, implant length is the dominant parameter in case of using a small diameter implant. Figures 3a and b also prove this new selection criterion, and minor effect of increasing implant diameter on the bone stresses.

Himmlova et al.[20] and Tawil et al.[21] indicated that stress distribution is mainly dependent on implant diameter than its length. Von Mises equivalent stresses decrease around the implant neck in response to increase in implant diameter more than increase in the implant length. This finding was in contrast with Pierrisnard et al.[22] Those authors concluded that stress within bone was virtually constant independent of surrounding bone support and implant length.

A limitation of this study is that the structures constructed as finite element model (s) were assumed to be homogeneous, isotropic, and linear elastic while the cortical bone of the mandible is transversely isotropic and nonhomogeneous in living tissue. In addition, there is a difference in cortical bone thickness, bone density, and buccolingual width in the mandible. Despite its limitations, using the finite element method for analyzing the biomechanical behavior of bony sections such as human mandible and maxilla is preferred, especially when focusing on the occurrence and osteosynthesis of bone stresses.[23]

CONCLUSIONS

Within limitation of this study, it can be concluded that:

• The ratio of implant side area to cross-sectional area is new real criterion and can be considered as the most effective for dental implant selection. This conclusion matches a previously obtained result by Abdel Azim et al.[18] when recommended to use twin small diameter implants over large diameter one

• Threaded implant showed better behavior over the plain ones as increasing the value of the ratio between side area and cross-section area reduces the stresses transferred to the cortical and spongy bones

• It is recommended to use the implant with higher ratio of side area to cross-section area to reduce stresses exerted on jaw bone.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.