Measuring shared variants in cohorts of discordant siblings with applications to autism

Significance

We developed a statistical method that detects if shared ancestral genetic variants contribute to a disorder by analyzing common variant data from cohorts that include discordant sibling pairs. We applied this method to two published datasets of autism families and found strong evidence that shared ancestral genetic variants contribute to autism spectrum disorders.

Abstract

We develop a method of analysis [affected to discordant sibling pairs (A2DS)] that tests if shared variants contribute to a disorder. Using a standard measure of genetic relation, test individuals are compared with a cohort of discordant sibling pairs (CDS) to derive a comparative similarity score. We ask if a test individual is more similar to an unrelated affected than to the unrelated unaffected sibling from the CDS and then, sum over such individuals and pairs. Statistical significance is judged by randomly permuting the affected status in the CDS. In the analysis of published genotype data from the Simons Simplex Collection (SSC) and the Autism Genetic Resource Exchange (AGRE) cohorts of children with autism spectrum disorder (ASD), we find strong statistical significance that the affected are more similar to the affected than to the unaffected of the CDS (P value ∼ 0.00001). Fathers in multiplex families have marginally greater similarity (P value = 0.02) to unrelated affected individuals. These results do not depend on ethnic matching or gender.

Autism spectrum disorders (ASDs), a collection of developmental delay syndromes characterized by deficient social skills and communication, receive a strong contribution from genetics: identical twins have much higher concordance than dizygotic twins or siblings (1–3), and children with ASD have a greater incidence of de novo likely-gene-disrupting mutations than unaffected siblings (4–6). We estimate based on exome sequencing that germ-line mutation contributes to at least 30% of autism in families with a single affected child (simplex ASD) (7).

Nonidentical siblings have a significantly higher concordance than expected by chance, and this observation argues for a role for heredity (8). In fact, a role for transmission of strong-acting variants from the mother has recently been published (9, 10). The question that we address with our study is whether there is a role for contribution from variants of small effect. Statistically unexpected sharing of certain common variants among the affected would serve as evidence. Without a counterbalancing strong positive selection, only variants of small negative effect would be sufficiently persistent in the population to leave a trace of the common genetic background in which they initially arose.

There have been persistent reports of such evidence from case–control studies (11, 12). These approaches universally use a liability threshold model developed by Yang et al. (13, 14) applied initially to estimate the genetic contribution to quantitative traits, such as height, on a simple random sample from the population. The proper use of this method, as specified in a theoretical analysis, was that the trait should be under neutral selection, that the cases and controls should be ethnically matched but not be close relatives, and that the underlying liability should be Gaussian. A method for computing the significance of the contribution was also provided dependent on the above assumptions. Generally speaking, these assumptions have been ignored in the application to ASD: it is not a neutral trait and therefore, will destroy a Gaussian distribution; hence, its quantitation is problematic. Moreover, homogeneity between the cases and controls is difficult to achieve except with inbred populations, which bedevil almost all genetic inference from case–control studies when the overall signal depends on the aggregation of many small effects. There is no effective statistical method that can differentiate between the subtle ethnic imbalance in the prevalence of a disease caused by nongenetic factors on one hand and contributions from many genetic variants of small effects on the other.

To address these issues but especially, the problem of subtle ethnicity imbalance in case–control studies, we use a nonparametric method based on cohorts of discordant sibling pairs (CDS). We exploited the Simons Simplex Collection (SSC) of more than 2,000 ASD simplex families with discordant siblings and introduced a test statistic affected to discordant sibling pairs (A2DS). Our method scores similarity based on shared common variant patterns and makes no assumption about an underlying genetic model. It has a minimal dependence on ethnic background, and the statistical significance is determined by permuting the affected status of the discordant sibling pairs and establishing a distribution of the score. Applying a standard measure of genetic relation (14) between each individual of a test population and each component of the discordant siblings, we determine if, in aggregate, the test individuals are closer to the affected than to the unaffected components of the CDS. We show that test subjects with ASD are significantly closer to the affected than the unaffected siblings and that, in contrast, the unaffected siblings or the parents in simplex families show no greater similarity to either component of the CDS. We obtain statistical signal using a variety of subsets of affected test subjects and conclude that gender and ethnicity are not confounding variables.

To confirm our findings, we turned to samples from the Autism Genetic Resource Exchange (AGRE), a collection of multiplex families. Although the genotype data were collected independently and to a lower density, we see a statistically strong signal that the affected individuals of the AGRE have closer genetic relation to the affected of the SSC than their unaffected SSC siblings. Interestingly, the fathers in the AGRE, but not the mothers, also show stronger relatedness to the affected than the unaffected of the SSC. The latter observation requires additional investigation, because it has only marginal statistical significance.

Results

Statistical Design.

We developed a statistic designed to ask if an individual affected person, $g_t$, is more closely related to an unrelated affected person, $g_s^a$, than to the unrelated affected person’s discordant sibling, $g_s^u$. Hence, we use the term A2DS. We reasoned that, by using unaffected siblings, we control as well as is theoretically possible for ethnic biases and allow for the later determination of significance using a permutation test on the labels “affected” and “unaffected.”

We used a standard measure of genetic relation (13, 14), $gr\left(g_1,g_2\right)$, between two individuals, $g_1$ and $g_2$, based on shared variants normalized for variant frequency as expressed in Eq. 1:

$$gr\left(g_1,g_2\right)=\frac{1}{N_p}{\displaystyle \sum _{all\hspace{0.17em}SNPs}}\frac{(g_{1k}-2f_k)(g_{2k}-2f_k)}{F_k},$$ [1]

where $N_p$ is the total number of SNPs, $f_k$ is allele frequency of the kth SNP, $g_{1k}$ and $g_{2k}$ are the observed numbers of alleles of two individuals at the kth SNP, and F_k $=2f_k(1-f_k)$, an SNP frequency normalization factor. In this study, the allele frequencies are estimated from the parents of the SSC.

The difference, $gr\left(g_t,g_s^a\right)-gr\left(g_t,g_s^u\right)$, is thus a measure of how much closer $g_t$ is to $g_s^a$ than to $g_s^u$. Aggregating over all pairs of individuals in a test set, T, and all sibling pairs in a cohort of discordant siblings, CDS, and taking the average, we arrive at the $A2DS\left(T,CDS\right)$ as expressed in Eq. 2:

$$A2DS\left(T,CDS\right)=\frac{1}{N_{CDS}{N}_T-n_a}{\displaystyle \sum _{t\in T,s\in CDS,s\ne t}}gr\left(g_t,g_s^a\right)-gr\left(g_t,g_s^u\right),$$ [2]

where N_T and N_CDS are the number of test individuals and the number of the discordant sibling pairs, respectively, and n_a is the size of overlap $T{{\displaystyle \cap }}^{}CDS$. Because T and CDS can overlap, we exclude comparisons of a test individual with his/her own family. Eq. 2 formulates A2DS as a statistic over the population, but it can be rewritten as a statistic over the variants aggregated over the variants. This reformulation is found in SI Methods, where we relate A2DS to more familiar test statistics. In particular, we show that A2DS essentially measures transmission distortion. Global transmission distortion tests are plagued by the problem that nearby allele states are dependent because of linkage disequilibrium. However, the statistical significance of the test statistic A2DS is determined by permuting the affected status within the sibling pairs to properly account for these dependencies and thereby, derive a distribution on the statistic, from which significance can be computed.

Genotype Data.

The collections for which we have genotyping data are the SSC (10,220 individuals from 2,591 families) (15) and the AGRE (6,259 individuals from 1,374 families) (16) genotyped on multiple Illumina platforms and in the public domain, with additional description in SI Methods. The first is composed of 2,113 quads families (parents, an affected, and at least one unaffected offspring) and 474 trios (parents and an affected offspring). It is important to note that the genotyping of members of the same family was always by the same array platform at the same time. Therefore, there will be no batch effect affecting our test statistics. We built our cohort of discordant siblings from the quads (CDS) and used it as described above with a minor modification, namely when families had more than one unaffected sibling. In these 290 cases, we used all unaffected siblings by averaging their genotypes. In some tests, we formed subsets of the CDS based on ethnicity and gender. The test sets were derived from the SSC and the AGRE. For the test sets of the AGRE, we took only one affected child per family. Details of data merging and filtering are found in SI Methods.

Significant Sharing Among Affected of the SSC and the AGRE.

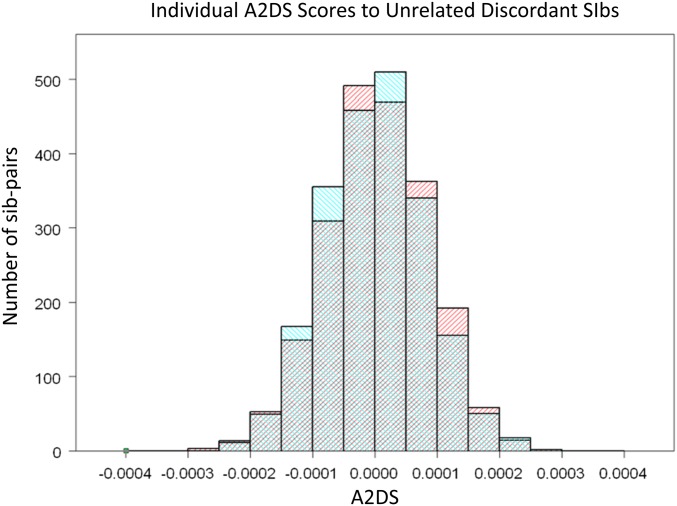
A2DS from a test set T to a CDS is the average score of individuals of the test set to the CDS. We drew our first test sets from the CDS itself using affected and unaffected each as test sets. The distributions of scores for individual affected and unaffected are presented as histograms in Fig. 1. The distributions of the individual scores of the two sets are reasonably similar in shape and symmetric, but the distribution for the affected is slightly shifted to the right. The difference in mean using the affected individuals as test (5.02 × 10⁻⁶) and the mean using the unaffected as test (−5.53 × 10⁻⁷) is about 5% of the SD of the individual scores.

Fig. 1.

A2DS scores of individual affected (red) vs. unaffected (blue) as the test sets. It can be seen that the distribution of the affected shifted toward the right compared with the distribution of the unaffected.

To determine if this shift was statistically significant, we formed a distribution of means of tests and CDS sets created by randomly permuting the labels affected and unaffected. We recalculated the mean for each of 100,000 permutations. We then asked if the observed mean of a test set was significantly in the tail of that distribution. When the test set is the affected, the one-sided P value of its mean is about 0.003 (Table 1, row 2). By contrast, when the unaffected siblings in quads are used as the test set, we calculate a one-sided P value of 0.38 (Table 1, row 4). Thus, the unaffected are slightly more closely related to themselves than to the affected but not significantly so. Therefore, whereas the genotypes of the affected show a significant degree of ascertainment-based clustering, their unaffected siblings do not. By the same token, neither the test set of SSC mothers nor that of the SSC fathers show any statistically greater similarity to either component of the CDS (Table 1, rows 5 and 6).

Table 1.

Main results of statistical significance tests based on A2DS

Test index	Test set (T)	DS	A2DS (×106)	Estimated P value
1	SSC affected n= 2,591	SSC DS n = 2,113	5.99	1 × 10−5*
2	SSC affected in quads n = 2,113	SSC DS n = 2,113	5.02	0.00306*
3	SSC affected in trios n = 4,78	SSC DS n = 2,113	10.29	0.01104*
4	SSC unaffected in quads n = 2,113	SSC DS n = 2,113	−0.55	0.3753
5	SSC fathers n = 2,591	SSC DS n = 2,113	0.24	0.4405
6	SSC mothers n = 2,591	SSC DS n = 2,133	−0.20	0.5475
7	SSC white affected n = 1,816	SSC white DS n = 1,489	5.21	0.0078
8	SSC affected n = 2,591	SSC male–male DS n = 924	6.53	0.0003
9	SSC male affected n = 2,246	SSC male–male DS n = 924	5.27	0.0078
10	AGRE affected n = 1,374 (one affected selected from each family based on IQ)	SSC DS n = 2,113	11.40	0.01478*
11	AGRE unaffected n = 615 (one unaffected sibling selected from each family)	SSC DS n = 2,113	−0.53	0.5695
12	AGRE mothers n = 1,232	SSC DS n = 2,113	2.28	0.2241
13	AGRE fathers n = 1,142	SSC DS n = 2,113	6.34	0.0206
14	AGRE + SSC affected n = 2,591 + 1,374	SSC DS n = 2,113	7.87	4 × 10−5*

Columns 2 and 3 list the test sets and corresponding discordant sibships (DS). Column 4 shows the A2DS value ×10⁶, and column 5 shows the estimated P values from 10,000 random permutations, except where indicated.

^*Estimated P values from 100,000 random permutations.

In the first of independent confirmations, the affected individuals from the SSC trio families also show greater similarity to the affected than the unaffected of the SSC quads (Table 1, row 3: P value of 0.01). Combining affected individuals from trios with those from quads as the test set, we obtain a P value of about 0.00001 (row 1 of Table 1).

The CDS can be restricted to address concerns about gender and ethnicity. Because of gender bias in ASD, more than one-half of the unaffected siblings are female, whereas the vast majority of the test subjects are male. Concerned that the results might somehow reflect subtle gender bias in the genotyping process, we restricted the CDS to the male–male discordant pairs. The results are found in Table 1 for all male affected (Table 1, row 7: P value = 0.008) and all affected (Table 1, row 8: P value = 0.003) test subjects. Similarly, strong evidence remains (P value = 0.008) if we restrict the CDS to children of self-described ethnically “white” parents, choose the test population by the same criterion, and recompute variant frequencies (Table 1, row 7).

We next sought confirmation from the AGRE collection of multiplex families. These families were genotyped at a different time and place (16) than the SSC, on Illumina chips, and at a lower density of SNPs in general. Using the SNPs that are genotyped in both SSC and AGRE, we observe again significantly greater genetic relation between the affected of the AGRE to the affected than to the unaffected in SSC quads (P value = 0.015 in Table 1, row 10), and no particularly difference from the AGRE unaffected siblings (P value = 0.57 in Table 1, row 11) or the mothers (P value = 0.22 in Table 1, row 12). Interestingly, we do observe greater relatedness of the fathers of the AGRE to the affected individuals of the SSC than to the unaffected siblings (P value = 0.02 in Table 1, row 13).

Combining all affected individuals from the AGRE and the SSC as the test set against the CDS of the discordant SSC sibling pairs, we get a strong genetic relatedness between the affected population with a P value less than 0.0001 (Table 1, row 14).

Interpreting the Strength of the A2DS Score.

Beyond statistical evidence for an unexpected excess of shared ancestral variants, the A2DS score itself measures the strength of that sharing. Because of linkage disequilibrium, a shared ancestral variant causes an increase in the A2DS score measured from multiple SNP agreements on Illumina arrays. The score from the AGRE affected individuals (1.14 × 10⁻⁵) is twice the score from affected individuals of SSC quads (5.02 × 10⁻⁶), in keeping with an expectation that the affected of the multiplex families will have a higher load of such variants than the affected of the simplex families.

The A2DS score can be seen to be the mean score over every SNP locus over the population (Eq. S3). However, interpreting this in terms of “extra” sharing requires estimates of linkage disequilibrium. Taking an approximate approach, we assume that the average span of linkage disequilibrium for a shared variant is about 45 kb or about 9 SNP loci on a 600,000 SNP Illumina array. Then, a single extra sharing of one ancestral variant forces agreement at about 9 of 600,000 SNPs, increasing the A2DS score by ∼15 × 10⁻⁶, three times what we observe for the A2DS score on the quads of the SSC. If the score is linear with the number of shared causal variants, as it must be, that number averages to an extra 0.33 sharing per pair of unrelated affected children than is observed per an unrelated affected/unaffected pair.

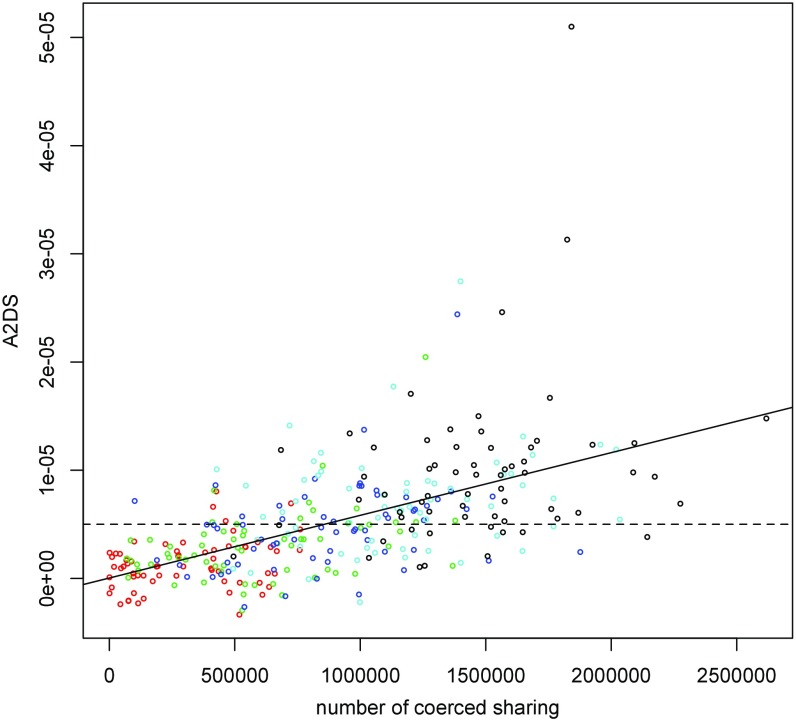
Another approach, using perturbation–simulation, yields a similar answer. We “coerce” sharing between randomized sibling pairs and compute A2DS, obtaining a relationship between the number of coerced sharing and the score. We first randomize the affected status labels of the siblings in the quad families of the SSC, so that the A2DS score is distributed about zero. Then, we coerce sharing between families, one locus at a time. A coerced sharing is made by swapping the chromosome of a locus between the siblings of a family to bring the affected from families into greater concordance with each other. A scatterplot of the number of coerced sharing with the A2DS score is shown in Fig. S1. As predicted, we observe a roughly linear relation that allows us to conclude that the observed A2DS score of the SSC quads (5.02 × 10⁻⁶) requires on the order of 8 × 10⁵ extra sharing in ∼2.23 million pairs of families (∼2,113²/2). This number averages to ∼0.36 more sharing between unrelated affected individuals than between unrelated affected and unaffected individuals. A detailed description of the procedure that we used can be found in SI Methods.

Fig. S1.

A2DS of perturbed SSC quad genotypes. Each dot represents a perturbed SSC quad with coerced sharing at one (red), two (green), three (blue), four (light blue), or five (black) loci. The vertical axis is the A2DS score of the perturbation. The dashed horizontal line is the observed A2DS score of the SSC quads. The other solid straight line is the least square fit to the dots. The projection of the intersect of these two lines onto the x axis occurs at a value of 8 × 10⁵.

SI Methods

Relationship Between A2DS and Association Test.

By changing the order of summation of Eq. 2, we can write

$$A2DS=\frac{1}{N_{CDS}{N}_T-n_a}\frac{1}{N_p}{\displaystyle \sum _{all\hspace{0.17em}SNPs}}{A}_k,$$ [S1]

where like before, $N_p$ is the total number of SNPs, and $A_k$ is indexed over all SNPs by k. $A_k$ can be written as follows:

$$A_k={\displaystyle \sum _{t\in T,s\in CDS,s\ne t}}\frac{(g_{tk}-2f_k)(g_{sk}^a-2f_k)}{F_k}-\frac{(g_{tk}-2f_k)(g_{sk}^u-2f_k)}{F_k}={\displaystyle \sum _{t\in T,s\in CDS,s\ne t}}\frac{(g_{tk}-2f_k)(g_{sk}^a-g_{sk}^u)}{F_k}={\displaystyle \sum _{t\in T,s\in CDS}}\frac{(g_{tk}-2f_k)(g_{sk}^a-g_{sk}^u)}{F_k}-{\displaystyle \sum _{s=t\in T{{\displaystyle \cap }}^{}CDS}}\frac{(g_{tk}-2f_k)(g_{sk}^a-g_{sk}^u)}{F_k}=\frac{1}{F_k}{\displaystyle \sum _{t\in T}}(g_{tk}-2f_k){\displaystyle \sum _{s\in CDS}}(g_{sk}^a-g_{sk}^u)-{\displaystyle \sum _{s=t\in T{{\displaystyle \cap }}^{}CDS}}\frac{(g_{tk}-2f_k)(g_{sk}^a-g_{sk}^u)}{F_k}.$$ [S2]

We consider first the case where the test set T and the set of discordant siblings DS have zero intersect (e.g., rows 3 and 10–13 in Table 1). Then, we have $A_k=1/F_k{\displaystyle {\sum }_{t\in T}\left(g_{tk}-2f_k\right)}{\displaystyle {\sum }_{s\in CDS}(g_{sk}^a-g_{sk}^u)}$. The first term of the multiplication is the difference between the allele frequency of the test samples and the frequency in the general population, and the second term of the multiplication is the difference of the allele frequencies between the affected siblings and the unaffected siblings. The multiplication is positive if these two terms are of the same direction and negative if they are of the opposite directions. This statistic can be viewed as using the test set to validate the discoveries made by a discordant sibling study. In our case, the control set frequencies derive from the parents, although the control frequencies can be obtained in other ways.

Next, we consider when our data are from quads, two parents and two discordant siblings, as for the SSC in rows 2 and 4 of Table 1. In this case, $f_k$ is the allele frequency of the parents. Under Hardy–Weinberg Equilibrium, $F_k$ represents the expected proportion of parents with heterozygous genotypes. Then, the term ${\displaystyle {\sum }_{t\in T}\left(g_{tk}-2f_k\right)}$ represents the transmission distortion observed in the test to be normalized by $F_k$. This term thus has essentially the same information found in a Transmission Disequilibrium Test on the parent–child trios. Similarly, the term ${\displaystyle {\sum }_{s\in CDS}(g_{sk}^a-g_{sk}^u)}$ is the transmission distortion observed between the affected and unaffected siblings. Multiplying these two terms is a reasonable test statistic for transmission test on quads of parents–discordant siblings.

In the cases where the test sets are affected children (i.e.,$g_{tk}=g_{sk}^a$), the remaining term of $A_K$, which is to be subtracted, can be broken into two parts:

$${\displaystyle \sum _{s\in T{{\displaystyle \cap }}^{}CDS}}\frac{(g_{sk}^a-2f_k)(g_{sk}^a-g_{sk}^u)}{F_k}={\displaystyle \sum _{s\in CDS}}\hspace{0.17em}\frac{{(g_{sk}^a-2f_k)}^2}{F_k}-{\displaystyle \sum _{s\in CDS}}\hspace{0.17em}\frac{(g_{sk}^a-2f_k)(g_{sk}^u-2f_k)}{F_k}.$$ [S3]

The second part of the right-hand side of the above equation is invariant under permutation of affected status within a family. The first part varies, and it measures the variation among the affected from the expected allele counts. Note that its value increases if the genotypes of the affected do not follow the expected distribution. However, unlike the first term of Eq. S2, it does not measure the overall shift in allele frequency. The value increases if some families tend to have more allele 1 and other families tend to have more allele 2, but the overall allele frequency is the same as expected. Therefore, this part does not measure the association between the disease and a particular allele. Rather, it is a statistic for detecting genetic linkage to the disease at this locus. Hence, by its subtraction, the statistic $A_k$ can be viewed as a statistic for genetic association that excludes signal coming from genetic linkage.

Genotyping Data and Preprocessing.

SSC.

We obtained genotyping data of SSC samples that were genotyped on three different Illumina platforms as shown in Table S1.

Table S1.

The number and types of families genotyped on each of three platforms

Platform	Families	Individuals	SNPs
Human1M v1	333	1,354	1,072,814
Human1M v3	1,189	4,626	1,199,033
Omni 2.5	1,069	4,240	2,440,283

For this study, we selected SNPs that are genotyped for all SSC samples for this study. We further selected autosomal SNPs with minor allele frequency (MAF) > 0.01 and excluded SNPs that violate the Hardy–Weinberg Equilibrium (tested on all parents self-reported as white with ${\mathrm{\chi }}^2$ > 9). A total of 554,426 SNPs were used for computing A2DS. For the analysis in which only white families (defined as both parents self-reported as white) are used, we further exclude SNPs with MAF that is less than 0.01 among the white parents and use the remaining 540,025 SNPs for our test.

AGRE.

From a previous study (16), we obtained imputed genotypes at 5,814,564 variants of 1,493 AGRE families (6,259 individuals). We excluded from the AGRE individuals with known chromosomal abnormalities, such as Fragile X, trisomy, 15q duplication, etc. From each of the remaining 1,374 families, we selected one child diagnosed with autism as our “test set.” For a family of multiple affected siblings, the one with the lowest IQ score was selected if IQ was available; otherwise, we selected an affected randomly. Parents and unaffected siblings whose genotypes are available (1,142 fathers, 1,232 mothers, and 615 unaffected siblings) were also used as test sets in separate analyses.

From the available SNPs, we extracted 401,614 SNPs that are also genotyped for all SSC samples. After filtering for Hardy–Weinberg violation and excluding those on the X and Y chromosomes, a total of 396,512 SNPs are used for computing A2DS.

A2DS for Sibships with More than Two Unaffected.

Some SSC families have two or more unaffected siblings. To accommodate families with multiple affected and unaffected individuals, we extend the A2DS as

$$A2DS={\displaystyle \sum _{t\in T,\hspace{0.17em}s\in DS,t\ne s}}Gr\left(A_t,A_s\right)-Gr\left(A_t,U_s\right),$$

where $\mathit{Gr}({\mathit{A}}_{\mathit{t}},{\mathit{A}}_{\mathit{s}})$ denotes the genetic relation between a group of affected siblings in the test set and the affected in a discordant sibship, and $\mathit{Gr}({\mathit{A}}_{\mathit{t}},\hspace{0.17em}{\mathit{U}}_{\mathit{s}})$ represents the genetic relationship to the unaffected in a discordant sibship. For sibships with exactly one affected and one unaffected, Gr(.,.) is the genetic relationship between two individuals $gr\left(g_1,g_2\right)$ as defined in Eq. 2. For general sibships, we compute $\mathit{Gr}({\mathit{A}}_1,{\mathit{A}}_2)$ as the average genetic relationship between the individuals of A₁ and he individuals of A₂:

$$Gr\left(A_1,A_2\right)=\frac{{\displaystyle \sum _{g_1\in A_1,g_2\in A_2}gr\left(g_1,g_2\right)}}{n_1{n}_2},$$

where n₁ and n₂ are numbers of individuals in A₁ and A₂., respectively.

Perturbation Experiments.

Perturbation experiments were devised to “explore” the magnitude of A2DS score. Understanding the score one allele at a time is complicated by linkage disequilibrium. We, therefore, coerce sharing, whole chromosomes at a time. We start by a random permutation of disease status among SSC discordant sibling pairs followed by randomly selecting a “risk” allele at one to five loci. The loci are chosen to fall on different chromosomes, so that coercion at one locus does not interfere with coercion at another. For the first locus and each sibling pair whose genotypes differ at the locus, we swap the genotypes of the entire chromosomes, so that the affected receives an excess of risk allele. (A more precise procedure for doing this would require phasing of the chromosomes in the affected and swapping only one of the relevant parental chromosomes.) Those sibling pairs with the same genotype at the locus are left unchanged. Thus, the affected always have more risk alleles than the unaffected. The total number of coerced sharing is calculated as the number of pairs of unrelated affected individuals who now have more agreement at the locus than they had before the perturbations. This number is simply n₁n₂, where n₁ is the number of sibling pairs that are swapped, and n₂ is the number of sibling pairs in whom the affected already has more risk alleles than the unaffected. We then randomly select a second locus on a different chromosome and similarly swap the genotypes of the chromosome to coerce the agreement as before. We keeping doing this up to five SNPs on five distinct chromosomes and compute A2DS each time. This entire process is repeated 60 times, and the results are shown in Fig. S1.

Discussion

ASD is clearly a disorder with a strong genetic contribution. A portion of this contribution is attributable to de novo or germ-line mutation, but germ-line mutation cannot explain high sibling concordance. A genetic explanation of the latter must be sought in transmission. Some of the transmitted variants could come from recent highly penetrant mutation, and there is some evidence for such a mechanism (9, 10). However, that mechanism seems insufficient to explain the entirety of the transmitted component.

As of now, there is sparse evidence for even a single ancestral variant found by genome-wide association studies (17). Case–control studies reported in the literature claim evidence for a global genomic “signal” as a shared common variant bias in the ASD population (11, 12). These reports would indicate the existence of shared ancestral causal variants in linkage disequilibrium with common variants. These undiscovered variants would have persisted sufficiently long in the human population to become widely distributed but by their sheer number, have escaped individual identification.

We have questioned the validity of these reports, in part because in studies using unrelated control populations, signal caused by subtle differences in the genetic background often is present and cannot be rigorously excluded. We, therefore, sought evidence for shared ancestral causal variants using discordant siblings, in which ethnic bias is rigorously corrected. For this purpose, we developed A2DS, in which we use a standard measure of genetic relation, and ask whether a given test population is more closely related to the affected than to the unaffected of a pair of discordant siblings in CDS. Statistical strength is then determined from a distribution of the measure created by randomly permuting the affected status of the siblings.

Using our test, A2DS, we find strong statistical evidence that the cohort of affected individuals in SSC quad families shares slightly more with each other than with the cohort of unaffected siblings. Confirmation comes from the affected in the trio families of the SSC and the affected of the AGRE multiplex collection. Combining all sets, the P value is less than 1/10,000. The significance is not attributable to ethnic makeup or gender bias within the ASD populations. All of the affected subpopulations show roughly the same score (from 5.02 × 10⁻⁶ to 11.4 × 10⁻⁶). By contrast, unaffected siblings from either the SSC or the AGRE are not significantly closer to the affected SSC quads (−0.5 × 10⁻⁶). Thus, although the affected populations are enriched in certain common variants, the SSC siblings do not seem to be.

We expect stronger signal from a multiplex population, and indeed, the affected of the AGRE score higher (11.4 × 10⁻⁷) than the affected of the SSC quads (5.02 × 10⁻⁶). We looked further for signal in the parents of the AGRE and the SSC. We make one important observation. Fathers of the AGRE show significantly higher relatedness to the SSC affected than to the unaffected siblings. Parents of the SSC and the mothers of the AGRE do not. The AGRE fathers’ A2DS score (6.3 × 10⁻⁶) has a P value at 0.02 and therefore, is only of marginal significance. Thus, this intriguing observation requires additional validation either with more powerful methods or on larger cohorts.

The high A2DS score from fathers may be consistent with the gender bias in autism diagnosis (8). We hypothesize two types of variant, “strong” and “weak” and that most multiplex families transmit a strongly penetrant allele. These alleles would likely be transmitted by the mother who because of female resistance, is more able to carry a strong variant without impairment (8). Moreover, because such alleles would be highly penetrant, they are unlikely to persist in a population and survive to be shared, and thus, they would not contribute to A2DS scores. This hypothesis has statistical support from two recent analyses of the SSC (9, 10). When the strong variants in the mothers of the multiplex families are insufficient on their own to induce ASD in their progeny, the affected progeny might have additional weak variants that come from the parents. We anticipate that these weak variants will not be pathogenic in individuals that lack a strong genetic determinant and perhaps are not at all under strong negative selective pressure. Therefore, the weak variants could persist from ancestors and contribute to the A2DS score. We next propose that the father has more opportunity to carry these weak variants than the mother, because she already carries a strong variant.

The same hypothesis that explains the extra sharing of variants from the fathers’ genomes makes a testable strong prediction between discordant siblings, especially if the unaffected sibling is male. Namely, we should observe diminished sharing of the maternal genome because of the transmission of highly penetrant alleles from the mother. The predicted maternal sharing between concordant affected siblings would not be observed by A2DS, because being strongly penetrant, it would be of recent origin.

The A2DS measure is general and can be applied to evaluating the contribution of shared variants for any phenotype in which two siblings can be separated by that phenotype. In essence, it is a global transmission distortion test, where significance is judged by permutation tests between siblings. Our formulation is only one of several that could have been chosen for this purpose. Although our method requires discordant sibs, a similar method can be established from trios of affected and parental genome information. Provided such information, the parental phases can be separated into transmitted and nontransmitted to the affected child. One can then measure genetic similarities between the transmitted and nontransmitted parental alleles using permutation to determine significance. Unlike discordant sib methods, care must be exercised with trio methods, because genotyping anomalies and allele-driven embryonic lethality can create biases. With that caveat, our preliminary investigations with trio-based methods confirm our results, giving us confidence in both methods.

The A2DS or similar global transmission distortion tests can give us evidence of the existence of transmitted causal variants that are sufficiently ancient to be shared by apparently unrelated affected individuals. However, the method based on common variant SNP arrays holds little promise for identifying those alleles with cohorts of this size. We have looked for signal from specific loci and find no statistical significance after adjusting for multiple testing. However, we believe that transmission distortion analysis based on whole-genome sequence might lead to some identification of functional variants with transmission bias that are rare in the general population.