Significance
The plant cortical microtubule array is a dynamic self-organizing structure that controls the mechanics of plant growth by guiding the deposition of wall material, and is required for asymmetric cell growth, the basis for plant morphogenesis. The array is acentrosomal, i.e., its self-organization is a distributed process. Acentrosomal microtubule arrays are also present in animals, e.g., in the basal cortex of polarized epithelial cells and fertilized Xenopus eggs. Microtubule-severing enzyme katanin is essential for normal array organization and its response to internal and external stimuli. Here, we formally identify the requirements for microtubule ordering through katanin action, including one previously unknown. This understanding provides access to the adaptive control of cell wall structure and plant growth and development.
Keywords: katanin, cortical microtubule array, microtubule dynamics, self-organization, plant cell biology
Abstract
Plant morphogenesis requires differential and often asymmetric growth. A key role in controlling anisotropic expansion of individual cells is played by the cortical microtubule array. Although highly organized, the array can nevertheless rapidly change in response to internal and external cues. Experiments have identified the microtubule-severing enzyme katanin as a central player in controlling the organizational state of the array. Katanin action is required both for normal alignment and the adaptation of array orientation to mechanical, environmental, and developmental stimuli. How katanin fulfills its controlling role, however, remains poorly understood. On the one hand, from a theoretical perspective, array ordering depends on the “weeding out” of discordant microtubules through frequent catastrophe-inducing collisions among microtubules. Severing would reduce average microtubule length and lifetime, and consequently weaken the driving force for alignment. On the other hand, it has been suggested that selective severing at microtubule crossovers could facilitate the removal of discordant microtubules. Here we show that this apparent conflict can be resolved by systematically dissecting the role of all of the relevant interactions in silico. This procedure allows the identification of the sufficient and necessary conditions for katanin to promote array alignment, stresses the critical importance of the experimentally observed selective severing of the “crossing” microtubule at crossovers, and reveals a hitherto not appreciated role for microtubule bundling. We show how understanding the underlying mechanism can aid with interpreting experimental results and designing future experiments.
Plant cells are constrained by their cellulose-based cell walls. This fact poses two important requirements for development: (i) consistent cell wall anisotropy within tissues to ensure coherent growth and (ii) precise local controllability of cell wall properties to produce complex cell shapes (e.g., ref. 1) and accommodate the development of new plant organs (e.g., ref. 2). The central organizing system that mediates these requirements is the plant cortical microtubule (MT) array. Individual MTs self-organize into this often strikingly ordered structure, which is known to regulate the insertion of cellulose synthase complexes into the plasma membrane (3) and subsequently guide their movement during cellulose microfibril deposition (4), thereby playing a key role in cell growth and development. The organizational state of the array, in turn, depends on cell type (5) and may change in response to mechanical (6), environmental stimuli, and developmental patterning processes (7). Acentrosomal and cortical MT arrays also occur in other eukaryotic systems, including protists and animals (e.g., refs. 8–10).
The core mechanism behind the self-organization of the array is described by a consensus model that has been developed over the past few years. Cortical MTs are attached to the plasma membrane, where they interact with each other through collisions. A single MT can undergo multiple interactions during its lifetime due to the dynamic instability of individual MTs (11), i.e., the stochastic switching between growing and shrinking phases. These switching events are called catastrophes and rescues.
When a growing cortical MT impinges on an obstructing MT, the outcome of this collision depends strongly on the angle between the two MTs. After shallow-angle encounters, with , the growing MT will typically bend and continue its way along the obstructing MT, a process we refer to as “bundling” (elsewhere also referred to as entrainment or zippering) (12, 13). For larger-angle encounters, the impinging MT may either cross over the obstructing one and continue growth in its original direction, or, after a short pause, switch to a shrinking state (13), which is called an “induced catastrophe.”
These interactions are sufficient to create spontaneous collective alignment of cortical MTs, as shown by both computer simulations (14–16) and analytical models (17, 18). The causative mechanism at play has been called “survival of the aligned” (17). Induced catastrophes suffered by “discordant” MTs can significantly shorten their lifetime in comparison with a majority of concordant (aligned) MTs, which have few collisions among themselves. With a sufficient number of collisions per average MT lifetime, small biases in an initially isotropic state will be reinforced, resulting in the spontaneous appearance of a majority of aligned MTs that are longer-lived and therefore attain longer average lengths.
A number of recent results point to a key role for the MT-severing protein katanin (19–22) in setting up alignment of the cortical array (23, 24) as well as its reorientation upon external cues (25, 26). At first sight, these findings seem at odds with the survival-of-the-aligned mechanism. It has been reported that, after severing, the newly formed plus end of the lagging MT typically starts in the shrinking state (27, 28). Previous theoretical work on noninteracting MTs has shown that, under this condition, severing uniformly along the full length of MTs does not affect the total number of MTs but does reduce average MT length (29). These shorter MTs would have fewer interactions per average MT lifetime and, consequently, a reduced potential for alignment.
Experiments suggest, however, that katanin actually promotes alignment. Loss-of-function mutations of the katanin p60 subunit result in reduced MT alignment in a range of cell types. The cells in these mutants tend to be more bulged, and the plants exhibit an overall dwarfed phenotype (20, 22). Ref. 19 also reported delayed MT alignment. Additionally, overexpression of RIC1, a protein that stimulates katanin activity, results in highly aligned arrays in pavement cells, which normally do not have aligned arrays (30).
Interestingly, in plants, MT severing appears to preferentially occur at crossover sites (31), and it has recently been shown that this requires the activity of katanin (26, 24, 32). Strikingly, these recent experimental observations also show that it is the “crossing” MT which is preferentially severed (26, 24), rather than the “crossed-over” one.
Here we dissect the influence of MT severing on the alignment process of the cortical array using both computer simulations and theoretical arguments. In the simulations, we systematically address the roles of crossover-specific versus random severing, the significance of severing only the crossing MT at crossovers, and the importance of bundling following shallow-angle encounters. Our results show that katanin-mediated severing can indeed promote array alignment, but only when severing is more likely for the crossing MT and the probability of severing at shallow-angle crossovers is low. Our work uncovers an additional requirement for severing-mediated alignment of the cortical array: a previously unknown role for MT bundling. These insights lead to the understanding of mechanisms by which tuning MT severing can be used to control the organizational state of the array.
Results
Key Aspects of the Modeling Framework.
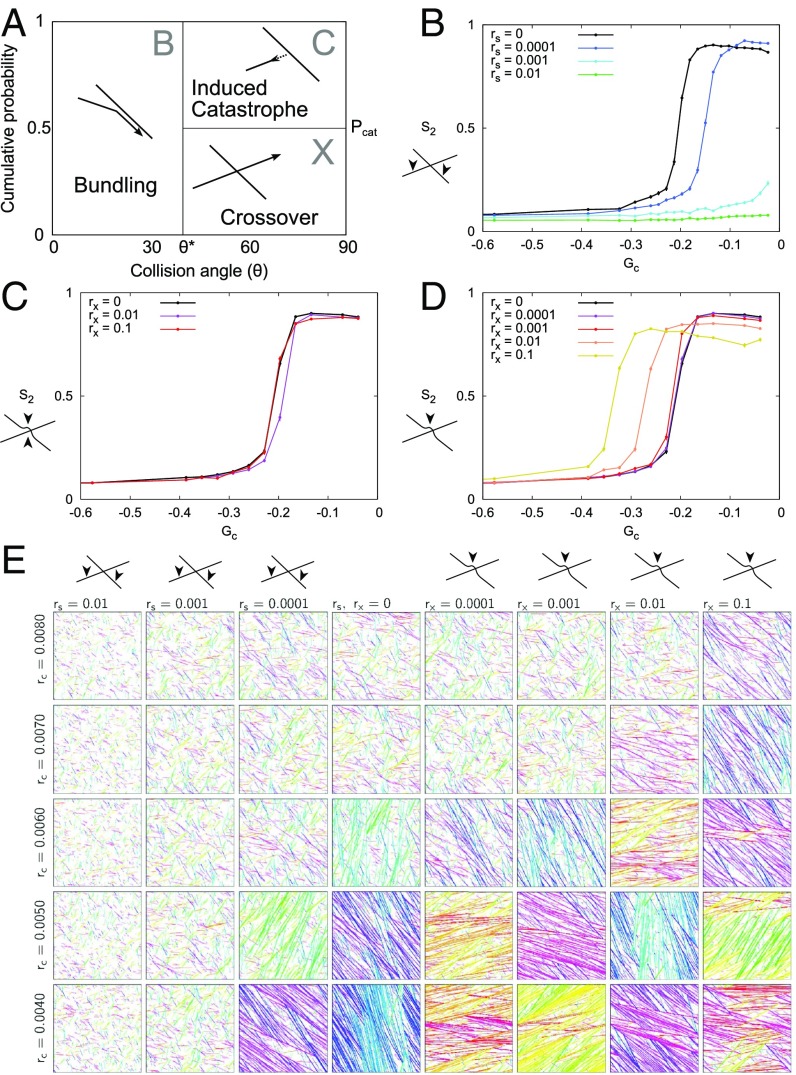
We model cortical MTs as series of connected line segments, where one free end, the plus end, exhibits dynamic instability, and the other free end, the minus end, shows steady depolymerization (“treadmilling”), characterized by parameters (SI Appendix, Table S1) that are based on experimental observations (16). MT collisions with relative angles result in bundling. Collisions at larger angles result in either an induced catastrophe (with probability ) or a crossover (Fig. 1A). As default, we used (16, 33, 34). In between collisions, MTs grow in straight lines.
Fig. 1.
Location of severing determines its effect on alignment. (A) Angle-dependent collision outcomes. Bundling (“B”) occurs for collision angles ; for larger angles, induced catastrophes (“C”) occur with probability , and, otherwise, MTs cross over (“X”). (B–D) Alignment () as a function of . (B) Random severing (rates per micrometer per second as indicated). (C and D) Crossover severing (rates per crossover per second as indicated) for (C) aselective (either side of crossover) and (D) crossing only. In B–D, error bars show the SEM, with n = 100 independent simulations per data point. (E) Representative snapshots (SI Appendix, Unbiased Selection of Snapshots) for various induced catastrophe rates and severing rates ( and ) at T = 30 h. MTs are colored according to their orientation, to enhance the visibility of domains with different orientations.
In our simulations, we characterize the strength of the interactions between the MTs using a control parameter . This parameter, originally derived from a theoretical model (Materials and Methods), combines all dynamic instability parameters and the nucleation rate in a single dimensionless number. Generically, alignment occurs when the control parameter exceeds a critical value (Materials and Methods). In most biologically relevant cases, , and its value can be interpreted as (minus) the ratio of the typical length scale between interactions and the average MT length in the absence of interactions. This interpretation intuitively suggests ways in which alignment can be enhanced by making less negative (see also Table 1). The control parameter has proven very useful in investigating the effects of various processes on MT alignment, even outside the scope in which it was derived (16, 33, 35).
Table 1.
Impact of changes in MT dynamics
| Primary effect | compensated∗ | ||||
| Change | Possible switch | If aligned | stMTs | l0† | |
| A D | –‡ | ∼§ | |||
| D A | |||||
| D A | — | — | — | ||
| A D | |||||
| A D | N/A∗ | N/A | N/A | ||
| N/A | D A | ∗ | N/A | ||
Through rc , where applicable. †Theoretical average equilibrium length of noninteracting MTs. ‡Dash denotes no change. §Negligible change.
To quantify the degree of alignment of our simulated cortical arrays, we use the order parameter , originally formulated to measure the degree of alignment in liquid crystals (Materials and Methods). takes values between 0, for a perfectly isotropic (disordered) system, and 1, for a system in which all MTs are aligned exactly parallel or antiparallel.
By measuring the order parameter for a range of values of the control parameter , we can compare, in a straightforward manner, how phenomena that are not part of , such as severing, influence the system’s potential for alignment (e.g., see ref. 35). Using this framework, we investigated several modes of MT severing.
Localization and Selectivity of Severing Determines Effect on Alignment.
Random severing reduces the potential to align.
We first tested the theory-based (29) prediction that random severing would reduce the potential to align also in the full interacting system. For this analysis, we introduced a uniform severing rate per unit of MT length (in micrometers per second) in our simulations. Increasing reduced the regime of control parameter values () for which the system can align, to the point that alignment became impossible with the highest reported severing rates (Fig. 1 B and E). Moreover, in line with the theoretical predictions for the noninteracting MTs (29), we found that the MT length distributions were no longer exponential, as without severing (refs. 18 and 36; see also SI Appendix, Fig. S2A), and contained fewer long MTs (SI Appendix, Fig. S1).
Severing both crossed-over and crossing MTs has a neutral or weakly positive effect on alignment.
We then incorporated the experimentally observed preference for severing at crossovers (24, 26, 31) into our simulations using a constant rate (per second) per intersection. Per event, either the crossed or the crossing MT bundle was selected with equal probability, upon which one MT within that bundle was severed (“aselective cross-over severing”). With the default parameters, this mode of severing had very little effect on alignment propensity (Fig. 1C). To investigate whether this mode of severing is truly without impact, or whether two opposing effects happened to cancel out each other with the default probability of having an induced catastrophe, we repeated these simulations with . Strikingly, aselective crossover severing now resulted in a marked increase in the average degree of alignment close to (SI Appendix, Fig. S3B). The degree of alignment, however, was much lower than with , and alignment was unstable (SI Appendix, Unstable Alignment with Aselective Crossover Severing and Fig. S3 C–J). In conclusion, aselective crossover severing has, at best, a weakly positive effect on alignment, or no impact at all.
Preferential severing of crossing MTs at crossovers strongly enhances alignment.
All current experimental measurements show a strong bias toward severing the crossing MT rather than the crossed-over one: 97% vs. 3% (24), 330 vs. 192 events (26). Concentrating all severing events to the crossing MTs at crossovers (“crossing-only severing”) resulted in a significant increase of the parameter regime of spontaneous alignment compared with no severing (Fig. 1 D and E). When varying the severing bias at crossovers between the aselective and crossing-only variants, the size of the aligned regime increased gradually with increasing preference for the crossing MT () (SI Appendix, Fig. S4).
Shallow-Angle Interactions Must Be Protected from Severing.
The original survival-of-the-aligned mechanism works by selective punishment of discordant MTs. Combining the results with random severing and crossing-only severing in this context suggests the following mechanism for enhancing alignment: (i) severing acts as a punishment of MTs (Fig. 1B), although weaker than induced catastrophes, because, initially, a leading growing MT bit remains beyond the crossover; (ii) when severing primarily affects the crossing MTs at crossovers, this punishment is mostly targeted to discordant MTs; and (iii) severing then confers additional punishment of discordant MTs, on top of induced catastrophes, so the parameter regime of spontaneous alignment is increased.
If this mechanism is true, then crossing-only severing will only promote alignment if it is, indeed, primarily affecting discordant MTs. In our simulations thus far, this requirement is met, because collision angles of 40° all result in bundling. Consequently, there are no crossovers with angles of 40°, so no “delayed punishment” through severing is possible for these interactions. Previous work without severing shows that alignment is still possible when bundling is replaced by crossovers (16, 18). This change in dynamics, however, exposes shallow-angle interactions to crossover severing, which would be detrimental to ordering; this is, indeed, what we observed (Fig. 2A), in stark contrast to Fig. 1D with bundling.
Fig. 2.
Bundling normally protects nearly aligned MTs from crossover severing. (A) Without bundling, severing at crossovers is detrimental to MT alignment. (B) The theoretically estimated effect of protecting angles less than from severing: Spontaneous alignment may occur in the gray area (). The thick red curve assumes that severing at intersections is equally effective as direct induced catastrophes, an assumption that necessarily overestimates their effectiveness and thus provides an upper bound. The thin red curve shows predictions for 50% effectiveness, illustrating the nonlinear approach toward this theoretical maximum. The cartoons at the bottom show the interaction functions used for C corresponding to the colored arrows: dark gray represents induced catastrophes, light gray represents crossovers that may be severed later, and white represents crossovers that are protected from severing. (C) The negative effect of crossing-only severing on alignment decreases if shallow angles (below = 20°, 40°, and 60°) are protected from severing and turns into a positive effect for = 40° and 60°. With less frequent induced catastrophes (), the potential impact of crossing-only severing is even larger (SI Appendix, Fig. S5). Error bars represent SEM, with n = 100 independent simulations per data point.
In the same vein, crossing-only severing should promote alignment, also without bundling, if shallow-angle crossovers are somehow protected from severing. To test this prediction, we introduced a “protected angle” , below which no severing occurs; with this, we included crossing-only severing in the theory by ref. 17 as an -times-weaker form of punishment than induced catastrophes. This approach is supported by the shapes of MT length distributions (SI Appendix, MT Length Distributions and Fig. S2) and the way in which the severing rate affects the aligned regime (SI Appendix, Increasing Crossing-Only Severing Rates and Fig. 3).
Fig. 3.
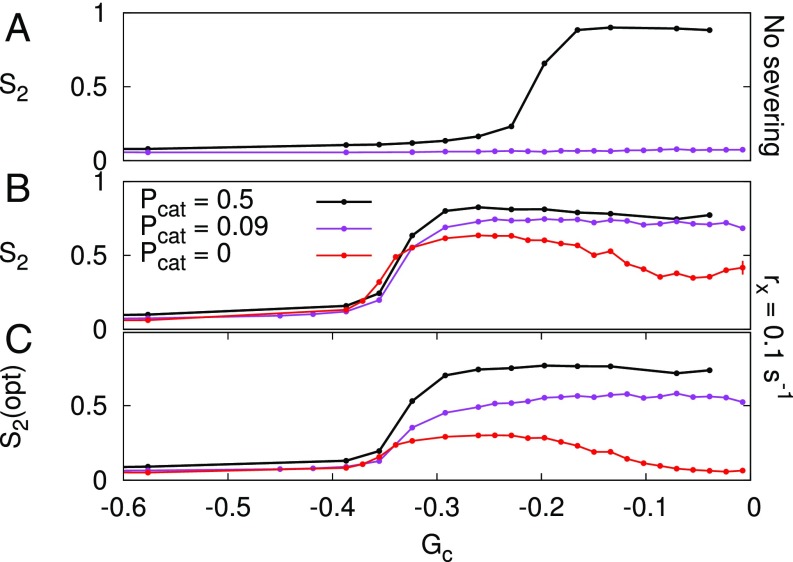
Crossing-only severing is essential for alignment if induced catastrophes are rare, but is insufficient if they are absent. Bundling occurs for . (A) Without severing, the reduced induced catastrophe probability is insufficient to find an aligned regime. (B) With high severing (), some degree of alignment occurs over the same range of parameters for all three values of . (C) Using optical instead of normal to measure alignment, i.e., counting every stretch of MT bundle as a single MT, regardless of the actual number in the bundle, alignment disappears toward in the absence of induced catastrophes. Also, for intermediate values of , the arrays would appear poorly aligned. Error bars represent SEM, with n = 100 independent simulations per data point. For other values of and buildup of alignment over time, see SI Appendix, Figs. S6–S8.
This theoretical consideration predicted a transition from a detrimental effect on alignment to a positive effect on alignment (at ) with increasing (Fig. 2B). We confirmed this reversal of effects with simulations (Fig. 2C). The maximum enhancement of alignment was even more pronounced with more crossovers (; SI Appendix, Fig. S5).
These results suggest that bundling plays a critical role in supporting katanin action: Bundling concentrates katanin severing to large-angle interactions by preventing the occurrence of shallow-angle crossovers.
Crossing-Only MT Severing Requires Subsequent Catastrophes to Promote Alignment.
Treating crossing-only severing as a weak form of induced catastrophes raises two questions: (i) Does the effectiveness of crossing-only severing depend on induced catastrophes? (ii) Can crossing-only severing also induce alignment independently, i.e., without induced catastrophes? Central to these questions is the mechanism that removes the leading MT fragments after severing. What is the relative contribution in this removal of induced catastrophes, spontaneous catastrophes, and a combination of bundling (to adopt the majority orientation) and minus end treadmilling? We investigated the importance of catastrophes by repeating the crossing-only severing simulations (with bundling) of Fig. 1D with fewer () and no () induced catastrophes. With , as with the default , we found a well-aligned regime for the high severing rates ( and ), albeit with a somewhat reduced maximum average degree of alignment (Fig. 3 and SI Appendix, Fig. S6). Without any induced catastrophes, the maximum degree of alignment further declined. Moreover, the “optical” version of the alignment parameter—for which each bundle is counted as a single MT, regardless of how many MTs are part of it—was much lower still. Particularly the arrays with would visually appear disordered over the entire parameter range (SI Appendix, Figs. S7 and S8).
We conclude that, in the absence of induced catastrophes, crossing-only severing can, at best, induce a low to moderate degree of alignment. Furthermore, such alignment could only be induced if is not too high, that is, if sufficiently many spontaneous catastrophes occur. This result means that crossing-only severing can only induce alignment with help of enough catastrophes.
Severing and MT Stability.
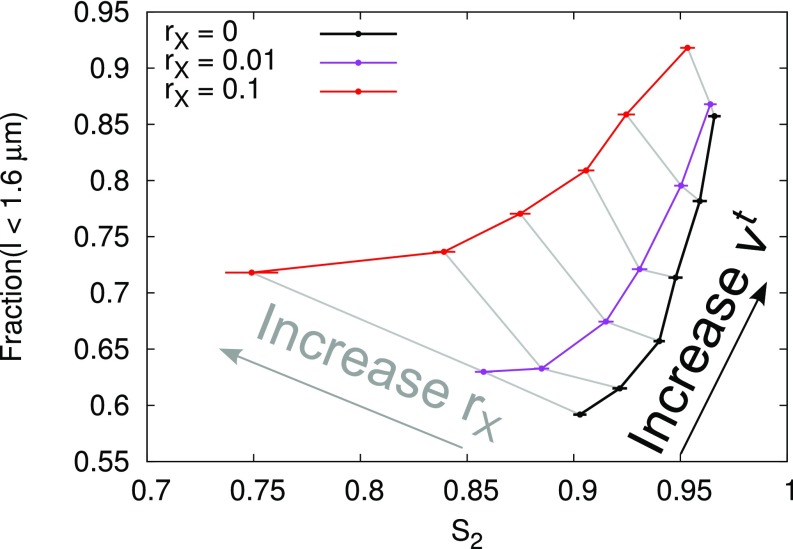
To allow the reader to predict how various mutations and chemical treatments affecting MT stability interact with katanin-mediated severing, we varied each of the remaining parameters: rescue rate (), plus end growth () and shrinkage () velocity, and minus end retraction velocity (). In the absence of severing, such changes are accounted for in the survival-of-the-aligned theory [“primary effect” in Table 1; either a switch from disordered (D) to aligned (A) is possible, or the reverse]. That is, they affect (MT length and array density) in such a way that the critical value for the transition between disorder and alignment remains the same. The presence and magnitude of crossing-only severing did not change this finding (SI Appendix, Figs. S9 and S10 and Table 1). We noted, however, increased maximum levels with increasing and, very mildly, also with increasing , but not with or . Increasing thus could have two effects: complete loss of alignment if becomes too small, or increased alignment. Ref. 37 suggested that short treadmilling MTs (stMTs) could enhance alignment, so we quantified the MT length distributions of MTs that grow against the majority orientation (SI Appendix, Measuring Length Distributions of Discordant MT Populations, Figs. S11 and S12, and Table S2). We found that, even when we fixed the value of (through ), the simulations with high had more discordant short MT segments () and fewer long ones. We also observed an increase in short MTs with decreasing , but this was accompanied by a small decrease in maximum . Increasing also increased the abundance of the shortest MTs and decreased maximum levels (Fig. 4 and SI Appendix, Fig. S11 E and F). Increases in stMT abundance occurred both correlated and anticorrelated with increases in maximum alignment, so this class of MTs is not a significant driver of array alignment in our simulations.
Fig. 4.
Opposite correlations between order and short MTs for crossing-only severing and minus end treadmilling. Increasing resulted in increased and increased the fraction of short MTs (1.6 m) with and without crossing-only severing (three curves as indicated in legend). For any given value of , increasing resulted in an increase of the short MTs but a decrease of . The ranges from 0.01 to 0.06 m/s, and identical values of are connected by gray lines (SI Appendix, Measuring Length Distributions of Discordant MT Populations).
Discussion
Supported by our simulations, we have extended the theory underlying the survival-of-the-aligned mechanism for spontaneous alignment of plant cortical MTs (17, 35), to explain two previously conflicting findings: (i) the theoretical finding that katanin-mediated MT severing reduces average MT length, which should result in less alignment (29), and (ii) the experimental observations that katanin-mediated severing critically contributes to normal alignment in plants (19, 20, 22, 38).
The core of the survival-of-the-aligned mechanism is that spontaneous alignment occurs if the amount of interactions exceeds a threshold, and this happens only if discordant MTs, i.e., growing against the majority direction, are sufficiently “punished”; this results in a difference in average MT life time between discordant and concordant (i.e., aligned) MTs, which in turn causes the isotropic (i.e., disordered) state to become unstable, thus driving spontaneous alignment.
Our simulations using random severing confirm that severing acts as a punishment, i.e., leads to reduced MT lengths and lifetimes; this only happens because the newly formed plus end starts in the shrinking state, as is observed in vitro (27, 28). We have found that only when severing occurs at crossovers and specifically targets the crossing MTs, the difference between concordant and discordant MTs is enhanced. These conditions are experimentally observed: In Arabidopsis, MT severing predominantly occurs at MT crossover sites (24, 26, 31) and predominantly affects the crossing MTs (24, 26). The observed biases were sufficient to enhance alignment in our model.
Our mechanistic approach allowed us to uncover a major hidden requirement of severing enhanced alignment: shallow-angle encounters must be protected from severing. This protection naturally occurs through bundling, as is supported by our simulations without bundling (Fig. 2). Experiments from two independent labs support that the katanin-mediated severing rate is independent of the crossover angle (24, 26), suggesting that bundling is required for this protection. Together, this provides a mechanistic explanation of why MT bundling may be essential for the self-organization of the plant cortical MT array in real cells.
Our simulations show that MT severing, depending on the model parameters, can induce MT ordering (Fig. 1D). This finding suggests that MT severing is a potential target for regulating MT organization in vivo. Interestingly, overexpressing the p60 subunit of the katanin complex can lead to progressive loss of MT length and alignment in Arabidopsis (39), suggesting a proper balance between catalytic (p60) and regulatory (p80) katanin subunits is crucial for normal MT organization. Other experimental data suggest that katanin-mediated severing activity can be regulated through interactions between RIC1 and katanin p60 (30), and in a blue light-dependent manner through photoreceptors PHOT1/PHOT1 (26). Moreover, the MT array responds far less to mechanical perturbations in katanin loss-of-function mutants (25). All of these findings suggest that tuning MT severing is indeed an important target for responding to environmental stimuli and changing MT organization (40).
The stMTs were absent in the katanin loss-of-function mutant (37); this can be understood from the fact that katanin not only severs MTs at crossovers, but is also responsible for their release from nucleation sites (32). Without either process, few treadmilling MTs are expected. Ref. 37 reported a twofold to threefold increase in the abundance of stMTs in the spr2 mutant petiole cells. SPR2 is proposed to protect crossover sites from severing (23). Our simulations, however, cannot explain the increased stMT abundance in spr2 by increasing alone, because this produced only a small increase in stMT abundance and was correlated with a decrease of alignment. It is, however, conceivable that stMTs could play a role in MT organization because of factors such as MT age and/or length-dependent properties that affect MT reorientation and are not accounted for in our simulations. Once such effects have been firmly experimentally established, it will be interesting to incorporate them. We found that substantial changes in or produced a change in stMT abundance of the experimentally observed magnitude, and, only with , this change correlated with increased alignment (SI Appendix, Figs. S11 and S12). Our results thus suggest that MT treadmilling properties are potentially potent targets for controlling MT organization.
During blue light reorientation of the hypocotyl array, a subpopulation of severing-created plus ends started in the growing state, and 1.7 times as many severing events affected the crossing MTs of the new (longitudinal) orientation (26). In terms of our framework, this renders katanin-mediated severing as an amplifier rather than repressor of the discordant (longitudinal) MT population, exactly what is needed to initiate reorientation. Additional enhancement of the discordant MT population could occur if the cell would temporarily enter the unbound growth regime, as this hampers the removal of leading MT stubs (Fig. 3). This regime could be reached by decreasing the spontaneous catastrophe rate and/or shrinkage velocity and/or increasing the growth velocity and/or rescue rate. Neither option, however, imposes a final directionality to the array, so a complete reorientation requires additional mechanism(s) to favor and fix the new orientation. Which of different possible mechanisms are involved in a particular type of reorientation remains a topic for further investigation.
In conclusion, our work provides mechanistic understanding of the role of MT severing in MT alignment, and why MT severing is an excellent target to induce changes in MT organization in vivo. Our results, moreover, encourage measurements of minus end treadmilling parameters in mutants that show MT organization phenotypes.
Materials and Methods
Basic Simulation Methods and Parameters.
All simulations have been carried out using CorticalSim version 1.26.1 (16); this is a fast, event-based simulation platform that explicitly includes all individual MTs. MTs can grow straight at their plus ends with , or shrink with . They can switch between these states with catastrophe rate and rescue rate , respectively (41). All minus ends show steady retraction (treadmilling) with (12). New MTs are nucleated with a uniform isotropic nucleation rate of . The effect of MT–MT collisions depends on the relative angle . For , bundling occurs. For larger angles, induced catastrophes occur with probability , or the MTs cross over one another (Fig. 1A). The same interaction function is also used by other researchers, with varying values for (14, 15). These basic dynamic parameters are the same as in our previous simulation studies (16, 33, 34). We have used a periodic simulation domain, i.e., with dimensions similar to a plant cell circumference. Source code is available (42).
Modes of Katanin Action.
In all cases, a severing event results in the severing of a single MT. The newly formed MT plus end starts in the shrinking state, and the newly formed minus end immediately starts treadmilling. In the “random” mode, katanin severs MTs with a constant rate per unit length (per micrometer per second); this makes the computation of simulation events dependent on the, continuously varying, total MT length density. For technical details, see the supporting information of ref. 16.
In the crossover mode, intersections are severed with constant rate per intersection. Zhang et al. (24) reported an average waiting time until severing of 41 s 14 s in transverse arrays (mode: ), indicating that our highest used rate of is high but still in a realistic ballpark. Typically, a single MT is selected for severing from the bundle (possibly consisting of one MT only) that arrived second at the intersection. We call this “crossing-only severing.” The second bundle usually corresponds to the bundle on the cytoplasmic side of the intersection. We also performed “aselective crossover severing” simulations in which either bundle was selected at random (Fig. 1C and SI Appendix, Fig. S3), upon which a single MT from the selected bundle was severed.
We introduced a protected angle below which no severing occurs. This modification is only used in Fig. 2 and SI Appendix, Fig. S5, whereas, in the default simulations, the presence of bundling effectively results in a protected angle of 40°.
Measuring Alignment: S2.
To measure the degree of alignment, we use the planar order parameter (16, 33),
| [1] |
with as the length of individual MT segments and as the absolute orientation of the segment within the simulation domain. increases monotonically from 0 (perfectly isotropic system) to 1 (all MTs with exactly the same orientation, disregarding segment polarity). A corresponding angle indicates the orientation of the alignment and takes values from to (−90 to 90°).
Control Parameter Gc.
Control parameter , which combines all dynamic instability parameters and the nucleation rate, was originally derived without minus end treadmilling (17, 18) and has subsequently been extended to include treadmilling in the absence of MT bundling (33),
| [2] |
For , there is no intrinsic bound on MT growth, which, in practice, results in an absence of steady-state solutions with biologically relevant densities, so that natural systems can, at most, transiently exist with . We use parameter to vary , which we emphasize using the subscript c. With our default parameters, .
Critical Value G∗ of Gc.
The mean field theory in Hawkins et al. (18) predicts that the system will align for , and not for smaller . The biologically relevant range for alignment is thus . In the absence of severing, the value of depends on the zeroth and second Fourier coefficient of interaction function as
| [3] |
with
| [4] |
and as the (relative) collision angle (16).
Due to the spatial correlations that typically occur in real (and simulated) cells, the transition between isotropic and aligned states typically deviates somewhat from the theoretical value, but remains a powerful concept to predict the direction of change (16).
To predict the effects of crossing-only severing in the absence of bundling, we assume that it effectively functions as an times-as-effective induced catastrophe, based on the detrimental effects random severing on alignment. This results in
| [5] |
with as a step function that is 1 for collision angles larger than protected angle and zero otherwise.
Supplementary Material
Acknowledgments
We thank Pier Siersma for his input during the initial stages of this work. The work of B.M.M. is part of the research program of the Foundation for Fundamental Research on Matter, which is part of the Netherlands Organisation for Scientific Research.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. O.H. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1702650114/-/DCSupplemental.
References
- 1.Xu T, et al. Cell surface- and rho gtpase-based auxin signaling controls cellular interdigitation in Arabidopsis. Cell. 2010;143:99–110. doi: 10.1016/j.cell.2010.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vermeer JEM, et al. A spatial accommodation by neighboring cells is required for organ initiation in Arabidopsis. Science. 2014;343:178–183. doi: 10.1126/science.1245871. [DOI] [PubMed] [Google Scholar]
- 3.Gutierrez R, Lindeboom JJ, Paredez AR, Emons AM, Ehrhardt DW. Arabidopsis cortical microtubules position cellulose synthase delivery to the plasma membrane and interact with cellulose synthase trafficking compartments. Nat Cell Biol. 2009;11:797–806. doi: 10.1038/ncb1886. [DOI] [PubMed] [Google Scholar]
- 4.Paredez A, Somerville C, Ehrhardt D. Visualization of cellulose synthase demonstrates functional association with microtubules. Science. 2006;312:1491–1495. doi: 10.1126/science.1126551. [DOI] [PubMed] [Google Scholar]
- 5.Ehrhardt D. Straighten up and fly right – Microtubule dynamics and organization of non-centrosomal arrays in higher plants. Curr Opin Cell Biol. 2008;20:107–116. doi: 10.1016/j.ceb.2007.12.004. [DOI] [PubMed] [Google Scholar]
- 6.Hamant O, et al. Developmental patterning by mechanical signals in Arabidopsis. Science. 2008;322:1650–1655. doi: 10.1126/science.1165594. [DOI] [PubMed] [Google Scholar]
- 7.Shibaoka H. Plant hormone-induced changes in the orientation of cortical microtubules: Alterations in the cross-linking between microtubules and the plasma membrane. Annu Rev Plant Biol. 1994;45:527–544. [Google Scholar]
- 8.Bouck GB, Ngo H. Cortical structure and function in euglenoids with reference to trypanosomes, ciliates, and dinoflagellates. Int Rev Cytol. 1996;169:267–318. doi: 10.1016/s0074-7696(08)61988-9. [DOI] [PubMed] [Google Scholar]
- 9.Reilein A, Yamada S, Nelson WJ. Self-organization of an acentrosomal microtubule network at the basal cortex of polarized epithelial cells. J Cell Biol. 2005;171:845–855. doi: 10.1083/jcb.200505071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Elinson RP, Rowning B. A transient array of parallel microtubules in frog eggs: Potential tracks for a cytoplasmic rotation that specifies the dorso-ventral axis. Dev Biol. 1988;128:185–197. doi: 10.1016/0012-1606(88)90281-3. [DOI] [PubMed] [Google Scholar]
- 11.Desai A, Mitchison TJ. Microtubule polymerization dynamics. Annu Rev Cell Dev Biol. 1997;13:83–117. doi: 10.1146/annurev.cellbio.13.1.83. [DOI] [PubMed] [Google Scholar]
- 12.Shaw S, Kamyar R, Ehrhardt D. Sustained microtubule treadmilling in Arabidopsis cortical arrays. Science. 2003;300:1715–1718. doi: 10.1126/science.1083529. [DOI] [PubMed] [Google Scholar]
- 13.Dixit R, Cyr R. Encounters between dynamic cortical microtubules promote ordering of the cortical array through angle-dependent modifications of microtubule behavior. Plant Cell. 2004;16:3274–3284. doi: 10.1105/tpc.104.026930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Allard JF, Wasteneys GO, Cytrynbaum EN. Mechanisms of self-organization of cortical microtubules in plants revealed by computational simulations. Mol Biol Cell. 2010;21:278–286. doi: 10.1091/mbc.E09-07-0579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eren EC, Dixit R, Gautam N. A 3D computer simulation model reveals the mechanisms for self-organization of plant cortical microtubules into oblique arrays. Mol Biol Cell. 2010;21:2674–2684. doi: 10.1091/mbc.E10-02-0136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tindemans SH, Deinum EE, Lindeboom JJ, Mulder B. Efficient event-driven simulations shed new light on microtubule organisation in the plant cortical array. Front Phys. 2014;2:9. [Google Scholar]
- 17.Tindemans SH, Hawkins RJ, Mulder BM. Survival of the aligned: Ordering of the plant cortical microtubule array. Phys Rev Lett. 2010;104:058103. doi: 10.1103/PhysRevLett.104.058103. [DOI] [PubMed] [Google Scholar]
- 18.Hawkins RJ, Tindemans SH, Mulder BM. Model for the orientational ordering of the plant microtubule cortical array. Phys Rev E. 2010;82:011911. doi: 10.1103/PhysRevE.82.011911. [DOI] [PubMed] [Google Scholar]
- 19.Burk D, Liu B, Zhong R, Morrison W, Ye Z. A katanin-like protein regulates normal cell wall biosynthesis and cell elongation. Plant Cell. 2001;13:807–828. [PMC free article] [PubMed] [Google Scholar]
- 20.Bichet A, Desnos T, Turner S, Grandjean O, Höfte H. Botero1 is required for normal orientation of cortical microtubules and anisotropic cell expansion in Arabidopsis. Plant J. 2001;25:137–148. doi: 10.1046/j.1365-313x.2001.00946.x. [DOI] [PubMed] [Google Scholar]
- 21.Stoppin-Mellet V, Gaillard J, Vantard M. Functional evidence for in vitro microtubule severing by the plant katanin homologue. Biochem J. 2002;365:337–342. doi: 10.1042/BJ20020689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bouquin T, Mattsson O, Naested H, Foster R, Mundy J. The Arabidopsis lue1 mutant defines a katanin p60 ortholog involved in hormonal control of microtubule orientation during cell growth. J Cell Sci. 2003;116:791–801. doi: 10.1242/jcs.00274. [DOI] [PubMed] [Google Scholar]
- 23.Wightman R, Chomicki G, Kumar M, Carr P, Turner SR. Spiral2 determines plant microtubule organization by modulating microtubule severing. Curr Biol. 2013;23:1902–1907. doi: 10.1016/j.cub.2013.07.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhang Q, Fishel E, Bertroche T, Dixit R. Microtubule severing at crossover sites by katanin generates ordered cortical microtubule arrays in Arabidopsis. Curr Biol. 2013;23:2191–2195. doi: 10.1016/j.cub.2013.09.018. [DOI] [PubMed] [Google Scholar]
- 25.Uyttewaal M, et al. Mechanical stress acts via katanin to amplify differences in growth rate between adjacent cells in Arabidopsis. Cell. 2012;149:439–451. doi: 10.1016/j.cell.2012.02.048. [DOI] [PubMed] [Google Scholar]
- 26.Lindeboom JJ, et al. A mechanism for reorientation of cortical microtubule arrays driven by microtubule severing. Science. 2013;342:1245533–1245533. doi: 10.1126/science.1245533. [DOI] [PubMed] [Google Scholar]
- 27.Walker RA, Inoué S, Salmon ED. Asymmetric behavior of severed microtubule ends after ultraviolet-microbeam irradiation of individual microtubules in vitro. J Cell Biol. 1989;108:931–937. doi: 10.1083/jcb.108.3.931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tran PT, Walker RA, Salmon ED. A metastable intermediate state of microtubule dynamic instability that differs significantly between plus and minus ends. J Cell Biol. 1997;138:105–117. doi: 10.1083/jcb.138.1.105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tindemans SH, Mulder BM. Microtubule length distributions in the presence of protein-induced severing. Phys Rev E. 2010;81:031910. doi: 10.1103/PhysRevE.81.031910. [DOI] [PubMed] [Google Scholar]
- 30.Lin D, et al. Rho GTPase signaling activates microtubule severing to promote microtubule ordering in Arabidopsis. Curr Biol. 2013;23:290–297. doi: 10.1016/j.cub.2013.01.022. [DOI] [PubMed] [Google Scholar]
- 31.Wightman R, Turner S. Severing at sites of microtubule crossover contributes to microtubule alignment in cortical arrays. Plant J. 2007;52:742–751. doi: 10.1111/j.1365-313X.2007.03271.x. [DOI] [PubMed] [Google Scholar]
- 32.Nakamura M, Ehrhardt DW, Hashimoto T. Microtubule and katanin-dependent dynamics of microtubule nucleation complexes in the acentrosomal Arabidopsis cortical array. Nat Cell Biol. 2010;12:1064–1070. doi: 10.1038/ncb2110. [DOI] [PubMed] [Google Scholar]
- 33.Deinum EE, Tindemans SH, Mulder BM. Taking directions: The role of microtubule-bound nucleation in the self-organization of the plant cortical array. Phys Biol. 2011;8:056002. doi: 10.1088/1478-3975/8/5/056002. [DOI] [PubMed] [Google Scholar]
- 34.Lindeboom JJ, et al. Cortical microtubule arrays are initiated from a nonrandom prepattern driven by atypical microtubule initiation. Plant Physiol. 2013;161:1189–1201. doi: 10.1104/pp.112.204057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Deinum EE, Mulder BM. Modelling the role of microtubules in plant cell morphology. Curr Opin Plant Biol. 2013;16:688–692. doi: 10.1016/j.pbi.2013.10.001. [DOI] [PubMed] [Google Scholar]
- 36.Dogterom M, Leibler S. Physical aspects of the growth and regulation of microtubule structures. Phys Rev Lett. 1993;70:1347–1350. doi: 10.1103/PhysRevLett.70.1347. [DOI] [PubMed] [Google Scholar]
- 37.Chomicki G, Wightman R, Turner SR. A specific class of short treadmilling microtubules enhances cortical microtubule alignment. Mol Plant. 2016;9:1214–1216. doi: 10.1016/j.molp.2016.05.008. [DOI] [PubMed] [Google Scholar]
- 38.Webb M, Jouannic S, Foreman J, Linstead P, Dolan L. Cell specification in the Arabidopsis root epidermis requires the activity of ectopic root hair 3-a katanin-p60 protein. Development. 2002;129:123–131. doi: 10.1242/dev.129.1.123. [DOI] [PubMed] [Google Scholar]
- 39.Stoppin-Mellet V, Gaillard J, Vantard M. Katanin’s severing activity favors bundling of cortical microtubules in plants. Plant J. 2006;46:1009–1017. doi: 10.1111/j.1365-313X.2006.02761.x. [DOI] [PubMed] [Google Scholar]
- 40.Nakamura M. Microtubule nucleating and severing enzymes for modifying microtubule array organization and cell morphogenesis in response to environmental cues. New Phytol. 2015;205:1022–1027. doi: 10.1111/nph.12932. [DOI] [PubMed] [Google Scholar]
- 41.Vos J, Dogterom M, Emons A. Microtubules become more dynamic but not shorter during preprophase band formation: A possible “search-and-capture” mechanism for microtubule translocation. Cell Motil Cytoskeleton. 2004;57:246–258. doi: 10.1002/cm.10169. [DOI] [PubMed] [Google Scholar]
- 42.Tindemans SH, Deinum EE. 2017 Data from “Corticalsim v1.26.1.” Zenodo https://dx.doi.org/10.5281/zenodo.801851.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.