Potential high-T_c superconducting lanthanum and yttrium hydrides at high pressure

Significance

Theoretical predictions and subsequent experimental observations of high-temperature superconductivity in dense hydrogen-rich compounds have reinvigorated the field of superconductivity. A systematic computational study of the hydrides of lanthanum and yttrium over a wide composition range reveals hydrogen-rich structures with intriguing electronic properties under pressure. Electron–phonon coupling calculations predict the existence of new superconducting phases, some exhibiting superconductivity in the range of room temperature. Moreover, the calculated stabilities indicate the materials could be synthesized at pressures that are currently accessible in the laboratory. The results open the prospect for the design, synthesis, and recovery of new high-temperature superconductors with potential practical applications.

Abstract

A systematic structure search in the La–H and Y–H systems under pressure reveals some hydrogen-rich structures with intriguing electronic properties. For example, LaH₁₀ is found to adopt a sodalite-like face-centered cubic (fcc) structure, stable above 200 GPa, and LaH₈ a C2/m space group structure. Phonon calculations indicate both are dynamically stable; electron phonon calculations coupled to Bardeen–Cooper–Schrieffer (BCS) arguments indicate they might be high-T_c superconductors. In particular, the superconducting transition temperature T_c calculated for LaH₁₀ is 274–286 K at 210 GPa. Similar calculations for the Y–H system predict stability of the sodalite-like fcc YH₁₀ and a T_c above room temperature, reaching 305–326 K at 250 GPa. The study suggests that dense hydrides consisting of these and related hydrogen polyhedral networks may represent new classes of potential very high-temperature superconductors.

Extending his original predictions of very high-temperature superconductivity of high-pressure metallic hydrogen (1), Ashcroft later proposed that hydrogen-rich materials containing main group elements might exhibit superconductivity at lower pressures, as the hydrogen in these structures may be considered “chemically precompressed” (2). These proposals, which were based on the Bardeen–Cooper–Schrieffer (BCS) (3) phonon-mediated theory of superconductivity, have motivated many theoretical and experimental efforts in the search for high-temperature superconductivity in hydrides at elevated pressures (4–10). Theory has predicted the stability of a variety of dense hydride structures for which BCS arguments give superconducting transition temperatures, T_cs, that are very high (11–18).

In recent times, compression of hydrogen sulfides has provided a new incentive in hydride superconductivity, one in which theory played an important role. First, theoretical calculations predicted H₂S to have a T_c of ∼80 K at pressures above 100 GPa (19). Compression of H₂S led to the striking discovery of a superconducting material with a T_c of 203 K at 200 GPa (20). Moreover, the critical temperature exhibits a pronounced isotope shift consistent with BCS theory. It was proposed that the superconducting phase is not stoichiometric H₂S but SH₃, with a calculated T_c of 194 K at 200 GPa including anharmonic effects (21, 22). A subsequent experiment (23) suggested that the superconducting phase is cubic SH₃, in agreement with a theoretical study that gave T_c = 204 K within the harmonic approximation (24). Compression of another hydride, PH₃, was reported to reach a T_c of ∼100 K at high pressures (25). Subsequent theoretical calculations predicted possible structures and calculated T_cs close to the experimental results (26–28). The experimental picture for these materials remains not entirely clear, and the synthesis of the superconducting phases, which has been reproduced for hydrogen sulfide, is path-dependent (23).

There is great experimental and theoretical interest in searching for related materials with both higher T_c and potentially broader ranges of stability. To date, simple hydrides with the highest predicted superconducting T_cs are MgH₆ (271 K at 300 GPa) (29), CaH₆ (235 K at 150 GPa) (17), and YH₆ (264 K at 120 GPa) (30). In searching for other high-T_c superconducting hydrides, here we investigated theoretically possible high-pressure crystal structures of La–H and Y–H. We predict the existence of new stable hydride phases of these elements, with remarkably high T_cs at attainable pressures. The search for low-energy crystalline structures of La–H was performed using particle swarm optimization methodology implemented in the CALYPSO code (31, 32). This method has been applied successfully to a wide range of crystalline systems ranging from elemental solids to binary and ternary compounds (33–35) and has proven to be a powerful tool for predicting crystal structures at high pressures (36–39). Structure searches were performed in the pressure range of 150–300 GPa using models consisting of 1–4 formula units. In general, the structure search was terminated after the generation of 1,500 structures. Structural optimizations, enthalpies, electronic structures, and phonons were calculated using density-functional theory (DFT). Structure relaxations were performed using DFT using the Perdew–Burke–Ernzerhof (40) generalized gradient approximation. Phonon dispersion and electron–phonon coupling (EPC) calculations were performed with density functional perturbation theory. Ultrasoft pseudopotentials for La and H were used with a kinetic energy cutoff of 80 Ry. A q mesh of 6 × 6 × 6 and k mesh of 24 × 24 × 24 for fcc-LaH₁₀ structure in the first Brillouin zone (BZ) was used in the EPC calculations. The superconductivity calculations were performed with the Quantum-ESPRESSO package (17)·

Results

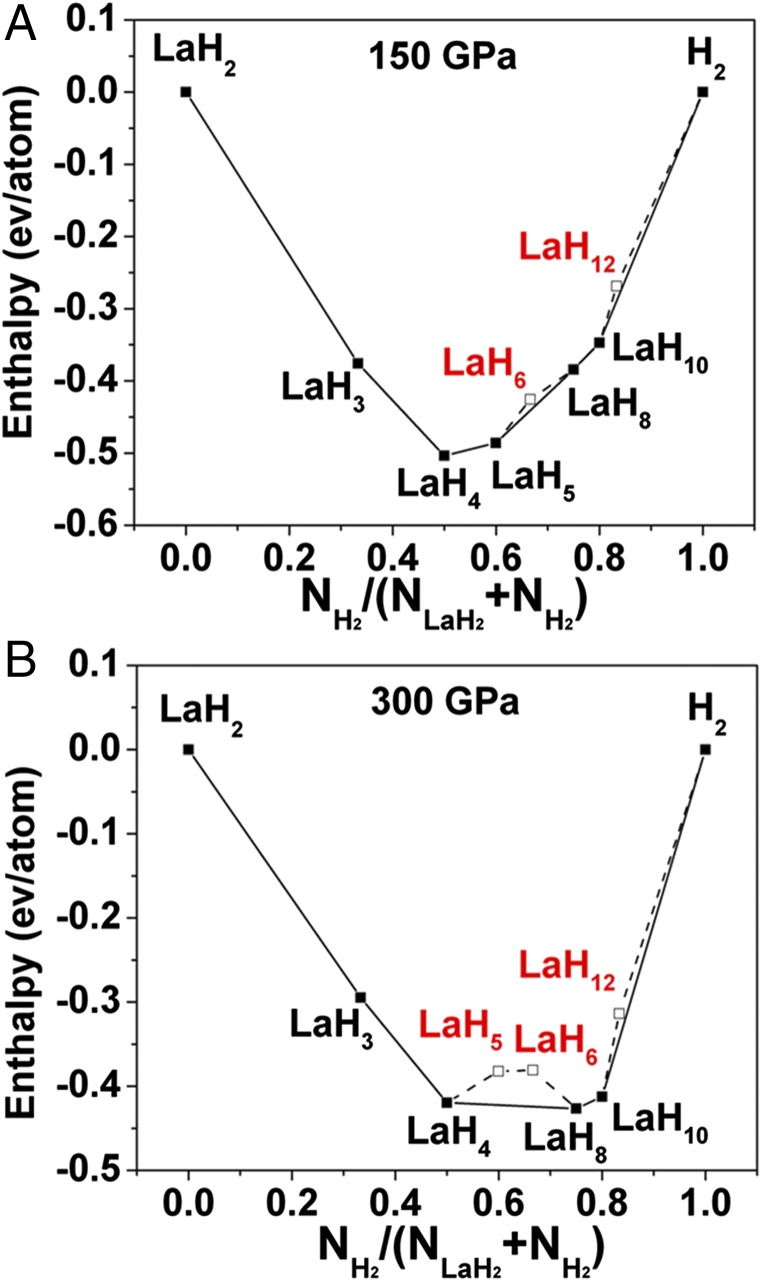
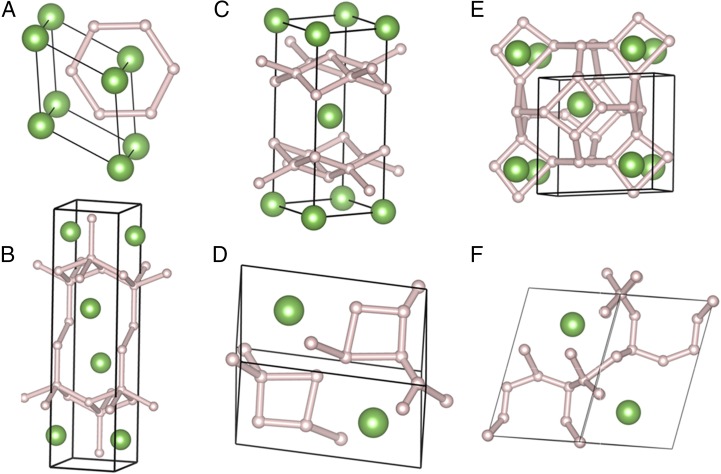
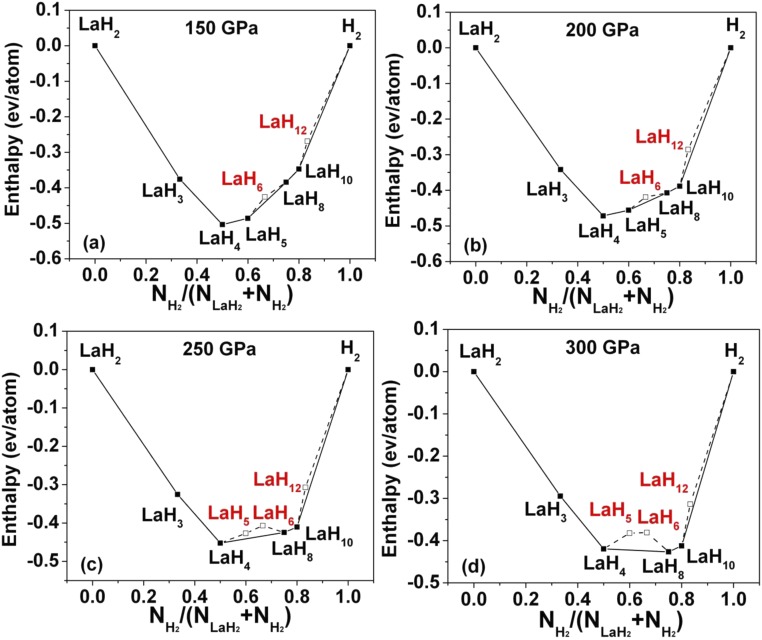
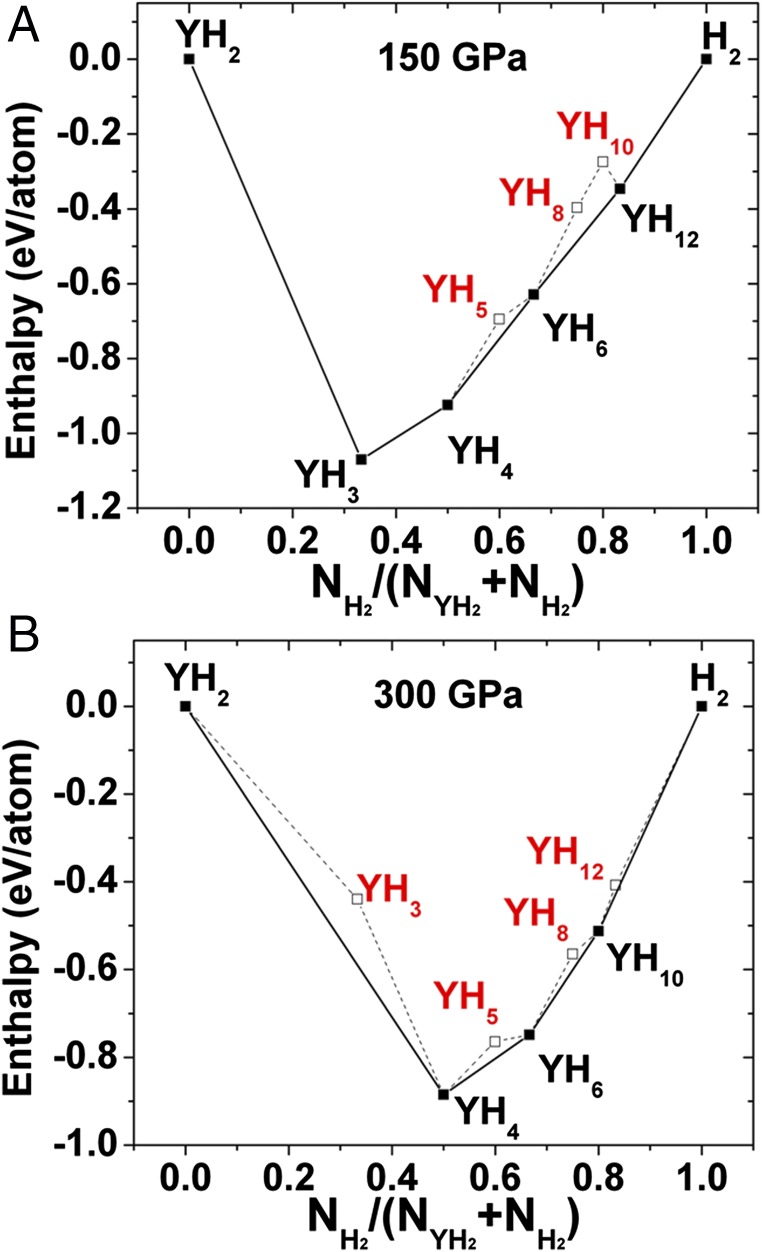
We began with structure searches at ambient pressure for LaH₂. The fcc structure is found to be stable at low pressure, in agreement with experiment. Thinking the high-pressure regime would be most productive for new stoichiometries, we moved directly to 150 and 300 GPa. We first performed structure prediction at 150 and 300 GPa for LaH_x (x = 1–12). LaH₂, LaH₃, LaH₄, LaH₅, LaH₈, and LaH₁₀ are found to be stable at 150 GPa (Fig. 1). Note that this figure is plotted with LaH₂ as the lanthanum-rich endpoint, because this composition has the most negative enthalpy/atom at every pressure considered. Fig. 2 shows the computed geometries for the most stable phases we found at each stoichiometry, for n = 2–8. Interestingly, the stable phase predicted for LaH₆ is not sodalite-type but an R-3m structure. The convex hull shows that LaH₆ is not stable from 150 to 300 GPa (Fig. S1); LaH₅ in a P-1 structure is stable from 150 to 200 GPa. LaH₂ adopts a C2/m structure with a H–H distance of 1.53 Å, LaH₃ adopts a Cmcm structure with H–H distance of 1.42 Å, and LaH₈ has a C2/m structure with H–H distance of 1.02 Å (all at 300 GPa).

Fig. 1.

Formation enthalpy of predicted structures in the La–H system at (A) 150 GPa, (B) 300 GPa. The x axis is the concentration of hydrogen pairs in the stoichiometric compositions considered as described by the generic formula (H₂)_x(LaH₂)_1−x (0 < x < 1). The enthalpies are shown relative to the ground states of H₂ and LaH₂ at each pressure.

Fig. 2.

Predicted lanthanum hydride structures. (A) LaH₂, (B) LaH₃, (C) LaH₄, (D) LaH₅, (E) LaH₆, and (F) LaH₈. Large and small spheres represent La and H atoms.

Fig. S1.

Formation enthalpy of predicted structures in the La–H system at (A) 150, (B) 200, (C) 250, and (D) 300 GPa. The x axis is the concentration of hydrogen pairs in the stoichiometric compositions considered as described by the generic formula (H₂)_x(LaH₂)_1−x (0 < x < 1). The enthalpies are shown relative to the ground states of H₂ and LaH₂ at each pressure.

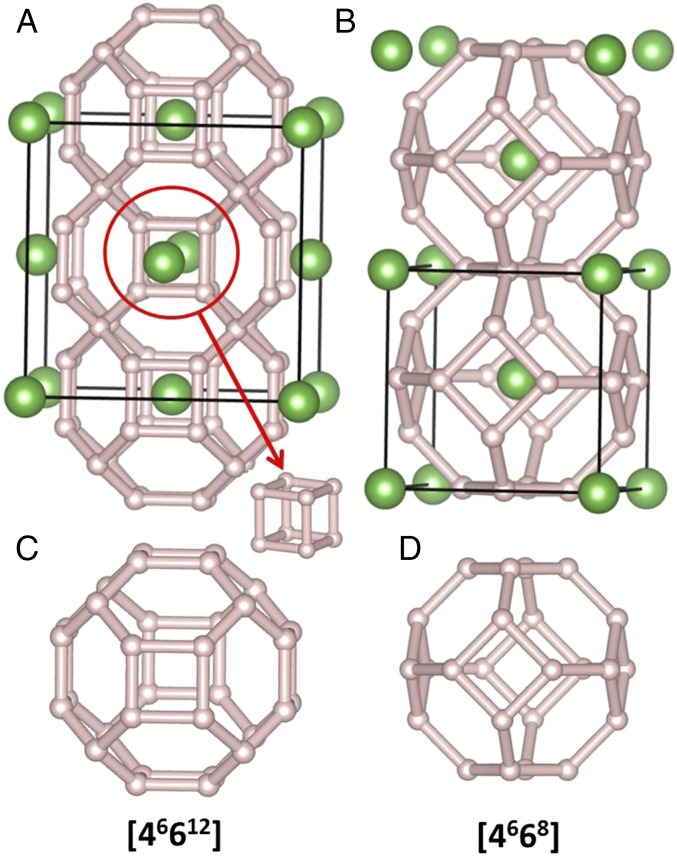
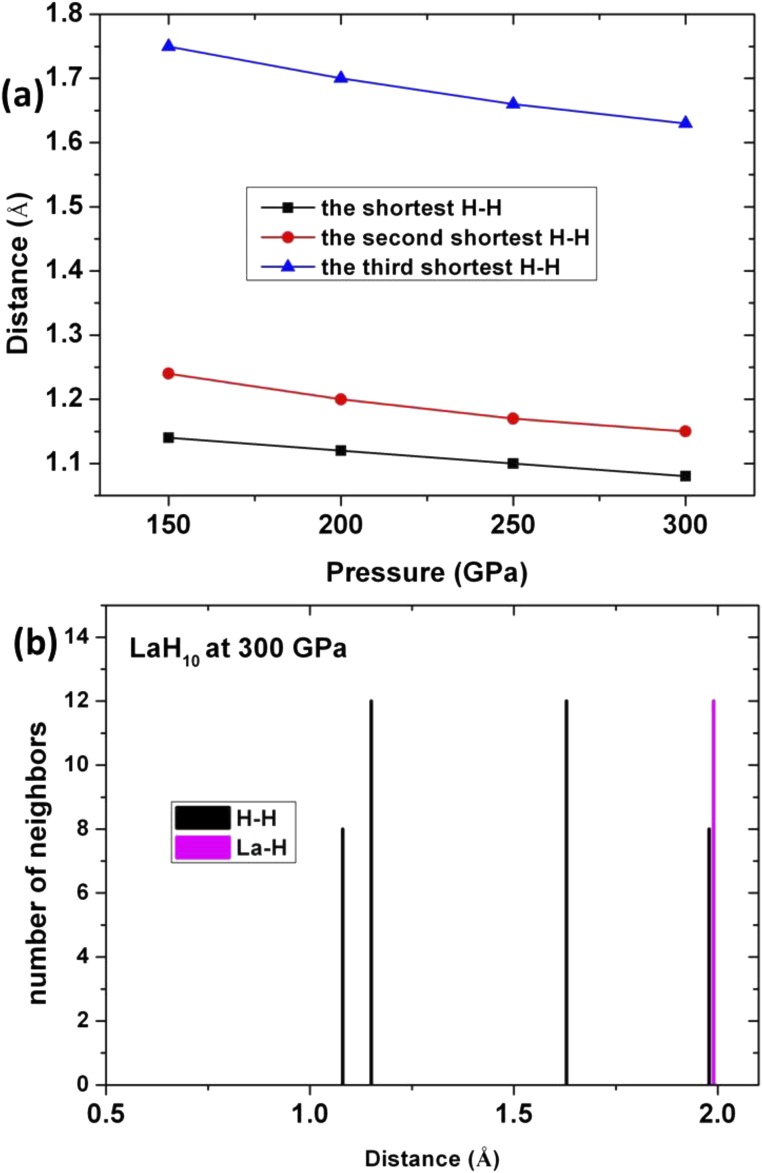
Most interestingly, we find that LaH₁₀ adopts a sodalite-like structure with the La atoms arrayed on an fcc rather than a bcc lattice (Fig. 3). To illustrate the difference between fcc LaH₁₀ and previous sodalite-like bcc CaH₆/YH₆ structure, Fig. 3B shows the sodalite-like LaH₆ structure. The fcc-LaH₁₀ structure contains [4⁶6¹²] polyhedra which contain hydrogen cubes (Fig. 3 A and C), whereas conventional sodalite is built up of [4⁶6⁸] polyhedra (Fig. 3 B and D). The H network, made of different atoms, is known in the clathrate and zeolite community as AST (41). The La atoms sit at the 4b Wyckoff position (0, 0, 0), the H atoms at the 32f position (0.12, 0.38, 0.12) and 8c position (0.25, 0.25, 0.75). The shortest H–H distance is 1.1 Å (250 GPa), which is close to H–H distance predicted for atomic metallic hydrogen near 500 GPa (1 Å) (1). In contrast, the H–H distance in sodalite-type CaH₆ is 1.24 Å at 150 GPa.

Fig. 3.

Crystal structure of sodalite-like LaH₁₀ (A) and LaH₆ (B) at 300 GPa. In the LaH₁₀ structure, the red circle highlights the cube hydrogen units. The bottom shows the [4⁶6¹²] (C) and [4⁶6⁸] (D) hydrogen polyhedra in these structures.

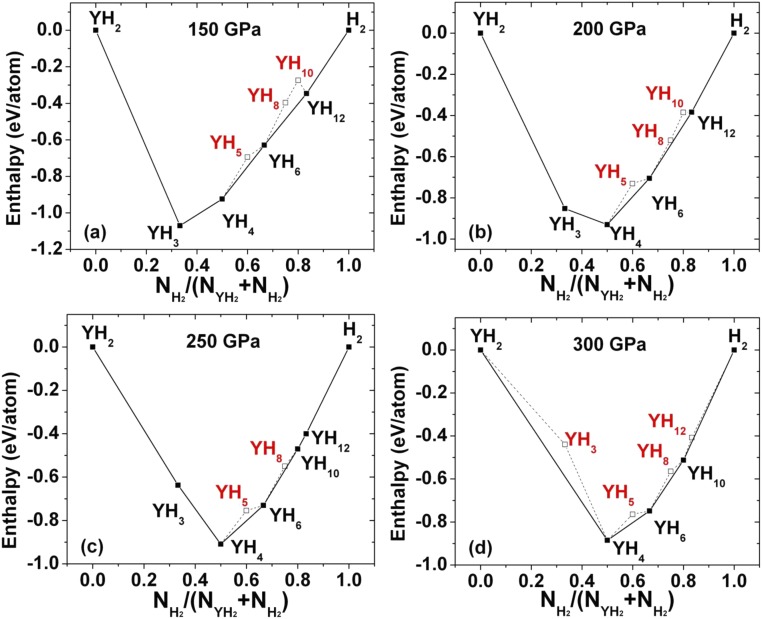
The above structures of LaH₁₀ encouraged us to explore the Y–H system at similar pressures (Fig. S2). Previously, YH₃ was predicted to adopt an fcc structure of Y, with atomic H located in the tetrahedral and octahedral interstitial sites. The compound was predicted to be superconducting with a maximum T_c is 40 K near 18 GPa (μ* = 0.1) (16). Another theoretical study suggested two energetically competing hydrogen-rich polymorphs YH₄ and YH₆ (30). At 120 GPa, both are predicted to be superconductors with maximum T_c of 95 K and 264 K for YH₄ and YH₆, respectively. Our calculations indicate that YH₆ is stable in the sodalite structure up to 300 GPa (Fig. 4 and Fig. S2). As expected, YH₁₀ adopts the same structure as LaH₁₀ over a range of pressures. We predict that YH₁₀ is the energetically stable phase from 250 to 300 GPa, and is dynamically stable down to 220 GPa.

Fig. S2.

Formation enthalpy of predicted structures in the Y–H system at (A) 150, (B) 200, (C) 250, and (D) 300 GPa. The enthalpies are shown relative to the ground states of H₂ and YH₂ at each pressure.

Fig. 4.

Formation enthalpy of predicted structures in the Y–H system at (A) 150 GPa, (B) 300 GPa. The enthalpies are shown relative to the ground states of H₂ and YH₂ at each pressure.

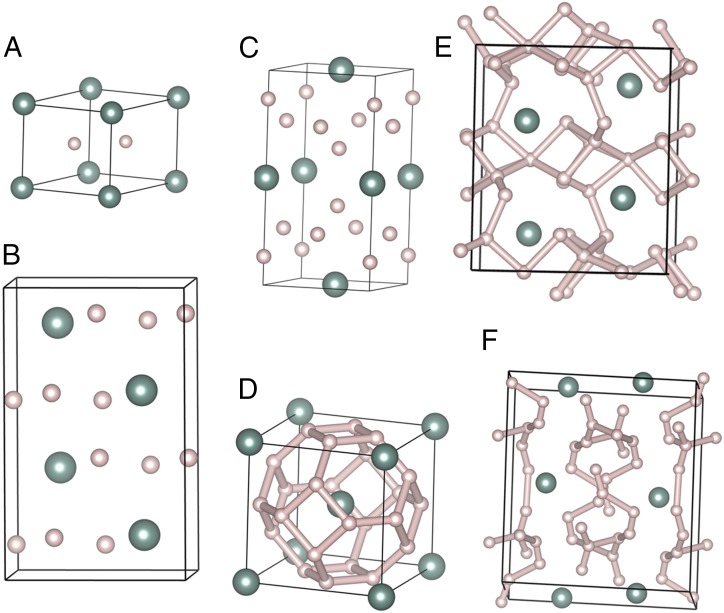
Fig. 5 shows computed YH_n geometries for the most stable phases found at each stoichiometry, for n = 2, 3, 4, 6, 8, and 12. The YH₂ adopts a P6/mmm structure with H–H distances of 1.46 Å at 300 GPa. The YH₃ is stable from 150 to 250 GPa and adopts a Pnma structure with H–H distances of 1.54 Å at 300 GPa (Fig. S2). The YH₄ adopts an I4/mmm structure with H–H distances of 1.37 Å at 300 GPa. It is interesting to see that YH₆ has the same sodalite structure as CaH₆ from 150 to 300 GPa with H–H distances of 1.19 Å at 300 GPa and is stable from 150 to 300 GPa. We found YH₈ is unstable from 150 to 300 GPa with a Cc structure (Fig. S2). The YH₁₂ is stable from 50 to 250 GPa and is a C2/c structure with shortest H–H distances of 0.79 Å at 250 GPa.

Fig. 5.

Predicted yttrium hydride structures. (A) YH₂, (B) YH₃, (C) YH₄, (D) YH₆, (E) YH₈, and (F) YH₁₂. Large and small spheres represent Y and H atoms.

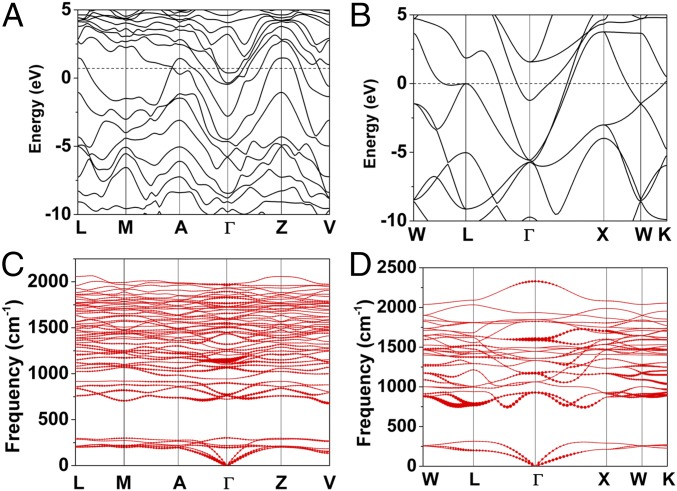
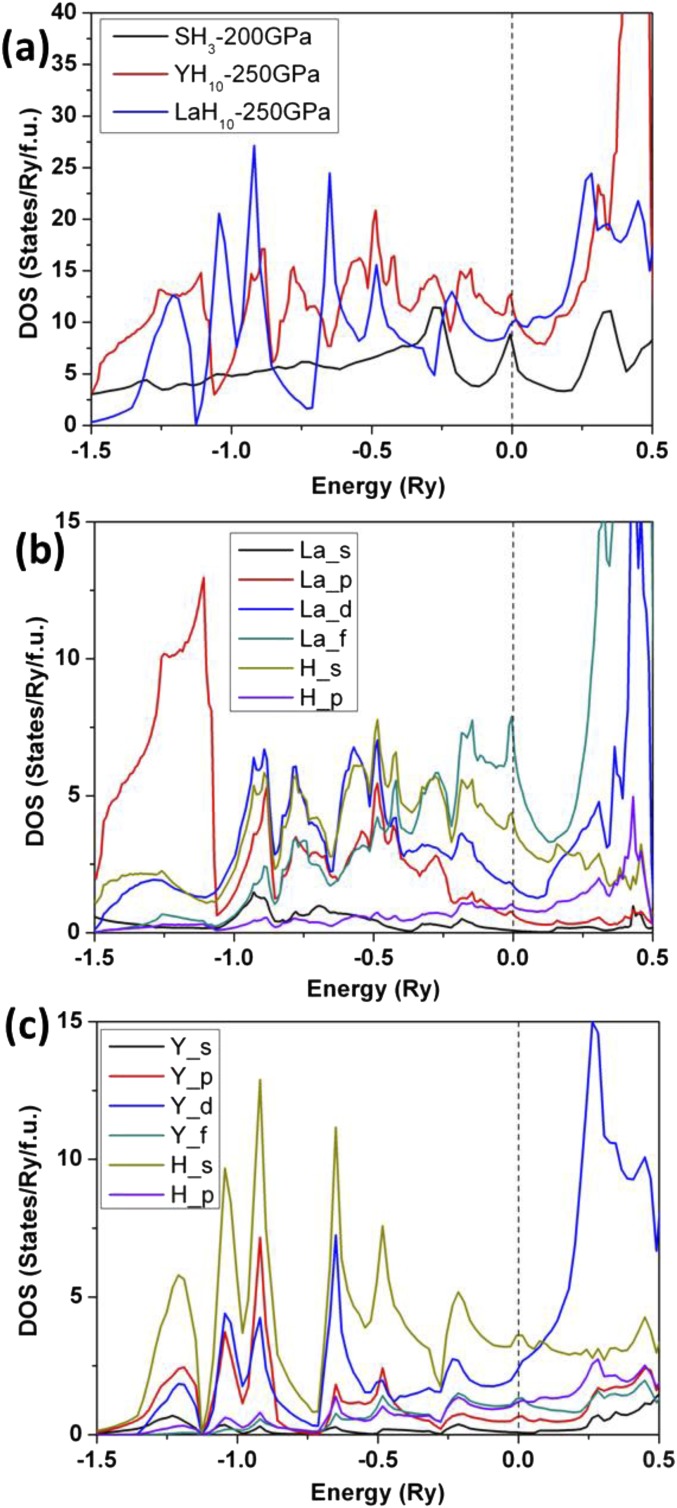
Before calculating possible superconducting properties we analyze the electronic band structures of the C2/m-LaH₈ and fcc-LaH₁₀ structures. The band dispersion shows the metallic character of both structures at these pressures (Fig. 6). The fcc LaH₁₀ is a good metal with several bands crossing the Fermi level along many directions. This fact manifests itself in a noticeable density of electronic states at the Fermi level: 10.0 states/Ry, which is a factor of 1.4 higher than that previously found in SH₃ (42) at an optimal pressure of 200 GPa (Fig. S3). Remarkably, not only the d electrons of La and s electrons of H contribute to N(E_f) but also f electrons of La; moreover, the latter contribution is dominant. This is due to the fact that external pressure destabilizes La 6s and La 5d orbitals to a greater extent than La 4f: the first two have five and two nodes in their radial wave functions, respectively, whereas the latter has none. This is in sharp contrast with the YH₁₀ system, where only the d electrons of Y and s electrons of H are the main contributors to N(E_f). Phonon calculations reveal no imaginary frequencies for LaH₈ and LaH₁₀ over a wide pressure range, indicating dynamic stability. Specifically, we find that the structure shown for LaH₁₀ is dynamically stable down to 210 GPa. The EPC calculations for different phonon modes indicate that there are no significant contributions in particular directions (Fig. 6 C and D). Note that there are no high-frequency vibrations, consistent with the absence of molecular H₂ entities. The highest frequency for the structure here (2,000 cm⁻¹) can be compared to the 2,600 cm⁻¹ calculated for atomic metallic hydrogen in the Cs-IV structure at 500 GPa (43); the lower frequency for the former suggests still weaker H–H interactions in the hydride.

Fig. 6.

Calculated electronic band structures of (A) LaH₈ and (B) LaH₁₀ at 300 GPa. The phonon spectrum for (C) LaH₈ and (D) LaH₁₀ at 300 GPa. Red solid circles (Bottom) show the EPC with the radius proportional to the respective coupling strength.

Fig. S3.

Calculated total and partial DOS. (A) The total density for SH₃ at 200 GPa, LaH₁₀ at 250 GPa, and YH₁₀ at 250 GPa. (B and C) The partial density for LaH₁₀ and YH₁₀ at 250 GPa.

Electron-coupling calculations for LaH₄ give a relatively small λ of 0.43. The estimated T_c is 5–10 K at 300 GPa with the typical choice of the Coulomb potential of μ* = 0.1–0.13. Using the McMillan equation (44), we calculated T_c using the spectral function [α²F(ω)], again with μ* = 0.1–0.13, as previously used in superconductivity calculations for Y (15), La (45, 46), SH₃ (24), CaH₆ (17), YH₆ (30), and other superconductors.

$$T_c=\frac{{\omega }_{\mathit{log}}}{1.2}\mathit{exp}\left(\frac{-1.04\left(1+\lambda \right)}{\lambda -{\mu }^{\ast }(1+0.62\lambda )}\right).$$ [1]

Here, λ is the first reciprocal moment of α²F(ω),

$$\lambda =2{\displaystyle {\int }_0^{\infty }\frac{{\alpha }^{2}F\left(\omega \right)}{\omega }}d\omega \approx {\displaystyle \sum _{qj}{\lambda }_{qj}}\omega \left(\mathit{q}\right),$$ [2]

and ω(q) is the weight of a q (wave vector of crystal vibrations) point in the first BZ. The EPC spectral function α²F(ω) is expressed in terms of the phonon linewidth γ_qj arising from EPC,

$${\alpha }^{2}F\left(\omega \right)=\frac{1}{2\pi N_f}{\displaystyle \sum _{qj}\frac{{\gamma }_{qj}}{{\omega }_{qj}}}\delta \left(\omega -{\omega }_{qj}\right)\omega \left(\mathit{q}\right).$$ [3]

In this equation, N_f is the electronic density of electron states at the Fermi level. The linewidth γ_qj of a phonon mode j at wave vector q, arising from EPC is given by

$${\gamma }_{qj}=2\pi {\omega }_{qj}{\displaystyle \sum _{nm}{\displaystyle \int \raisebox{1ex}{$d^{3}k$}\!\left/ \!\raisebox{-1ex}{${\mathrm{\Omega }}_{bz}$}\right.}}|g_{kn,k+qm}^j{|}^2\times \delta \left({\xi }_{kn}-{\xi }_F\right)\times \delta \left({\xi }_{k+qm}-{\xi }_F\right),$$ [4]

where the sum is over the first BZ, with Ω_BZ as the volume of the BZ, and ξ_kn are the energies of bands measured with respect to the Fermi ξ_F level at point k. Here, g^j_kn,k+qm is the electron–phonon matrix element for scattering from an electron in band n at wave vector k state to band m at wave vector k+q via a phonon with wave vector q.

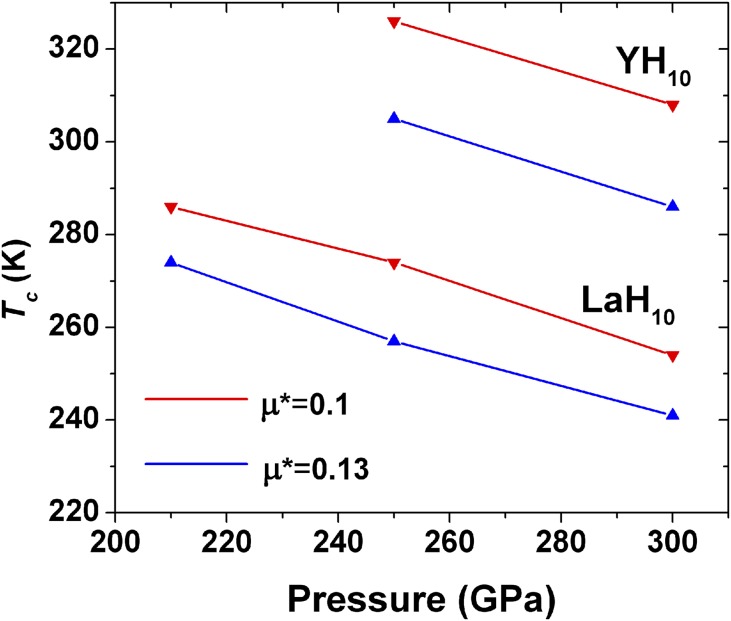
The calculated electron-coupling parameter for LaH₈ at 300 GPa is relatively large (λ = 1.12), and the calculated T_c is 114–131 K, assuming μ* = 0.1–0.13 (Eq. 1). That result encouraged us to calculate the T_c of LaH₁₀. Previous theoretical studies also found that sodalite-structured hydrides (e.g., CaH₆ and YH₆) were associated with calculated high-T_c superconductivity. In the LaH₁₀ structure, the predicted shortest H–H distance is 1.1 Å (Fig. S4) at these pressures, indicating some H…H interactions and no clear distinction between stretching and bending vibrations. As a result, all H vibrations effectively participate in the EPC process, which appears to enhance high superconductivity. The calculated EPC is quite large (λ = 2.2). T_c was estimated from α²F(ω) by numerically solving the Eliashberg equations (17, 30) with μ* = 0.1–0.13. Coulomb repulsion is taken into account in terms of μ* scaled to a cutoff frequency. At 250 GPa, the estimated T_c of LaH₁₀ is 257–274 K with μ* = 0.1–0.13. The calculated T_c is found to decrease with increasing pressure (Fig. 7 and Table S1). The predicted T_c for YH₁₀ is very high (Fig. 7) using similar EPC calculations. At 250 GPa, the λ is 2.56 and gives a T_c of 305–326 K with μ* = 0.1–0.13 based on numerically solving the Eliashberg equations. The T_c of YH₁₀ increased by ∼30 K relative to YH₆ (30) despite the fact that λ decreases (from 2.93 to 2.56). But, this change is offset by the higher average ω_log calculated for YH₁₀ compared with YH₆ (1,282 K versus 1,124 K), as a result of the higher hydrogen content in the former. The information of all predicted structures for La–H and Y–H is summarized in Table S2.

Fig. S4.

(A) Distance between H atoms in LaH₁₀ as a function of pressure. (B) Histogram of H–H and La–H distances in LaH₁₀ at 300 GPa.

Fig. 7.

Calculated T_c of LaH₁₀ and YH₁₀ as a function of pressure.

Table S1.

T_c of La–H and Y–H systems at different pressures calculated using the McMillan and Eliashberg equations

Compound	Pressure, GPa	λ	wlog, K	Tc, K; μ* = 0.1 McMillan	Tc, K; μ* = 0.13 McMillan	Tc, K; μ* = 0.1 Eliashberg	Tc, K; μ* = 0.13 Eliashberg
LaH4	300	0.43	1,624	10	5	10	5
LaH8	300	1.12	1,591	131	114	150	138
LaH10	210	3.41	848	238	219	286	274
LaH10	250	2.29	1,253	232	212	274	257
LaH10	300	1.78	1,488	215	196	254	241
YH10	250	2.58	1,282	265	244	326	305
YH10	300	2.06	1,511	255	233	308	286

Table S2.

Lattice parameters and atomic positions for predicted La–H and Y–H systems

Compound	Pressure, GPa	Space group	Lattice parameters, Å, degree	Atomic positions
LaH2	300	P6/mmm	a = b = 2.65	La 0.000 0.000 0.000
			c = 2.58	H 0.666 0.333 0.500
			α = 90	H 0.333 0.666 0.500
			β = 90
			γ = 120
LaH3	300	Cmcm	a = 2.62	La −0.000 0.885 0.250
			B = 9.99	La 0.500 0.385 0.250
			C = 2.65	La −0.000 0.114 0.750
			α = 90	La 0.500 0.614 0.750
			β = 90	H 0.500 0.808 0.750
			γ = 90	H 0.500 0.962 0.750
				H −0.000 0.462 0.750
				H 0.500 0.037 0.250
				H 0.000 0.537 0.250
				H −0.000 0.751 0.750
				H 0.500 0.251 0.750
				H −0.000 0.248 0.250
				H 0.500 0.748 0.250
				H −0.000 0.691 0.250
				H 0.500 0.191 0.250
				H −0.000 0.308 0.750
LaH4	300	I4/mmm	a = b = 2.53	La 0.000 0.000 0.000
			c = 5.87	La 0.500 0.500 0.500
			α = 93.33	H 0.500–0.000 0.750
			β = 93.33	H 0.000 0.500 0.750
			γ = 93.33	H 0.500 0.000 0.250
				H 0.000 0.500 0.250
				H 0.500 0.500 0.831
				H 0.000 0.000 0.331
				H 0.500 0.500 0.168
				H 0.000 0.000 0.668
LaH6	300	R-3m	a = b = c = 3.53	La 0.776 0.776 0.776
			α = 93.33	La 0.223 0.223 0.223
			β = 93.33	H 0.291 0.709 0.000
			γ = 93.33	H 0.000 0.291 0.709
				H 0.709 0.000 0.291
				H 0.709 0.291–0.000
				H −0.000 0.709 0.291
				H 0.291–0.000 0.709
				H 0.727 0.272 0.500
				H 0.500 0.727 0.272
				H 0.272 0.500 0.727
				H 0.272 0.727 0.500
				H 0.500 0.272 0.727
				H 0.727 0.500 0.272
LaH8	300	C2/m	a = b = 3.42	La 0.491 0.491 0.778
			c = 8.40	La 0.508 0.508 0.221
			α = β = 135.1887	H 0.731 0.233 0.413
			γ = 60.2893	H 0.766 0.268 0.586
				H 0.268 0.766 0.586
				H 0.233 0.731 0.413
				H 0.738 0.738 0.133
				H 0.998 0.998 0.639
				H 0.932 0.932 0.874
				H 0.241 0.241 0.419
				H 0.701 0.701 0.670
				H 0.261 0.261 0.866
				H 0.001 0.001 0.360
				H 0.067 0.067 0.125
				H 0.758 0.758 0.580
				H 0.298 0.298 0.329
				H 0.252 0.747–0.000
				H 0.747 0.252–0.000
LaH10	300	Fm-3m	a = 4.78	La 0.500 0.500 0.500
			b = 4.78	H 0.639 0.120 0.120
			c = 4.78	H 0.120 0.639 0.120
			α = 90	H 0.120 0.120 0.639
			β = 90	H 0.120 0.120 0.120
			γ = 90	H 0.360 0.879 0.879
				H 0.879 0.360 0.879
				H 0.879 0.879 0.879
				H 0.879 0.879 0.360
				H 0.250 0.250 0.250
				H 0.750 0.750 0.750
YH2	300	P6/mmm	a = b = 2.53	Y 0.000 0.000 0.000
			b = 2.4	H 0.333 0.666 0.500
			α = 90	H 0.666 0.333 0.500
			β = 90
			γ = 120
YH3	300	Pnma	a = 5.8888	Y 0.143 0.750 0.675
			b = 3.6288	Y 0.356 0.250 0.175
			c = 2.9464	Y 0.856 0.250 0.324
			α = 90	Y 0.643 0.750 0.824
			β = 90	H 0.906 0.502 0.836
			γ = 90	H 0.593 0.497 0.336
				H 0.093 0.002 0.163
				H 0.406 0.997 0.663
				H 0.093 0.497 0.163
				H 0.406 0.502 0.663
				H 0.906 0.997 0.836
				H 0.593 0.002 0.336
				H 0.866 0.750 0.324
				H 0.633 0.250 0.824
				H 0.133 0.250 0.675
				H 0.366 0.750 0.175
YH4	300	I4/mmm	a = b = 2.52	Y 0.500 0.500 0.500
			c = 5.15	Y −0.000–0.000–0.000
			α = 90	H −0.000 0.000 0.354
			β = 90	H 0.500 0.500 0.854
			γ = 90	H −0.000 0.000 0.645
				H 0.500 0.500 0.145
				H 0.500 0.000 0.750
				H 0.000 0.500 0.750
				H 0.500 0.000 0.250
				H 0.000 0.500 0.250
YH6	300	Im-3m	a = 3.37	Y 0.500 0.500 0.500
			b = 3.37	Y 0.000 0.000 0.000
			c = 3.37	H 0.000 0.750 0.500
			α = 90	H 0.500 0.000 0.250
			β = 90	H 0.000 0.500 0.250
			γ = 90	H 0.000 0.250 0.500
				H 0.250 0.000 0.500
				H 0.750 0.000 0.500
				H 0.500 0.250 0.000
				H 0.000 0.500 0.750
				H 0.500 0.000 0.750
				H 0.500 0.750 0.000
				H 0.750 0.500 0.000
				H 0.250 0.500 0.000
YH8	300	Cc	a = b = 3.23	Y 0.458 0.793 0.264
			c = 4.89	Y 0.793 0.458 0.764
			α = β = 90.86	H 0.779 0.944 0.606
			γ = 120.79	H 0.533 0.337 0.422
				H 0.961 0.241 0.069
				H 0.802 0.971 0.949
				H 0.241 0.388 0.561
				H 0.788 0.458 0.161
				H 0.132 0.123 0.264
				H 0.975 0.302 0.445
				H 0.944 0.779 0.106
				H 0.337 0.533 0.922
				H 0.241 0.961 0.569
				H 0.971 0.802 0.449
				H 0.388 0.241 0.061
				H 0.458 0.788 0.661
				H 0.123 0.132 0.764
				H 0.302 0.975 0.945
YH10	300	Im-3m	a = 4.6	Y 0.000–0.000–0.000
			b = 4.6	H 0.750 0.750 0.750
			c = 4.6	H 0.250 0.250 0.250
			α = 90	H 0.379 0.862 0.379
			β = 90	H 0.862 0.379 0.379
			γ = 90	H 0.379 0.379 0.379
				H 0.379 0.379 0.862
				H 0.620 0.137 0.620
				H 0.137 0.620 0.620
				H 0.620 0.620 0.137
				H 0.620 0.620 0.620
YH12	300	C2/c	a = b = 4.42	Y 0.708 0.291 0.250
			c = 3.21	Y 0.291 0.708 0.750
			α = β = 70.41	H 0.308 0.942 0.139
			γ = 81.15	H 0.073 0.034 0.009
				H 0.657 0.767 0.244
				H 0.872 0.692 0.921
				H 0.059 0.382 0.728
				H 0.514 0.695 0.158
				H 0.057 0.691 0.360
				H 0.965 0.926 0.490
				H 0.232 0.342 0.255
				H 0.307 0.127 0.578
				H 0.617 0.940 0.771
				H 0.304 0.485 0.341
				H 0.691 0.057 0.860
				H 0.926 0.965 0.990
				H 0.342 0.232 0.755
				H 0.127 0.307 0.078
				H 0.940 0.617 0.271
				H 0.485 0.304 0.841
				H 0.942 0.308 0.639
				H 0.034 0.073 0.509
				H 0.767 0.657 0.744
				H 0.692 0.872 0.421
				H 0.382 0.059 0.228
				H 0.695 0.514 0.658

Discussion

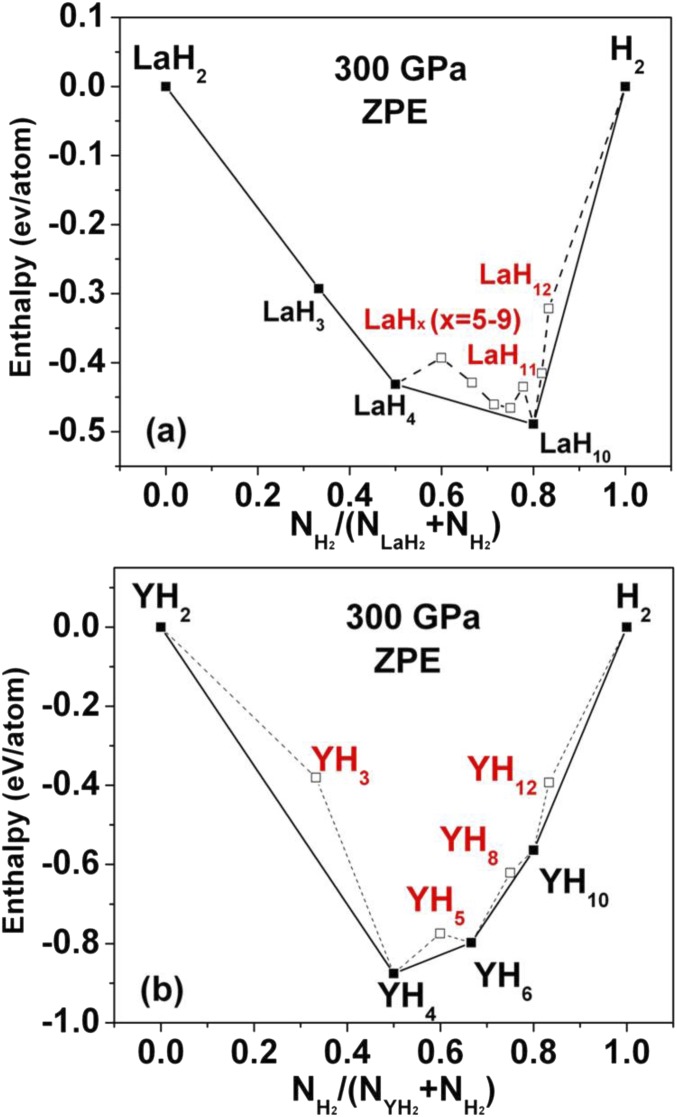
We now examine the above results, including various assumptions and comparisons with previous studies. Because zero-point energy (ZPE) has been shown to play an important role in determining the stability of hydrogen-rich materials, we consider its effect. We recomputed the formation enthalpies of different phases in La–H and Y–H systems at 300 GPa by including ZPE (Fig. S5). The phases LaH₁₀ and YH₁₀ are still stable; therefore, the above conclusions are not altered by considering zero-point vibrations. The authors of ref. 30 focused on the YH₆ stoichiometry, and the authors did not consider hydrogen compositions higher than 1:8. To understand the role of the La atoms in stabilization of clathrate hydrogen structure, we computed the “formation volume” V_LaH10 − V_H10 − V_La, where V_LaH10 is the volume of LaH₁₀, V_H10 is the volume of hydrogen in the sodalite-like structure, and V_La is the volume of La at 300 GPa. We found the formation volume to be negative: −4.66 A³ per primitive cell. This suggests that the La atoms help to stabilize the clathrate hydrogen structure.

Fig. S5.

Formation enthalpy of predicted structures in the (A) La–H and (B) Y–H system at 300 GPa including ZPE.

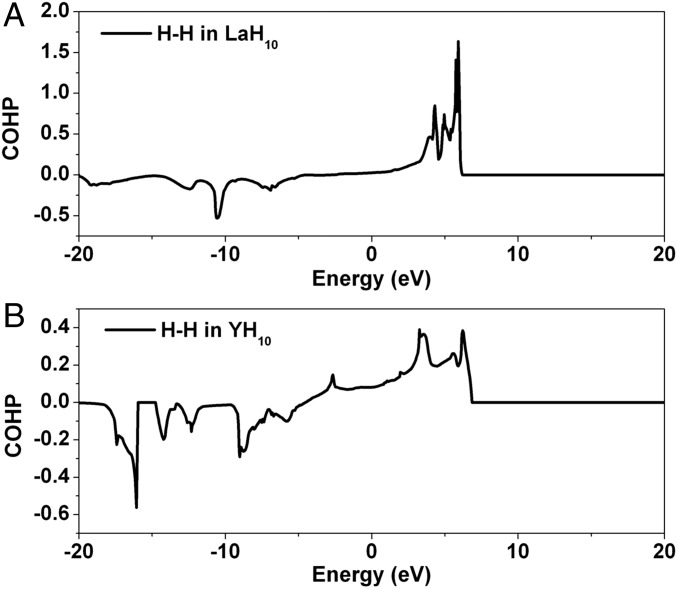
We also investigated the bonding in these hydrides by a crystal orbital Hamiltonian population (COHP) analysis. The COHP provides an atom-specific measure of the bonding character of states in a given energy region (47). A negative COHP indicates bonding and positive COHP indicates antibonding. As Fig. 8 shows, predictably most of the states below the Fermi level are H–H bonding for LaH₁₀ and YH₁₀. The interesting difference is that some H–H antibonding states are occupied in the yttrium hydride.

Fig. 8.

COHP for pairs of H–H in (A) LaH₁₀ and (B) YH₁₀ at 300 GPa.

We comment on the reliability of the present predictions of very high-T_c superconductivity by comparing our results with existing experimental data and additional BCS calculations for related superconductors. We calculated a T_c of 6–7 K for fcc La under ambient pressure using μ* = 0.1–0.13, which is close to previous theoretical (46) and experimental work (T_c = 6 K) (48), and consistent with high-pressure behavior (T_c = 13 K at 20 GPa) (45, 48). Likewise, our method gives the T_c of elemental Y under pressure to be 15–16 K using μ* = 0.1–0.13, which is also consistent with previous theoretical (15) and experimental studies (T_c = 17 K at 89 GPa) (49). All of our calculations were carried out using the harmonic approximation. It is well known that in many hydrides anharmonicity tends to lower T_c (50). For the well-studied SH₃ system, however, such an effect is weak: T_c is lowered from its harmonic 204 K value (24) only to 194 K (21) at 250 GPa, and both are close to the reported experiment T_c at that pressure (20).

There is a good reason to think that hydrogen-rich hydrides should behave similarly to pure hydrogen. Recent first-principles calculations of metallic hydrogen in structures with space groups I4₁/amd and Cmca-4 predict anharmonic behavior that differs from calculated results for hydrides with relatively low hydrogen content (51, 52). Whereas in the I4₁/amd the inclusion of anharmonicity slightly lowers T_c (i.e., from 318 to 300 K at 500 GPa), the situation is drastically different in the Cmca-4 phase, where the calculated T_c increases by a factor of 2 with anharmonicity introduced, such that the phase is predicted to be a superconductor above 200 K. In this context it is also worth noticing that anharmonic vibrations may enhance the electron–phonon matrix elements, e.g., in the case of disordered materials (53).

In summary, exploration of La–H and Y–H systems at high pressures reveals stable hydrogen-rich phases with calculated unusually high superconducting temperatures. To be realistic, we should be careful about these high T_cs. Although well-calibrated on low T_c elemental superconductors, more high-T_c compounds need to be studied––we only have SH₃ mentioned above (with its attendant ambiguities––not in the T_c, measured, but in the structure). The predicted stabilities of the phases are in the range of current high-pressure techniques, although the megabar pressures required present challenges for combined synthesis and characterization. On the other hand, it may also be possible to synthesize these and related materials metastably at lower pressure. For instance, one might reason from the fact that Y (54) itself has a distorted fcc structure that it may be possible to produce sodalite-like YH₁₀ at a metal–hydrogen interface. The exploration, theoretical and experimental, of high hydrides of heavy metals is thus a promising field (55–58).

SI Text

Table S1 presents calculated T_cs of LaH_n (n = 4, 8, and 10) and YH₁₀ at high pressures for different models and parameters. It is seen that the McMillan and Eliashberg equations lead to similar results for small λ. For larger λ, however, the Eliashberg equation predicts higher T_c values. Table S2 contains the lattice parameters and atomic coordinates for the predicted structures.

We compare the calculated density of states (DOS) for LaH₁₀, YH₁₀, and SH₃ in Fig. S3. In the case of SH_3, we found a DOS at the Fermi level of 7.1 states/Ry which is close to the value of 6.93 states/Ry found in the previous work (42). The calculated N(E_f) of LaH₁₀ and YH₁₀ at 250 GPa is larger than that of SH₃ at 200 GPa. For LaH₁₀, both the d and f electrons of La as well as the s electrons of H contribute to N(E_f). Indeed, the f-electron contribution is dominant, which is in sharp contrast with the YH₁₀ system, where only the d electrons of Y and s electrons of H are the main contributors to N(E_f).

The distances between H atoms in LaH₁₀ as a function of pressure are shown in Fig. S4. Each La atom is coordinated with 12 hydrogen atoms. H atoms are 4-coordinated, with bond distances of 1.08 and 1.15 Å (see also Fig. 3). Finally, the formation enthalpy of predicted La–H and Y–H structures at 300 GPa including ZPE is shown in Fig. S5.